中学数学ではたくさん「角度の問題」が出てくるよね?
中でもなぜかでてきやすいのが、この不思議な図解↓
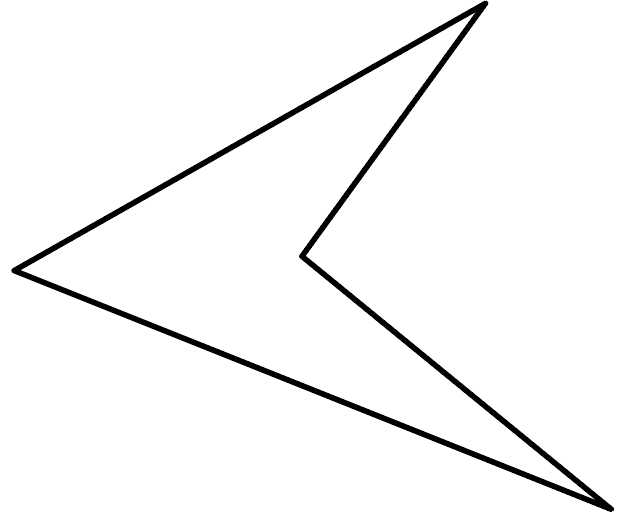
ブーメランのように見えてくるし、矢じりのようにも見えてくるし、「く」にも見えてくる。
いや、紙飛行機のようにも見えなくは、ない。
角度によっては「人」に見えるときも、ある。
じつはこの四角形にはちゃんと名前がついていて、業界では
凹四角形(おうしかくけい)
と呼んでいるんだ。
これは、
1つの内角の大きさが180度を超える四角形のこと
だね。
この問題は難しそうに見えるけど、じつはめちゃくちゃ簡単だよ。
この四角形が出てきたら、次の法則を覚えておけば大丈夫。
ズバリ、
「3つの尖った内角」をたすと「溝の角度」になる
っていう裏技。
たとえば、「尖った部分の角度」がそれぞれ
だとしよう。
このとき、矢じりの裂け目、ブーメランが曲っている角度は、a・b・cをぜーんぶ足した角度になるんだ。
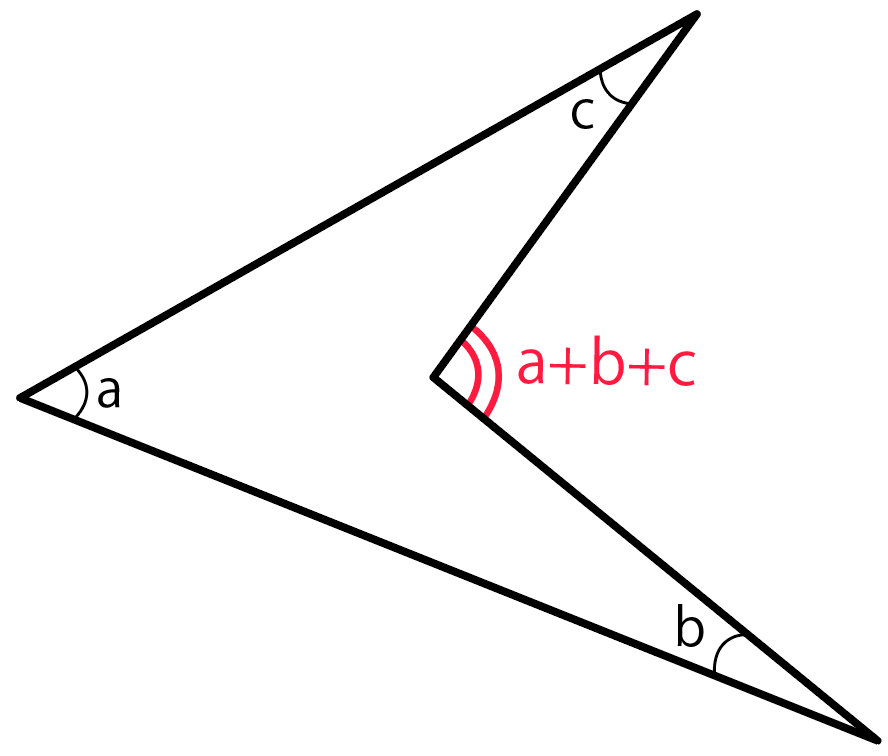
いやあ、こりゃ不思議だね。
これを応用してやると、次のような問題も一発でとけるようになるよ。
xの角度を求めなさい。
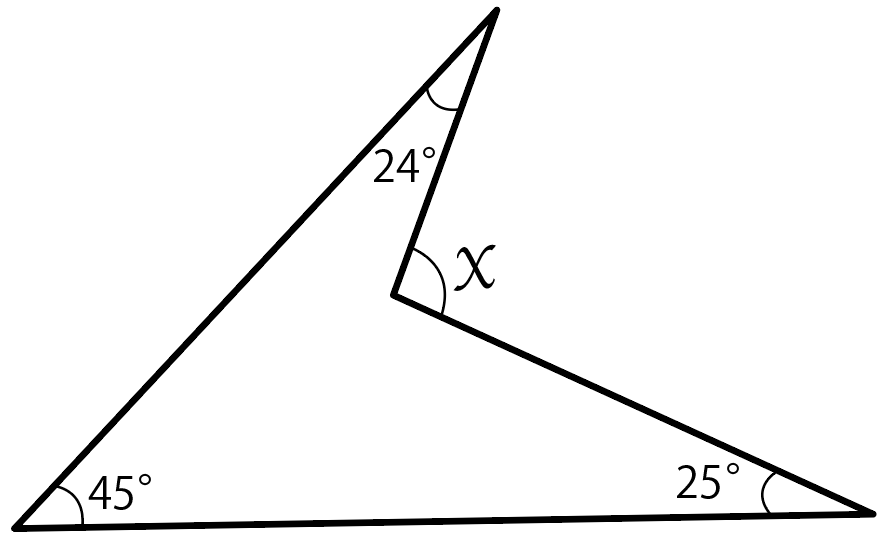
この場合、ぜーんぶの角度を足してやって、
45 + 24 + 25
= 94度
で、Xの角度は94度ってわけさ。
いやあ、ぜーんぶ足すだけなんて超楽。
それじゃあ、なぜブーメラン型の四角形の角度は求めやすいんだろうね??
いろいろ求め方があるけど、一番しっくりきているのは三角形の外角の定理を使う方法かな。
念のために復習すると「三角形の外角の定理」とは、
2つの内角をたすと、残りの内角に接する外角になる
ってやつだったね。
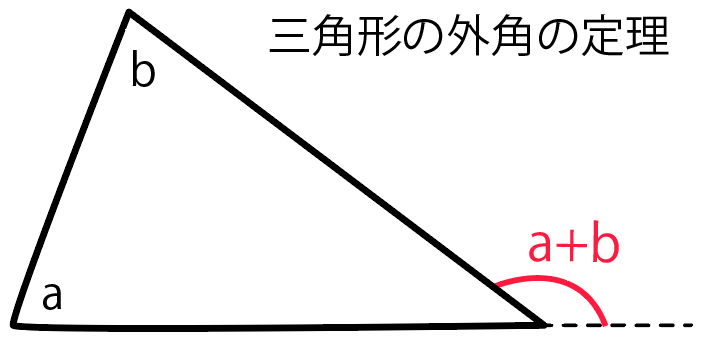
まずは補助線を引いてみよう。
ブーメランの1辺から向かい側に向かって補助線を引っ張ってやる。
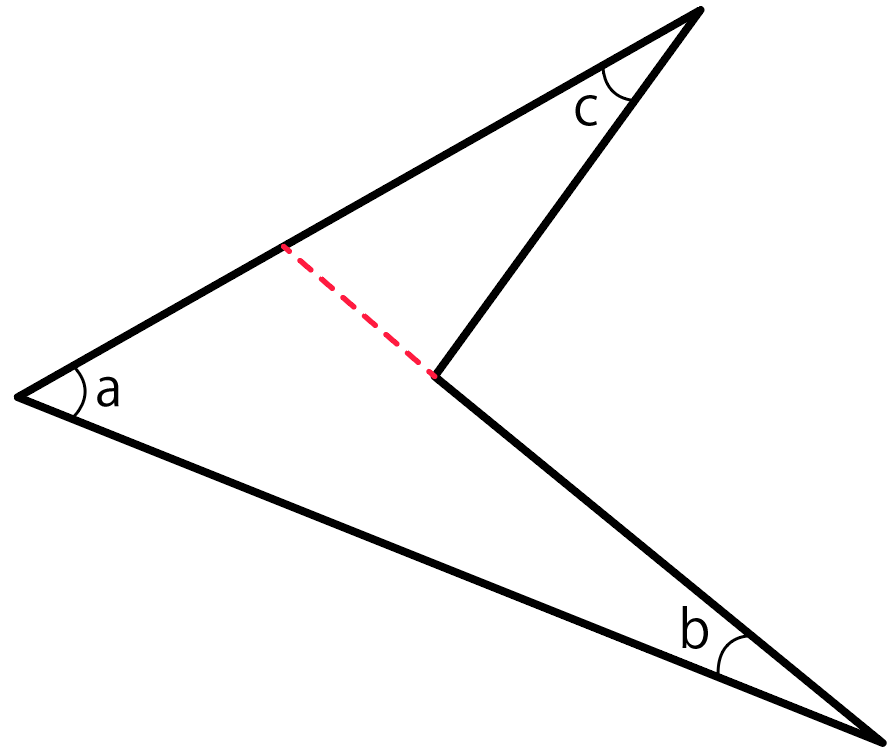
そして、三角形を2つ作る。
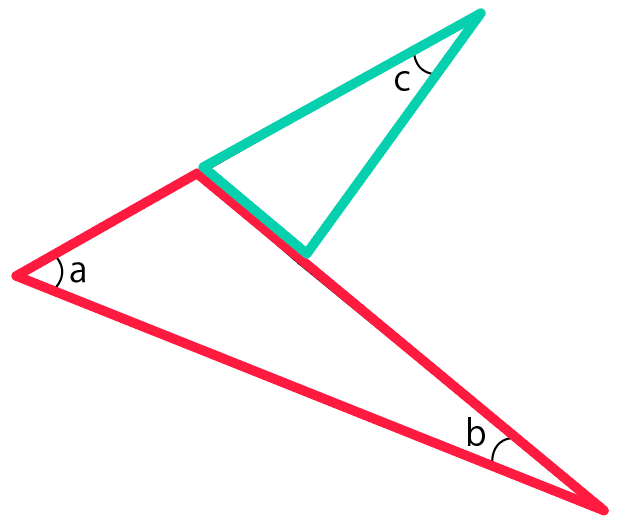
あとは2つの三角形で、三角形の外角の定理を2回使うだけ。
まず手前の「赤い三角形」で外角の性質を使ってみよう。
すると、外角の大きさはaとbを足したやつになるはず。
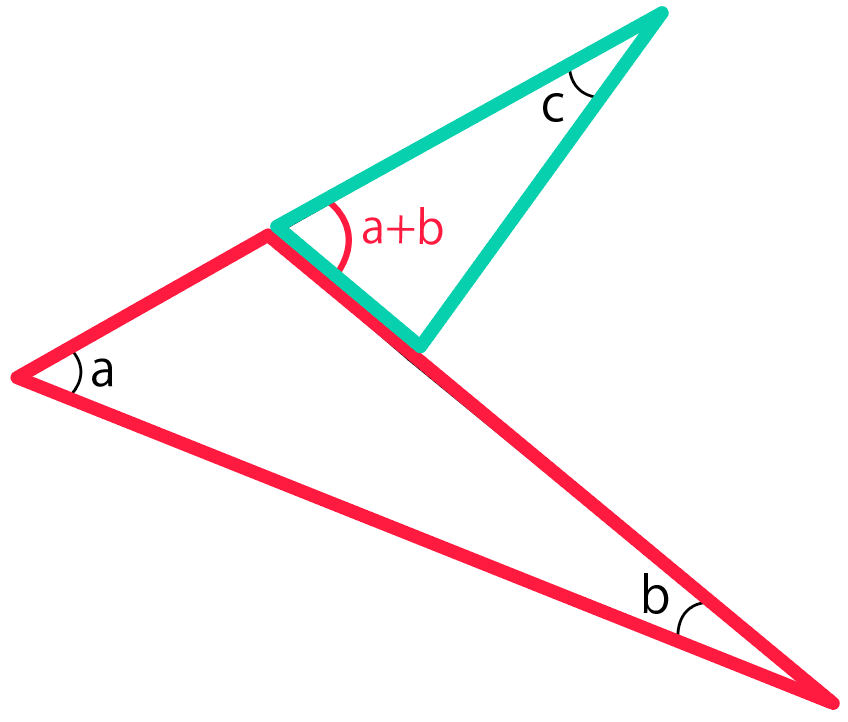
そして、緑の三角形でもう一回、外角の定理を使っていくよ。
この三角形に注目してみると、
という2つの内角になっているから、これらを足すと外角は
a+b+c
になるはずだ。
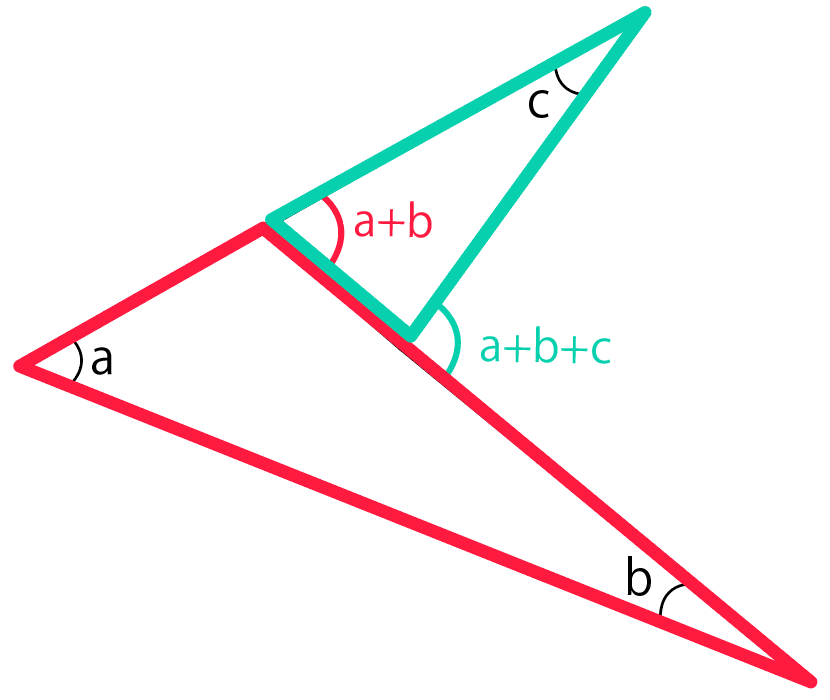
これで、ブーメランの尖ってる角度をたすと、曲っている角度になると証明できたね。
こんな感じで、ブーメラン型の四角形は解き方を知っていれば楽勝。
テストにでてきたらむしろガッツポーズしてもいい。
ただ、なぜそうなるかまで押さえておくと、応用問題まで対応できるようになるから勉強してみてね。
そんじゃねー
Ken
この記事を書いているKenだよ。下痢に、勝ったね。
中学数学ででてくる円錐の問題には
とかいろいろあるけど、もう1つでてきやすいのが
円錐を転がす問題
だね。
例えば次のような問題↓
半径4cmの底面である円錐を滑らずに転がしてみたところ、円錐が4回転してちょうど一周しました。この円錐の側面積を求めなさい。
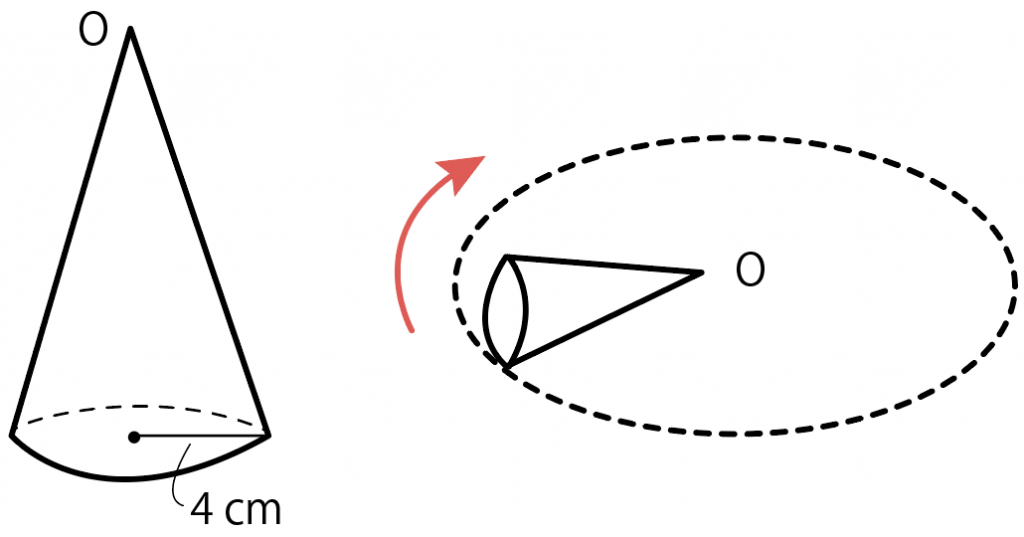
わざわざ円錐を転がすぐらいだから難しそうだけど、ゆっくり解いていけば大丈夫。
まずは円錐の転がった距離を求めてみよう。
図でいうと、この円の円周の長さだね↓
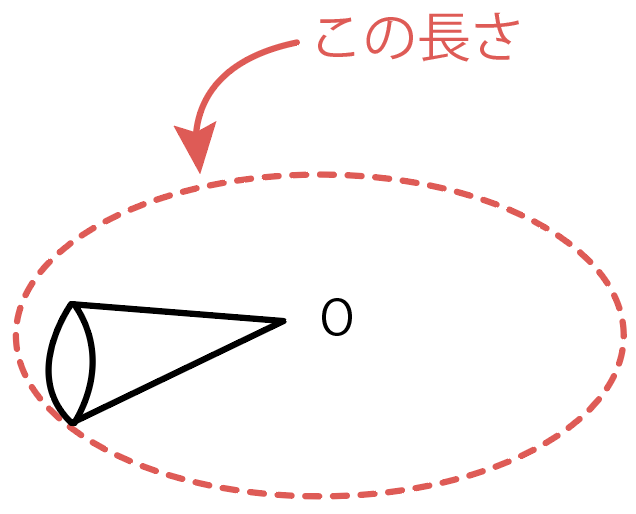
円錐が転がらずに回ったとすれば、円錐の底面のふちが移動した距離は、
回転数 × 底面の円周の長さ
で求められるよ。
この問題だと、
だから、
回転数 × 底面の円周の長さ
= 4 × 8π
= 32π
になるね。
次は母線の長さを求めよう。
母線とは、「円錐の頂点から底面への長さ」のことだね。
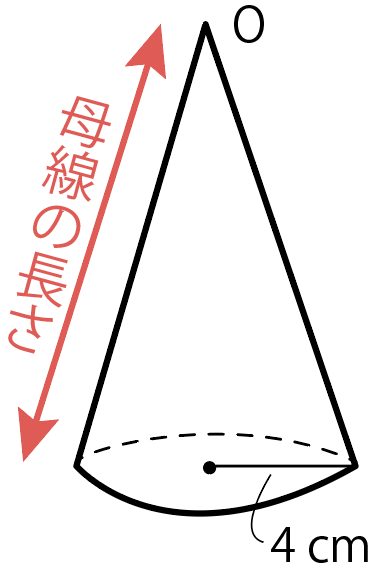
この母線を求めるためには
母線が作る円の円周長さ = 円錐のふちが動いた距離
という方程式を作ればいいよ。
母線をrとしてやると、
母線が作る円の円周長さ = 円錐のふちが動いた距離2πr = 32π
r = 16 cm
となって、母線の長さは16 cm になるはずだ。
母線が16 cm とわかったから、問題の円錐はこんな感じになってるね↓
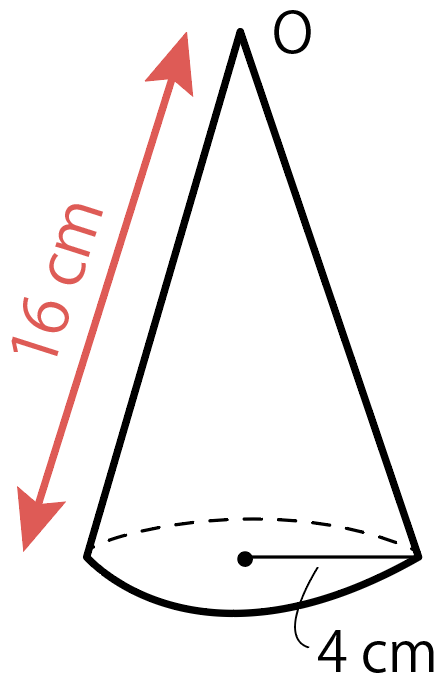
ここで冷静になって、側面積を求める前に円錐の展開図をかいてみよう。
円錐の展開図は
でできているよね?
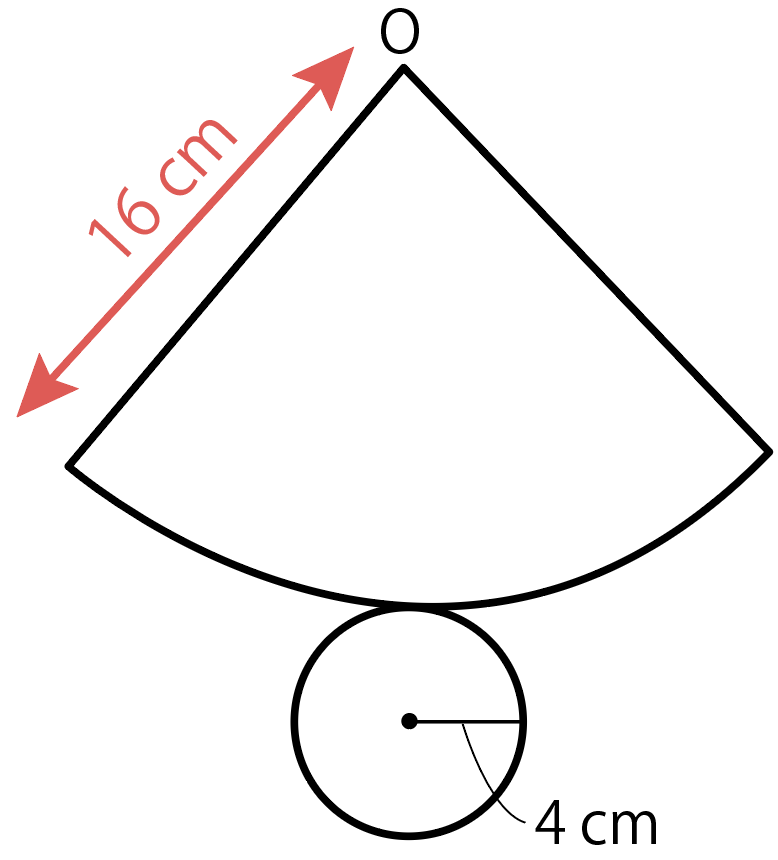
つまり、円錐の側面積は「扇形」になるわけだ。

半径×半径×中心角÷360
で求められる。
だから、面積を求めるためには「扇形の中心角」が必要になってくるんだね。
側面の扇形の中心角を X として方程式を作ってみよう。
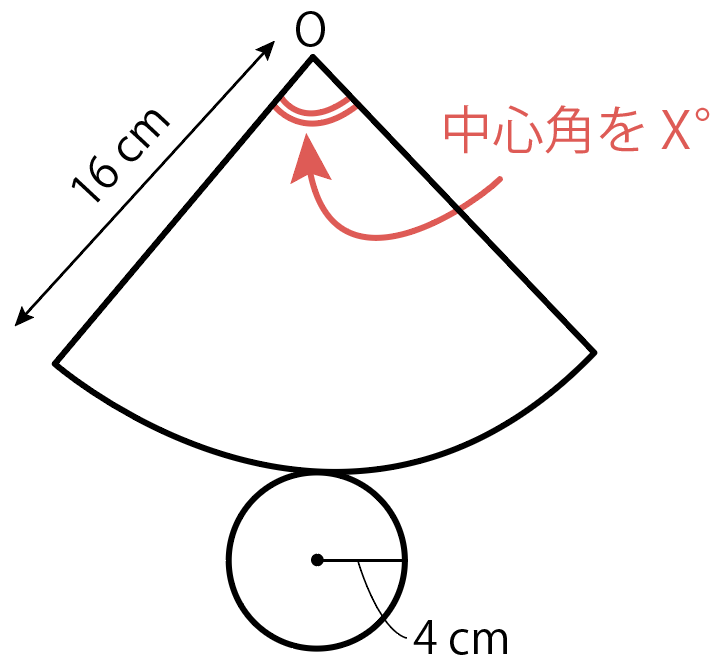
扇形の弧の長さ = 底面の円周の長さ
という方程式を作って、中心角を求めればいいね。
例題では、
16× 2π × X ÷ 360 = 8π
という式ができて、
X =90°
になるはず。
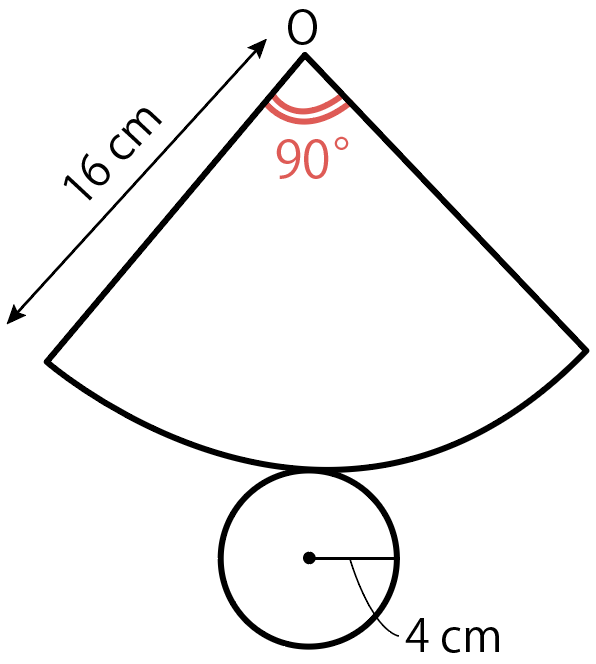
「扇形の中心角の求め方」がいまいちわからない時はこの記事で復習してみてね↓
いよいよ扇形の面積の公式を使って、側面積を求めていこう。
扇形の面積の公式は
半径×半径×円周率×中心角÷360
で求められるから、
16の2乗×π ×90÷360
= 64π [cm²]
が正解だね。
こんな感じで、円錐が転がっちゃう応用問題もステップを踏んでやれば大丈夫。
転がる問題を解くために必要なのは、
の3つだけ。
ひるまずにチャレンジしてみてね。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。音声入力、最高。
中3数学で勉強する方程式は「二次方程式」。
こいつは「次数が2の方程式のこと」なんだけど、解き方が6つもあるせいで、なかなかに解くのが難しい問題だね。
しかも、ただでさえ二次方程式は厄介なのに、たまに、
分数を含む二次方程式
というモンスターが出現することがあるんだ。
今日はこのパターンの二次方程式の解き方をマスターしていこう。
たとえば次のような問題があるよ。
次の二次方程式を解きなさい
X²ー3分の1X = 8
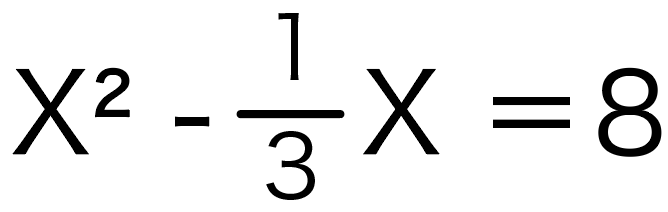
分数が紛れ込んでいる二次方程式の問題は、厄介だからこそテストや宿題に出やすい。。
次の3つのステップで瞬殺してみようぜ。
まず最初にやるべきことは、分数を消し去ること。
分数なければいつも通りの二次方程式になるから簡単になるよね。
じゃあどうやって二次方程式から分数を削除するのかっていうと、
分母の最小公倍数を両辺にかければいいんだ。
この分数の消し方は、
とまるまる一緒だね。
さて、例題の二次方程式を見てみよう。
次の二次方程式を解きなさい
X²ー3分の1X = 8
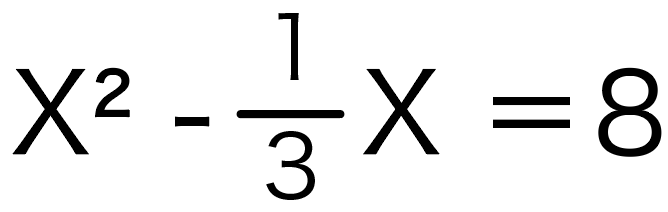
よーく見てみると分数の項が1つで、
ー3分の1X
しかない。

1つしか分数の項がないから、分母の最小公倍数はこの分母の3になるね。
ってことで両辺に3をかけてやると、
になる。

分数が消えたか確認してみてね。
あとはいつも通り二次方程式を解くだけでいいんだ。
例題を見てみよう。
3X²ーX = 24
はx2乗の項とxの項、整数の項がそれぞれ1つずつある二次方程式。
みやすいようにすべての項を左辺に寄せてみよう。
すると、こうなる↓
3X²ーX – 24 = 0
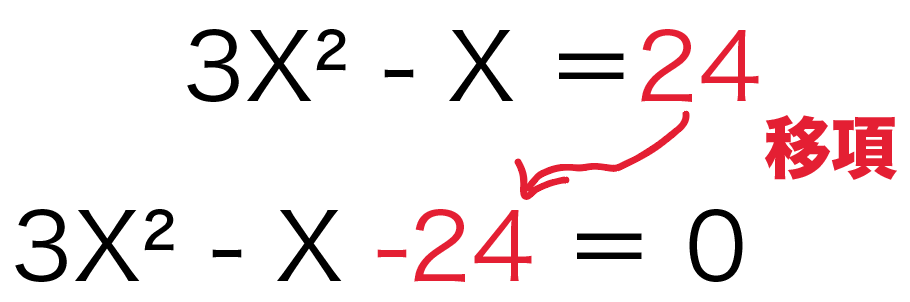
あとは二次方程式をいつも通りとくだけ。
「3X²ーX – 24 = 0」は公式で因数分解できないけど、たすき掛けの因数分解なら使えそう。
3X²ーX – 24 = 0
でたすき掛け因数分解を使ってやると、
3X²ーX – 24 = 0
(X-3) (3X+8) = 0
になるね。

たすき掛け因数分解を忘れちゃった時はこの記事で復習してみてね↓↓
(X-3 ) と(3X-8)のどっちかが0のとき、(X-3) (3X-8)が0になるから、
の2通りの等式ができるはずだね。

よって、この2つの方程式を解くと答えは、
x =3, -3分の8
だ。
以上が分数を含む二次方程式の解き方だったよ。
ポイントはやはり、
一番最初に分数を消し去るということ。
分数がなくなればいつも通りに二次方程式の解き方でとけばいいから、
の6つの二次方程式の解き方が使えるようになるんだ。
テストにも出やすいからよーく復習してこう。
そんじゃねー
Ken
やあ、Dr.リードだよ。今日は「逆」だよ。逆。
これまで勉強してきた、三平方の定理には、
三平方の定理(ピタゴラスの定理)の逆
っていうのがあるんだ。

逆は中2数学で習ったやつだったね。
忘れてるやつも多いと思うから、逆を復習しつつ、
三平方の定理でも逆が言えるのか??
を見ていこう。
=もくじ=
まずは数学の「逆」を復習してみよう。
数学の「逆」とはずばり、
ある命題の「仮定」と「結論」を入れ替えたもの
なんだ。
数学の命題とは、「正しいか、正しくないかを考える事柄のこと」だったね。
たとえば、次のような命題があるとするよ。
x =2, y = 3 ならば x+y = 5

仮定と結論をいれかえて、逆を作ってみると、
x+y = 5 ならば x =2, y = 3
になるね。

この命題の逆は正しいかな?
「x+y=5」を満たすxとyの組み合わせって「x=2, y = 3」以外にもありそうだよね?
たとえば、「x = 0、 y = 5」とかね。
だから、この場合は逆にすると命題が成り立たないね。
この例みたいに、
ある命題は正しいけど、逆は正しい場合もあるし、正しくない場合も両方あり得るんだ。
では、三平方の定理の逆はどうだろ。
三平方の定理(ピタゴラスの定理)とはこうだったな。
【三平方の定理(ピタゴラスの定理)】
直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、
a²+b² = c²
が成り立つ。

この三平方の定理(ピタゴラスの定理)で逆をつくってみようか。
三平方の定理の仮定と結論は、
だ。
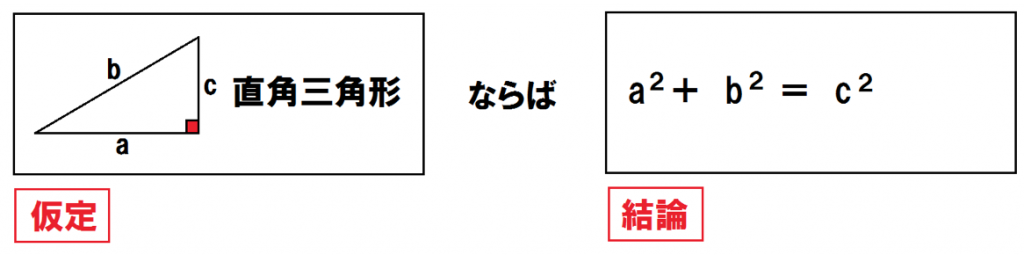
この逆をつくってみると、
になるね。
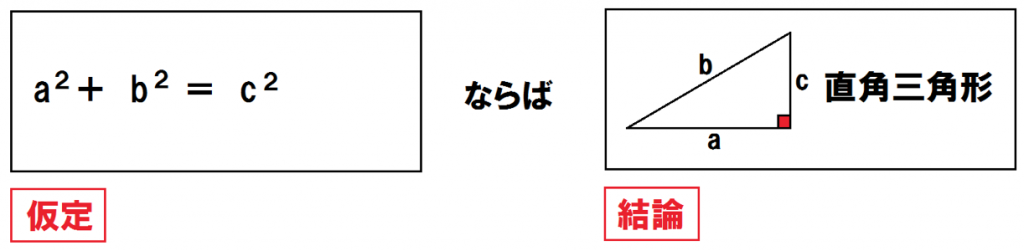
つまり、三平方の定理(ピタゴラスの定理)の逆は、
「a²+b² = c²」ならば「直角三角形である」
だ。
はてさて、これは正しいのかな?
三平方の定理の逆の証明してみるか。

わかりきってても、きっちりいくぜぃ。
下の図のような△ABCと△DEFがある。
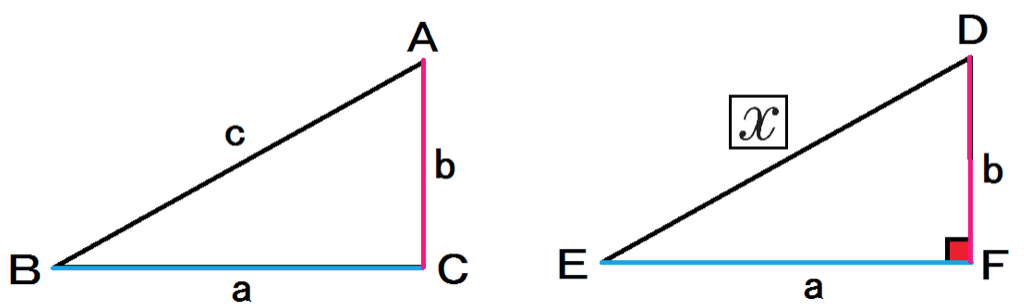
【仮定】
△ABCにおいて a²+b² = c²
△DEFは直角三角形である。
【証明】
△ABC と△DEF について、
仮定より、 a²+b² = c²・・・(1)
△DEFは直角三角形なので 三平方の定理より
a²+b² = x² ・・・(2)
(1)・(2)より、
c² = x²
c も x も正の数なので 、
c = x
△ABCと △DEF の3つの辺がそれぞれ等しいので、
△ABC ≡△DEF
よって ∠BCA =∠EFD=90°
したがって、
△ABC は直角三角形である。
この証明からわかるのは、
三平方の定理の逆も正しい!
ってこと。
中学生ならこの証明で十分かな!

三平方の定理の逆をつかった問題を解いてみよう。
練習問題
次の1辺の三角形があります。直角三角形となるのはどれですか。
(1) 3 cm 4 cm 5 cm
(2) 2 cm √7 cm √10 cm
(3) 15 cm 13 cm 7 cm
(4) 2 cm 2 cm √6 cm
(5) 2√5 cm 2√6 cm 2√7 cm
(6) 2√5 cm 2√5 cm 2√10 cm
2ステップで解けちゃうぜ。
一番長い斜辺は5 cmだから、斜辺の2乗は5² = 25。
他の2辺のに乗の和は、
3² + 4² = 25
になるね。
三平方の定理が成り立つから、直角三角形である!

斜辺は√10cmだから、斜辺の2乗は、
(√10)² = 10
になる。
他の2辺の2乗の和は、
2² + (√7)² = 11
三平方の定理が成り立たないから、直角三角形ではない。

一番長い辺の斜辺は15 cm。
斜辺の2乗は 15² = 225。
他の2編の2乗の和は、
7² + 13² = 218
三平方の定理が成り立たないから直角三角形ではない。

斜辺は√6 cmだから、斜辺の2乗は、
(√6)² = 6
になる。
他の2辺の2乗の和は、
2² + 2² = 8
三平方の定理が成り立たないから直角三角形ではない。

斜辺は2√7 cmだ。
斜辺の2乗は(√7)² = 7
他の2辺の2乗の和は、
(2√5)² + (2√6)² = 44
三平方の定理が成り立たないから直角三角形ではない。

斜辺は2√10 cmだから、斜辺の2乗は (2√10)² = 40になる。
他の2辺の2乗の和は、
(2√5)² + (2√5)² = 40
三平方の定理が成り立つから、直角三角形。

三平方の定理の逆はどうだったかな?
散々「ピタゴラスった!」から慣れたようだね。
つぎは立体で三平方の定理を使えるようになってみよう!
それじゃあな!
Dr.リード
やあやあ、Dr.リードだよ。
3年生の数学もいよいよ大詰め。
今日は、高校入試でよく出てくる、
正四角錐の高さを求める問題
を解説していくぞ。
正四角錐って、底面が正方形で、先っちょが尖ってる立体のことだったね。

ちょうど、エジプトのピラミッドが正四角錐だな。
正四角錐の高さを求めるためには、中3で勉強した三平方の定理も使っていくぞ。
正四角錐の高さの求め方はつぎの4ステップだ。
つぎの例題をいっしょに解いていこう。
練習問題
つぎの正四角錐の立体の高さを求めなさい。
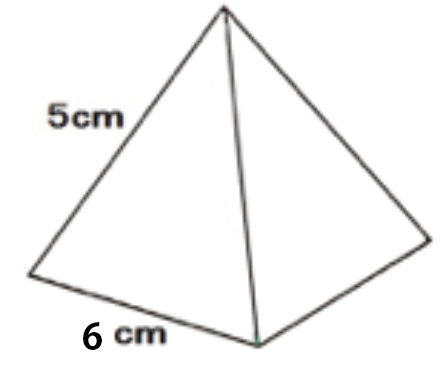
まずは、補助線をガンガン入れる。直角にも印をつけるといい。
正四角錐の中の直角三角形を見つけやすくするためだ。
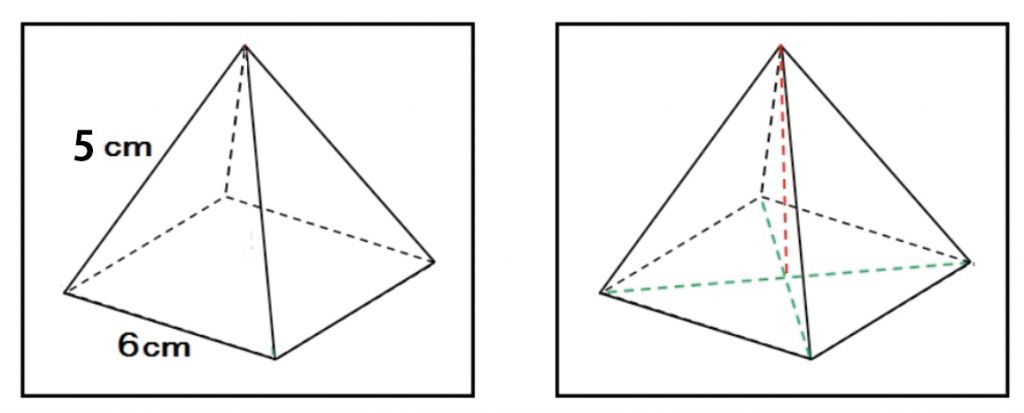
つぎは、正四角錐の底面に注目してみよう。
底面の正方形の対角線の長さを計算していくんだ。
底面は1辺が6cmの正方形だったな?
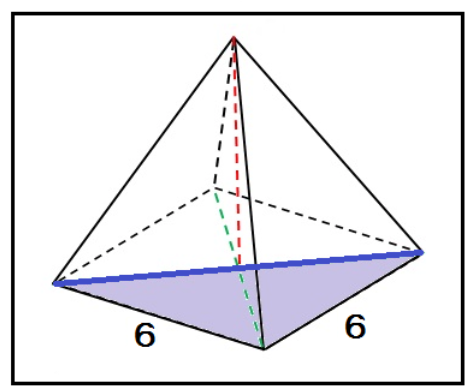
この正方形の半分の直角三角形で三平方の定理を使ってやると、
6² + 6² = x²
x = √72 = 6√2
になるぞ。
ってことは、正四角錐の底面の対角線の半分の長さは、
6√2÷2 = 3√2
だ。
つぎは、正四角錐の頂点からの垂線に注目。
垂線をふくむ直角三角形を探して、三平方の定理を使えばいいんだ。
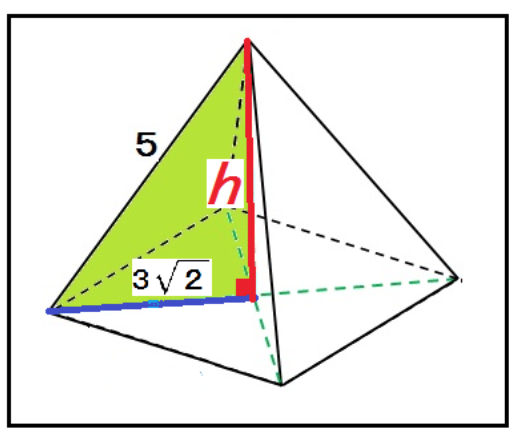
さっき見つけた正四角錐の頂点からの高さを求めてみよう。
使うのは、もちろん、
三平方の定理!
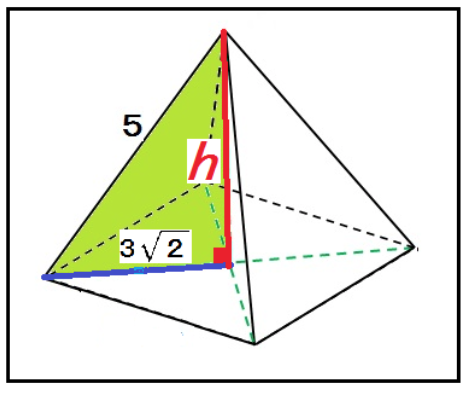
正四角錐の頂点からの高さをhとしてやると、
5² = (3√2)² + h²
h = √7
になるね。
つまり、この正四角錐の高さは√7 cmってわけ!
正四角錐の高さの求め方はどうだったかな?
つぎの4ステップで計算できちゃったな。
入試問題によく出てくるから復習しておこう。
正四角錐の高さが計算できたら次は円錐の高さに挑戦してみよう。
じゃあな
Dr.リード
tomo の中学1年生の数学の記事をまとめました。
数学の基本中の基本。プラスマイナスをマスター!
文字をつかった計算!
いよいよ方程式の解き方!文章題にもチャレンジしてみよう。
比例、反比例という関数を勉強していくよ。
面積の求め方から作図まで!
今度は平面じゃなくて立体!
体積や表面積を計算してみよう。
統計学の基礎を勉強していくよ。
tomo の中学2年生の数学を単元ごとにまとめたよ。
中学数学の復習の参考にしてね。

文字式の復習!
等式変形や文章題にチャレンジしていくよ。
2つ以上の方程式から答えを出す連立方程式!
「一次関数」とは次数が1の関数。
連立方程式をつかって解いていくよ。
平面図形の角度や性質をマスターしよう。
苦手な子も多い図形の証明。
コツをつかめばいけそうな気がするよ。
確率の基礎。サイコロやコインの確率を計算しよう。
tomo の中学3年生の数学の単元ごとにまとめてみたよ。
テストや試験の復習に参考にしてね!

二次方程式を解くために必要な計算方法を勉強していくよ。
二次方程式や三平方の定理で活躍する「平方根の計算方法」を勉強していくよ。
いよいよ二次方程式を解いていくよ。
二次方程式を使って次数が2の関数を勉強していこう。
相似な図形にチャレンジ!
円周角と中心角を使いこなせ!
ピタゴラスが発見した定理を駆使しよう!
統計学の基礎をマスター!
こんにちは!この記事を書いてるKenだよ。ナンは1つでいいね。
三角形の角の二等分線の定理・性質
っておぼえてるかな??
念のために復習しておくと、
「三角形の二等分線と底辺の交点」と「各頂点の長さの比」が、他の辺の2辺と等しい
っていう定理だったよね??
言葉じゃわかりづらいから図をみてみよっか。
たとえば、
の△ABCで、∠Aの二等分線との交点をDとすると、
AB : AC = BD : DC = a : b になってるんだ。
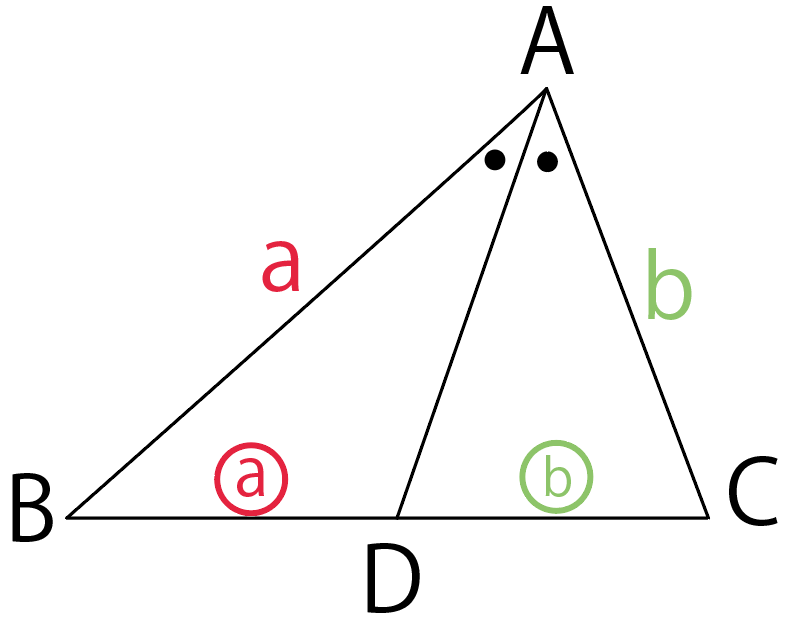
なぜ、三角形の角の二等分線の性質が使えるのかわからない??
そういうときは、角の二等分線の定理の証明の記事を読んでみてね。
今日はこの定理を使った問題を解説していくよ。
つぎの問題を解いてみよっか。
つぎの△ABCにおいて、線分BDの長さを求めなさい。
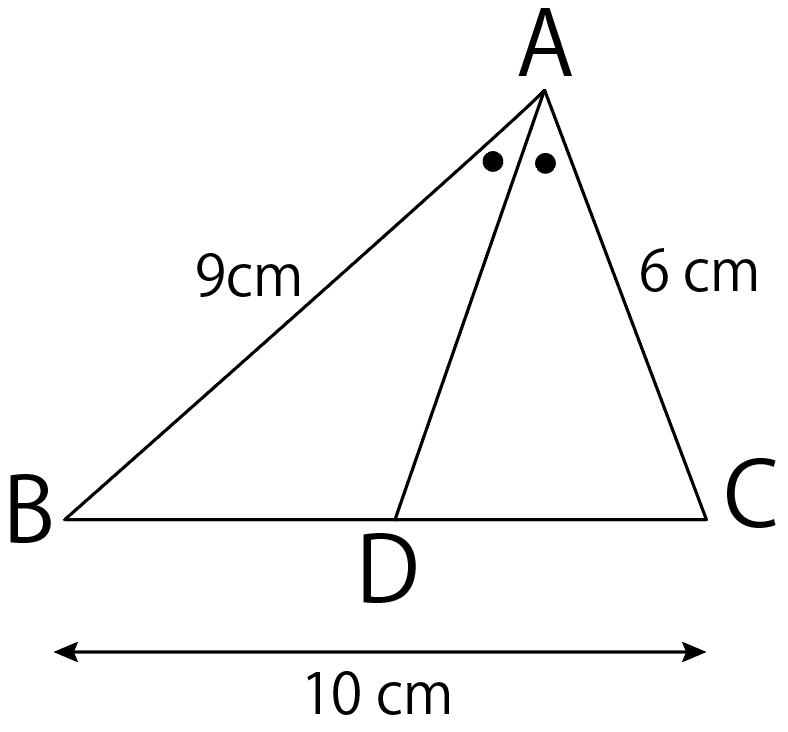
このタイプの比の問題はつぎの3ステップで解けちゃうんだ。
まずは、三角形の2つの辺の比を求めてみよう。
練習問題でいうと、
の2辺だね。
こいつの辺の比を求めてみると、
AB : AC = 9 : 6 = 3 :2
になる!
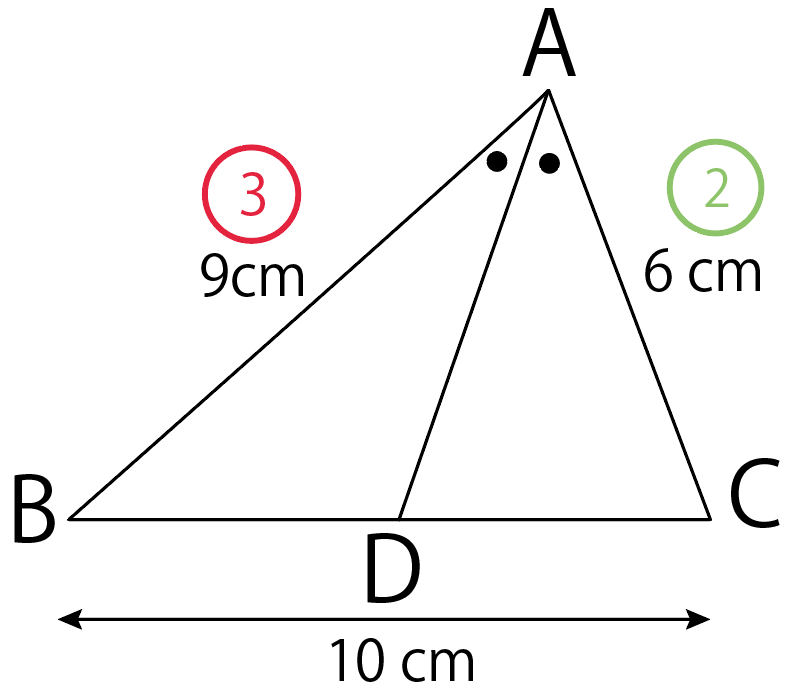
これが第一ステップ。
いよいよ三角形の角の二等分線の定理の出番だ。
さっき求めた「三角形の2辺の比」と「二等分線と底辺の交点でできた線分の比」が等しいってことがいえるからね。
練習問題でいうと、
AB : AC = BD : DC
が言えるわけ。
ステップ1で、AB : AC = 3 : 2がわかったから、
BD : DC = 3 : 2
ってことがわかるね。
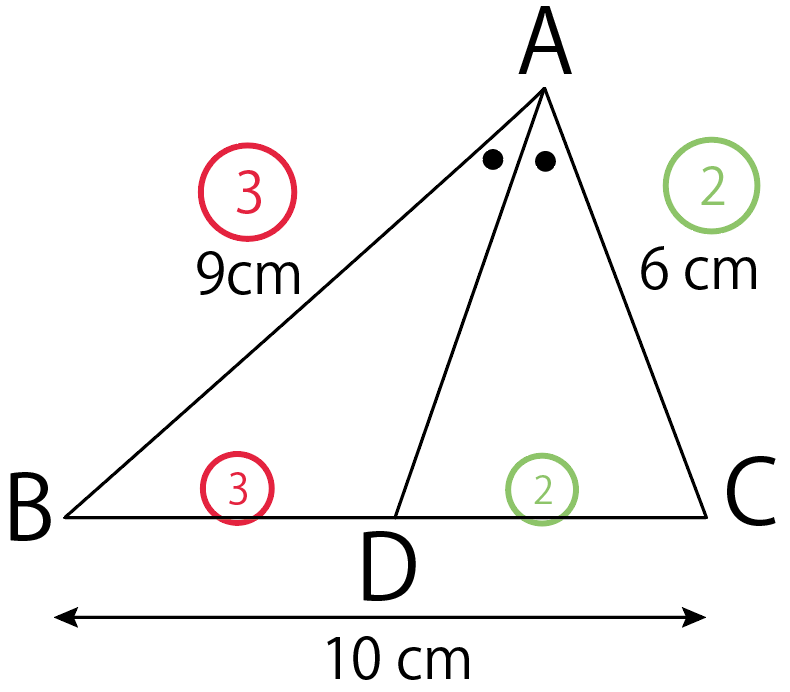
これが第二ステップ!
求めた辺の比を使って、辺の長さを計算しよう。
練習問題でいうと、
BD : DC = 3 : 2
っていう比をつかって、BDの長さを求めればいいね。
底辺BCの長さは10cmだったから、
BD = 10 × 5分の3 = 6 cm
になるんだ。
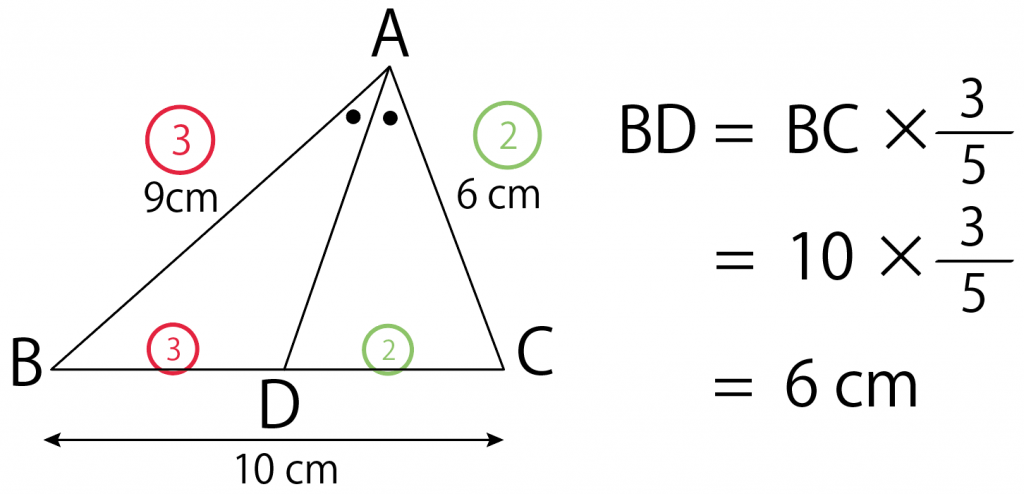
角の二等分線の性質の問題はどうだったかな??
の3ステップでだいたい解けそうだったね。
最後につぎの応用問題を解いてみよう!
つぎの△ABCにおいて、AE : EDを求めなさい。
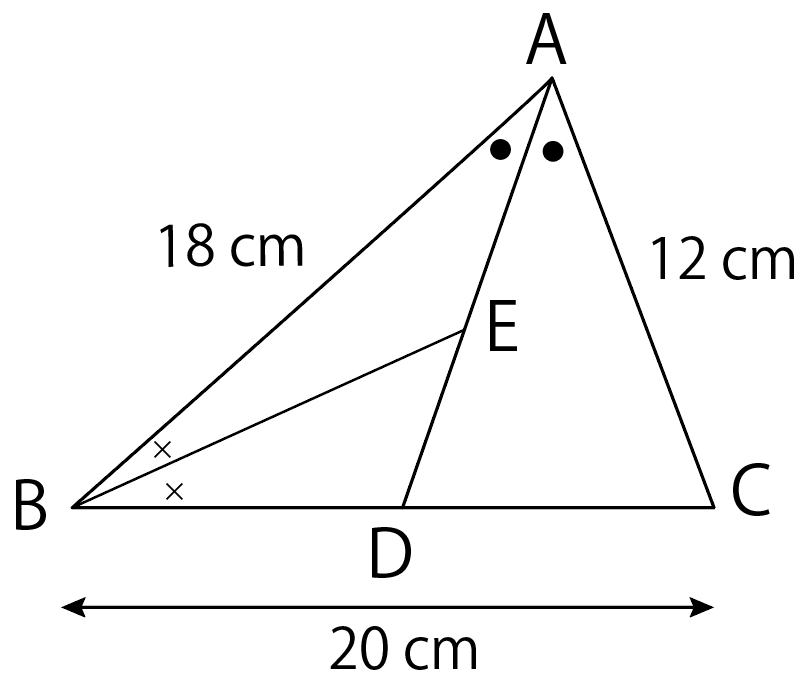
そんじゃねー
Ken
こんにちは!この記事を書いてる Kenだよ。分子を振動させたね。
中2と中3数学の平面図形で、
三角形の「合同条件」と「相似条件」
を勉強してきたよね。

両方とも数学の証明のために必要なアイテムだから、テスト前には覚えなきゃいけないね。
念のためおさらいしておくと、
だったね。
でもさ、この2つの条件ってちょっと似てない??
ごちゃ混ぜにしちゃうことあるよね。
そこで今日は、
三角形の合同条件と相似条件をごちゃ混ぜにしないために、整理して覚えてみよう!
合同条件と相似条件の似ているところと、違うところを中心に復習していくよ。
三角形の合同条件と相似条件をうまく覚えるために、3つの種類に分類してみたよ。
| 3つの何かが等しい条件 | 2つの角が等しい条件 | 2辺を角で挟んだ条件 | |
|---|---|---|---|
| 合同条件 | 3つの辺がそれぞれ等しい | 両端の角とその間の辺が等しい | 2つ辺とその間の角が等しい |
| 相似条件 | 3つの辺の比がすべて等しい | 2つの角がそれぞれ等しい | 2つの辺の比とその間の角が等しい |
まず1つ目の条件の種類は、
3つの「何か」が等しいやつだ。
合同条件と相似条件をそれぞれ見ていこっか。
「3つの辺の長さ」がすべて等しいっていう条件は合同条件だ。
この条件を満たす三角形たちは合同である、ってことが言えるわけね。
たとえば、次の2つの△ABCと△DEFを想像してみて。
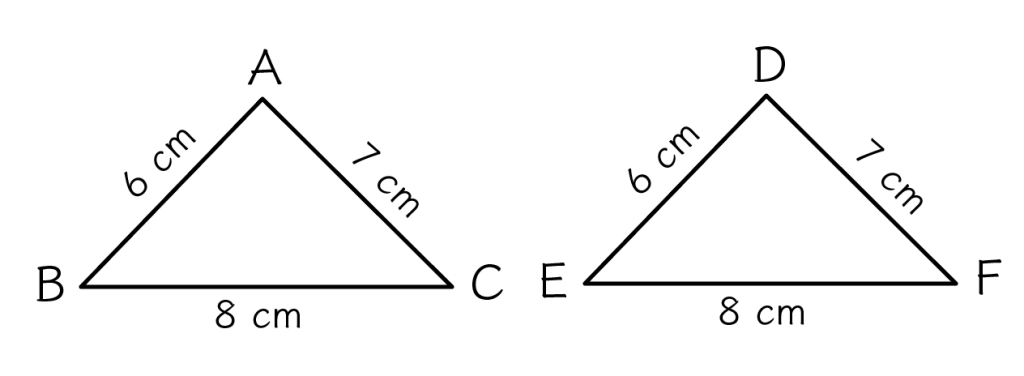
と、
この2つの三角形は合同って言えるんだ。
なぜなら、すべての3つの辺の長さがそれぞれ等しいからね。
「3つの辺の比」がすべて等しいとき、2つの三角形は相似って言えるんだ。
たとえば、2つの△ABCと△DEFを想像してみて。
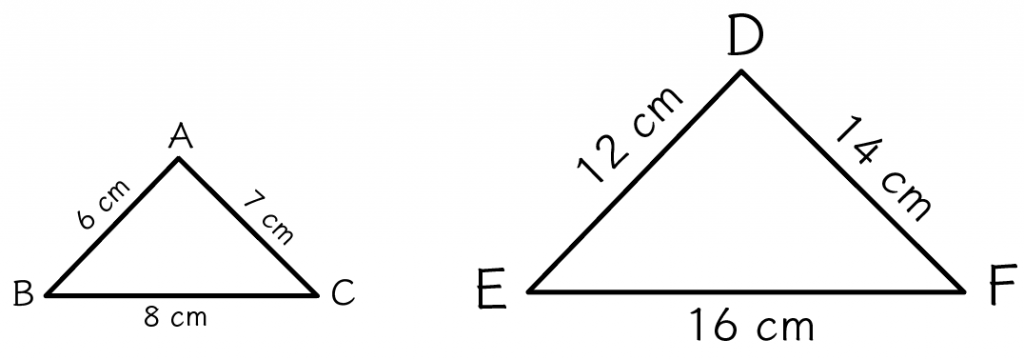
と
だ。
この2つの三角形は相似になってるはず。
なぜなら、
になっていて、すべての辺の比が全部1:2で等しくなってるね。
つぎの条件は、2つの角が等しい条件だ。
2つの角が等しいことを使った条件が、なんと偶然にも合同条件と相似条件に1つずつ存在しているんだ。
まず三角形の合同条件には、
1つの辺とその両端の角がそれぞれ等しい
っていう条件があるよ。
つまり、
1つの辺が等しくて、それを挟んでいる2つの角が等しかったら合同が言えるってわけね。
たとえば、つぎの2つの△ABCと△DEFを想像してみて。
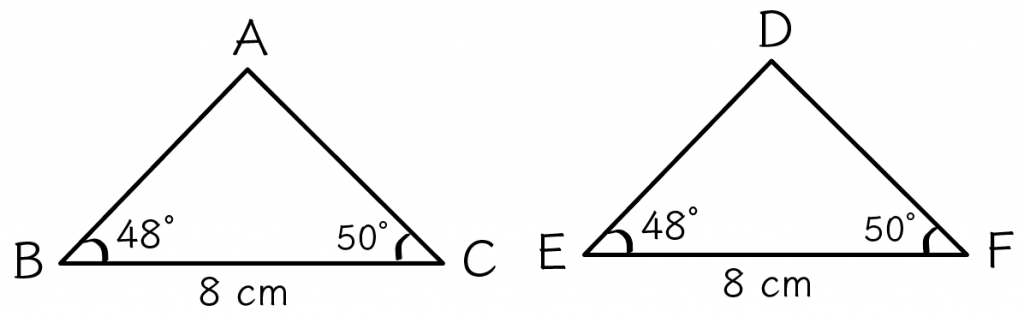
と、
この2つの三角形はへんのひとつの辺の長さが等しくて、その両端の額の大きさが等しいよね。
だから、この2つの三角形は合同であると言えるんだ。
ふたつめの相似条件は、2つの角がそれぞれ等しいっていうやつだね。
この相似条件は1番簡単で、でてきやすい相似条件なんだ。
たとえば、次の△ABCと△DEFを想像してみて。
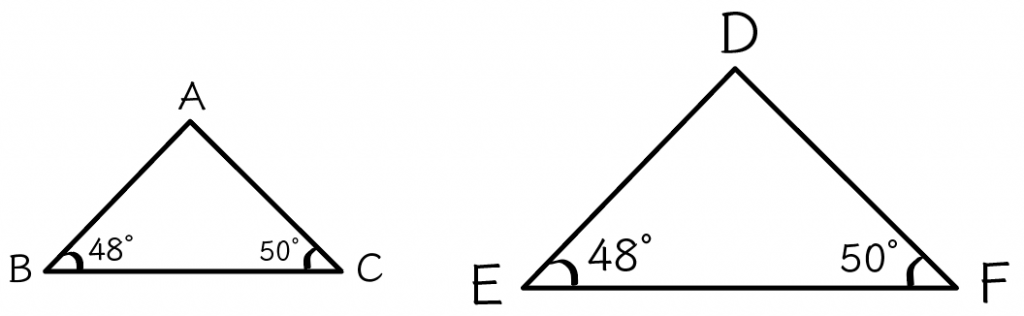
この場合、2つの三角形は、「2つの角がそれぞれ等しい」っていう相似条件に当てはまるから、相似であるといえるんだ。
つぎは、2つの辺が角を挟んじゃってる条件だ。
合同条件と相似条件には2つあるよ。
最後の合同条件は、
2つの辺との間の角がそれぞれ等しい
ってヤツ。
等しい辺たちが等しい1つの角を挟んでいれば、2つの三角形は合同って言えるんだ。
たとえば、つぎの△ABCと△DEFを想像してみて。
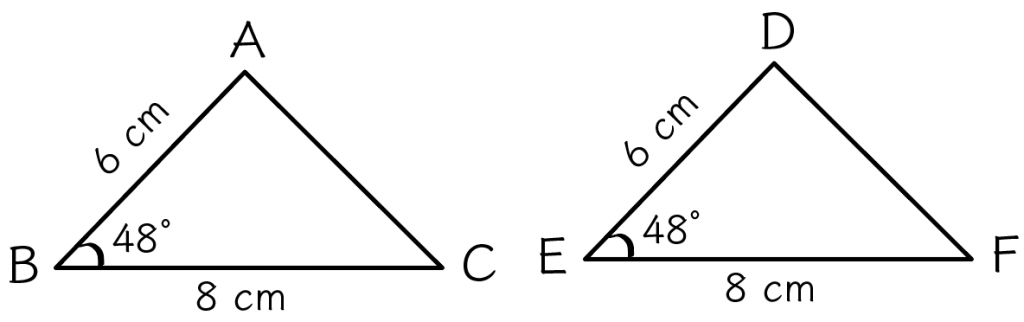
と、
この2つの三角形は、2つの辺(BCと EF、 ABとDE)が等しくて、
なおかつ、その辺に挟まれた間の角(∠ABC と∠DEF)が等しいから合同って言えるんだ。
最後の相似条件は、
2組の辺の比とその間の角がそれぞれ等しい
ってヤツね。
つぎの△ABCと△DEFを想像してみて。
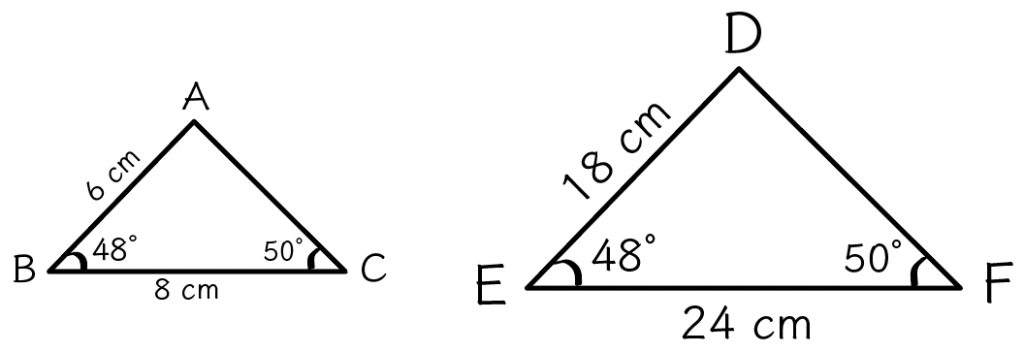
と、
この2つの三角形は相似なんだ。
なぜなら、
で2組の辺の比が1:3で等しくなっていて、なおかつ、その2辺の間に挟まってる角の、∠ABCと∠DEF が等しくなってるからね。
三角形の合同条件と相似条件は思い出せたかな??
最後にもう一回復習してみよう。
| 3つの何かが等しい条件 | 2つの角が等しい条件 | 2辺を角で挟んだ条件 | |
|---|---|---|---|
| 合同条件 | 3つの辺がそれぞれ等しい | 両端の角とその間の辺が等しい | 2つ辺とその間の角が等しい |
| 相似条件 | 3つの辺の比がすべて等しい | 2つの角がそれぞれ等しい | 2つの辺の比とその間の角が等しい |
どちらも証明問題に必要な条件だから、しっかりテスト前には覚えておこうね。
そんじゃねー
Ken
どうも、Drリードだぞい。
中3数学では、
三平方の定理(ピタゴラスの定理)を勉強してきたよな?
簡単に復習すると、
直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、
a²+ b² = c² が成り立つ
ってやつだったな。

さあ、この定理を使いこなせるようになるんだぞ。
今回はそのための基礎トレーニングだ。
三平方の定理をつかった問題でよく出てくるのは、
直角三角形の辺の長さを求める問題。
今日はこの問題を4つのパターンに分けてみたぞ。
問題集では、いろいろな直角三角形がでてくるし、簡単なのも難しいのも混じっているからな。
初めは解けなくっても、がっくりこないで、
負けんぞ!!
と構えとけ。

まず1つ目の問題は、
直角三角形の辺の長さを三平方の定理の公式で求めるタイプ。
これは、
三平方の定理の公式に、辺の長さを代入して計算するだけだから簡単だ。
たとえば、つぎの練習問題な。
練習問題1.
つぎの直角三角形の辺の長さxを求めてください。
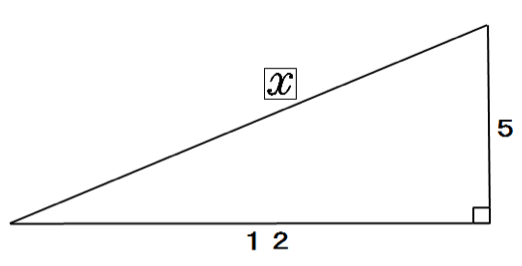
辺の長さが2桁でも気にすんな。
三平方の定理(ピタゴラスの定理)の公式にぶち込めばいいんだ。
x² = 5² + 12²
x = 13
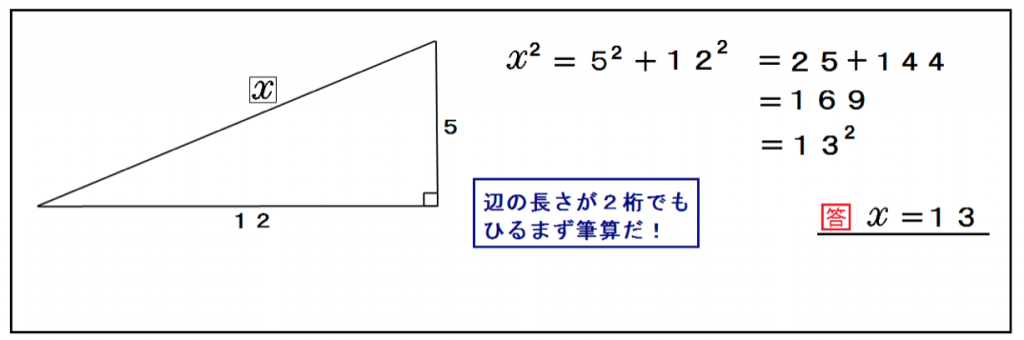
直角三角形と言えども、いつも右下に直角が来るとは限らんぞ。
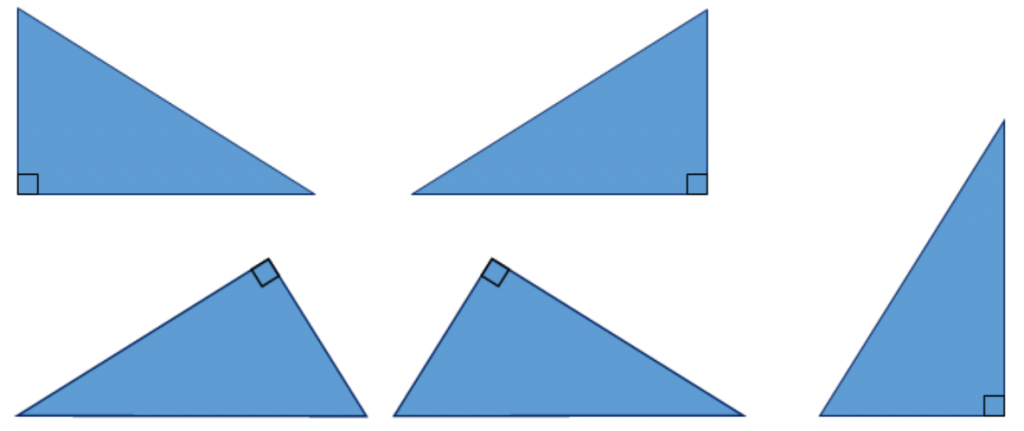
なっ。向きが変わると、斜辺がどれなのかうっかりしてしまうよ。
要注意だな。
2つ目のタイプは、
三平方の定理の計算に「平方根・ルートの計算」が混じってるやつだ。
たとえば、次のような練習問題。
練習問題2.
つぎの直角三角形の辺の長さxを求めてください。
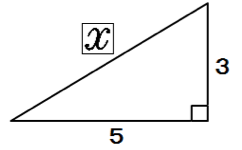
三平方の定理で直角三角形の辺の長さを計算してみると、
x² = 3² + 5²
x = √34
になるね。

答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。
つぎは、直角二等辺三角形の辺の長さを三平方の定理で計算する問題。
たとえば、三平方の定理を発見したピタゴラスも悩んだと知られる次の問題だ。
練習問題3.つぎの直角三角形の辺の長さxを求めてください。
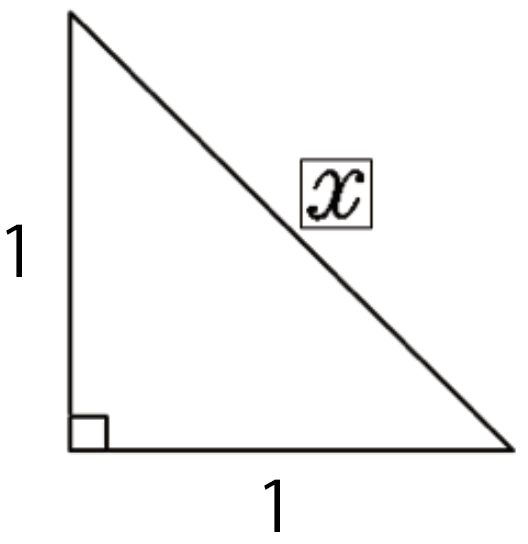
直角二等辺三角形だけど、さっきの計算問題と同じだ。
三平方の定理の公式を使ってやると、
x² = 1² + 1²
x = √2
になるぞ。
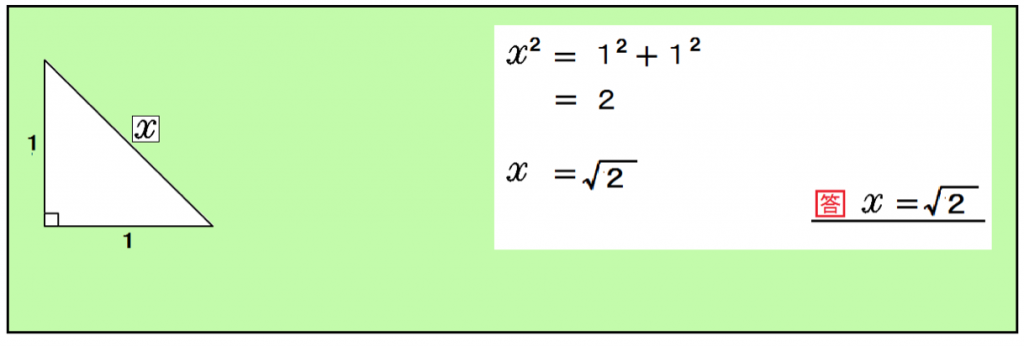
この直角二等辺三角形からピタゴラスは「無理数」を発見したと言われているんだ。
でも、ピタゴラスの生きてた時代は、まだまだ自然科学より宗教の勢力の方が主流でな。
ピタゴラス学派がうっかり、そして見事にピタゴラスの定理を見つけたんだが、
2乗して2になる数なんて、まだ見つかってなかった。
やや、これを発表したら、世の中大変なことになる・・・・
ってんで、長いこと秘密にしてたらしいぞ。

今は平和だ。
無理数はある!!と大声で言えるいい時代だ。(。)
つぎは、
直角三角形が2つくっついてる問題な。
たとえば、次の練習問題だ。
練習問題4.
つぎの直角三角形の辺の長さxを求めてください。
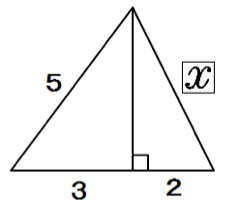
このタイプの問題では、高さを新しい文字で置いて2つの三角形の辺を出していくぞ。
まず、大きい三角形の高さをyとしてみよう。
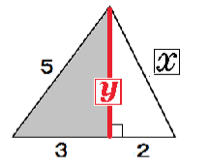
まず、灰色の直角三角形でyを計算してみる。
5² = 3² + y²
y = 4
そして、残りの白い直角三角形でxを出せばいいのさ。
x² = 4² + 2²
x = 2√5
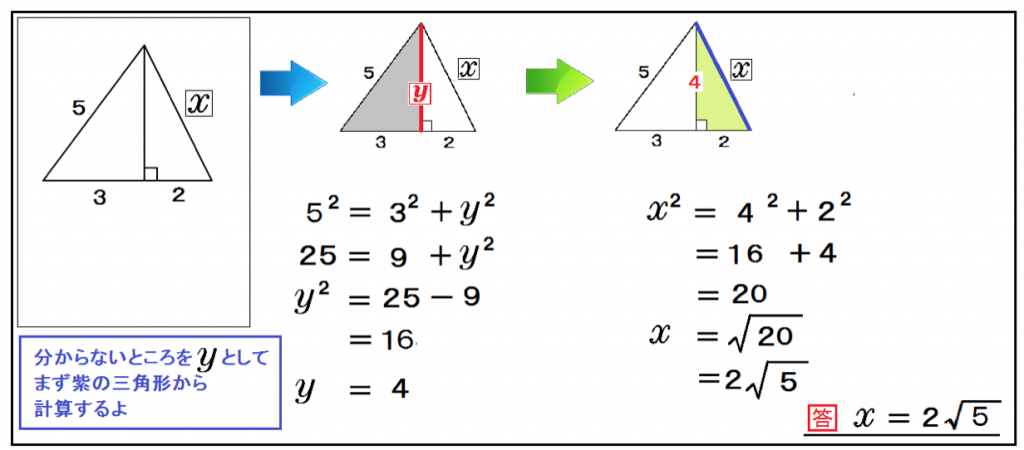
解き方大体わかっただろ??
じゃあつぎの計算問題にもチャレンジしよう。
練習問題5.
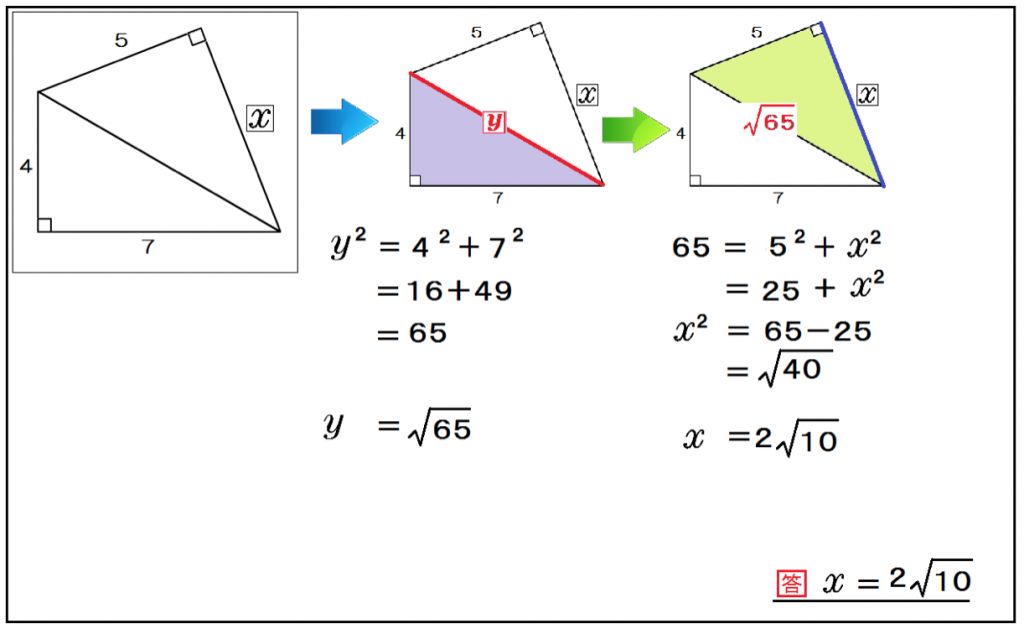
つぎの直角三角形の辺の長さxを求めてください。
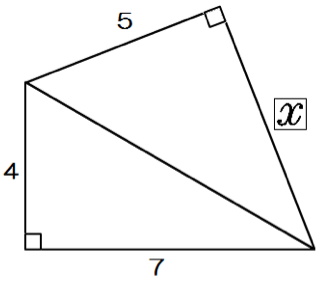
この問題も解き方はおんなじだ。
まず、真ん中の辺をyとして、yから計算すればいいんだね。
y² = 4² + 7²
y = √65
つぎはxを計算!
65 = 5² + x²
x = 2√10
三平方の定理で、直角三角形の辺の長さを求める問題はどうだった?
今日勉強した問題のパターンは4つだったな?
これだけの基本パターンやったら、少しは自信がついたな。
慣れるまではピタゴラスの定理の式に丁寧に数値を代入してくれ。


それじゃあな
Drリード
こんにちは!この記事を書いてる Kenだよ。ゆれた、ね。
中3数学で相似を勉強していると、
中点連結定理(ちゅうてんれんけつていり)
を習うよね??
中点連結定理とはその名前の通り、
三角形の辺の中点を連結したときに使える定理のこと
をいうんだ。
三角形の2つの辺の中点を結んであげるとね、
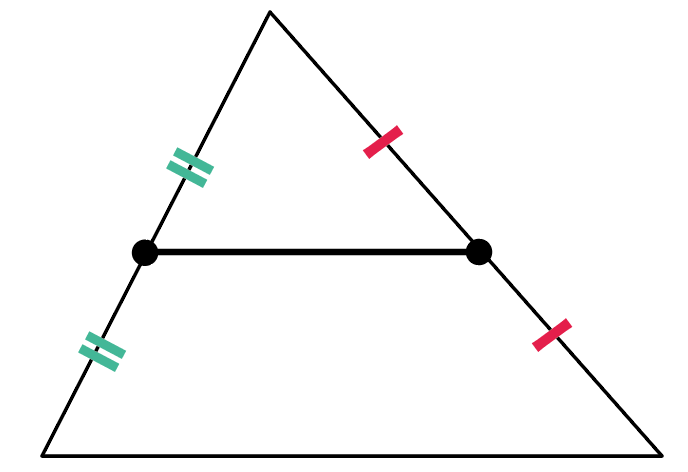
なんと、その中点を結んでできた辺の長さは、底辺の長さの半分になっていて、
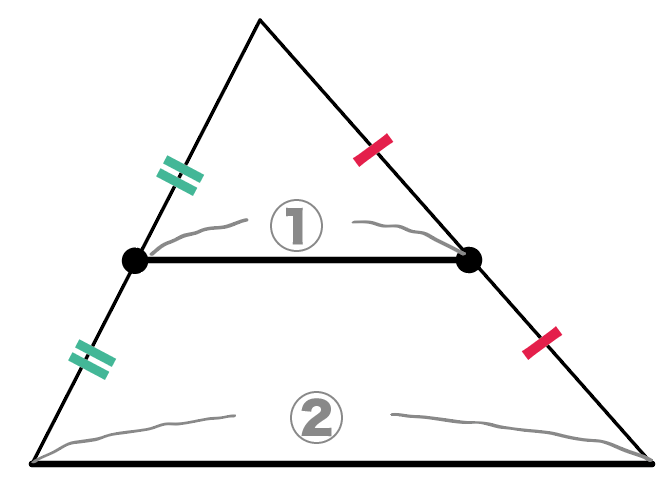
なおかつ、底辺と平行になっているんだ!
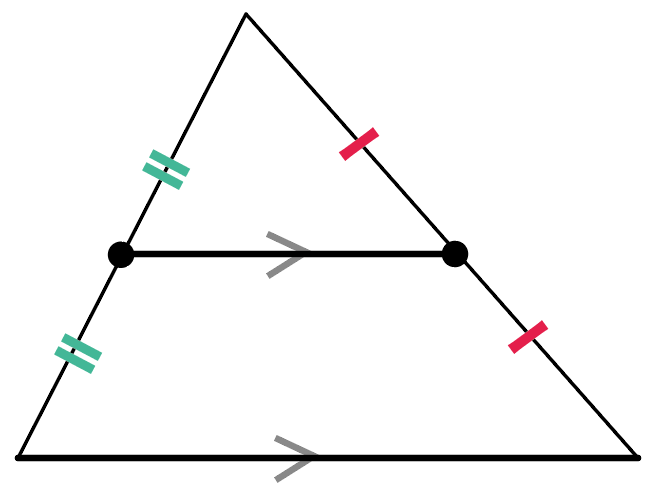
これが中点連結定理の正体。
つまり、中点連結定理の中身を開けてみると、おもに2つに分かれてるわけ。

三角形の中点を結ぶだけで底辺の半分の線が引けて、しかも、そいつは底辺に平行でもあるっていうんだ。
むちゃくちゃ楽チンな定理だね。
えっ。中点連結定理は役に立つのかって??
今日はそんな疑ってるみんなのために、実際に中点連結定理を使ってみよっか。
つぎの△ABCを想像してみて。
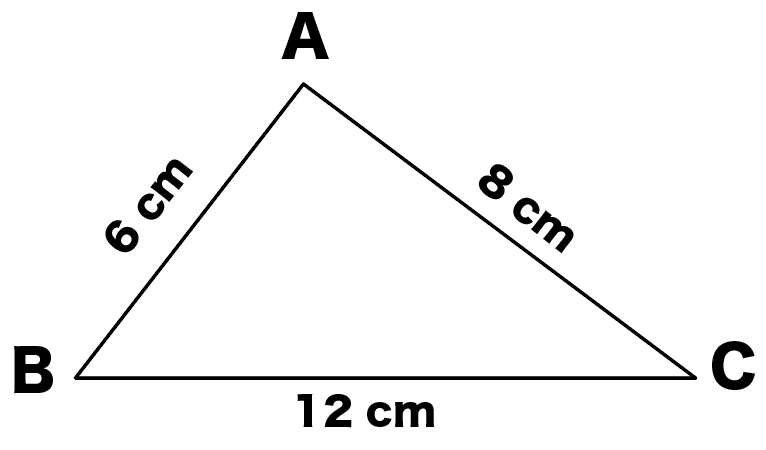
こいつの、辺 ABとACの中点 Mと Nを結んでみたんだ。
∠ACB=48°のとき、
を求めてみよっか!
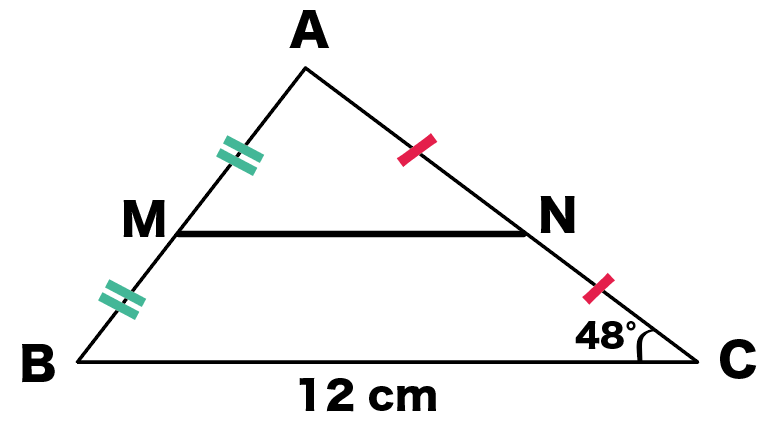
まずはMNの長さを求めてみよう。
MとNはそれぞれ三角形の辺の中点だから、さっき勉強した中点連結定理が使えるね。
中点連結定理では、三角形の辺の中点を結ぶと、
「結んだ線分の長さ」は「底辺の半分の長さ」になる
って習ったね?
だから、MNの長さは底辺BCの半分になるはずなんだ。
よって、
MN = 1/2 BC = 12×1/2 = 6cm
になるよ。
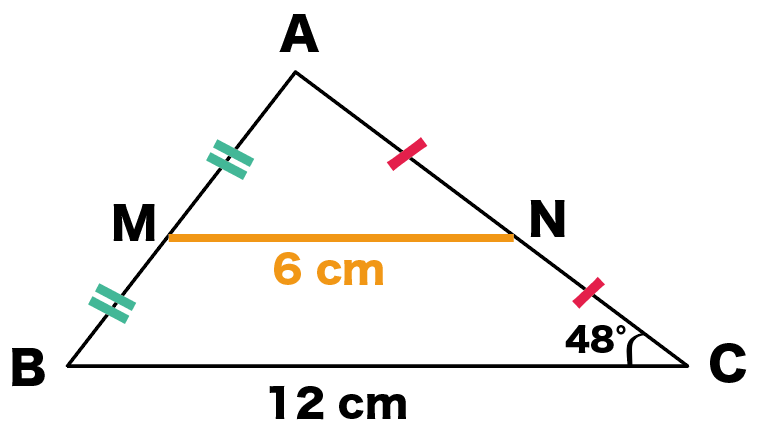
中点連結定理を使ってやると、中点を結んだ線分の長さを1秒ぐらいで計算できちゃうんだ。
ね?便利でしょ??
つぎは、∠ANMの大きさを求めてみよっか。
中点連結定理のもう1つの性質の、
三角形の辺の中点を結んだ線分は底辺に平行になる
を使うと求めることができるよ。
MとNは△ABCの辺のそれぞれ中点になってるよね??
だから、中点連結定理を使うと、
MN//BC
ってことがわかる。
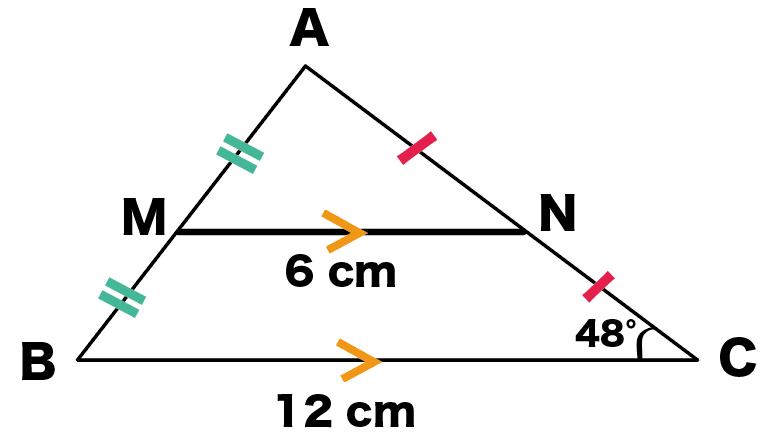
平行な線分同士の同位角は等しいから、同位角の位置にある、
は等しいはずなんだ。
問題によると、∠ACB = 48° だから、
∠ANM = ∠ACB = 48°
になるってわけ!
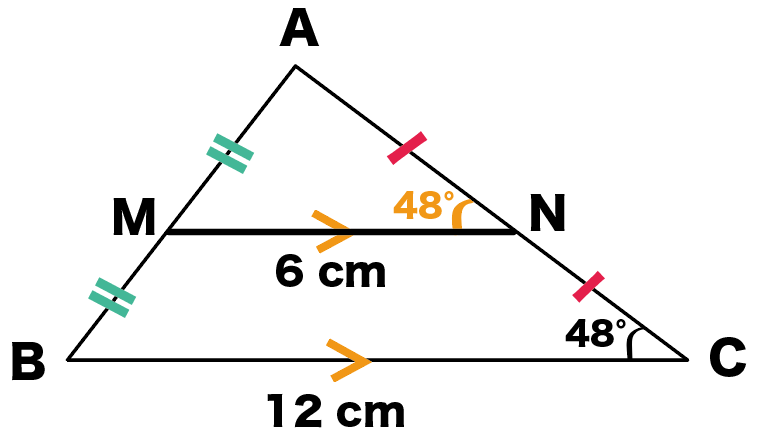
やったね!
これで中点連結定理の平行になる性質も使うことができた!
中点連結定理はどうだったかな?
最後にもう一回復習しておこっかー!
【中点連結定理】
三角形の2辺の中点を結ぶと、
結んでできた線分は、底辺の長さの半分になり、
しかも、底辺に平行である。

中点連結定理を使った証明問題はよく定期テストにも出てくるから、しっかりおさえておいてね。
そんじゃねー
Ken