サイコロでゾロ目がでる確率を計算できる公式は??
こんにちは!この記事をかいているKenだよ。焼き肉は週一でいいね。
サイコロを2個以上投げたとしよう。
このとき、「ぜんぶ同じ目になること」を「ゾロ目がでる」ってよんでいるよ。
たとえば、サイコロを4つふったとしよう。
ぜんぶの目が4になったら「ゾロ目」がでたっていうんだ。

ゾロ目をだすといいことばかりだ。
ボーナスがもらえたり、ワープできたりと、かなりお得。
それだけめずらしくてラッキーってことなんだ。
だからこそ、
サイコロでゾロ目がでる確率
ってむちゃくちゃ気になるよね?
今日は、
サイコロをふってゾロ目がでる確率を3秒で計算できる公式
を紹介していくよ。
よかったら参考にしてみて。
サイコロでゾロ目がでる確率の計算公式
サイコロの数をnとしよう。
ゾロ目になる確率は、
6/6^n
になるよ。

ただし、nは2以上にかぎるけどね!
たとえば、サイコロ4つのゾロ目の確率を計算してみよう!

サイコロの数は4だから、
「n」 に「4」を代入すればいいわけだ。
すると、
(4つのサイコロでゾロ目がでる確率)
= 6 ÷ 6^4 = 1/ 216
になるはず。
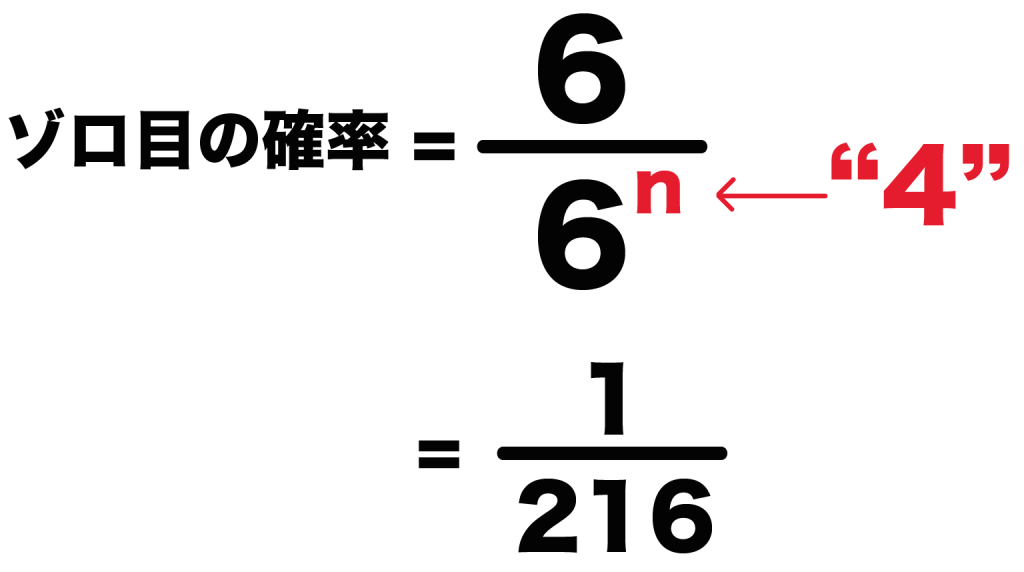
つまり、
1/216っていう確率で、
「3の目」が4つでるかもしれないし、

「1の目」が4つでるかもしれないんだ。

どう??簡単な公式でしょ??
なぜサイコロのゾロ目の確率公式がつかえるの??
でもさ、
なぜゾロ目の確率が計算できるんだろう??

nに「サイコロの数」をいれるだけ。
簡単すぎる。
ぜったいあやしいよね??。
だから、
なぜゾロ目の確率公式がつかえるのか???
っていうことを確認していこう。
ゾロ目の場合の数は「6」??
サイコロを何個ふっても、
「ゾロ目がでる場合の数」って「6」なんだ。
なぜなら、
サイコロの目が同じになる場合の数は1~6で1つずつだからね。
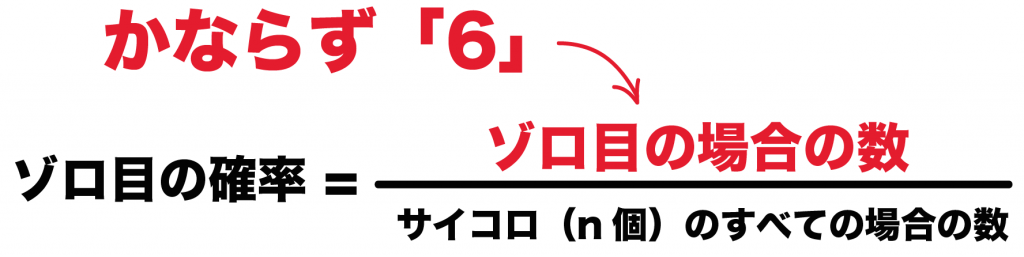
だから、1000個サイコロをふろうが、1万個サイコロをなげようが、
ゾロ目になる場合の数は6通りになるんだ。

すべての場合の数は?
あとは分母の、
すべての場合の数を求めるだけ!
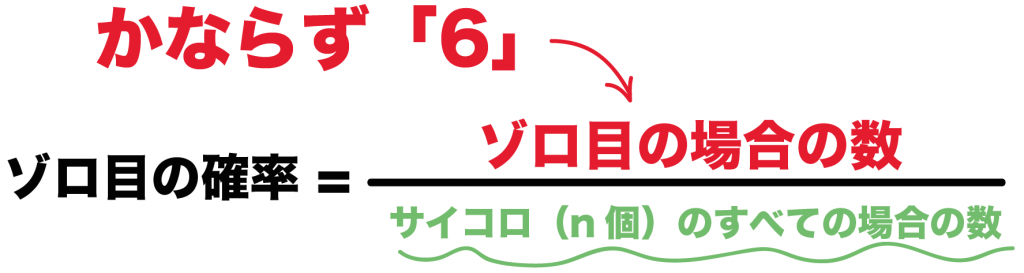
6のn乗
だったね??
なぜなら、1個のサイコロは6通りの目をもっているからね。
n個のときは6をn回かけると場合の数になるんだ。
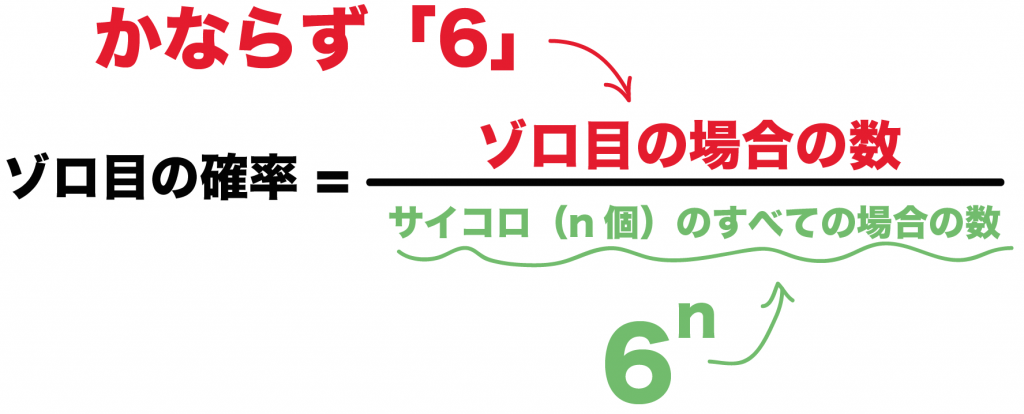
だから、n個のサイコロをふったときにゾロ目がでる確率は、
6/6^n
になるよ。

どう?スッキリしたかな!?
まとめ:サイコロでゾロ目がでる確率の公式はシンプル!
サイコロでゾロ目がでる確率の公式は簡単。
n個サイコロをふったとすれば、
6/6^n
の公式で計算できちゃうんだ。
じゃんじゃん計算していこう。
そんじゃねー
Ken









