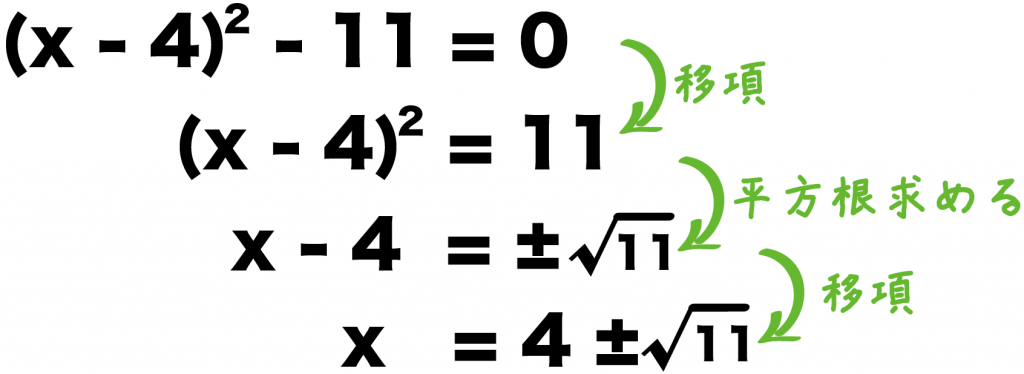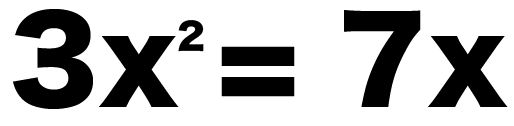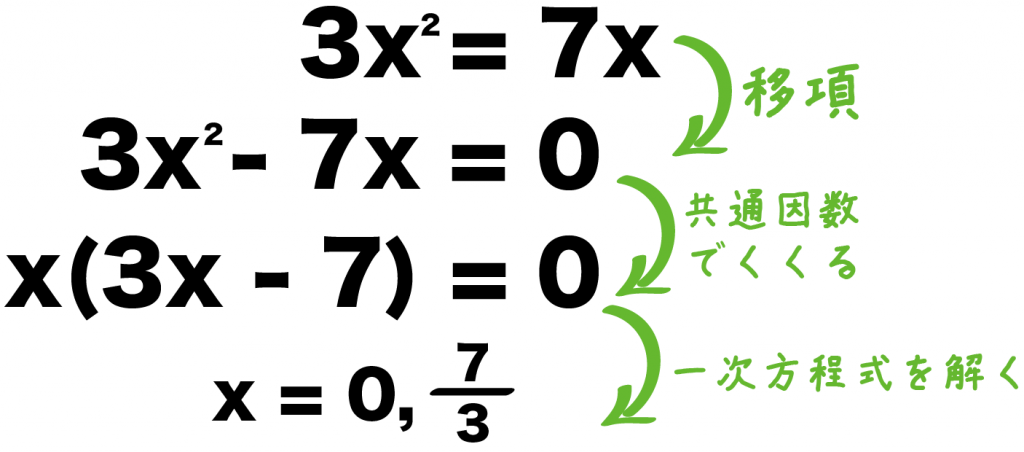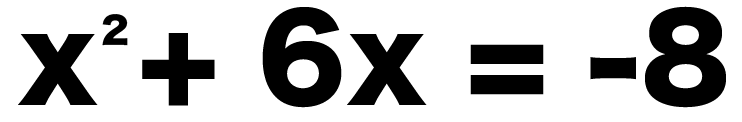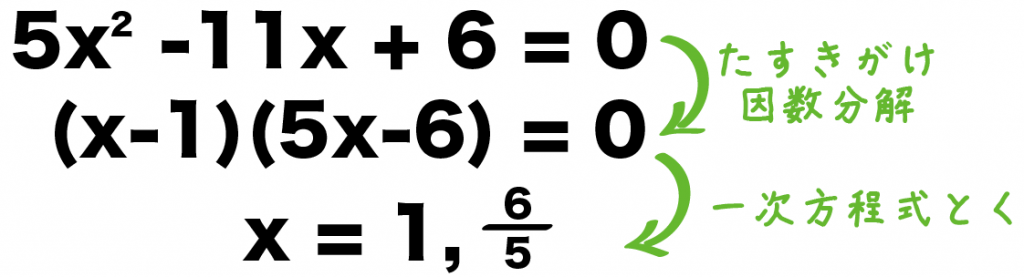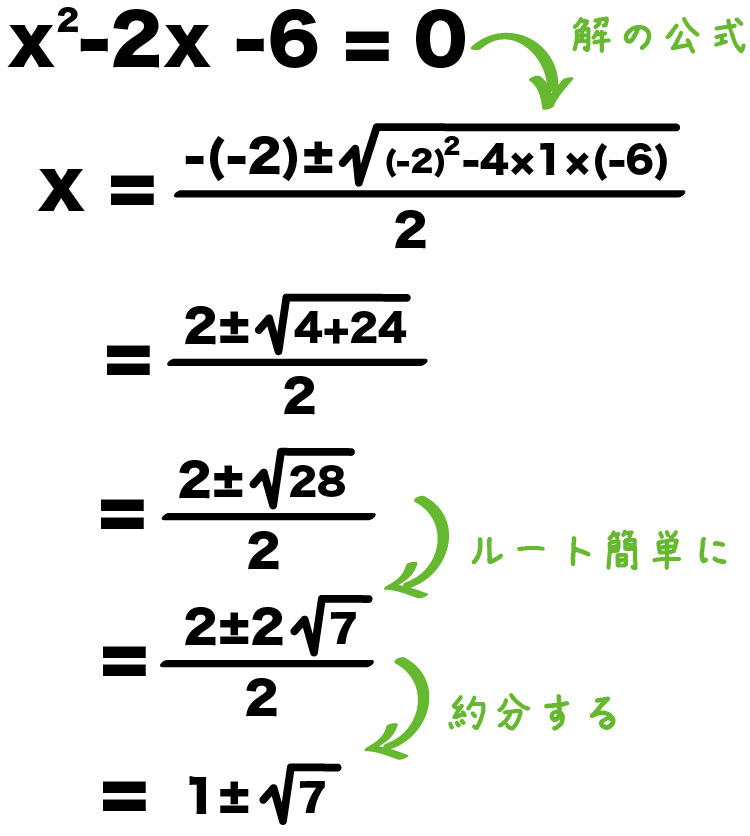【中3数学】二次方程式の解き方を見分ける1つのコツ
二次方程式の解き方を見分けるコツ??
こんにちは!この記事をかいているKenだよ。スペース最高。
二次方程式の解き方をたくさんならってきたね。
ざっと数えるだけ、6つもある。
解き方がたくさんあって便利なんだけど、
どの解き方つかえばいいかわからないんだよね。
せめて、
二次方程式の解き方を見分けるコツ
とかあれば助かる・・・・
そこで今日は、特別に、
二次方程式の解き方の見分け方
を紹介するよ。
よかったら参考にしてみてね。
二次方程式の解き方を見分ける1つのコツ
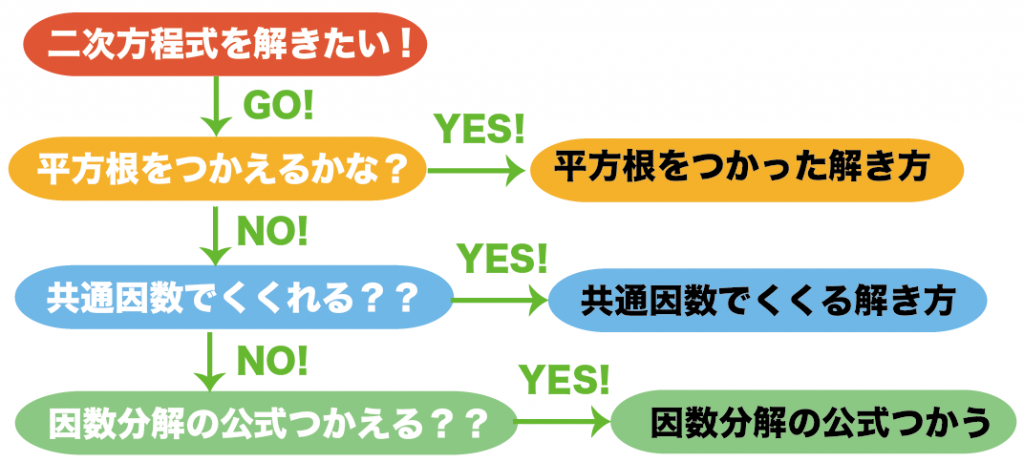
二次方程式の解き方を見分けるコツは1つ。
それは、
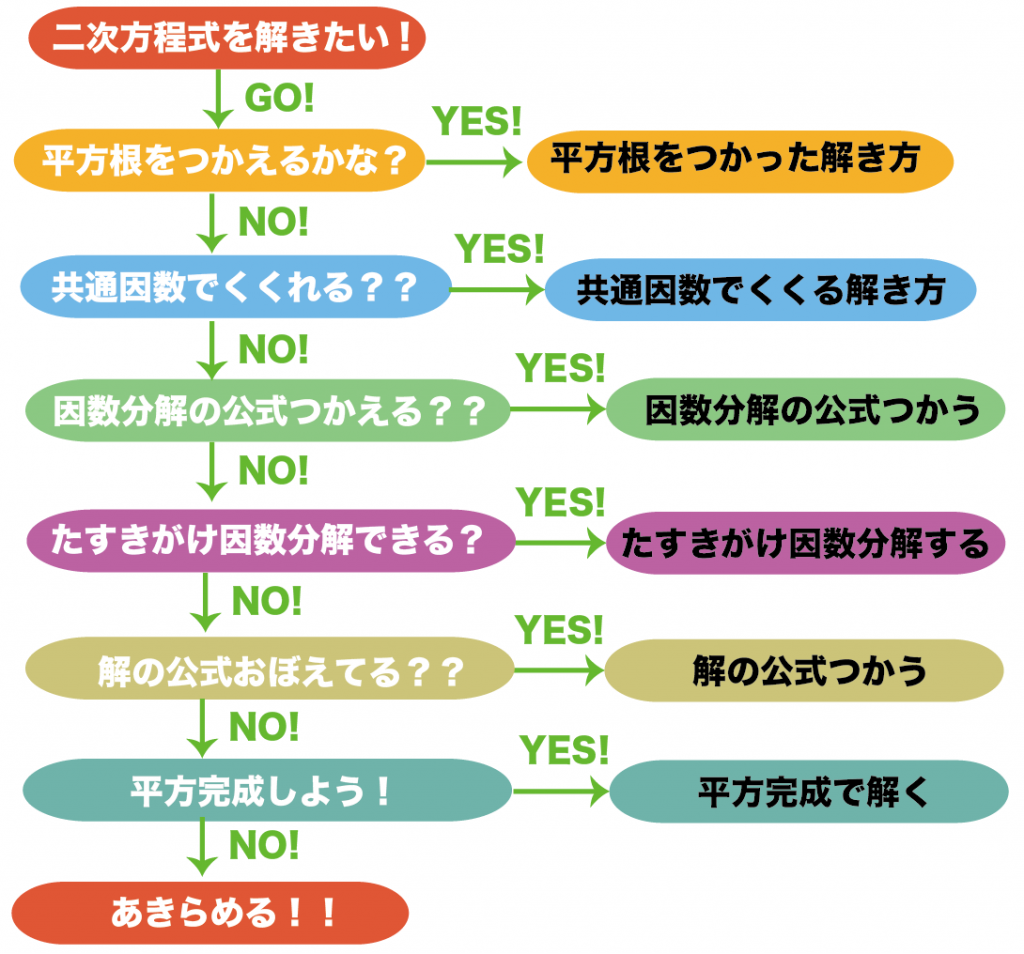
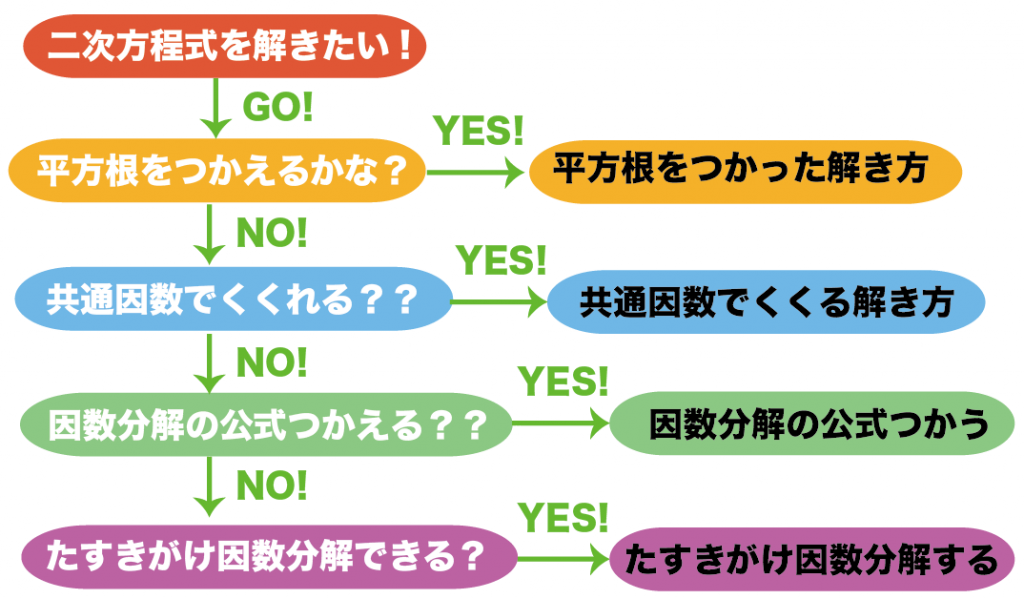
消去法で解き方を選ぶ
だ。
- 平方根の解き方がつかえる??
- 共通因数でくくれる??
- 因数分解の公式をつかえる??
- たすきがけの因数分解できる??
- 解の公式をつかう??
- 平方完成をつかう。
っていう6つの解き方がつかえるか、上から確認していくのさ。
全部の解き方で解けなかったら諦めよう。
それぞれの解き方を確認してみようね。
解き方1.「 平方根でイケル??」
平方根を使えるか確認してみて。
見分け方のコツは1つ。
それは、二次方程式のかたちが
(xをふくむ式)の2乗 = A
になっているか、もしくはソレに変型できるか確認すればいいのさ。
たとえば、
(x-4)² -11 = 0
っていう二次方程式があったとしよう。
こいつはみたかんじ、
(xをふくむ式)² = A
の形にもっていけそうだ。
だって、11を右辺に移項すればいいだけだからね。
このタイプの2次方程式なら、
- 移項
- 平方根を求める
- 移項
の3ステップでとけちゃうよ。
くわしくは、平方根をつかった二次方程式の解き方を復習してみて。
実際に右辺に11を移項して解くと、
(x-4)² -11 = 0
(x-4)² = 11
x – 4 = ± √11
x = 4±√11
になるね。
平方根をつかう解き方がいちばん簡単。
こいつで二次方程式が解けるか、まず確認してみて。
解き方2. 「共通因数でくくれる??」
共通因数でくくれるか確認しよう。
項が2つの二次方程式のとき、つかうことが多いね。
たとえば、つぎの二次方程式とか↓↓
3x² = 7x
この二次方程式の解き方なら、3ステップでとけちゃう。
- 移項する
- 共通因数でくくる
- 一次方程式を解く
⇒くわしくは「因数分解の公式をつかわない二次方程式の解き方」をよんでね。
実際にといてみると、
3x² = 7x
3x² – 7x = 0
x(3x – 7) = 0
x = 0, 3分の7
になるね。
解き方3. 「因数分解の公式つかえる??」
平方根でも解けないし、共通因数でもくくれない・・・・
そんなときは、
因数分解の公式をつかった二次方程式の解き方
だ。
この解き方では、
因数分解の公式で二次式を因数分解して、一次方程式をつくっていくよ。
たとえば、つぎのような問題ね。
x² + 6x = -8
このタイプの二次方程式は3ステップでとけちゃう。
- 移項
- 因数分解の公式つかう
- 一次方程式をとく
⇒くわしくは「因数分解をつかった解き方」をよんでみて。
実際に、さっきの二次方程式の、
x² + 6x = -8
を因数分解の公式をつかってといてみると、
x² + 6x = -8
x² + 6x + 8 = 0
(x +2) (x+4) = 0
x = -2, -4
になるね。
因数分解の公式をよーく復習しとておいてね。
解き方4. 「たすきがけ因数分解つかえる??」
因数分解の公式つかえねえええー
そんなときは、
たすきがけの因数分解がつかえるか粘ってみよう。
たとえば、つぎの二次方程式で活躍するね。
5x² – 11x + 6 = 0
因数分解の公式を使おうとしても・・・・・
ぐっっっっ
使えない!!
ってなるはず。
そういうときは「たすきがけの因数分解」をつかえばいい。
2次方程式の係数を、
- xの2乗の係数
- 定数項
- xの係数
の順番にヨコにかく。
んで、
かけたら「xの2乗の係数」、「定数項」になる数字をたすきがけで考えると、
1 -1 -5
5 -6 -6
———–
5 6 -11
になる。
よって、二次方程式は、
5x² – 11x + 6 = 0
(x-1)(5x-6) = 0
になるね。
今まで通り、一次方程式をといてやると、
x = 1, 5分の6
になるね。
解き方5. 「解の公式をつかう」
因数分解の公式も、たすきがけも無理。
そんなときは最終兵器、
解の公式
をつかおう。
解の公式はどんな二次方程式でもとける公式だったね??
覚えにくいけど、むちゃ便利なんだ。
たとえば、つぎの二次方程式とかね。
x² – 2x -6 = 0
この二次方程式はどうがんばっても、因数分解の公式はつかえない。
たすきがけ因数分解でもかすりもしない。
・・・・・こまった・・・・・・
そんなときは、解の公式の出番だ。
3ステップでとけちゃうよ。
- 解の公式に代入
- √を簡単に
- 約分
二次方程式の係数を公式に代入すると、
x² – 2x -6 = 0
x = 2±√(2² -4×1×-6)/2
= 2±√(4 +24)/2
= 2±√28/2
= 2±2√7/2
= 1±√7
になるね!
これでどんな二次方程式もとけちゃう!
安心だ〜〜
解き方6. 「平方完成をつかう」
もしも、だよ。
もしも、解の公式を忘れたらどうしたいいんだろう??
因数分解の公式もつかえないし、共通因数でもくくれない。
そんなやばいときに役にたつのが、
平方完成による因数分解の解き方
だ。
平方完成は、解の公式を証明するときにつかった解き方だよ。
だから、解の公式を忘れても、解の公式っぽく二次方程式がとけちゃうのさ。
たとえば、さっきの2次方程式、
x² – 2x -6 = 0
を平方完成でといてみようか。
平方完成の解き方は4ステップだよ。
- x以外を右辺に移項
- xをふくむ式の2乗をつくる
- 平方根を求める
- x以外を右辺に移項
この解き方で二次方程式をといてみると、
x² -2x – 6 = 0
x² -2x = 6
x² -2x +1 -1 = 6
(x-1)² = 7
x-1 = ±√7
x = 1 ±√7
になる。
これは解の公式でだした解とおなじ。
解の公式を忘れたときに大活躍だ。
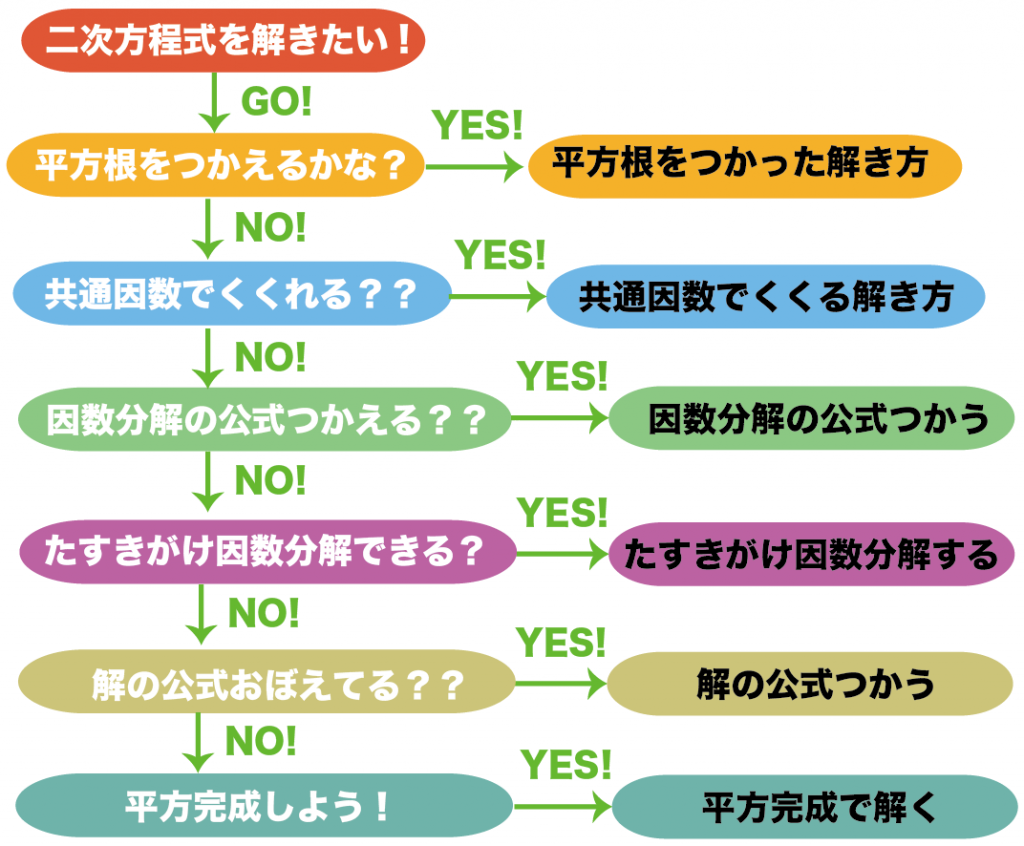
まとめ:二次方程式の解き方のコツは消去法!
二次方程式の解き方はありすぎる。
どれを使ったらいいかわからないね。
心がけてほしいコツは、
消去法で解き方を選んでいく
ということ。
がつかえるか順番に確認していってね。
きっと、どれかしらで解けるはずだよ。
そんじゃねー
Ken