一次関数の変域の求め方を知りたい!
こんにちは!この記事をかいているKenだよ。換気は大事だね。
一次関数の変域の問題ってよくでるよね。
たとえば、つぎのような問題さ。
例題
1次関数y = -3x+7について、xの変域が -1 ≦ x ≦ 9のとき、yの変域を求めなさい。
一次関数の変域とかあきらかにむずそうだけど、
基本をおさえればチョー簡単なんだ。
今日はこのタイプの問題を攻略するためにも、
一次関数の変域の求め方がわかる3ステップ
を紹介するよ。
よかったら参考にしてみて。
一次関数の変域の求め方がわかる3つのステップ
3ステップで変域を求められるよ。
- 変域の端と端を代入する
- 小さい方を左、大きい方を右にかく
- 不等号は同じやつを使う
例題をいっしょにといてみよう!
1次関数y = -3x+7について、xの変域が -1 ≦ x ≦ 9のとき、yの変域を求めなさい。
Step1. 変域の端と端を代入する
まず、変域の端と端を代入してやろう。
たとえば、xの変域が○ ≦ x ≦ □だとしたら、
- x = ○
- x = □
を一次関数に代入すればいいんだ。
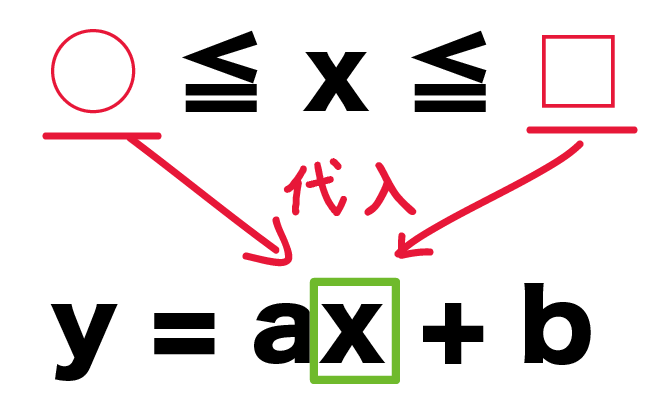
例題でわかっているのはxの変域の、
-1 ≦ x ≦ 9
だね。
この変域の端っこの、
- x = -1
- x = 9
を一次関数 y = -3x + 7 に代入すればいいんだ。

x = -1 を代入すると、
y = -3x + 7
= -3 × (-1) + 7
= 10
になる。
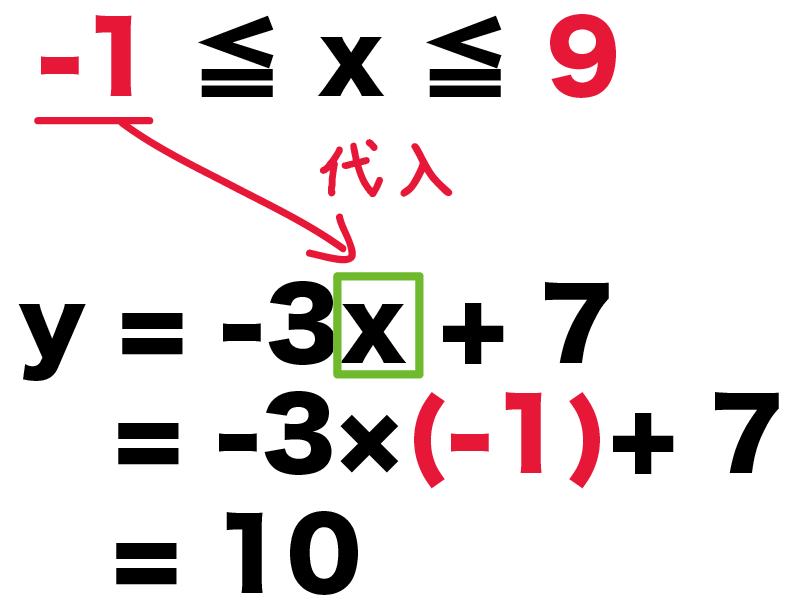
一方、x = 9を代入してやると、
y = -3x + 7
=-3 × 9 + 7
= – 20
になるね。
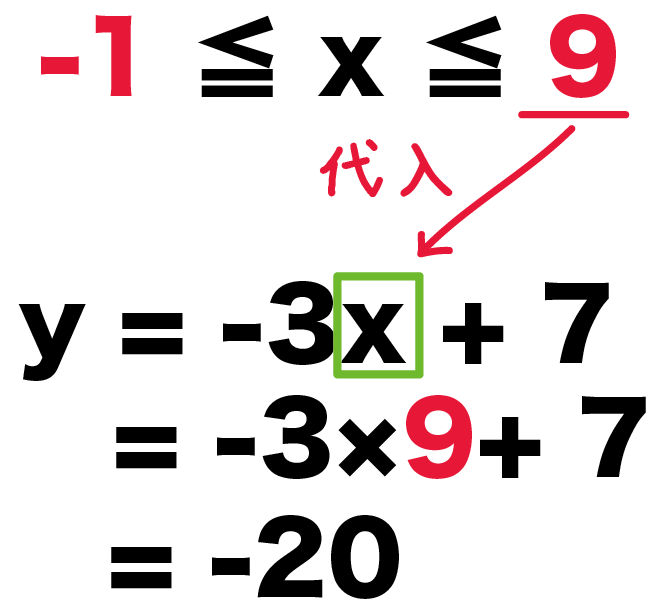
これが第1ステップ!
Step2. 小さい値を左、大きい値を右にかく
さっき計算した2つの値のどちらが大きいのか??
を比べてみよう。
そして、
大きい値を右に、小さい値を左にかくんだ。

例題では、
- y = 10
- y = -20
の2つをゲットできたね??
こいつらを比べてみると、
明らかに10のほうがでかい。
-20のほうが小さいね。
だから、10を右に、-20を左にかいてみて。

これが第2ステップ!
Step3. 不等号でむすぶ!
最後は不等号で結んでみよう。
使う不等号は、
問題でわかってる変域と同じものを使うよ。
例題でいうと、xの変域は「≦」を使ってるよね??
だからyの変域も「≦」を採用するのさ。
例題をみてみよう。
「大きい値」と「小さい値」の間に「y」をかく。

そして、
「小さい値」・「大きい値」と「y」を「≦」で結んでやるのさ。
-20≦y≦10

これでyの変域が求まったよ。
おめでとう。
なぜ一次関数の変域が求められるんだろう??
でもさ、なんで変域が求められるんだろう??
話がうますぎるよね。
じつは、ここだけの話なんだけど、
一次関数がまっすぐだからなんだ。
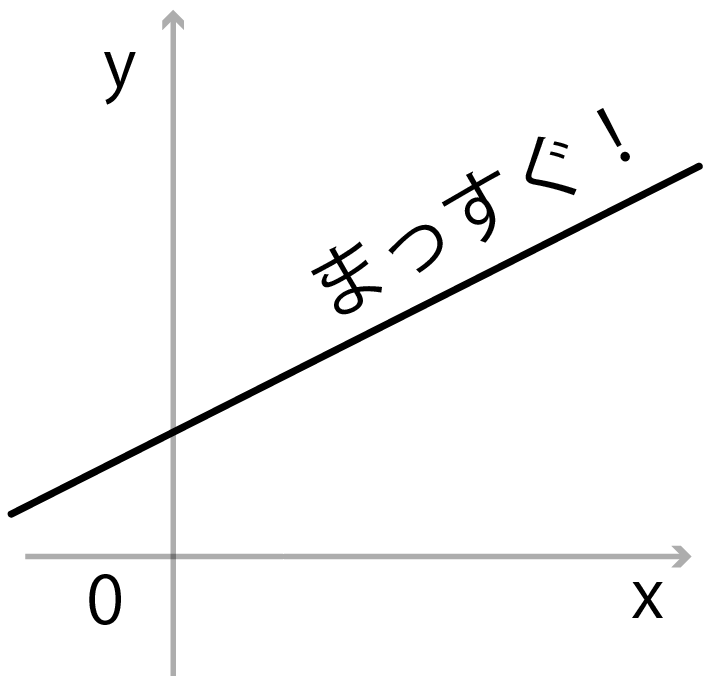
xの変域の端っこと端っこのy座標が、
yの変域の端っこと端っこになっているよ。
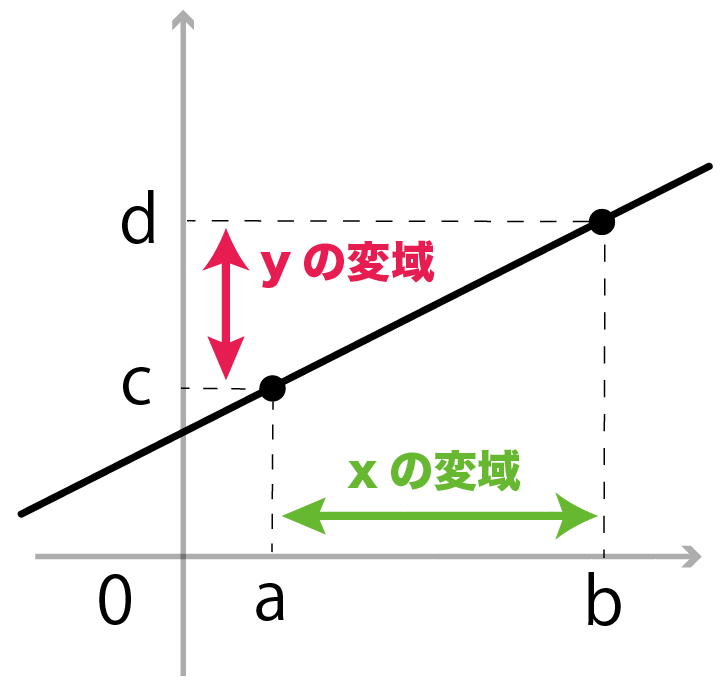
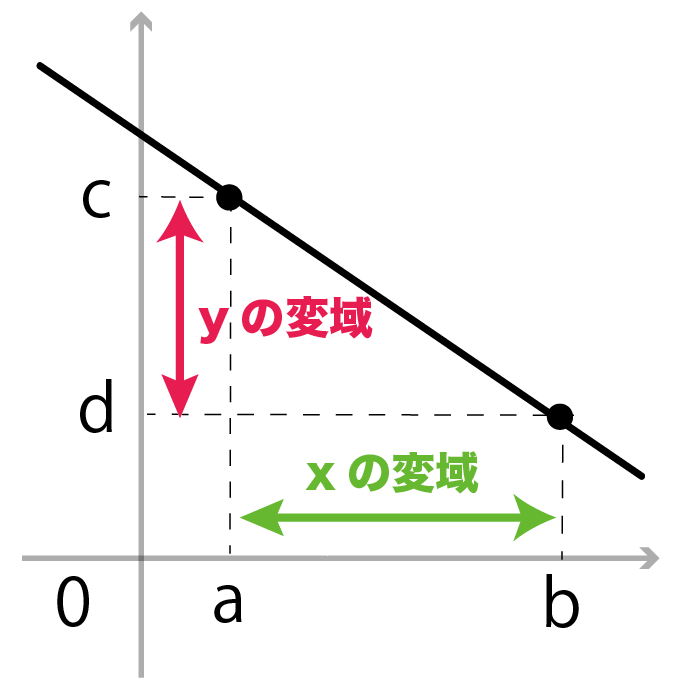
これは傾きがマイナスでも同じだね。
もし、一次関数が波だっていたり、
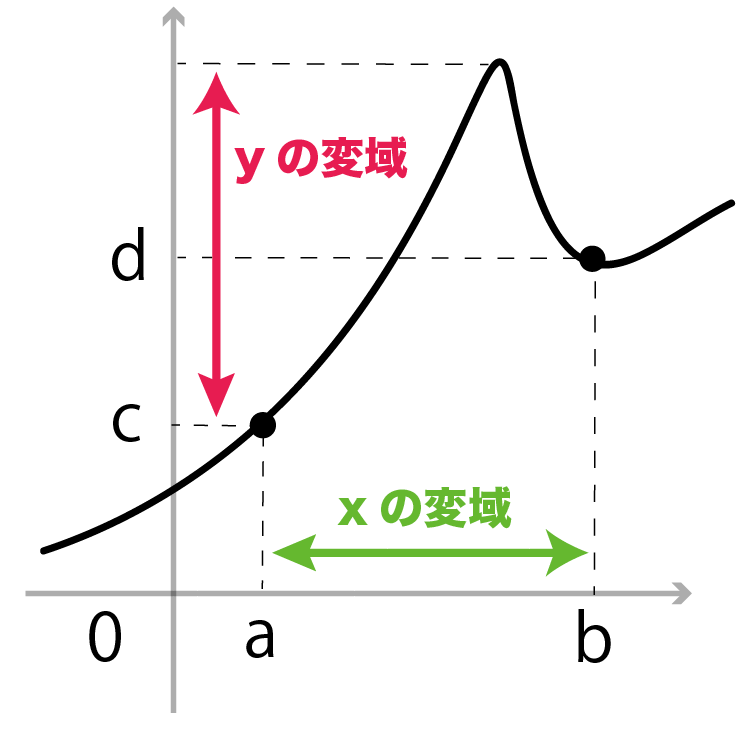
ギザギザしていたら変域はこのやり方だと無理。

なぜなら、変域の端っこ以外に、
最大値とか最小値がいるかもしれないからね。
一次関数がまっすぐだからこそ、変域の端っこが最大値・最小値になる
ってことを覚えておこう!
まとめ:一次関数の変域の求めるためには端をつかえ!
一次関数の変域の求め方は簡単。
- 変域の端っこを2つ代入
- 小さい順に並べ替える
- 不等号で結ぶ
の3ステップでいいんだ。
問題をといて変域に慣れていこう!
そんじゃねー
Ken









