回転移動の書き方がいまいちわからない??
こんにちは、この記事を書いているKenだよ。コーヒーは一日一杯までだね。
中1数学の平面図形で勉強する図形の移動には、
- 平行移動
- 回転移動
- 対称移動
の3種類があるって勉強してきたね。どれもテストで狙われやすいやつばっかだけど、一つ一つ順番にみていこう。

今日は2つめの「回転移動」の書き方をわかりやすく解説していくね。
テスト前に参考にしてみてね。
超わかりやすい!回転移動の書き方
回転移動では回転移動の性質を使うと一発で終わるんだ。
教科書によると、
対応する点は、回転の中心からの距離が等しく、回転の中心と結んでできた角の大きさはすべて等しい
という性質があるって書いてある。
これはどういうことなんだろう??
たとえば、点Oを「回転の中心」として三角形ABCを回転移動させてやるとしよう。
このとき、対応する点BとB’は、
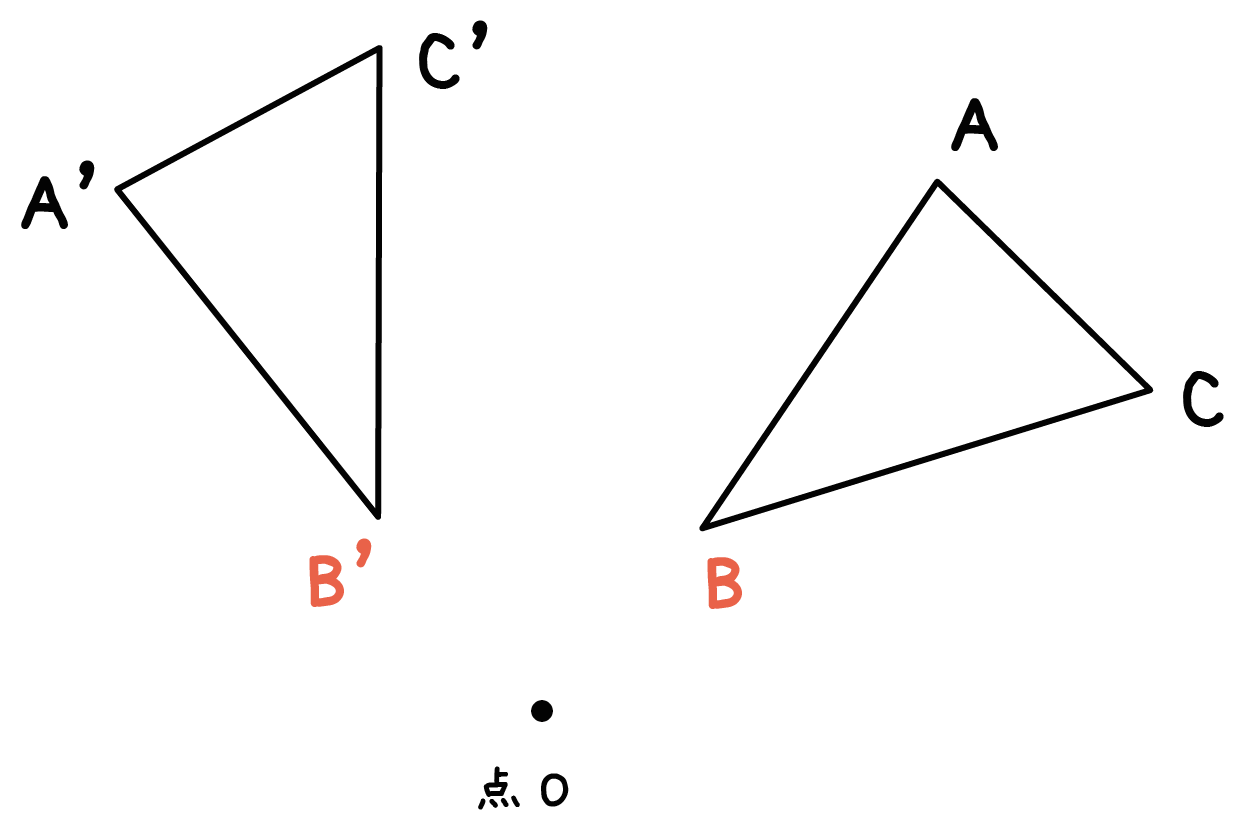
回転中心Oからの距離が等しい ( 線分OB=線分OB’)。
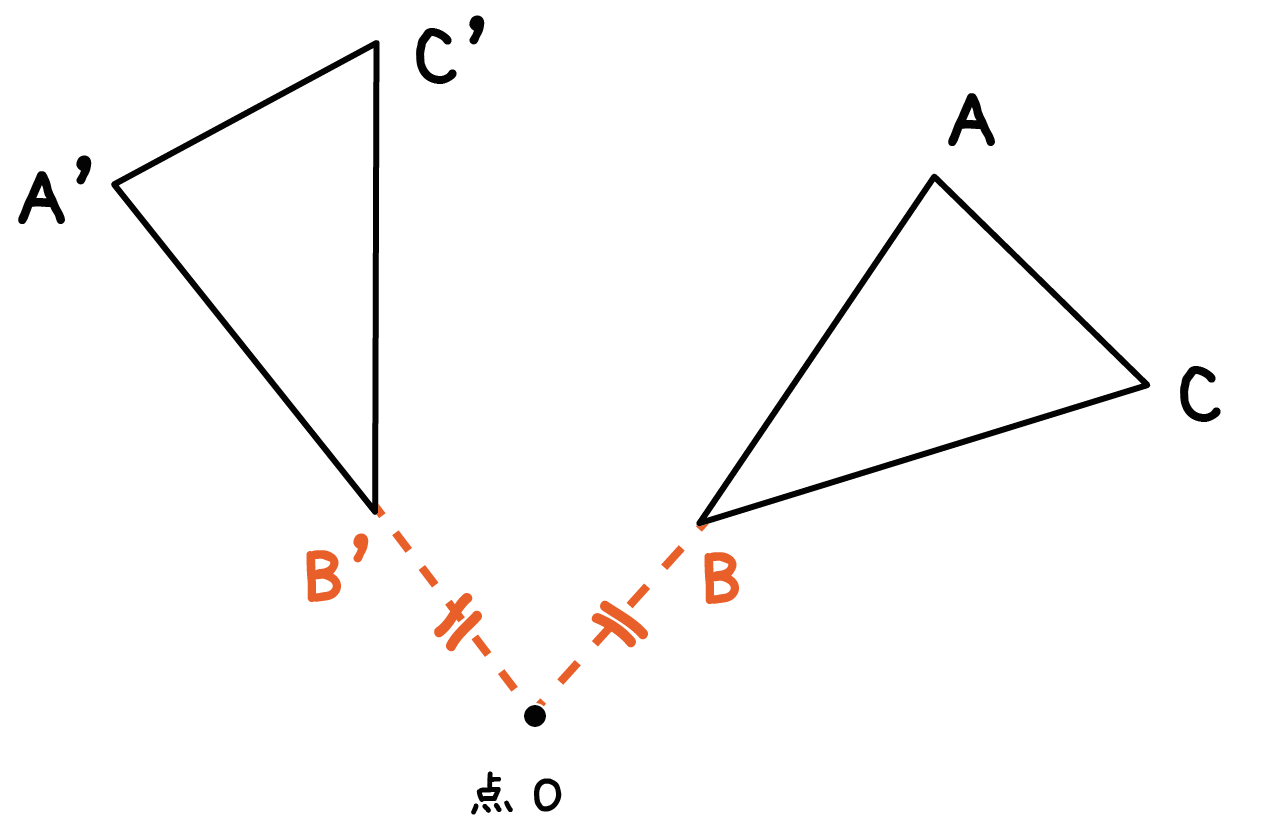
さらに、回転の中心と結んでできた角の大きさ(角BOB’)は、
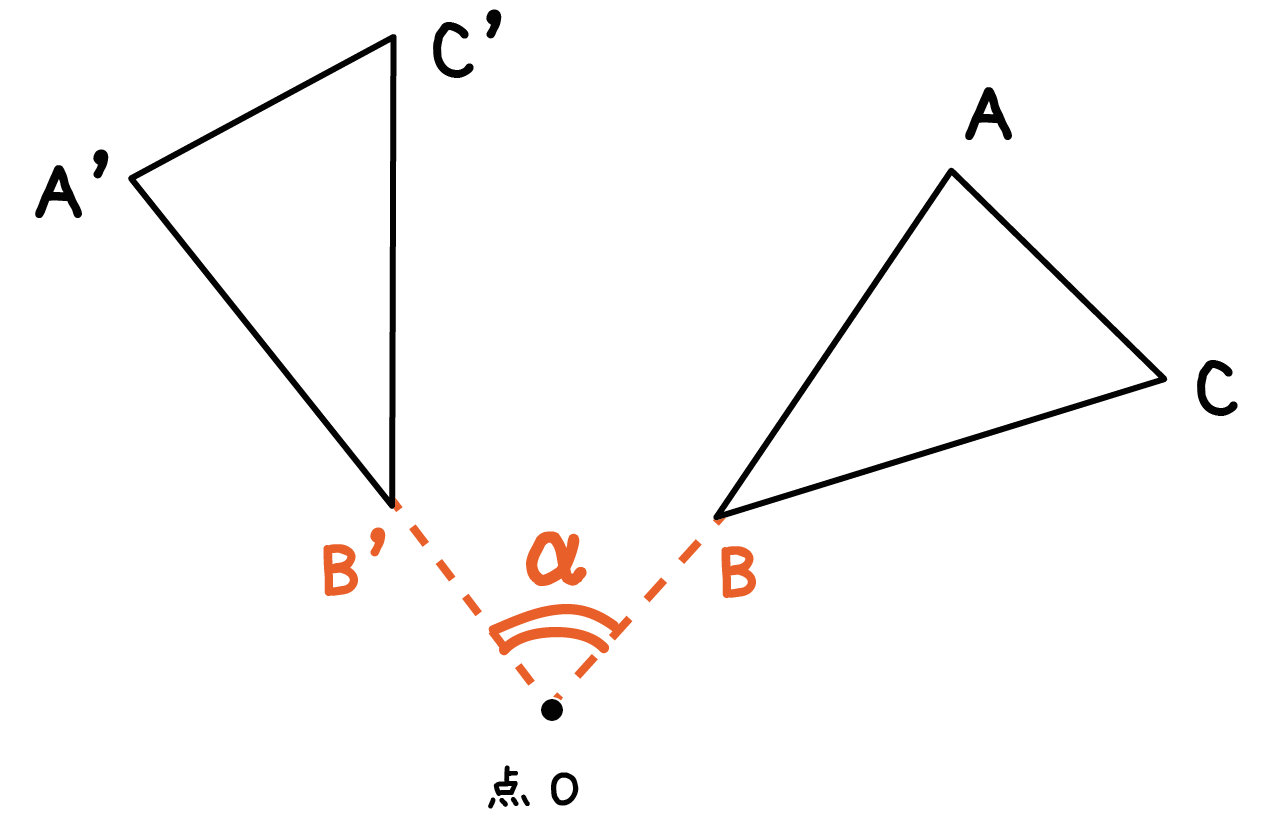
他の頂点の場合のそれとすべて等しい (角BOB’ = 角AOA’ = 角COC’)ってことなんだ。
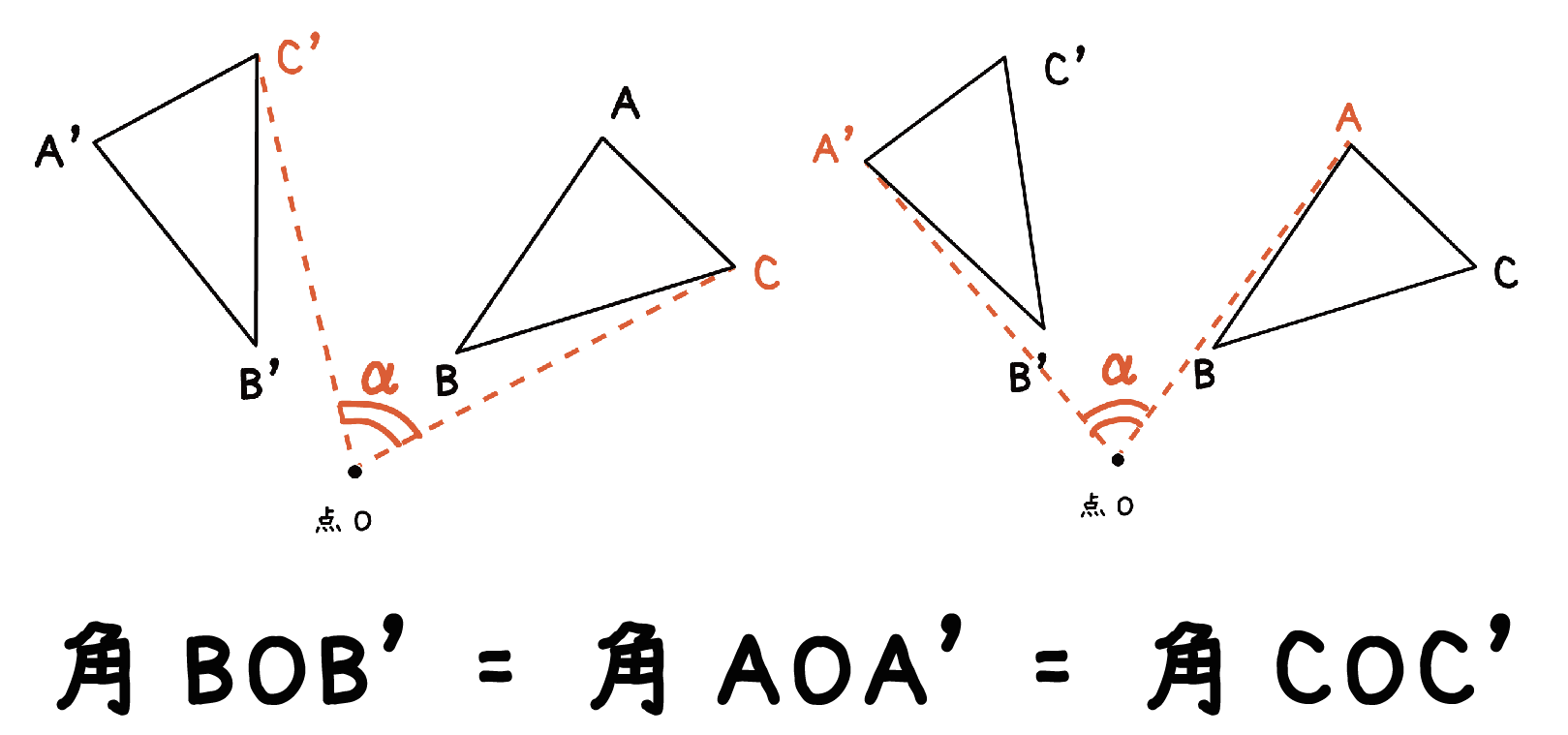
これが回転移動した図形の性質だね。
こいつらをウマくつかってやれば、自由自在に回転移動できるようになるよ。
5つのステップでわかる!回転移動の書き方
それじゃあ、さっそく回転移動の書き方を解説していこう。
よーくみてみると、回転移動はつぎの5つのステップで書けることがわかる。
Step 1. 「回転の中心」と「図形の頂点」を結ぶ
「回転の中心」と「1つの図形の頂点」を結んであげよう。
そして、あたらしい線分をつくってあげるんだ。
たとえば、
三角形ABCをOを中心に反時計まわりに90°回転移動させよ!
っていう問題があったとしよう。
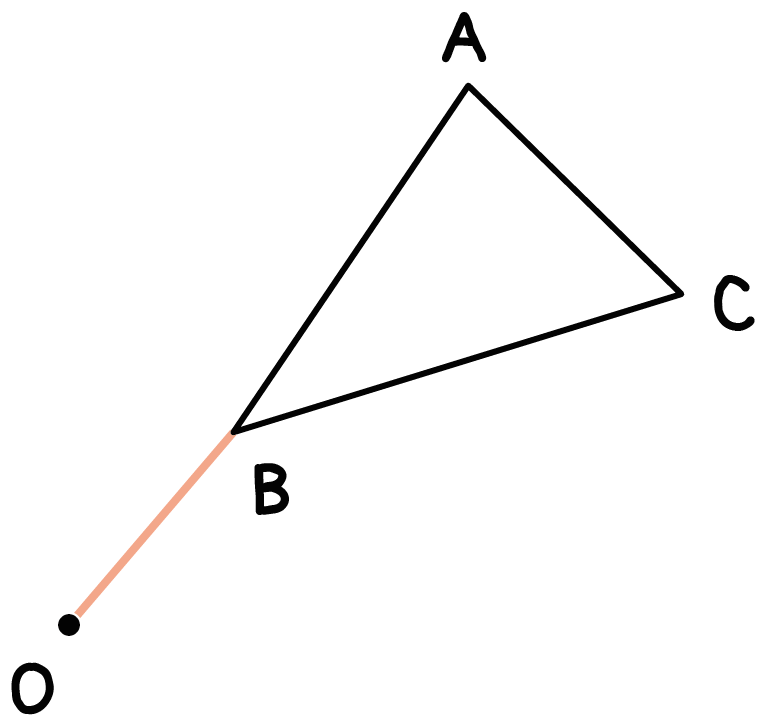
この場合なら、OとBを結んで線分をOBをつくってあげるって感じ。
これが第一ステップさ。
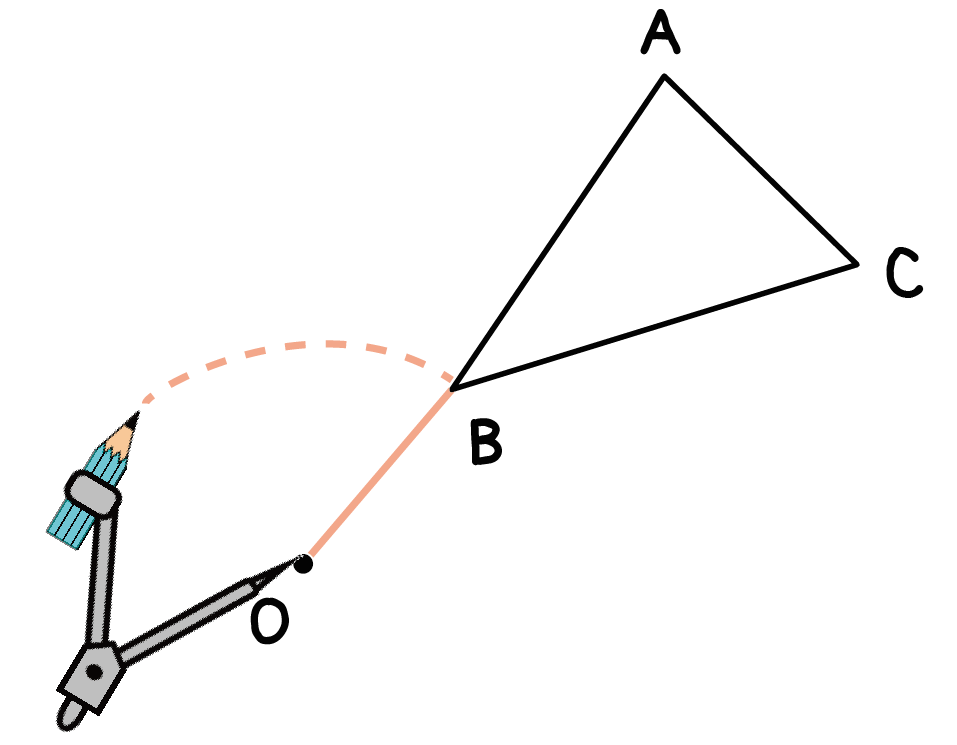
Step 2. 「あたらしい線分」を半径とした「孤」をかく
つぎは、コンパスの出番だ。
ステップ1でつくった線分を半径として、回転の中心から「孤」を書いてみよう!
コンパスの針を「回転の中心O」において、
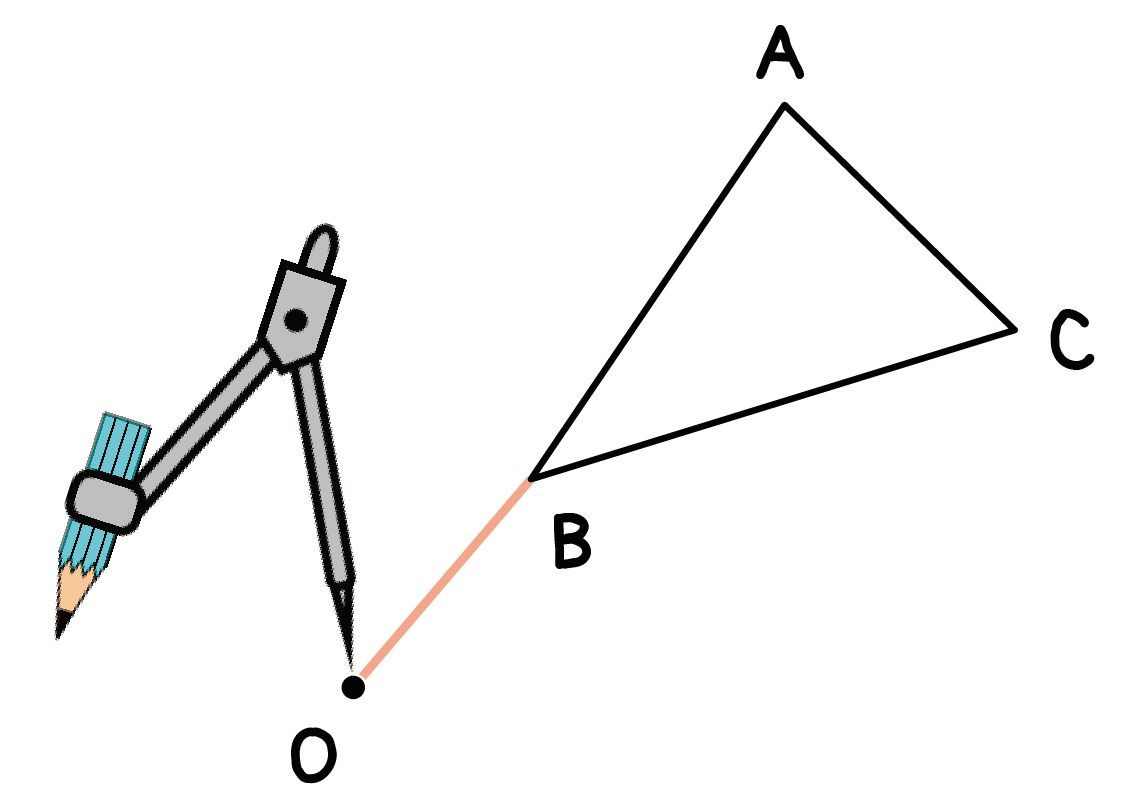
コンパスの鉛筆側を頂点Bにあわせ、
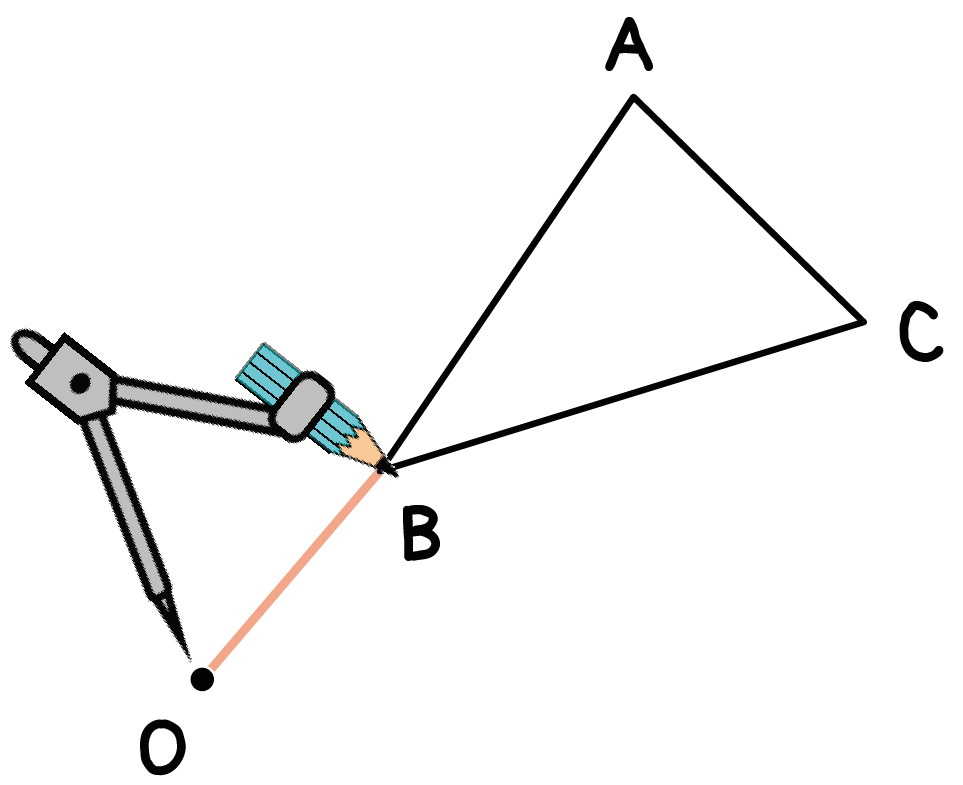
反時計回りに90°以上の孤をてきとーに書いてあげよう。
Step 3. 半径から「回転させる角度」を測る
つぎは、回転させる角度をはかっちゃおう。
この例題では、反時計まわりに90°図形を回転移動させる問題だから、
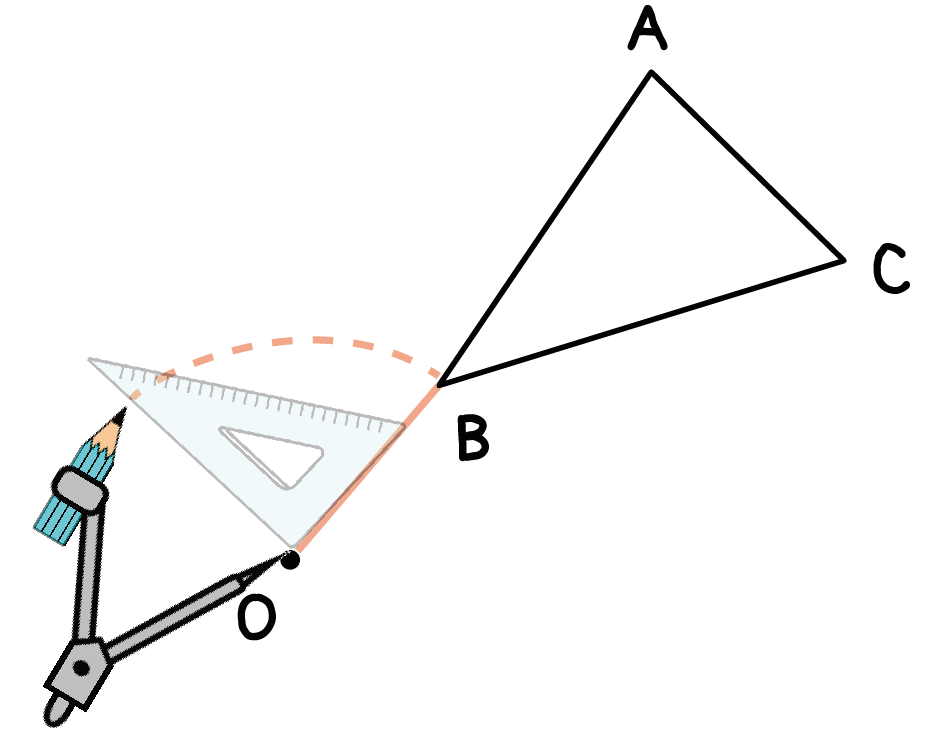
孤の半径となっている線分OBから反時計回りに90°の角度をはかってあげよう。
角度を測る方法としては、
- 分度器をつかう(0~180°まで対応)
- 三角定規(30°、45°、60°、90°など対応可能)
- コンパス(垂線の作図で90°、垂線と角の二等分線をつかって45°)
などがあるよ。もし、分度器を使うな!って問題でいわれたら、三角定規とコンパスでねばってみよう!!
Step4. 孤の上に回転させる角度で「点」をうつ
回転させる角度を測った??
あとは、その角度上の孤に「点」をうってあげるだけ。
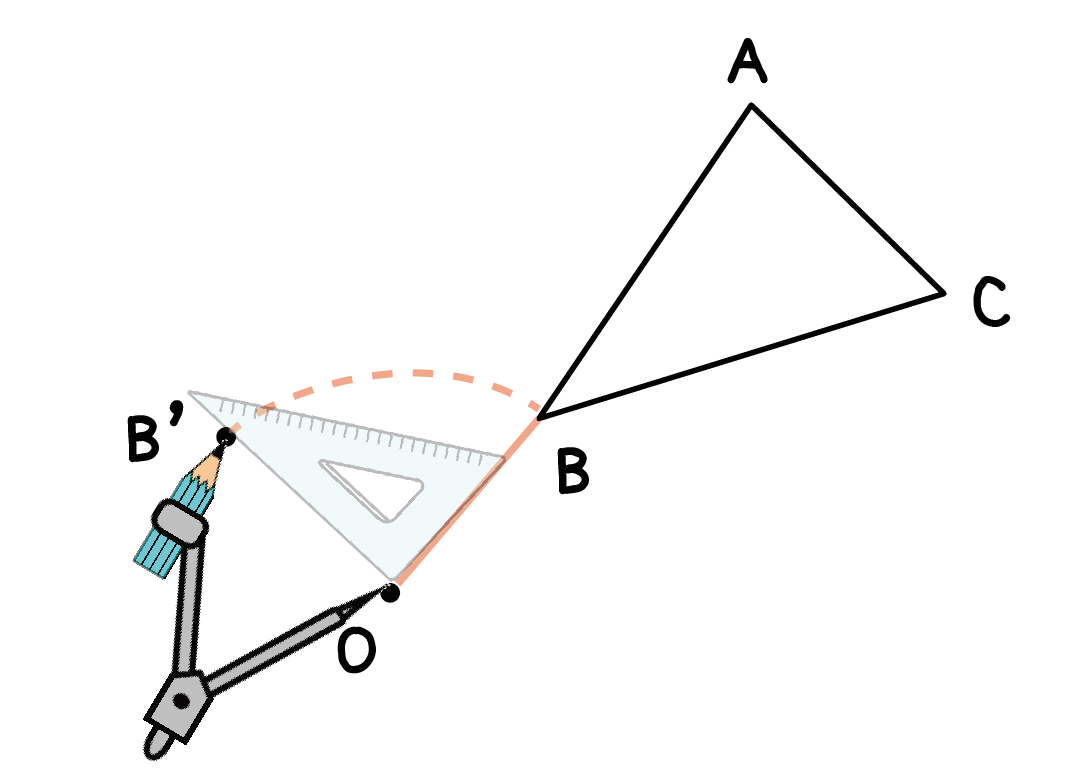
さっきの例でいえば、
孤の90°の角度上に点B’がうてる。
Step 5. 「1~ 4の手順」を各頂点で繰り返す
同じ手順をのこりの頂点でもやってみよう。
この例題だと、点AとCだ。
点Bと同じように、
- 線分をつくって
- 孤をかいて
- 角度はかって
- 点をうつ
という動作を繰り返せばいいんだ。
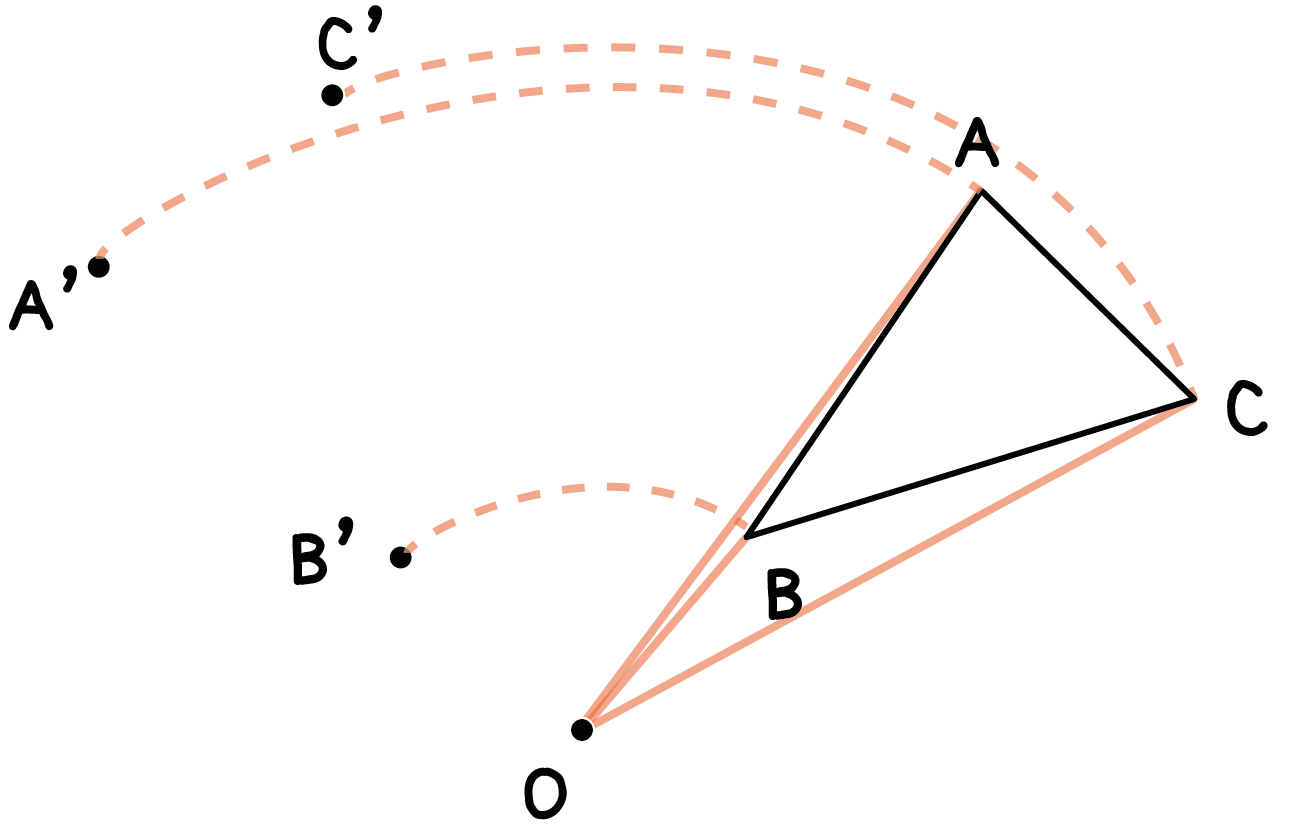
そんで、ぜんぶ書き終えたら結んでみよう!
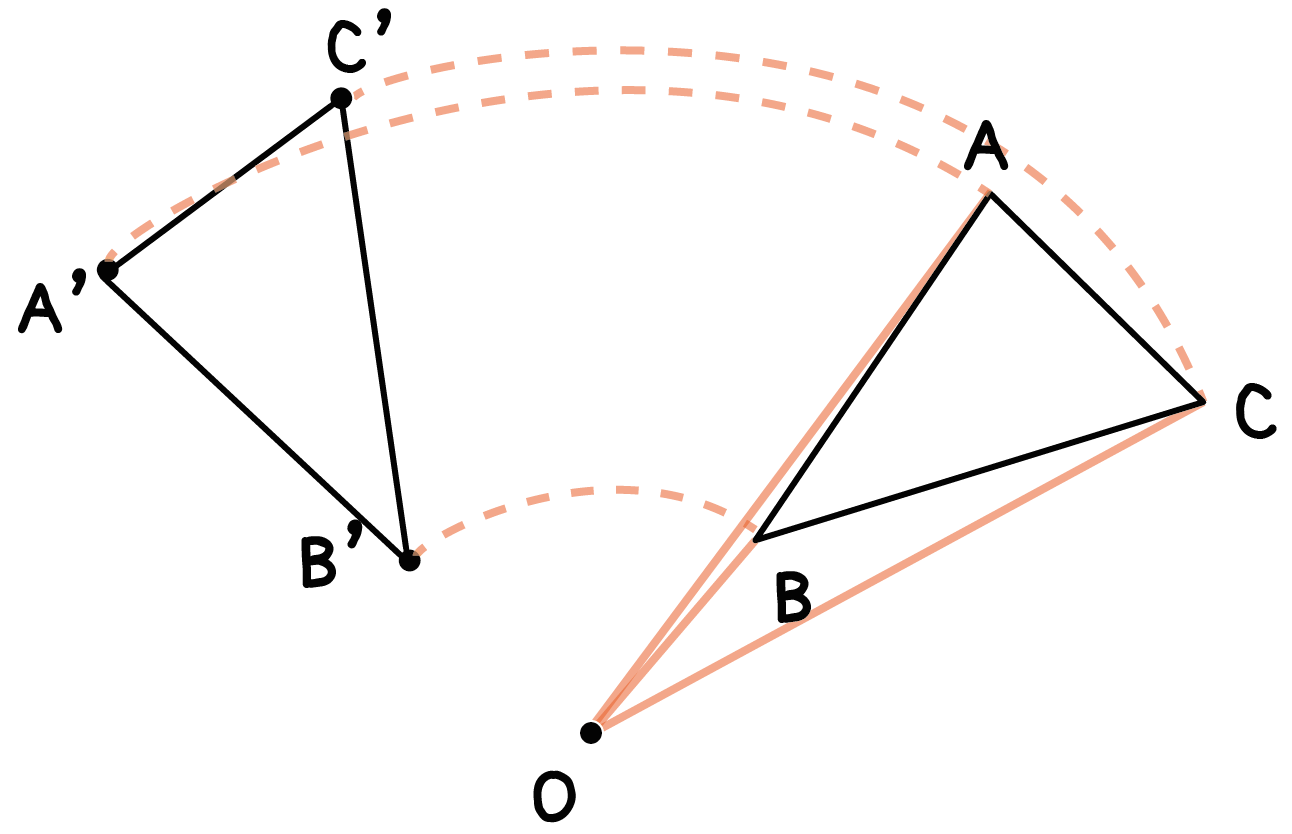
この新しくできた三角形A’B’C’が「回転移動した図形」だ!
やったね! 疲れたー
まとめ:回転移動の書き方はたった5つのステップである
回転移動の書き方はどうだった???
コンパス、三角定規、分度器っていう3つのアイテムでチョちょいのちょい。
テストでも落ち着いて図形を移動させていこう!
次回は対称移動の書き方を解説していくね。
そんじゃねー
Ken









