くじ引きの確率の問題の公式ってあるの？？

こんにちは！この記事をかいているKenだよ。オレンジは目覚めにいいね。

 

中学数学の確率でたまーに、

くじ引きの問題

ってあるよね？？

たとえば、

6本のうち当たりくじが4本あるとき、当たりくじをひく確率を求めなさい。

っていう感じで。

 

 

 

こういう問題はむずかしそう。

だけど、公式をつかえば5秒で確率を計算できるんだ。

 

 

くじ引きの確率を5秒で計算できる公式

つぎの公式で計算できるよ。

 

（当たりor はずれを引く確率）

＝（当たりorはずれの本数）÷（残りのくじ本数）

 

あ、くじを1回引く場合だけどね。

 

 

 

 

 

たとえば、6本のうち2本が当たりくじだとする。

 

 

くじを1回ひいて「当たりくじ」がでる確率を求めてみよう。

 

• 当たりくじ： 2本
• ぜんぶのくじ数：6本

だよね。

公式をつかってやると、

（当たりくじを引く確率）
＝（当たりくじの本数）÷（ぜんぶのくじ数）
＝　2 ÷ 6
= 3分の1

になるんだ。

 

 

 

 

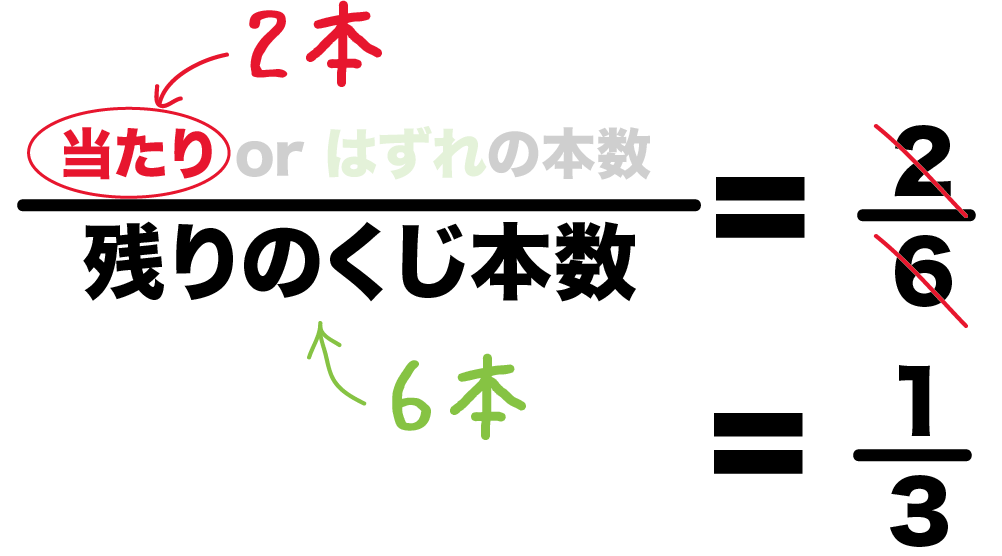
「当たりくじの数」を「残りのくじ数」でわるだけ。

簡単でしょ！？

 

 

なぜ、くじ引きの確率が公式が使えるんだろう！？

でもさ、なんで公式が使えるんだろう？？

ちょっと怪しいよね。。

この公式がつかえる理由は、

1つ1つのくじ引きを区別しているから

なんだ。

 

「当たりくじ」たちはすごく似ている。

ぶっちゃけ、どれも同じ。

 

 

 

だけど、確率を計算するときは同じじゃだめなんだ。

こいつらを区別しないといけない。

 

たとえば、

• あたりくじ、その1
• あたりくじ、その2

みたいな感じでね。

 

 

当たりくじだけじゃなくて、はずれでも同じ。

見た目は同じだけど、別ものとしてあつかってやろう。

 

 

 

だから、「当たりくじのひき方」だったら、

• 当たりくじ(1)
• 当たりくじ(2)

の2通りがあるはず。

 

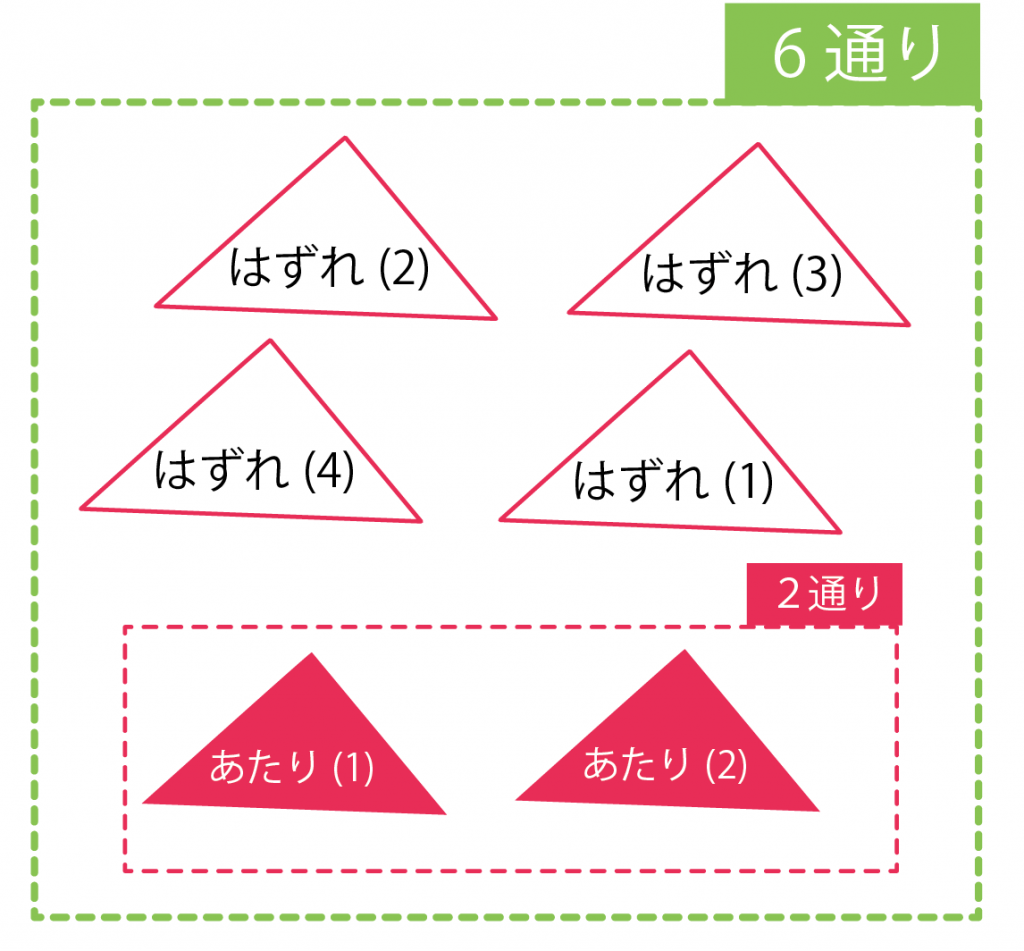
ぜんぶのくじ引きは、6通りのひきかたがある。

だから、確率の公式をつかってやれば、

（当たりくじの場合の数）÷（すべてのくじ引きの場合の数）

= 2÷6
=3分の1

になるんだ。

 

おめでとう！

くじ引きの確率もマスターだね。

 

 

まとめ：くじ引きの確率の問題は公式で1発！

くじ引きの確率の問題？？

おそれることはない。

ただ、公式で計算すればいいんだ。

くじの1つ1つが区別されるっておぼえておこう。

そんじゃねー

Ken