円錐の高さの求め方がわからない！
こんにちは！この記事をかいているKenだよ。トマトはヘルシーだね。
円錐の高さを求める問題
ってたまにでるね？？
こいつは中1数学でならった
と、
中3でマスターする「三平方の定理」でといていくんだ。
かなりくせ者だね。
今日はコイツを攻略するために、
円錐の高さの求め方がわかる3ステップ
を解説していくよ。
よかったら参考にしてみて。
円錐の高さの求め方がわかる3ステップ
3ステップで求められるよ。
- 側面の弧の長さを求める
- 底面の半径をだす
- 三平方の定理をつかう
例題をといてみよう！
例題
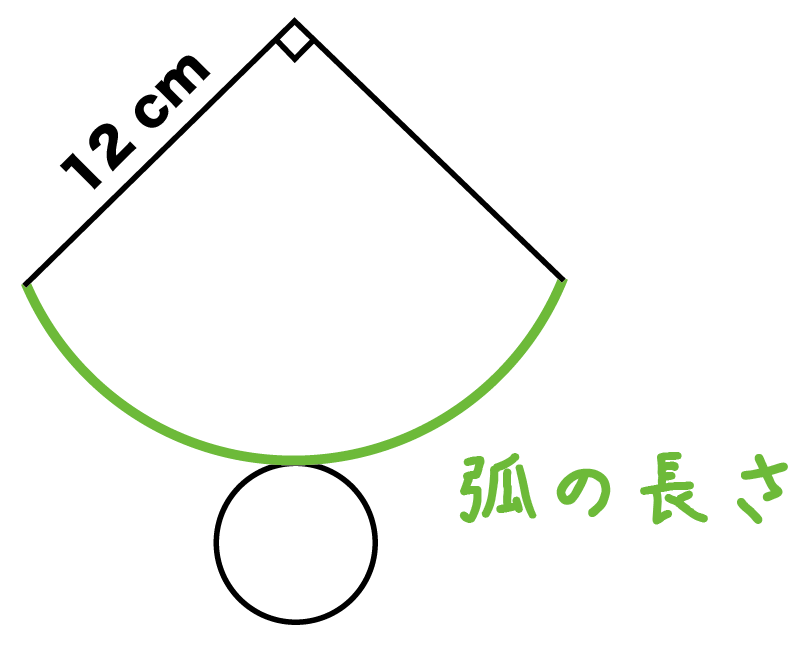
下の図は円錐の展開図です。円錐の側面が、半径12cm、中心角90°のとき、円錐の高さを求めなさい。
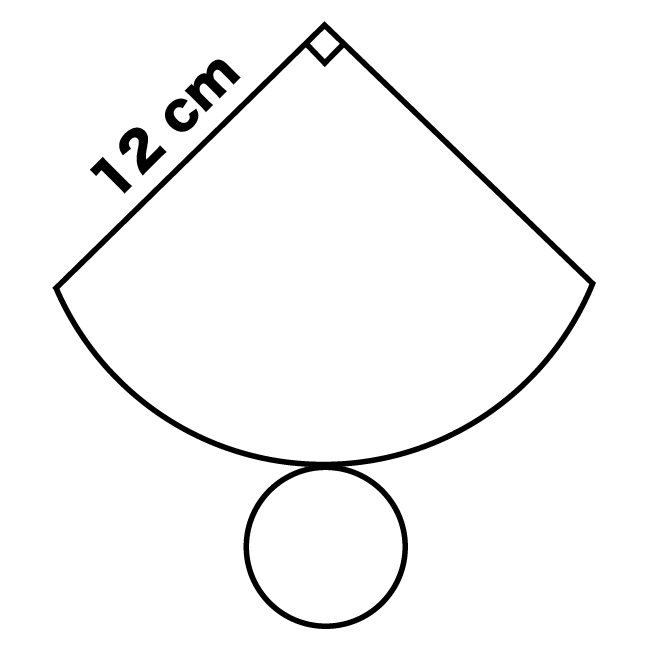
Step1. 弧の長さをだす
まずは円錐の側面の、
弧の長さ
を計算しよう。
えっ。
弧の長さの出し方がわからないって？？
円錐の側面は「おうぎ形」だったね。
だから、
をつかえばいいんだ。
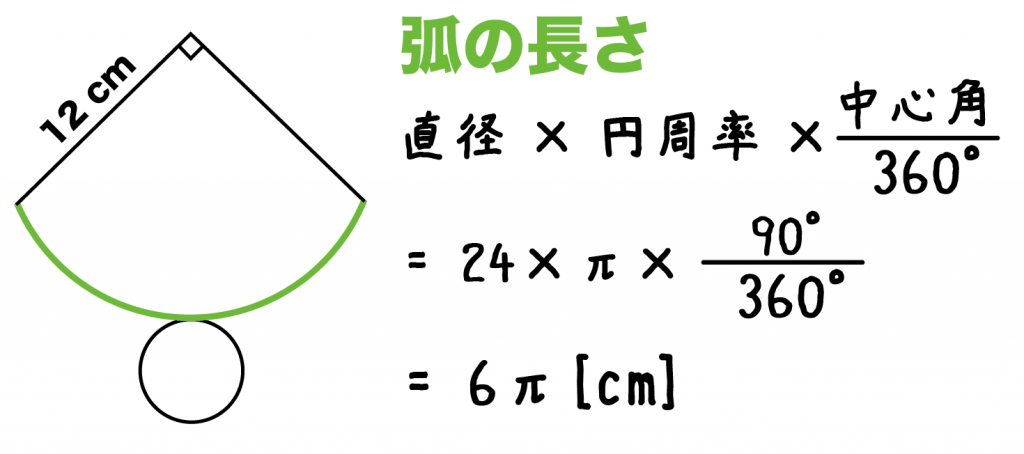
扇形の弧の長さは、
直径×円周率×中心角÷360
で計算できたね。
例題の扇形は、
- 半径： 12cm
- 中心角：90°
だ。
公式をつかってみると、
（扇形の弧の長さ）
= （直径）×（円周率）×（中心角）÷ 360
= 24 × π × 90 ÷ 360
= 6π
になる。
これが第1ステップ！！
Step2. 底面の半径を計算する！
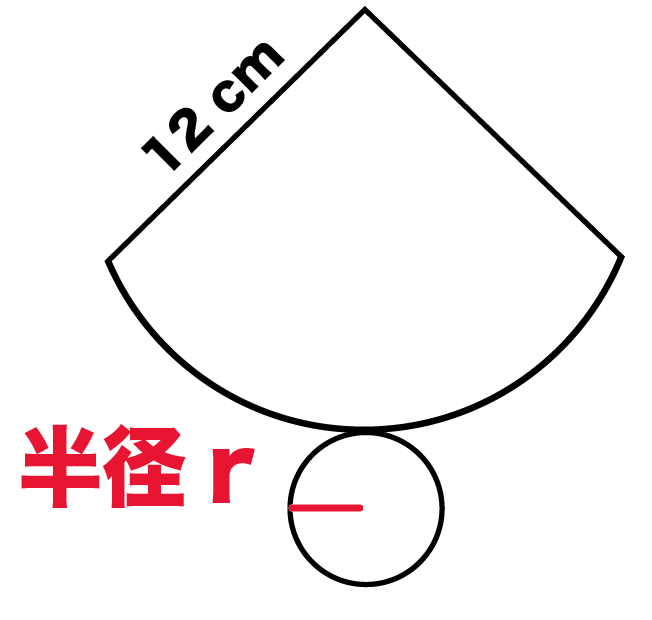
つぎは円錐の底面に注目。
半径を計算するんだ。
半径の長さをrとして方程式をたてるよ。
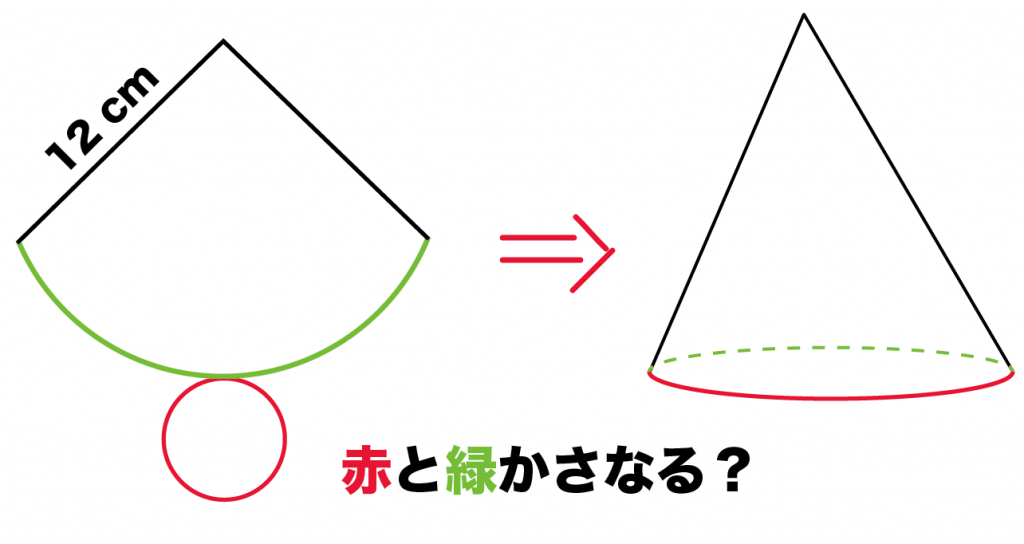
円錐の展開図をくみたてると、
「底面の円」
と
「側面の弧」
がかさなるでしょ？？
だから、
（底面の円周の長さ）＝ （側面の扇形の弧の長さ）
っていう方程式がつくれるんだ。
（底面の円周の長さ）＝ （側面の扇形の弧の長さ）
（直径×円周率）＝ （直径×円周率×中心角÷360°）
2 × r × π ＝ 2 × 12 × π × 90° ÷ 360°
r = 3 [cm]
になるね！
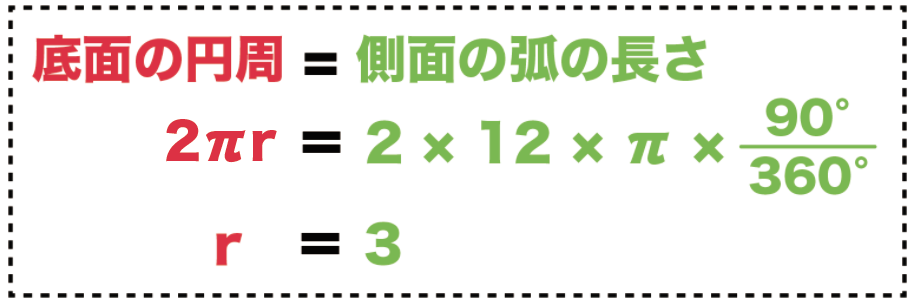
底面の半径は「3 cm」ってことさ。
第2ステップ終了！
Step3. 三平方の定理をつかう！
最後は三平方の定理をつかうよ。
円錐をナイフできってやると、
直角三角形がでてくるでしょ？？
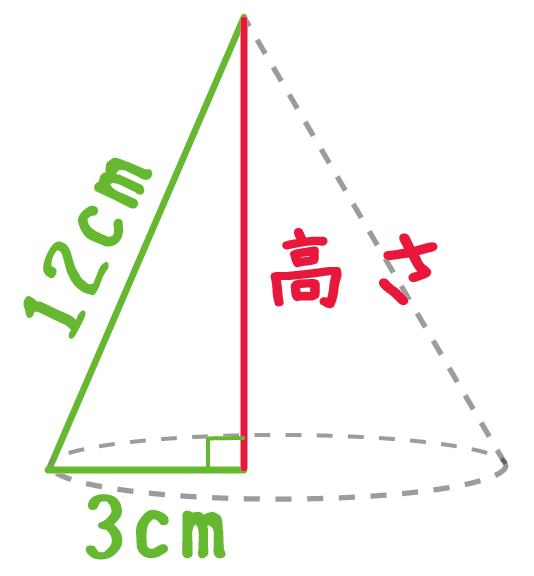
三平方の定理をつかうと、
（円錐の高さ）
＝ √（斜辺の二乗）- （その他の1辺の二乗）
＝ √ （12）² – 3²
＝ √135
になるね。
おめでとう。
円錐の高さもゲットだね！
まとめ：円錐の高さの求め方は三平方の定理でとどめ！
円錐の高さを求めるのはむずそう。
だけど、基本をおさえれば大丈夫。
- 弧の長さをだす
- 底面の半径をだす
- 三平方の定理つかう
の3ステップで、
じゃんじゃん求めていこう。
そんじゃねー
Ken
