中央値(メジアン)の求め方がわからない??
こんにちは!この記事をかいているKenだよ。チャーハン炒めまくったね。
中学数学の資料の活用では、
中央値(メジアン)
を勉強するよね。
この単元はけっこうムズい。
メジアンとかモードとかわけのわからんカタカナでてくるし、
正直、わからんこと多いはずだ。
そこで今日は、苦手を克服してもらうために、
中央値(メジアン)の求め方がわかる3ステップ
を紹介するよ。
メジアンを出したいときに読んでみて^^
中央値(メジアン)の求め方・出し方がわかる3ステップ
さっそく中央値を求めていこう。
つぎの3ステップで計算できちゃうんだ。
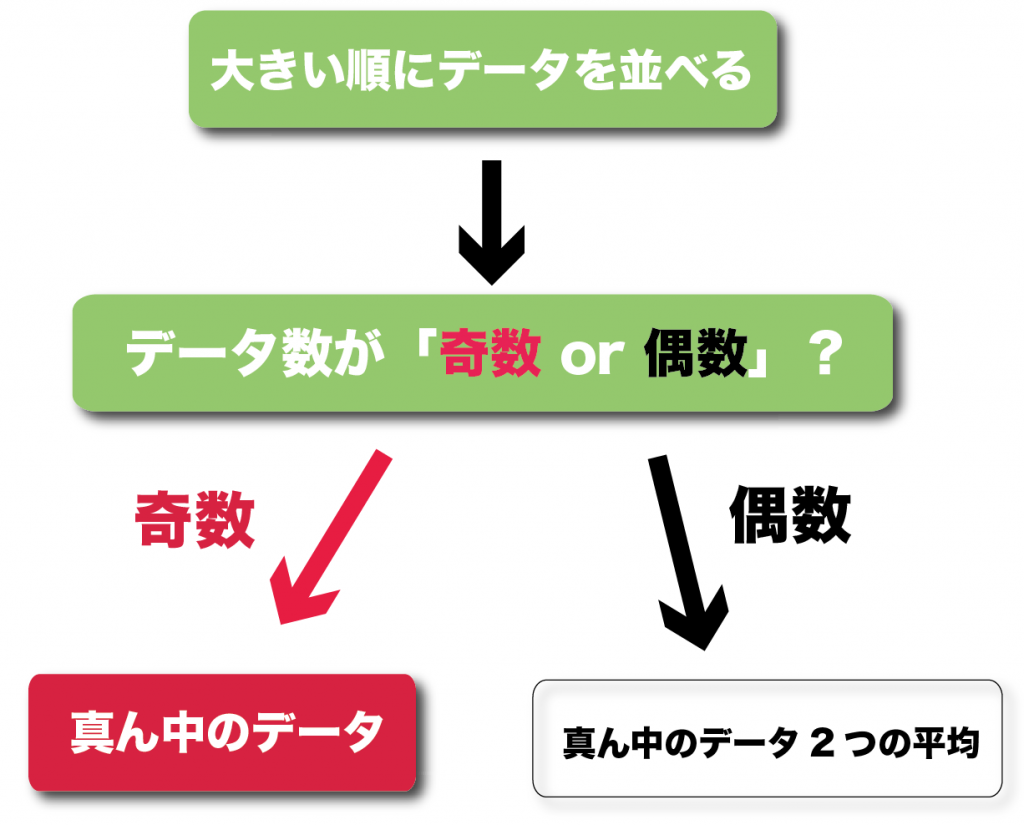
- 大きい順にデータを並べる
- データ数が「偶数または奇数」か調べる
- 真ん中の値をみつける
つぎの例題をといてみようね。
例題
下の表は、ある中学校の10人の生徒の砲丸投げの記録のデータです。10人の生徒の砲丸投げの中央値を求めなさい。
- Aさん: 7 m
- Bさん: 4 m
- Cさん: 5 m
- Dさん: 9 m
- Eさん: 11 m
- Fさん: 3 m
- Gさん: 4 m
- Hさん: 12 m
- Iさん: 6 m
- Jさん: 7m

Step1. 大きい順に並びかえる!
データを並びかえてみよう!
上から大きい順番にならびかえるんだ。
砲丸投げでスゴかったやつから順番にならびかえると、
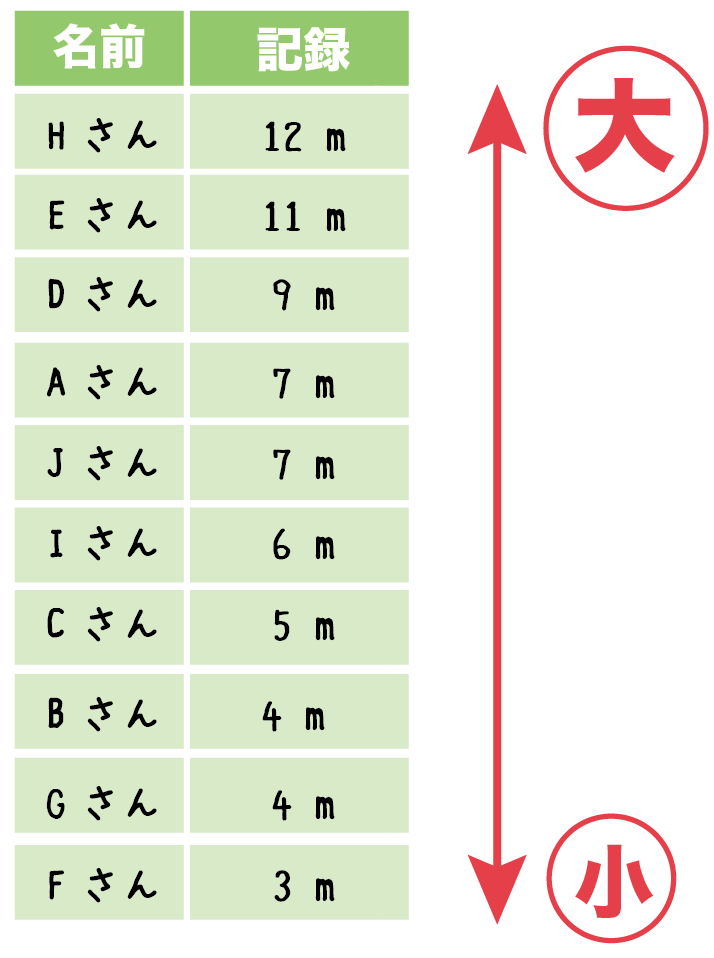
こんな感じになるね↓↓
- Hさん: 12 m
- Eさん: 11 m
- Dさん: 9 m
- Aさん: 7 m
- Jさん: 7 m
- Iさん: 6 m
- Cさん: 5 m
- Bさん: 4 m
- Gさん: 4 m
- Fさん: 3 m
Step2. データ数は「奇数or偶数」??
データの数をかぞえよう!
1、2、3、4・・・・
って感じでね!
ここでみてほしいのが、
データ数が「奇数」なのか「偶数」なのか???
ということだよ。
例題のデータは、10人の砲丸投げ記録だったね??
ってことは、
ぜんぶで10つのデータがあるわけだ。
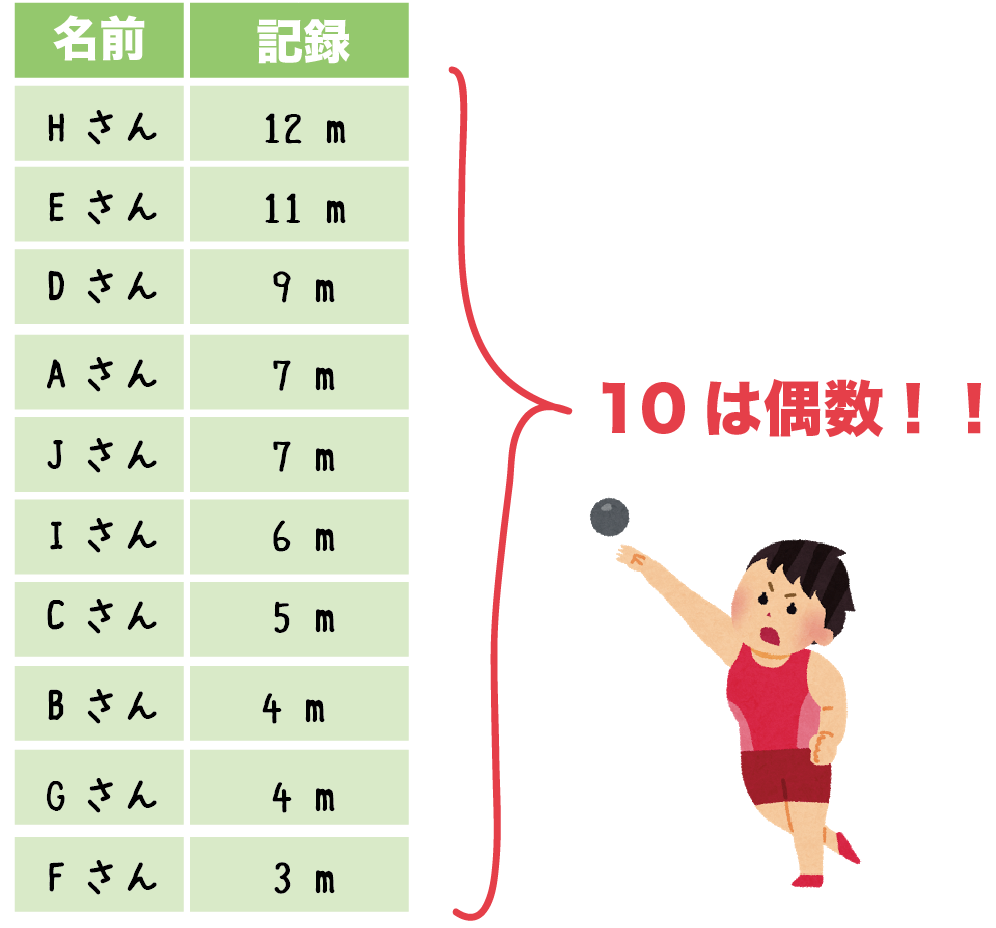
つまり、データ数は偶数だ!
Step3. 真ん中のデータをさがす
中央値は、
大きい順(or 小さい順)に並び替えたときの真ん中のデータ
のことだったね??
並び替えて真ん中のデータをえらべばいいわけさ。
ただ、注意してほしいのが、
データ数が「奇数」か「偶数」かによって真ん中の値の選び方がちがう
ってこと。
データ数が「偶数」のときは、
2つの真ん中の平均値をだすんだ。

真ん中の値は、
- Jさん: 7 m
- Iさん: 6 m
だね?
こいつらの平均をとってやると、
{(Jさんの記録) + (Iさんの記録)}÷2
= (7 + 6 ) ÷2
= 6.5
になる。
これが中央値だよ!

※データ数が「奇数」のときはどうする??
データ数が奇数のときはどうすんのって話だよね?
ちょっと気になる。。
さっきの例題で、Fさんが風邪で休んだとしよう。
すると、
砲丸投げをした生徒は9人になる。

つまり、データ数が奇数になるわけ。
奇数のときは偶数のときより簡単!
真ん中の数がそのまま「中央値(メディアン)」になるからね。
例題でいうと、
ちょうど真ん中の「7」がメジアンだ。
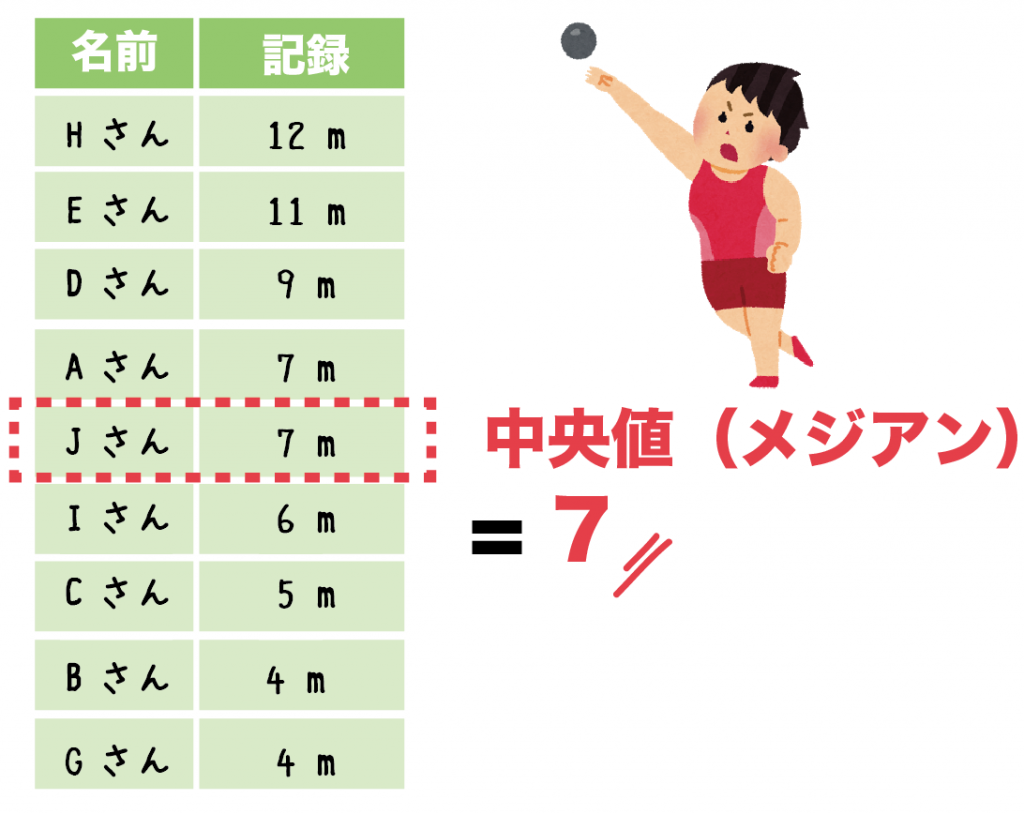
これで奇数のときも偶数のときも大丈夫だね!
まとめ:中央値の出し方は2通りある!
中央値の出し方には、
- データ数が「偶数」のとき
- データ数が「奇数」のとき
の2通りあるんだ。
- 大きい順にデータを並べる
- データ数が「偶数または奇数」か調べる
- 真ん中の値をみつける
という3ステップをおぼえちゃおう。
中央値なんてちょちょいのちょいさ!
そんじゃねー
Ken









