円錐の展開図の書き方・作図方法がわからない！！

こんにちは、この記事をかいているKenだよー。緑ペンがほしいね。

 

円錐の表面積を求めなさいっ！

っていう問題はけっこうでる。先生はだしたくなる。

だけど、

円錐の表面積を求めるの

はけっこうムズい。できれば避けて通りたいね・・・・

このピンチを助けてくれるのが、

円錐の展開図を作図する

ということなんだ。

円錐を切り取ったら円錐はどんな紙切れになるのか？？

円錐の展開図の書き方を知っていると、いとも簡単に表面積まで計算できちゃうんだ。

今日は、その、

円錐の展開図の書き方・作図法

をわかりやすく解説していくね。

 

 

円錐の展開図の書き方・作図の4つのステップ

さっそく、円錐の展開図の書き方をみていこう。だれでも簡単にかけるように4つのステップで作図していくよー

つぎの例題をみてみよう！

 

例題

つぎの円錐の展開図を作図してね!!（直径4cm、母線の長さ6cm）

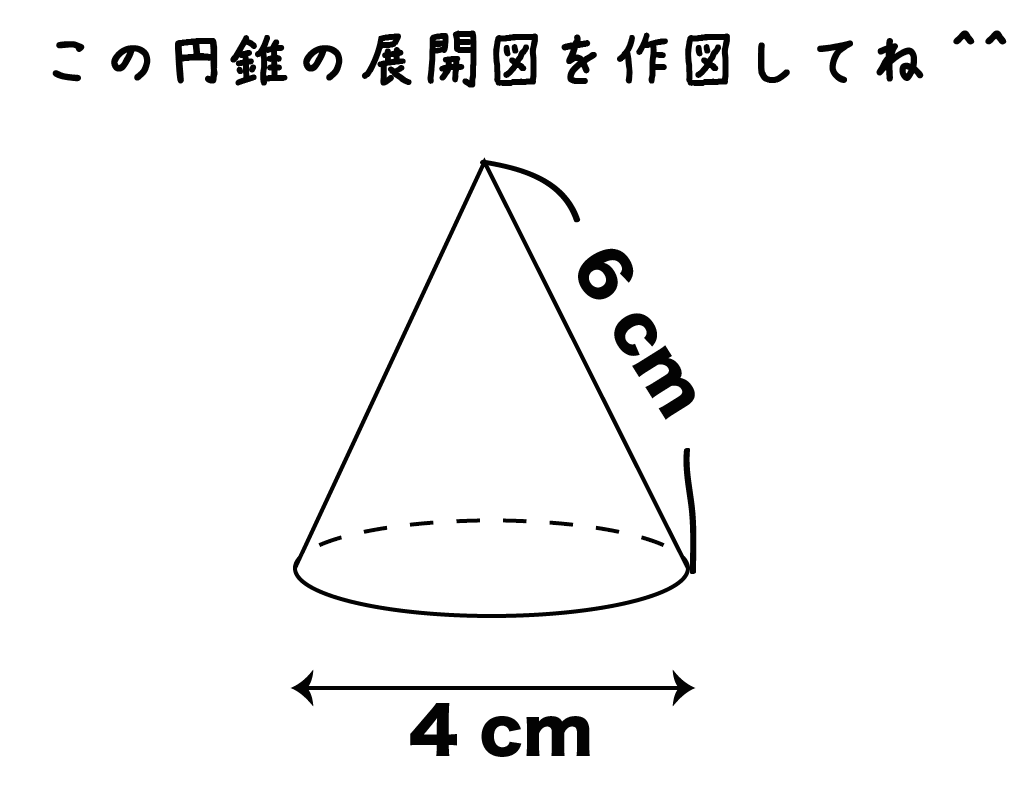
円錐の展開図の問題では、

だいたいこうなるっ！

ていう展開後をさきにイメージしておくとわかりやすいんだ。

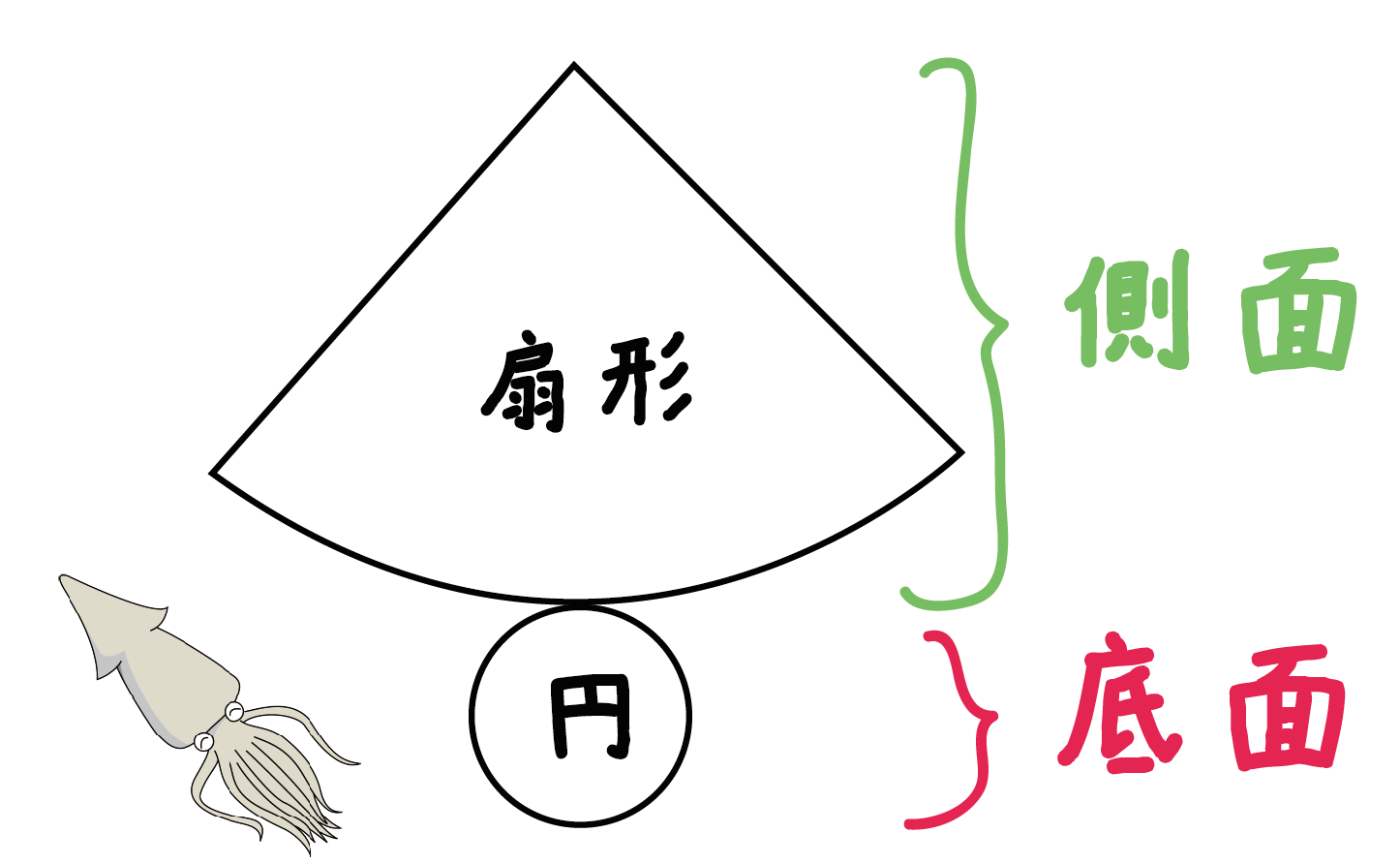
側面が扇形になって、底面の円がぴょこっとつくって展開図になるよ。

そこらへんのイカに似ているねw

それじゃあ、この展開図をぴしっとかいていこう！

 

 

Step1. 底面の「円周の長さ」を計算するっ！

まずは底面の円に注目しよう。

円周の長さを求めてあげるのが第一ステップだ。

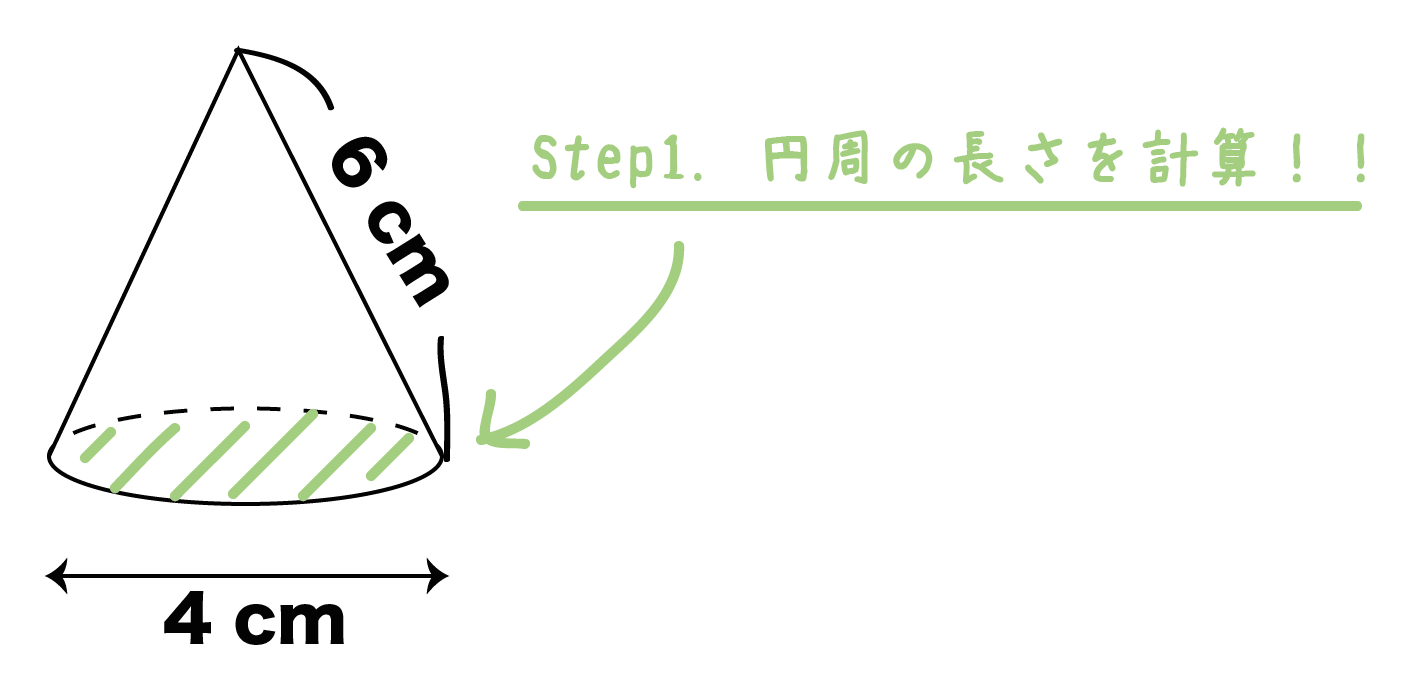
円周の長さは、

「直径×円周率」で求められたよね？？　だから例題では、

円周の長さ =  4 π [cm]

になるよ。

 

 

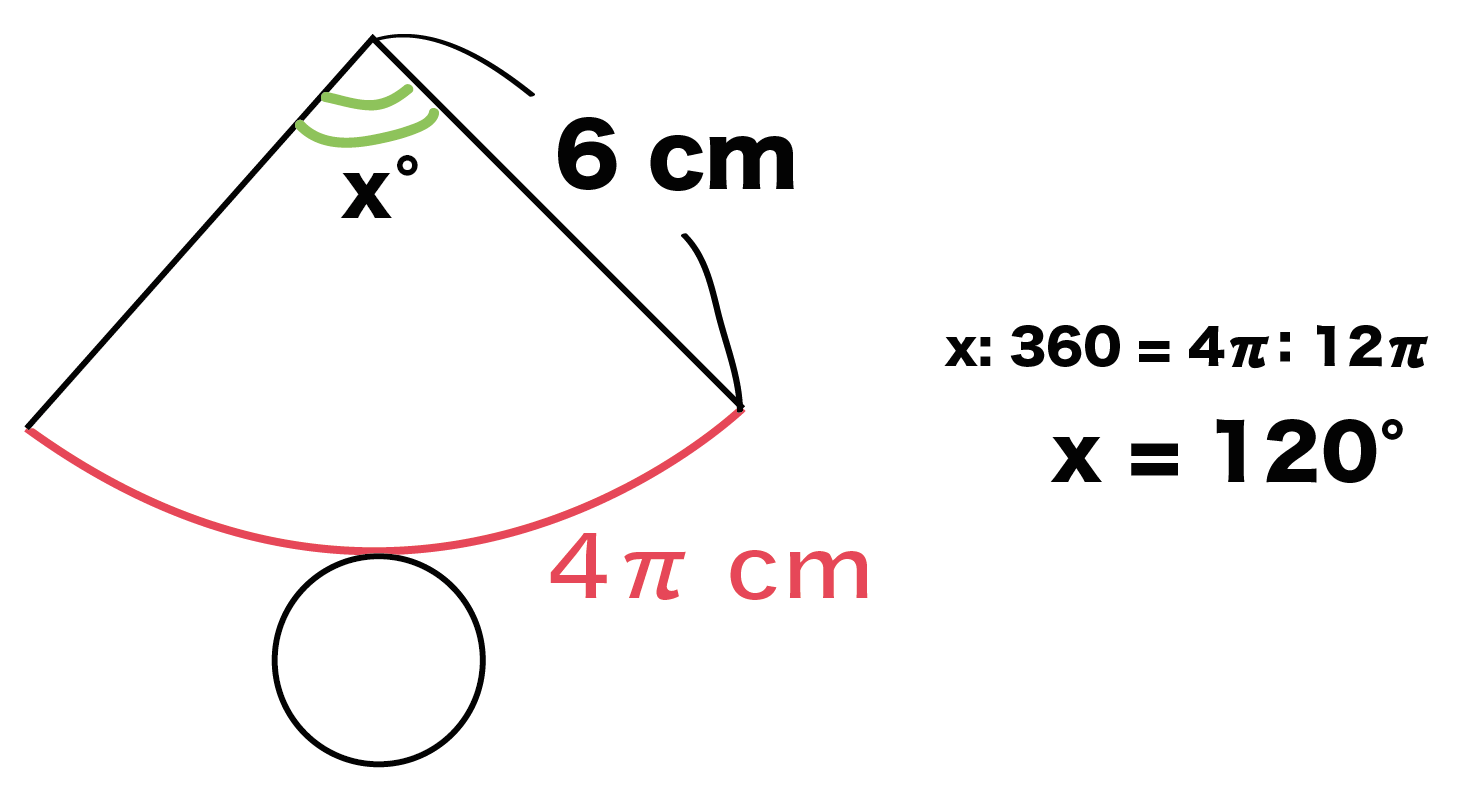
Step2. 側面の「扇形の中心角」を求める

つぎは円錐の側面の展開図をかくためのステップだ。

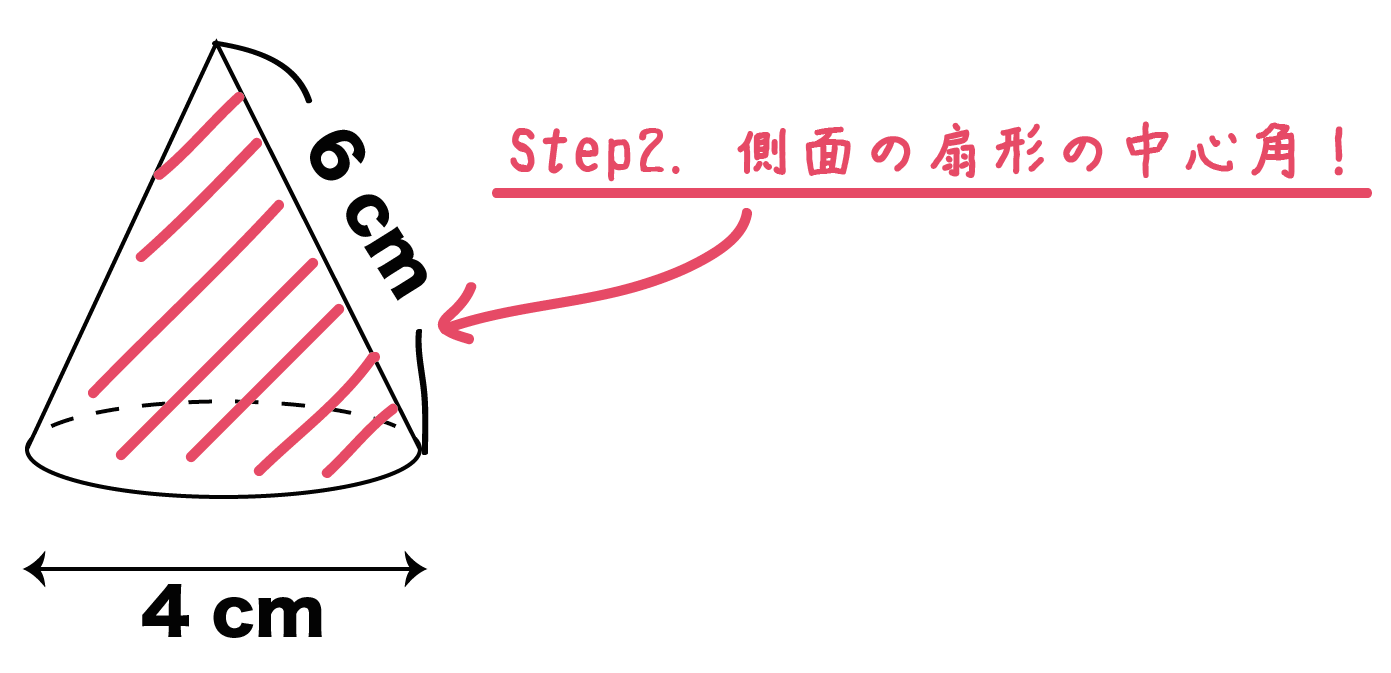
ここでは、円錐の側面を展開したときにできる「扇形の中心角」を求めるんだ！

Step1で「底面の円周の長さ」を求めたよね？？

じつは、円錐の展開図ではソレが「扇形の弧の長さ」になっているんだ。

扇形の中心角の求め方を参考に計算してやると、

x : 360 = 4π : 12π

x = 120°

になるね！

 

 

Step3. 扇形をかくっ！

求めた中心角をもとに側面の扇形をかいてみよう。

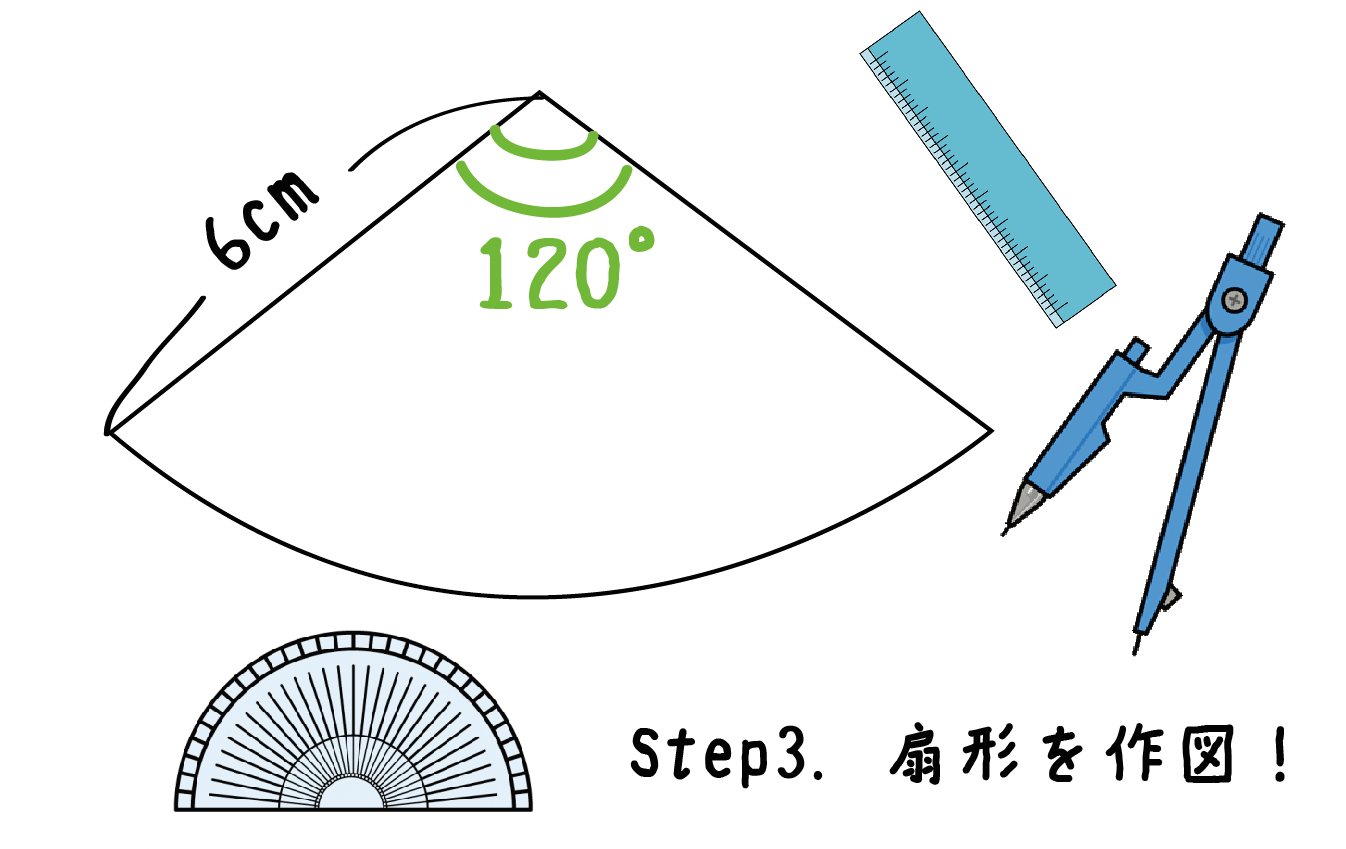
コンパスと定規、あわよくば分度器をつかってね。

例題でいうと、

中心角120°、半径6cmの扇形をかけばいいんだ。

 

 

Step4. 扇形の弧に円をちょこんとのせる！

いよいよ最後のステップだ。

さっきかいた扇形の展開図に、底面の円をのせてあげよう。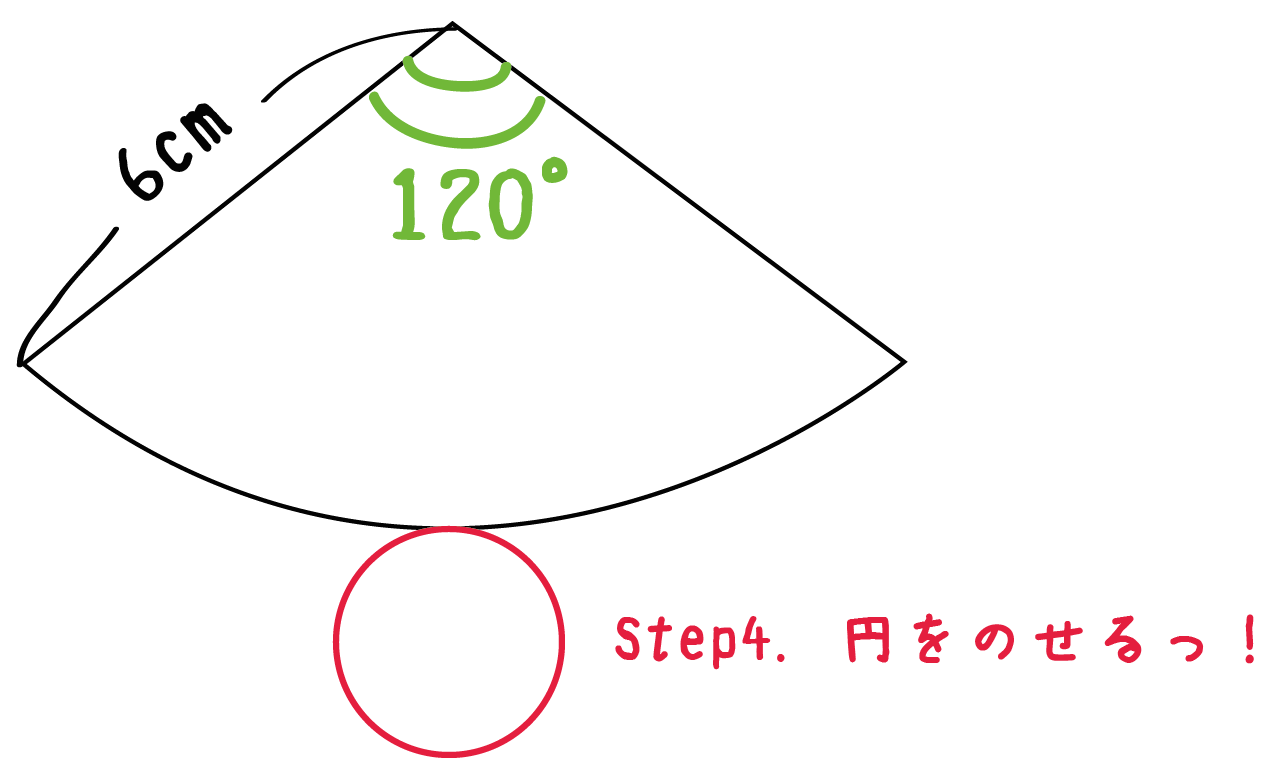 

円をのせる位置は「扇形の弧の上」ならどこでもいい。ただ、美しい円錐の展開図を作図したかったら、

「扇形の中心の真下」に「円の中心」がくるようにする

といいよ。

ただ、大切なのは位置よりも、

扇形と円が1点で接しているかどうか

ということ。

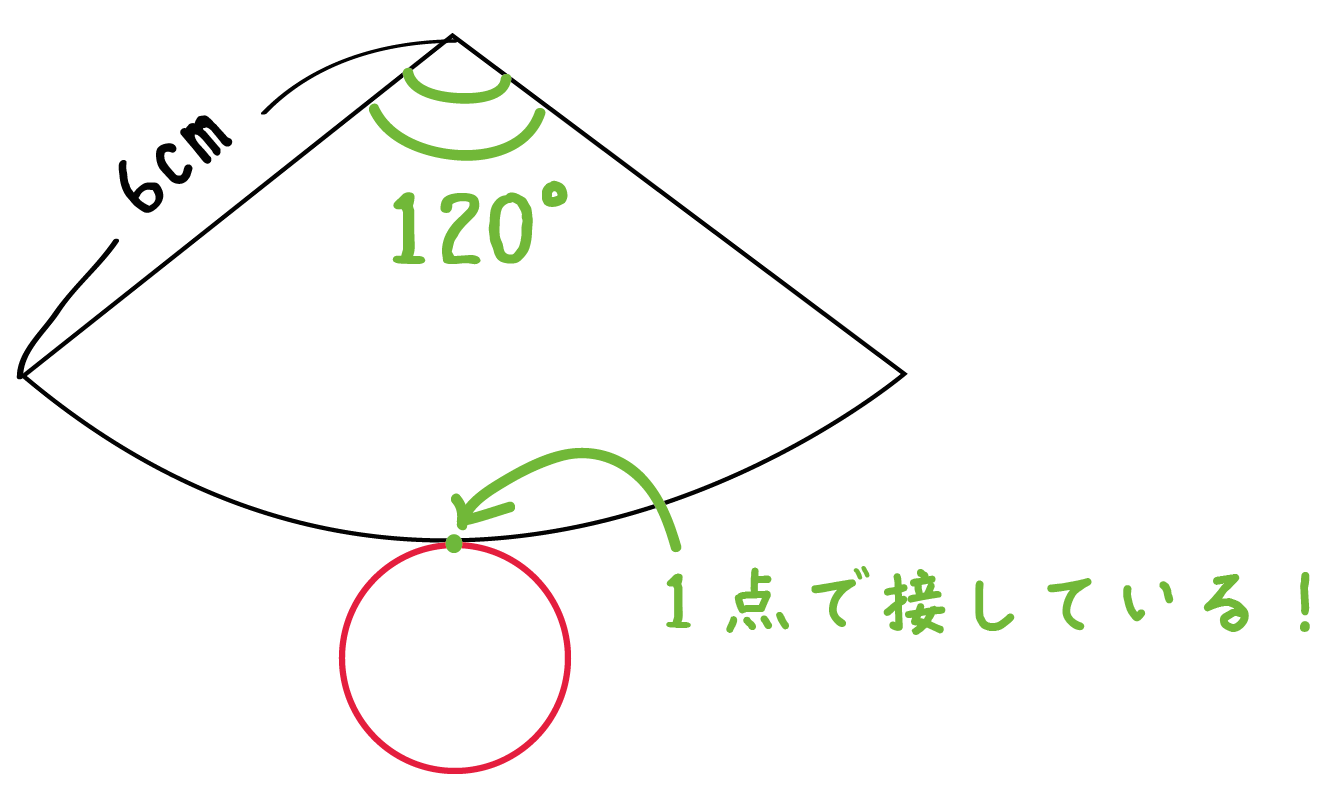
これは円柱の展開図の書き方でも触れたことだったね。

扇形に接している円になるようにしよう！

 

 

まとめ：円錐の展開図は4ステップで簡単にかける！

これで円錐の展開図は終了！

たったの4ステップでかけちゃったんだ。なかなかに簡単でしょ？？

円錐の表面積を求める前に、展開図を作図できるようにしておこう！

そんじゃねー

Ken