度数分布表からの平均値の求め方がわからん??
こんにちは!この記事をかいているKenだよ。山、みたいね。
平均値の求め方はわかってる。
だって、
「データの合計」を「データの個数」で割ればいいんでしょ??

ちょろいよ。
たとえば、A・B・C・D君のテストの平均値を求めてみよう。
かりに、4人の点数が、
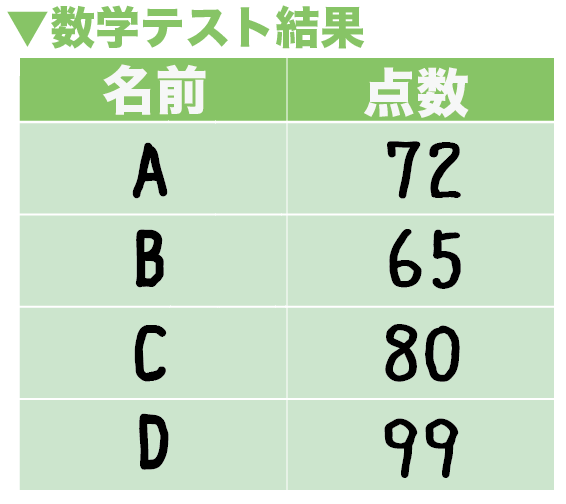
- A君: 72点
- B君: 65点
- C君: 80点
- D君: 99点
だとするね。
こいつらの平均点は、
(データの合計)÷(データの個数)
= (72 + 65 + 80 + 99)÷ 4
= 79
になる。
ぶっちゃけ、楽勝だね!
だけどさ、
度数分布表から平均を求めるとき
ってどうすればいいんだろ??
テストや宿題ででてくるのに、教科書にのってない。。
こいつは困ったね。
そこで今日は、
度数分布表からの平均値の求め方
を5ステップで解説してみたよ。
度数分布表からの平均値の求め方がわかる5ステップ
度数分布表から平均値を求めるときは、
つぎの公式をつかうよ。
「(階級値×度数)の合計」÷「度数の合計」

「階級値」と「度数」をかけたものをぜーんぶたして、
「度数の合計」でわればいいんだ。
えっ、言葉だけじゃよくわからん??
実際に例題をといてみよう!
例題
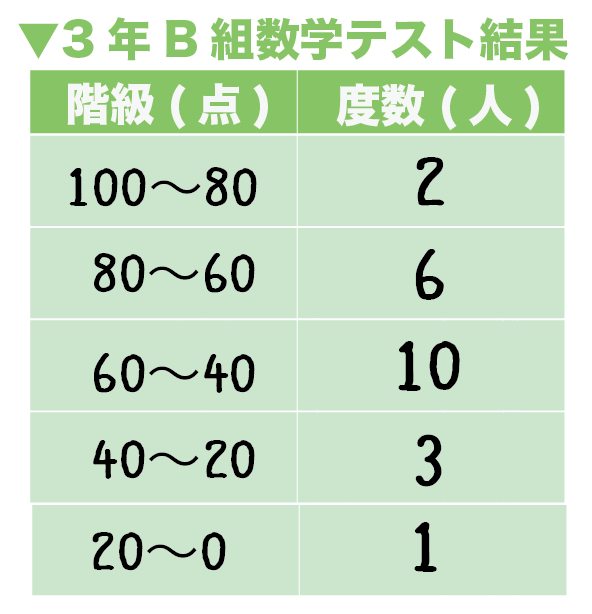
つぎの度数分布表は3年B組の期末テストの点数の分布をあらわしたものです。この度数分布表から平均値を求めなさい。
つぎの5ステップで計算できちゃうよ。
- 階級値をだす
- 「階級値×度数」を計算する
- 度数の合計をだす
- 「階級値×度数」の合計をだす
- 公式をつかう
Step1. 階級値をだす!
各階級の「階級値」を計算してみよう!
階級値の求め方は、
(階級の端+階級の端)÷ 2
だったよね??

たとえば、階級が「100~80」だったら、
(100 + 80 ) ÷ 2
= 90
になるってわけ。
こんな感じで、階級の端っこの平均をだせばいいんだ。
例題の階級値をぜーんぶだしてやると、
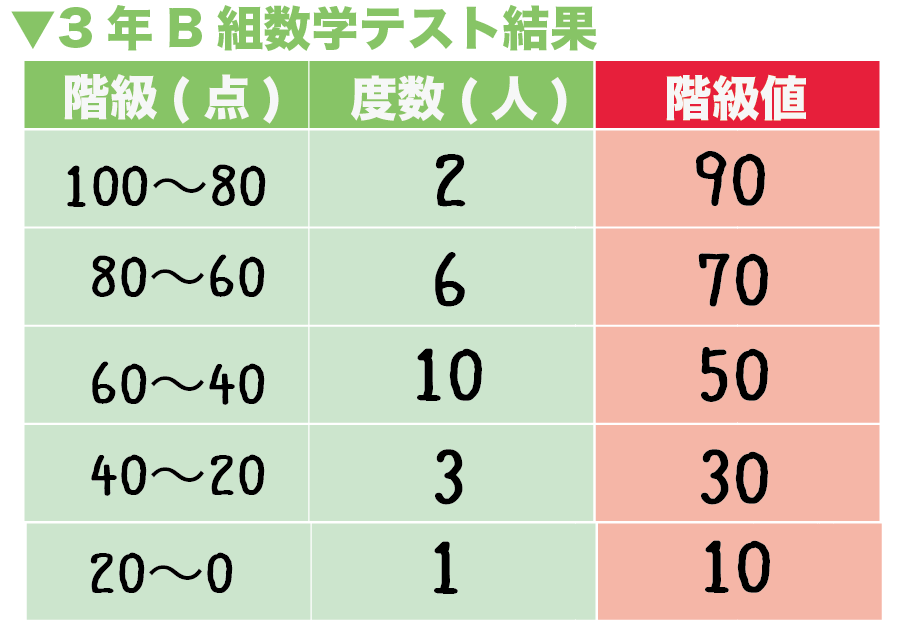
- 階級 100 ~ 80 : 階級値 90
- 階級 80 ~ 60: 階級値 70
- 階級60 ~ 40: 階級値 50
- 階級40 ~ 20 : 階級値 30
- 階級20 ~ 0 : 階級値 10
になるね。
これが第1ステップ!!
Step2. 「階級値×度数」を計算する!
つぎはさっき計算した、
階級値
と
度数
をかけてみよう。

例題で「階級値×度数」を計算してみると、
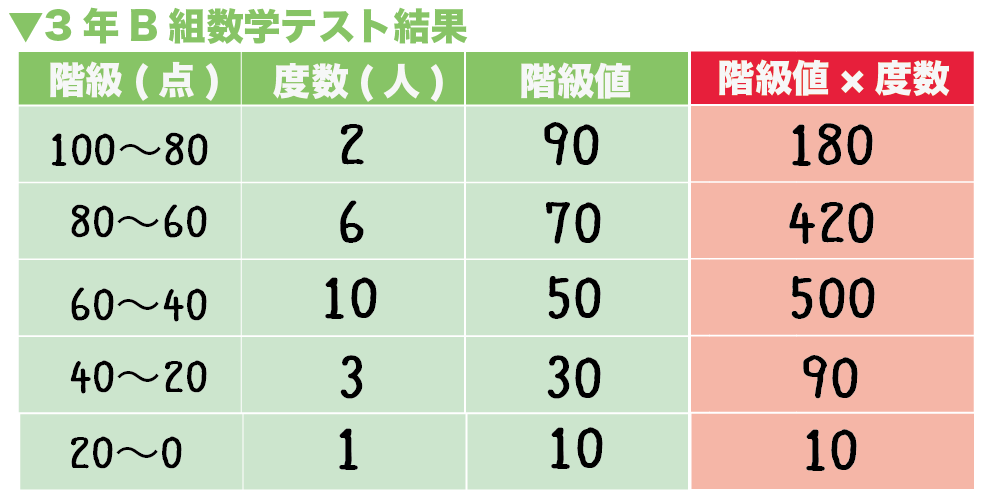
- 階級 100 ~ 80 : 90 ×2 = 180
- 階級 80 ~ 60: 70 × 6 = 420
- 階級60 ~ 40: 50 × 10 = 500
- 階級40 ~ 20 : 30 × 3 = 90
- 階級20 ~ 0 : 10 × 1 = 10
になるね。
慎重にかけ算をしてみよう!!
Step3. 「度数」の合計をだす
おつぎは、
度数の合計
を計算しよう。
ぜーんぶの階級の「度数」をたせばいいのさ。
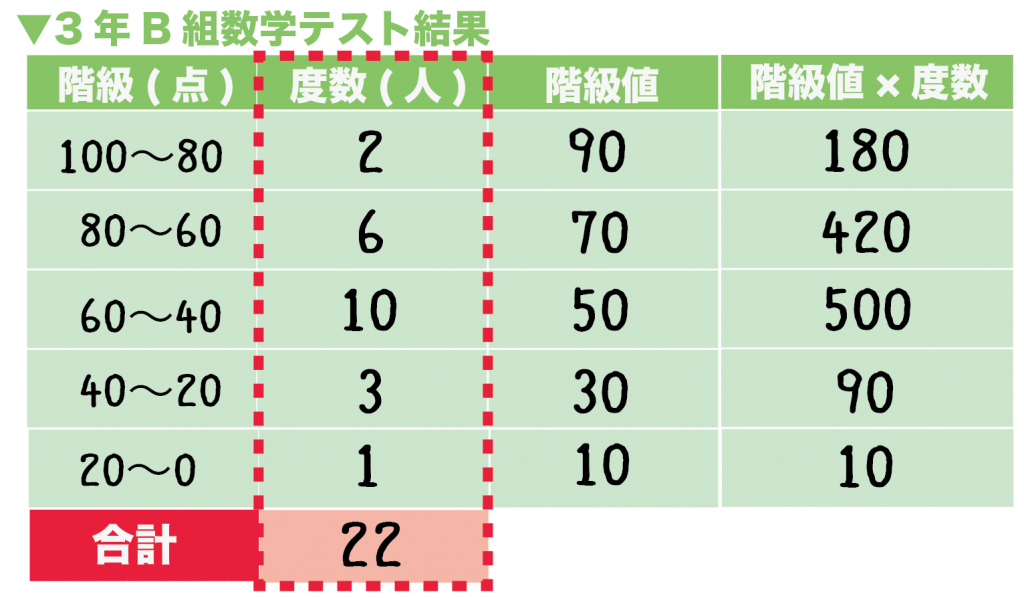
例題でいうと、各階級の度数は、
- 階級 100 ~ 80 : 2
- 階級 80 ~ 60: 6
- 階級60 ~ 40: 10
- 階級40 ~ 20 : 3
- 階級20 ~ 0 : 1
だったね??
こいつらをぜんぶ足してやると、
2 + 6 + 10 + 3 + 1
= 22
になる!
Step4. 「階級値×度数」をたしたる!
「階級値×度数」の合計もだしてみよう!
ぜーんぶの階級の「階級値×度数」をたせばいいんだ。
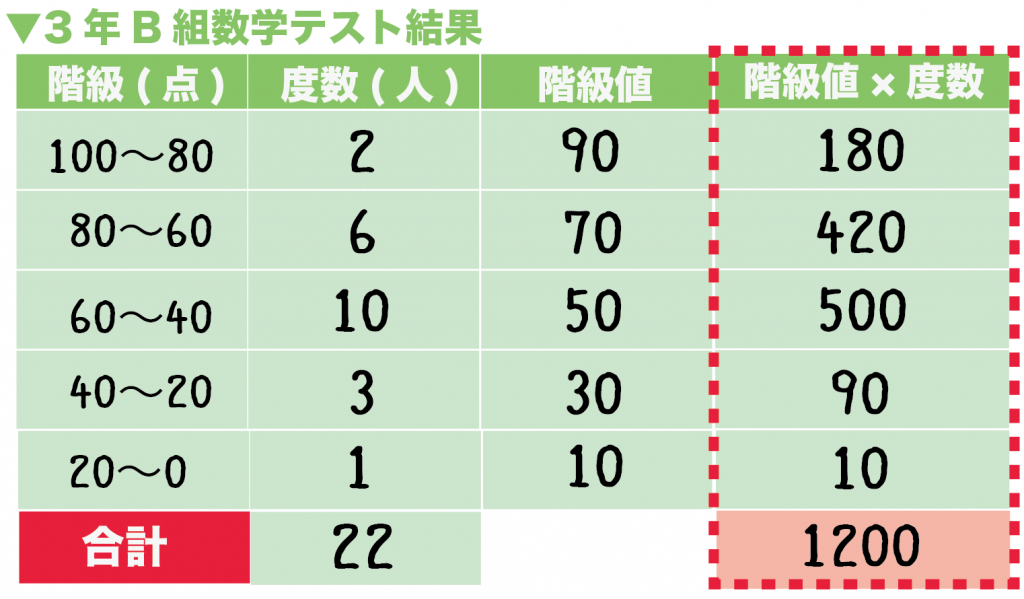
例題の「階級値×度数」は、
- 階級 100 ~ 80 : 180
- 階級 80 ~ 60: 420
- 階級60 ~ 40: 500
- 階級40 ~ 20 : 90
- 階級20 ~ 0 : 10
だったよね??
こいつをぜんぶたしてやると、
180 + 420 + 500 + 90 + 10
= 1200
になるね。
Step5. 公式をつかう!
最後に平均値の公式をつかおう!
度数分布表から平均値を求める公式は、
「(階級値×度数)の合計」÷「度数の合計」

だったね??
Step4まででそろえた、
- (階級値×度数)の合計
- 度数の合計
を公式にぶちこんでみよう。
例題では、
- (階級値×度数)の合計:1200
- 度数の合計: 22
を公式にいれて計算してやると、
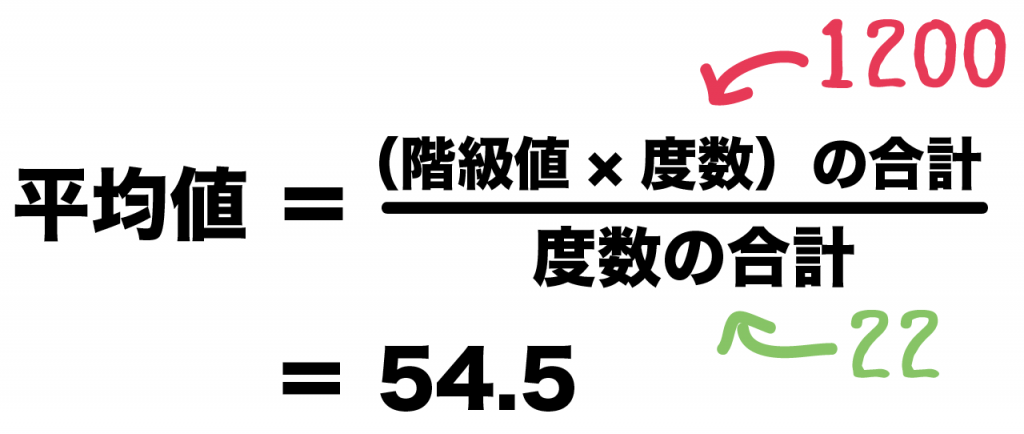
(階級値×度数の合計)÷(度数の合計)
= 1200 ÷ 22
= 54.5※小数点第二位を四捨五入
になる!
おめでとう!
どんな度数分布表からも平均値を求められるね。
まとめ:度数分布表から平均値を求め方は足し算・かけ算・割り算をつかえ!
度数分布表から平均値をだすのはむずい。
だけど、ふたをあけてみると案外簡単。
使ってるのは、
- 足し算
- かけ算
- 割り算
の3つだからね。
求め方さえおぼえちまえば、計算は簡単なんだ。
度数分布表からガンガン平均値を求めていこう!
そんじゃねー
Ken









