3つのサイコロの確率の求め方がわからない!
こんにちは!この記事をかいているKenだよ。水、うまいね。
3つのサイコロの確率の問題ってたまにでてくる。
サイコロが2つの確率ならけっこう簡単だったね。
だけど、
サイコロが1つ増えたらちょームズくなるんだ。

なぜなら、
サイコロ3つだと表がかけないからね。
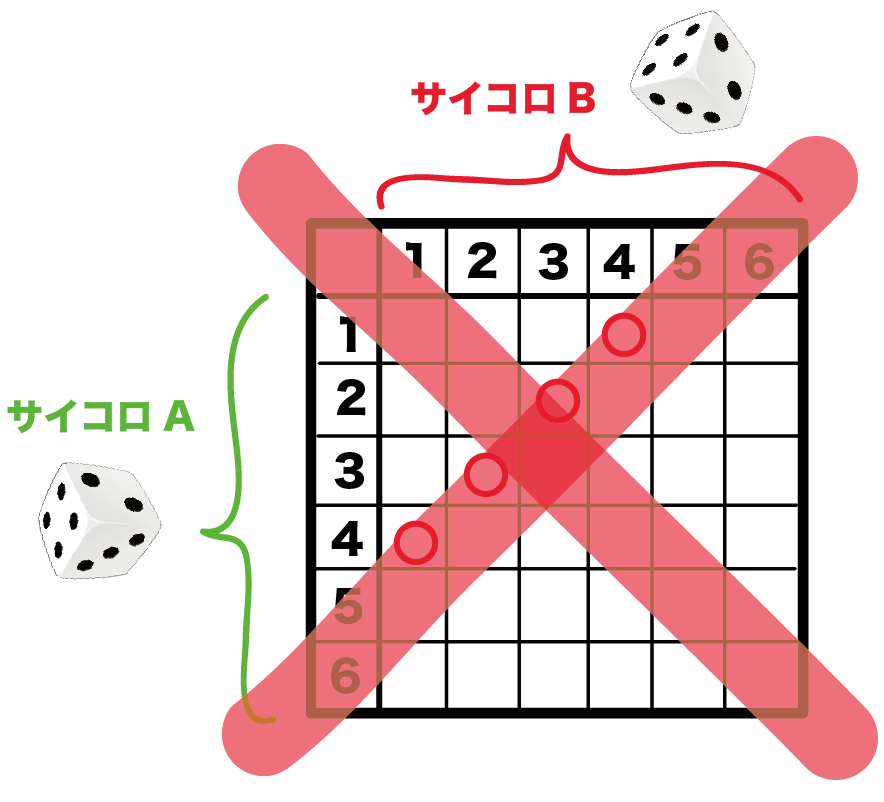
今日はこのやっかいな
「3つのサイコロの確率の問題」の解き方をわかりやすく解説していくよ。
よかったら参考にしてみて。
3つのサイコロの確率の求め方がわかる3ステップ
サイコロ3つの確率の問題は3ステップでとけちゃうよ。
- 樹形図をかく
- 場合の数をかぞえる
- 確率の公式をつかう
例題をといてみよう。
3つのサイコロを同時に振ったとき、目の和が5になる確率を求めよ。

Step1. 樹形図をかく!
樹形図をかいてみよう。
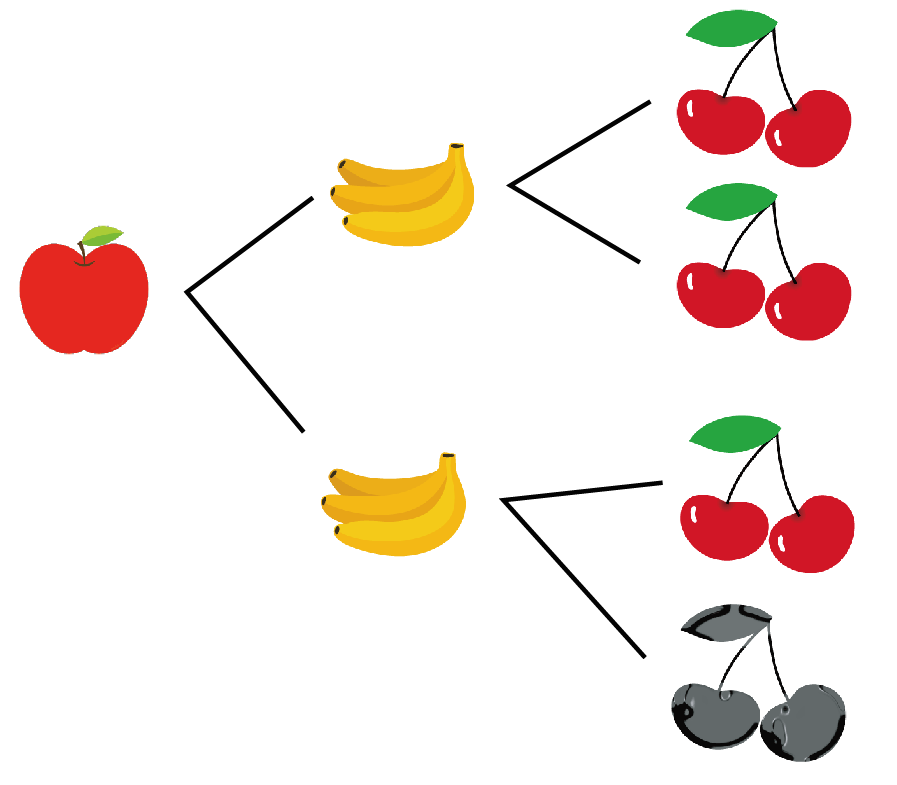
中学数学では樹形図で場合の数をかぞえていくんだ。
例題では、
3つの目の和が5になる
場合の数をしらべなきゃいけないね。
3つのサイコロを、
- サイコロA
- サイコロB
- サイコロC
としてみよう。

樹形図で「3つの目の和が5になる」場合の数をかぞえてみると、
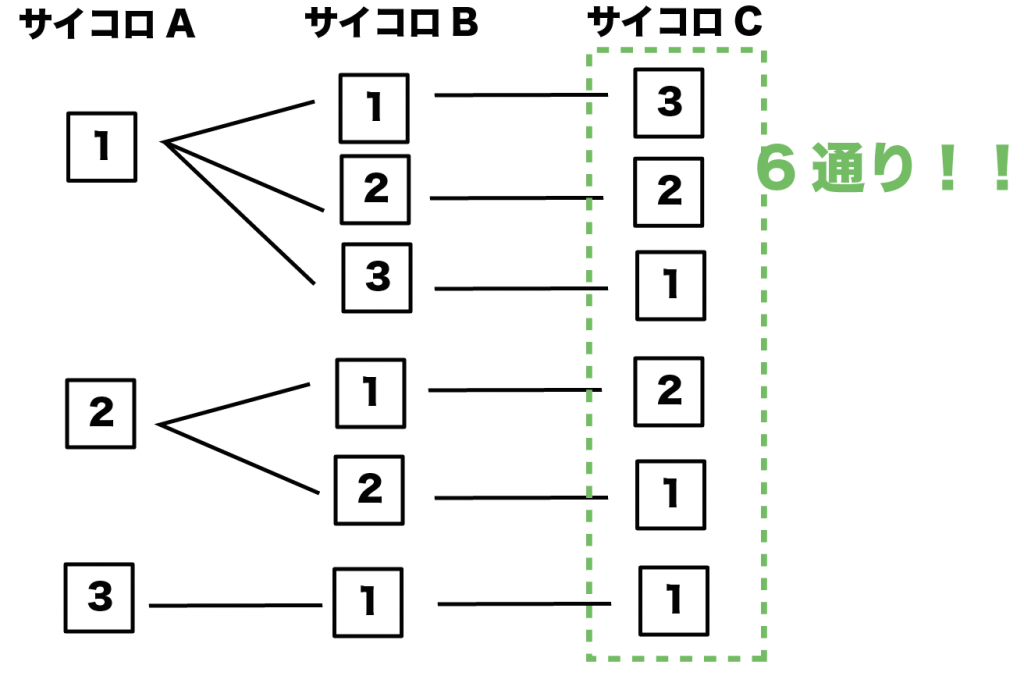
ぜんぶで6通りありそうだね!
Step2. すべての場合の数を調べる
ぜーんぶの目の場合の数をしらべよう。
サイコロ1つの目のパターンは6つ。
ってことは、サイコロを3つ同時にふったときの目の出方って、
6×6×6
= 216
になるはずだね。

Step3. 確率の公式で計算する!
最後に確率の公式で計算してみよう。
「樹形図でかぞえた場合の数」を「すべての場合の数(216)」でわればいいんだ。

例題だと、
- 3つの目の和が5になる場合の数:6通り
- すべての場合の数:216通り
だったね??
ってことは、
サイコロ3つの目の和が5になる確率は、
(サイコロの目の和が5になる場合の数)÷(すべての場合の数)
= 6÷216
= 36分の1
になるね。

おめでとう!
3つのサイコロの確率をマスターしたね。
まとめ:サイコロ3個の問題は根性と樹形図でとく!
3つのサイコロの問題は正直、
近道がない。
ガッツと樹形図のスキルが必要だね。
問題をガンガンといてなれていこう!
そんじゃねー
Ken









