回転体の見取り図の書き方がわからない??
こんにちは、この記事をかいているKenだよ。できれば鼻をかみたくないね。
空間図形で「回転体」っていうモンスターを勉強するよね。
「回転体」とは教科書によると、
1つの平面図形を、その平面上の直線lのまわりに1回転させてできる立体
のことってかいてある。
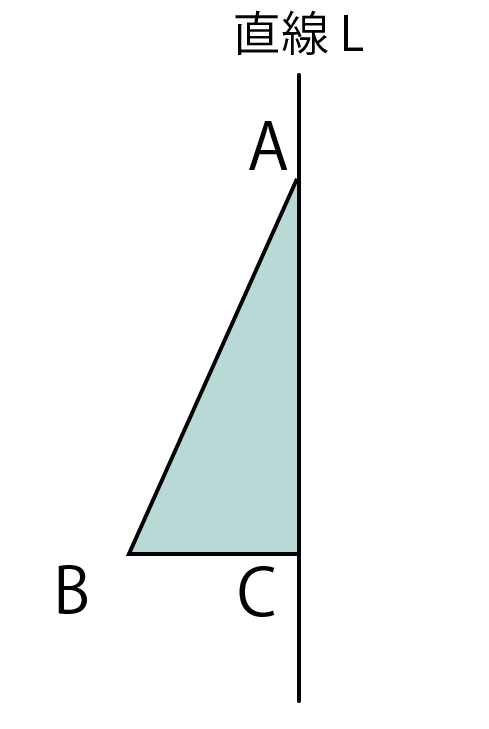
たとえば、直角三角形ABCを直線Lのまわりに1回転させて立体を作図してみると、
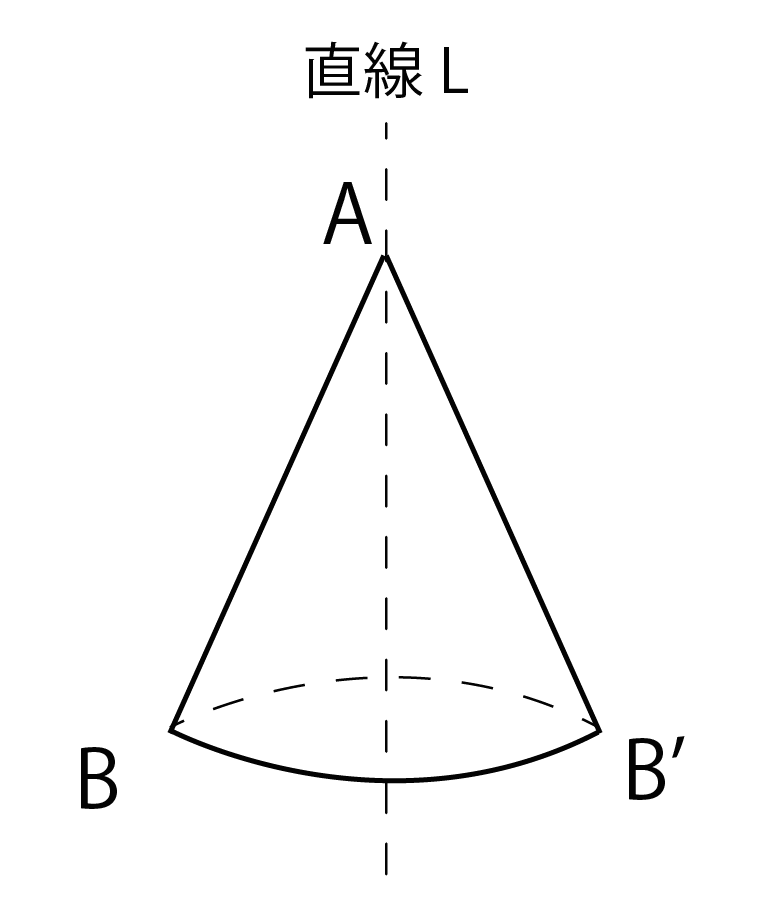
三角錐ABB’っていう立体ができちゃうんだ。
このとき、回転によってできた立体(この場合、三角錐ABB’)を「回転体」、直線Lを「回転の軸」って呼んでるわけだね。
それじゃあ、どうやって、回転体の見取り図をかくんだろう?? これができたら、回転体の体積を簡単に求められるよね。
そこで今日は、
回転体の見取り図の書き方
をわかりやすく解説していくよ。たった4ステップで作図できちゃうんだ。困ったときに参考にしてみてね。
「回転体の見取り図」の書き方がわかる4ステップ
見取り図の書き方を解説しながら、つぎの例題をといていくよ。
つぎの長方形ABCDを直線Lを回転の軸として、1回転してできる回転体の見取り図をかきなさい。
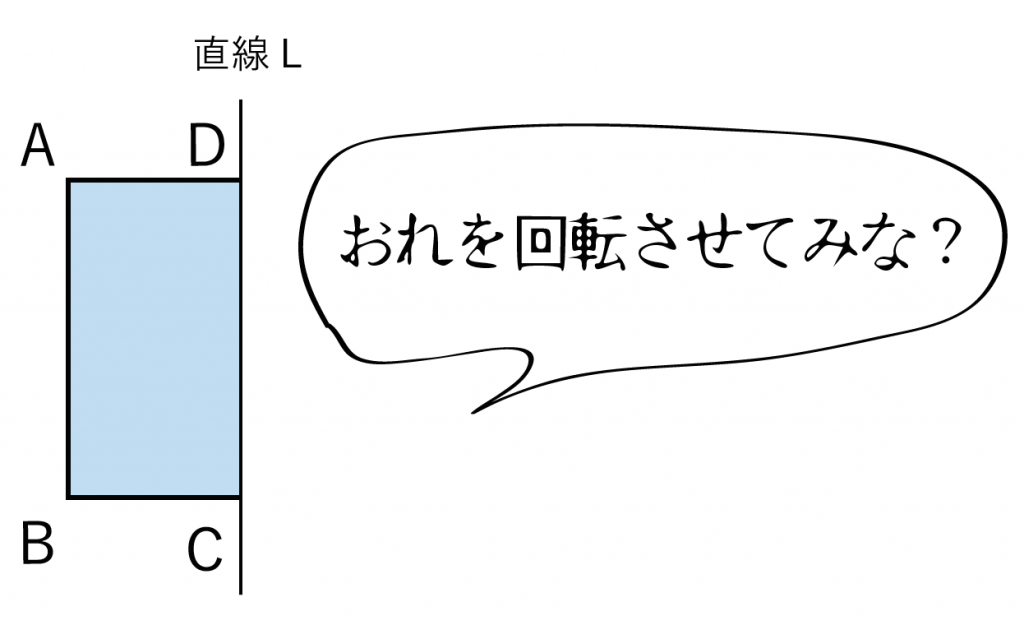
さっそく書き方をみてみよう!!
Step 1. 「回転の軸」で「対称移動」させる!
まずは与えられた平面図形を「回転の軸」で対称移動させた図形をかいてみよう。いわゆる線対称というやつだ。
対称移動をちょっと忘れていたら対称移動の書き方の記事をみてみてね。
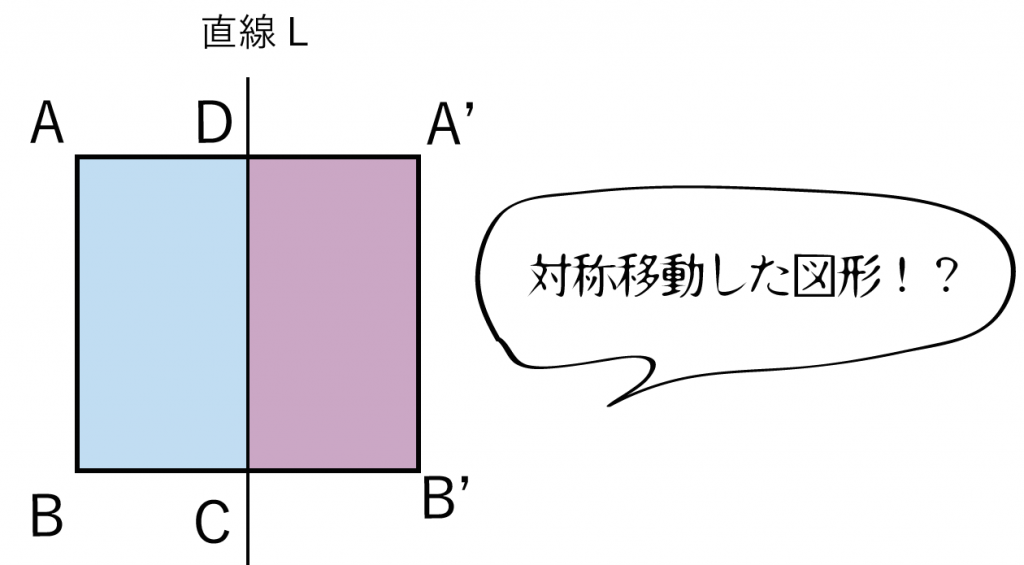
例題でいえば、
長方形ABCDを直線Lで対称移動させた図形は「長方形DA’B’C」になるね。ちょっとパープルの色をしているやつさ。
どう?? 回転の軸で対称移動できた??
Step 2. 「回転の軸」上にない「頂点」を「細長い円」でむすぶ
つぎに、「回転の軸」にのっかっていない頂点に注目してみよう。対称移動させた「対応する頂点」を細長い円(楕円)でむすぶんだ。
ちょっとわかりづらいから例題をみてみよう。
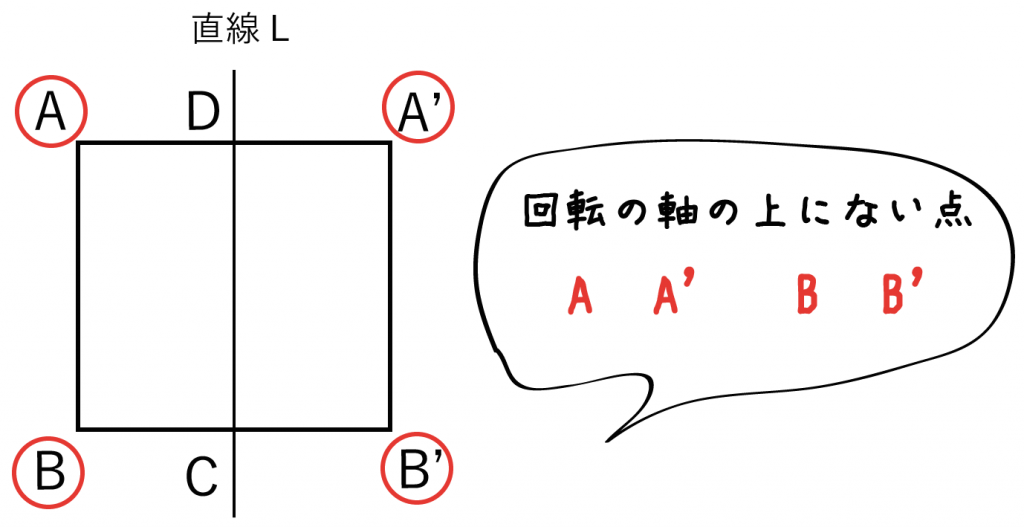
「回転の軸」上にない頂点は、
- A
- B
- A’
- B’
の4点だね。そのうち、対称移動させた図形同士の対応する頂点はつぎの2組。
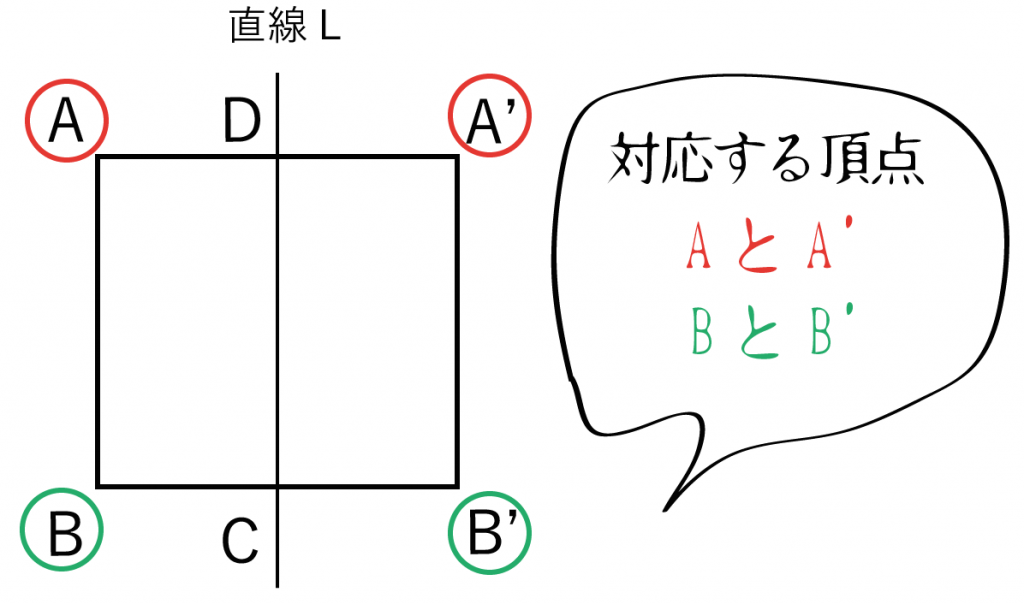
- AとA’
- BとB’
そして、この対応する頂点同士を「細ながーい円」でむすんであげるんだ。
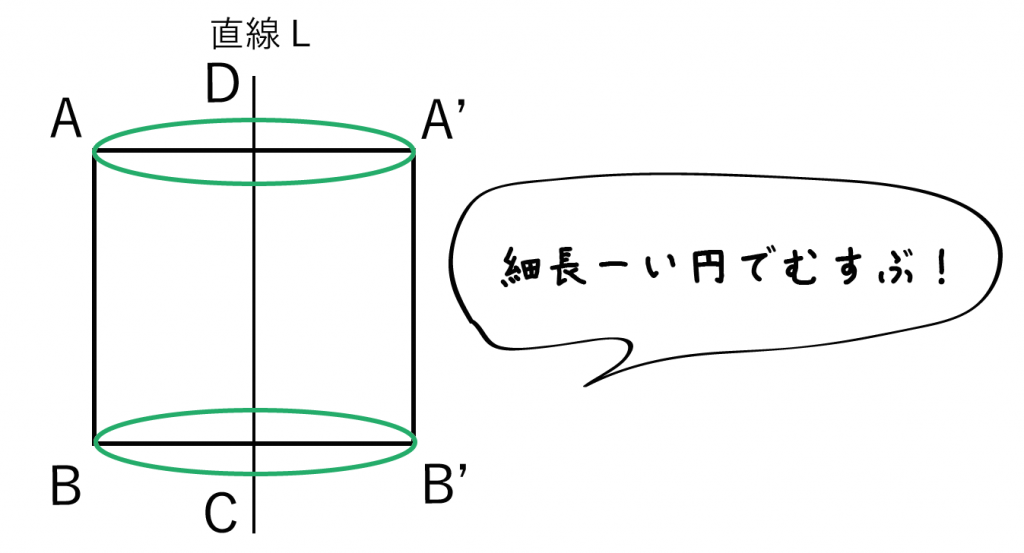
対応する頂点同士を円の両端にしてね。
上図のようにぴったりと細長い円をうめこんでやろう!
Step3. 外から見えない線を「点線」にするっ!
立体の見取り図では、立体の中の線は「点線」になってるんだ。
だから、ここでも見えないはずの線を「点線」にしてあげよう!
例題では、細長い円を埋め込んだだけだと、こうなっているね↓↓
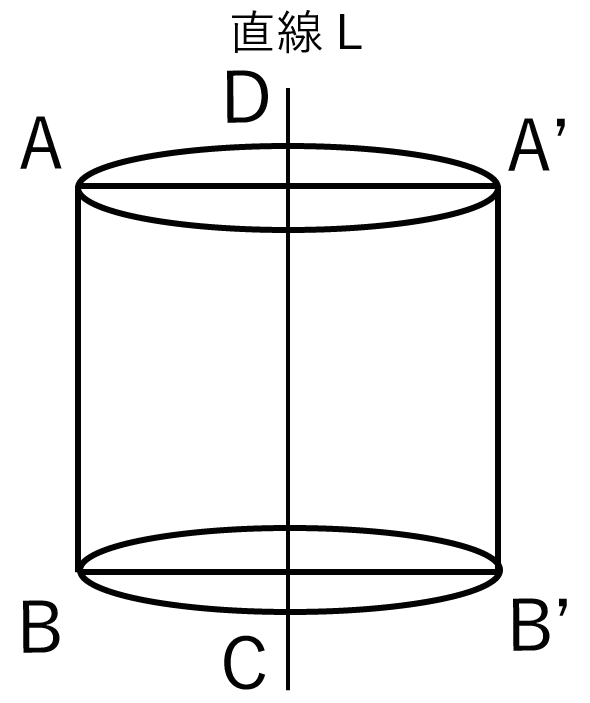
だけれども、円BB’の上の弧(緑のやつ)は外からみたら見えないはずの線。
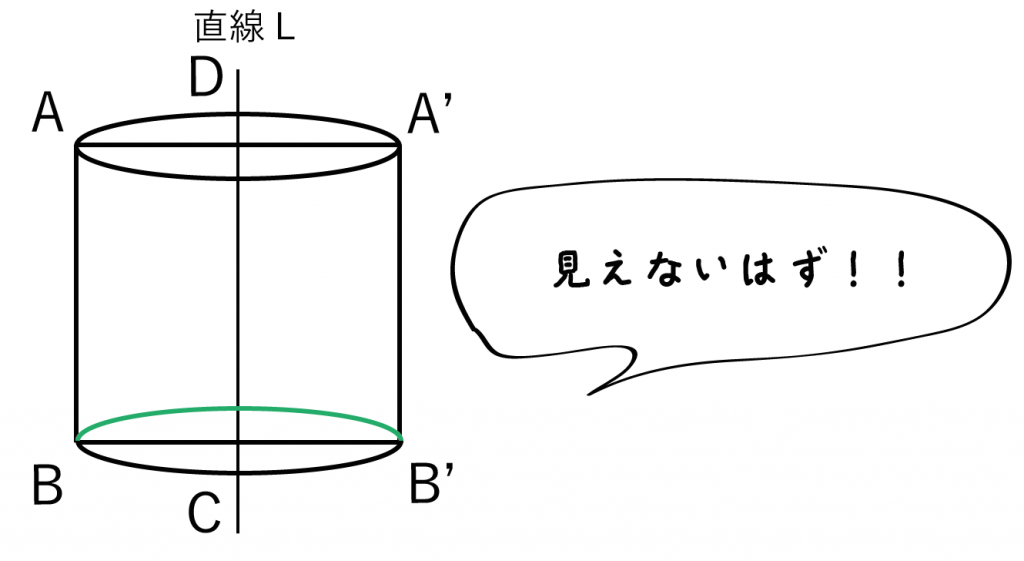
だからこいつを点線にしてあげよう↓↓
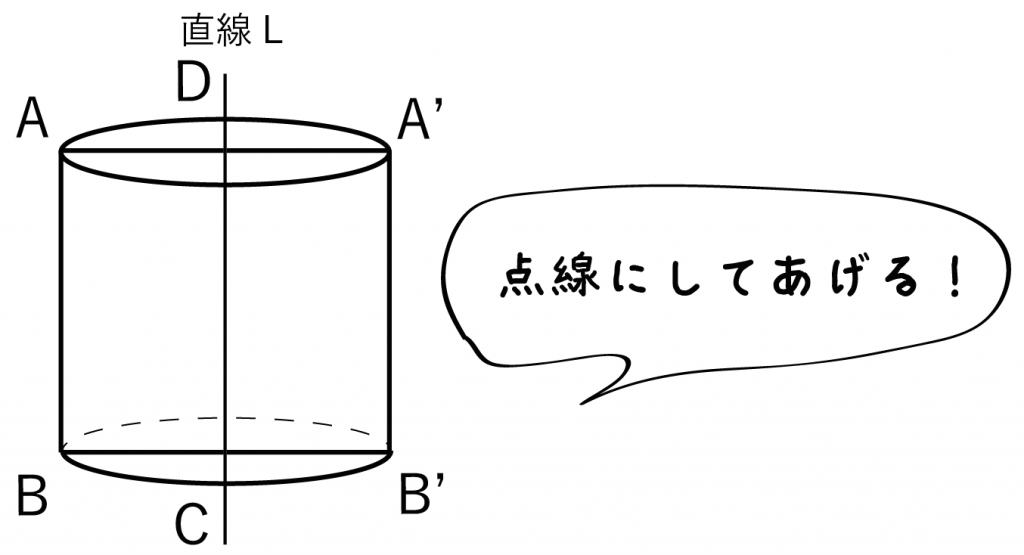
Step 4. 「回転体の半径の線」を消す!
いよいよ最後のステップ。
あとは回転体の半径の線を削除すればいいだけ!
例題でいうと、
- 線分AA’
- 線分BB’
の2つだね。
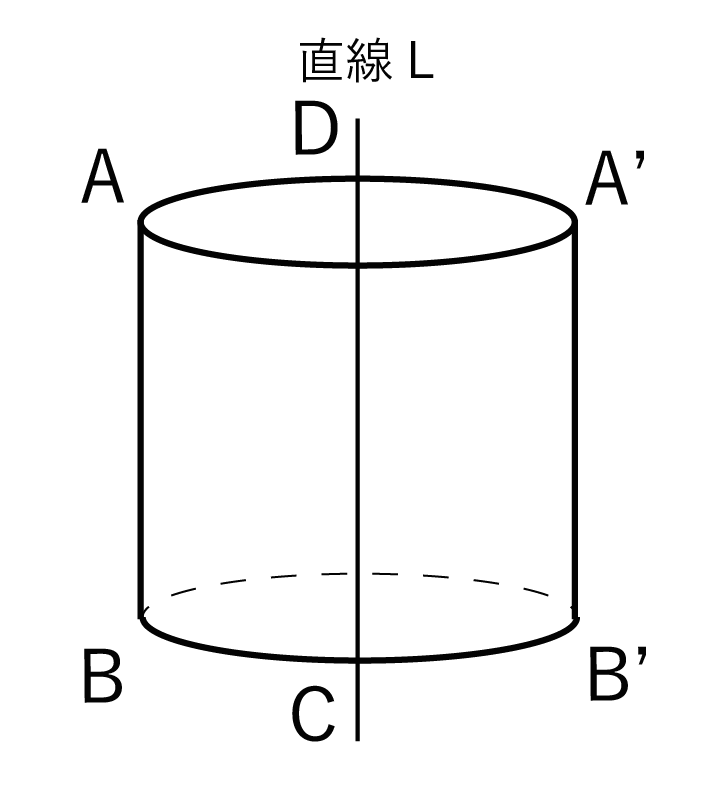
どう?? きれいな円柱ができたでしょ!?
おめでとう。回転体の見取り図が無事にかけたね。
まとめ:回転体の見取り図の書き方は4ステップでOK!!
回転体の見取り図はかけるようになったかな??
次回は「回転体の体積」の記事をかいていくよ。
よかったら参考にしてみてね。
そんじゃねー
Ken









