対頂角の性質はなぜ使えるの??
こんにちは!この記事をかいているKenだよ。チャーシューは2つまでだね。
対頂角(たいちょうかく)って知ってる??
教科書ではつぎのように書いてあるね。
2つの直線が交わっているとき、交点のまわりに4つの角度ができる。
そのうち、向かい合っている角同士のことを「対頂角」という。

名前だけでもカッコいいけど、
もっとすごいのはその性質。
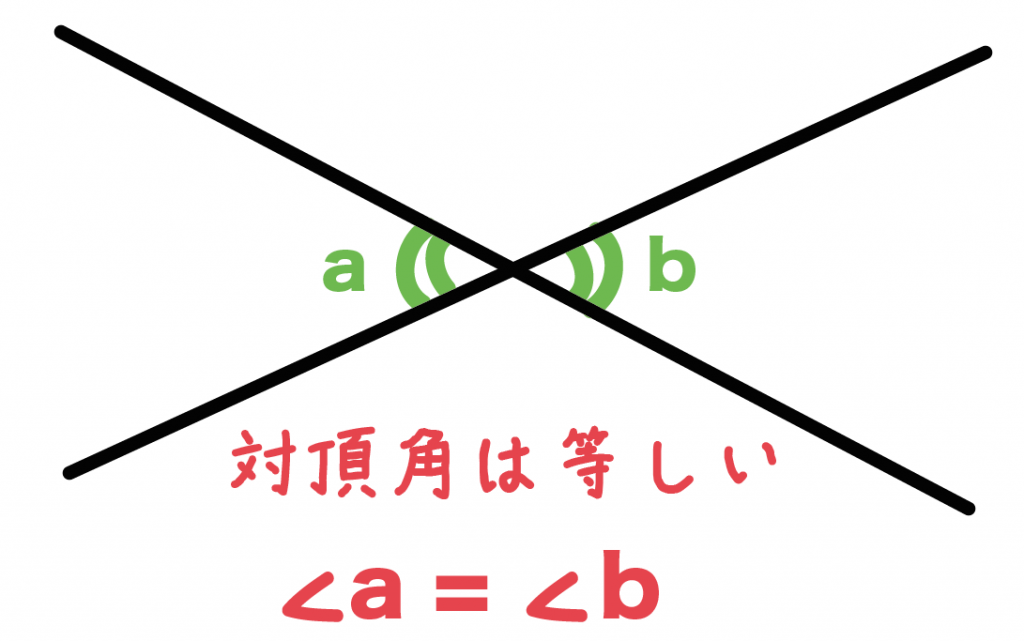
なんと、
対頂角は等しい
ってことが言えるんだよ。
対頂角の角たちを
- a
- b
とすると、
角 a = 角 b
ってことがいえるんだ。
この性質はむちゃくちゃ便利だけど、
なぜ、対頂角が等しいといえるのか??
が気になるよね。
今日はコイツをふかぼっていくよ!
3ステップでわかる!対頂角の性質の証明
コツはたった1つ。
それは、
1つの直線ごとに角度を確認していけばいいんだ。
つぎのように、
直線lとmが交わっていて、
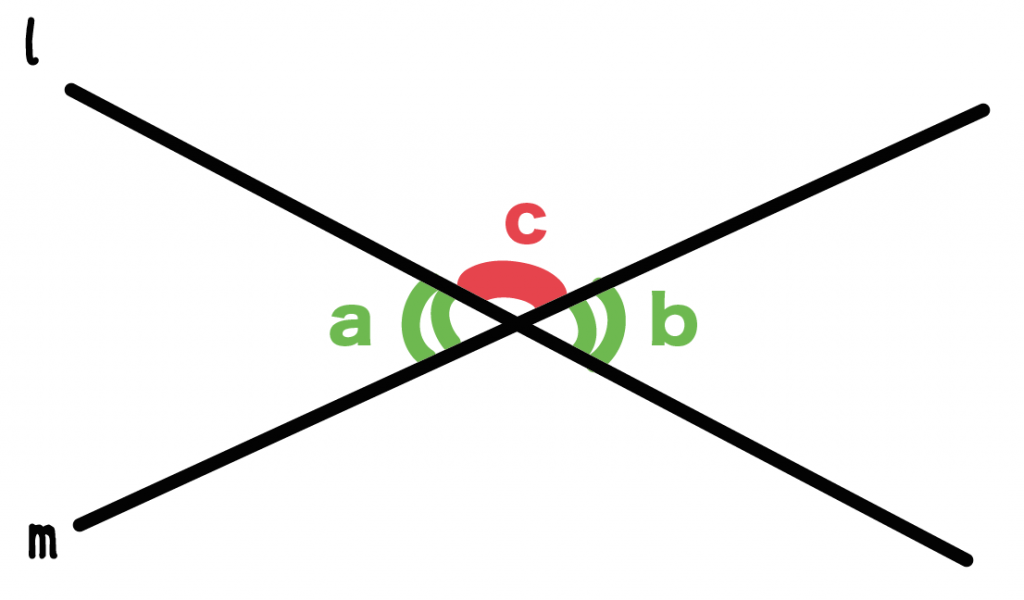
その周りにできる角を図のように
- a
- b
- c
とおいてみよう。
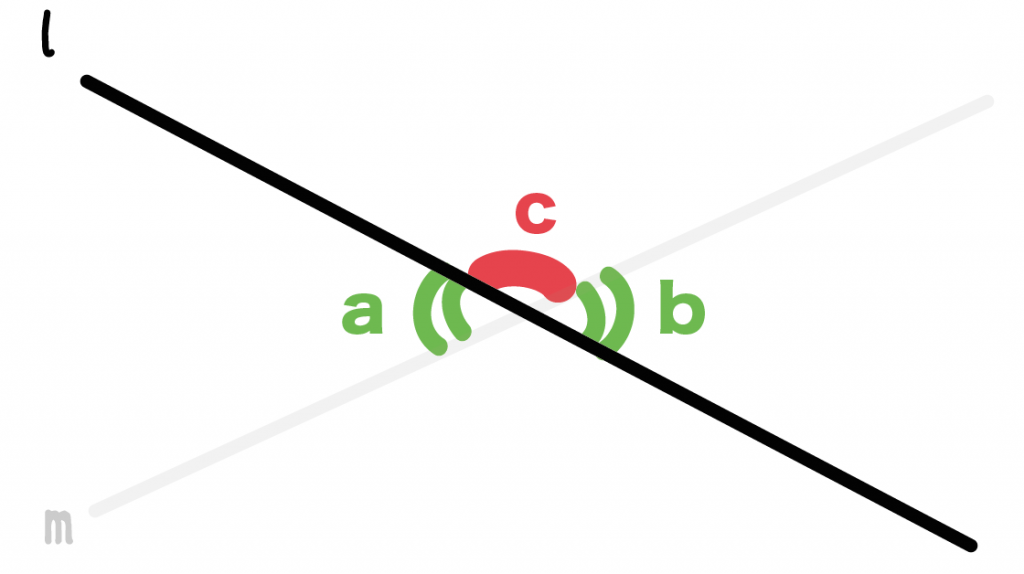
Step 1. 「直線mだけに注目したとき」
まずは直線mに注目するよ。
よーくみてみると、
「角a」と「角c」でちょうど1直線になっている
ってことに気づかない??
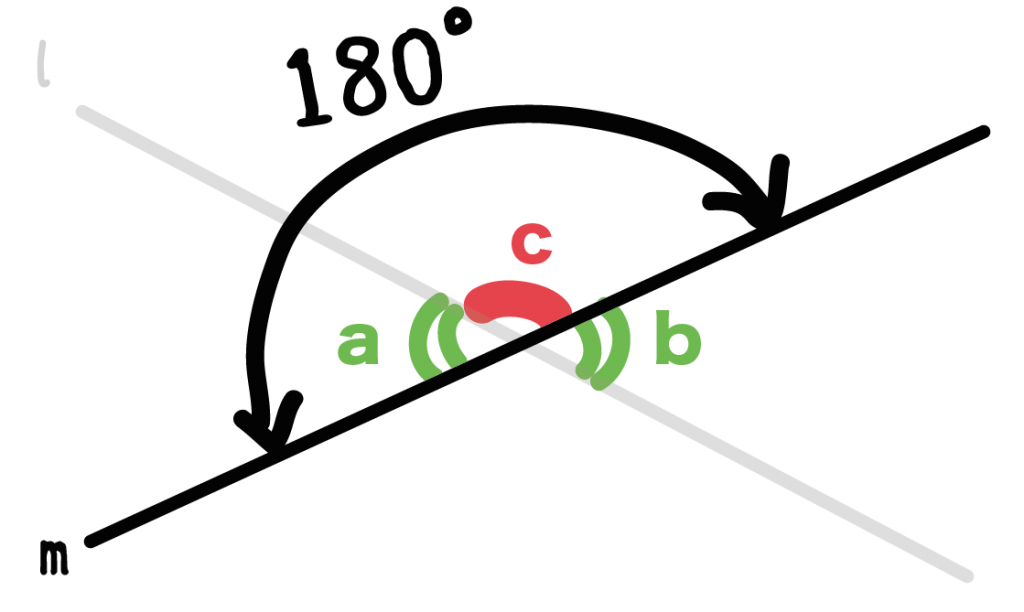
直線の角度は180°だ。
つまり、
角度a + 角度c = 180°
になるね。
等式を変形してやると(角度aについて)、
角度a = 180° – 角度c ・・・・・(1)
になる。この式を(1)としてあげよう。
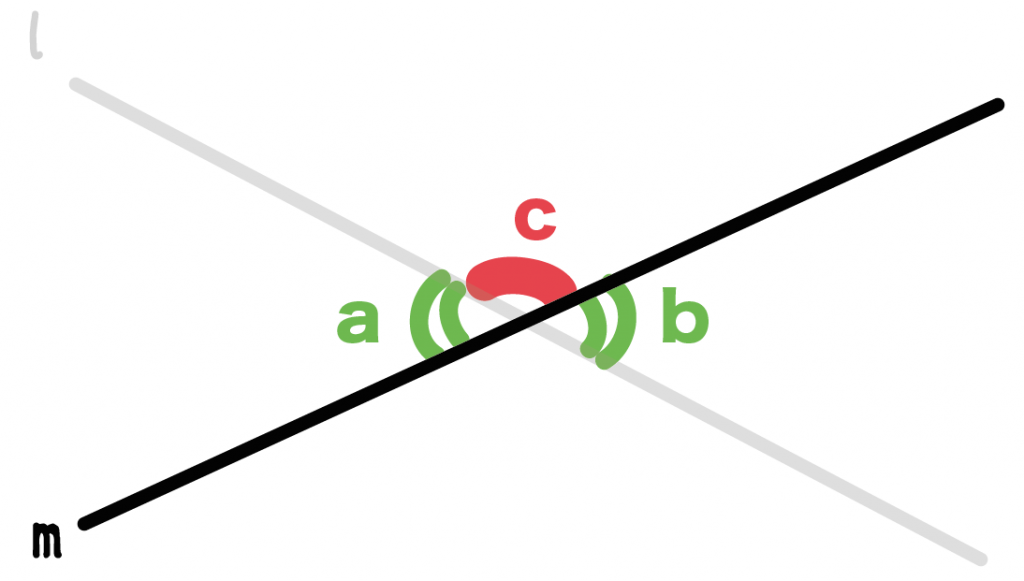
Step 2. 「直線lだけに注目したとき」
つぎは直線lだね。
さっきみたいに、
「角b」と「角c」を組み合わせると1直線(l)になってるでしょ??
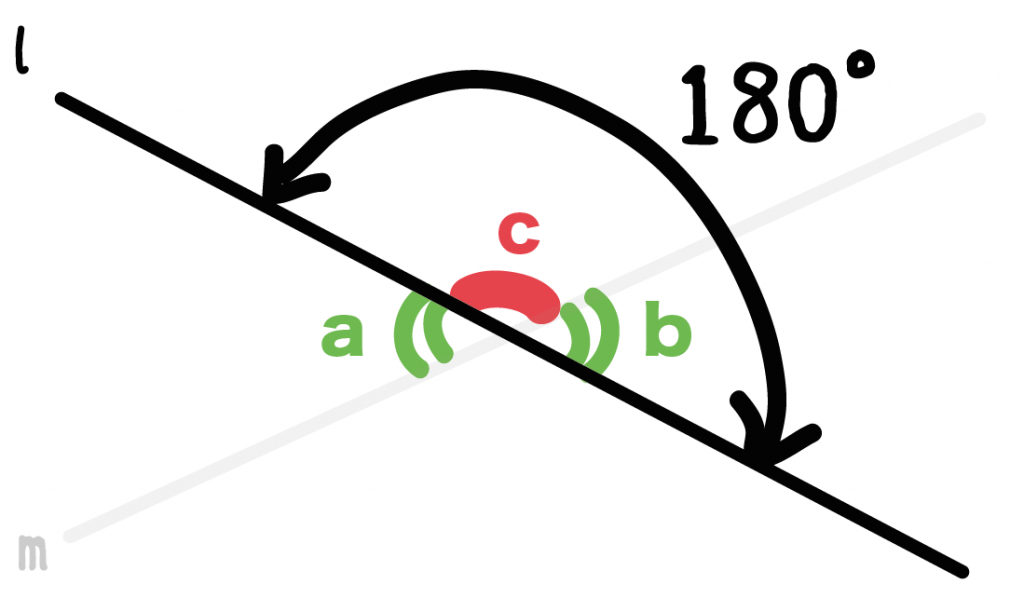
直線の角度は「180°」だから、
角度b + 角度c = 180°
になるね。
等式の変形をしてやると、
角度b = 180° – 角度c ・・・・(2)
になるね。
この等式を(2)としてあげよう。
Step3. 等式を組み合わせる
ここにきて、
- 角a = 180° – 角c ・・・・・(1)
- 角b = 180° – 角c ・・・・・(2)
の2つの式がでそろった。
(1)と(2)の右辺がまったく同じになってるよね??
ってことは、
(1)=(2)
が言えるね。つまり、
「角a」 =「角b」
になるね。
角aと角bは対頂角だから、
対頂角は等しい
といえるのさ。
どう?スッキリした??
まとめ:対頂角の性質は3ステップで証明できる!
対頂角は便利だから今後もガンガンつかってくよ。
だけど、
しっかりとなぜ対頂角が等しいといえるのか?
ってことも忘れずに勉強しておいてね。
そんじゃねー
Ken