円錐の側面積の求め方の公式って??
こんにちは、この記事をかいているKenだよ。うなぎの骨ってウマいね。
円錐の側面積の求め方にはチョー簡単な計算公式があるんだ。
「円錐の半径」をr、「母線の長さ」をLとすると、
「円錐の側面積」は次の式で求めることができる。
πLr
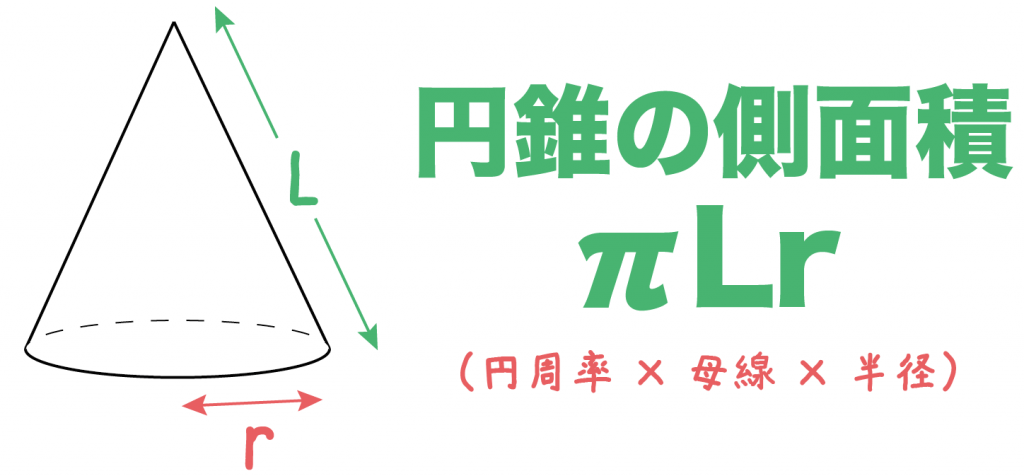
つまり、
(円周率)×(母線の長さ)×(底面の半径)
ってことだね。
むちゃくちゃシンプルだから覚えやすいけれど、テストで公式を忘れたらちょーヤバい。
そんなときに備えて、今日は「公式なしで円錐の側面積を計算する方法」をおぼえておこう!
円錐の側面積の求め方がわかる3ステップ
円錐の側面積は3つのステップでもとめることができるよ。
つぎの例題をといていこう!
例題
半径3cm、母線の長さ10cmの円錐の側面積を求めてくれ!
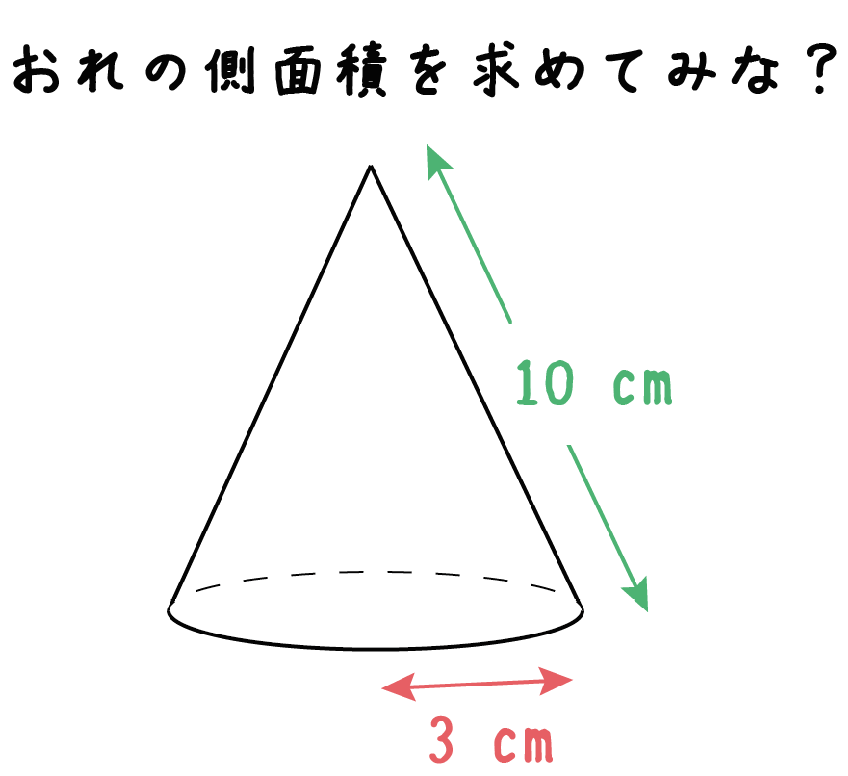
Step1. 底面の「円周の長さ」を求める!
まずは円錐の底面の「円周長さ」を計算しちゃおう!
直径×円周率
だったよね??
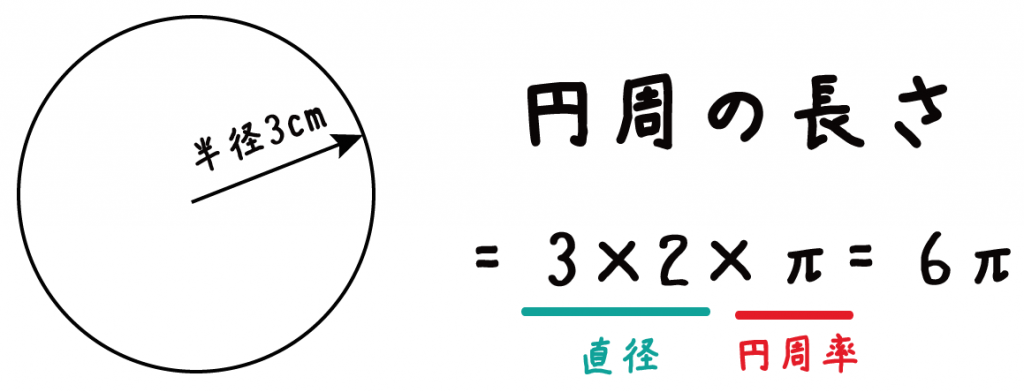
だから例題では、円周の長さは、
3×2×π = 6π
で求めることができるんだ!
Step2. 側面の中心角を求める!
つぎは円錐の側面の中心角を求めるよ。
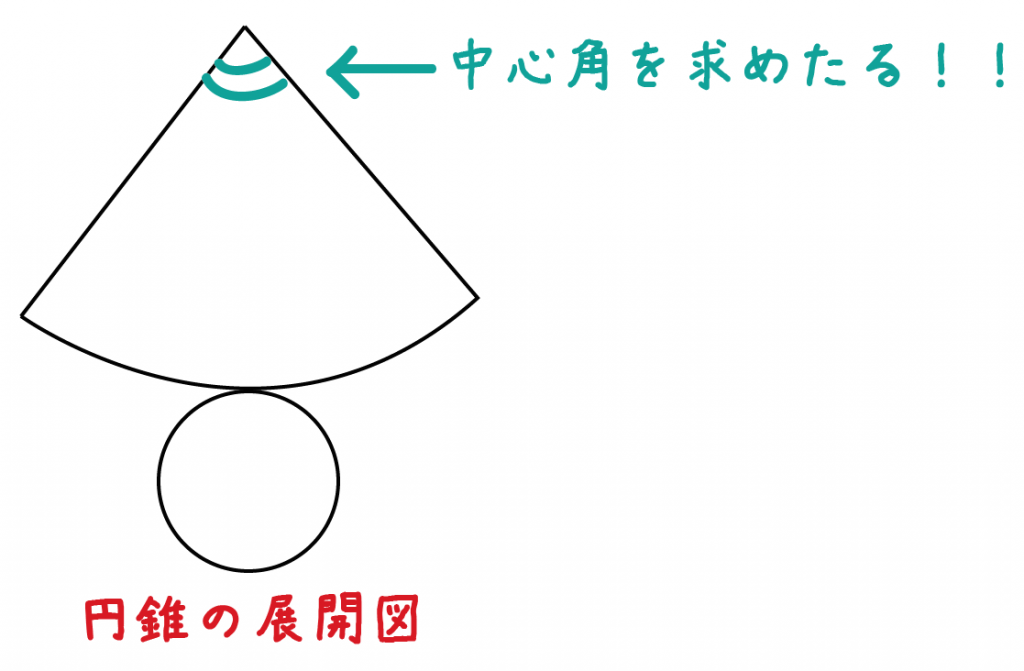
円錐の展開図の書き方で勉強したことを使えばいいんだ。
「円錐の底面の円周長さ」と「側面の扇形の弧の長さ」が等しいよ
っていう方程式をたててみる。
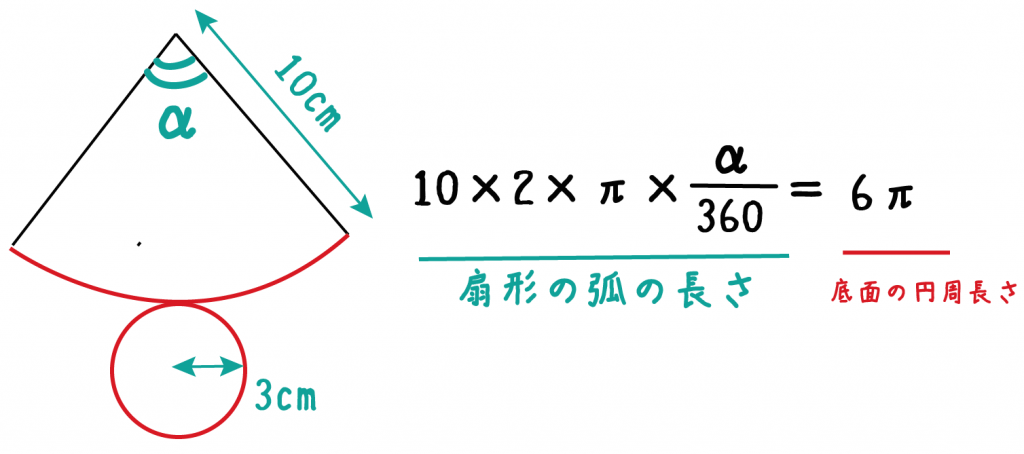
例題で「側面の中心角」をαとしてやると、
10×2×π×α/360 = 6π
になる。このαについての方程式をといてやると、
α = 108°
っていう中心角がゲットできるね!
Step3. 側面積(扇形の面積)をだす!
中心角が求まったね??
最後に、円錐の側面の「扇形の面積」と計算してあげよう。
扇形の面積は、
(半径)×(半径)×(円周率)×(中心角)÷360だったよね??
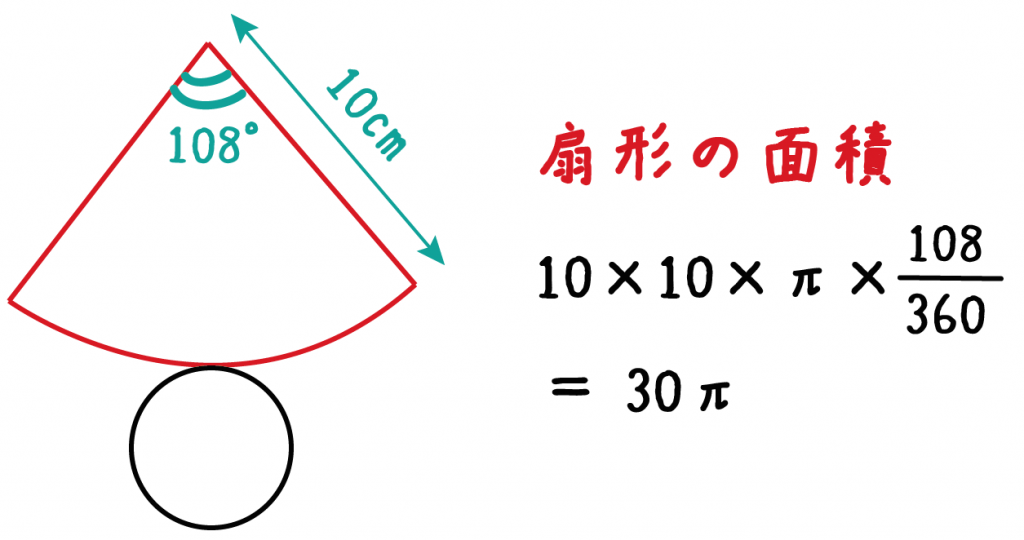
だから、例題の側面の扇形の面積は、
10×10×π×108/360
= 30π
になるんだ!
これはいちばん最初に紹介した、
円錐の側面積 = 円周率(π)×母線(10)×半径(3)
っていう公式の結果と同じだね!!おめでとう!
まとめ:円錐の側面積の求め方は公式に頼らなくてもいい
円錐の側面積を求める問題ってたくさんでてくると思うんだ。
この手の問題でいちばん大切なのは、
公式に頼らない側面積の求め方を知っている
ということ。
求め方さえわかっていれば、公式を忘れても焦らなくていいからね。テスト前に復習してみてね。
そんじゃねー
Ken









