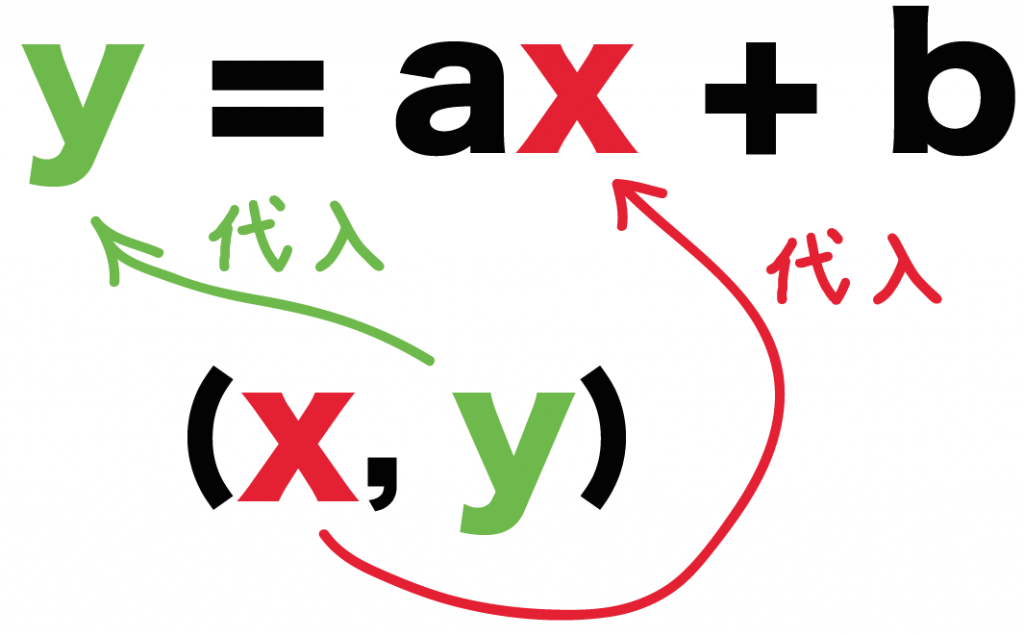2点を通る直線の式の求め方って??
こんにちは!この記事をかいているKenだよ。焼き肉のたれは便利だね。
一次関数でよくでてくるのは、
二点の直線の式を求める問題だ。
たとえば、つぎのようなヤツ ↓↓
例題
つぎの一次関数の式を求めなさい。
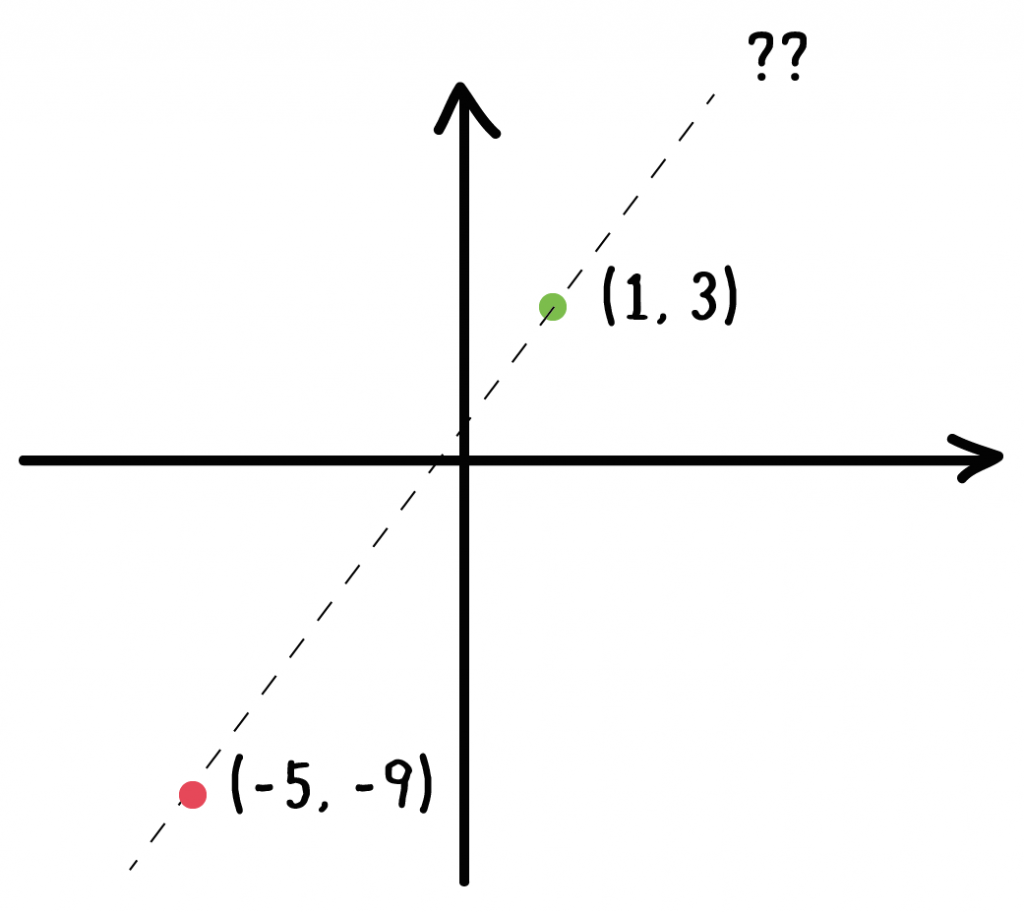
グラフが、2点(1, 3)、(-5, -9)を通る直線である。
今日はこのタイプの問題を攻略するために、
2点を通る直線の式の求め方
を3ステップで解説していくよ。
二点を通る直線の式の求め方がわかる3ステップ
二点を通る直線の式を求める問題には、
- 変化の割合から求める方法
- 連立方程式をたてて求める方法
の2つがある。
どっちか迷うかもしれないけれど、
ぼくが中学生のときは断然、
2番目の「連立方程式をてて求める方法」をつかってたんだ。
シンプルでわかりやすかったからね。計算するだけでいいんだもん。
ってことで、
今日は「連立方程式をたてて求める方法」だけを語っていくよー!
さっきの例題、
例題
つぎの一次関数の式を求めなさい。
グラフが、2点(1, 3)、(-5, -9)を通る直線である。
で直線の式を求めていこう!!
Step1. xとyを「一次関数の式」に代入する
2つの点のx座標とy座標を、
1次関数の式「y = ax + b」に代入してみよう。
例題の2つの座標って、
- (1, 3)
- (-5, -9)
だったよね??
このx座標・y座標を「y = ax + b」に代入すればいいんだ。
すると、
- 3 = a + b
- -9 = -5a + b
っていう2つの式がゲットできるはずだ。
Step2. 引き算してbを消去する
2つの式同士を引き算しよう。
「+b」という共通項を消しちまおうってわけ。
連立方程式の加減法の解き方といっしょだね。
例題の、
- 3 = a + b
- -9 = -5a + b
を引き算してやると、
12 = 6a
になるね。
これをaについてとくと、
a = 2
になる。
つまり、
傾き(変化の割合)は「2」になるってことだね。
Step3. aを代入してbをゲットする
あとは「b(切片)」を求めればゲームセットだ。
さっき求めた「a」を代入してやるだけで、
b(切片)の値がわかるよ。
例題をみてみて。
aの値の「2」を「3 = a+b」に代入してやると、
3 = 2 + b
ってなるでしょ?
これをといてあげると、
b = 1
って切片の値が求まるね。
これで、
- a = 2
- b = 1
っていう2つの値をゲットできた。
ということは、
2点を通る一次関数の式は、
y = 2x + 1
になるのさ。
おめでとう!! これで二点を通る直線の式もマスターしたね。
まとめ:二点を通る直線の式は「加減法」で攻めろ!
2点を通る直線の式は、
- 座標を代入
- 計算
- aを代入
の3ステップで大丈夫。
そんじゃねー
Ken