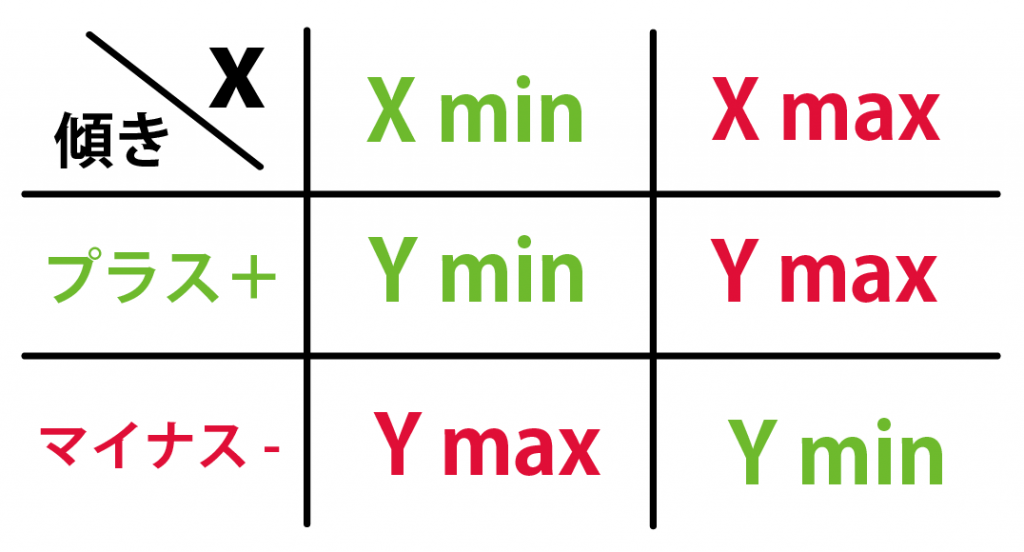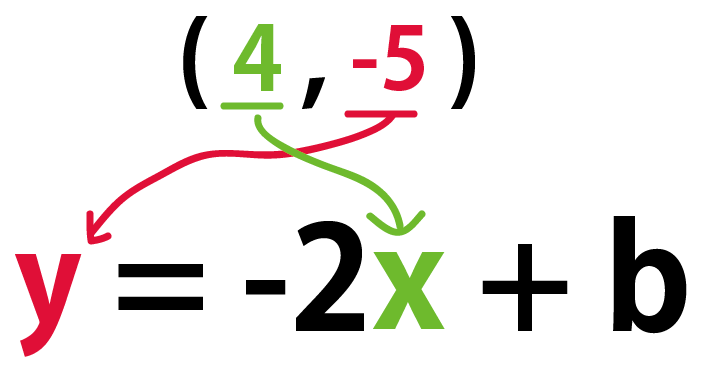一次関数の変域の応用問題を解きたい！
こんにちは！この記事をかいているKenだよ。汗かきたいね。
一次関数の変域の求め方の基礎はわかった。
だけど、ときどき、
変域の応用問題ってでてくるよね。
たとえば、つぎのような問題さ。
y=-2x+bのxの変域がc≦x≦4のとき、yの変域が-5≦y≦5である。bとcを求めなさい。
いっけん楽勝にみえる。
だけどじつは、うっかりミスを誘うトラップ問題なんだ。
今日はこの変域の問題の解き方を3ステップで解説していくよ。
よかったら参考にしてみてね。
一次関数の変域の応用問題の解き方がわかる3ステップ
例題をいっしょにといていこう。
y=-2x+bのxの変域がc≦x≦4のとき、yの変域が-5≦y≦5である。bとcを求めなさい。
この手の問題はつぎの3ステップでとけちゃうよ。
Step1. 傾きの符号をチェックする
まずは問題で登場する、
一次関数の傾きの符号をチェックしよう！
傾きが＋なのか？？
それとも、とんでもなくマイナスなのか？？
さらっと調べてみよう。
例題の関数の、
y = -2x + b
に注目してみて。
こいつの傾きは「-2」。
あきらかにマイナスがついちゃってるよね？？
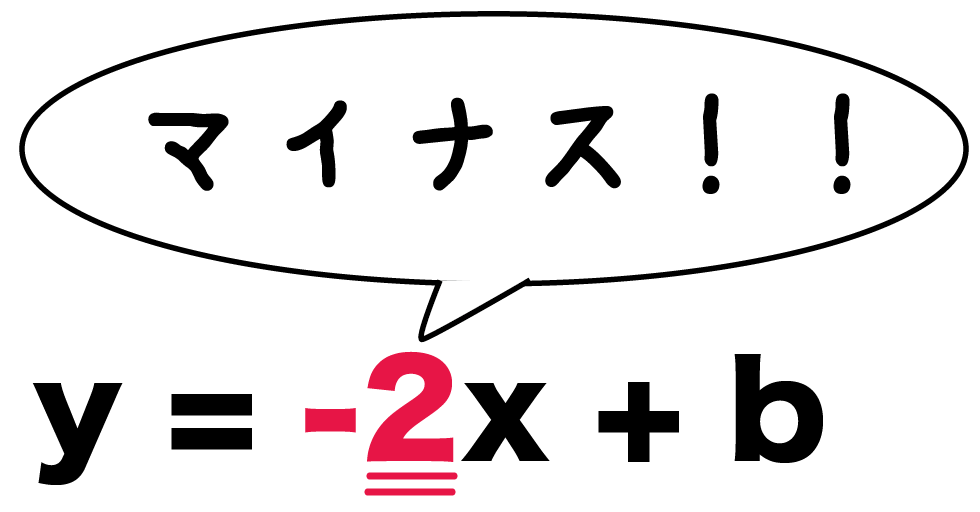
ってことで、例題の傾きは負の数だ。
Step2. 直線が通る2点を求める！
つぎは、
xが大きくなるとyはどうなるか？？
を考えてみよう。
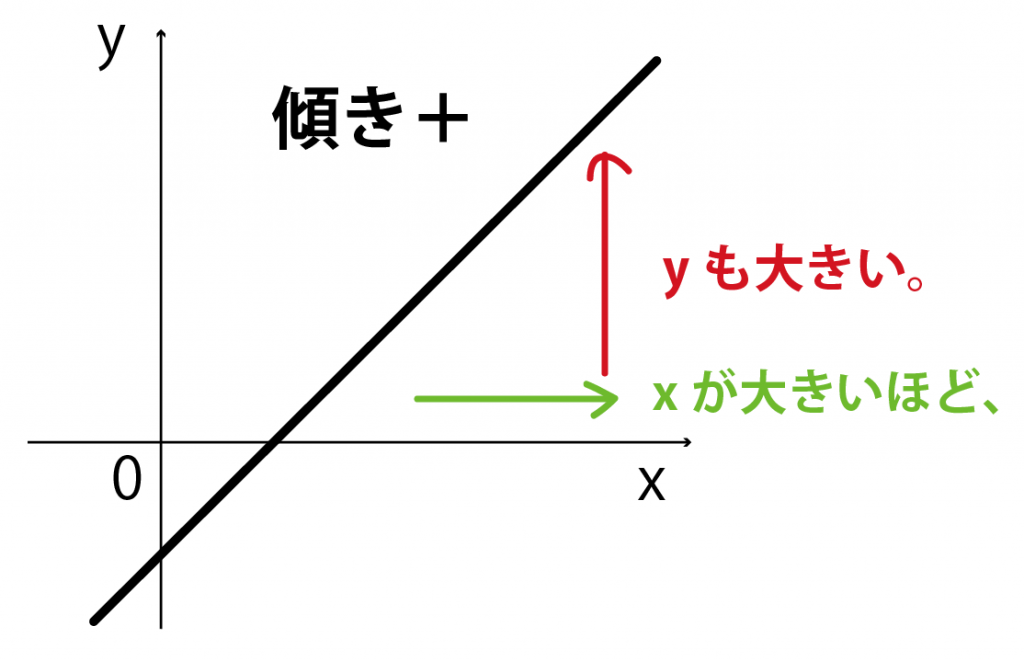
もし、一次関数の傾きが＋のとき、
xが大きければ大きいほどyも大きいね？
だから、xが最大値になるとき、yも最大値になるってわけ。
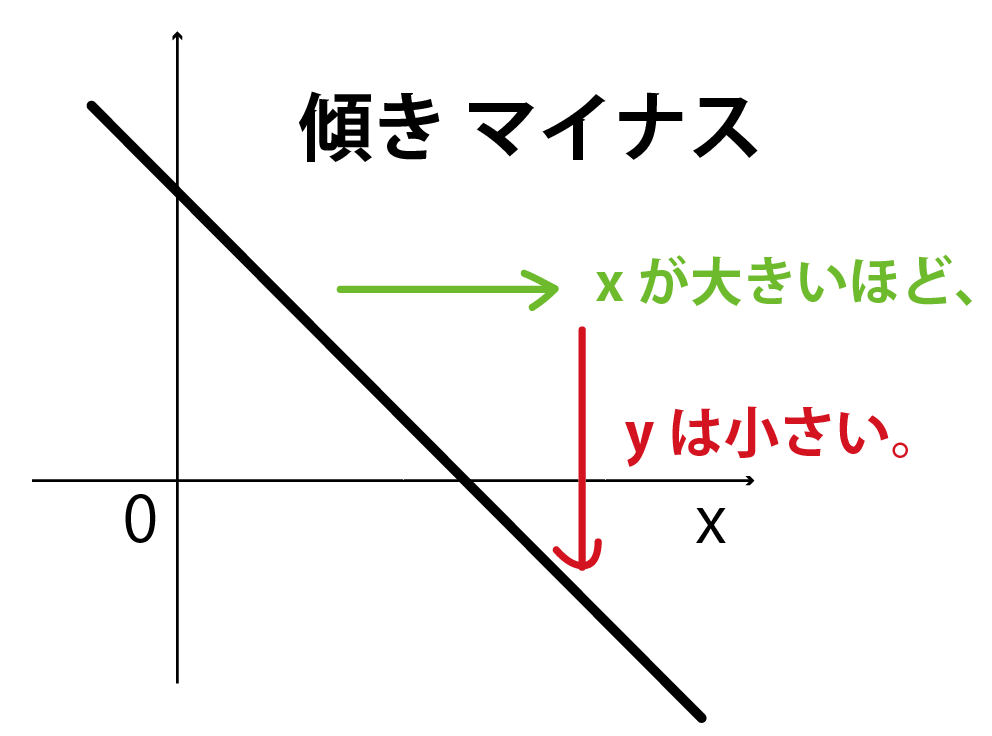
逆に、傾きが -のとき、
xが大きければ大きいほどyは小さくなっちゃう。
だから、xが最大値のときはyは最小値になるわけさ。
つまり、これをまとめるとつぎのようになる↓↓
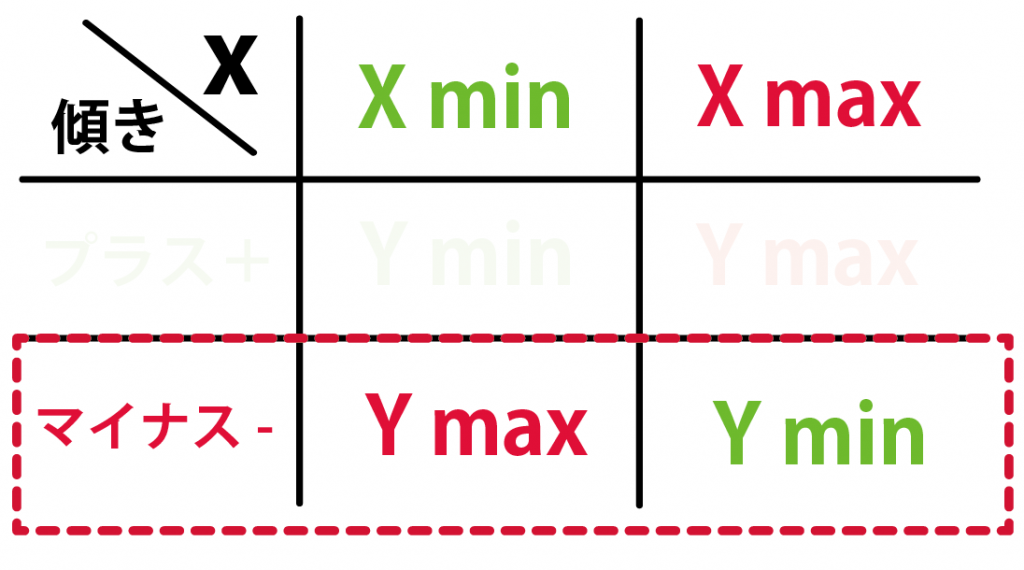
- 傾きが「＋」： xが最大値のとき、yは最大値。xが最小値のとき、yは最小値
- 傾きが「−」： xが最大値のとき、yは最小値。xが最小値のとき、yは最大値
※ min：最小値、 max: 最大値
例題をみてみよう。
一次関数の傾きは「マイナス」だったよね？？
xとyの変域から最小値・最大値をだしてみると、
- x： 最小値 = c, 最大値 = 4
- y : 最小値 = -5, 最大値 = 5
になってるね。
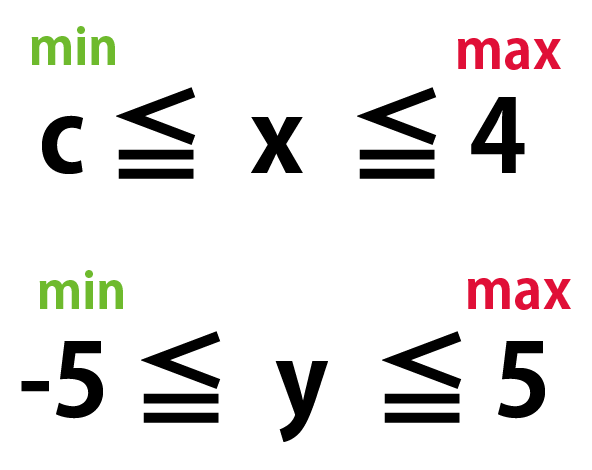
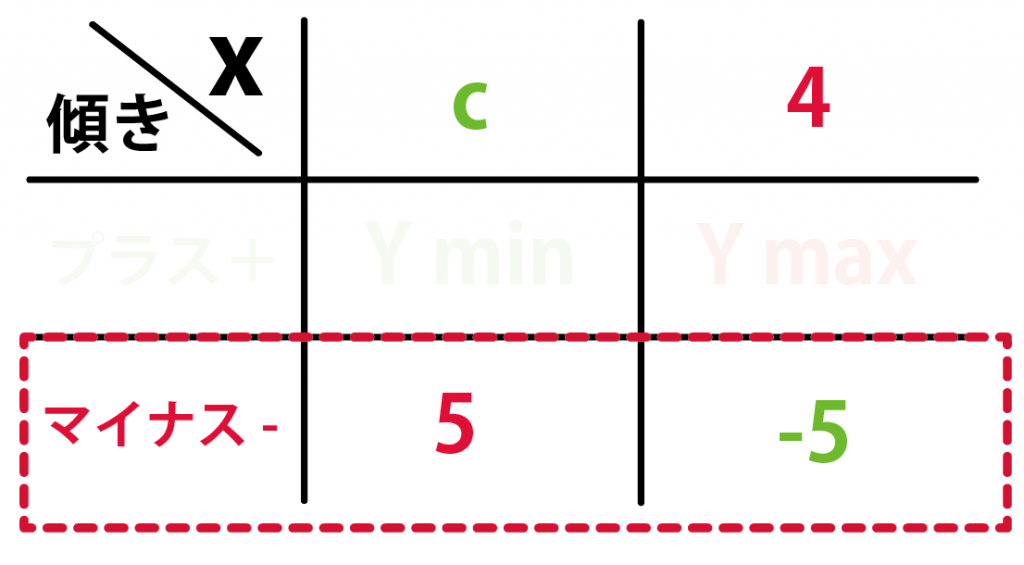
んで、一次関数の傾きがマイナスだから、
- xが最小値cのとき、yは最大値5
- xが最大値4のとき、yは最小値-5
になるんだ！
つまり、
y = -2x + b は、
- (c, 5)
- (4, -5)
の2点を通るんだ。
こんな感じで、
xとyの組み合わせをみつけるのが第2ステップだよ。
Step3. 座標を直線の式に代入する！
最後は、2つの座標を式に代入してみよう。
例題の直線は、
- (c, 5)
- (4, -5)
の2点を通るはずだったね？？
こいつを直線の式、
y = -2x + b
に代入してbを求めればいいんだ。
さっそく、y = -2x + bに（4, -5)を代入すると、
y = -2x + b
-5 = -2 × 4 + b
b = 3
になるね。
つぎは、bの値がわかった一次関数の、
y = -2x + 3
に（c, 5）を代入してcを求めてみよう。
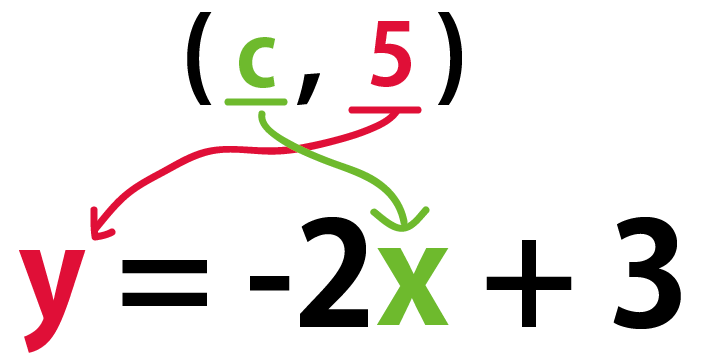
すると、
y = – 2x + 3
5 = – 2c + 3
c = -1
になるよ。
これで文字の正体がわかったね。
- b = 3
- c = -1
おめでとう。
まとめ： 一次関数の応用問題はグラフをかかなくても楽勝！
一次関数の変域の問題はよく、
グラフをかけば解ける
っていわれる。
だけどね、ぶっちゃけグラフなんていらん。
傾きの符号をみて、xとyの組み合わせを考えればいいんだ。
応用問題におそれず挑んでいこう！
そんじゃねー
Ken
