「少なくとも」がついた確率の求め方がわからん!
こんにちは!この記事をかいているKenだよ。もやしは安いね。
確率でたまーに、
「少なくとも」
がつく問題でてくるよね???
たとえば、つぎのようなやつだ↓↓
例題
4枚のコインをなげて少なくとも1枚が表になる確率を求めなさい。
こんな感じで、「少なくとも」がついている問題は、
ふつうに解くとメンドイ。
楽な計算方法をつかってみよう!
そこで今日は、
「少なくとも」がついた確率の求め方
を3ステップで解説していくよ。
よかったら参考にしてみて。
「少なくとも」がつく確率の求め方の3ステップ
「少なくとも」がつく確率の問題。
世の中にはたくさんある。
今回紹介するのは、
少なくとも1枚/回がAになる確率
を求める問題の解き方だよ。

この手の問題は3ステップで計算できちゃうんだ。
- 「ぜんぶAにならない」をさがす
- 確率を計算
- 「1」から確率をひく
さっきの例題を解説していくよー
例題
4枚のコインをなげて少なくとも1枚が表になる確率を求めなさい。

Step1. 「ぜんぶAにならないこと」をみつける
まずは、
ぜんぶAにならないこと
をみつけよう。

例題では、
少なくとも1枚表になる確率
を求めるんだったよね??
Aにあたるのは、
表になる
ってこと。
つまり、「ぜんぶAにならないこと」は、
ぜんぶ表にならないこと
だね。

これが第1ステップだ!
Step2. 「ぜんぶAにならないこと」の確率を計算
つぎは、さっきの、
ぜんぶAにならないこと
の確率を計算してみよう!

例題でいうと、
コインを4回なげて、ぜんぶ表にならない確率
ってことだね。
これは、
コインを4回なげてぜんぶ裏になる確率
ってこと!
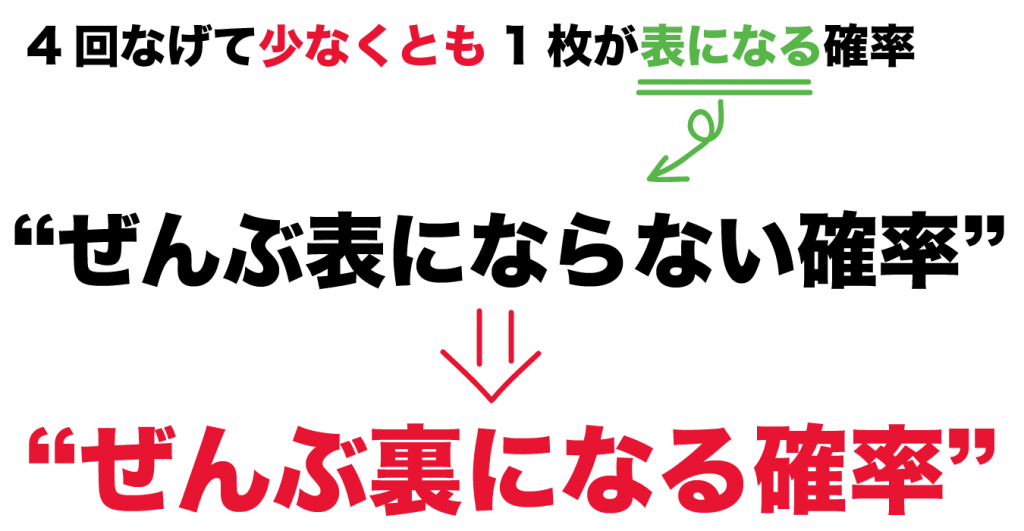
コインを4枚なげると、表裏の組みあわせはぜんぶで16通り。
ぜんぶ裏になる場合の数は1通りしかない。
よって、ぜんぶ裏になる確率は、
16分の1
になるはず!
>>コインの確率の求め方はこちら

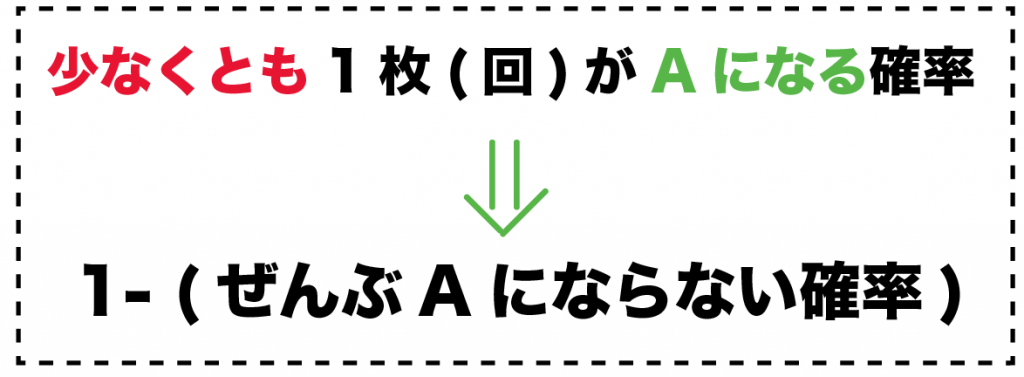
Step3. 「1」から確率をひく
最後に、その確率を1からひいてみよう。
つまり、
1 – (ぜんぶAにならない確率)
を計算すればいい。
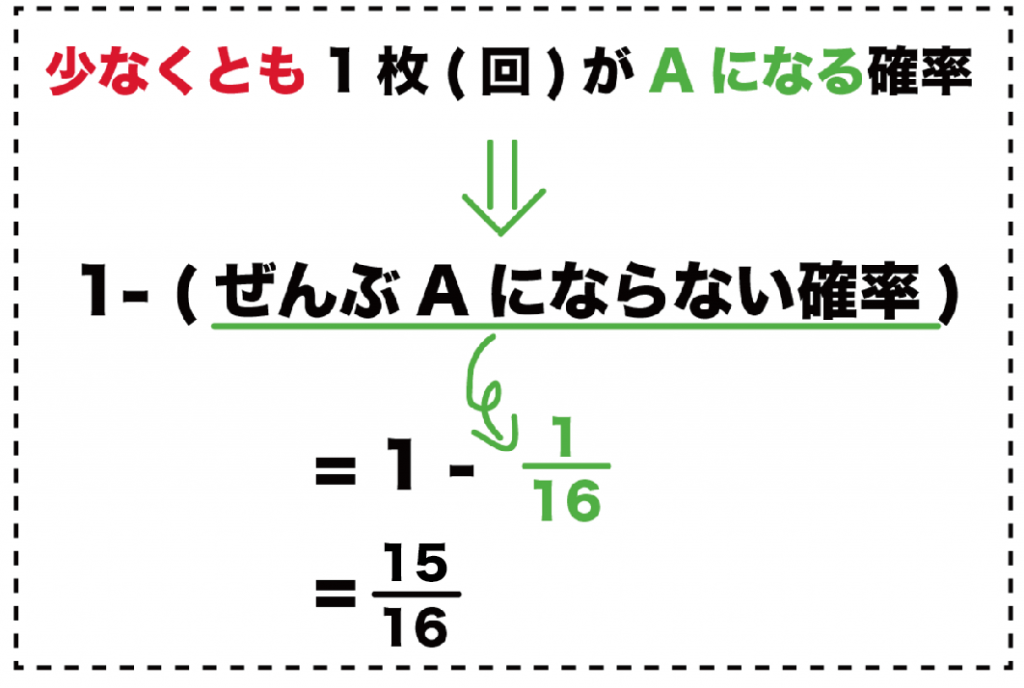
例題では、「ぜんぶAにならない確率」は、
16分の1
だったよね??
よって、
1 – (ぜんぶAにならない確率)
= 1- (16分の1)
= 16分の15
になるんだ。
おめでとう。
「少なくとも」の確率問題も攻略だね!!
なぜこんな確率の解き方をするの??
でもさ、
なぜメンドイ方法で計算するんだろう??
って思うない??
ふつうに確率の求めればいいじゃない!?
って切れてるヤツもいるかもしれない。

この解き方を使う理由は、
「少なくとも1枚(回)がAになる」場合の数が多すぎるからなんだ。
ふつうに計算すると、場合の数をかぞえるときに苦戦する。

だから、ストレートに確率を計算するんじゃない。
「ぜんぶAにならない場合の数」を数えて確率をだすんだ。
「少なくともAにならない確率」と、
「ぜんぶAにならない確率」を足したら1になるはずだね??
だって、どちらかは絶対に起きるからね。
つまり、足したら1、100%起きる確率になるのさ。

だから、
ゼッタイに起きる確率の「1」から「ぜんぶAにならない確率」
をひいてやると、
「少なくともAにならない確率」
を計算できちゃうんだ。
どう??スッキリしたかな??
まとめ:「少なくとも」がつく確率は1からひこう!
「少なくとも」がつく確率の問題は、
1から「ぜんぶAにならない確率」をひいてみよう!
これで計算が早くなるはず。;
じょじょに慣れていこうね!
そんじゃねー
Ken









