中央値(メジアン)を求める意味あるの??
こんにちは!この記事をかいているKenだよ。抹茶最高。
中学数学で、
中央値(メジアン)を求める問題
ってでてくるよね??
復習すると、中央値とは、
大きい順にならべたときに真ん中にくる値
のことだったね。
中央値の求め方はマスターした。
何度だってメジアンをだすことができそう・・・!
だけれども、
何度も何度も中央値(メジアン)をもとめてるとこう思わない?
そう、
中央値を求める意味ってあるのかなあ??
ってね。

そんな疑問を解消するために、
中央値(メジアン)を求める意味を解説していくよ。
中央値(メジアン)をだす意味とは??
中央値をだす意味はずばり、
特殊なデータがいてもぶれない代表値
だからだ。
代表値としてよくつかわれるのは平均値。
こいつはデータの中に変わったやつがいると、
ぶれぶれになっちゃうんだよ。

例として中央値の求め方でとりあげた、
砲丸投げの例をみてみよう。

Aさん〜Jさんまで10人が砲丸投げに挑戦した話だったね。
砲丸投げの記録をデータにしてみたんだ。
体育の先生が、
こいつらのパワーはどれくらいなのか??
ってことをみるために代表値を参考にしているよ。
今回はつぎの2つのパターンをみてみよう。
- 飛び抜けたやつがいないケース
- むちゃくちゃすげえやつがいたケース
ケース1. 飛び抜けたやつがいないとき
みんな同じぐらいの記録だったケースだ。
すごすぎるやつもいないし、
しょぼすぎるやつもいない。
たとえば、つぎの記録データが得られたとしよう。

- Aさん: 7 m
- Bさん: 4 m
- Cさん: 5 m
- Dさん: 9 m
- Eさん: 11 m
- Fさん: 3 m
- Gさん: 4 m
- Hさん: 12 m
- Iさん: 6 m
- Jさん: 7m
このとき、平均値をだしてみよう。
平均値の出し方をつかえば、
平均値 =(全部のデータの合計)÷(データ数)
= (7 + 4 + 5 + 9 + 11 + 3 + 4 + 12 + 6 ) ÷ 10
= 6.1
になるね!
この平均値という代表値をみた先生は、
ふーん、近頃の若いヤツはこんなもんかあー
って納得するはず。
ケース2. 飛び抜けてすごいやつがいるとき
つぎは、
他とあきらかに違うデータがいるときだ。
このとき、
平均値は変な数値になってしまうんだ。
たとえば、砲丸投げの例をもう1回考えてみよう。
Aさんがこの日だけ、むちゃ覚醒したんだ。
世界記録を塗り替る宇宙記録100mをだしちゃっとしよう。

このときの平均値を計算してみよう。
平均値 =(全部のデータの合計)÷(データ数)
= (100 + 4 + 5 + 9 + 11 + 3 + 4 + 12 + 6 ) ÷ 10
= 15.4
すると、Aさんの宇宙記録のせいで、
平均がぐんと上がっているよね??
なんと、
平均が15.4m。
Aさん以外、ひとりも15m以上とばせてないのにだよ??
それなのに平均が10だなんておかしいじゃないか!
これじゃあ代表値の役割をはたしていないね。
そんなとき、代表値に「中央値(メジアン)」をつかってやれば一件落着。
メジアンをだしてやると、
(中央値)= {(真ん中1 )+ (真ん中2)} ÷ 2
= (7 + 6)÷2
= 6.5
になるね!
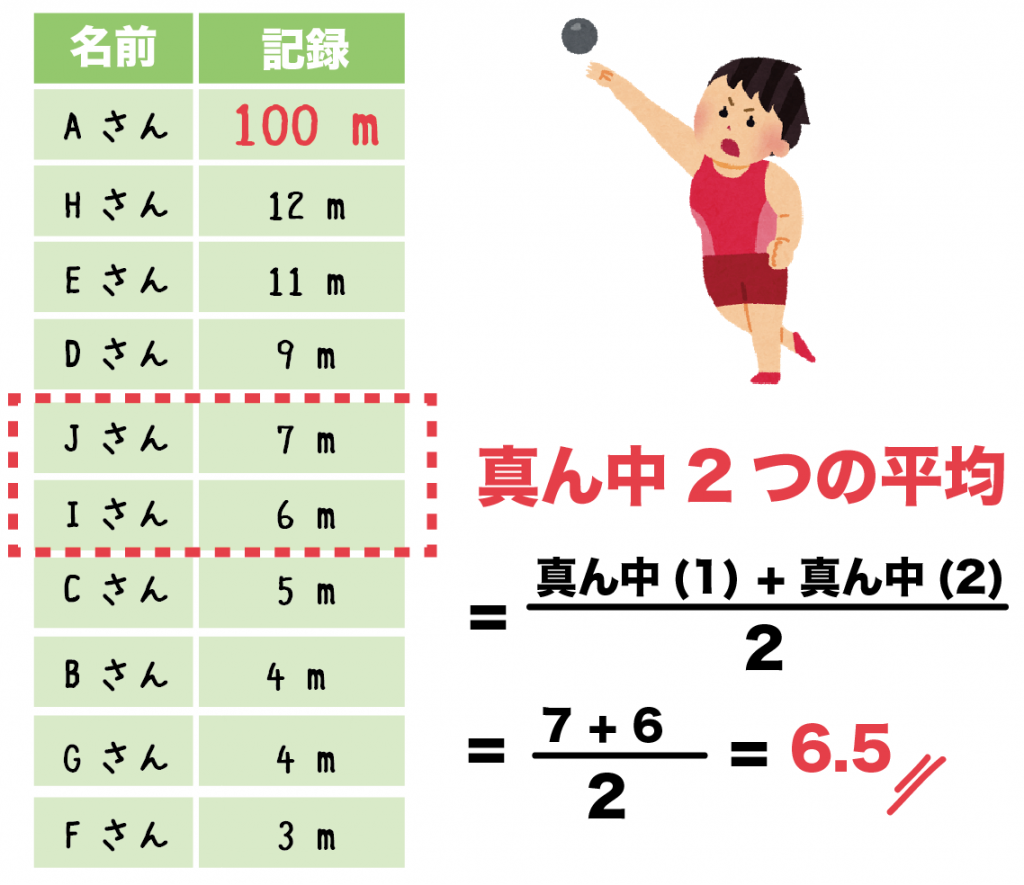
※中央値の求め方はコチラ
この中央値は平均値15.1とくらべるとかなり妥当。
ちょうど真ん中の記録って感じだ。
ぶれる前の平均値の「6.1」にだいぶちかい。
これなら体育の先生もまどわされずにすむね。
こんな感じで、中央値は、
特殊なデータの影響をうけにくい代表値なんだ。
よーくおぼえおこう!
まとめ:中央値を求める意味は、ある!
平均値は計算しやすくて便利。
中央値みたいにデータを並び替えなくていいからね。
たくさん使うチャンスがあるかもしれない。
だけれども、
中央値にはぶれにくい
っていうメリットがあるんだ。
とびぬけたデータがいるときの代表値として存在する意味があるんだ。
中央値の出し方をマスターしてガンガンつかっていこう!
そんじゃねー
Ken









