一次関数でいう「変化の割合」とは何者?!?
こんにちは!この記事をかいているKenだよ。麻婆豆腐うめえよ。
一次関数で知っておきたいのは、
変化の割合
というキーワードだ。
こんな言葉、滅多に使わないよね??
おれ、変化の割合のこと・・・好き・・・
なんてセリフは出てこないはずだ。
そんなよくわからない、
「変化の割合」
をわかりやすく説明していくよ。
よかったら参考にしてみてね。
一次関数の「変化の割合」とは・・・??
一次関数の「変化の割合」とは、
xが1増えたらyがいくら増えるのか、減るのか
の数値のこと。
「yの増加量」を「xの増加量」でわってやれば「変化の割合」になるんだ。
変化の割合 = yの増加量/ xの増加量
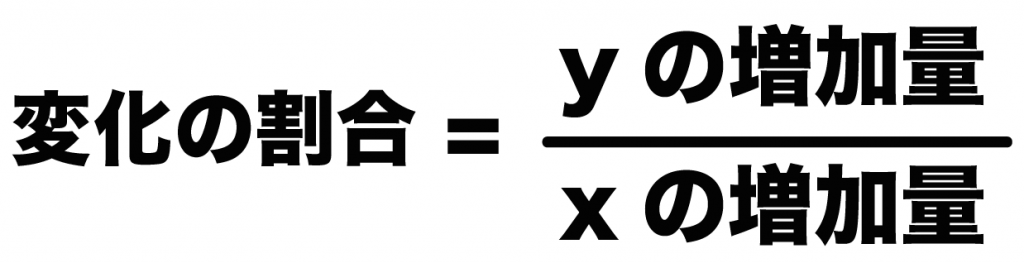
たとえば、
xが2増えたとき、yが10増えたとしよう。
このとき、
- xの増加量:2
- yの増加量:10
だよね。だから変化の割合は、
(yの増加量)÷(xの増加量)
= 10 ÷ 2
= 5
になるね。
つまり、xが1増えたらyが5増える一次関数ってことなのさ。
ここまで大丈夫??
一次関数の変化割合の特徴って??
もう一方踏み込んで、
一次関数における変化の割合の特徴
をつかんでおこう。
最大の特徴は、
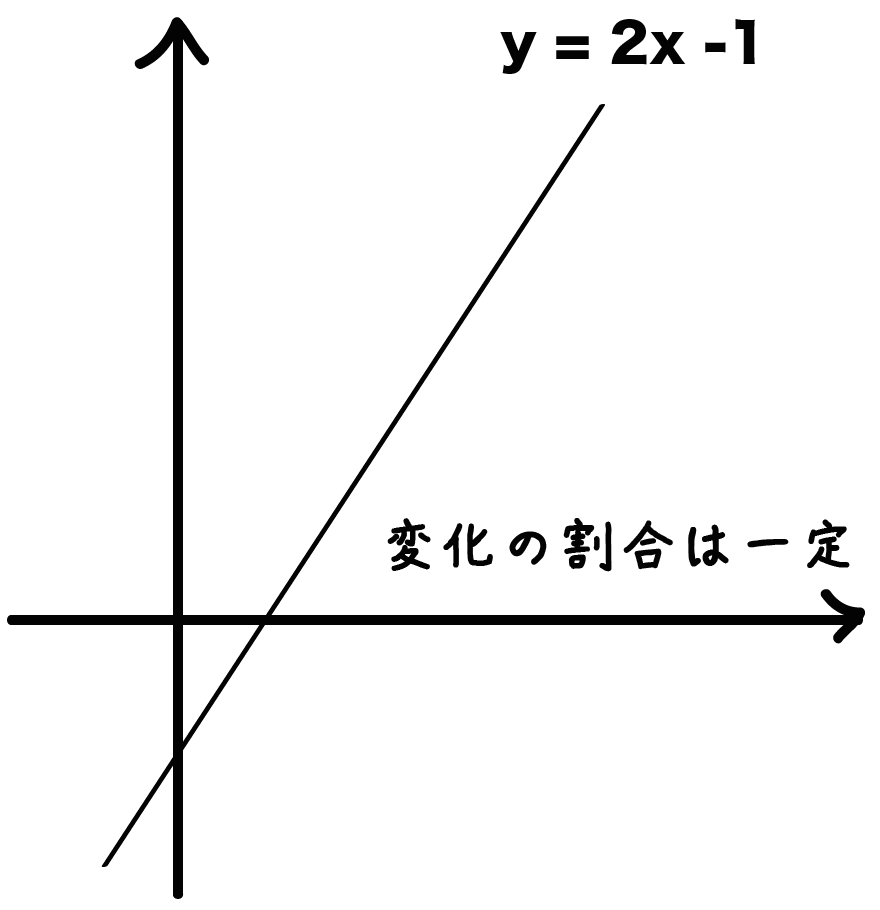
1次関数の変化の割合はずーーーっと一定
ってことなんだ。
つまり、一次関数の途中で「変化の割合」が変わったりしないんだ。
たとえば、
y = 2x +1
という一次関数があったとしよう。
こいつは、
- xが2だけ増加したとき
- xが10だけ増加したとき
も、変化の割合はずっと2で同じなんだ。
ゼッタイに変わらない。
これが一次関数の変化の割合の特徴さ。
逆に、一次関数でもへったくれでもない関数だったらどうなる??
そう。
変化の割合は一定じゃない。
もうね、コロコロ変わるんだ。
たとえば、つぎのようにクレイジーな関数がいたとしたら、
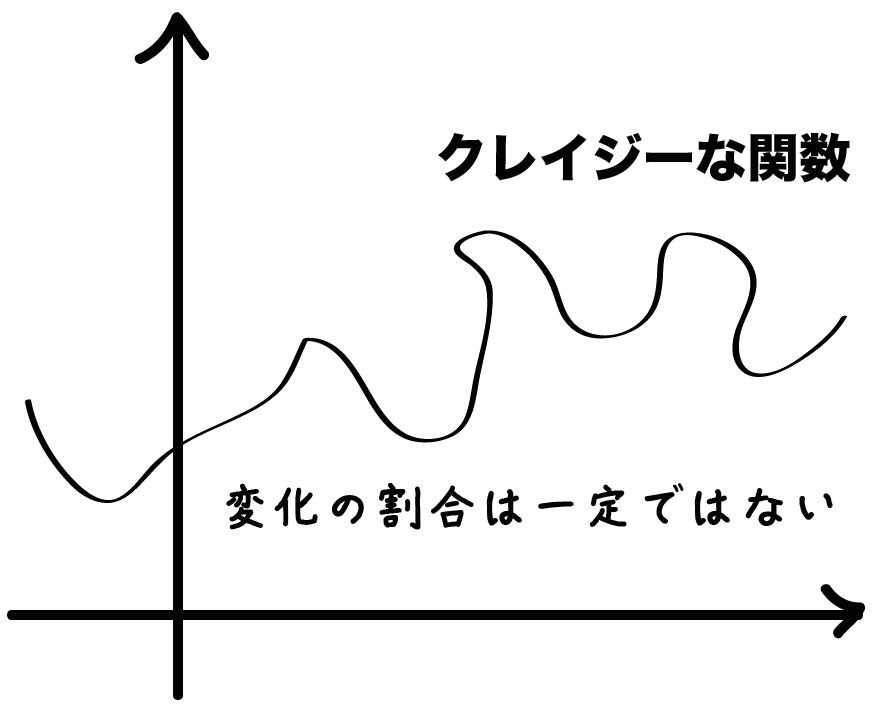
変化の割合はまさに暴れ馬。
xがどの範囲で変化するかによって、ぜんぜん変化の割合がちがうんだ。
一次関数では「変化の割合」が一定である
ってことをおぼえておこう。
まとめ:1次関数の「変化の割合」とは「xが1増えた時のyの増加量」
一次関数の変化の割合もわかったかな??
コツさえつかめれば問題がとけるようになるから、
ゆっくりと勉強していこうね。
そんじゃねー
Ken










