平行線の性質はむちゃくちゃ使える？？
こんにちは！この記事をかいているKenだよ。川にはまっているね。
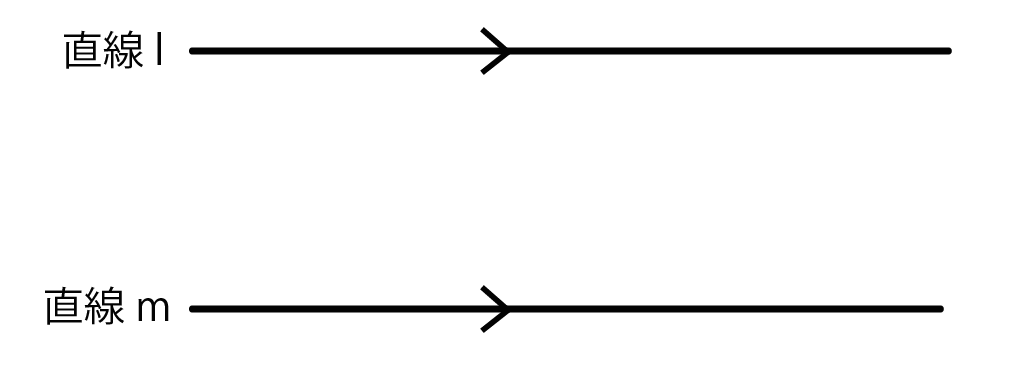
平行線が2本あったとしよう。
名は、
「直線l」と「直線m」
という。
ある日コイツらに、
直線nが交わったとしよう。そう、いきなりだ。
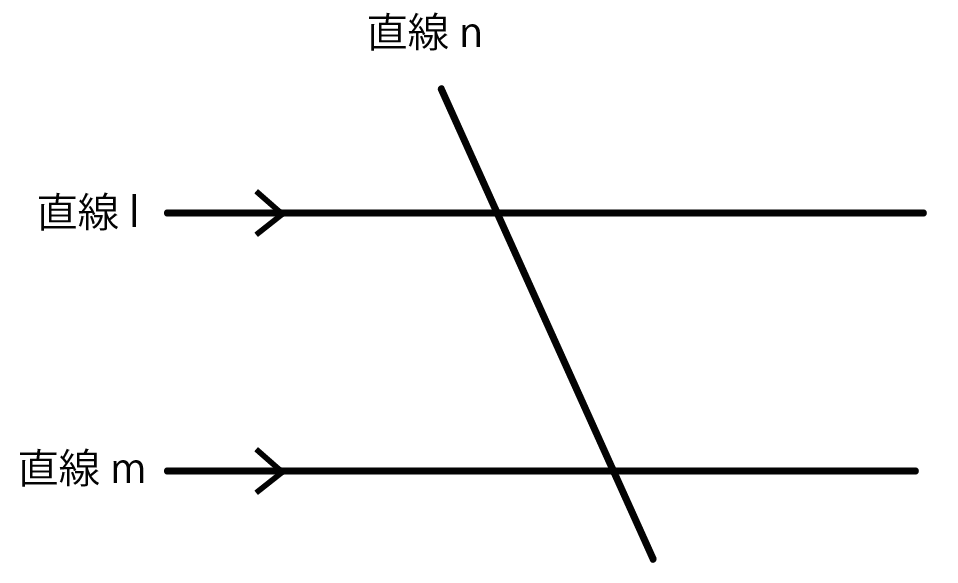
もちろん、平行線の直線lとmはビックリしている。
だけど、この時点で、
平行線の性質
がつかえるようになる。
それは、
2つの直線に1つの直線が交わっているとき、
- 同位角が等しい
- 錯角が等しい
という性質だ。
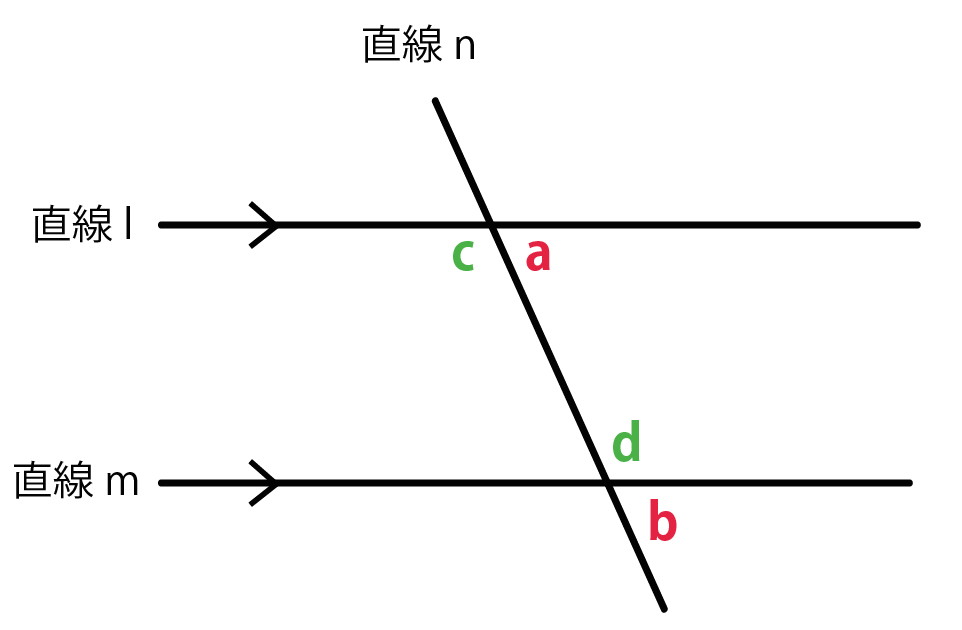
図でいうと、
- 同位角が等しい（a = b）赤
- 錯角が等しい（c = d）緑
だね。
今日は平行線の性質をつかって、
問題をといてみよう！
平行線の性質で問題をクリアする方法
つぎの問題をといてみよう。
例題
下の図で、l // m のとき、角度x の大きさを求めなさい。
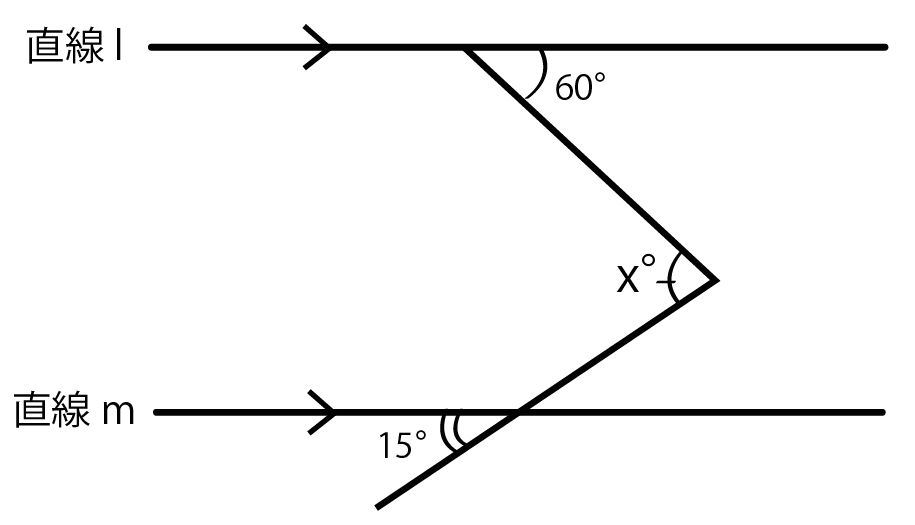
この手の問題は3ステップで攻略できちゃうよ。
Step1. 新たな平行線nをひく！
直線lとmに平行なnをひいてあげよう。
ひく場所は、
角xの頂点のところだ↓↓
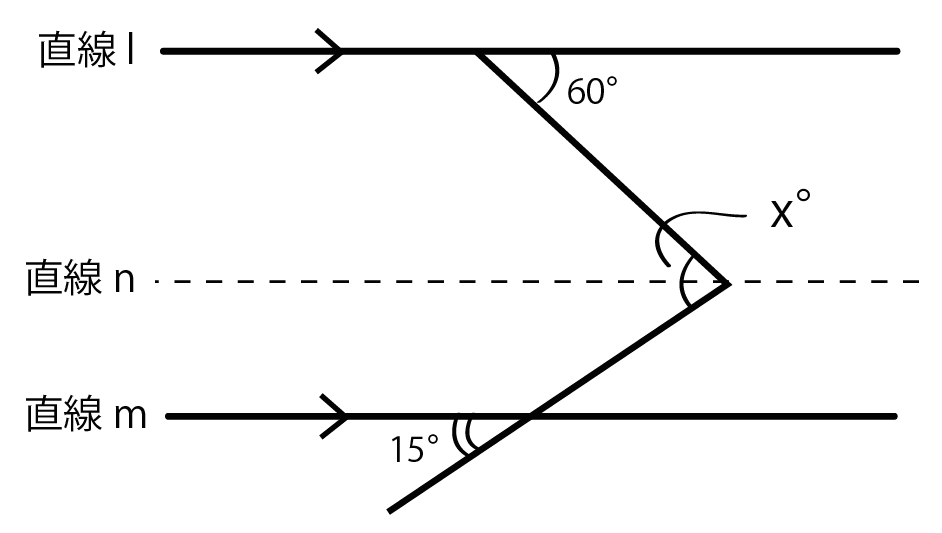平行線の性質をつかうために、平行線を増やしたわけさ！
Step2. 平行線の性質「同位角が等しい」を使う
平行線の性質の、
同位角が等しい
を使ってあげよう。
直線mとnに注目してみて。
コイツらで同位角が等しいことをつかってやると、
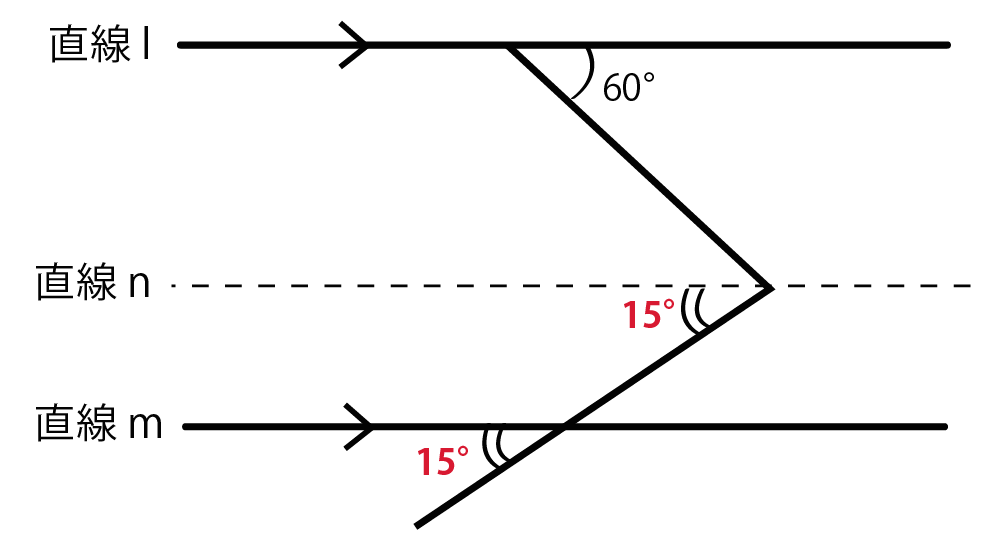
角xの下半分が15°になるね。
あともう少し！
Step3. 平行線の性質「錯角が等しい」を使う
つぎは、
錯角が等しい
という性質をつかおう。
直線lとnに注目してみて。
2つの直線は平行線だから、
錯角が等しいことをつかってみよう。
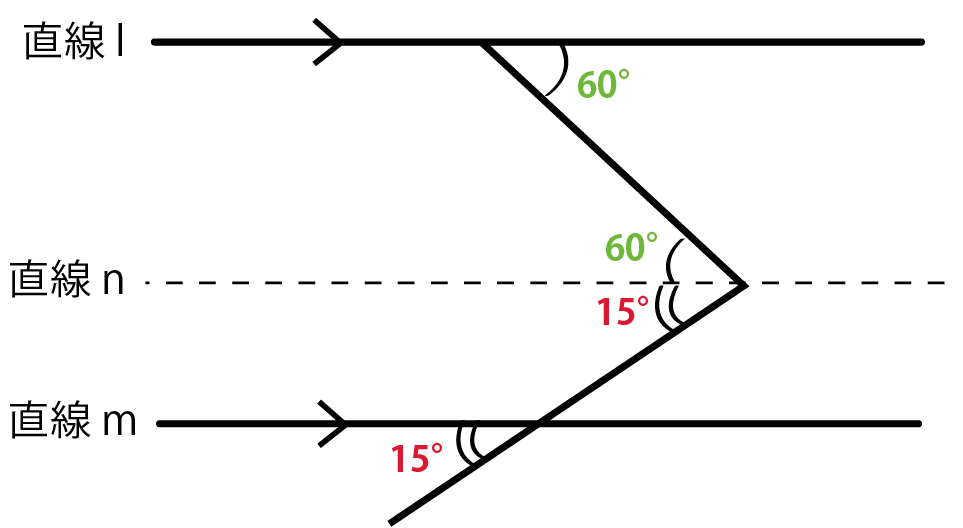
すると、
角xの上半分は60°になるね。
ってことで、
Step2と3の角たちをたすと、
角度x ＝ 75°
になる。
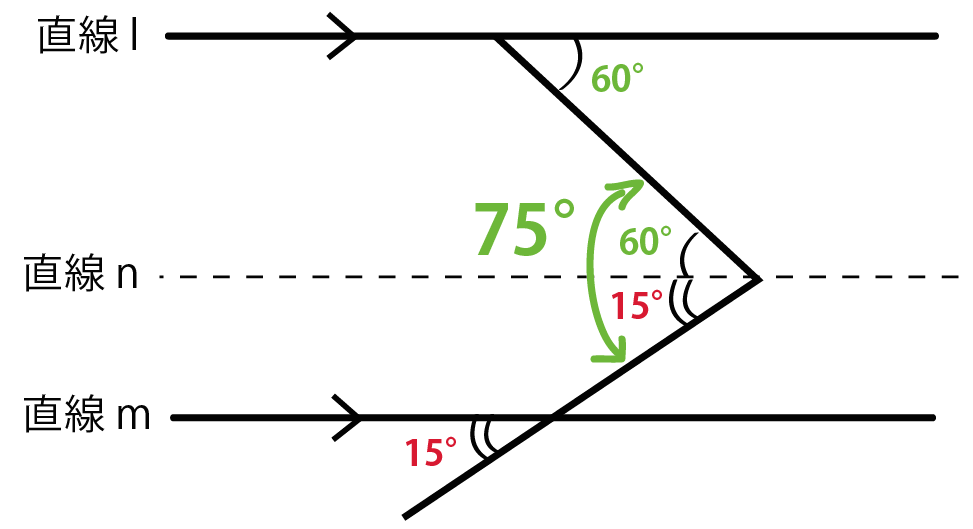
これで問題クリアだよ。おめでとう。
まとめ：平行線の性質は平行線が多いほど便利！
平行線の性質である、
- 同位角は等しい
- 錯角は等しい
はむちゃくちゃ便利。
ポイントは、
足らなかったら平行線を増やす
ということ。
これにつきるね。
必要だったら平行線をじゃんじゃん追加しよう！
そんじゃねー
Ken
