正多角形の外角の大きさをどうしても知りたい!
こんにちは!この記事をかいているKenだよ。鍋つくりたいね。
正多角形の外角の大きさがわからない・・・・・
そんなときは公式をつかえば一発。
正n角形の外角の1つの大きさは、
360°/n
になるんだ。
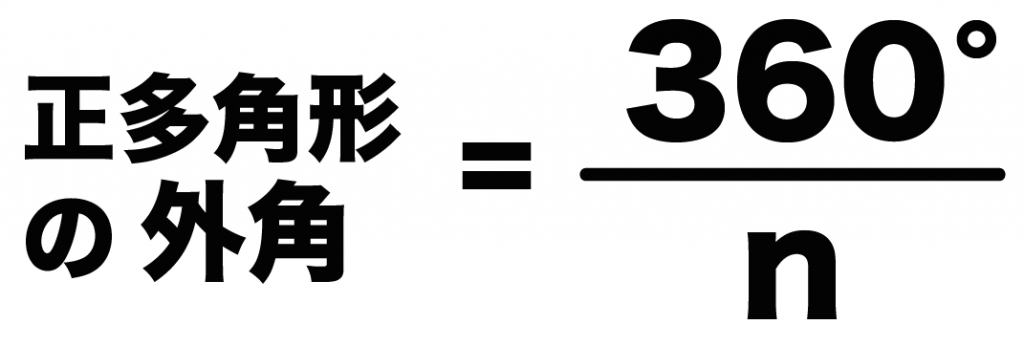
たとえば、正五角形の外角を求めてみよう。
公式のnに「5」を代入してやればいいから、
360°/ n
= 360°/ 5
= 72°
になるね。
つまり、正五角形の外角の1つの大きさが「72°」になっているってことさ。
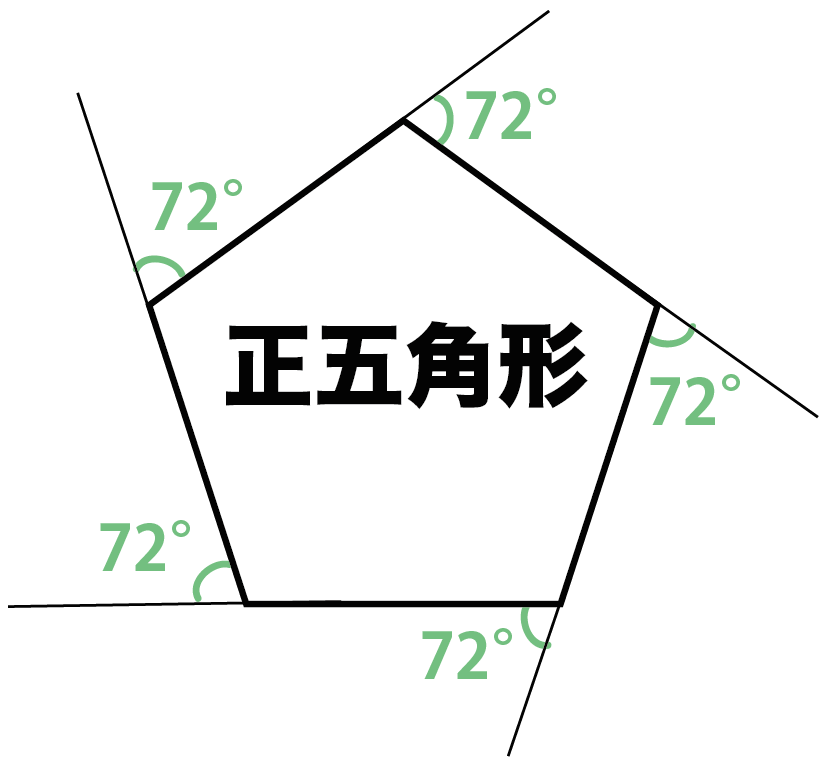
どう??神秘的でしょ??。
なぜ正多角形の外角の公式がつかえるの??
nに頂点の数をいれるだけでいい。
むちゃくちゃ便利だよね?
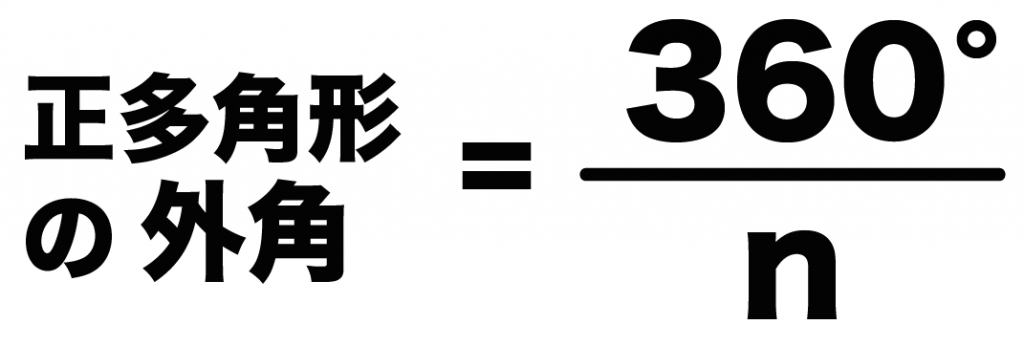
せっかくだから、
なぜ、
360°/n
で正計算できるか振り返ってみよう。
正多角形だろうが、何角形だろうが、
多角形の外角の和は360°になるって勉強したよね??

んで、
正多角形には「すべての内角が等しい」という性質がある。
ってことは、
内角と隣り合っている「外角もすべて等しい」ってことになるよ。
だから、正多角形の1つの外角の大きさは、
(多角形の外角の和)÷ n
= 360°/n
になるんだ。
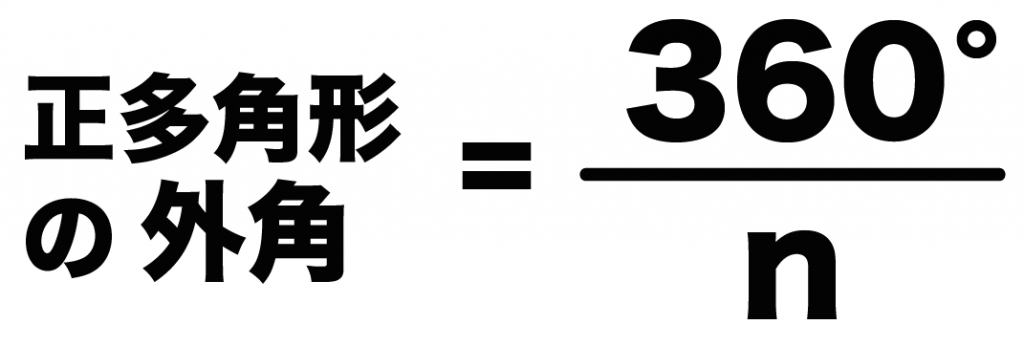
ただ公式をつかうだけじゃなくて、
なぜ、使えるのか??
ってこともおさえておこう!
まとめ:正多角形の外角の大きさはたまーにでてくる!
正多角形(n角形)の大きさは、
360°/n
で計算できちゃうよ。
テストで出たらガンガン得点をうばっていこう!
そんじゃねー
Ken









