ひし形(菱形)の面積の求め方の公式って??
こんにちは!この記事をかいているKenだよ。ドタキャンはきついぜ。
ひし形(菱形)の面積の求め方の公式は、
大きく分けて、
2つ
あるんだ。
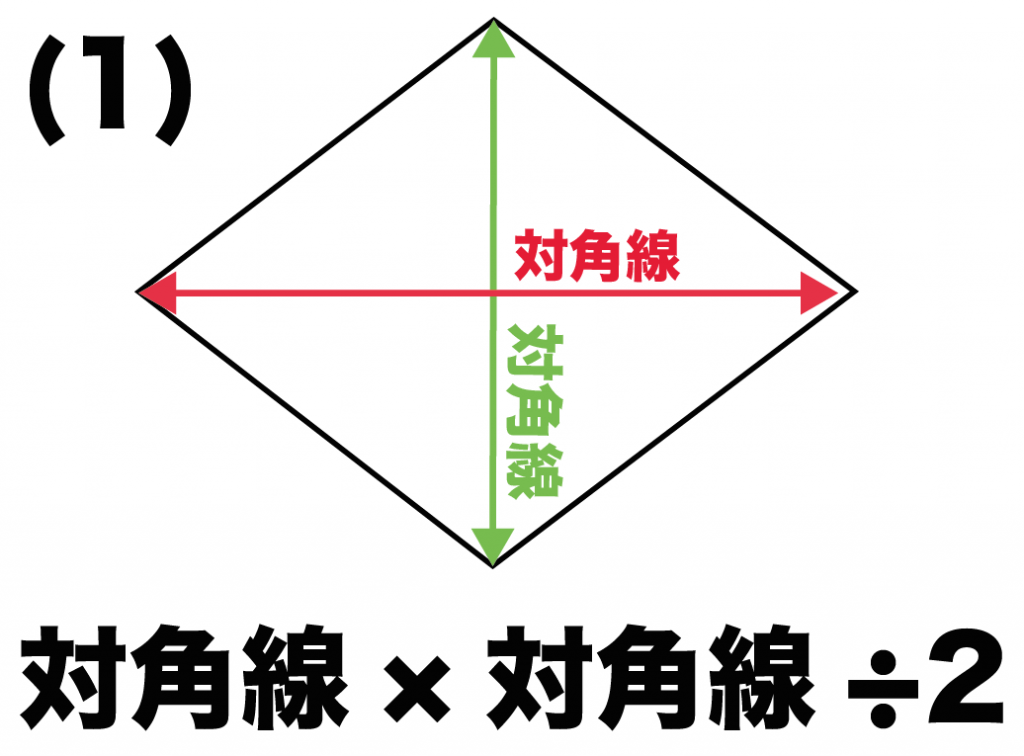
対角線×対角線÷2
ってやつ。
それと、
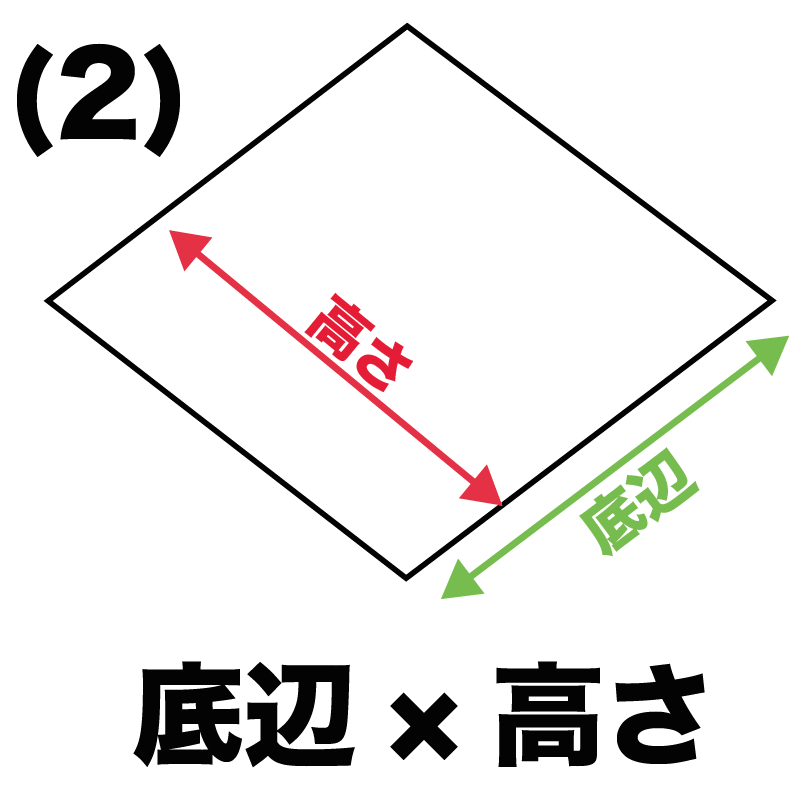
底辺×高さ
って公式だ。
どっちも便利だけど、
どっちの公式を使えば良いのか??
迷っちゃうよね。
そこで今日は、
ひし形の面積の求め方を2つわかりやすく解説してみたよ。
よかったら参考にしてみてー
〜もくじ〜
- 対角線をつかった公式
- 底辺と高さをつかった公式
対角線をつかったひし形の面積の求め方
対角線で「ひし形の面積」を計算できちゃう公式だ。
さっきも紹介したけど、
対角線×対角線÷2
で計算できちゃうんだ。

菱形の面積の公式をつかってみよう!
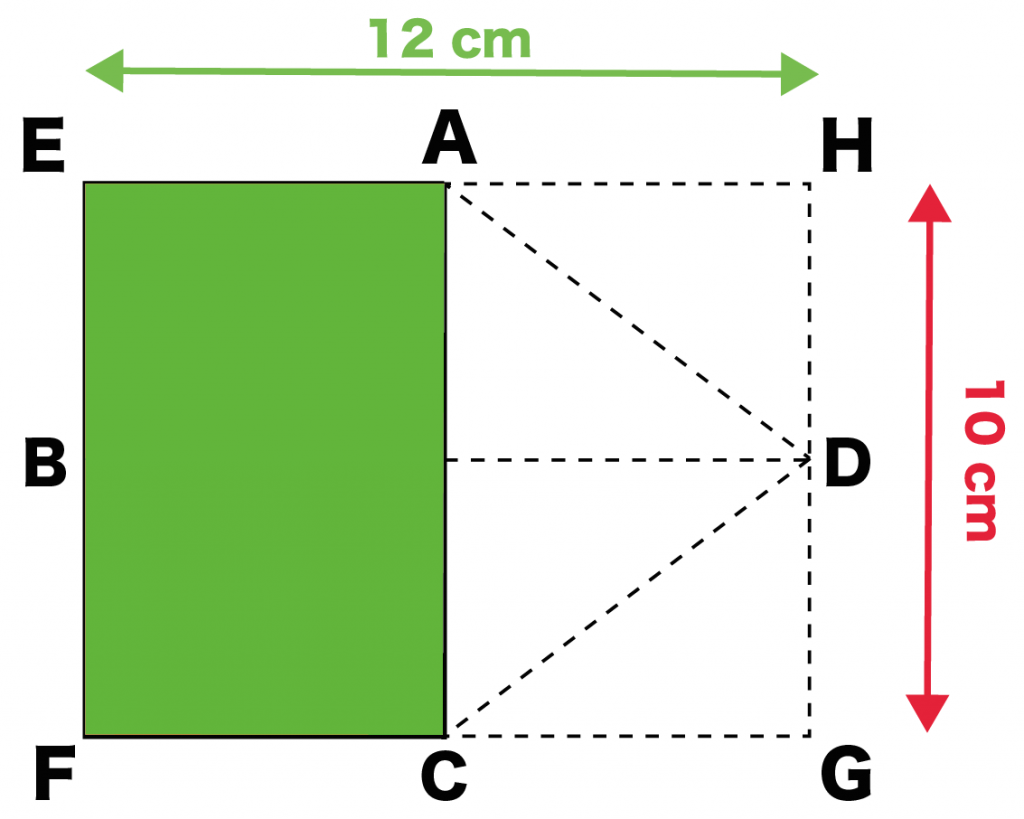
つぎの「ひし形ABCD」の面積を求めてみよう。
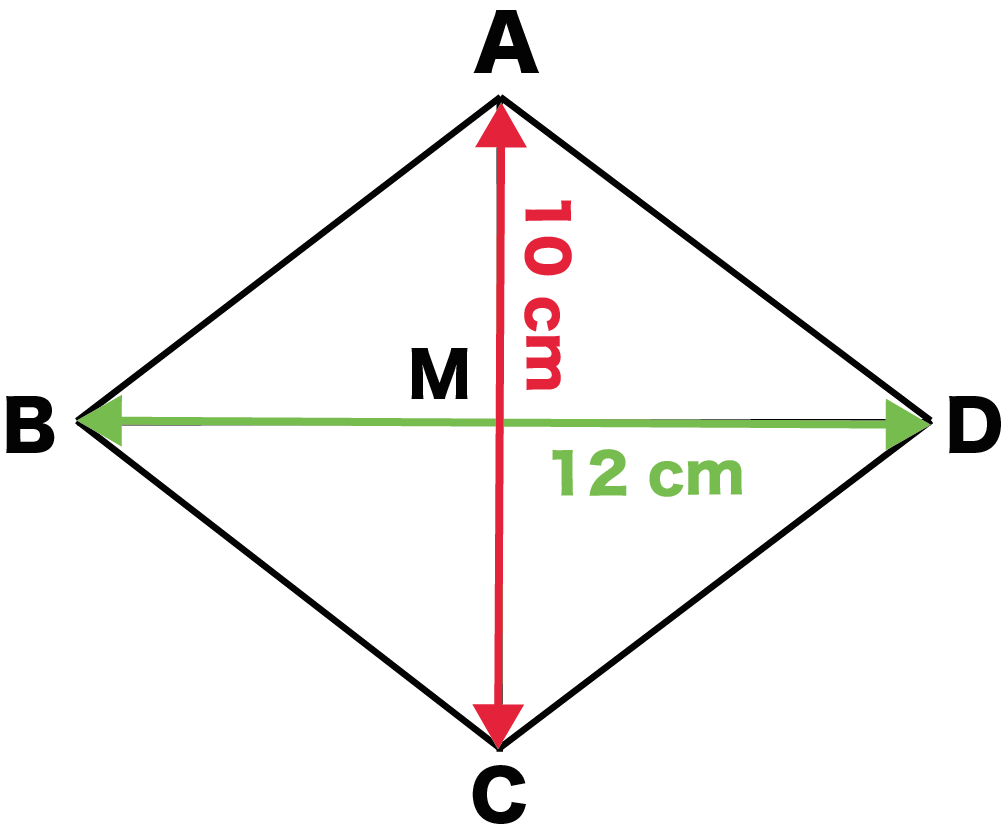
対角線AC・BDの長さがわかっているね??
だから、
対角線の公式をつかうと、
(対角線)×(対角線)÷2
= 10×12÷2
= 60 [cm^2]
になるね。
なんで公式がつかえるの??
でもさ、
なんで菱形の面積を公式で計算できるんだろう・・・
って思うよね。
じつは、
ひし形の4つの頂点を通る、
長方形の半分の面積になっているからなんだ。
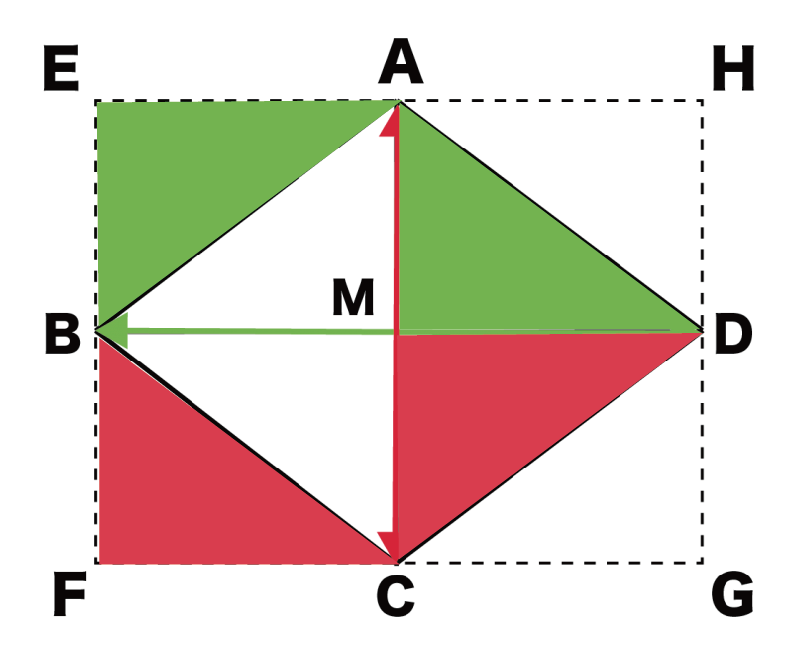
ひし形ABCDの周りに長方形EFGHをかいたとしよう。
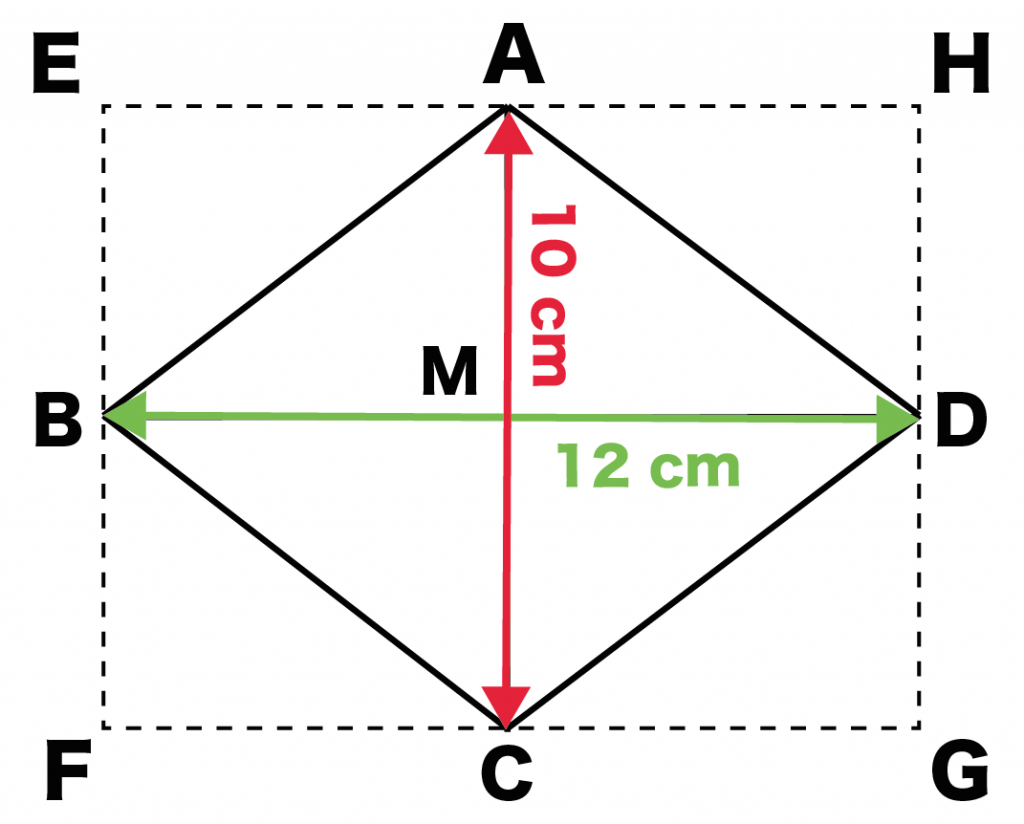
- △ADMと△AEB
- △DMCと△CFB
はそれぞれ合同になっているね。
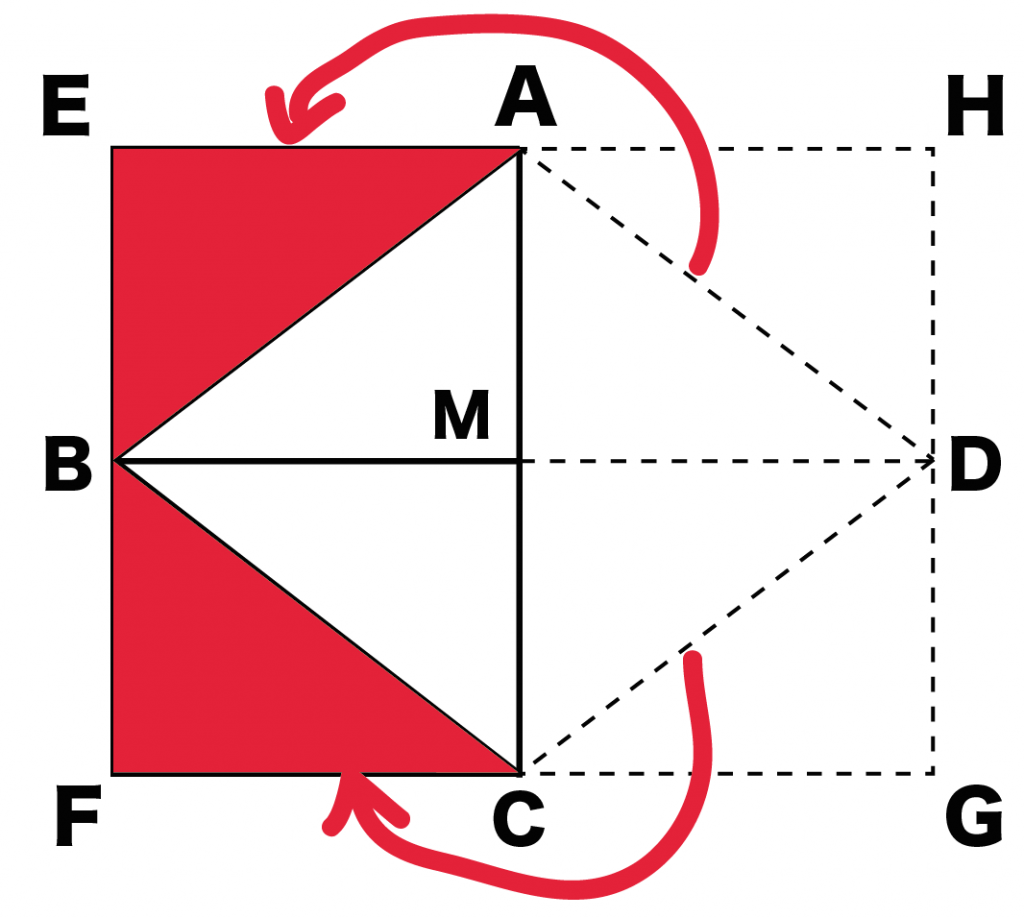
ってことは、
△ADMを△ABMの位置に、
△DMCを△CFBの位置に移動させてもいいわけだ。
つまり、
菱形ABCDは長方形AEFCと等しくなるってわけ。
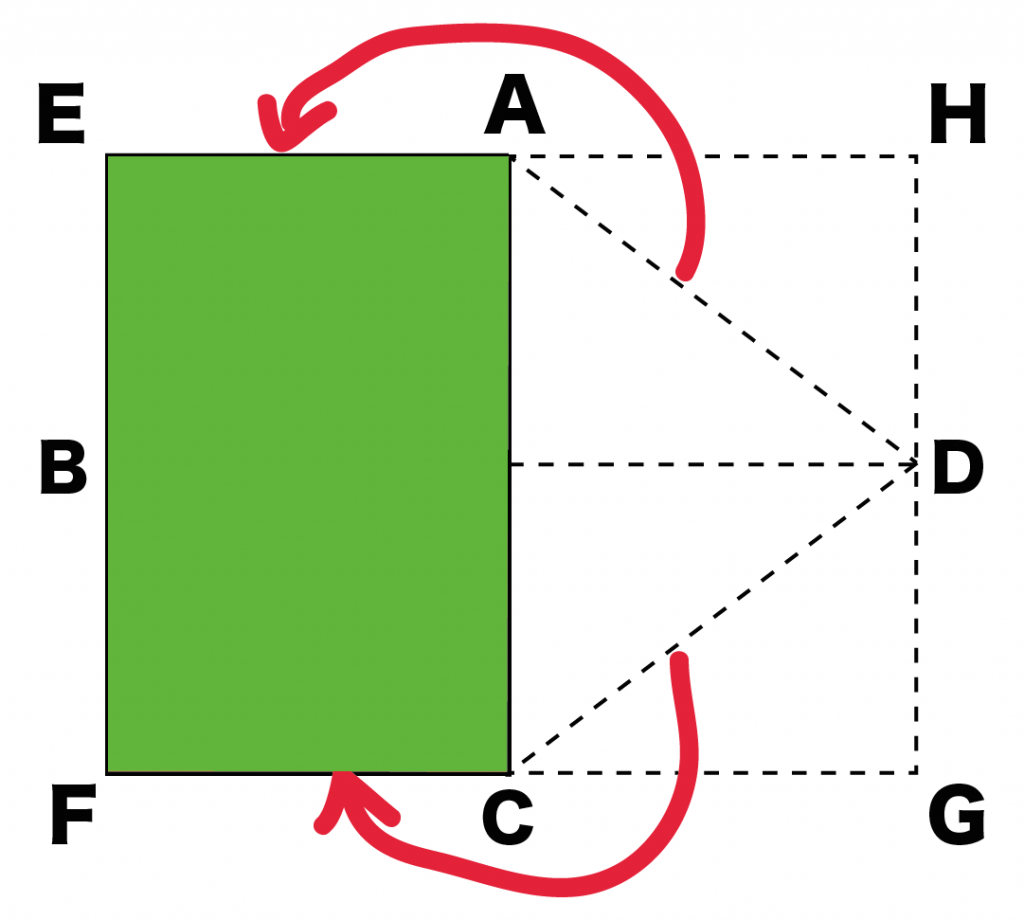
「長方形AEFCの面積」は長方形EFGHの半分になっているね??
よって、
(ひし形ABCDの面積 )=(長方形EFCA)
= (長方形EFGH)÷2
= (対角線)×(対角線)÷2
になるんだ。
底辺と高さをつかった菱形の面積の公式
つぎは、「底辺」と「高さ」をつかった公式だよ。
菱形の面積は、
(底辺)×(高さ)
で計算できちゃうんだ。

公式をつかってみよう!
たとえば、つぎのような菱形ABCDだね。

- 底辺:10cm
- 高さ:12cm
のひし形だとすると、こいつの面積は、
10×12
= 120[cm^2]
と計算できちゃうんだ。
なんで公式がつかえるの??
なぜ、
底辺×高さ
っていう公式がつかえるんだろう??
じつはこれは、
ひし形が平行四辺形であるからなんだ。

※詳しくはひし形の定義をみてね。
平行四辺形の面積は「底辺×高さ」で求められたよね??
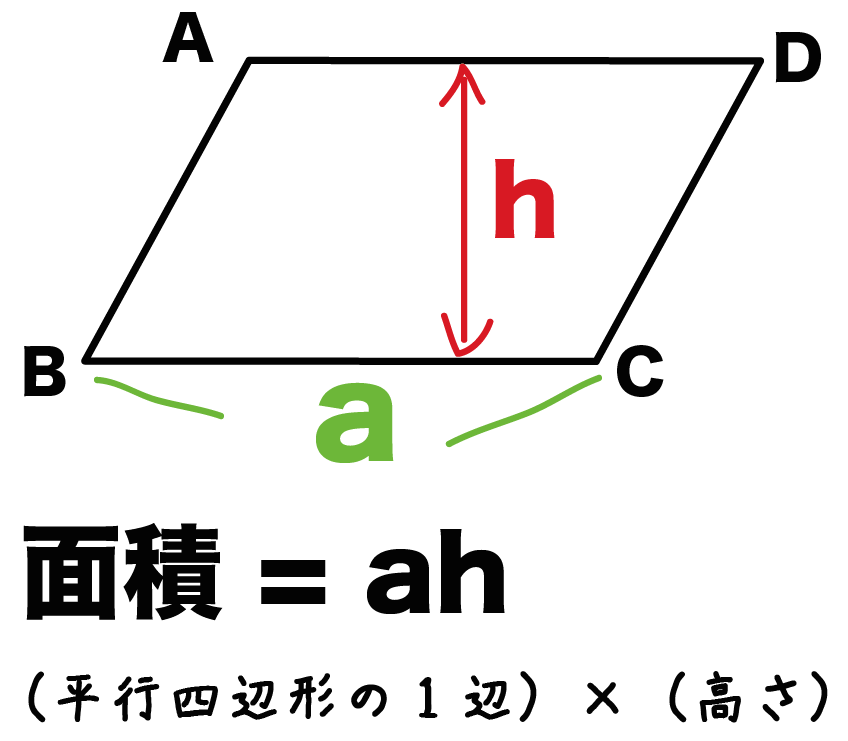
菱形は平行四辺形ともいえるから、
この面積の公式も使えちゃうってわけさ。
じゃんじゃん計算していこう!!
まとめ:ひし形の面積の求め方は2通りおさえよう!
ひし形の面積の求め方は、
- 対角線×対角線÷2
- 底辺×高さ
の2通りがあるよ。
問題によって使いわけていこう!
そんじゃねー
Ken









