直角三角形の合同条件なんて必要なん？

こんにちは！この記事をかいているKenです。納豆は3パックにかぎるね。

 

直角三角形の合同を証明したい！！

ってときあるよね？

そんなときに便利なのが、

直角三角形の合同条件

だよ。

 

こいつは裏技みたいなものでチョー便利。

三角形の合同条件をつかわなくても、

直角三角形の合同が証明できちゃうからね。

今日はこの合同条件を2つ紹介していくよ。

よかったら参考にしてみてね。

 

 

チョー便利な直角三角形の2つの合同条件

直角三角形の合同条件はつぎの2つさ。

• 斜辺と1つの鋭角がそれぞれ等しい
• 斜辺と他の1辺がそれぞれ等しい

 

えっ。ぜんぜんピンとこないって？！

うん、そうだよね。

でもコイツらってむちゃくちゃシンプルで、ようは、

「斜辺」と「角 or 辺」が等しい直角三角形同士は合同である

ってことを言っているんだ。

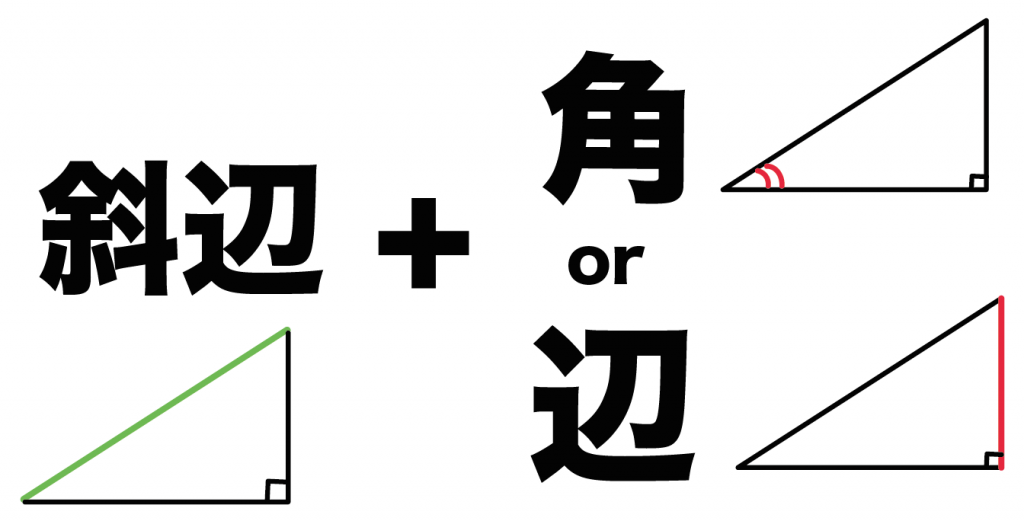
だから、

2つの直角三角形の「斜辺」が等しいってことがわかれば

合同を証明しやすくなるっわけさ。

それじゃあ、合同条件をくわしくみていくよ。

 

 

条件1.  「斜辺と1つの鋭角がそれぞれ等しい」

まずは、

斜辺

と、

1つの角（直角以外の角ね）

が等しい

という合同条件だ。

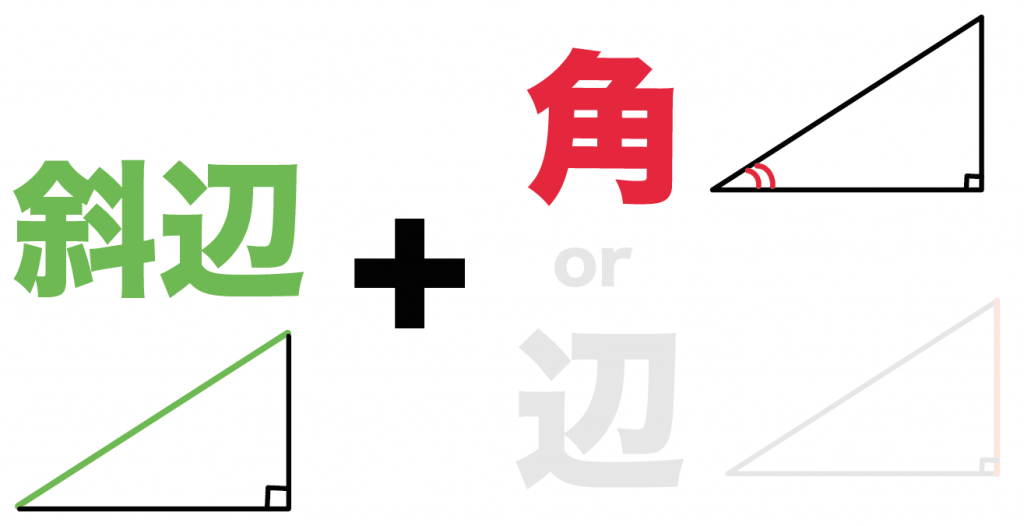
いちいち三角形の合同条件なんかに頼らなくても、

2つの直角三角形の合同がいえちゃうんだ。

 

たとえば、つぎの直角三角形ABCとDEFをみてみて。

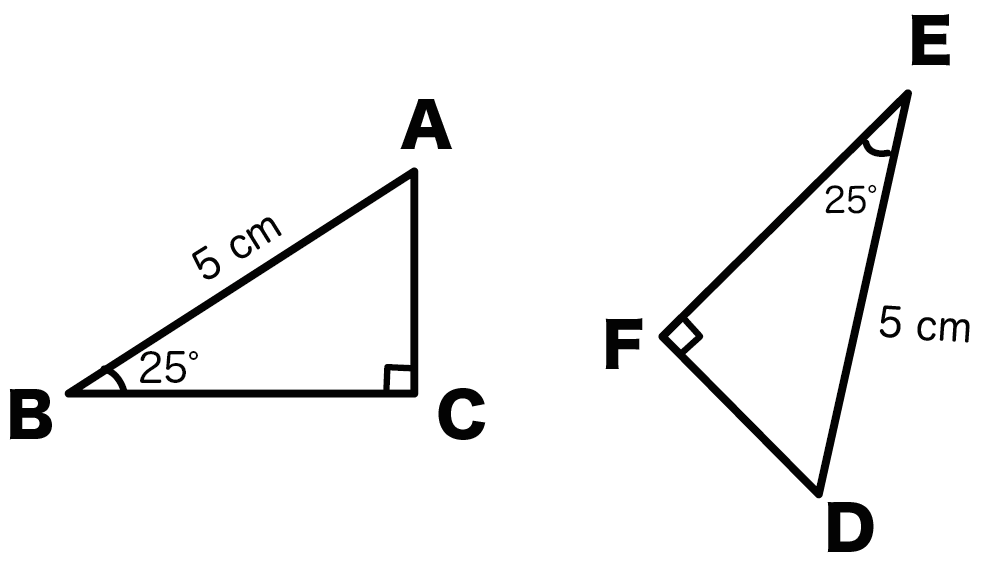こいつらはなんと、合同なんだ。

だって、

• 斜辺が等しい（AB = DE = 5 cm）
• 直角以外の角も等しい（角B = 角E = 25°）

だからね。

 

よって、

斜辺と1つの鋭角がそれぞれ等しい

っていう合同条件をつかえば

△ABC ≡ △DEF

がいえるんだ。

 

 

条件2. 「斜辺と他の1辺がそれぞれ等しい」

つぎは、

斜辺

と、

1つの辺（斜辺以外のやつ）

が等しい

っていう合同条件さ。

 

 

たとえば、つぎの三角形GHIとJKLがいい例だね。

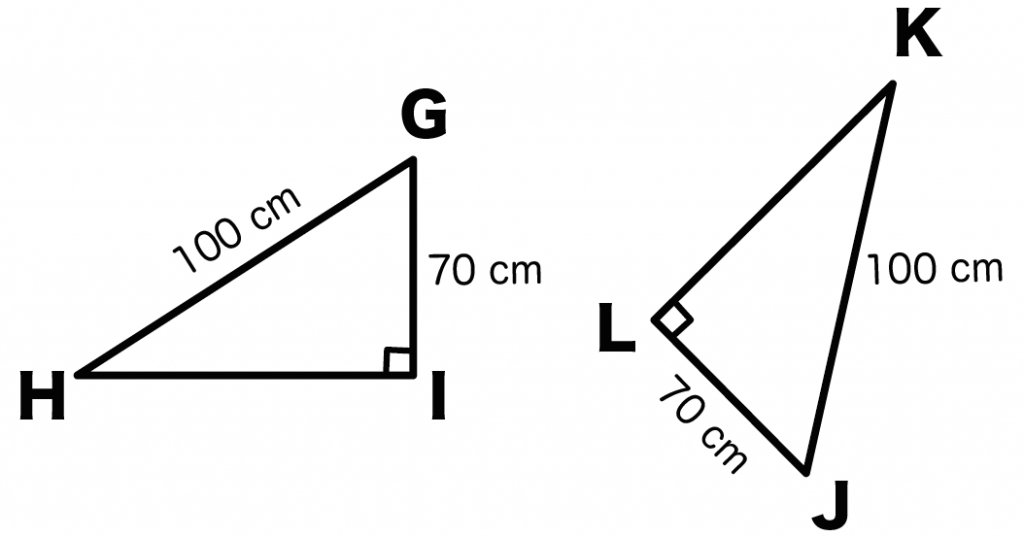
こいつらは合同な直角三角形だよ。

なぜなら、

• 斜辺が等しい（GH = JK = 100 cm）
• 斜辺以外の1つの辺が等しい（GI = JL = 70 cm）

からね。

 

こういうとき、

斜辺と他の1辺がそれぞれ等しい

っていう直角三角形の合同条件をつかえば、

△GHI ≡ △JKL

がいえるんだ。

 

 

 

まとめ：直角三角形の合同条件で近道しまくろう！

ぶっちゃけ、

直角三角形の合同条件なんてなくても大丈夫。

正直、いきていける。

 

だけど、

直角三角形の合同条件はつかえば、

問題を解くスピードがはやくなるんだ。

ガンガン使っていこう！

そんじゃねー

Ken