
中学数学の「データの活用」で出てくる箱ひげ図。
名前のインパクト、強すぎますよね。
箱に、ひげ、っすからね。
たぶん、こんなキャラクターイメージしちゃったんじゃないっすか。

でも、いえ。
箱ひげ図はキャラ名ではありません。
数学用語の一種なんです。
えっ、名前からしてゼッタイ難しそうですって??
安心してください。
箱ひげ図は、
四分位数がわかっていれば描けます。
今日は、
「箱ひげ図の書き方(中学数学)」
を、ステップを踏んでわかりやすく解説します。
~もくじ~
まず基本から。
箱ひげ図とは、
データの散らばり方を、ひと目で表す図
です。
サンプルを出すとこんな感じっすね。
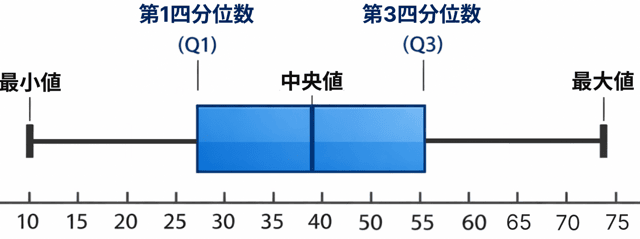
どう?? 全然ヒゲっぽくないでしょ。
この箱ひげ図は、
が一気にわかるのが特徴。
だからテストでもよく出るんすね。
箱ひげ図を書くために必要なのは、次の5つの数です。
この5つがそろえば、箱ひげ図は完成します。
えっ。ちょっと無理??
そんなときは中央値の求め方、
四分位数の求め方を復習しておきましょう。
では、実際に書いていきましょう。
まず、次のようなデータがあるとします。
9, 3, 11, 6, 5, 8, 13
箱ひげ図の書き方は次の6ステップ。
オッケー、まずは小さい順に並び替え。
すると、
3, 5, 6, 8, 9, 11, 13
こうなりますね。
次は、四分位数を求めます。
すると、こんな感じ。

やり方は四分位数の求め方を読んでみてね。
値の範囲が入るように、横に数直線を書きます。
ルールは簡単。
最小値〜最大値を必ず含むようにすればいいんす。
なので、数直線は「3 〜 13」をカバーする範囲にします。
メモリの間隔は・・・そうだな、2にしておこうか。辛いし。
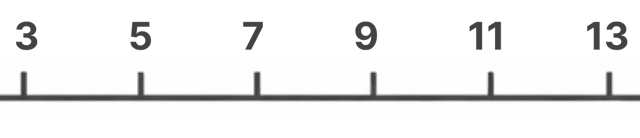
右端の矢印ヘッドは書かなくて大丈夫。
オッケー、次はいよいよ箱です。
まず、Q1 から Q3 までを「箱」で囲みます。
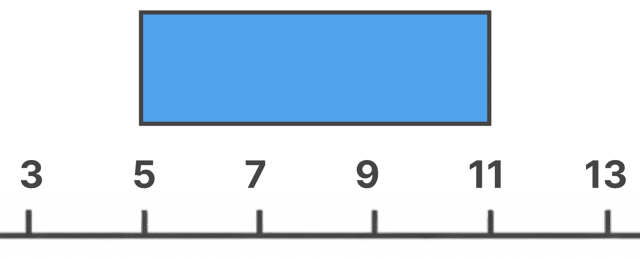
今回は
でしたよね。だから、こんな感じのボックスが登場。
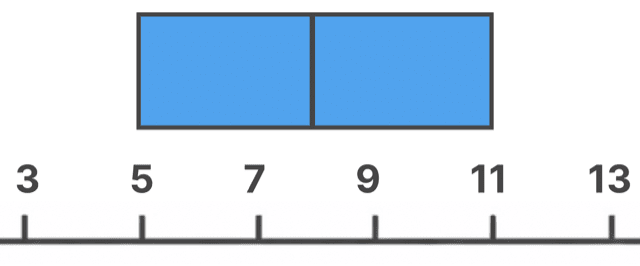
そして、箱の中に中央値の線を引こう。
今回は
だから、こんな感じ。
さて、お待ちかねのひげ、きました。
箱ひげ図の「ひげ」って、これっすね。
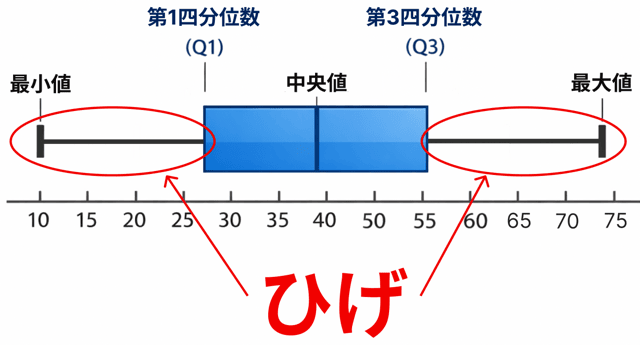
ひげの書き方は
箱の左端(Q1)から最小値まで線を引く。
箱の右端(Q3)から最大値まで線を引く。
です。
今回の場合は、
でしたから、こんな感じ。
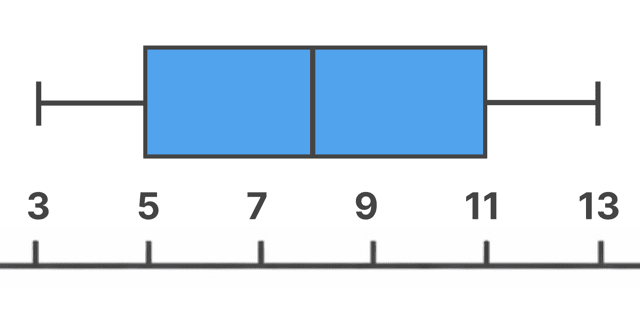
うん、はい。
これで、
箱ひげ図の完成!

テストで多いミスをまとめます。
特に、
箱は Q1 ~ Q3、ひげは端まで。
ここを間違えないようにしましょう。
箱ひげ図を見ると、
がすぐにわかります。
箱が長い → ばらつきが大きい
箱が短い → データが集中
という見方も、テストでよく聞かれますので要記憶。
箱ひげ図は、
だけでした。
見た目は難しそうですが、中身はシンプル。

そんじゃねー

中学数学で出てくる「四分位範囲」。
名前からして強そうですよね。
四分位??
範囲??
なにそれ???
しかも問題を見てみると、
でやり方が変わるっぽい…。
ってことで今日は、
「四分位範囲の求め方(奇数・偶数)」
を、中学生向けにわかりやすく解説します。
~もくじ~
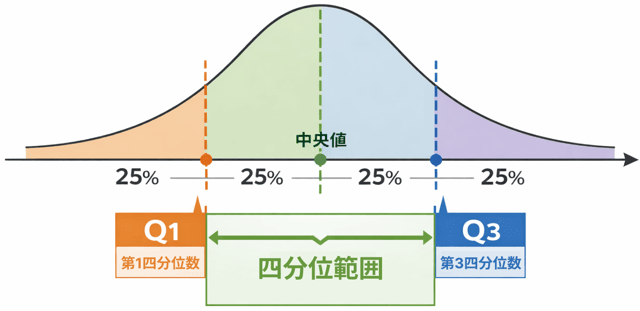
四分位範囲とはずばり、
データの散らばり具合を表す数
です。
平均との差とはちょっとちがって、
「真ん中の50%が、どれくらい広がっているか」
を見るための指標なのです。
そのために使うのが、
です。
つまり、四分位範囲を出すには、先に四分位数を求める必要があります。
やることはこの3ステップ。
詳しいやり方はこちらの四分位数の求め方の記事で復習しておきましょう。
四分位範囲の求め方の公式はこれ ↓
四分位範囲 = 第3四分位数 − 第1四分位数
そう、これだけです。
引き算1回です。
たとえば、四分位数の求め方を駆使して頑張った結果、
が得られたとします。

さて、四分位範囲の求め方は
四分位範囲 = 第3四分位数 − 第1四分位数
でしたね?
この公式にもろもろの値をぶち込んでみると、
四分位範囲
= 11 – 5
= 6
になります。
つまり、四分位範囲は6!
この
四分位範囲 = 第3四分位数 − 第1四分位数
という求め方はデータの個数が奇数だろうが偶数だろうが同じ。
問題は、
第3四分位数と第1四分位数の求め方が偶数と奇数の場合で異なるってことですね。
そこらへんの事情は、さっきからチラチラ登場している四分位範囲の求め方で復習しておいてくださいね。
はい、四分位範囲は、
が全部つながった用語でした。最後に紛らわしい「四分位数」と「四分位範囲」の違いをおさらいしておきましょう。
| 項目 | 四分位数 | 四分位範囲 |
|---|---|---|
| 意味 | データを4等分するときの区切りとなる数 | 真ん中50%のデータがどれくらい広がっているかを表す量 |
| 種類 | 第1四分位数(Q1) 第2四分位数(Q2・中央値) 第3四分位数(Q3) |
1種類のみ |
| 求め方 | データを小さい順に並べ、 4等分した位置の値を求める |
第3四分位数 − 第1四分位数 (Q3 − Q1) |
| 役割 | データの区切りの位置を知る | データのばらつきの大きさを知る |
| 単位 | 元のデータと同じ | 元のデータと同じ |
| 箱ひげ図での表し方 | 箱や線の区切りの位置 | 箱の横の長さ |

そんじゃねー

中学数学で登場する「四分位数(しぶんいすう)」。
中央値はなんとなくわかるけど、
四分位数??
なんか急に専門用語っぽい〜
なんて思っちゃいますよね。
しかも問題をよく見ると、
で、やり方が変わるみたいで混乱しがちです。
今日は、
「四分位数の求め方(奇数・偶数それぞれ対応)」
を中学生向けにやさしく解説します。
~もくじ~
そもそもからいきましょう。
四分位数とはずばり、
データを4つに分けたときの区切りになる数
です。
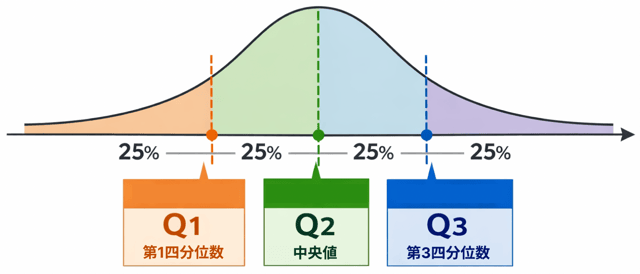
ポイントはここ ↓
小さい順に並べたデータを4等分する
ってこと。
そのときに出てくるのが、
です。
中学数学では、Q1 と Q3 を求められることが多いです。
四分位数は、次の3ステップで求めます。
ここから、奇数か偶数かで少しだけ分かれますよ。
たとえば、次のデータの四分位数を求めてみましょう。
9, 3, 11, 6, 5, 8
まず、小さい順に並べます。
すると、
3, 5, 6, 8, 9, 11
になる。
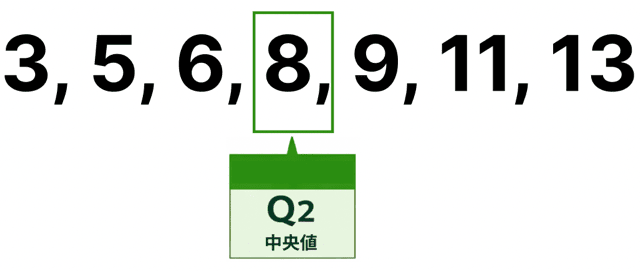
そして、データの真ん中は「8」。
これが中央値(Q2)ってわけっすね。
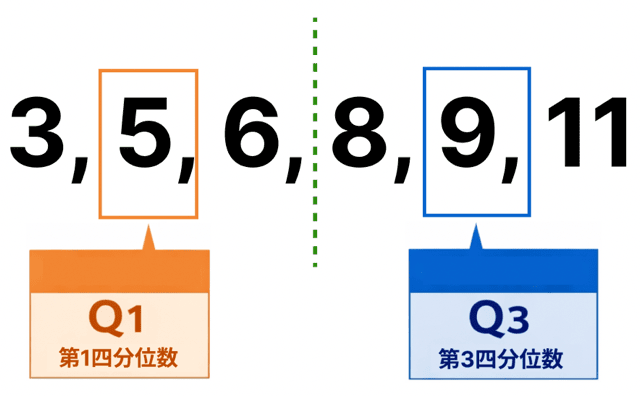
そして、中央値を除いて左右に分けます。
それぞれの中央値は、

これで四分位数が求まりましたね。
次は偶数の場合です。
6, 13, 5, 9, 3, 8, 11
さて、もう一度小さい順に並べます。
3, 5, 6, 8, 9, 11, 13
この場合だと、真ん中2つは「6」と「8」。
この2つの平均が中央値(Q2)になるんすね!
つまり、
(6 + 8) ÷ 2 = 7
です。

だがしかし、
中央値の値は、分けるための目安
として使うってポイントに注意です。
「左右それぞれの中央値を求める」っていう最後のステップでは、中央値は一旦脇に置来ましょう。
ってことで、中央値を無視して左右にわけると、
それぞれの中央値は、
となります。
テストで間違えやすいポイントをまとめます。
この4つを意識すればOKです。
四分位数は、
だけでした。
このあと、
へとつながっていきます。

そんじゃねー
「一次関数の利用」で必ず出てくるのが、
点が動く問題。
ちまたでは、
動点の問題
と呼ばれているやつだ。
一番テストに出てくるのは「1つの点が動くパターン」。
だけど、厄介なことに、たまーに、
「2つの点が動く」問題が出ることもある。
例えば次のような問題さ。
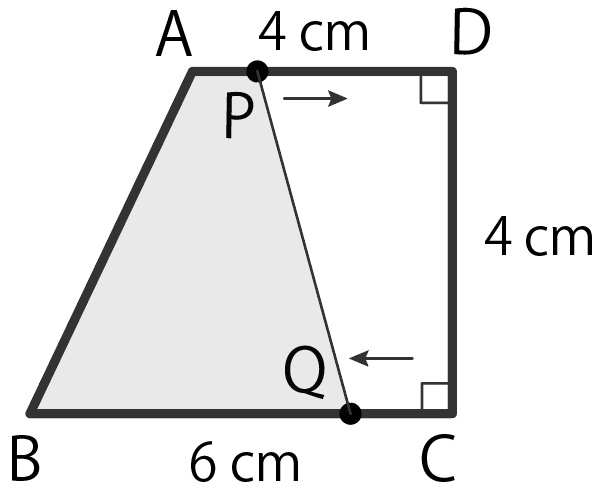
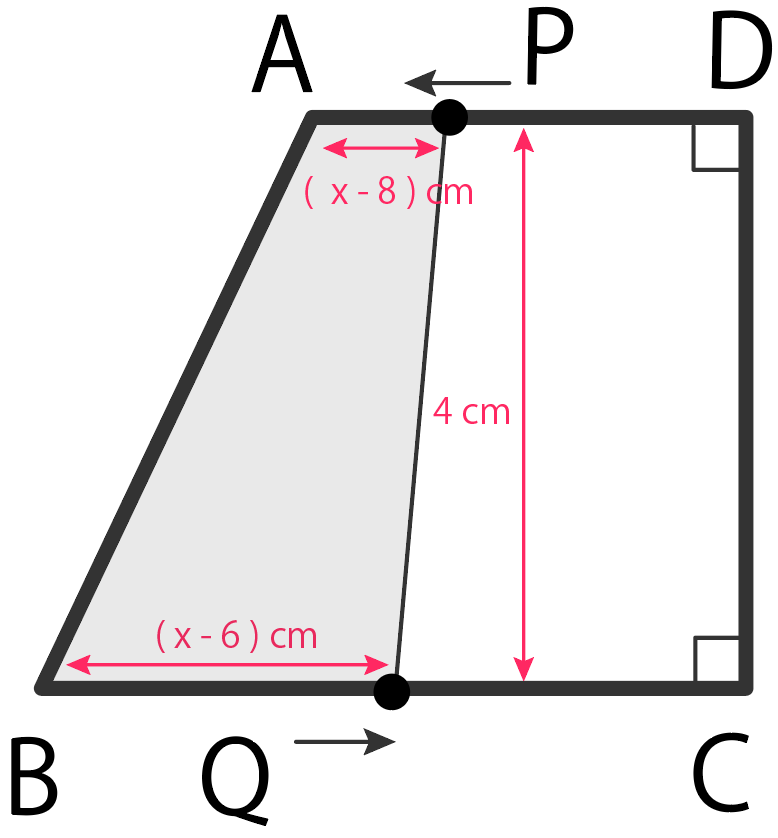
AD = 4 cm、BC = 6 cm、 CD = 4 cm、∠C = ∠D = 90°の台形ABCDがある。
2点P、QはそれぞれA、Cを同時に出発し、点Pは辺AD上を、点Qは辺BC上をどちらも毎秒 1 cmの速さで動く。
端まで行けば折り返し、12秒間動くものとする。点P、Qが動き始めてからx秒後の4点A、B、P、Qを結んでできる図形の面積をy cm² とする。
(1) 0 ≤ x ≤ 12のとき、xとyの関係を表すグラフをかきなさい。
(2)四角形ABQPの面積が、台形ABCDの面積の4分の1になるのは点P、Qが動き始めてから何秒後ですか。
今日はこの応用問題を気合いで乗り切っていこう。
一次関数の動点では、
変域がいくつできるのか?
と見通しをつけるといいよ。
この問題では
点PがAから、点QがCから毎秒1cmの速さで動く
という条件があるね?
しかも、辺の端まできたら折り返して、12秒間動く、らしい。
12秒で四角形ABQPの面積 (y)はどのように変化するんだろう??
分け方のポイントは、
動点が頂点に到着するタイミングで分ける
だよ。
ADはBCより短いから最初に、点PがDに着く。
そして、点Pに遅れてちょっとして点QがBに辿り着く。
PとQは、頂点にたどり着くタイミングが微妙に異なるから、4つの変域が考えられそう。
それぞれの変域で、四角形ABCDの面積の変化をみればいいんだ。
まずはPがAを出発してからDに着くまで。
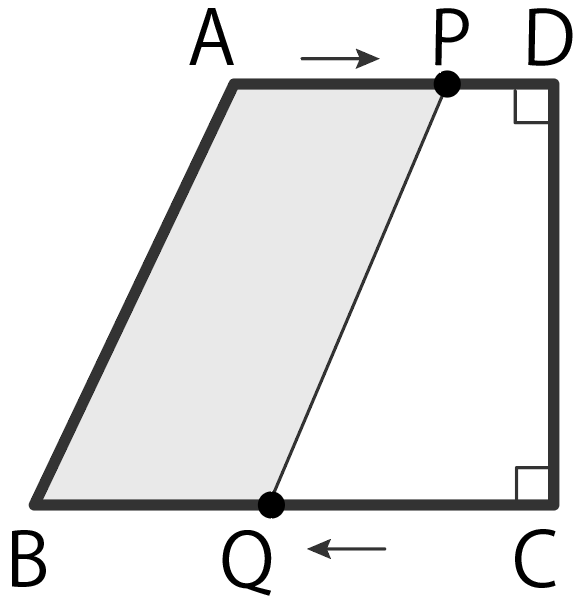
図をかくとわかるけど、四角形ABQPは台形になる。
で、面積を求めるために、
という辺の長さが必要だね。
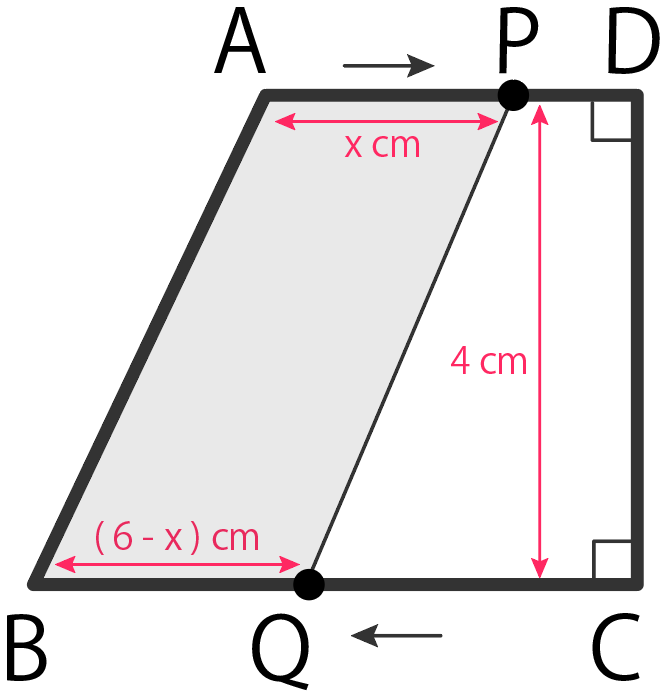
ポイントはBQの長さ。
QはCからスタートしてBに向かっているから
$$CQ= x cm$$
そして、そいつをBCの長さ 6 cm から引いたやつがCQの長さになるから、
$$BQ= BC – CQ$$
$$= 6 – x$$
になる。
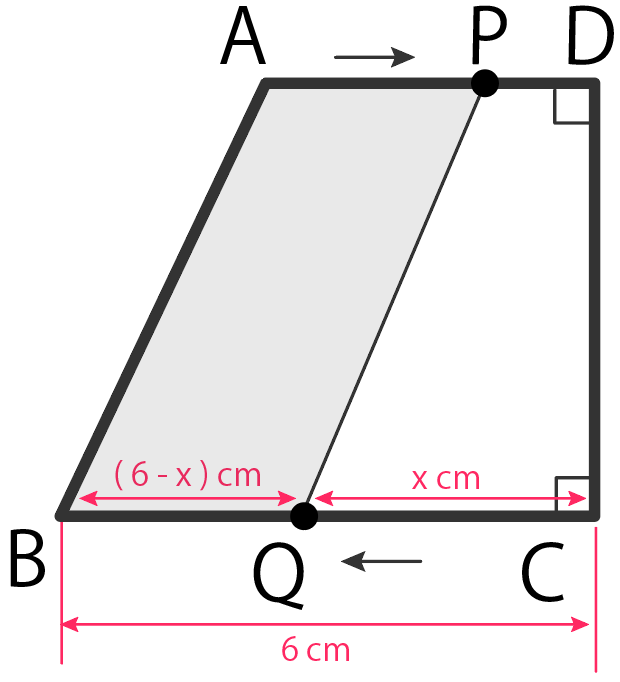
さて。ここで台形ABQPの面積yを計算しよう。
(上の辺+下の辺)×(高さ)÷2
だったから、
$$y = (AP+BQ)× DC ÷ 2$$
$$= (x +6 -x)× 4 ÷ 2$$
$$= 12$$
になる。
0〜4秒では、台形ABQPの面積はずーっと12ってこと。
PがDに到着して、折り返しを始めたら、四角形ABQPの面積は変化するよ。
この場合、APの長さが変化してきていて、
$$8 – x$$
になってるはず。
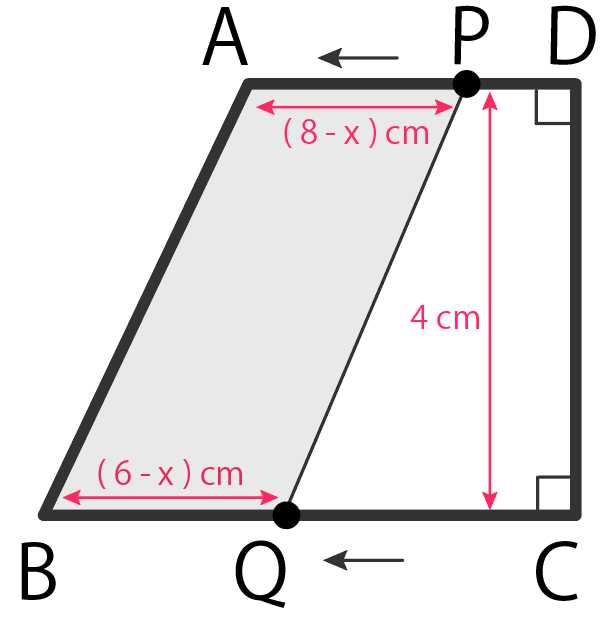
ADを2倍した長さから、Pが動いた距離「x」を引くとAPになるね。
ただ、相変わらず四角形ABQPは台形さ。
同じように台形の面積 y を計算すると、
$$y = (AP+BQ)× DC ÷ 2$$
$$= (8-x +6 -x)× 4 ÷ 2$$
$$= -4x + 28$$
になる。
この式から分かるのは、
このフェーズ($0 ≤ x ≤ 4$)では時が経つにつれて面積が小さくなるってこと。
お次はPがDに到着して、PがAに戻るまでの時間。
6〜8 秒までだね。
ここでのポイントは、BQの長さが変化していること。
QはBに到着して、折り返しているから、
BQ=
Qが進んだ距離 – BCの長さ
= x – 6
になる。
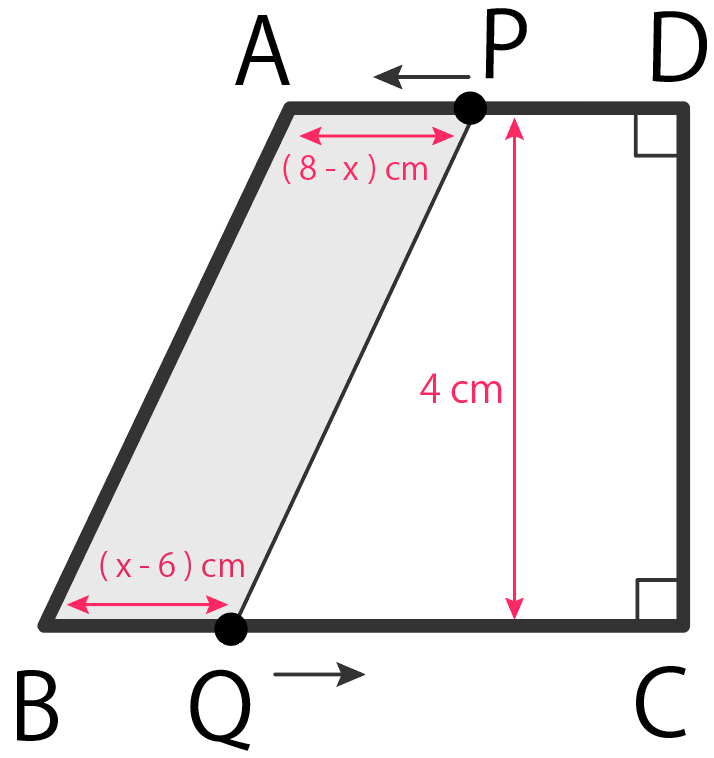
すると、四角形ABQP(というか台形)の面積yを計算すると、
$$y = (AP+BQ)× DC ÷ 2$$
$$= (8-x +x – 6)× 4 ÷ 2$$
$$= 4$$
になるね。
あら不思議。
またまた面積yが一定になっちゃった。
最後はQがCに戻るまで。
このタイミングは、Pが2回目にDに到着するタイミングでもあるとも言えるね。
変域で表すと
$$8 ≤ x ≤ 12$$
になる。
この時ポイントは、APの長さが変化していること。
PはAに到着して、折り返してDを目指しているはず。
だから、
APの長さ
=Pが進んだ距離 – ADの2倍の距離
= x – 8
になる。
四角形ABQP(というか台形)の面積yを計算すると、
$$y= (AP+BQ)× DC ÷ 2$$
$$= (x – 8 +x – 6)× 4 ÷ 2$$
$$= 4x – 28$$
になる。
ふう、これで全部の変域における関数式が出せたぜ。
それぞれの式をグラフにするとこんな感じ。
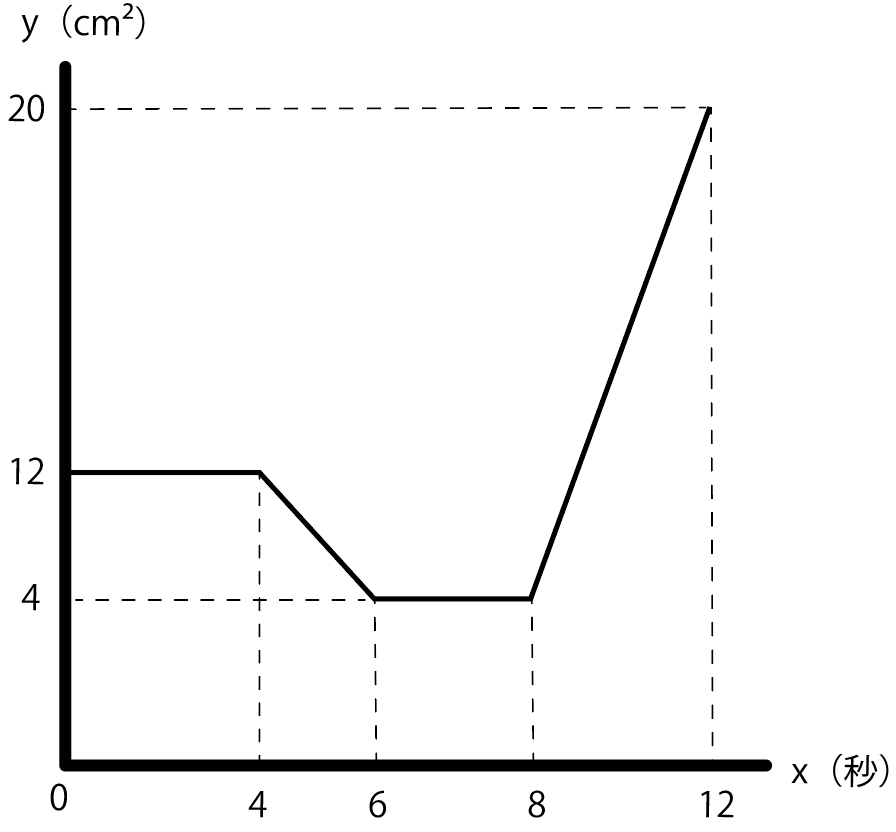
あと1つやることがある。
それは、例題の(2)の
四角形ABQPの面積が、台形ABCDの面積の4分の1になるのはいつ?
に答えること。
つまり、これ、
yが特定の値になる時のxを求めよ
という問題だ。
まずは「台形ABCDの面積の4分の1」がいくつか探っていこう。
台形ABCDは上辺が4、下辺が6、高さが4の台形だから、
$$(4 + 6 )× 4 ÷ 2$$
$$= 20 cm²$$
という面積になる。この4分の1は「$5 cm²$」だ。
ここで、さっき適当にかいたグラフに注目。
yが「5 」になっている箇所を探してみると、2つヒットだ。
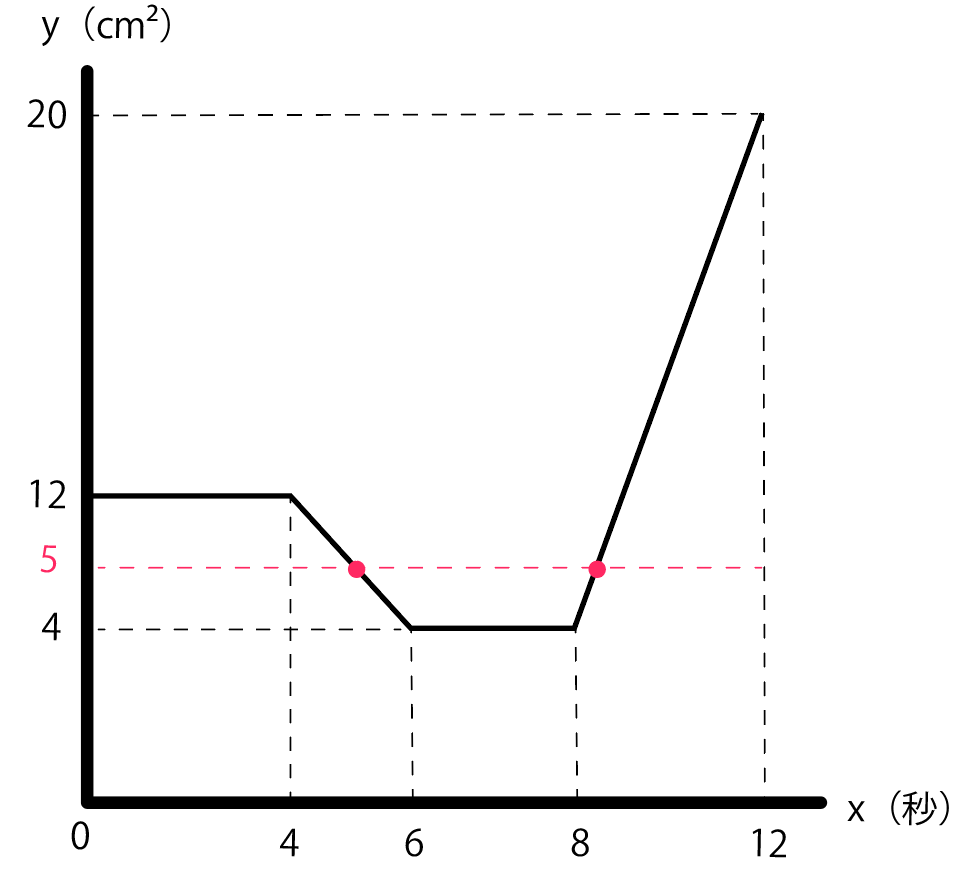
という2つの変域でyが5になる瞬間があるじゃないか。
ということで、これら2つの変域の関数にそれぞれ$y=5$を代入して、その時のxを求めればいいことになる。
まず、QがBに着くまで($4 ≤ x ≤ 6$)の場合。
$$y = -4x + 28$$
に $y = 5$を代入すると、
$$5 = -4x + 28$$
$$x= \frac{23}{4}$$
になるね。
あと1つは、QがCに戻るまで($8 ≤ x ≤ 12$)の場合。
$$y = 4x -28$$
に$y = 5$を代入しよう。
すると、
$$5 = 4x -28$$
$$x = \frac{33}{4}$$
になる。
ってことで、四角形ABQPの面積yが$5 cm²$になる時間は、
の2つだ。
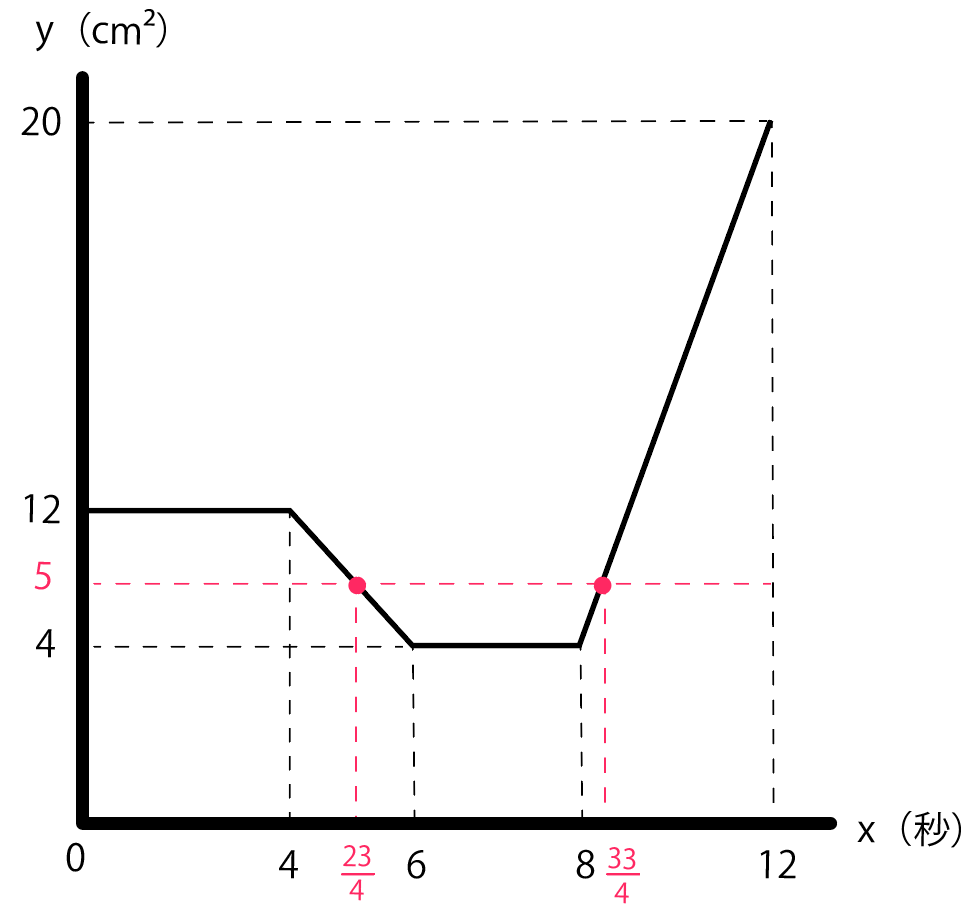
いやーほんとおつかれさま。
動点が2つあるとこんなに厄介だとは思わんかったな。
応用問題では出現することがあるから対策しておこう。
そんじゃねー
Ken
前回、「平行な2直線の求め方」を勉強してきたね?
今回はそれと似たようなやつで、
ある直線に「垂直な」式を求める問題
にチャレンジしよう。
例えば、次のような問題↓
状況を図にかくとこんな感じ。
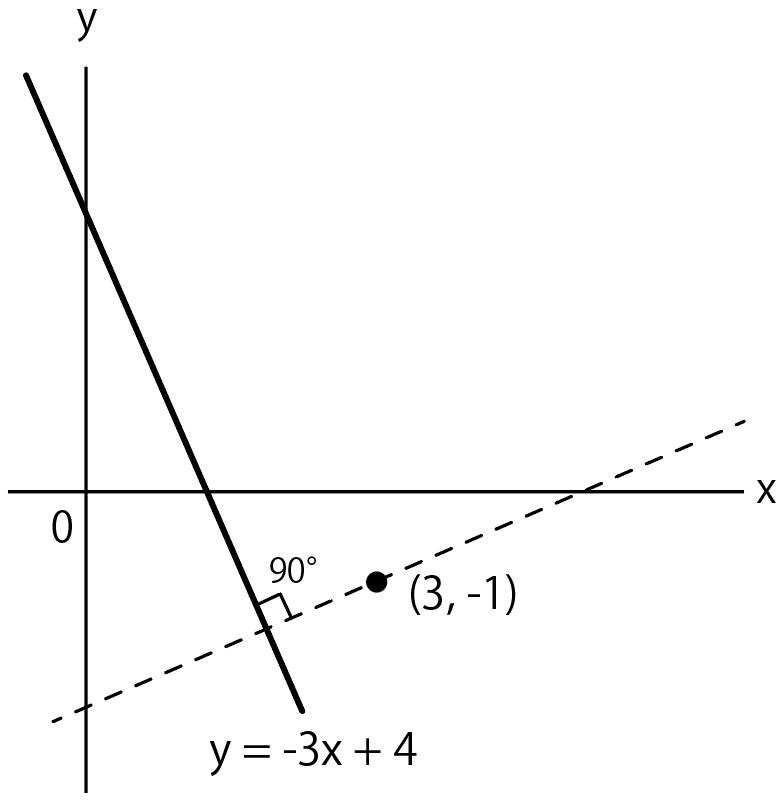
点線になっている一次関数の式を求めるんだ。
この手の問題は次の方法で解けるはず。
2直線が垂直だったらわかること。
それは、
2直線の傾きをかけたら 「- 1」になる
こと。
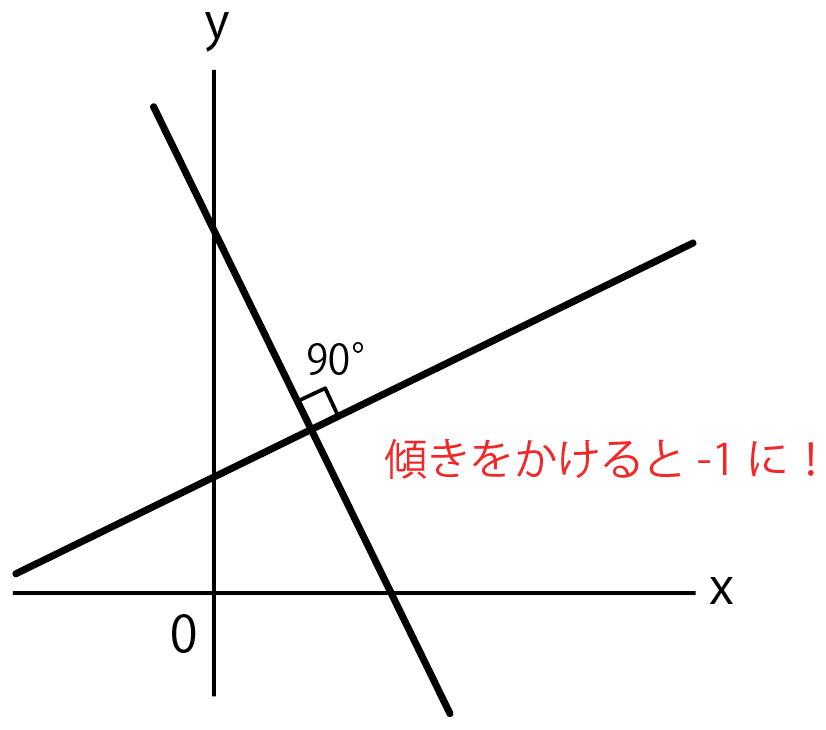
例えば「$y = – 3x + 4$」に垂直な直線の傾きを考えてみよう。
傾き「- 3」にかけたら 「- 1」になる傾きを求めればいいんだ。
求めたい直線の傾きを「a」とすると、
$$- 3 a = -1$$
$$a = \frac{1}{3}$$
と出てくるね。

って感じで、垂直ってヒントから、一次関数の傾きがわかっちまうんだ。
さっきのステップで$y = ax + b$の傾きが分かった。
あとは座標を代入して「切片b」を求めよう。
例題では
点(3, – 1)を通る
っていうヒントがあったから、この座標を代入しよう。
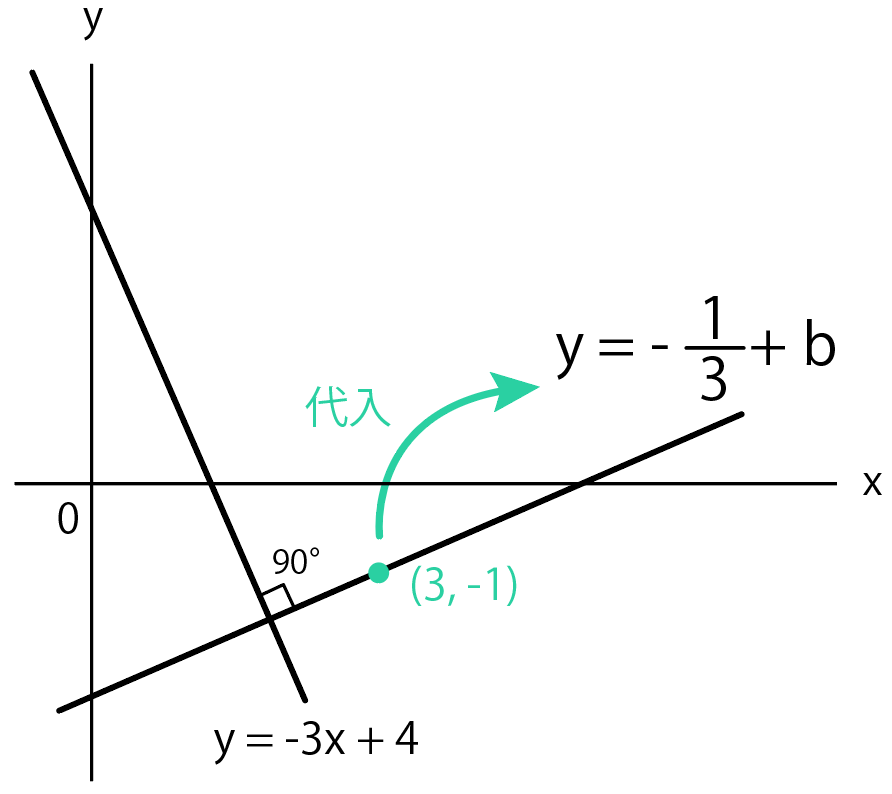
すでに傾きは$\frac{1}{3}$とわかったから、
$$y = \frac{1}{3} x + b$$
$$-1 = \frac{1}{3} × 3 + b$$
$$b = -2$$
となるね。
ここで疑問に思うのが、
垂直な2直線の傾きをかけたらなぜ「- 1」になるのか?
ってこと。
シンプルでわかりやすいけど、理由を教えてもらえないとしっくりこないよね。
これを証明するには、中学3年生でならう三平方の定理を使うよ。
例えば$y =mx$、$y = nx$という1次関数(比例)があったとしよう。
そして、直線上にx座標が「1」の点A、Bがあるシチュエーションを想像してくれ。
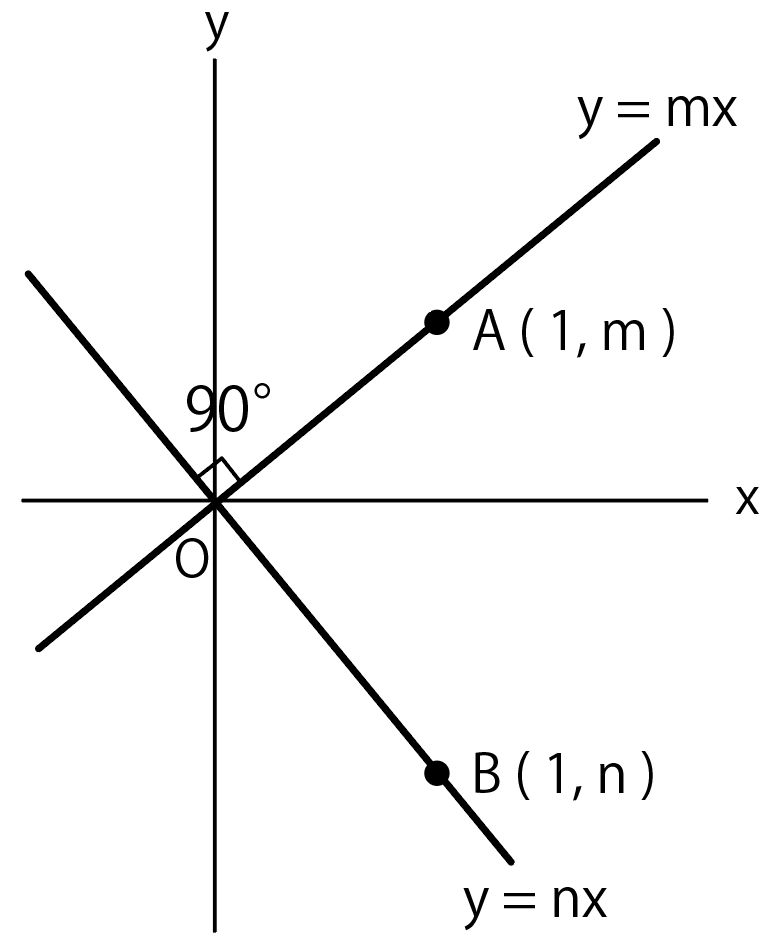
このとき、ABの長さはAのy座標からBのy座標を引いて
$$m – n$$
になるはず。
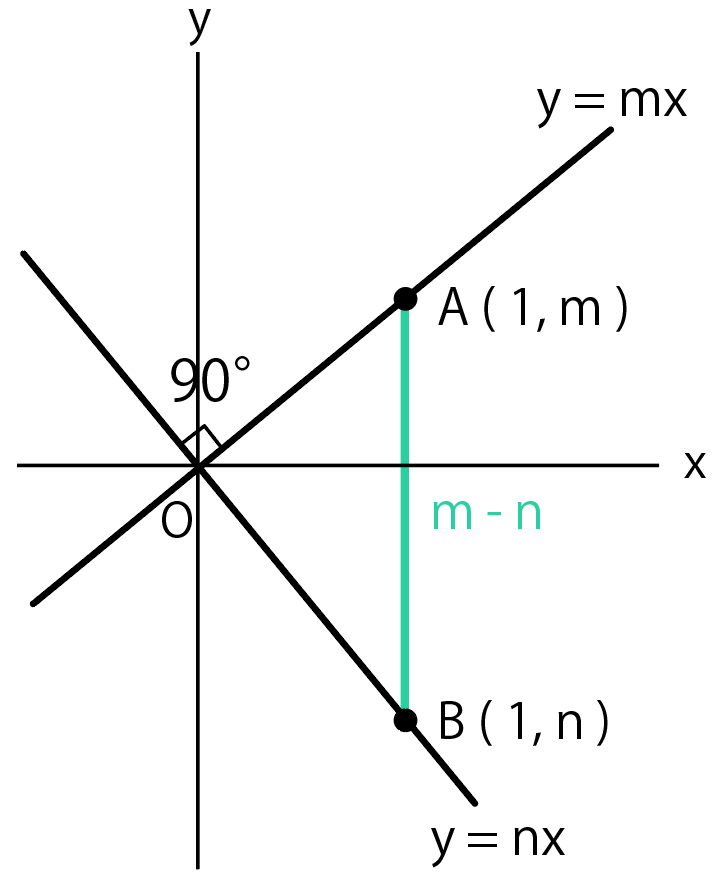
三平方の定理を使うと
$$OA =\sqrt{(1² + m²)} $$
$$OB = \sqrt{(1² + n²)}$$
と計算できる。
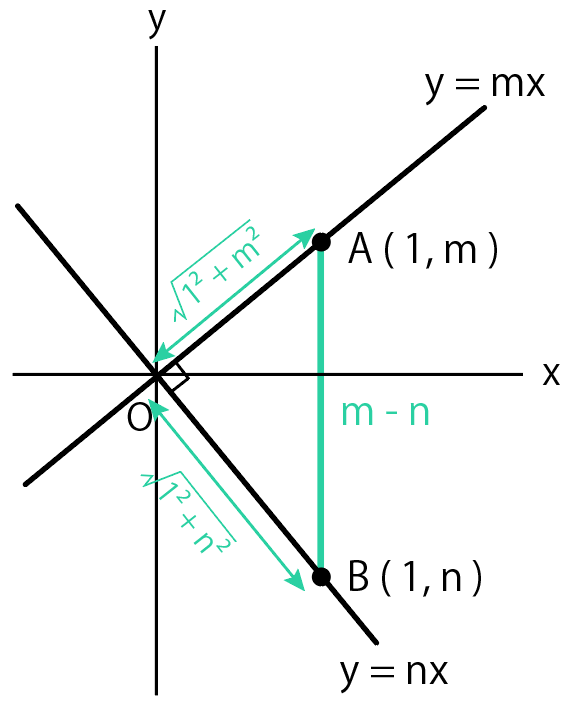
直角三角形OABに注目して、三平方の定理を使うと、
$$AB² = OA² + OB²$$
$$(m – n)^2 = {\sqrt{(1² + m²)}}^2 + {\sqrt{(1² + n²)}}^2$$
$$2mn = -2$$
$$mn = -1$$
となる。
「m」と「n」は垂直な直線の傾きだから、
垂直な2直線の傾きをかけると-1になる
って証明できるね。
こんな感じで、垂直な直線の傾きをかけると -1 になるから便利。
ついでに、なぜそうなるのかを理解しておけば怖いものなしだ。
テストに出てきやすいからよーく復習しておこう。
そんじゃねー
Ken
一次関数でわりと出てくるのは
平行な直線の式を求めよ
ってやつ。
例えば次の問題↓
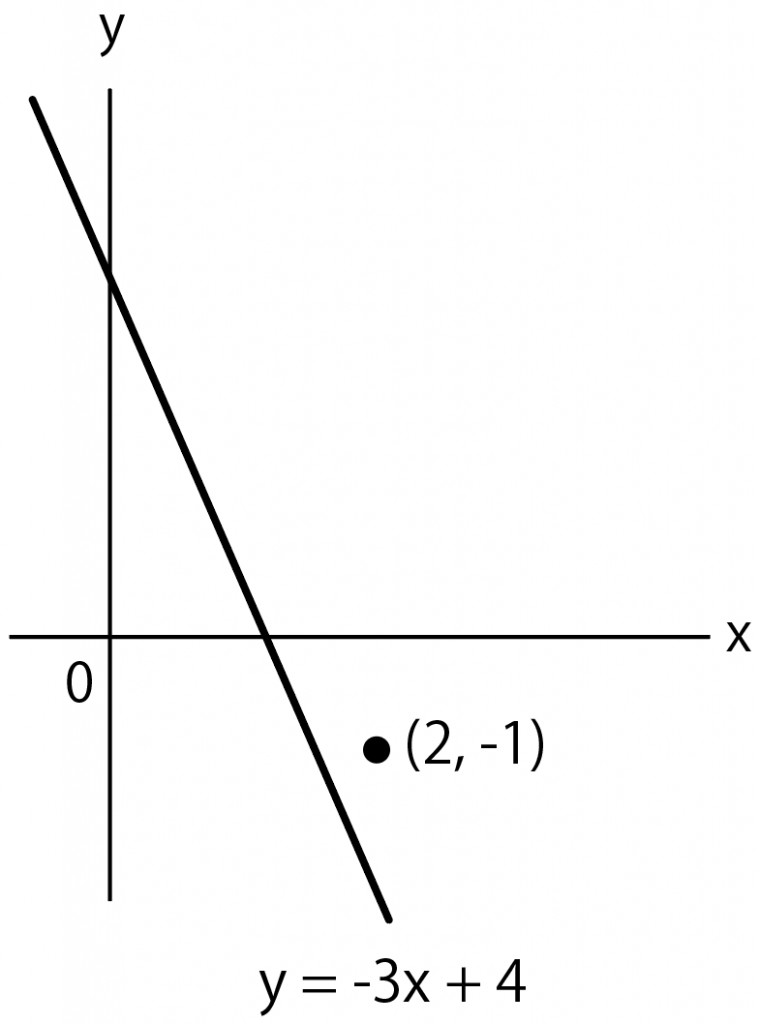
よく出てくるわりに、解き方がワンパターン。
1度解けるようになれば大丈夫。
一次関数の「傾き」から求めよう。
問題文でわかっているのは
「とある直線」と平行
ってこと。
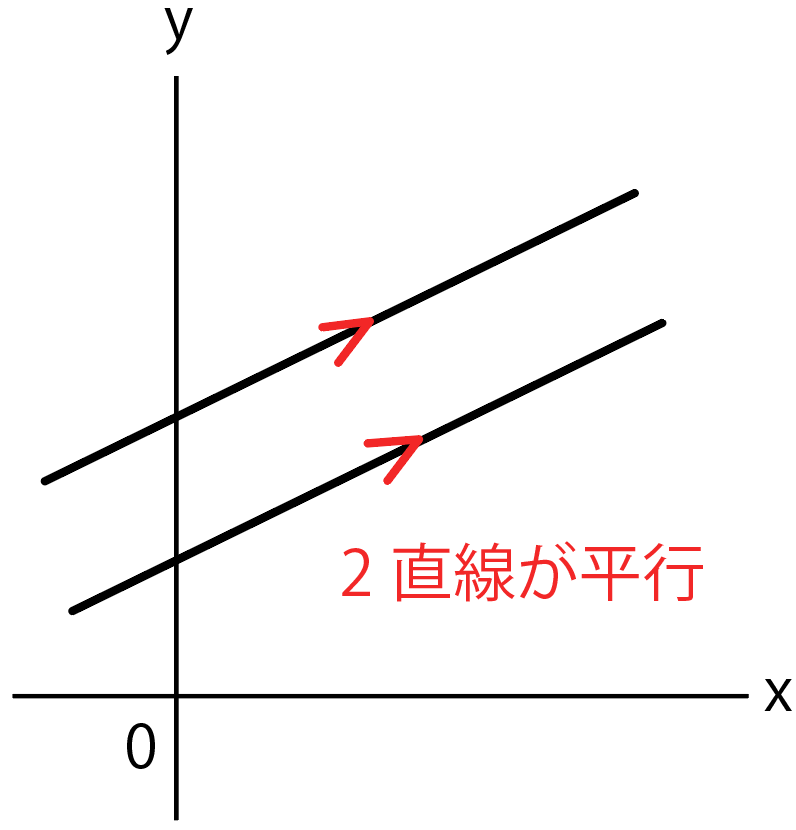
2直線が平行だとわかることが1つ。
それは、
傾きが等しい
ってこと。
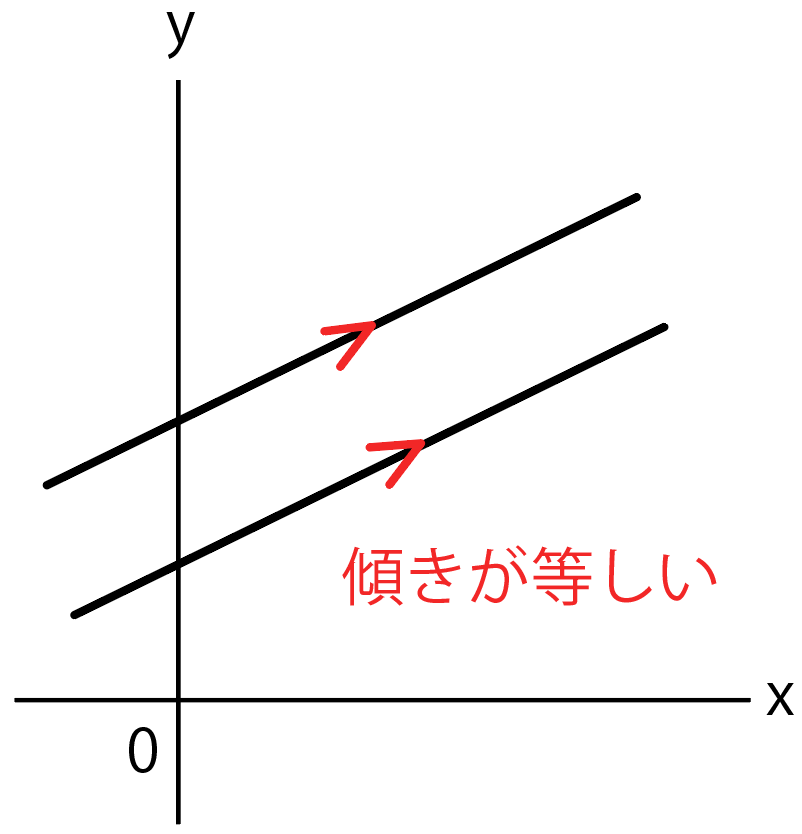
一次関数の「傾き」とは、変化の割合のことで、
xが1増加したとき y がどれぐらい変化するか?
を表していたね。
2つの直線が平行ってことは、
xが1変化した時の y の変化量も同じであるはず。
変化の割合(傾き)が違っていたとしたら、平行ではなく、どっかしらで交わっちゃう。
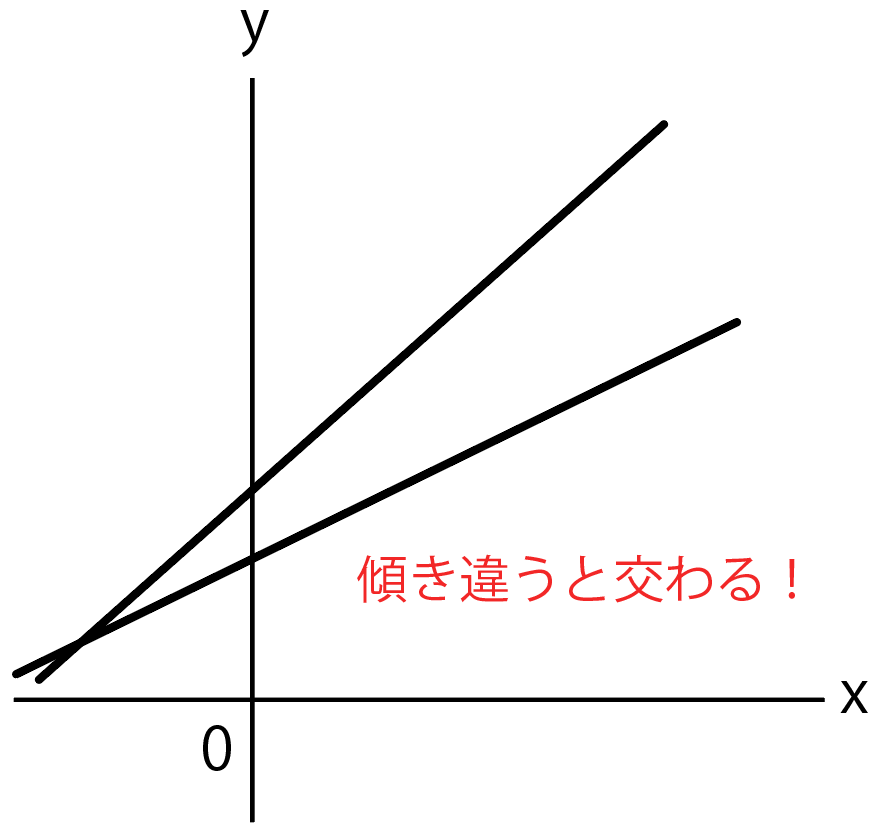
よって、平行な2直線の傾きは等しいはずだね。
例題では
直線 y = – 3 x + 4 と平行
って言ってるから、求めたい傾きは、 y = – 3 x + 4 の傾き「-3」と等しいはず。
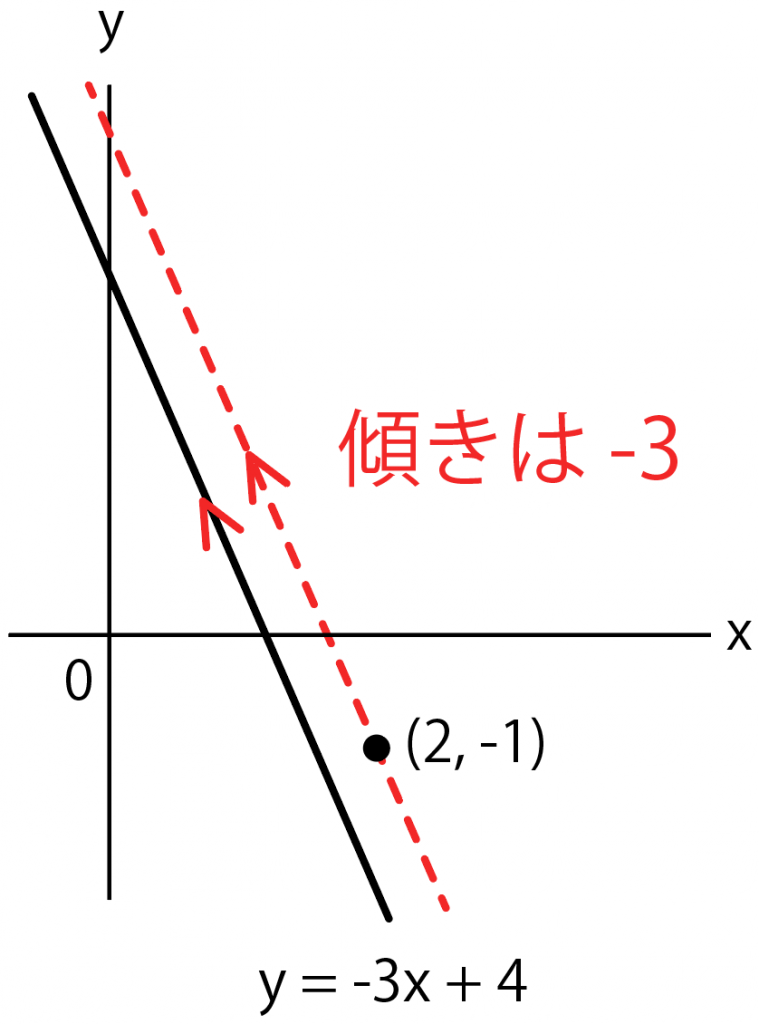
一次関数 y = ax + bの傾き「a」が「-3」ってことだから、
y = -3x + b
になる。
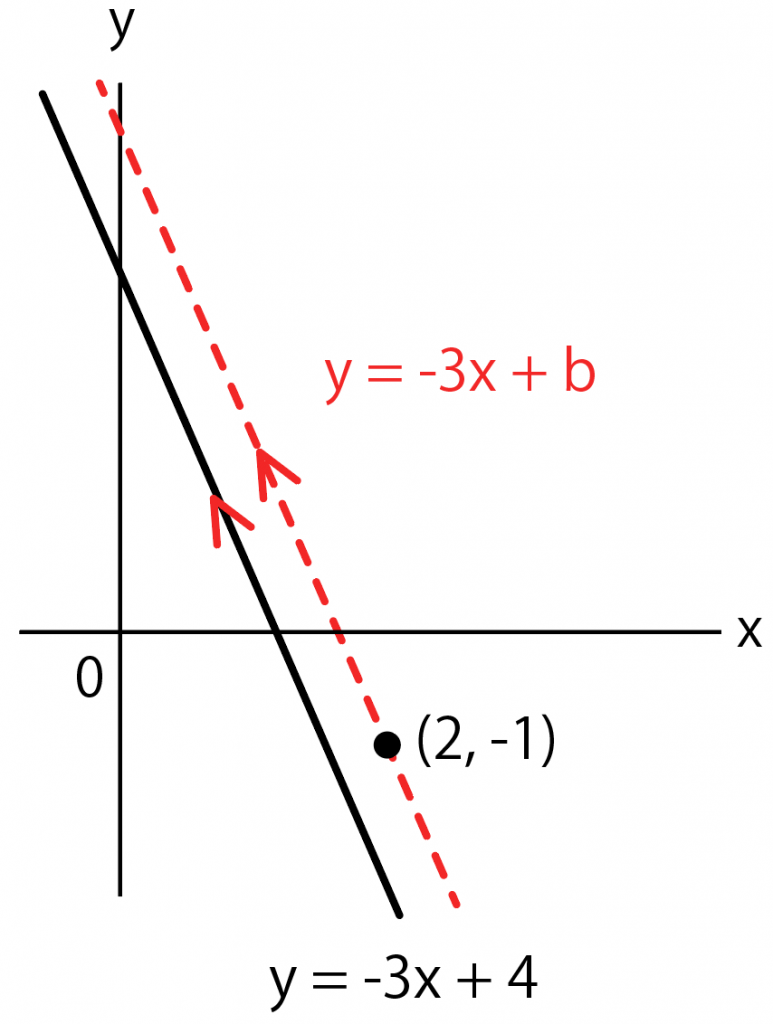
これでステージクリアにしたいけど、まだ解けたことにならないよ。
なぜなら、一次関数y =ax + bのうち、切片「b」が不明だからさ。
bの正体をつかんだらはじめて、直線の式が求められたことになる。
ってことで、切片bを求めるため、座標を直線の式に代入しよう。
例題だと、
y = -3x + b
に
点(2, -1)
という座標を代入するんだ。
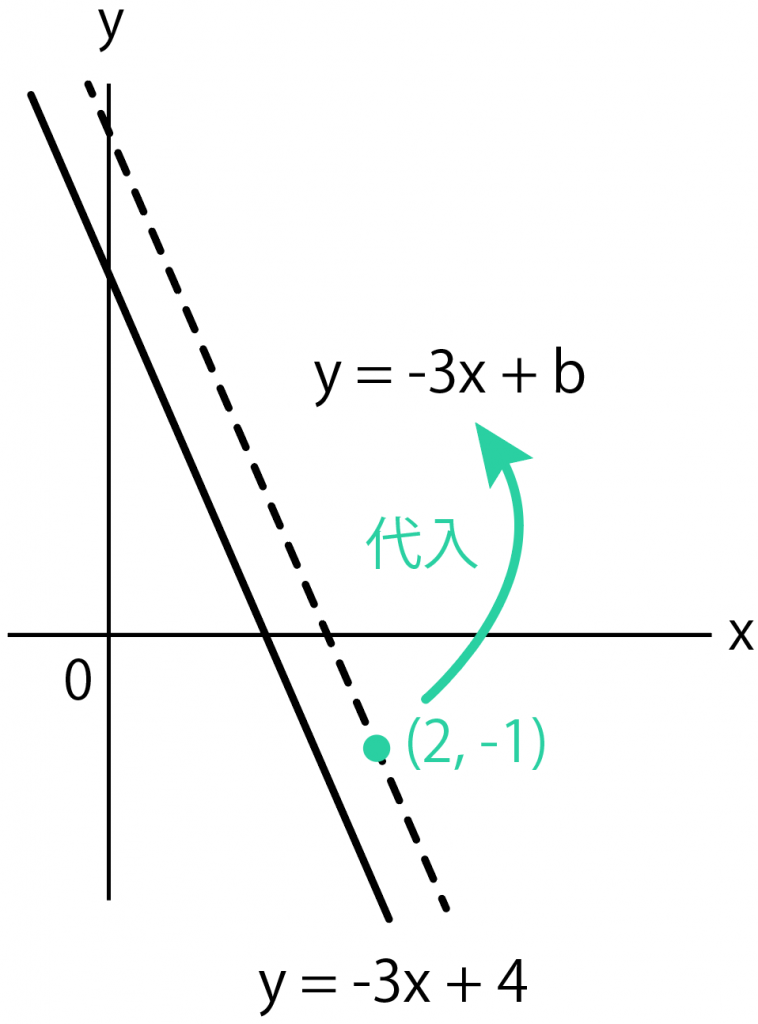
すると、
y = -3x + b
-1= -3 × 2 + b
b = 5
になる。
つまり、切片bは「5」だから、直線の全体の式は、
y = -3x + 5
になるはず。
こんな感じで、
「2直線が平行」 → 「傾きが等しい」
を知っていれば難しいことはないね。
次は「垂直な2直線の式の求め方」を勉強していこう。
そんじゃねー
Ken
中学数学では「角度を求める問題」が出てくるけど、中でも厄介なのが
図形が折られちゃっているパターンだ。
例えばこんな感じの問題↓
長方形の紙を次のように折りました。角度xを求めなさい
じつは、図形の折り返しの問題もカンタン。
2つのコツを知っていれば解けるようになるよ。
図形を折り返ししても、
元の図形の「長さ」や「角度」は変わらない
ことが大原則。
つまり、
折る前の図形
と
折られて移動した図形
はまったく同じってことだね。
たとえば、この三角形を
こんな感じでおったら、
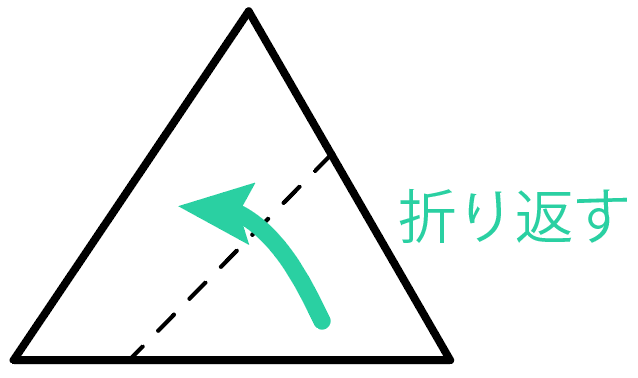
こうなって、
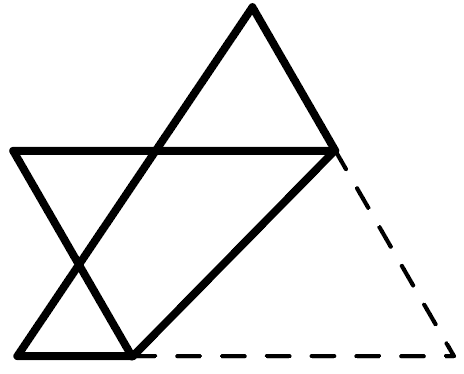
AとBはまったく同じ三角形ってわけ。
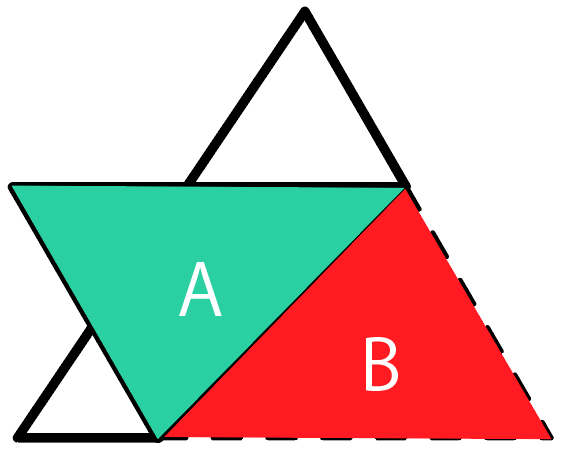
業界用語でいうと、2つの図形は「合同」といえるね。
合同であることから、
折り返して移動しても「辺の長さ」や「角度」は変わらない、と言えるんだね。
なぜなら、合同な図形は対応する角度、
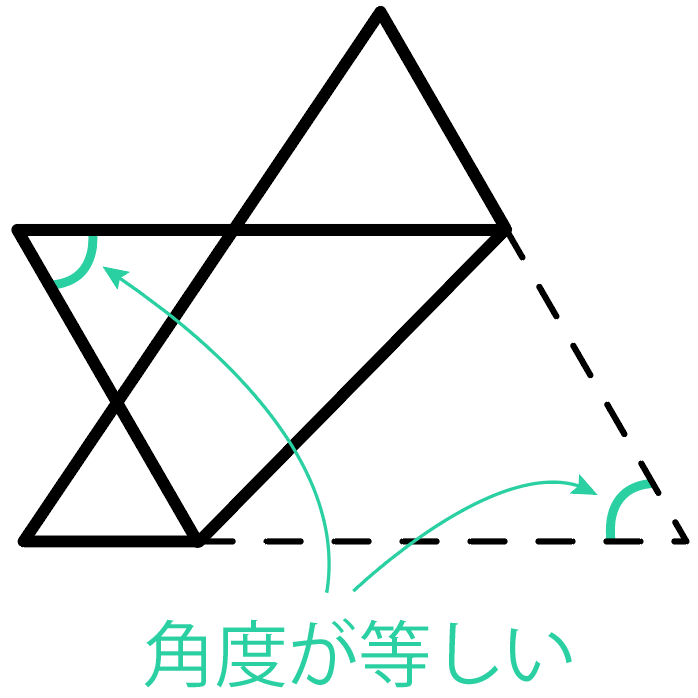
辺の長さがそれぞれ等しいっていう性質があるからだ。
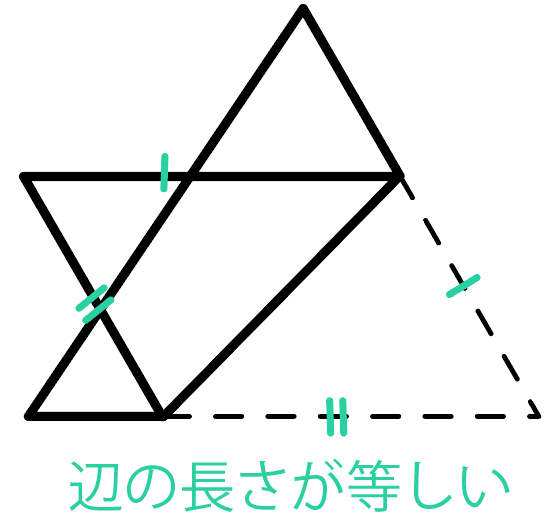
詳しくは「合同な図形の性質」を復習してみてね。
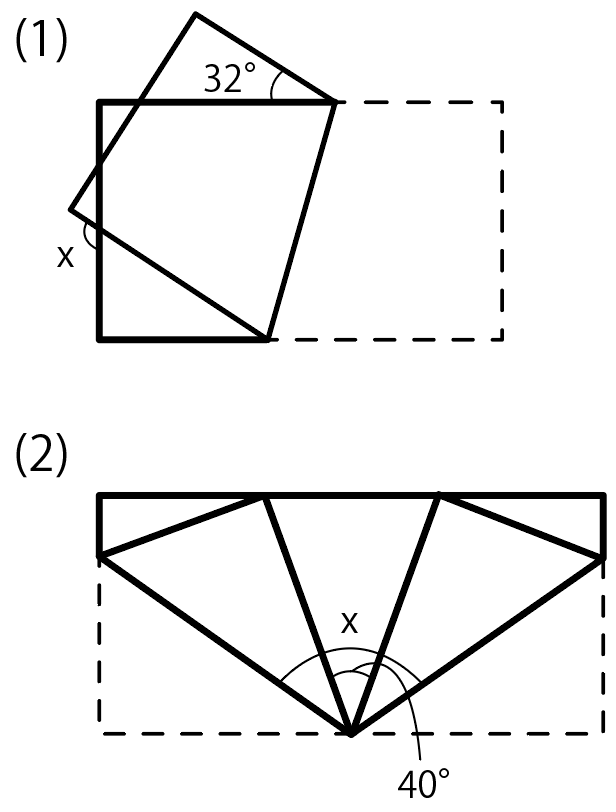
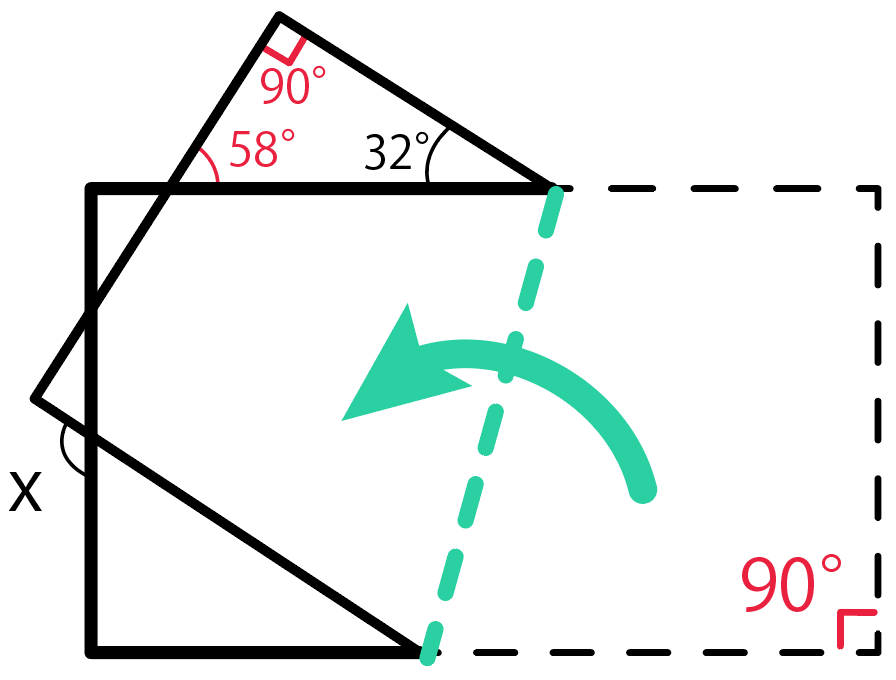
ここで1つ目の図形を見てみよう。
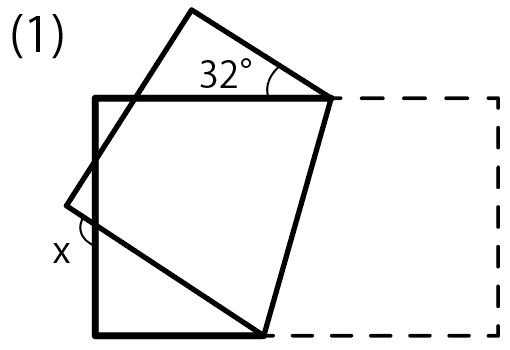
ここが折り目になっていて、
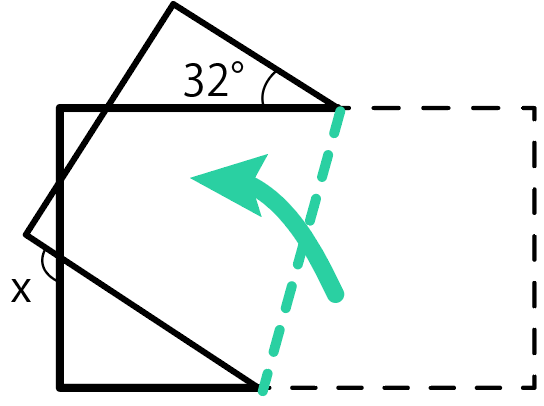
右下の四角形(台形)が左上に移動したわけだ。
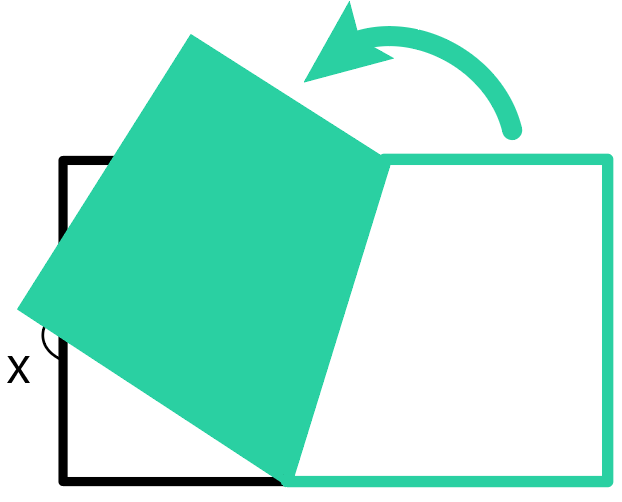
「折る前の図形」と「移動した実線の図形」は合同。
つまり、長さや角度はそのままだから、角度がすでにわかってるところがあるね。
左上の角度は90度。
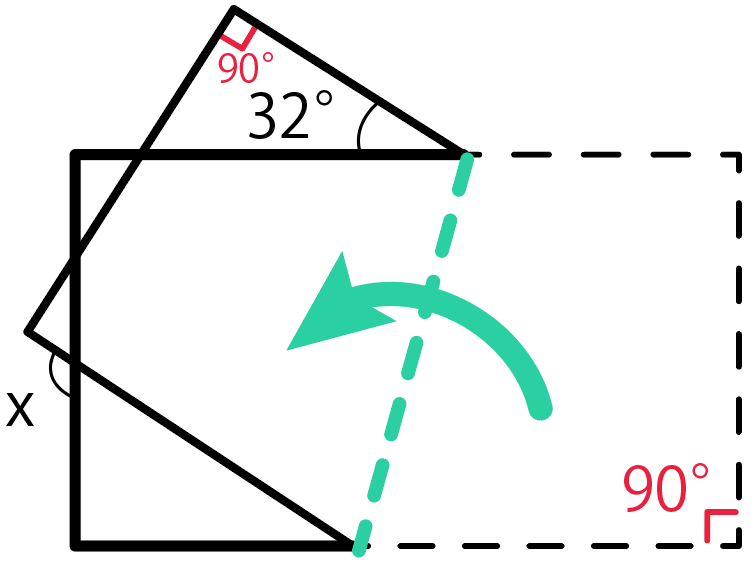
そして、三角形の内角の和は180度だから、180から90と32を引いて、
180 – 90 – 32
= 58
となって、残りの内角で58度。
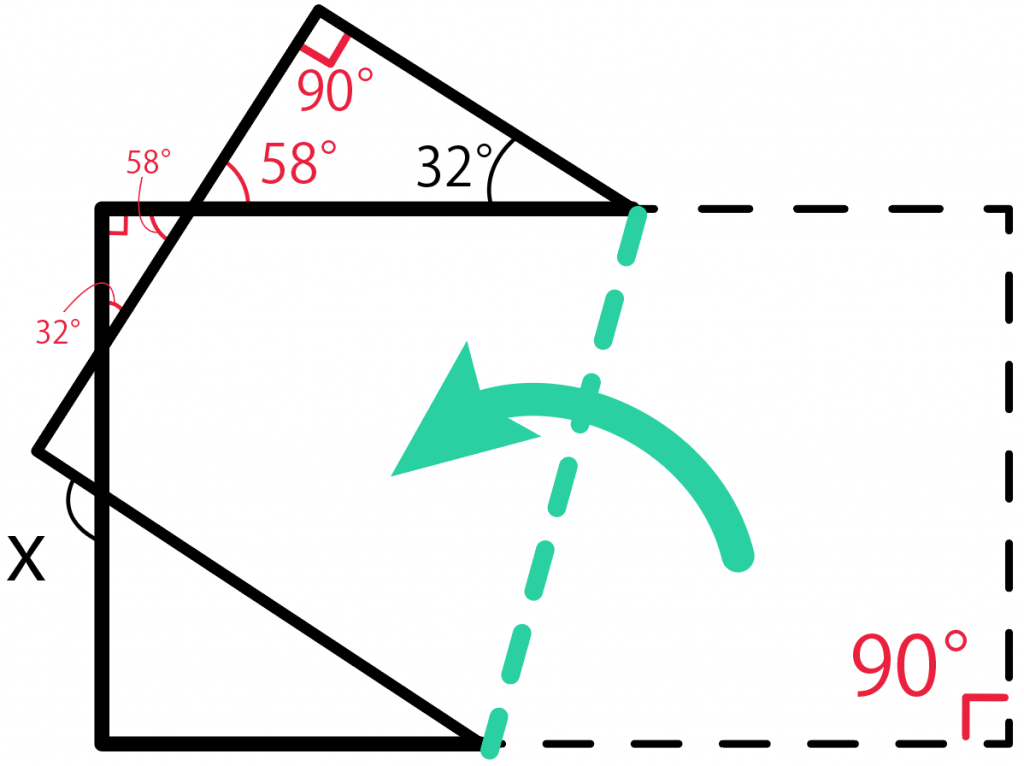
さらに対頂角を使って、小さい三角形の内角の1つも58度。
三角形の内角の和は180で、1つが直角90度だから、残りは32度。
で、さらに小さな三角形で対頂角を使う。
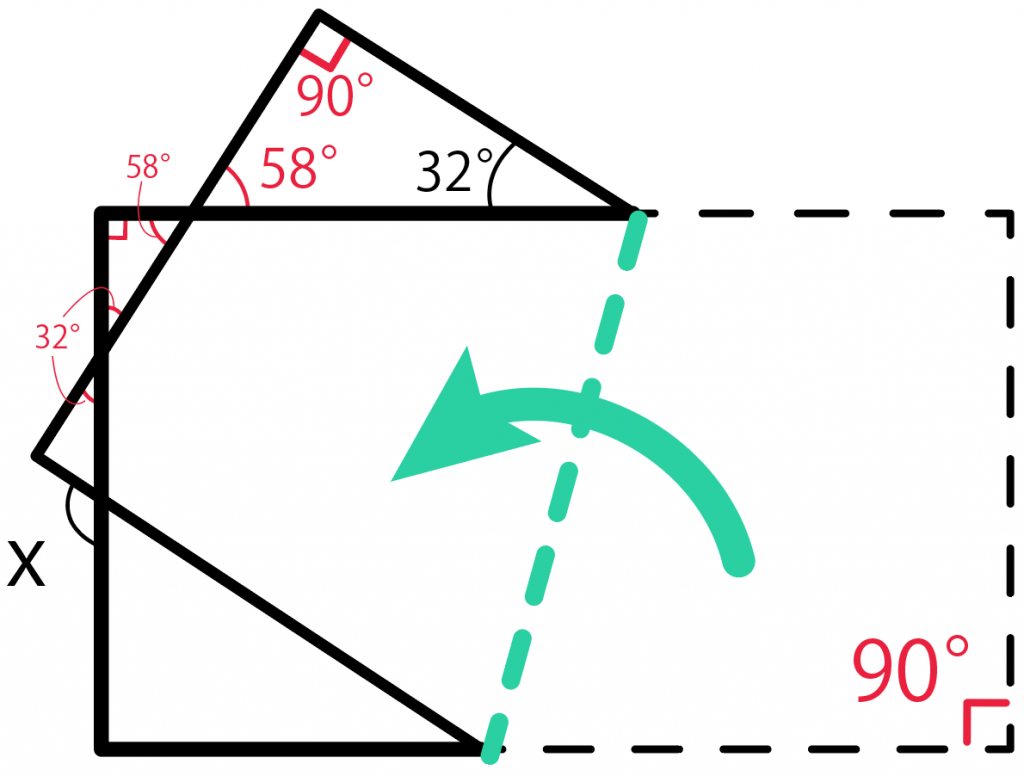
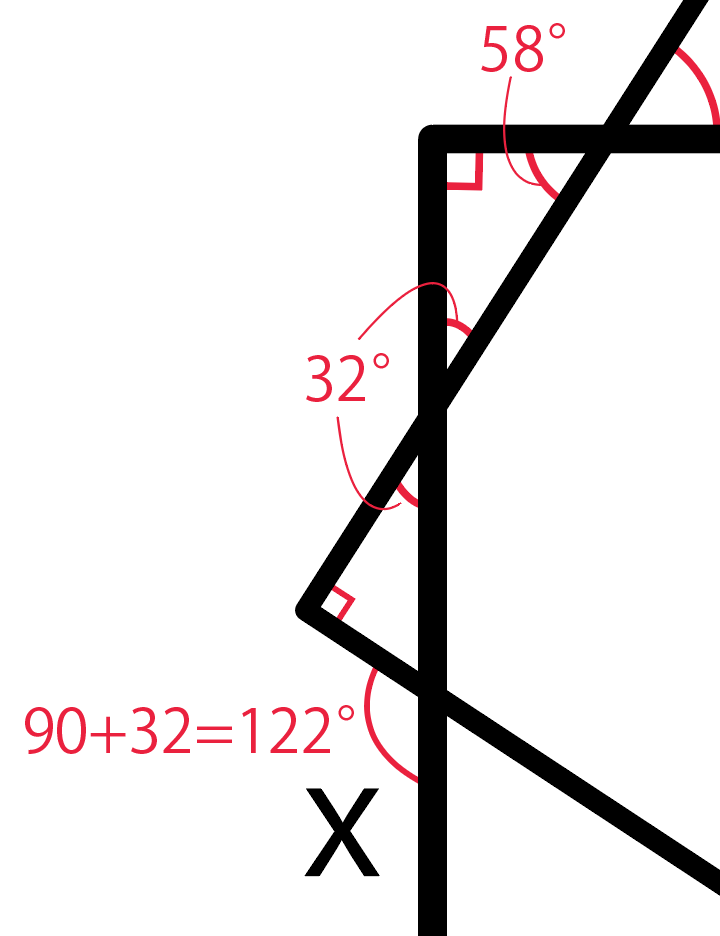
あとはミニ三角形で「外角の性質」を使って
90 + 32
=122
で、xは「122度」になるはず。
こんな感じで、
折り返しても長さや角度が変わらない
と知っておけば、折り返しの問題も解けるはずだよ。
さっきのことを応用してやると、図形の折り目は「角の二等分線」になってるはずだ。
なぜなら、折る前と折った後の図形が合同だからだね。
2つ目の例題を見てみよう。
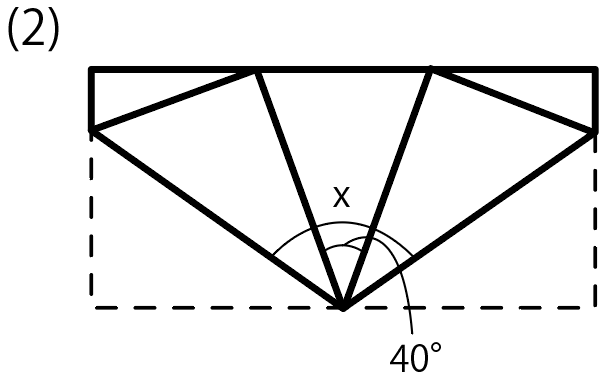
この図形は2箇所で折られていて、折り目が2箇所ついているね。
折り目が「角の二等分線」であることを使うと、
折り目を挟んでいる角度が等しい
ことになる。
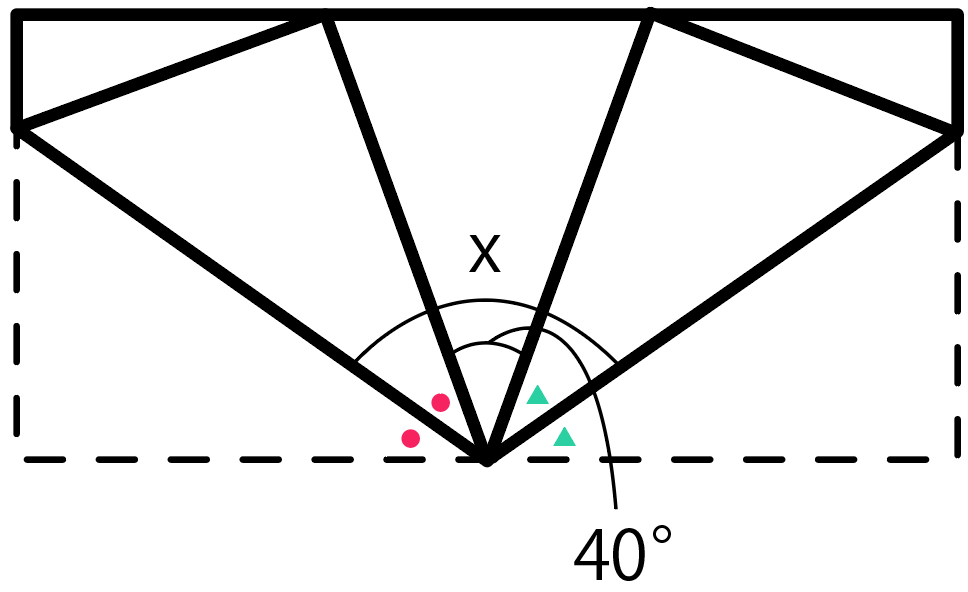
それぞれa、bと置いてやると、
2a + 2b + 40 = 180
っていう方程式が作れるね。
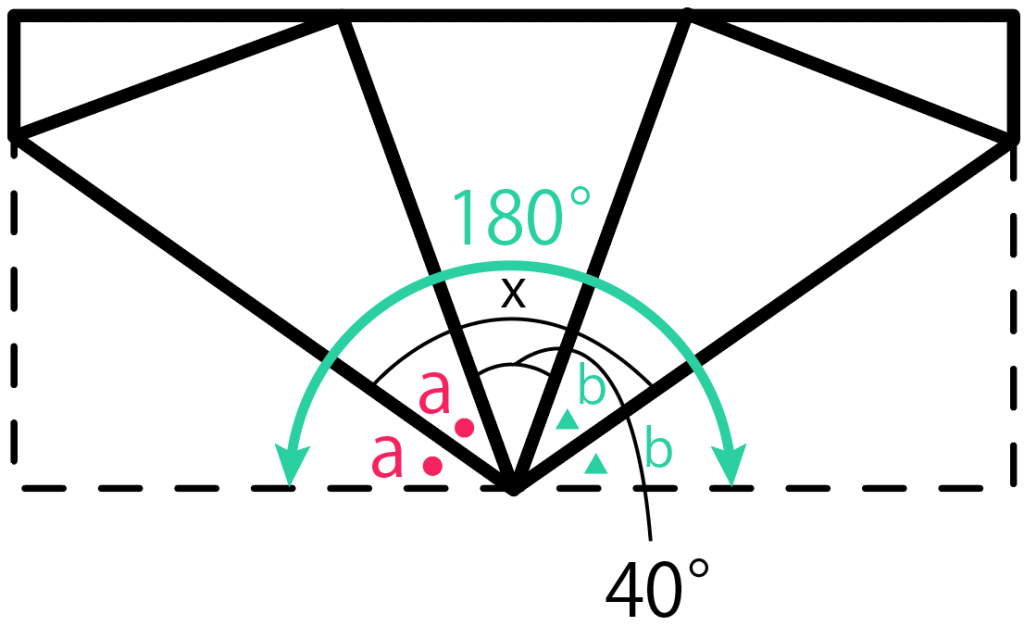
「 a + b 」について解いてあげると、
2a + 2b + 40 = 180
a + b = 70
ってなる。
この問題ではラッキーなことに、
角度 xは「a とbを足したもの」に「40度」を加えたものだ。
よって、「a + b + 40」がxになるはずだね。
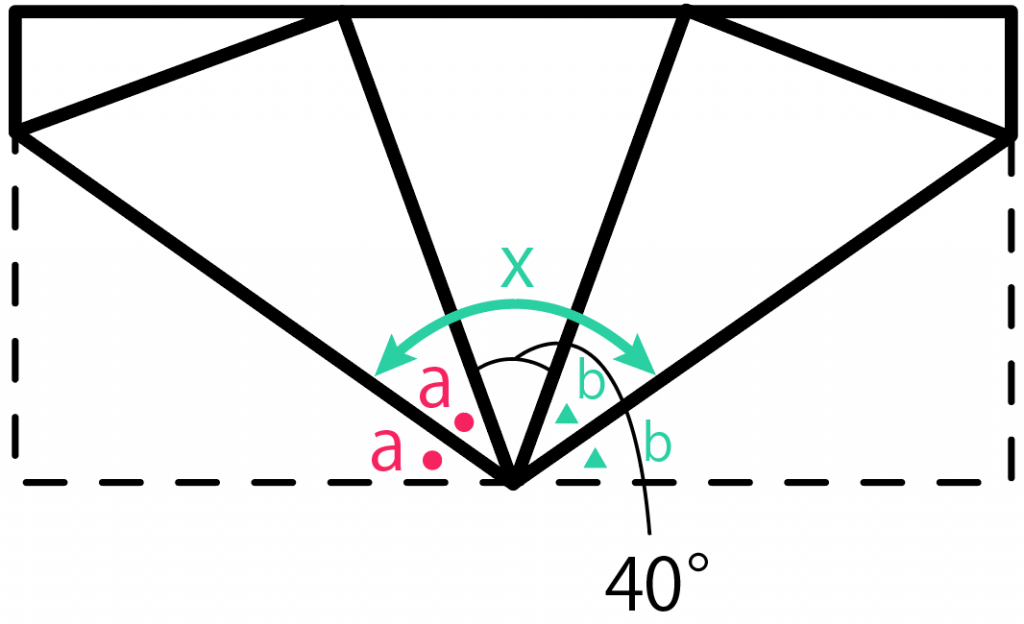
ってことで、「a + b + 40」を計算してみると、
a + b + 40
=70 + 40
= 110
と出てくる。
つまり、xは110度ってわけ。
こんな感じで、図形を折り返している角度の問題は、
さえ知っていれば大丈夫。
ガンガン問題を解いていこう。
そんじゃねー
Ken
中学生の連立方程式で厄介なのはやっぱり、
文章問題
だよね。
いわゆる連立方程式の利用っていう単元だ。
中でも狙われやすいタイプは、
「道のり・速さ・時間」についての文章題だ。
例えば、次のような問題↓
この問題は次の3ステップで解けるよ。
まずはやってほしいのが、一旦、とりあえず、
図を書いて整理する
ってこと。
方程式の文章問題では、読んでもわかんなくて、ごっちゃになる時がある。
そういう時も落ち着いて、
問題の情報を「図」とか「絵」でかいてみるんだ。
うだうだ悩んでるよりも、図をかけば1歩進むことになるね。
今回の例題を整理してみると、こんな感じかな↓
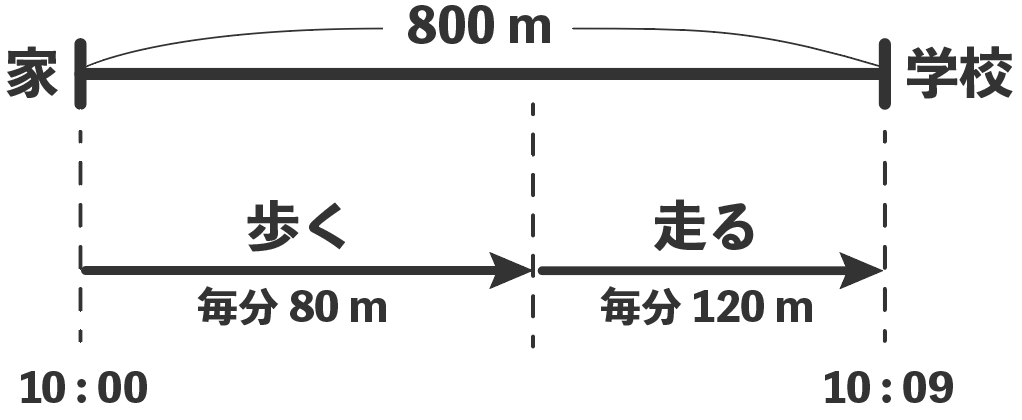
すべての文章問題ってわけじゃないけど、9割の文章題では、
「問題で求めたいもの」を文字でおくと解けるよ。
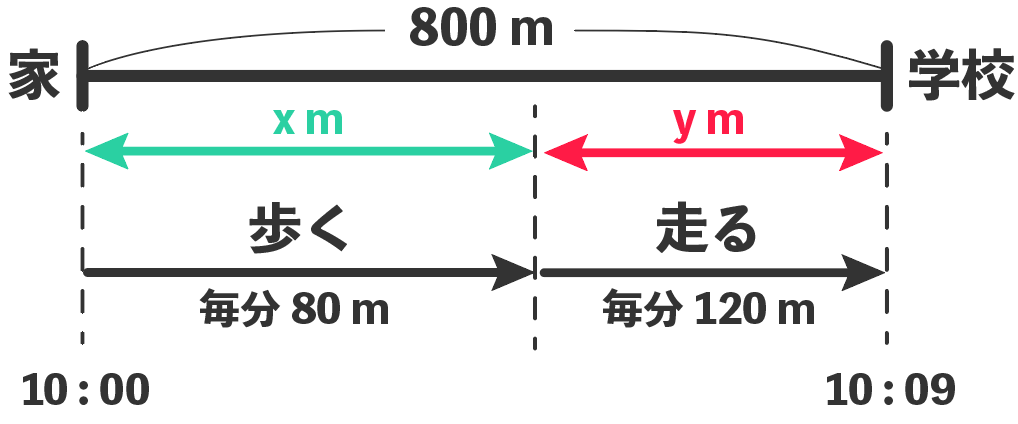
この例題では、
それぞれ何m進みましたか?
って聞かれてるね。
ということは、
を求めればステージクリアだから、こいつらをそれぞれ、
と置いてみよう。
これらをさっきの図に書き込むとこうなる↓
まずは1つ目の方程式を作ろう。
連立方程式は「x」と「y」の2つの文字を使ってるから、2つ式が必要だね。
一番簡単なのが、
道のりに関する式だ。
さっき描いた図をみるとわかるけど、
「毎分80mの速さで歩いた距離」と「毎分120 mで走った距離」を足すと800mになるはずだね。
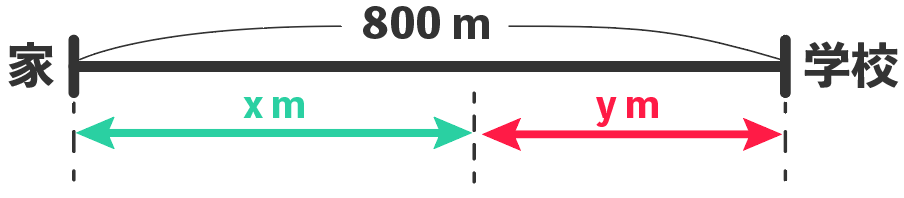
つまり、
x + y = 800
という式が作れるはずだ。
もう1つは「道のり」じゃなくて「時間」についての等式を作ってみよう。
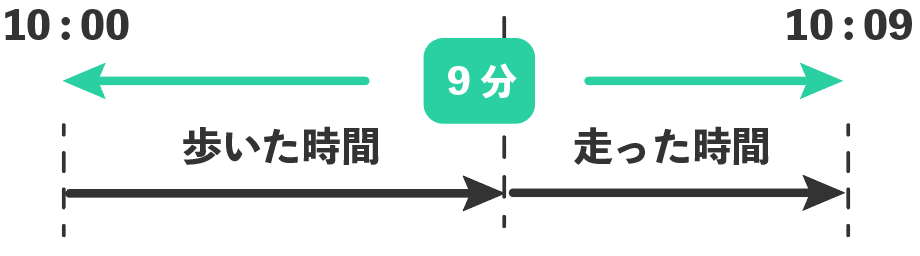
まず「Aさんが家から学校までにかかった時間」を求めてみる。
問題文によると、
10時に出発して10時9分についた
とあるから、到着までの時間は9分だ。
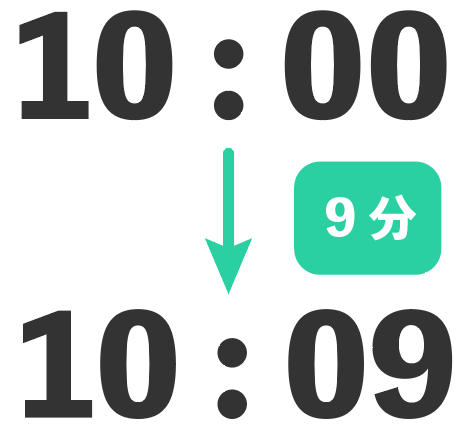
その「9分」に等しいはずなのが、
の合計。
つまり、
(毎分80 mで歩いた時間)+(毎分120 m で走った時間)= 9分
という式を作ればいいね。
「道のり・速さ・時間の公式」を使うと、
(時間) = (道のり)÷(速さ)
だから、「歩いた時間」と「走った時間」はそれぞれ、
になるね。
だから、
(毎分80 mで歩いた時間)+(毎分120 m で走った時間)= 9分
(歩いた距離 )÷ (歩いた速さ)+ (走った距離) ÷ (走った速さ) = 9分
x ÷ 80 + y ÷ 120 = 9
80分のx + 120分のy = 9
という式ができて、これが2つ目の等式になる。
最後に連立方程式を解いていこう。
Step4までで求めた連立方程式はこいつら↓
なんと、まさしく分数を含む連立方程式。
この手の問題は、
分数を消し去すことから始めよう。
分数が含まれているのは2つ目の式で、分数の分母は
の2つ。
こいつらの最小公倍数は240だから、240を両辺にかけてやると、次のようになる。
3x + 2y = 9 × 240
あとは加減法で解くだけ。
1つ目の式を2倍して、2つ目の式から引いてやると、
3x + 2y = 9 × 240
– ) 2x + 2y = 800 × 2
—————————–
x = 9 × 240 – 800×2
x = 560
と、xが出てくるはず。
このxを1つ目の式の
x + y = 800
に代入すると、
560 + y = 800
y = 240
と、yの値まで出てきたよ。
ここで冷静になって、xとyが何を表しているか考えると、
だったね。
ということで、この問題の答えは、
歩いた距離は560 m、 走った距離は240 m
になるんだ。
つまり、Aさんは歩いた距離が長くて、最後に少し走っただけになるね。
こんな感じで、道のり・速さの文章題も情報を整理すれば大丈夫。
あとは「道のり・速さ・時間」の公式を理解して、それを使えば解けるはずだ。
これさえできれば、どんな速さの応用問題でも大丈夫。
「ちょっと連立方程式の解き方が危ういな・・・・」
と思ったら、
を復習してみよう。
そんじゃねー
Ken
中学数学ではたくさん「角度の問題」が出てくるよね?
中でもなぜかでてきやすいのが、この不思議な図解↓
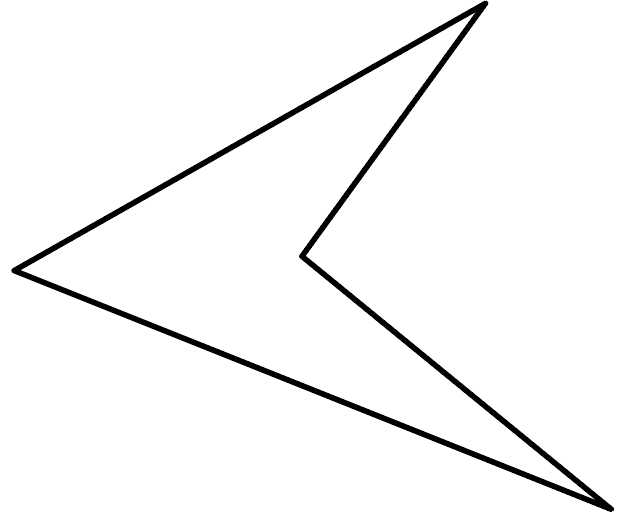
ブーメランのように見えてくるし、矢じりのようにも見えてくるし、「く」にも見えてくる。
いや、紙飛行機のようにも見えなくは、ない。
角度によっては「人」に見えるときも、ある。
じつはこの四角形にはちゃんと名前がついていて、業界では
凹四角形(おうしかくけい)
と呼んでいるんだ。
これは、
1つの内角の大きさが180度を超える四角形のこと
だね。
この問題は難しそうに見えるけど、じつはめちゃくちゃ簡単だよ。
この四角形が出てきたら、次の法則を覚えておけば大丈夫。
ズバリ、
「3つの尖った内角」をたすと「溝の角度」になる
っていう裏技。
たとえば、「尖った部分の角度」がそれぞれ
だとしよう。
このとき、矢じりの裂け目、ブーメランが曲っている角度は、a・b・cをぜーんぶ足した角度になるんだ。
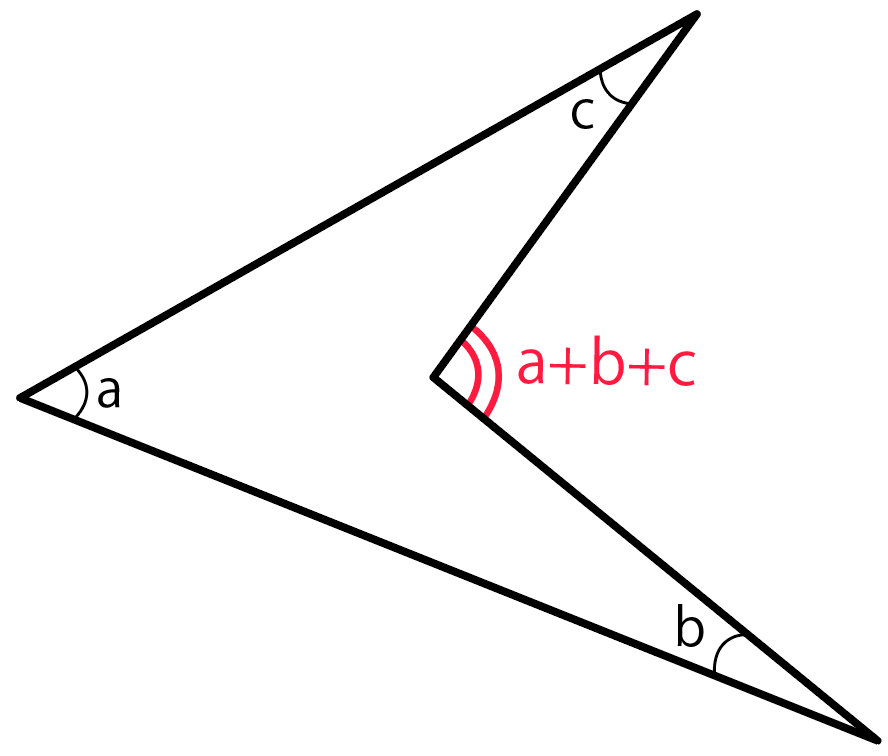
いやあ、こりゃ不思議だね。
これを応用してやると、次のような問題も一発でとけるようになるよ。
xの角度を求めなさい。
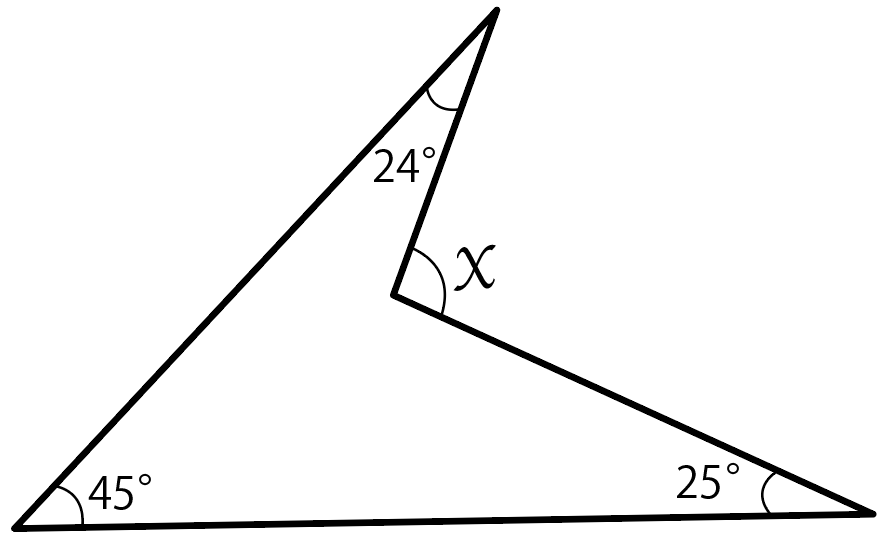
この場合、ぜーんぶの角度を足してやって、
45 + 24 + 25
= 94度
で、Xの角度は94度ってわけさ。
いやあ、ぜーんぶ足すだけなんて超楽。
それじゃあ、なぜブーメラン型の四角形の角度は求めやすいんだろうね??
いろいろ求め方があるけど、一番しっくりきているのは三角形の外角の定理を使う方法かな。
念のために復習すると「三角形の外角の定理」とは、
2つの内角をたすと、残りの内角に接する外角になる
ってやつだったね。
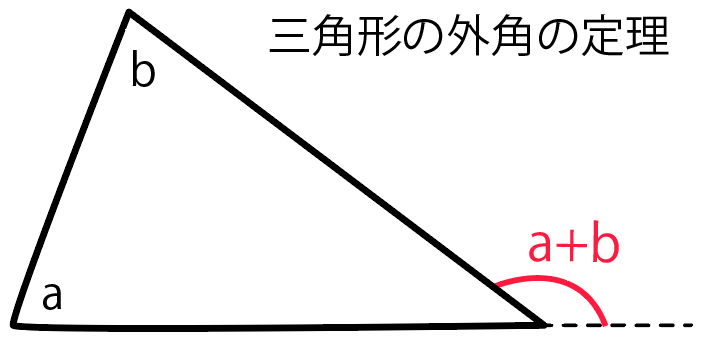
まずは補助線を引いてみよう。
ブーメランの1辺から向かい側に向かって補助線を引っ張ってやる。
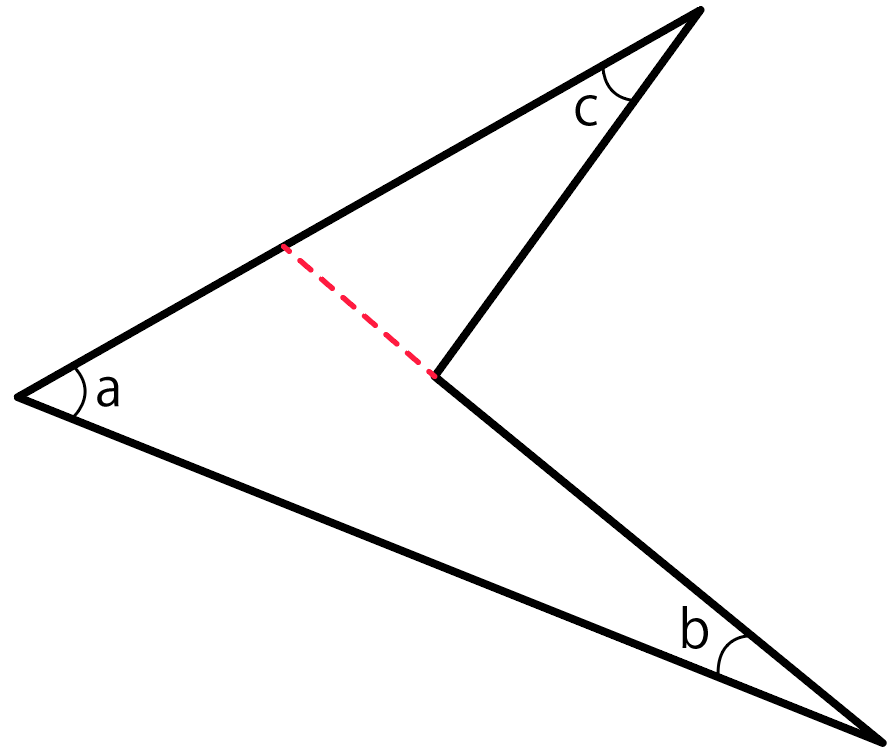
そして、三角形を2つ作る。
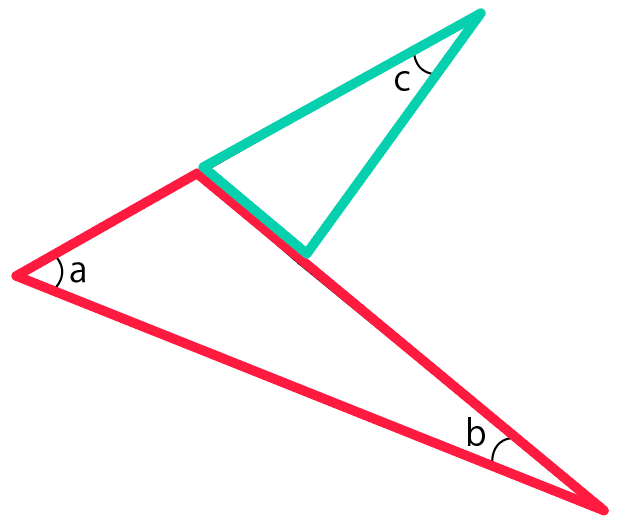
あとは2つの三角形で、三角形の外角の定理を2回使うだけ。
まず手前の「赤い三角形」で外角の性質を使ってみよう。
すると、外角の大きさはaとbを足したやつになるはず。
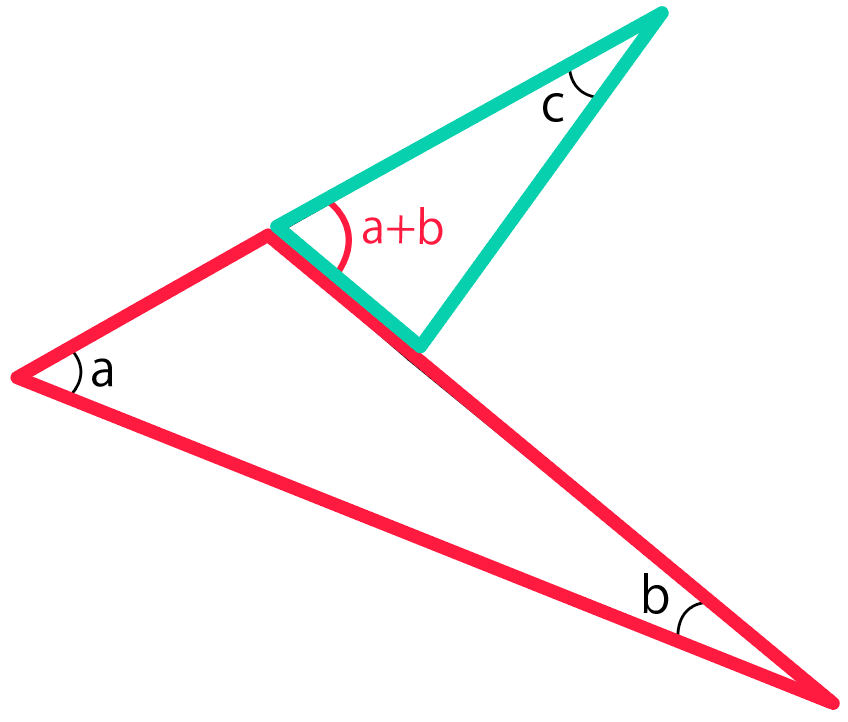
そして、緑の三角形でもう一回、外角の定理を使っていくよ。
この三角形に注目してみると、
という2つの内角になっているから、これらを足すと外角は
a+b+c
になるはずだ。
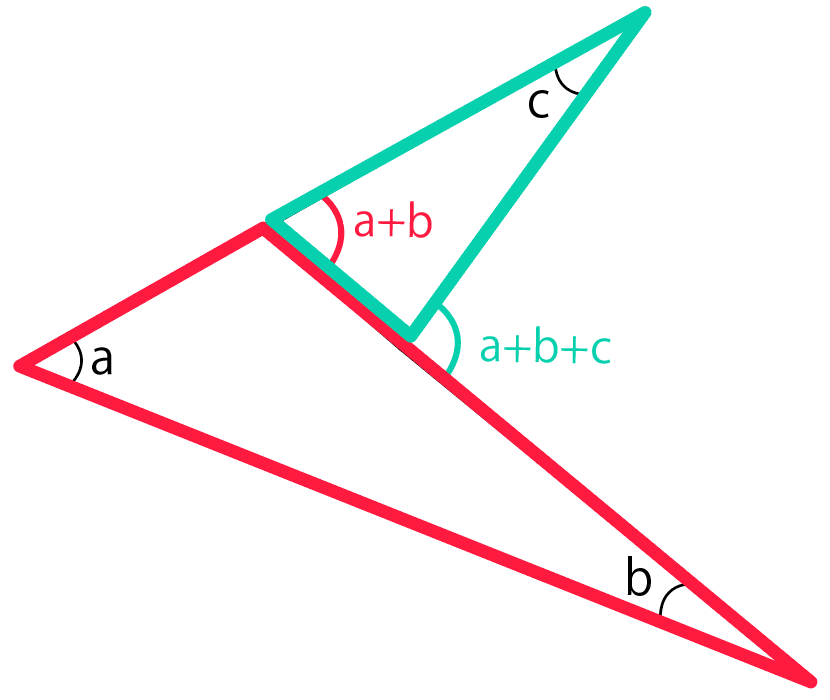
これで、ブーメランの尖ってる角度をたすと、曲っている角度になると証明できたね。
こんな感じで、ブーメラン型の四角形は解き方を知っていれば楽勝。
テストにでてきたらむしろガッツポーズしてもいい。
ただ、なぜそうなるかまで押さえておくと、応用問題まで対応できるようになるから勉強してみてね。
そんじゃねー
Ken
tomo の中学2年生の数学を単元ごとにまとめたよ。
中学数学の復習の参考にしてね。

文字式の復習!
等式変形や文章題にチャレンジしていくよ。
2つ以上の方程式から答えを出す連立方程式!
「一次関数」とは次数が1の関数。
連立方程式をつかって解いていくよ。
平面図形の角度や性質をマスターしよう。
苦手な子も多い図形の証明。
コツをつかめばいけそうな気がするよ。
確率の基礎。サイコロやコインの確率を計算しよう。
こんにちは!この記事を書いてる Kenだよ。分子を振動させたね。
中2と中3数学の平面図形で、
三角形の「合同条件」と「相似条件」
を勉強してきたよね。

両方とも数学の証明のために必要なアイテムだから、テスト前には覚えなきゃいけないね。
念のためおさらいしておくと、
だったね。
でもさ、この2つの条件ってちょっと似てない??
ごちゃ混ぜにしちゃうことあるよね。
そこで今日は、
三角形の合同条件と相似条件をごちゃ混ぜにしないために、整理して覚えてみよう!
合同条件と相似条件の似ているところと、違うところを中心に復習していくよ。
三角形の合同条件と相似条件をうまく覚えるために、3つの種類に分類してみたよ。
| 3つの何かが等しい条件 | 2つの角が等しい条件 | 2辺を角で挟んだ条件 | |
|---|---|---|---|
| 合同条件 | 3つの辺がそれぞれ等しい | 両端の角とその間の辺が等しい | 2つ辺とその間の角が等しい |
| 相似条件 | 3つの辺の比がすべて等しい | 2つの角がそれぞれ等しい | 2つの辺の比とその間の角が等しい |
まず1つ目の条件の種類は、
3つの「何か」が等しいやつだ。
合同条件と相似条件をそれぞれ見ていこっか。
「3つの辺の長さ」がすべて等しいっていう条件は合同条件だ。
この条件を満たす三角形たちは合同である、ってことが言えるわけね。
たとえば、次の2つの△ABCと△DEFを想像してみて。
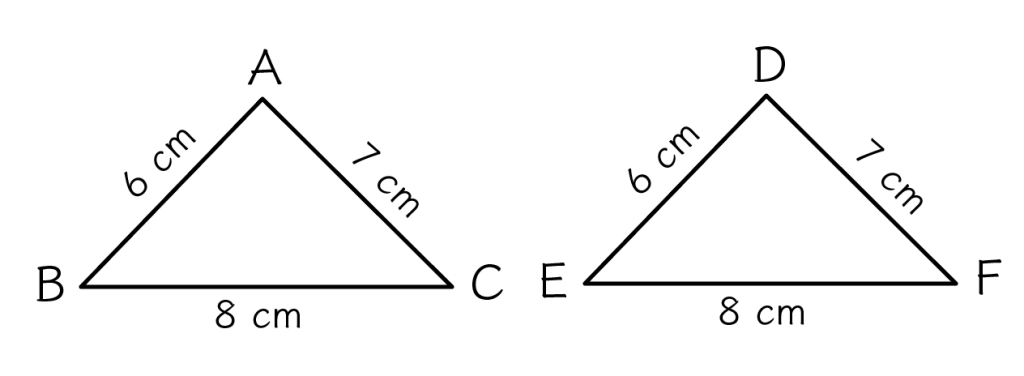
と、
この2つの三角形は合同って言えるんだ。
なぜなら、すべての3つの辺の長さがそれぞれ等しいからね。
「3つの辺の比」がすべて等しいとき、2つの三角形は相似って言えるんだ。
たとえば、2つの△ABCと△DEFを想像してみて。
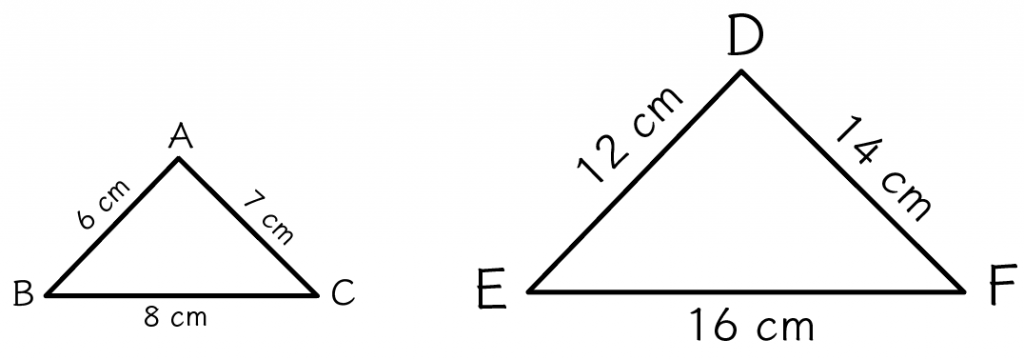
と
だ。
この2つの三角形は相似になってるはず。
なぜなら、
になっていて、すべての辺の比が全部1:2で等しくなってるね。
つぎの条件は、2つの角が等しい条件だ。
2つの角が等しいことを使った条件が、なんと偶然にも合同条件と相似条件に1つずつ存在しているんだ。
まず三角形の合同条件には、
1つの辺とその両端の角がそれぞれ等しい
っていう条件があるよ。
つまり、
1つの辺が等しくて、それを挟んでいる2つの角が等しかったら合同が言えるってわけね。
たとえば、つぎの2つの△ABCと△DEFを想像してみて。
と、
この2つの三角形はへんのひとつの辺の長さが等しくて、その両端の額の大きさが等しいよね。
だから、この2つの三角形は合同であると言えるんだ。
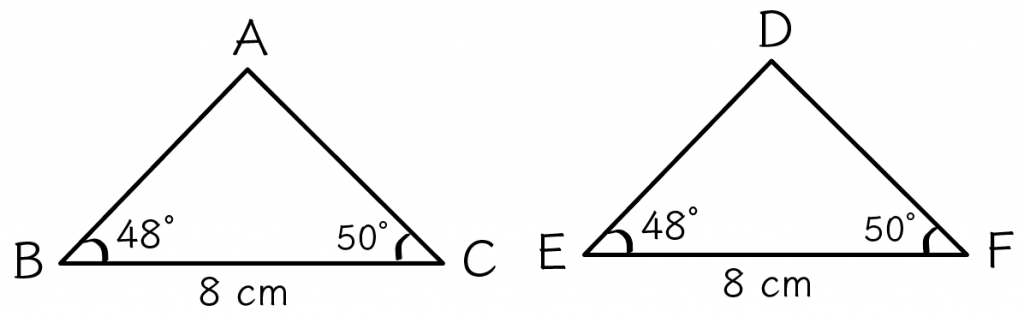
ふたつめの相似条件は、2つの角がそれぞれ等しいっていうやつだね。
この相似条件は1番簡単で、でてきやすい相似条件なんだ。
たとえば、次の△ABCと△DEFを想像してみて。
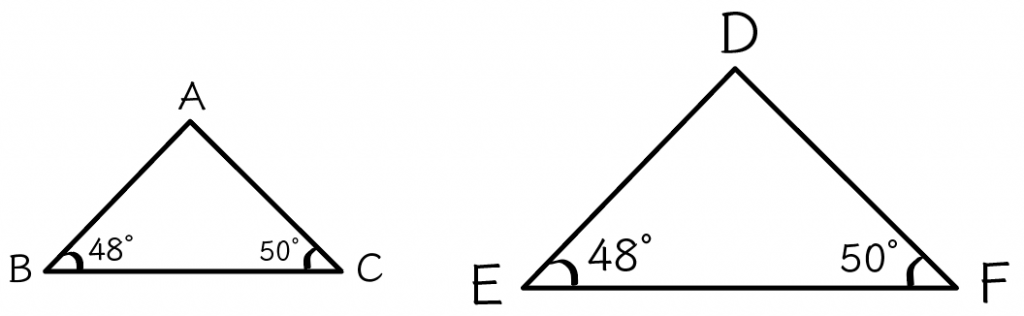
この場合、2つの三角形は、「2つの角がそれぞれ等しい」っていう相似条件に当てはまるから、相似であるといえるんだ。
つぎは、2つの辺が角を挟んじゃってる条件だ。
合同条件と相似条件には2つあるよ。
最後の合同条件は、
2つの辺との間の角がそれぞれ等しい
ってヤツ。
等しい辺たちが等しい1つの角を挟んでいれば、2つの三角形は合同って言えるんだ。
たとえば、つぎの△ABCと△DEFを想像してみて。
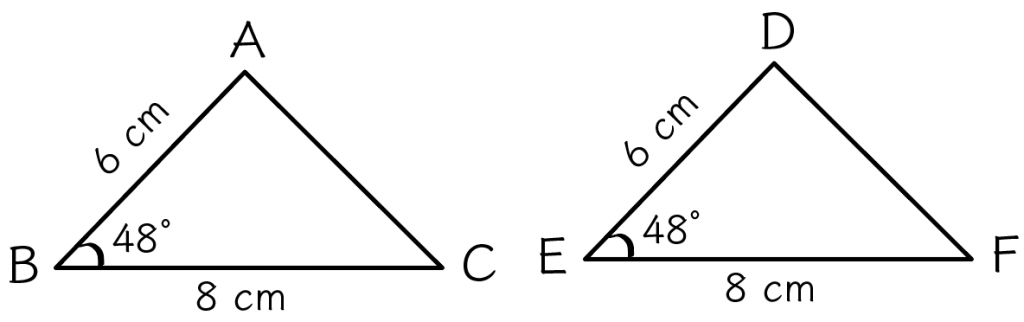
と、
この2つの三角形は、2つの辺(BCと EF、 ABとDE)が等しくて、
なおかつ、その辺に挟まれた間の角(∠ABC と∠DEF)が等しいから合同って言えるんだ。
最後の相似条件は、
2組の辺の比とその間の角がそれぞれ等しい
ってヤツね。
つぎの△ABCと△DEFを想像してみて。
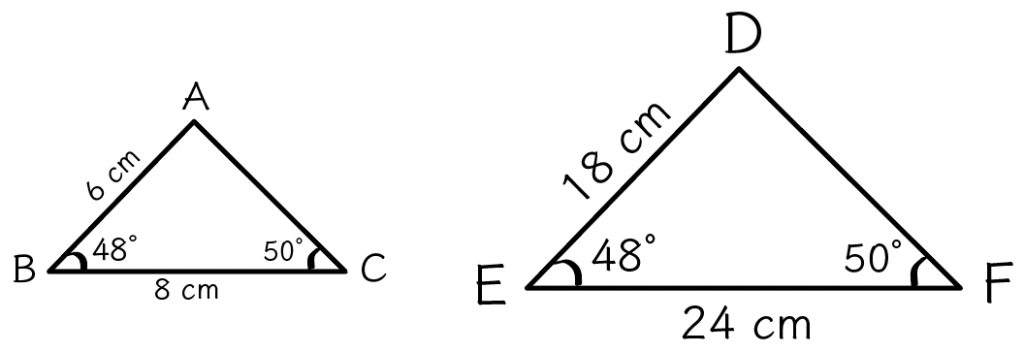
と、
この2つの三角形は相似なんだ。
なぜなら、
で2組の辺の比が1:3で等しくなっていて、なおかつ、その2辺の間に挟まってる角の、∠ABCと∠DEF が等しくなってるからね。
三角形の合同条件と相似条件は思い出せたかな??
最後にもう一回復習してみよう。
| 3つの何かが等しい条件 | 2つの角が等しい条件 | 2辺を角で挟んだ条件 | |
|---|---|---|---|
| 合同条件 | 3つの辺がそれぞれ等しい | 両端の角とその間の辺が等しい | 2つ辺とその間の角が等しい |
| 相似条件 | 3つの辺の比がすべて等しい | 2つの角がそれぞれ等しい | 2つの辺の比とその間の角が等しい |
どちらも証明問題に必要な条件だから、しっかりテスト前には覚えておこうね。
そんじゃねー
Ken
ある日、数学が苦手なかなちゃんは、
星がかけなくて困っていました。

だああー!
星かけねえええええ
おっ、苦戦してるね!
定規で一筆書きするといいよ。
へー!
やってみよっかなあー
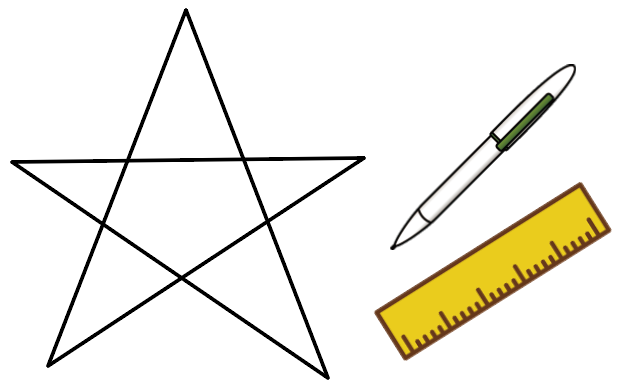
わ!かけた!
でしょでしょ??
じつはね、
数学の問題には、
星形の角度を求める問題
があるんだ。
たとえば、こんな感じ↓↓
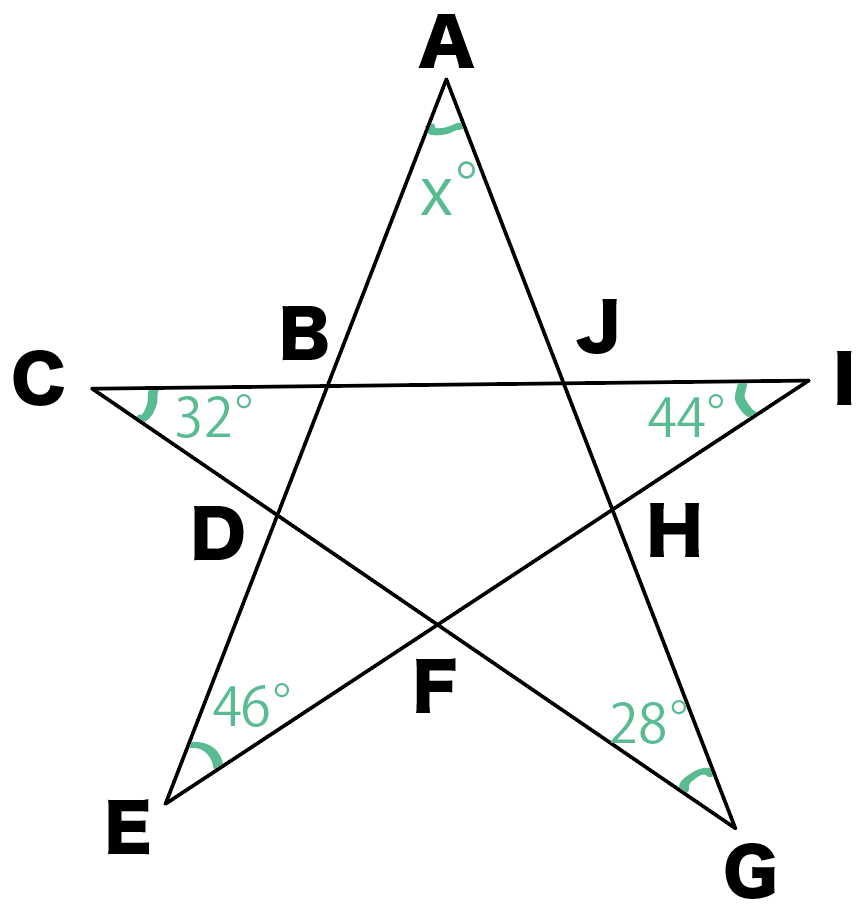
つぎの星形の角度のxを求めなさい。
ひょえー!
雰囲気むずそーー
いや!
基本おさえちゃえば大丈夫。
いっしょにといていこう!
はい!!
星形の角度の求め方はつぎの3ステップだよ。
へー!
3ステップならできそう!
いけるいける!
それじゃあ、
さっきの星形の問題をといていこう。
つぎの星形の角度のxを求めなさい。

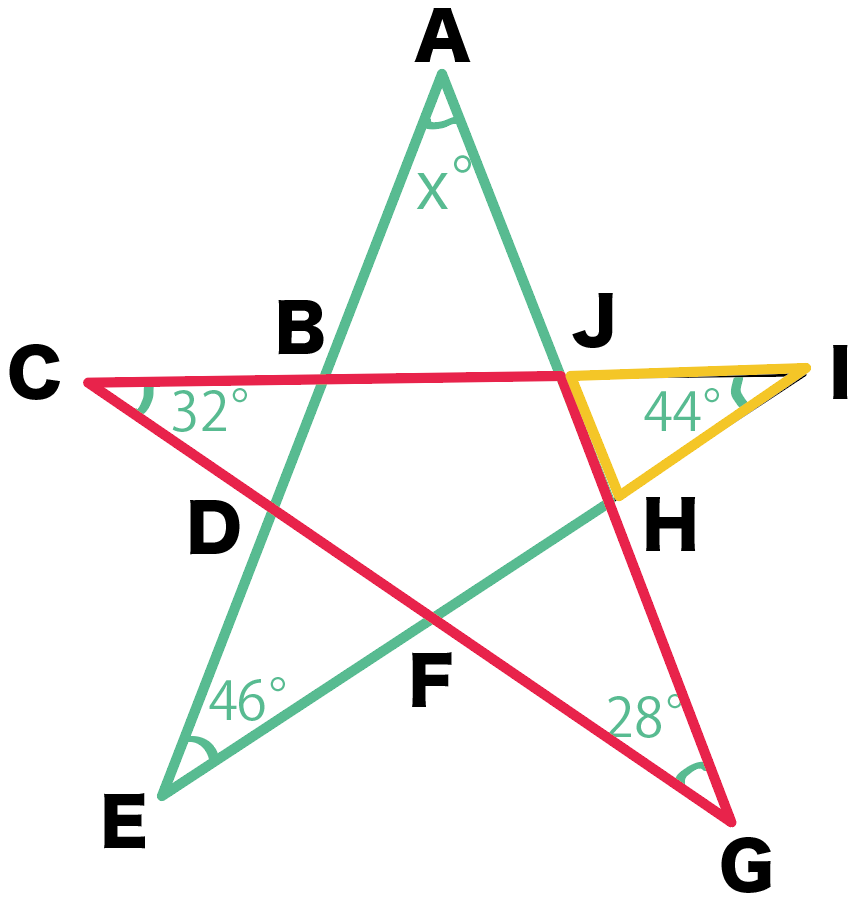
星形を、
「3つの三角形」
にわけて考えてみよう。
えっと・・・・
3つ??
そうそう。
星形の中に、
色んな図形が見えてこない??

三角形と….
あっ、
五角形もある!!
そう!
今回は、その中の3つの三角形に注目しよう。
練習問題でいうと、
の3つだね。
ひー
なんでその3つなんだろう?
それはね……
ひ、み、つ
えっ!
外角の定理ってなんだっけ??
っていう人もいると思って、
ちゃんと用意しといたよ!
さ、さすがすぎる!!
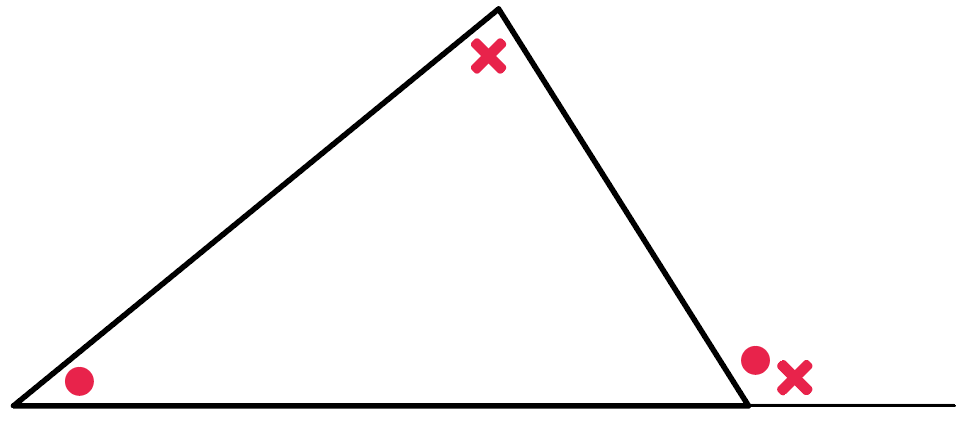
簡単にいうと、
三角形の内角を2つ足すと、
接してない外角になる
ってやつ。
下の図でいうと、
○と×をたしたら、
外角は「○+×」になるってわけ。
ああああああー
思い出してきたようなきがする!
これを星形の中の、
3つの三角形で考えてみよう!
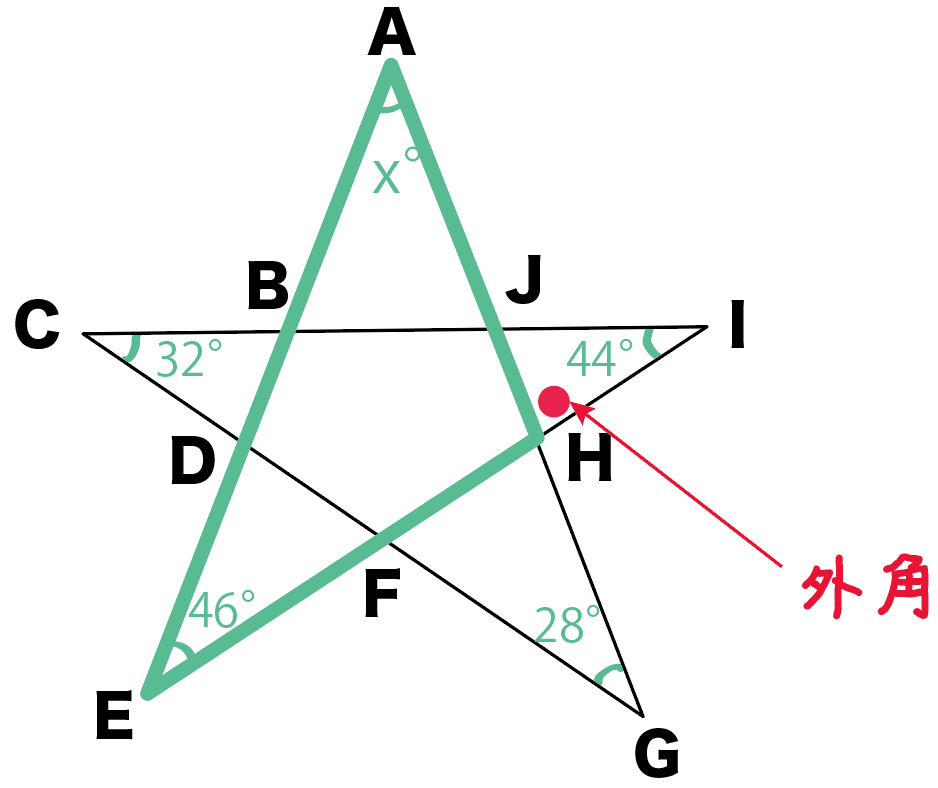
外角になりそうなところ……
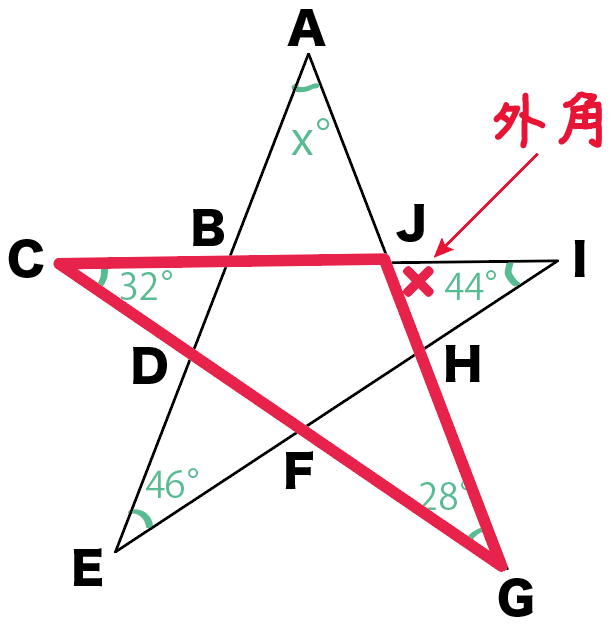
あっ、あった!
△AEHの外角は∠JHIだ!
いいね。
△CGJでも同じように考えると……
あっ!
△CGJでいうと、∠HJIが外角になってる!
三角形の外角の定理で、
角を移動させるとどうなる??
えっと・・・・、
あっ。
小さい三角形に集まってない!??
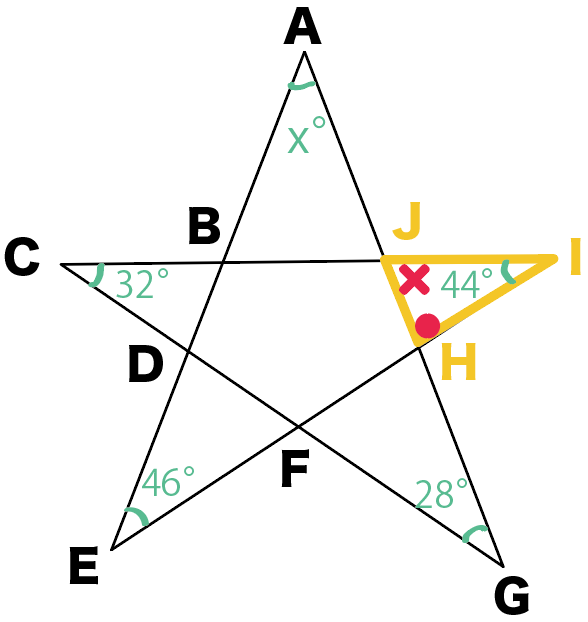
そう!
ぜんぶあわせて三角形の内角になってるね。
ということは??
三角形の内角の和は180度だから、
星の角度の和が180度になるってことだ!!
いいね!
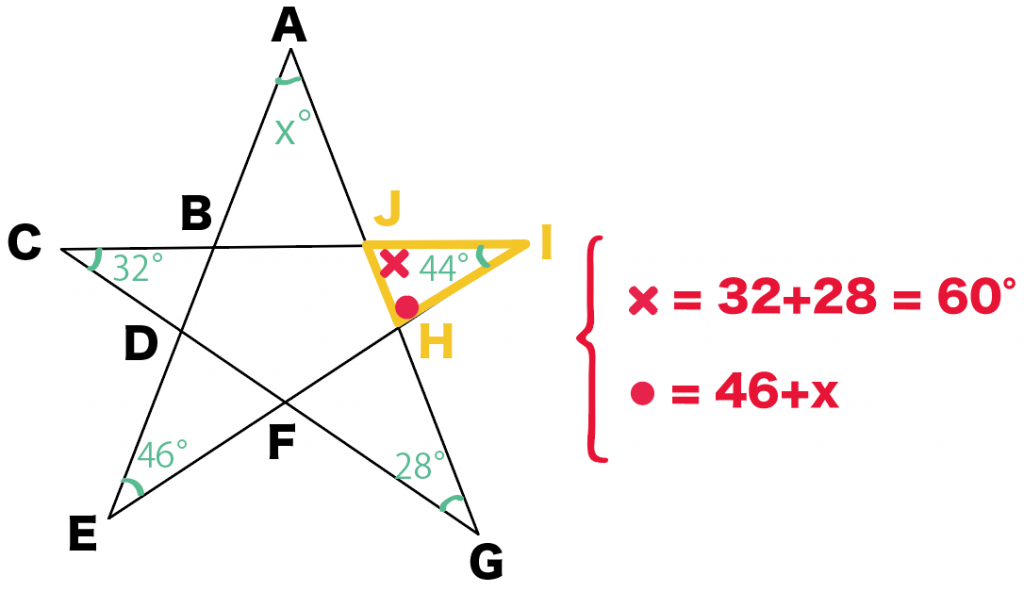
じゃあ、角xはいくつ??
えっと・・・、
三角形の外角の定理をつかうと、
になる。
うんうん
だから、△HIJの内角は全部で180度だから、
(46+x) + 60 + 44 = 180
x = 30°
だ!
xは30°!
星形の角度の求め方はどうだったかな?
の3ステップだったね。
これなら、
他の問題も解けそうかも!!
いいね、このことを利用した問題は、
まだまだたくさんあるんだ。
最初はよく分かんなかったけど、
特徴さえわかっちゃえば、分かりやすいね!!
そう!
どんな問題でも、
初めては分かりづらい。
けど、一度理解すれば大丈夫。
色んな問題が解けるようになるよ!
はい!
ありがとうございました!