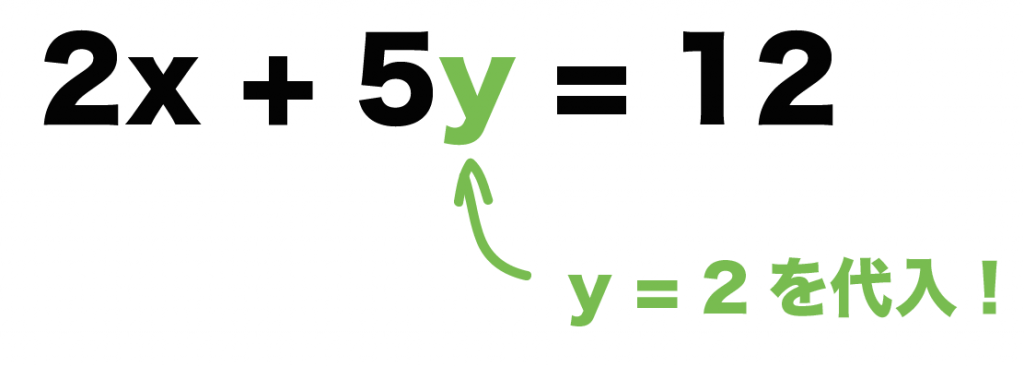連立方程式の加減法の解き方はムズい？？
連立方程式の加減法はチョー便利。
テストではだいたい「加減法」を使うからね！
「代入法」を使うのは結構だるいんだよ。
「加減法」なら楽できるってわけさ。
今日は、
連立方程式の解き方「加減法」をわかりやすく解説していくよ。
よかったら参考にしてみてね。
連立方程式の加減法の解き方がわかる4ステップ
つぎの例題をときながらみていこう！
つぎの連立方程式を、加減法で解きなさい。
$$\begin{cases}2x + 5y = 12\\3x – 7y = – 11\\ \end{cases}$$
加減法なら4ステップで解けちゃうよ。
Step1. 文字の係数をそろえる！
文字の係数をそろえちゃおう！
文字の項のうち、1つでも係数が一緒ならいいんだ。
例題の連立方程式をみてみると、
x・yの係数は一緒じゃない
ことがわかるよね？
たとえば上のxの係数は「2」だし、
下の$x$の係数は「3」だからね。ぜんぜん同じじゃない！
これは$y$だって同じことさ。
こういうときは、
それぞれの方程式に「ある数」をかけて係数をそろえるんだよ。
等式の性質のうち、
同じ数を両辺にかけても等式は維持される
ということを使ってやろう。
たとえば上の
$$2x + 5y = 12$$
の両辺に「3」をかけてやると、
$$6x + 15y = 36$$
になるよね？
これと同じように下の
$$3x – 7y = – 11$$
に「2」を両辺にかけてやると、
$$6x – 14y = -22$$
になる。
どっちの方程式でも「xの係数」が「6」になったね。
Step2. 文字を消す
文字の係数が同じになった？？
今度はその文字を消しちゃおう！
消し方は、
2つの方程式を「足し算」するか？
それとも「引き算」するか？
の2パターンさ。
消したい文字の符号が同じならば「引き算」。
符号が違うなら「足し算」すればいいんだよ。
例題ではxの係数は「6」で同じで、
さらに符号も「＋」だから一緒だね。
2つの方程式を「引き算」すればいいんだ ↓↓
- $$6x + 15y = 36$$
- $$6x – 14y = -22$$
引き算してやると、xが消されて、
$$29y = 58$$
になるね。
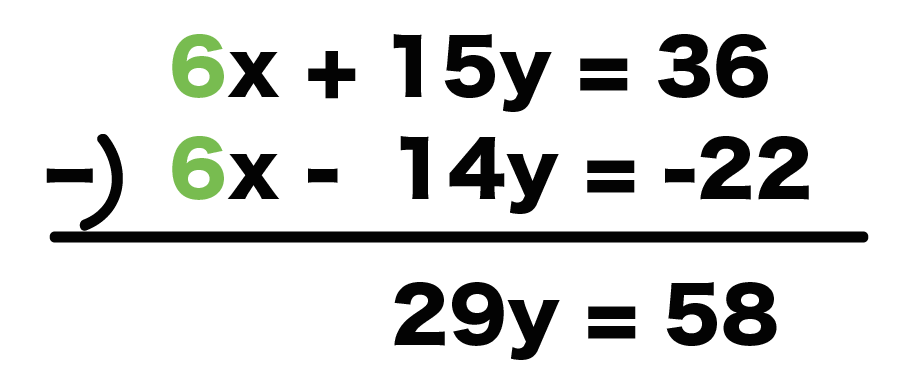
Step3. 一元一次方程式をとく！
文字が一つになった？？
文字が1つの方程式の解き方って中1数学でならったよね？？
勉強したことを使ってやればいいんだよ。
例題でいうと、
$$29y = 58$$
の両辺をyの係数「29」わってみよう。
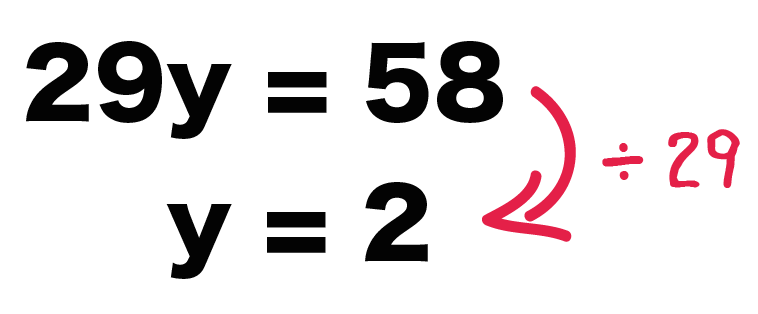
すると、
$$y = 2$$
っていう解がゲットできたね！
あとはxだけだ！
Step4. 解を代入するっ！
解を方程式に代入してみよう！
代入して方程式をとけばいいのさ。
例題の「$y = 2$」っていう解を
$$2x + 5y = 12$$
に代入してみよう。
すると、
$$2x + 5 × 2 = 12$$
になるね。
この方程式をとくと、
$$2x + 10 = 12$$
$$2x = 2$$
$$x = 1$$
になるね。これがxの解さ。
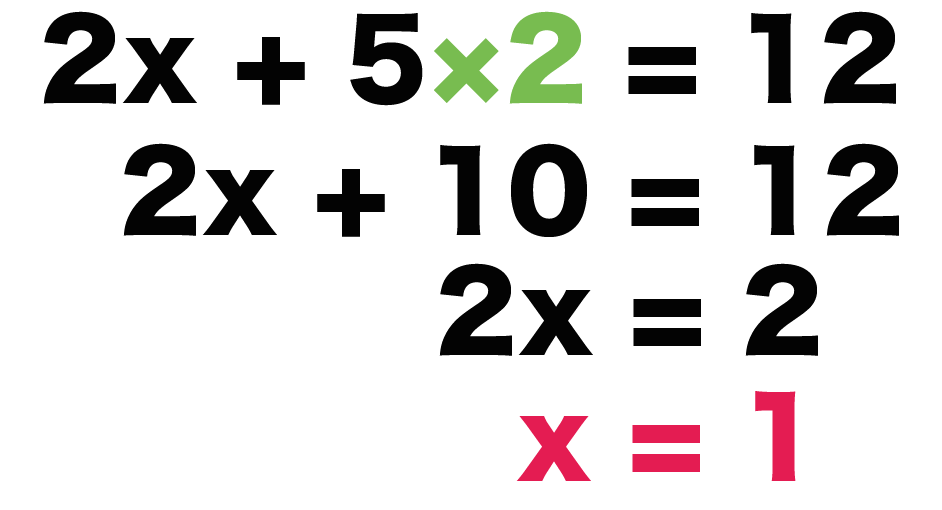
おめでとう！
これで連立方程式の解の
$$(x, y ) = (1, 2)$$
が得られたね。
まとめ：連立方程式の加減法は係数をあわせるだけ！
連立方程式の加減法はよく使うよ。
だからこそ、
時間がかかってもいい。
間違えずに解けるようにしたいね。
- 係数をあわせる
- 文字を消す
- 一元一次方程式をとく
- 代入する
っていう4ステップだけさ。
身に付くまで繰り返し問題を解いてみよう！
そんじゃねー
