3分でわかる！三平方の定理（ピタゴラスの定理）の公式とは？
妖練習 中学数学 三平方の定理 スーパードリル 350 (中学数学マスターシリーズ)
三平方の定理（ピタゴラスの定理）の公式とは？？
こんにちは！この記事を書いているKenだよ。電気最高。
中学3年生になると、
三平方の定理
を勉強していくよね？？
この定理は今から2500年ぐらい前に活躍した「ピタゴラス」っていう数学者が発見した定理だから、
ピタゴラスの定理
とも呼ばれてるやつね。
発見者の名前がついてるわけ。
この三平方の定理（ピタゴラスの定理）とは何かっていうと、
直角三角形の3つの辺の関係を表した公式
なんだ。
もうちょっと具体的にいうと、直角三角形には、
斜辺の2乗は、直角をはさむ辺を2乗して足したものと等しい
っていう関係があるんだ。
たとえば、斜辺の長さがc、その他の辺の長さがa・bの直角三角形ABCがあっとすると、
a² + b² = c²
っていう公式が成り立っているんだ。
たとえば、斜辺の長さが15cm、その他の辺の長さが12cm、9cmの直角三角形ABCをイメージしてみて。
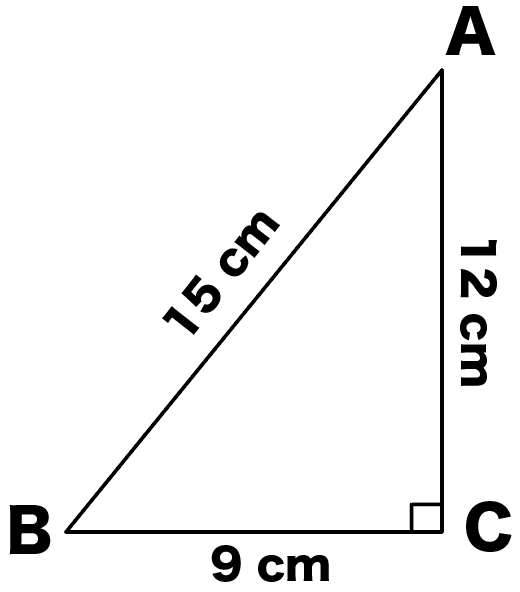
斜辺ABの2乗は、
AB²=15² = 225
一方、その他の辺のBCとACの2乗して足してみると、
AC²+ BC²
= 12² + 9² = 144 + 81 =225
だね！
おっ。両方225になって等しくなってんじゃん！
ピタゴラスの定理の公式すごいな。。
＞＞三平方の定理（ピタゴラスの定理）の証明はこちら
三平方の定理（ピタゴラスの定理）の公式の何がすごいのか？？
でもさ、
三平方の定理（ピタゴラスの定理）の公式のすごさがいまいちわからないよね？？
ぜんぜん生活に役に立ったないじゃん！
って思ってない？？
じつは、三平方の定理（ピタゴラスの定理）のすごいところは、
直角三角形の2辺の長さがわかれば、残りの辺の長さがわかる
ってところなんだ。
たとえば、斜辺の長さ13cm、その他一辺の長さが5cmの直角三角形DEFがあったとしよう。
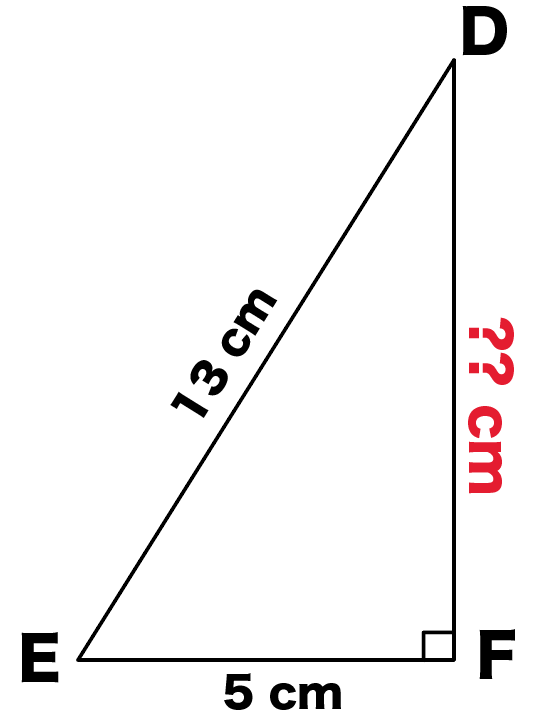
DFの長さって問題にも書いてないし、誰も教えてくれてないよね？？
でも、大丈夫。
三平方の定理（ピタゴラスの定理）を使えば求められるんだ。
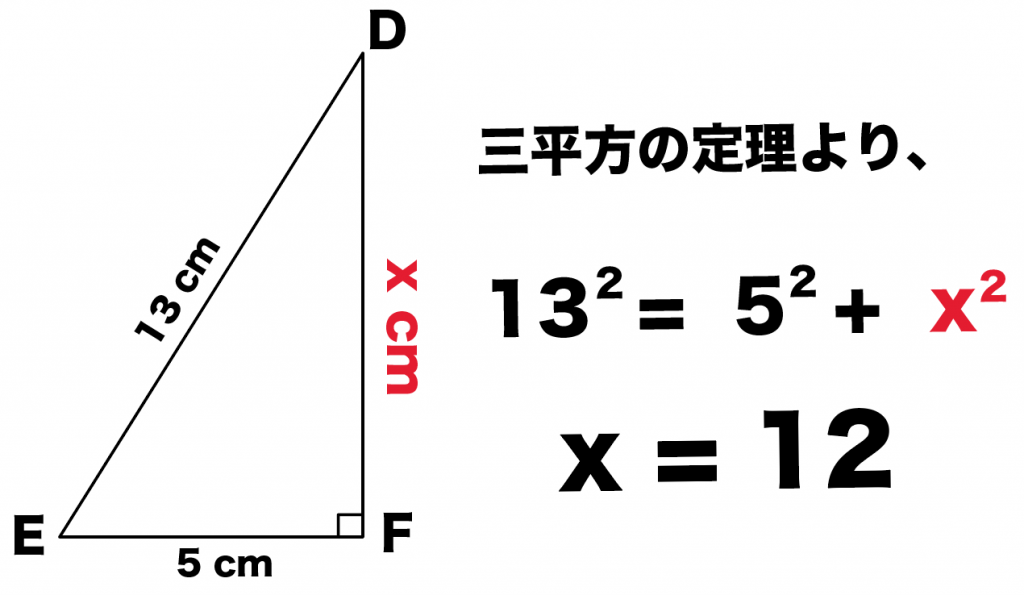
DFの長さをxcmとして、三平方の定理（ピタゴラスの定理）に代入してみると、
13² = 5² + x²
x = 12
あら不思議！
長さがわからない直角三角形の辺を求めることができたね。
＞＞三平方の定理（ピタゴラスの定理）の計算問題にチャレンジ！！
まとめ：三平方の定理（ピタゴラスの定理）の公式は便利だから絶対暗記！
三平方の定理（ピタゴラスの定理）の公式はめちゃくちゃ便利。
この公式なら、
だって計算できちゃうんだ。
入試問題や定期テストでむちゃくちゃよく出てくる定理だから、しっかりと覚えておこうね。
そんじゃねー
Ken
妖練習 中学数学 三平方の定理 スーパードリル 350 (中学数学マスターシリーズ)
