連立方程式に「分数」がいる？？
こんにちは、この記事をかいているKenだよ。ジムに通い始めたね。
分数がはいっている連立方程式
って、たまにあるよね？？
↓ たとえばこんな感じ ↓
例題
つぎの連立方程式を解きなさい。
$$\frac{x}{2} + \frac{y}{4} = 1$$
$$3x + 2y = 5$$
これみたいに、
分数がいるときは要注意！
テストでも間違えやすいところなんだ。
今日は、
分数がふくまれている連立方程式の解き方
をわかりやすく解説していくよ！
分数入りの連立方程式の解き方がわかる3ステップ
つぎの3ステップでとけちゃうよ！
例題をときながらみていこう！
例題
つぎの連立方程式を解きなさい。
$$\frac{x}{2} + \frac{y}{4} = 1$$
$$3x + 2y = 5$$
Step1. 分数をけすっ！
分数を消しちゃおう！
方程式から分数をなくすには、
分母の最小公倍数を両辺にかければいいんだ！
例題の分母の「2」と「4」の最小公倍数は「4」だね。
$$\frac{x}{2} + \frac{y}{4} = 1$$
に最小公倍数「4」をかければいいんだ。
左だけじゃなくて右にもかけてね！
すると、
$$2x + y = 4$$
になるよ。
ね？
分数がなくなったでしょー？
最小公倍数がわからないときは、
ぜんぶの分母を両辺にかけてやればいいよw
めんどいけど、確実に分母を消せるからね！
これで第一ステップ完了さ！
Step2. 文字をけす！
つぎは「文字」を消去してやろう！
連立方程式から文字を消す方法って、
- 加減法
- 代入法
の2つだったよね。
どっちを使うかわからないときは、
連立方程式の解き方のコツをみてみてね。
分母をはらったあとの連立方程式、
$$2x + y = 4$$
$$3x + 2y = 5$$
は「加減法」を使って解いてくよ！
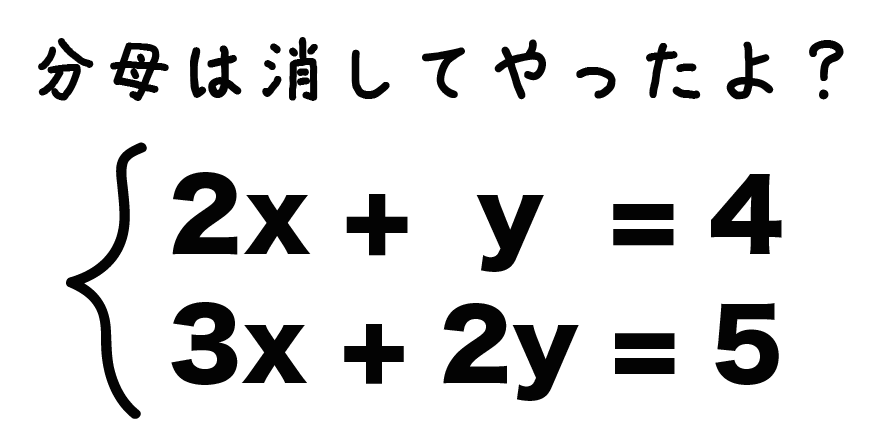
上の式を2倍して、上から式をひいてやると、
4x + 2y = 8
– ) 3x + 2y = 5
——————-
x = 3
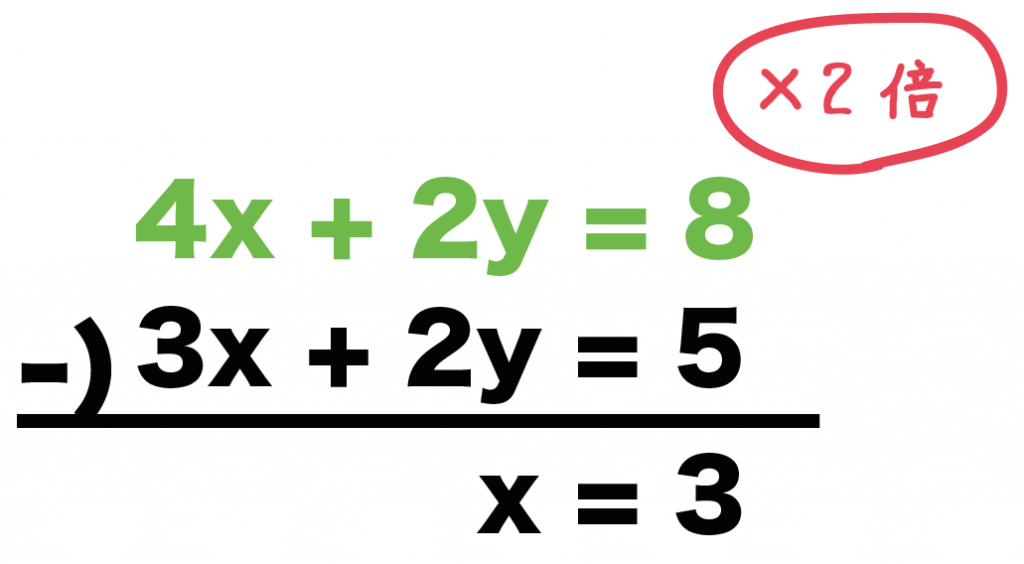
xの解が「3」になるよね！
こんな感じで、
文字を消去して解いていこう！
Step3. 解を代入する！
ゲットした解を代入してみよう。
計算できそうなヤツを選んで代入してくれ。
例題では、
$$3x + 2y = 5$$
に「$x = 3$」を代入してみようか！
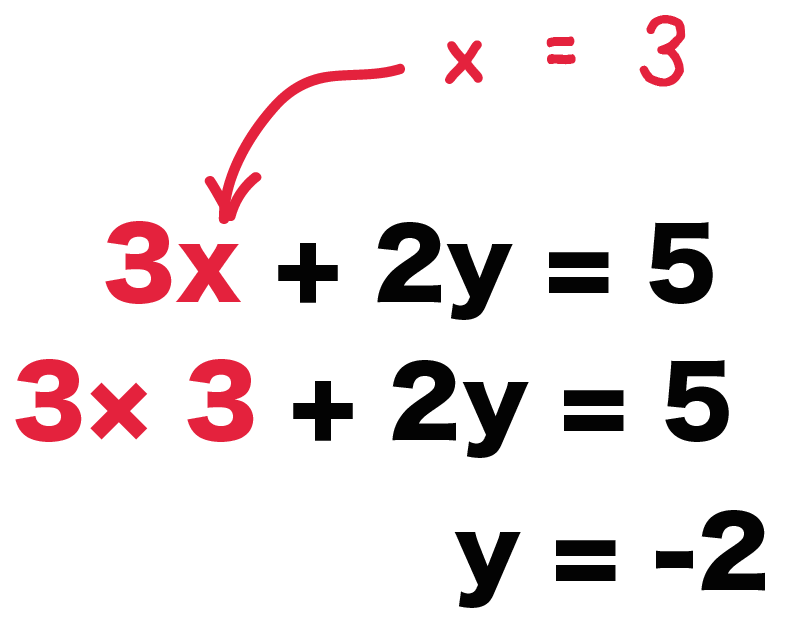
すると、
$$3 × 3 + 2y = 5$$
$$9 + 2y = 5$$
になるよ。
この方程式を中1数学でならった方程式の解き方でといてやると、
$$y = -2$$
になるね！
おめでとう！
これで連立方程式の解である
$$(x, y) = (3, -2)$$
がゲットできたね。
まとめ：分数の連立方程式はまずは「分母を払う」から
連立方程式に分数があるとむずかしそうだよね？？
だけど、
やることは案外すくないよ。
ただ、
分母をはらう
ってことを、最初にすればいいんだ。
慣れるまで問題を繰り返しといてみてね！
そんじゃねー！
Ken
