
二重根号の外し方の公式 って便利だよな。
二重根号の外し方の公式
$a>0, b>0のとき, $
$\sqrt{a+b+2\sqrt{ab}}=\sqrt{a}+\sqrt{b}$
$a>b>0のとき,$
$ \sqrt{a+b-2\sqrt{ab}}=\sqrt{a}-\sqrt{b}$
なんせ、2重のルートを1重にできるんだからな。
使い方もシンプルで、
という条件をみたす2つの数字のセットを見つけりゃいい。
でもさ、この二重根号の公式って何で使えるんだろうな。
ちょっと話がうますぎやしねえか。
ってことで、ここでは二重根号の公式の証明に挑戦しようぜ。
まずは二重根号の外し方の公式のうち、プラスバージョンからだ。
プラスの公式
$a>0, b>0のとき, $
$\sqrt{a+b+2\sqrt{ab}}=\sqrt{a}+\sqrt{b}$
中身の2ルートの前が「プラス」になっている場合の公式な。
まずはルートの中身($a+b+2\sqrt{ab}$)を因数分解するぞ。
こいつを因数分解すると次のようになる。
$$a+b+2\sqrt{ab}$$
$$=(\sqrt{a})^2+(\sqrt{b})^2+2\sqrt{ab}$$
$$=(\sqrt{a}+\sqrt{b})^2$$
この因数分解では中学数学の「因数分解の平方の公式」を使ってるな。
ってことで、二重根号($\sqrt{a+b+2\sqrt{ab}}$)は次のようになる。
$$\sqrt{a+b+2\sqrt{ab}}$$
$$=\sqrt{(\sqrt{a})^2+(\sqrt{b})^2+2\sqrt{ab}}$$
$$=\sqrt{(\sqrt{a}+\sqrt{b})^2}$$
お次はこの前習った「絶対値記号を使った平方根の外し方」を使うぞ。
$$\sqrt{a^2}=│a│$$
だったよな。
ルートの中身が「何か」の2乗になっていれば、その「何か」に絶対値記号をつけてルートを外せるんだ。
$\sqrt{(\sqrt{a}+\sqrt{b})^2}$の中身は「$\sqrt{a}+\sqrt{b}$」の2乗になってるな。ってことは、
$$\sqrt{(\sqrt{a}+\sqrt{b})^2}$$
$$=│\sqrt{a}+\sqrt{b}│$$
となる。
お次は絶対値記号を外すぞ。
絶対値記号を外す時の法則は次のもんだったな。
$$a≧0 のとき │a│ = a$$
$$a<0 のとき │a│ = -a$$
つまり、絶対値記号の中身が0以上なら符号をそのままはずせて、0より小さいなら符号を逆転させて絶対値記号を外すんだ。
二重根号を変形したやつを見てみるぞ。
$$│\sqrt{a}+\sqrt{b}│$$
絶対値記号の中身($\sqrt{a}+\sqrt{b}$)は、0より大きくなるよな。なぜなら、$a>0, b>0のとき,$っていう条件が二重根号のプラスの公式に与えられているからだ。
$a>0, b>0$なら$\sqrt{a}>0, \sqrt{b}>0$、つまりは$\sqrt{a}+\sqrt{b}>0$。
ということは、絶対値記号の中身が0より大きい!
そん時はそのまま絶対値記号外せるんだったよな。
つまり、
$$a>0, b>0より,$$
$$│\sqrt{a}+\sqrt{b}│$$
$$=\sqrt{a}+\sqrt{b}$$
となる。
これで二重根号のプラスの公式を証明できたぜ。
続いてはマイナスの公式の証明だ。
二重根号のマイナスの公式は次のようなものだったな。
マイナスの公式
$a>b>0のとき,$
$ \sqrt{a+b-2\sqrt{ab}}=\sqrt{a}-\sqrt{b}$
これもさっきのプラスの公式と同じ流れだから安心しろ。
$$\sqrt{a+b-2\sqrt{ab}}$$
$$=\sqrt{(\sqrt{a})^2+(\sqrt{b})^2-2\sqrt{ab}}$$
$$=\sqrt{(\sqrt{a}-\sqrt{b})^2}$$
$$=\sqrt{(\sqrt{a}-\sqrt{b})^2}$$
$$=│\sqrt{a}-\sqrt{b}│$$
$$a>b>0より, \sqrt{a}-\sqrt{b}>0$$
$$│\sqrt{a}-\sqrt{b}│$$
$$=\sqrt{a}-\sqrt{b}$$
うん、証明できたな。
ポイントは絶対値記号を外す時だ。二重根号のマイナスの公式を使う前提だった「$a>b>0$」に注目。
$a$が$b$より大きい、ってことは、$\sqrt{a}$の方が$\sqrt{b}$より大きいってことだな。
ってなわけで、絶対値記号の中身「$\sqrt{a}-\sqrt{b}$」は0以上だから、そのまま絶対値記号を外せるんだ。
二重根号の証明につかったのは、
だったな。

それじゃあ!

中学数学ではいろんな根号を外してきたな。
高校数学では2ステップぐらい上がって、
二重根号
を外していくぜ。
二重根号とは文字通り根号が2重になっているやつだ。
根号の中に根号がある、つまりは、ルートの中にルートがあるんだ。聞いただけでやっかいだろ?
例えば次のやつが二重根号だ。
$$\sqrt{7+2\sqrt{6}}$$
初めて見た時はビビるかもしれえねえが、安心しろ。
ありがたいことに、
二重根号を簡単に外せる公式があるんだ。それは次の2つだ。
$a>0, b>0のとき,$
$ \sqrt{a+b+2\sqrt{ab}}=\sqrt{a}+\sqrt{b}$
$a>b>0のとき,$
$\sqrt{a+b-2\sqrt{ab}}=\sqrt{a}-\sqrt{b}$
$2\sqrt{ab}$の符号がプラスなのかマイナスなのかで2パターン公式があるんだ。
どっちの公式でも使い方は大体一緒だ。
要は、
という条件をみたす2つの数字のセットを見つけりゃいいのさ。
そして、そのセットにそれぞれルートをつけたやつを足すのか、それとも引くのかするわけだ。
それじゃあ具体的な例を解いていこう。
$$\sqrt{7+2\sqrt{6}}$$
まずは最初に見たこいつな。
要は、
という条件をみたす2つの数字のセットを見つけりゃいいのさ。
そいつは・・・・そう、
のセットじゃあるまいか?
だって、こいつらたしたら「$7$」だし、かけたら「$6$」だもんな。
ってことで、二重根号の外し方の公式でいう$a$と$b$は、
となる。ゆえ、
$$\sqrt{7+2\sqrt{6}}$$
$$=\sqrt{6}+1$$
になるな。
たまに、二重根号の中に「2ルートがない」問題があるんだ。
例えば次のようなものがな。
$$\sqrt{7-4\sqrt{3}}$$
「2ルート」じゃなくて「4ルート」になっている・・・と。
こういう時はな、
2を強引に作って公式で突破していくぞ。
「4ルート」を「2ルート」にすればいいよな。ルートの中身に$2^2$をかけりゃ、「4ルート」を「2ルート」にできる。
$$\sqrt{7-4\sqrt{3}}$$
$$=\sqrt{7-2\sqrt{3×2^2}}$$
$$=\sqrt{7-2\sqrt{12}}$$
この変形が終わったら、あとは公式通り。
という条件をみたす2つの数字のセットを見つけりゃいいのさ。
そいつは・・・・そう、
のセットじゃあるまいか?
だって、こいつらたしたら「$7$」だし、かけたら「$12$」だもんな。
でも、この公式はマイナスバージョンであることに注意しようぜ。
マイナスバージョンの公式は
$$a>b>0$$
という条件がある。つまり「 $a$のほうがでかい」んだ。
ってことで、二重根号の外し方の公式でいう$a$と$b$は、
ゆえ、
$$\sqrt{7-2\sqrt{12}}$$
$$=\sqrt{4}-\sqrt{3}$$
$$=2-\sqrt{3}$$
になるな。
でもちょっと次の問題を見てほしい。
$$\sqrt{5+\sqrt{21}}$$
こいつも「2がない二重根号の問題」だ。が、しかし、こいつはちょっと厄介。
ルートの前に何もついてないパターンだ。
この場合、さっきみたいに「2ルート」を強引に作ると、二重根号の中身が分数になっちゃうんだ。
$$\sqrt{5+\sqrt{21}}$$
$$=\sqrt{\frac{5×2+2\sqrt{21}}{2}}$$
$$=\sqrt{\frac{10+2\sqrt{21}}{2}}$$
でもな、安心しろ。
分数があろうがなかろうが、やる事は同じだ。
つまり、
無理矢理、二重根号の中身に「2ルート」の形を作って公式に当てはめるだけだ。
すると次のようになる。
$$\sqrt{5+\sqrt{21}}$$
$$=\sqrt{\frac{5×2+2\sqrt{21}}{2}}$$
$$=\sqrt{\frac{10+2\sqrt{21}}{2}}$$
$$=\frac{\sqrt{10+2\sqrt{21}}}{\sqrt{2}}$$
あとは公式を分子の$\sqrt{10+2\sqrt{21}}$で使えばいいな。
という条件をみたす2つの数字のセットを見つけりゃいい。
そいつは・・・・そう、
のセットじゃあるまいか?
ってことで、
$$\sqrt{5+\sqrt{21}}$$
$$=\sqrt{\frac{5×2+2\sqrt{21}}{2}}$$
$$=\sqrt{\frac{10+2\sqrt{21}}{2}}$$
$$=\frac{\sqrt{10+2\sqrt{21}}}{\sqrt{2}}$$
$$=\frac{\sqrt{7}+\sqrt{3}}{\sqrt{2}}$$
$$=\frac{\sqrt{7}+\sqrt{3}}{\sqrt{2}}$$
$$=\frac{\sqrt{2}×(\sqrt{7}+\sqrt{3})}{\sqrt{2}×\sqrt{2}}$$
$$=\frac{\sqrt{14}+\sqrt{6}}{2}$$
オッケー、最後はちょっと厄介だったが、これでゲームクリアだ。

次はこの二重根号の公式がなぜ使えるのか、っていう証明をやっていこう。
証明までマスターしておけば、公式を本番で忘れても大丈夫だからな。
それじゃな!
tomo の高校数学 I の記事をまとめました。

平方根(ルート)の外し方は中学数学でもやってきたな。
高校でもルートはずしまくるんだが、ワンステップ進んで一味一味違う外し方を習得していくぜ。
なんとな、
絶対値記号で平方根を外す
んだ。
高校数学では次の法則を使っていくぞ。
$$\sqrt{a^2}=│a│$$
つまり、ルートの中身が「何かの2乗」なら、ルートを取っ払って、絶対記号をつければルートを外せるんだ。
例えば、
$$\sqrt{3^2}$$
を考えてみよう。
$3^2$は「3を2乗した数」だよな。
ルートの中身が「何かの2乗」なら、ルートを取っ払って、絶対記号をつければルートを外せる
から、
$\sqrt{3^2}$
$=│3│$
となる。
で、絶対記号の中身の「3」は0以上だから、絶対値記号もそのまま取っ払える。
$\sqrt{3^2}$
$=│3│$
$=3$
になるな。
これはルートの中身がマイナスの負の数を2乗しているパターンでも同じさ。
例えば、
$$\sqrt{(-10)^2}$$
だったら、ルートの中身が「-10を2乗した数」だ。絶対値記号を「-10」につければルートをおさらばできるから、
$\sqrt{(-10)^2}$
$=│-10│$
となる。で、絶対値記号の中身がマイナスならマイナスをつけて絶対値記号を外すんだったよな。ってことで、
$\sqrt{(-10)^2}$
$=│-10│$
$=-(-10)$
$=10$
となる。
なぜこの法則が使えるかって??
それは、ルート・平方根の意味に立ち返るとわかるぞ。
平方根(ルート)は
2乗したら「ある数」になる数のこと
だったよな。そして、ルートの中身にその「ある数」が入ってる。
例えば、$\sqrt{2}$ なら、そいつを2乗すれば中身の「$2$」になるって話さ。
だから、ルートの中身が何かの2乗だったら、そもそもルートの記号なんか必要ない。
その正体は、ルートの中身の数、ってことになる。
$\sqrt{9}$ ならその正体は「2乗して9になる数」。$3^2$は$9$だから、$3$になるはずだよな。
という流れを、高校数学では絶対値記号で表しているんだ。

普通の平方根を外せるようになったら、お次は二重根号を外そうぜ。
それじゃな!

絶対値とは、
ある数字の0からの距離
だったよな。

つまり、その数字が0からどれだけ離れているかを大きさで表したものだ。
例えば、「− 2の絶対値」は「2」、「− 15」の絶対値は「15」だ。
たとえるなら、絶対値は「数字のパワー」みたいなもんだ。
この絶対値は中学数学でも勉強したが、高校数学でもこいつがつきまとうぞ。
しかも、高校ではこの絶対値がさらに進化して、
絶対値の記号
が登場するんだぜ。
絶対値の記号は次のものだ。
│
どっからどうみても、縦棒だよな。こいつで数字を挟むと、その挟まれた数字の絶対値を表すことになるぞ。

例えば「2」をこの縦棒「│」で挟んでみると、
│2│
になるな。
この│2│は「2の絶対値」を表すんだ。
絶対値記号の意味を覚えられたら次は、絶対値記号を外す技をマスターするぞ。
絶対値記号を外す時に使える便利な法則があってな、次のものだ。
$$a≧0 のとき │a│ = a$$
$$a<0 のとき │a│ = -a$$
絶対値記号の中の数が0より以上だったら、その数と同じものが絶対値になる。
一方、絶対値記号の中の数が0より小さかったら、その数字にマイナスをつけた数字が絶対値になる、ってことを言ってるんだな。
たとえば、
$│− 5│$
なら、中の数字「-5」は0よりも小さい!
ゆえ、この絶対記号を外したら、その中の数字「-5」にマイナスをつけた数字が絶対値になるから、
$│− 5│$
$= -(-5)$
$= 5$
になるわけだ。
中学数学で何となく理解してできていたことを、高校数学では数式で表してるんだな。
でも、たまーに、ルートが混じった式に絶対値の記号がついているやつがいるんだ。
例えば、次のもの。
$│\sqrt{3} − 3│$
絶対値の記号の中身にルートがついていようがなかろうが、やる事は同じだ。
絶対値記号の中身が0以上か確認して、そうだったらそのまま中身を出せばいい。
中身が0より小さかったら、マイナスの符号をつけて出せばいいんだ。
さっきの例だと、記号の中身の
$\sqrt{3} − 3$
が0以上かどうかみてやりゃいいんだな。
ルート3の近似値は「ひとなみにおごれや」で、
1.730508..
だったな。
ってことは、
$\sqrt{3} − 3$
$≒1.7 – 3$
$≒- 1.3$
だ。つまり、
$\sqrt{3} − 3$は「0より小さくなりそう」だな。
したがって、絶対値記号の中身が0より小さくなるときはマイナスをつけて外せばいいから、
$│\sqrt{3} − 3│$
$=-(\sqrt{3} − 3)$
$=-\sqrt{3} + 3$
になるな。
でもな、絶対記号の中身がさ、ルートだけにとどまらず、
文字がはさまってる問題もたまにあるんだ。
例えば、次のやつ。
$│x+1│$
安心しろ。
文字が挟まっていようがなかろうが、やる事は同じだ。
絶対値記号の中身が「0以上か」判定してやるぞ。
でも、$x$という文字はどれぐらい大きいがわからないよな。
ルートのときみたいに推測できねえ。
こういう大きさがわからない文字のときは
場合分け
だ。
つまり、絶対値記号の中身が
の2パターンに場合分けをするんだ。
そして、それぞれのパターンで絶対値記号を外したときの値を考えるんだ。
さっきの例で考えてみるぞ。
$│x+1│$
中身の$x+1$が0以上の時、つまり不等号で表すと、
$x+1≧0$
つまりつまり、
$x≧-1$
のときだな。
その場合、絶対値記号の中身が0以上だから、そのまま絶対値記号を外すだけでオッケーだ。
$│x+1│$
$=x+1$
一方、中身の$x+1$が0より小さい時、つまり不等号で表すと、
$x+1<0$
つまりつまり、
$x<-1$
のときだな。
この場合は絶対値記号の中身が0より小さい!
ってことで、マイナスの符号をつけて絶対値記号を外すぞ。
$│x+1│$
$=-(x+1)$
$=-x-1$
ってことで、以上の流れをまとめると、
となる。
ふう、文字が入ってると場合分けが登場して少々厄介だが、やることは同じだったな。

ここでマスターした絶対値記号の外し方を使って、次回は「平方根の外し方(高校バージョン)」を勉強していこう。
それじゃな!

高校数学 I ではなんとな、
3乗の因数分解の公式
が登場するぜ。
それはこいつだ。
$$a^3+b^3 = (a+b)(a^2-ab+b^2)$$
それじゃあさっそく、この公式で因数分解してみようぜ。
トライする因数分解の問題は次のやつだ。
$$x^3+27$$
それぞれの項に注目してみると、
になってるな。
さっきの公式でいうと、
になっているはずだ。
ということで、この$a$と$b$を因数分解の公式にぶち込んでやると、次のようになるな。
$$x^3+27$$
$$=(x+3) (x^2-3×x+3^2)$$
$$=(x+3) (x^2-3x+9)$$
うん、こんな感じで公式を使えば3乗の因数分解もいっぱつで終了。まったく、便利な時代だぜ。
数学の教科書には、2種類の3乗の因数分解の公式のってるよな。
つまりマイナスバージョンの公式、
$$a^3-b^3 = (a+b)(a^2+ab+b^2)$$
も書いてあるんだ。
心配すんな、このマイナスの公式は覚えなくても大丈夫だ。
なぜなら、さっき紹介したプラスの公式「$a^3+b^3 = (a+b)(a^2-ab+b^2)$」から簡単に導けるからだ。
ズバリ、プラスの公式の$b$の代わりに$-b$を入れれば出てくるからだ。
試しにやってみるぞ。
$$a^3+b^3 = (a+b)(a^2-ab+b^2)$$
$$a^3+(-b)^3 = (a+(-b))(a^2-a(-b)+(-b)^2)$$
$$a^3-b^3 = (a-b)(a^2+ab+b^2)$$
ほら、出てきただろう??
ってことで、脳の記憶容量を節約するためにも、マイナスの公式は全ツッパのガン無視でも問題ないなんだ。
でもさ、プラスの公式だけでも覚えるの大変だよな。
$$a^3+b^3 = (a+b)(a^2-ab+b^2)$$
どっからどう見ても、明らかに、覚えづらいぜ。
でもな、この3乗の因数分解の公式公式は覚えなくても大丈夫だ。
なぜなら、3乗の展開公式の $(a+b)(a^2 – ab + b^2)=a^3+b^3 $ を逆にしただけ、だからな。
つまりは3乗の展開公式を覚えておけばよくて、3乗の因数分解の公式は覚えなくていいんだ。

ってことで、3乗の因数分解の公式に熱中するのもいいが、それと同時にここまで勉強してきた3乗の展開公式も復習しておこうな。
それじゃあ!

3乗の展開公式を勉強してきたけどさ、圧倒的に覚えづらいよな。
一応、お前らのために「3乗の展開公式の覚え方」考えてみたけど、どうも割に合わねぇってことに気がついたんだ。
そんなくそ覚えづらい3乗の展開公式を丸暗記しなくて済むよう、この公式を証明できるようにしようぜ。
つまりは、なぜこの公式で使えるのかという根本を知るんだ。公式を証明できるようにしておけば、テスト本番で忘れても自分で作れるからな。
それじゃあ、2つの3乗展開公式を1つずつ証明していくぞ。
次の3ステップで証明できるぜ。
$(a+b)^3$を一気に計算するんじゃなくて、細かい掛け算に分解するぞ。
3乗を「1乗× 2乗」の計算にわけて考えるんだな。
2乗の展開公式なら中学数学で死ぬほどを使って身に付いているし、1乗の計算はシンプルな掛け算だからな。
$(a+b)^3$を「1乗× 2乗」にわけると、次のようになるな。
$(a+b)^3$
$=(a+b)(a+b)^2$
で、$(a+b)^2$を2乗の展開公式で計算すると次のようになるな。
$(a+b)^3$
$=(a+b)(a+b)^2$
$=(a+b)(a^2+2ab+b^2)$
お次は分配法則だ。かっこを外すときに死ぬほどお世話になってきた法則だな。
この分配法則でさっきの計算式 $(a+b)(a^2+2ab+b^2)$ を展開しよう。
ポイントは後から前に分配法則を使うことだ。
後ろの$(a^2+2ab+b^2)$ から前の$(a+b)$に分配法則を使ってやるんだ。すると、次のようになる。
$(a+b)(a^2+2ab+b^2)$
$=a(a^2+2ab+b^2)+b(a^2+2ab+b^2)$
で、またまた分配法則で()を外してやるぞ。
$a(a^2+2ab+b^2)+b(a^2+2ab+b^2)$
$=a^3+2a^2b+ab^2+a^2b+2ab^2+b^3$
最後は同類項まとめる作業だ。
同類項とは「文字と文字がかけられている数が同じ項のこと」だったな。同類項を探して、同類項の係数を足し算でまとめればいいんだ。
ここまで変形してきた式に注目してくれ。
$a^3+2a^2b+ab^2+a^2b+2ab^2+b^3$
この式における同類項は、
だな。この同類項たちをまとめると、次のようになる。
$a^3+2a^2b+ab^2+a^2b+2ab^2+b^3$
$=a^3+3a^2b+3ab^2+b^3$
オッケー、こいつは紛れもなく$(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$っていう展開公式の右側だよな。意外にも簡単に証明できたぜ。
証明に使ったのは、
でどれも中学数学で勉強した内容だ。忘れちゃったら復習しといてくれよな。
2つ目の3乗の展開公式も証明していくぞ。大体1つ目の公式と同じ流れだから安心してくれ。
むしろ、2つ目の公式のほうが証明がシンプルでやりやすいぞ。
まずはこの公式の左辺を分配法則で展開してみよう。
$(a+b)(a^2 – ab + b^2)$
1つ目の公式の証明と同じく、後ろから前に分配法則を使うぞ。
$(a+b)(a^2 – ab + b^2)$
$=a(a^2 – ab + b^2)+b(a^2 – ab + b^2)$
そして、かっこをまたまた分配法則ではずすと、次のようになるな。
$a(a^2 – ab + b^2)+b(a^2 – ab + b^2)$
$=a^3 – a^2b + ab^2+a^2b – ab^2 + b^3$
同類項をまとめるぞ。
$a^3 – a^2b + ab^2+a^2b – ab^2 + b^3$ の同類項はこいつらだ。
この同類項をまとめると・・・・、そう、キレイさっぱり2つのグループとも0になる。
だから、
$a^3 – a^2b + ab^2+a^2b – ab^2 + b^3$
$= a^3 + b^3$
になるな。
こいつは紛れもなく2つ目の3乗展開公式 $(a+b)(a^2 – ab + b^2) =a^3+b^3$の右側だ。
ってことで、2つ目の3乗の展開公式の証明も終了だ!

次はこの3乗の展開公式を使って3乗の因数分解に挑戦していこう。
それじゃあな!

ここまでで3乗の展開公式を勉強してきたな。
だけどさ、どうだ、
これ覚えられるか?
そんなの無理って感じだよな。
文字と数字だけの公式だし、これは難易度が高すぎるわい。
そんなお前のために、今日はとっておきの3乗の展開公式の覚え方を紹介するぞ。
まずはこの展開公式だな。
$(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$
この公式で覚えづらいのは右側のこいつら、
$a^3 + 3a^2b + 3ab^2 + b^3$
だよな。
こいつらさえ覚えちゃえば、この3乗の展開公式をいつでも思い出せそうだ。
ズバリいっちまうぞ、次の覚え方でどうだ。
映画館に参上した3年A組のジジイがビー系の服装で見えない美人にビーチサンダル献上
それぞれのキーワードが次のように対応してるぜ。
映(a)画館に参上(3乗)した3年A組のジジイ(3aの二乗)がビー系(b)の服装で見(3)えない美人(b二乗)にビーチサンダル献上(b三条)
せっかくだからビジュアル化してみるか。

まぁこんな感じで、ちょっとホラーだが、3乗展開公式の1つ目は覚えられたはずだ。
それでは次の展開公式に移ろう。
$(a+b)(a^2 – ab + b^2)=a^3+b^3$
この公式の右辺はともかく、今度は左側を覚えなきゃいけないな。
$(a+b)(a^2 – ab + b^2) $
この3乗展開公式の覚え方は次の通り。
えびでえらいジジイを釣ったら毎日油でビジョビジョ
それぞれの言葉は次のように対応してるぜ。
え(a)び(b)でえらいジジイ(a二乗)を釣ったら毎(マイナス)日油(ab)でビジョビジョ(b二乗)
せっかくだからこいつもビジュアル化してみるぞ。

うーん、たまによくあることだよな。
ここまで俺の渾身の3乗展開公式の覚え方を紹介してきたけど、これもこれで大変だな、正直。
数学の公式は手で使って覚えるのが1番だ。
人生全て慣れ。
数学の公式は使いまくって、身に染みて覚えるもんなんだ。
そして、手に染み込ませるのと同じくらい効力を発揮するのが、数学の公式を証明できるようにしておくことだ。
つまり、なぜその公式で使えるのかを理解しておくんだ。
そうすりゃ、数学の公式をテスト本番で忘れても大丈夫だぞ。

ってことで、次は3乗展開公式の証明にチャレンジしよう。
それじゃなぁ!

中学数学では山のように式を展開してきたよな。
お世話になりまくった公式は次の3つだ。
忘れちゃったやつは随時復習しといてや。
でもな、残念ながら高校数学 I ではこいつらに加えて、
3乗の展開公式
が登場するぜ。つまり式を3乗するときに使える計算公式ってわけだ。
注目の公式は次の2つだ。
2つの項が足し算でつながっている式を3乗するときに使える公式だ。
例えば次の式を展開してみようぜ。
$$(2x+3)^3$$
さっきの公式でいうと、
になってるな。こいつらを公式に代入してみると、
$$(2x+3)^3$$
$$= (2x)^3 + 3(2x)^2×3 + 3(2x)×3^2 + 3^3$$
$$= 8x^3 + 36x + 54x + 27$$
$$= 8x^3 + 90x + 27$$
はい、出たな。これで$(2x+3)^3$っつう3乗の展開が一発でできるようになったんだ。
この公式は少々トリッキー。
をかけた時に使える展開公式だ。
こいつは非常に限定的で、たまにしか使えないけど、まあ、練習しとくか。次の計算問題に挑戦してみよう。
$$(x-2)(x^2+2x+4)$$
さっきの公式でいうと、
になってるな。こいつらを公式に代入してみると、
$$(x-2)(x^2+2x+4)$$
$$=(x^3-8)$$
になる。
お察しの通り、偶然に偶然が重ならない限り使えない計算公式だ。
だけどな、のちのち勉強する「3乗の因数分解」で大活躍する・・・と予告しておこう。
その時まで多めに見て待っといてくれよな。
教科書をみると、4つの3乗の展開公式が並んでるな。
えっ、もしかして妖精が間違えてるんじゃ・・・・と思ったそこのお前!
俺はな、あえて余計な公式を省いてやったんだぞ。感謝しろよ。
そう、俺は「bがマイナスバージョンの公式」を紹介しなかったんだ。
そう、こいつらね。
この余分な2つの公式は、正直、
覚える価値すらない。
なぜなら、プラスの公式の$b$に$-b$を代入すれば出てくるからな。
ほれ、やってみるぞ。
まずは1つ目の公式で$b$に$-b$を代入するぞ。
$$(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$$
$$(a-b)^3 = a^3 + 3a^2×(-b) + 3a×(-b)^2 + (-b)^3$$
$$(a-b)^3 = a^3 – 3a^2b + 3ab^2 – b^3$$
うん、$b$の代わりに$-b$ですべて解決だ。
ほれ、2つ目の公式もやってみるぞ。$b$の代わりに$-b$だ。
$$(a+b)(a^2 – ab + b^2) =a^3+b^3$$
$$(a-b)(a^2 – a × (-b) + (-b)^2) =a^3+(-b)^3$$
$$(a-b)(a^2 + ab +b^2) =a^3-b^3$$
ってな感じで、マイナスの3乗展開公式はすぐに出てくるから大丈夫。
覚えなくてもいいのさ。
心配なやつはプラスの展開公式だけ覚えておこう。
んで、

次は今回紹介した3乗の展開公式の覚え方を伝授するぞ。
それじゃな!

よう、消しゴムの妖精のクマシロだ。摩擦熱、最高。
今日は
降べきの順
を勉強していくぜ。
読み方は
こうべきのじゅん
だ。「おりるべきじゅん」ではないことに注意してくれよな。
こいつは「整式を整理する1つの方法」だ。家を掃除する1つの方法みたいなもんだ。
そのやり方のルールは次の通り。
「次数が大きい項」から順番に「左」に並び替える
だ。
実にシンプルだろ?
次数とは、
1つの項にかけられている文字の数
だったな。こいつは中学数学で習ったやつだから忘れたら随時復習してくれ。
だから例えば次の整式があったとする。
$$x^3+x^2+x^4$$
こいつを降べきの順で整理してみるぞ。
それぞれの項の次数は3、2、4だから、大きい順に並べかえると、次のようになるな。
$$x^4+x^3+x^2$$
これが降べきの順の基本ルールだ。
それじゃあ実際の例題解いてみよう。
やり方は次の3ステップ。
まずは同類項を探すんだ。
こいつも中学数学で習ったやつだったな。念のために復習しておくと、
同じ文字が同じ数だけかけられている項
を指すんだったな。例題では次のセットが同類項だ。
後はこいつらをまとめるだけだ。
同類項のまとめ方は、
文字を無視して、文字の前についている数(係数)をだけを考えて計算するんだ。
同類項のまとめ方忘れちまったら復習しといてな。
例題なら次のようになるな。
$$x^3+2x+3x^2-x+4x^2-5x^3-12$$
$$=x^3-5x^3+2x-x+3x^2+4x^2-12$$
$$=-4x^3+x+7x^2-12$$
最後に、少しきれいになった整式をさらに清潔に保つべく、トドメをさすぞ。
降べきの順、つまり、次数が大き順番に左から並び替えてやるんだ。
それぞれの項の次数をみると、次のようになってるな。
こいつを次数が大きい順に並び替えて次のようになる。これで降べきの順は終了!
$$=-4x^3+7x^2+x-12$$
さっきは文字が1つの問題だったけど、よくテストに出るのが文字が2つのパターンだ。
例えば次の例題だ。
このパターンでは「着目する文字」に注意しよう。
着目する文字以外は、文字でなく、
ただの数字
と思えばいいんだ。
例題をみると、
xについて着目せよ
と言っているな。
ってことで、この整式に含まれる「y」という文字は無視!
文字ではなくただの数字、と思えばいいんだ。
xについてだけ考えて同類項を探すと次の項セットが同類項だ。
さっきと同じように同類項たちをまとめてみるぞ。
$$2x^2+y+x^2y-11-x^3-x^2-5x^3$$
$$= 2x^2+x^2y-x^2-x^3-5x^3+y-11$$
$$= (2+y-1)x^2+(-1-5)x^3+(y-11)$$
$$= (y+1)x^2-6x^3+(y-11)$$
最後に次数が大き順番に並びかえると次のようになるな。
$$ (y+1)x^2-6x^3+(y-11)$$
$$= -6x^3+(y+1)x^2+(y-11)$$
うん、やり方は1つの文字のときの降べきの順と同じだ。
ただ、
着目しない文字を文字じゃないと思うこと。
それと、同類項をかっこでくるる手間が発生することが違うだけ。
このタイプの問題のよくある質問が、
マイナスを()の前につけるかどうか、と言うものだ。
これはぶっちゃけどっちでもいいな。
なぜなら、
降べきの順は整式の整理の方法だから、細かいところは好みだからだ。
一種の掃除の方法であり、大事なのは、掃除の目的であるきれいにすること。
だから、細かい事は好みなんだな。
教室の左から乾拭きしようが、右から水拭きしようが「教室をきれいにする」という目的を果たせは変わりねぇよな。
それと同じで、降べきの順の重要なルールである「次数が大きい項を左から順番に並び変える」だけ守っていればいいのさ。
どうやって掃除しようが関係ないってことだ。
俺の好みで言うと、

()の前はプラスで統一するといいな。
マイナスとか考えのめんどくさいし!
最後に昇べきの順(しょうべきのじゅん)も考えてみよう。
お察しの通り、これまでやってきた「降べきの順」の逆パターンだ。
つまり、
整式の項を次数が小さい順番に左から並び替えるんだ。
例えば、
$$x^3+x^2+x^4$$
なら次のようになるのが
$$x^2+x^3+x^4$$
そう、次数が小さい順番に項を左から並び替えってやればいいんだ。
OK、それじゃあね、とおさらばところだが、もう1つだけ気になることがある。
それは、
べき
という言葉。

なんだこいつは?
人気タレントの名前ではないだろうし、腹筋が割れる音でもないよな。数学教師の口癖でもなさそうだ。
その「べき」の正体はこのあやしい漢字だ。
冪
漢字辞典『漢辞海』によると次のように書いてあるな。
❶食物や食器をおおう布。ふきん。「蓋冪ガイベキ」
❷{数}同じ数どうしを何回か掛けた結果の数。「乗冪」
2つ目の意味の、
同じ数どうしを何回か掛けた結果の数
の意味が近そうだ。
つまり「べき」は、
指数のこと(数や文字のかけられている数)。
つまりつまり、文字や数の右上についているあの数字のことだ。
整式の1つの項に注目するなら、その項の次数だな。
だから、降べきの順は、
次数(べき)が降りるように、つまり、大きい方から小さいほうに並び替えること。
その逆の昇べきの順は、階段を上るように次数が小さい方から大きい順番に並び替えることを指すってこったな。
こんな感じで、この謎の「べき」という言葉に注目すれば、
をごっちゃにしないで済みそうだぜ。

降べきの順のやり方のついでに「べき」の意味もおぼえておこう
それじゃな!

よう、消しゴムの妖精のクマシロだ。消しカスは残してない、よな?
人間界の高校数学 I で最初に出てくるキーワードが
整式(せいしき)
だ。
響きですでにやばい感じするが、今日はこいつを学んでいくぞ。
ズバリいっちまうぞ。
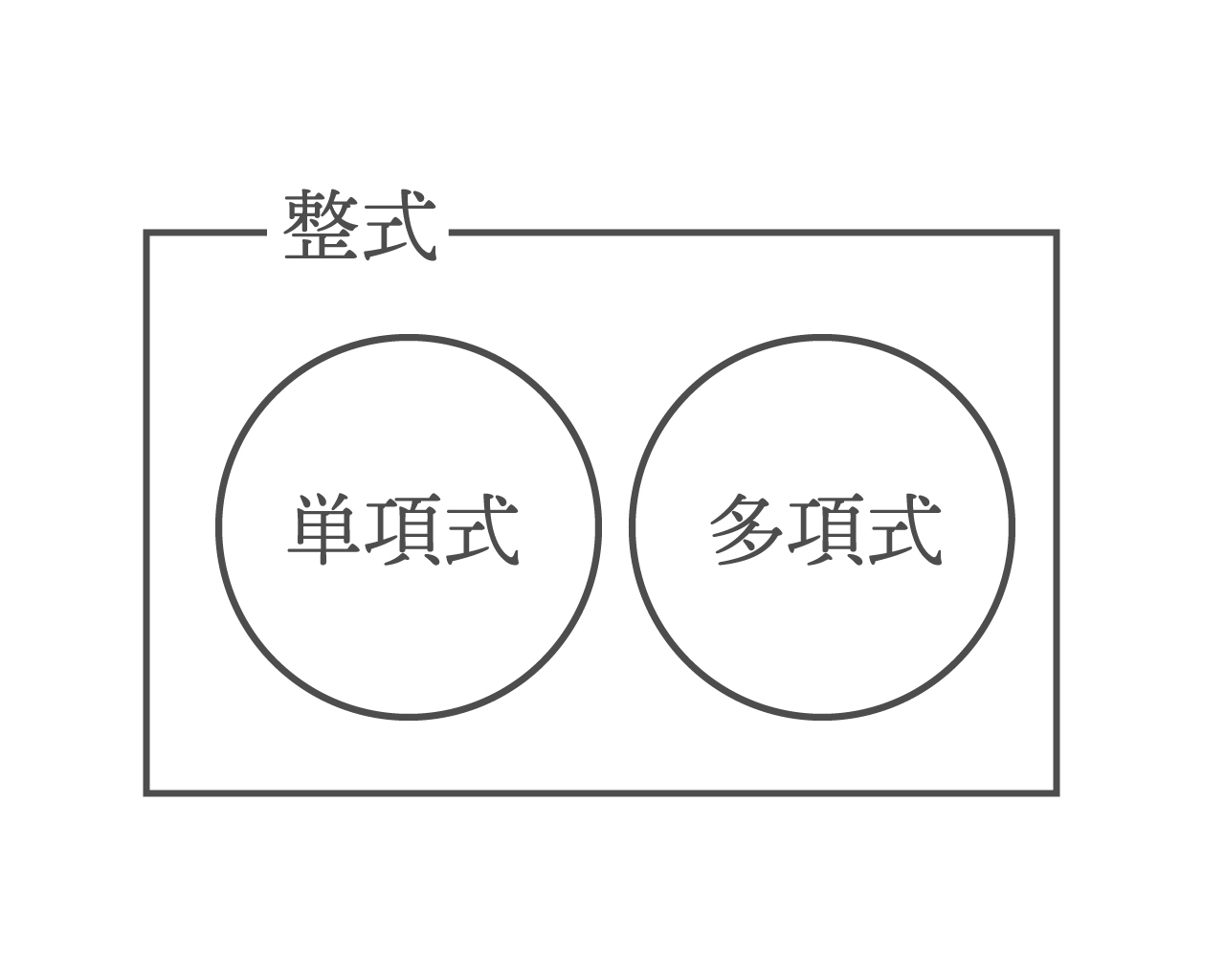
整式とは簡単にいうと、
単項式と多項式のこと
だ。図で表すとこんな感じだ。
えっ、単項式と多項式がわからないだって?
こいつらは中学数学で習ったやつらだったな。
ぴんときてないやつのために復習しておくか。
単項式とは、
「かけ算のみ」で表される「文字」と「数」の式のこと
のこと。たとえば、
$$5a$$
とかが単項式だ。
そうそう、文字と数字の掛け算のみで表されているだろう?

一方、多項式とは、
「かけ算」と「足し算」でできた「文字と数字の式のこと」
のことだ。たとえば、
$$2a+7$$
だな。単項式では登場しなかった足し算が混じってるのが多項式だ。

したがって、今回勉強する「整式」ってやつは、単項式のように掛け算だけの文字と数字でもいい。
多項式のように掛け算と足し算の組み合わせでもいいわけだ。
だから、まあ、整式の定義をかんたんにいっちまうと、
掛け算や足し算で成り立つ文字や数の式
だな。これを人間の数学界用語でいうと、
単項式と多項式のこと
ってなるんだな、うんうん。
いや、しかし、鋭いやつはもう勘づいているだろうが、もっと細かくいうならこうなるかもしれない。
整式は多項式である
と。
なぜなら、単項式は1種の多項式、と考えられるからだ。項がたまたま1つしかなかった多項式は単項式だもんな。だからさっきの整式の定義をあらわした図はこうなるな。
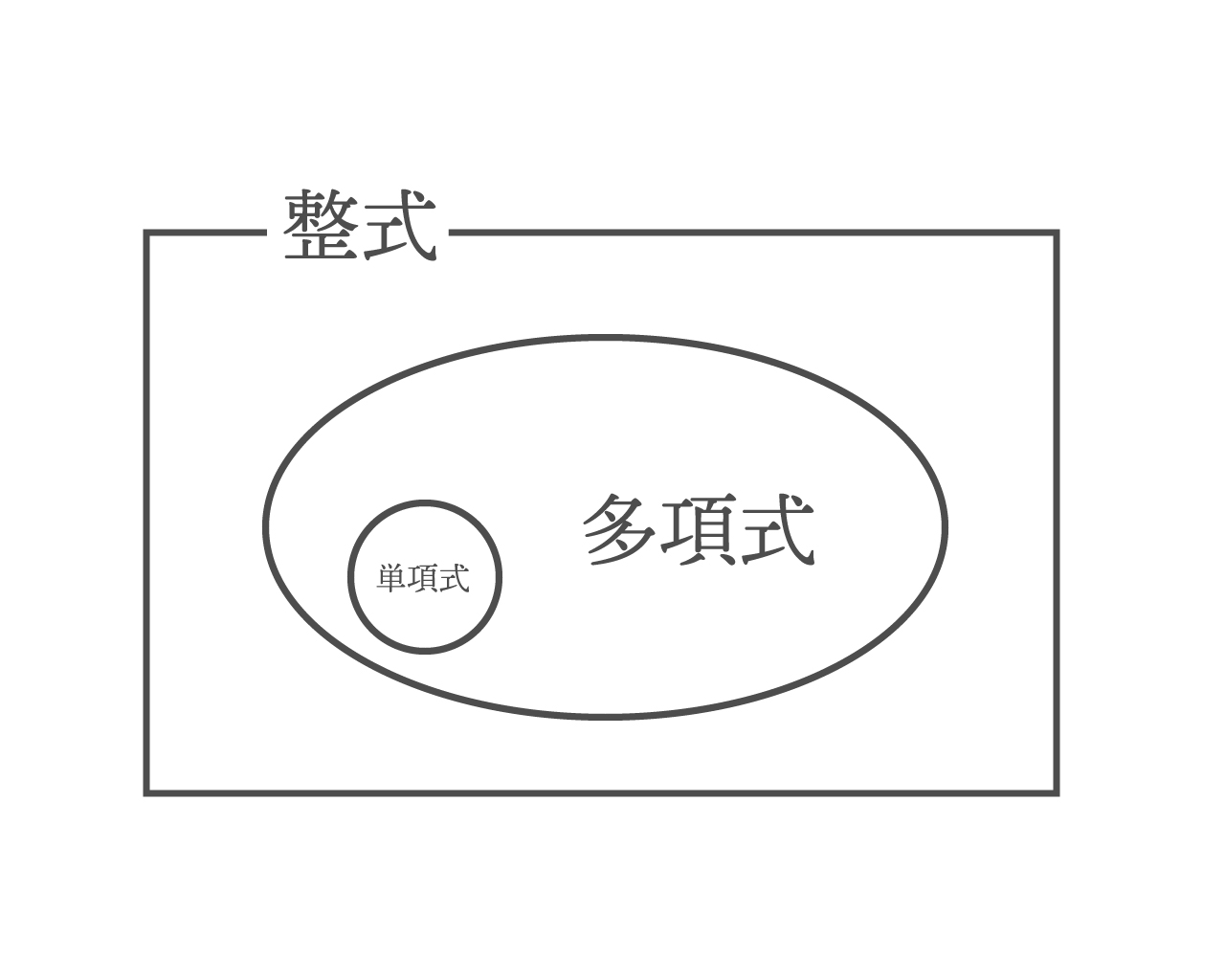
犬に例えるなら、多項式がチワワで、単項式が白いチワワだ。

ほら、考えてみろ。
チワワ中には黒いやつもいるし、

ブラウンカラーもいるだろ?

その中の一種がたまたま白いチワワだったわけであり、白いチワワはブラウンチワワと同じようにチワワであることは変わらねえ。
そんで、もっというなら整式はChihuahuaだな。Chihuahuaとチワワは同じ生物を指しているが、呼び方が違うだけだろ?
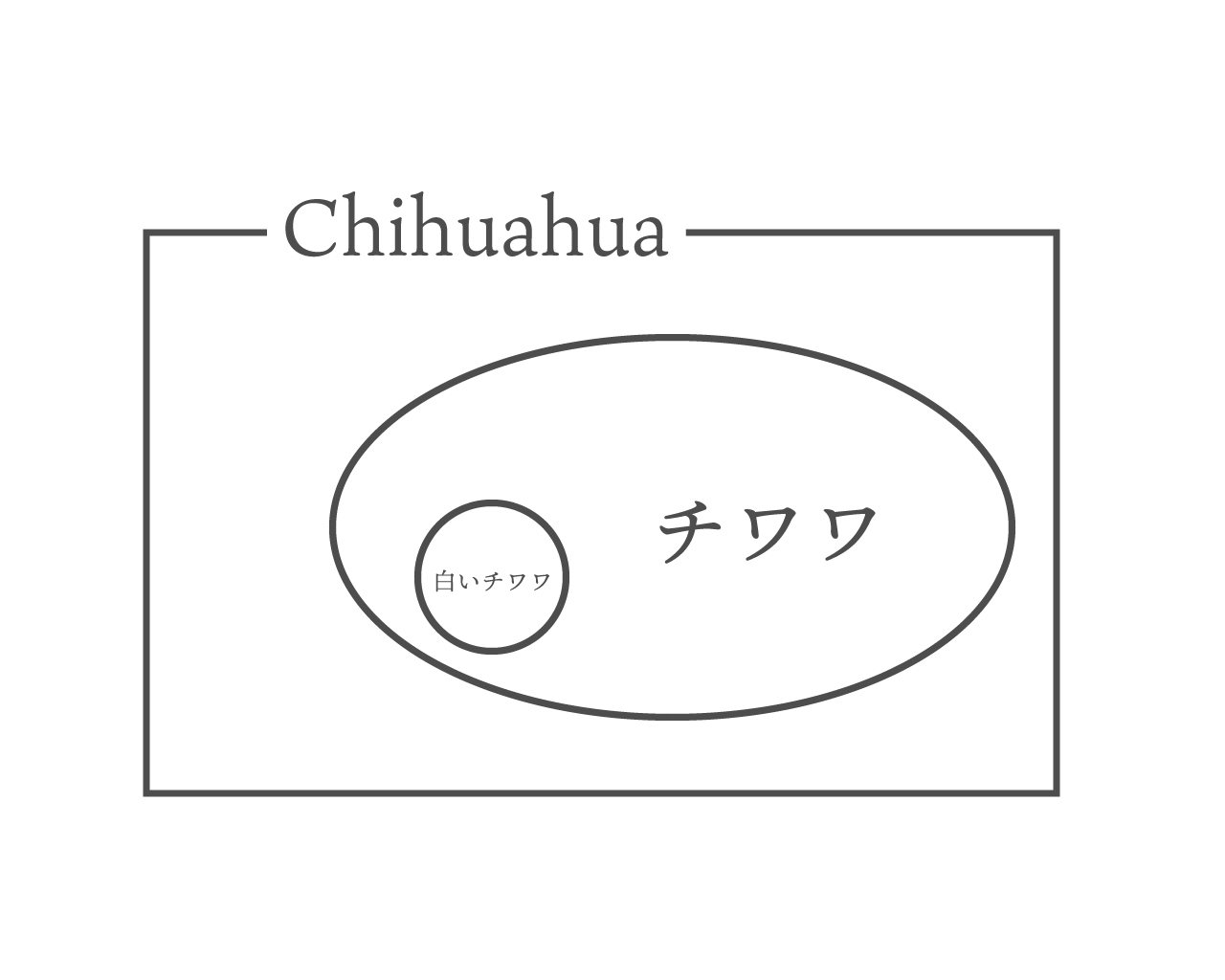
ってまあこんな感じで最後にまとめると、

整式はChihuahua、多項式はチワワ
だ。それじゃあな。