
今日は、
絶対値記号をふくむ方程式の解き方
を習得していくぞ。
じつは、この絶対値を含む方程式の解き方は厄介。なぜなら、
- 場合分けする場合
- 場合分けしない
の2つの解き方のタイプが存在していくからな。
お察しの通り、ぶっちゃけ、そう、
場合分けしないほうが楽に決まっている!!
でもな、世は世知辛くて、
全部が全部、100%、場合分けしない、ってわけにもいかないんだ。
それじゃあ、どんな時に、場合分けをしないで絶対値記号をふくむ方程式を解くことができるのか。
それは、方程式が次の形になっている時だ。
│文字式│ = 文字以外の項
例えば、
$$│x− 2│ = 6$$
だな。このタイプの方程式は、場合分けしなくてもとけるんだ。
場合は分けしないで済む絶対値記号をふくむ方程式の解き方
早速、場合分けしないで済む解き方を紹介していくぞ。
解き方は次の3ステップだ。
1. 絶対記号を外す
まずは絶対値記号を外していくぞ。
このタイプの方程式なら、次の法則が使えるんだ。
$a>0のとき、$
$│x│=a の解は x=±a$
これは数直線を書いてみるとわかりやすいよな。

$x$の絶対値が$a$ってことは、絶対記号の中にある$x$は
- $a$のプラスバージョン
- $a$のマイナスバージョン
の可能性がある。
例題に戻ってみよう。
$$│x− 2│ = 6$$
絶対記号の中身$x− 2$はプラスバージョンの$6$なのか、もしくは、マイナスバージョンの$-6$のどちらかになるはずだよな。
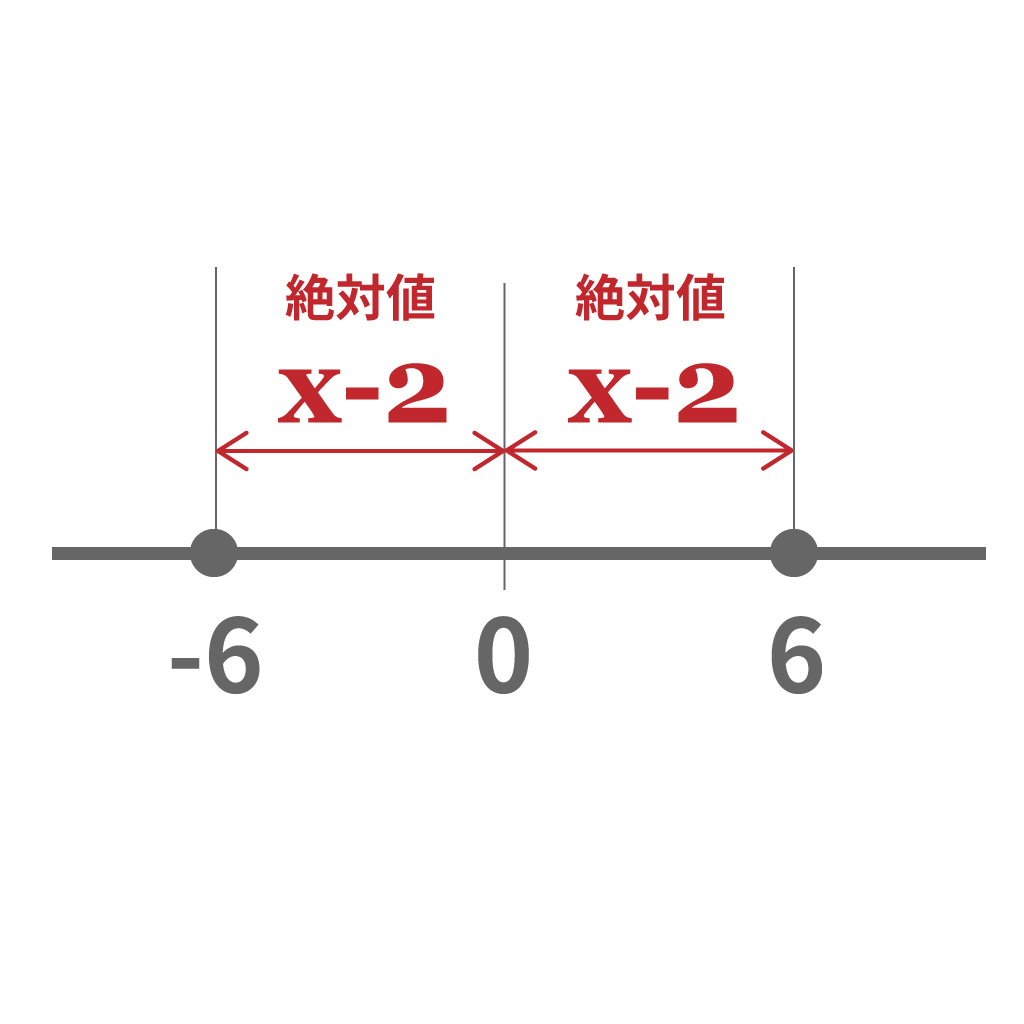
だから、
$$│x− 2│ = 6$$
$$x− 2 = ±6$$
となる。
今回みたいに、絶対値記号の中が文字の項1つだけじゃなくても問題ない。
なぜなら、その中身を何か別の文字を変えてやればいいからな。
例えば、$x− 2$を$A$とすれば、
$$│x− 2│ = 6$$
$$│A│ = 6$$
こうなって、さっきの法則、
$a>0のとき、$
$│x│=a の解は x=±a$
がつかえるんだ。
2. 移項する
絶対記号が外れたら、移項して方程式を解いていくぞ。
解き方は中学数学の解き方と同じだ。
(文字の項)=(文字以外の項)
に変形してやればいいんだ。
例題では左サイドの$-2$を右に持っていこう。
$$x− 2 = ±6$$
$$x = 2±6$$
3. 解を求める
後は方程式の解を求めるだけだ。
$$x = 2±6$$
って事は、
- $x = 2+6$
- $x = 2-6$
の2パターン解があるってことだ。
それぞれ計算してやると、
- $x= 8$
- $x= -4$
になるはずだ。
これがこの方程式の解なるわけだな。
以上、場合分けなしの絶対記号をふくむ方程式の解き方だ。

それじゃあ!









