
前回、「場合わけなし」の絶対値記号をふくむ不等式の解き方を勉強してきたよな。
今回は場合は分けありの絶対値記号をふくむ不等式の解き方を勉強していくぞ。
前回勉強してきた「場合分けなし」の解き方は例外中の例外中の例外だ。
それ以外のパターンの絶対値記号をふくむ不等式は、場合わけありで解いていこうな。
場合分けありの絶対値記号をふくむ不等式の解き方
早速、場合わけありのやり方を解説していくぞ。
次の例題を一緒に解いていこう。
$$│x-1│<\frac{1}{3}+2$$
場合分けする
まず場合分けをして絶対値記号を外していこう。
えっ、どうやって場合分けするのかって??
それはな、
- 絶対値記号の中身が0以上
- 絶対値記号の中身が0未満
の2通りで場合分けするんだ。
なぜなら、絶対値記号の中身が0以上か0未満かによって、絶対値記号を外した後の符号が変わるからだな。
絶対値記号の外し方を復習しとこうか。
- 絶対値記号の中身が0以上 → 符号そのままで外せる
- 絶対値記号の中身が0未満 → 符号を逆転させて外せる
ってことで、例題の不等式は次のように場合分けをして絶対値記号を外せるな。
絶対値記号の中身が0以上のとき($x-1≧0$)、つまり$x≧1$のとき、
$$x-1<\frac{1}{3}x+2$$
絶対値記号の中身が0未満($x-1 < 0$)、つまり$x > 1$のとき、
$$-(x-1)<\frac{1}{3}x+2$$
不等式をそれぞれ解く
ここまでで2つの不等式が誕生したな。
次はこれらの不等式をそれぞれ懇切丁寧に解いていくぞ。
ポイントは、一次不等式を解いた後にやってくる。
- 不等式の解
- 場合分けの条件
の共通範囲を求めなければならないんだ。
だから、これらの不等式たちは一次不等式というよりは連立不等式に近いな。
例題に戻って、2つの不等式をそれぞれ解いてやると次のようになる。
絶対値記号の中身が0以上のとき($x-1≧0$)、つまり$x≧1$のとき、
$$x-1<\frac{1}{3}x+2$$
$$3x-3<x+6$$
$$2x<9$$
$$x<\frac{9}{2}$$
条件$x≧1$との共通範囲は、
$$1≦x<\frac{9}{2}$$
になる。
絶対値記号の中身が0未満($x-1 < 0$)、つまり$x > 1$のとき、
$$-(x-1)<\frac{1}{3}x+2$$
$$-x+1<\frac{1}{3}x+2$$
$$-3x+3<x+6$$
$$-4x<3$$
$$x>-\frac{3}{4}$$
条件$x > 1$との共通範囲は、
$$-\frac{3}{4}<x<1$$
になる。
共通範囲を求める
ここまで2つの不等式の解が得られたな。
最後に、この2つの不等式の解の共通範囲を求めていこう。
例題だと、
- $1≦x<\frac{9}{2}$
- $-\frac{3}{4}<x<1$
の共通範囲を求めればいいよな。
すると、そいつはこうなるはずだ。
$-\frac{3}{4}<x<\frac{9}{2}$
迷った時は数直線で確かめるといいぞ。
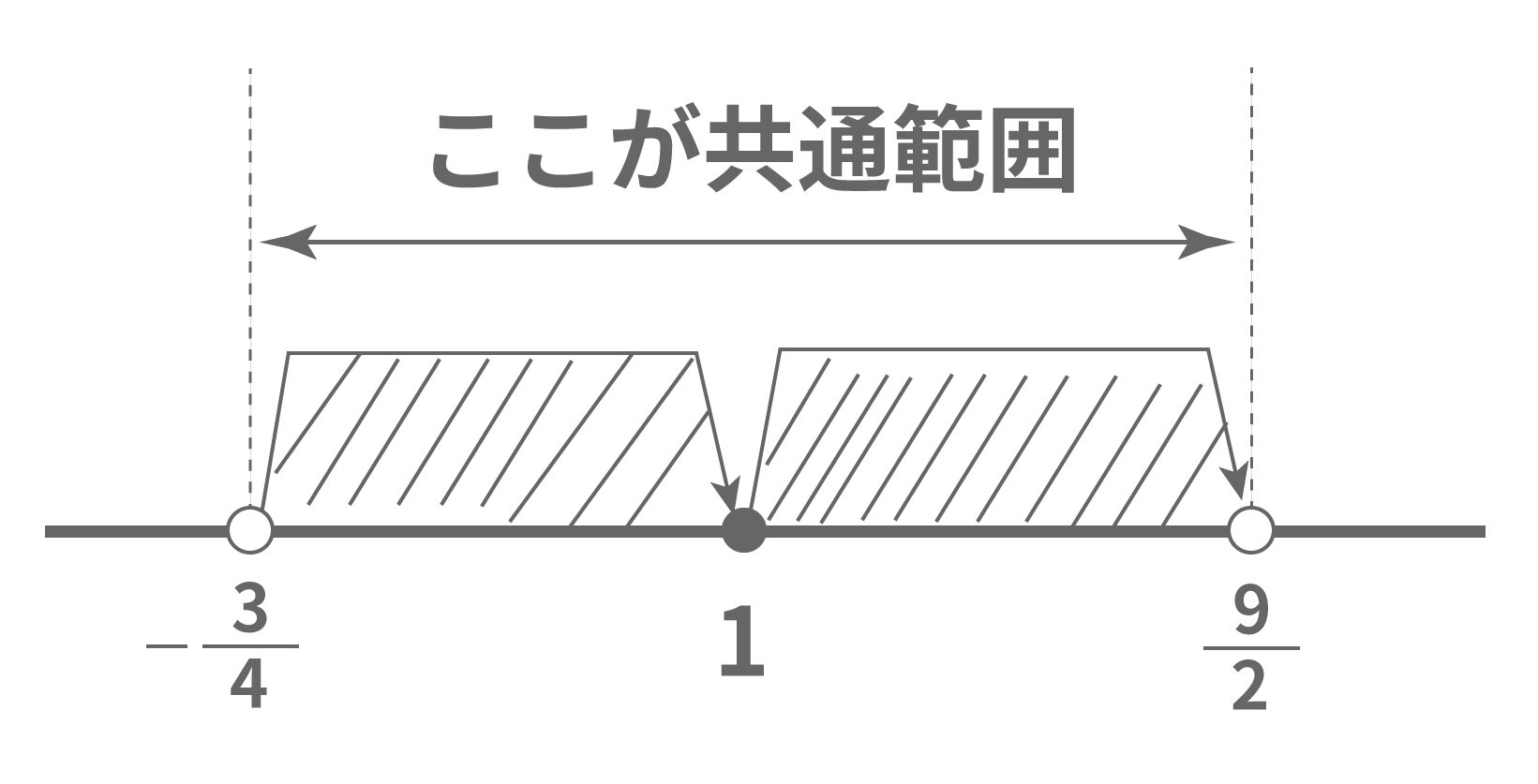
こんな感じで、場合分けありの解き方は厄介だ。
なんせ、共通範囲を求める作業が2回も発生しているからな。
めんどくさいかもしれないが、めんどくさいほど先生はテストに出したがるものだ。
怠らず油断せずに解き方を習得しておこう。
不等式の勉強はここらにして、次はお待ちかねの二次方程式を勉強していくぞ。

それじゃあなぁ!










