
高校数学で二次方程式を勉強していると、3秒に1回ぐらい目にするのが
実数(じっすう)
という言葉だ。
一体この「実数」とはどんな数なのか??
今日はその実数の意味をわかりやすく解説していくぞ。
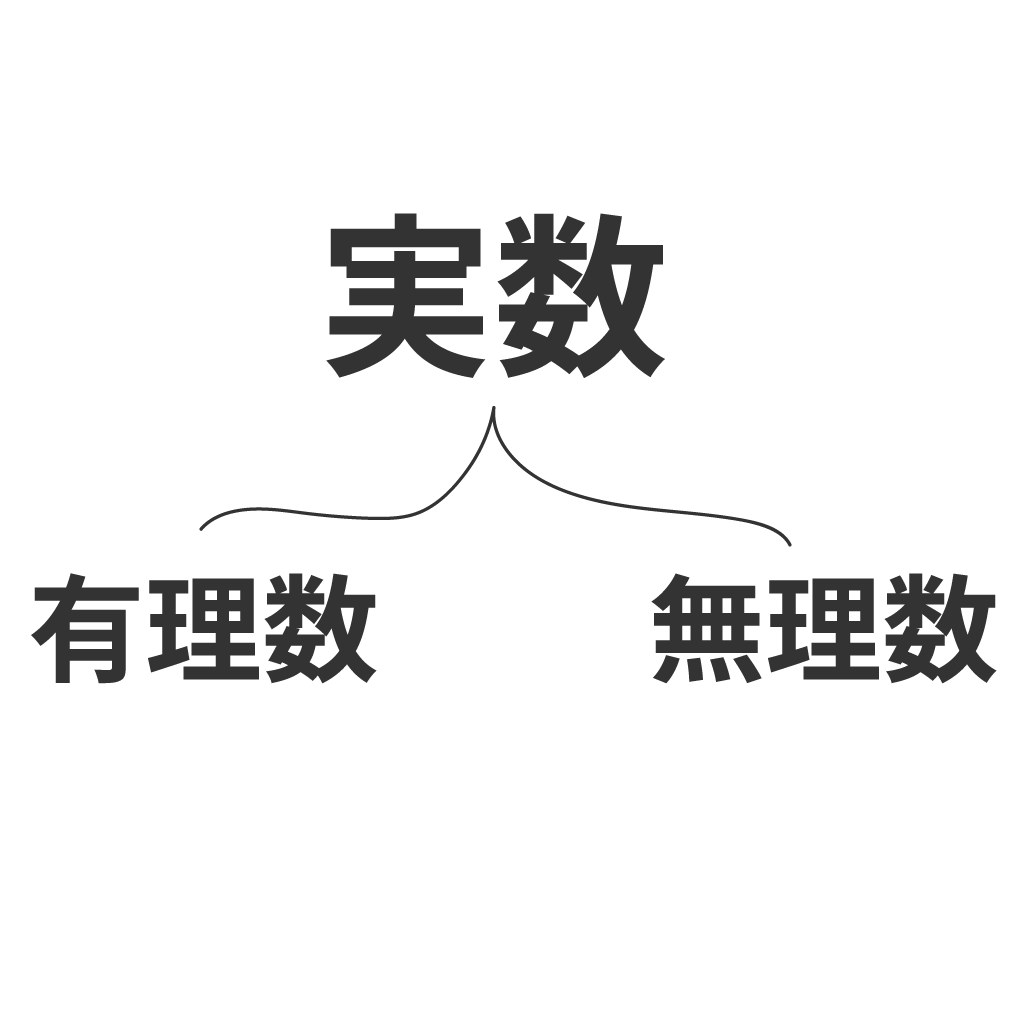
ズバリ実数とは、
有理数と無理数を合わせた数のこと
だ。
有理数と無理数は中学数学で勉強してきたよな?
ちょっと目が泳いだやつもいるだろうから、念のために復習しておこうか。
有理数とは、
分数で表せる数
だったな。
例えば、有理数の具体例には次のやつがあるぞ。
どいつもこいつも頑張れば分数で表すことができるからな。
一方、無理数とは、
分数で表せない数のこと
だ。例えば、平方根(ルート)とか、円周率のπバイとか、そういった数は無理数だったことを思い出してくれ。
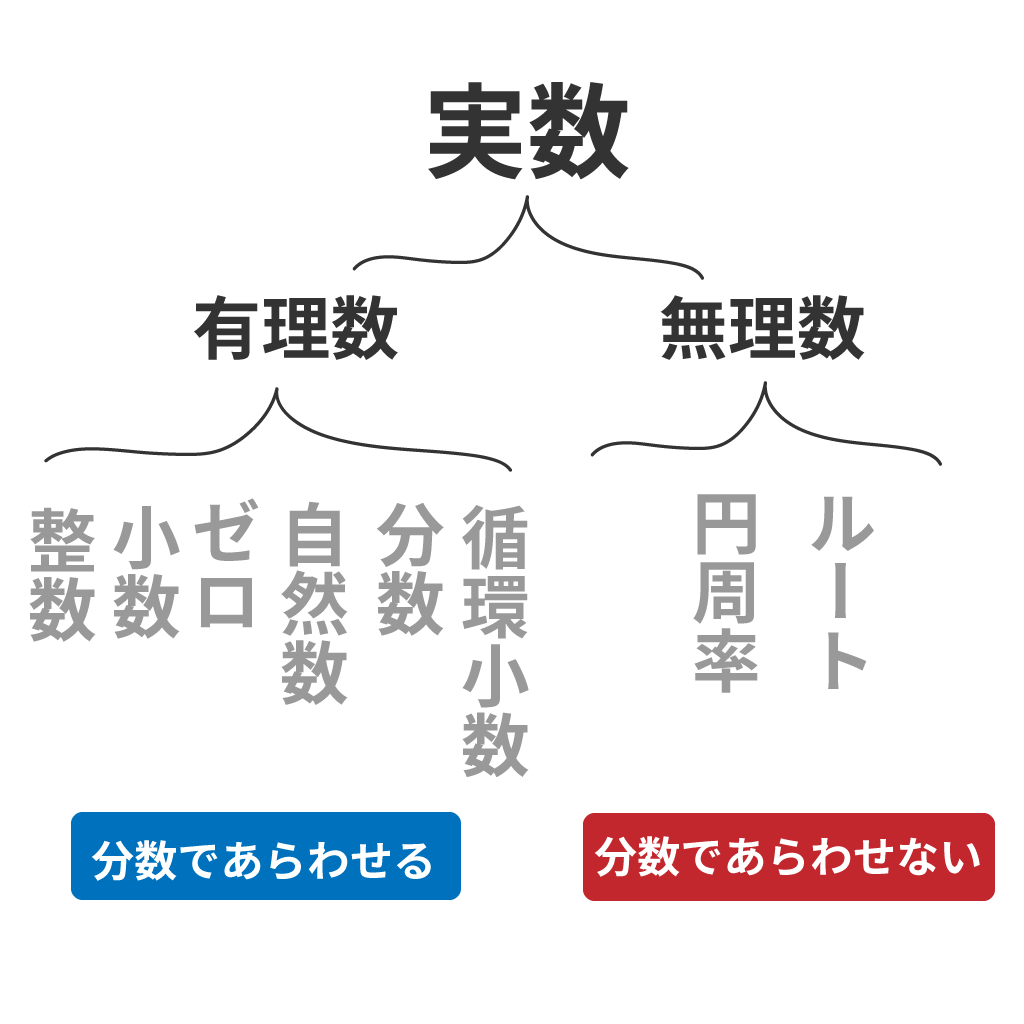
この無理数というやつは、
循環しない無限小数
だったこともついでに思い出してくれよな。つまり、無理数というやつは、小数点の続き方に規則性がないんだ。
たとえば、円周率πは、
3.1415926535…..
と無限に続いていくが、その続き方に規則性はない! だから、円周率を暗記することが一発芸になりうるわけさ。規則性あったら暗記するの楽だもんな。
という感じで、ここまでの流れをまとめておこう。
実数とは、
有理数と無理数を合わせた数
だから、
有理数も実数だし、無理数も実数なんだ。
でも、こう思っちゃいないか。
「私の知ってる、想像できるすべての数は実数なのかも…」
さすが、鋭いな。
実数というものは、
実際に存在するすべての数なんだ。だから、お前が頭で想像できる数字っていうのは、だいたい実数だ。
それじゃあ、実数以外の数なんてあるのか??
実際に存在していない「幻の数」なんてものは、この世にあるんだろうか。
じつは、人間の数学界では、そんな実数ではない幻の数があるんだな。
例えば、これから先、数学を勉強し続けたら巡り合うことになる
虚数(きょすう)
ってものがある。
虚数は、実際に存在しない数の具体例の1つだ。
その虚数の具体例をあげよう。
$$\sqrt{-1}$$
つまり、2乗したら「-1」になる数だ。
よーーく考えてみろよ、そんなのありえないよな?
だって、ある数に2乗、つまり2回かけたら、絶対正の数になっちまうからな。
ある数がプラスだろうとマイナスであろうと、2回かけたら答えはプラスだ。
なのに、2乗してもマイナスになる・・・・数・・・・なんて絶対にありえねえ!
でも、人間界ではそんなありえない数を無視せず「虚数」と名付けたんだ。
こんな感じで、人間の数学界では実数以外の数も取り扱っていくことを頭に入れとこう。
実数以外の数も数学界にあるとなると、
実数の見分け方
が気になってこないか??
そこで、そんなお前らのために、とっておきの実数の見分け方を伝授してやる。
それは、
数直線でその数がありそうなところを指で示せたら実数!
という見分け方だ。

例えば、0。
0の位置は数直線でここら辺ってわかるよな。
負の数の- 3とかもあそこら辺だし、分数の$\frac{1}{3}$もあそこら辺だろう。
無理数の円周率π・・・・・もいける。
だいたい3.14だからあそこら辺だし、ルートの2だって「ひとよひとよにひとみごろ」で1.4付近だとわかる。正確じゃなくてアバウトでいいんだ。
とにかく、その数がありそうなところを、数直線上で指で示せたら、そいつは実数だと覚えておこう。
さっき紹介した虚数の「$\sqrt{-1}$」。
こいつが数直線でありそうなところは・・・・・ないよな。
うん、いくら目に力を入れても到底浮かんでこねえ。
こんな感じで、ある数が実数かどうか問われたら、数直線を想像するんだ。
そして、その数がありそうなところを矢印で示せるかで見分けていこう。

それじゃあ!

前回、「場合わけなし」の絶対値記号をふくむ不等式の解き方を勉強してきたよな。
今回は場合は分けありの絶対値記号をふくむ不等式の解き方を勉強していくぞ。
前回勉強してきた「場合分けなし」の解き方は例外中の例外中の例外だ。
それ以外のパターンの絶対値記号をふくむ不等式は、場合わけありで解いていこうな。
早速、場合わけありのやり方を解説していくぞ。
次の例題を一緒に解いていこう。
$$│x-1│<\frac{1}{3}+2$$
まず場合分けをして絶対値記号を外していこう。
えっ、どうやって場合分けするのかって??
それはな、
の2通りで場合分けするんだ。
なぜなら、絶対値記号の中身が0以上か0未満かによって、絶対値記号を外した後の符号が変わるからだな。
絶対値記号の外し方を復習しとこうか。
ってことで、例題の不等式は次のように場合分けをして絶対値記号を外せるな。
絶対値記号の中身が0以上のとき($x-1≧0$)、つまり$x≧1$のとき、
$$x-1<\frac{1}{3}x+2$$
絶対値記号の中身が0未満($x-1 < 0$)、つまり$x > 1$のとき、
$$-(x-1)<\frac{1}{3}x+2$$
ここまでで2つの不等式が誕生したな。
次はこれらの不等式をそれぞれ懇切丁寧に解いていくぞ。
ポイントは、一次不等式を解いた後にやってくる。
の共通範囲を求めなければならないんだ。
だから、これらの不等式たちは一次不等式というよりは連立不等式に近いな。
例題に戻って、2つの不等式をそれぞれ解いてやると次のようになる。
絶対値記号の中身が0以上のとき($x-1≧0$)、つまり$x≧1$のとき、
$$x-1<\frac{1}{3}x+2$$
$$3x-3<x+6$$
$$2x<9$$
$$x<\frac{9}{2}$$
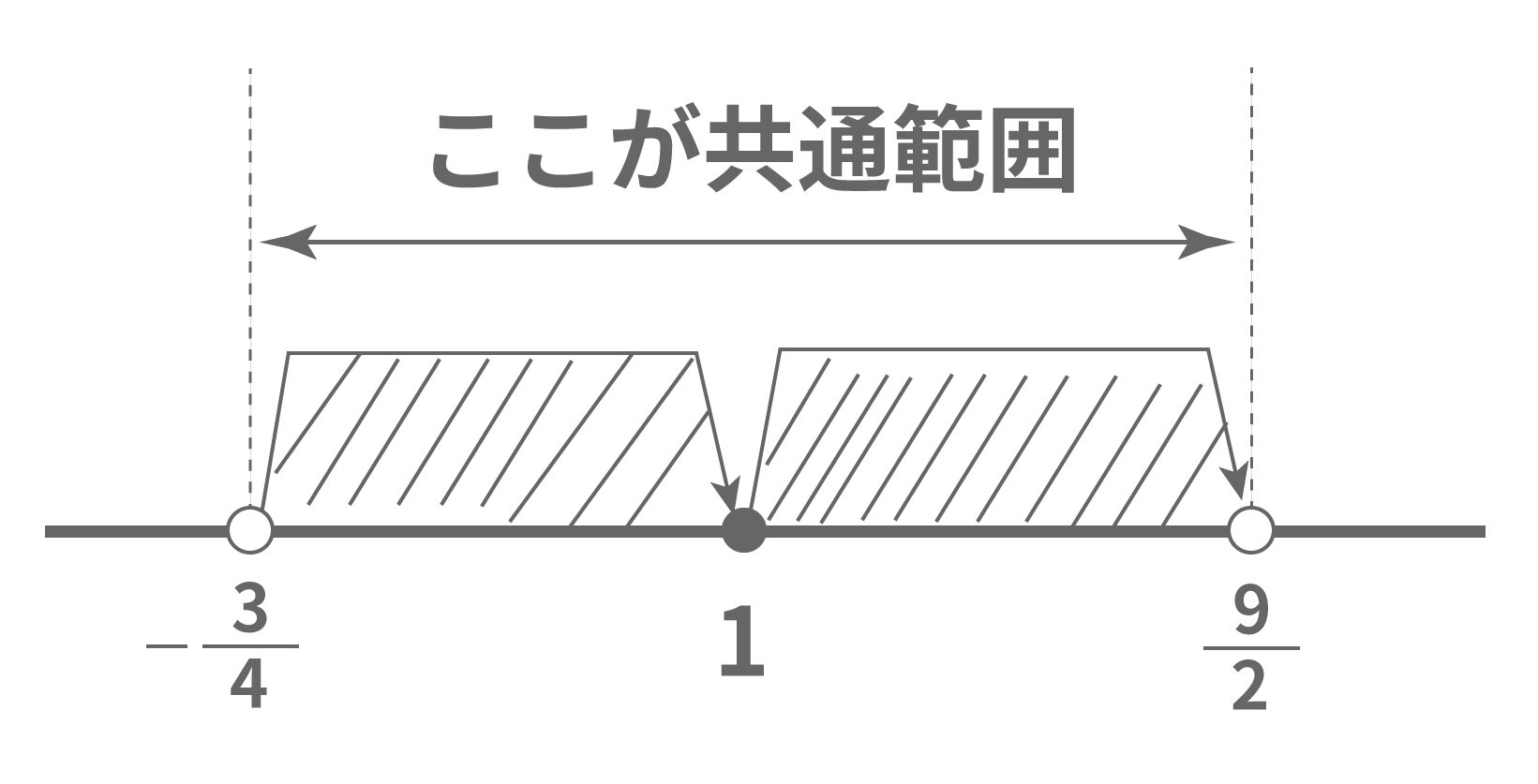
条件$x≧1$との共通範囲は、
$$1≦x<\frac{9}{2}$$
になる。
絶対値記号の中身が0未満($x-1 < 0$)、つまり$x > 1$のとき、
$$-(x-1)<\frac{1}{3}x+2$$
$$-x+1<\frac{1}{3}x+2$$
$$-3x+3<x+6$$
$$-4x<3$$
$$x>-\frac{3}{4}$$
条件$x > 1$との共通範囲は、
$$-\frac{3}{4}<x<1$$
になる。
ここまで2つの不等式の解が得られたな。
最後に、この2つの不等式の解の共通範囲を求めていこう。
例題だと、
の共通範囲を求めればいいよな。
すると、そいつはこうなるはずだ。
$-\frac{3}{4}<x<\frac{9}{2}$
迷った時は数直線で確かめるといいぞ。
こんな感じで、場合分けありの解き方は厄介だ。
なんせ、共通範囲を求める作業が2回も発生しているからな。
めんどくさいかもしれないが、めんどくさいほど先生はテストに出したがるものだ。
怠らず油断せずに解き方を習得しておこう。
不等式の勉強はここらにして、次はお待ちかねの二次方程式を勉強していくぞ。

それじゃあなぁ!

ここまでで絶対値の記号をふくむ方程式の解き方を2種類やってきたよな。
お察しのようにこの世界には、
絶対値記号がふくまれる不等式
も存在しているぜ。
ありがたいことに、この不等式の場合にも次の2種類の解き方があるんだ。
今日はそのうちの「場合分けしない」簡単な解き方を紹介していくぞ。
残念ながら、不等式の事情は方程式と同じだ。
例外中の例外をのぞけば、場合わけが必要だぜ。
で、その例外中の例外ってやつは、次のタイプの不等式だ。
│文字式│ 不等号 文字以外の項
絶対値記号に文字が挟まっていて、さらに不等号の逆サイドには文字がない問題ってわけな。
このタイプの問題では次の公式を使える。
公式
$a>0のとき、$
$│x│<aの解は -a<x<a$
$│x│>aの解は x<-a, a<x$
なぜこの公式が使えるのか?
それは数直線を書いてみるとわかるぞ。
絶対値とは
原点0からの距離
だったよな。
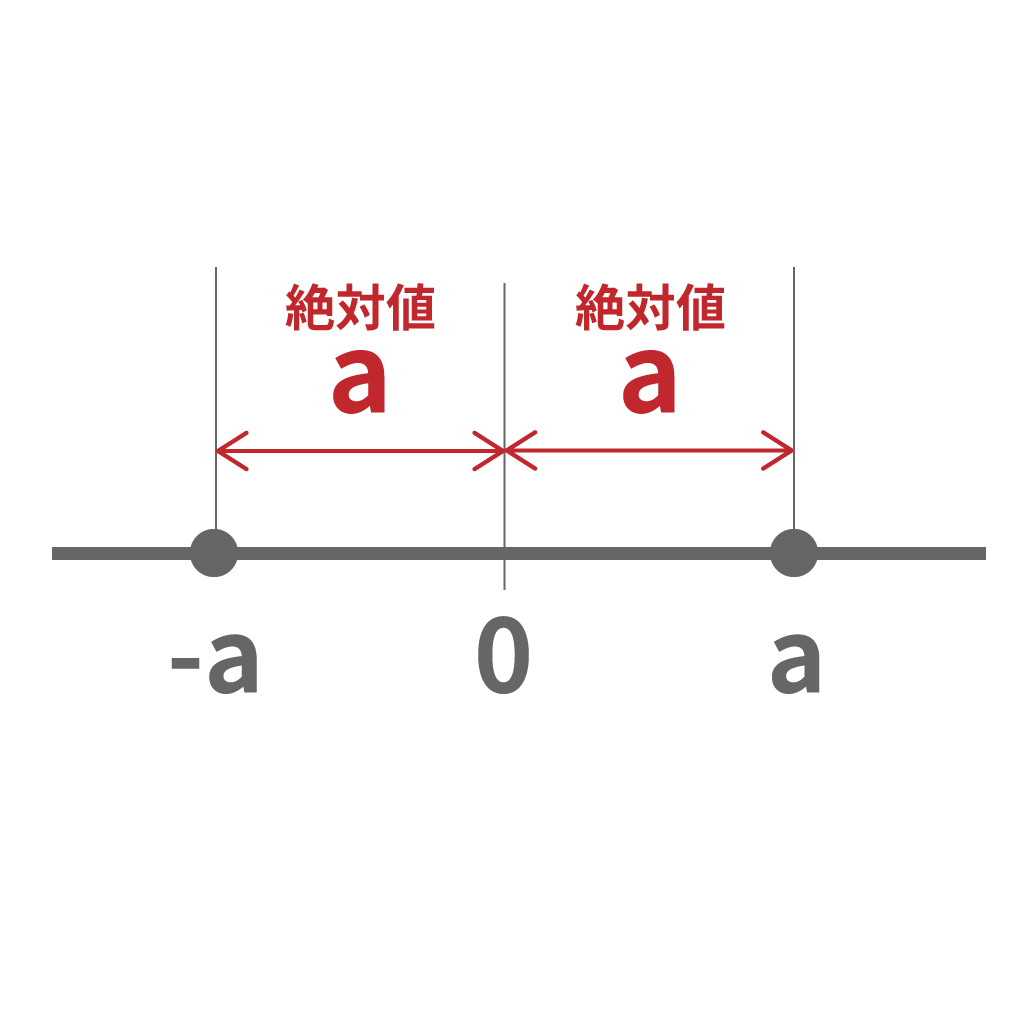
「絶対値がある数より大きい」っていうシチュエーションだったら、次の2つの可能性がある。
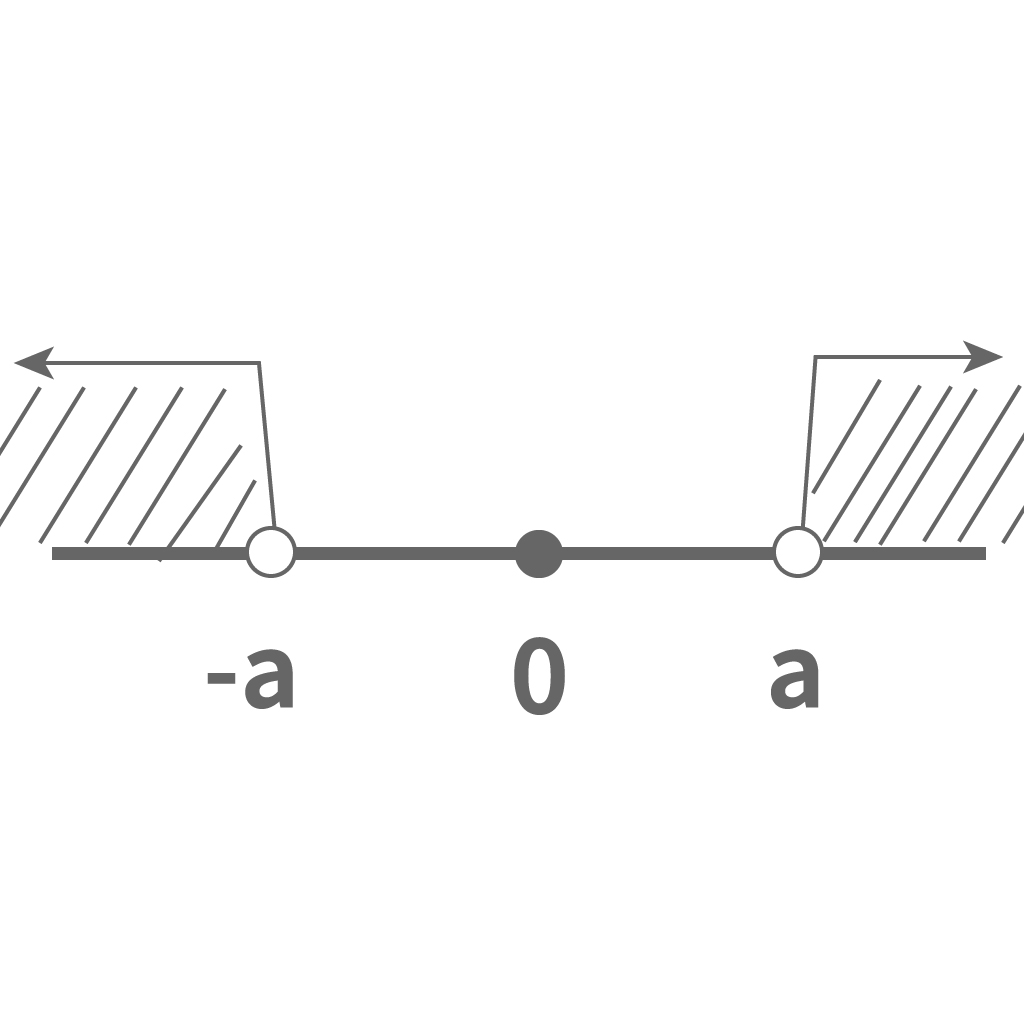
絶対値が小さい場合でも同じように考えればいいんだ。
絶対値がある数より小さいってことは
の間の範囲になる。
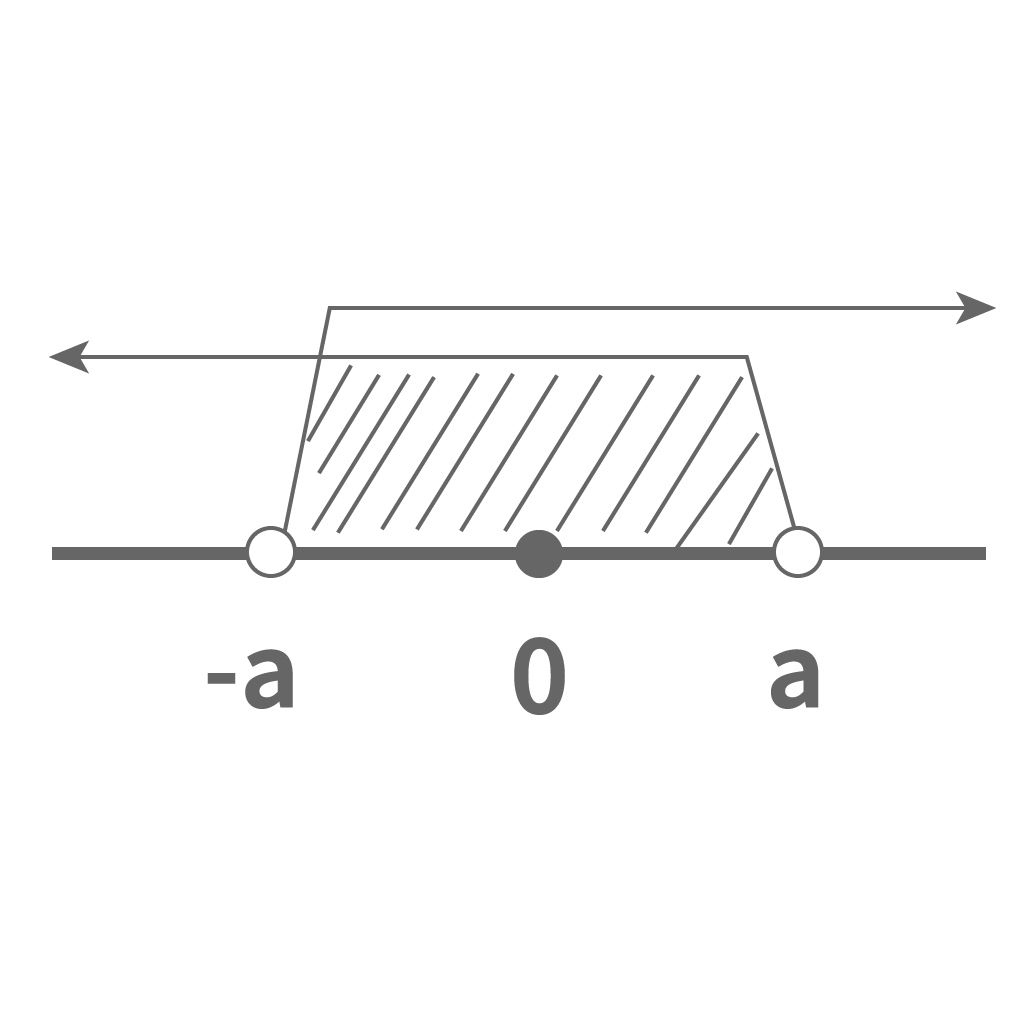
うん、この公式は便利そうだ。
でも、なぜ全てが場合しない方法で解けないのか気になるよな。
それはな、不等式の領域の境界に文字が入っていると、文字が変化したら不等式の領域もグラグラしちまうよな。
例えば、不等式の境界に$x$文字が含まれていたら、$x$が変化するとこの領域の境界も変化しちまう。
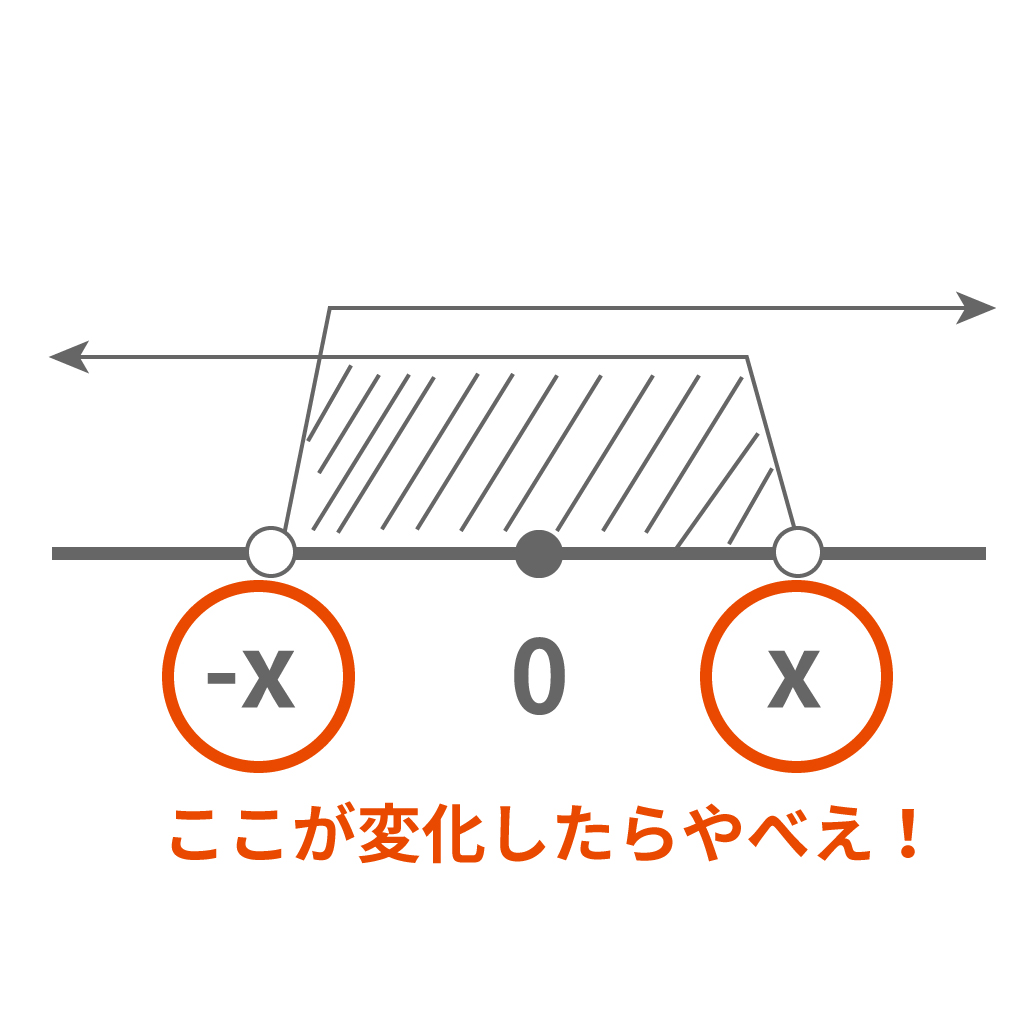
だから、この例外中の例外を除いて、俺たちは絶対値記号をふくむ不等式を見たら場合分けしなきゃいけないんだ。
それじゃあ早速実戦だ。
次の絶対値記号をふくむ不等式を解いてみよう。
$$│x│>2$$
オッケー、こいつぁ、うまい具合に
│文字式│ 不等号 文字以外の項
の形になってる不等式だな。
ってことで、場合分けしないでもいい。
だから、最初に見てきた公式のうちの次のものが使えるはずだ。
$a>0のとき、$
$│x│>aの解は x<-a, a<x$
今回は$a$が$2$ってわけだから、この絶対値記号をふくむ不等式は次のようになる。
$│x│>2$
$x<-2, 2<x$
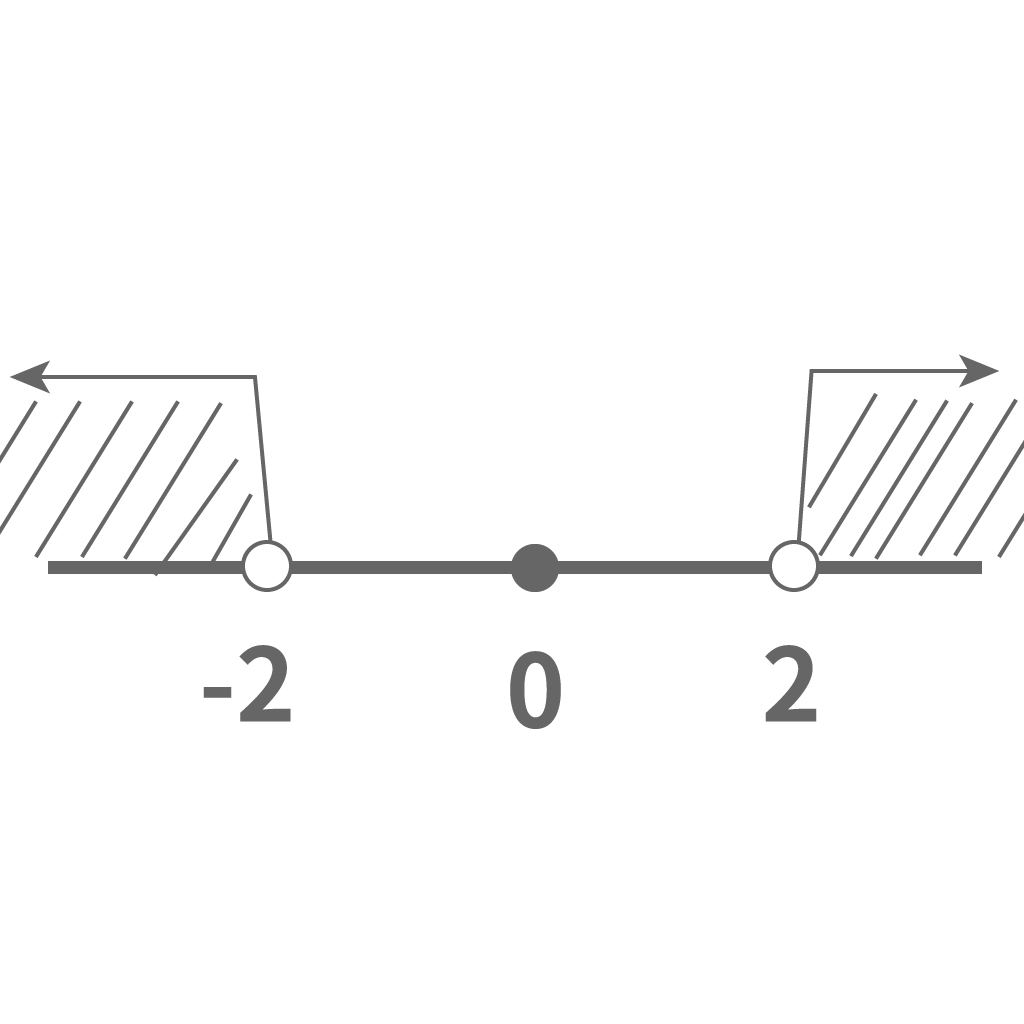

これに限るな。焦らずゆっくり着実に不等式を解いていこう。
次は「場合分けありの不等式の解き方」を勉強していこう。
そんじゃ!

前回は場合分けしない絶対値記号をふくむ方程式の解き方を勉強してきたな。
じつはな、あれは例外中の例外のラッキーパンチ。
残念ながら、現実はこうだ。
絶対値記号が含まれる方程式を見つけたら、
まず場合分けするもの
と思っておこうな。
本来すべての絶対値記号をふくむ方程は「場合分けが必要」なんだ。
今日はその場合分けバージョンの解き方を勉強していこう。
この解き方の基本は次のものだ。
絶対値記号を外して、あとはいつも通りに解く!
絶対値記号の外し方は次のものだったな。
$$a≧0 のとき │a│ = a$$
$$a<0 のとき │a│ = -a$$
つまり絶対値記号の中身が0以上ならそのまま記号を外せる。
中身が0より小さいなら マイナスをつけて絶対値記号を外せるんだ。
この法則を使って方程式に含まれ絶対値記号を外していくぞ。
でもさ、絶対値記号の中身って文字が入ってるよな。
文字は正体不明だから、0より小さいのかでかいのかわかんねぇってことだ。
この正体不明問題に対処するため、絶対値記号の中身が次の2パターン考えねえといけねえ。
この2パターンで場合分けをして、それぞれの場合で方程式を解いて解を求めていけばいいのさ。
以上が解き方の基本だ。
今回は次の例題を解いてみよう。
$│x− 3│ = 5x$
最初にやるべきなのは場合わけな。
の2パターンで考えていこう。
今回の例題では絶対値記号の中身は、
$$x-3$$
だ。ってことで、場合分けは次のようになる。
これを不等式で表すとこうなる。
そして、移項で整理するとこうなる。
それぞれのパターンで絶対値記号を外して方程式を作ってみるぜ。
$x≧3のとき、$
$ x-3 = 5x$
$x<3のとき、$
$-(x-3) = 5x$
2パターンできたらそれぞれの方程式を解いていくぞ。
解き方は中学中学で勉強してきた一次方程式のやり方と同じだ。
つまり、
(文字の項)=(文字以外の項)
となるように方程式を変形して、最後に文字の前の数(係数)で両辺をわりゃいいな。
このやり方で解いてやると次のようにそれぞれ解けるはずだ。
$x-3≧0のとき、$
$ x-3 = 5x$
$ x-5x = 3$
$ -4x = 3$
$ x = -\frac{3}{4}$
$x<3のとき、$
$-(x-3) = 5x$
$-x+3 = 5x$
$-6x = -3$
$x = \frac{1}{2}$
これでオッケーじゃあねえ〜と平和に行きたいところだが、ちょっと待った。
最後にやらなきゃいけないことがあるんだ。
それは、
解を吟味する
だ。
つまり、得られた解が本当に正しいのかチェックしなきゃいけないんだ。
じゃあ、どうやってチェックするのかって??
それはな、
最初に設定した「場合分けの条件」に解がマッチするか調べるんだ。
具体的に見てみるぞ。
まずは1つ目の解からだ。
$x≧3のとき、$
$ x = -\frac{3}{4}$
こりゃ、正しくねえ。
だって、解の$ -\frac{3}{4}$は$3$より小せえからな。
次、2つ目の解をチェック。
$x<3のとき、$
$x = \frac{1}{2}$
こりゃ、いけるな。
だって、解の$ \frac{1}{2}$は$3$より小せえからさ。
ってことで、この方程式の解は、
$x = \frac{1}{2}$
だけ、ってことになる。
以上が場合分けありの絶対値をふくむ方程式の解き方だ。
めんどくさいかもしれねえが、これも正しい解を得るためならやむを得ないことなんだ。
手間を惜しんでテストで間違えるより1000倍ぐらいマシだよな?
方程式に絶対値記号が入っていて、場合分けなしの例外形じゃなかったら場合わけしてこうな。

それじゃあ!

今日は、
絶対値記号をふくむ方程式の解き方
を習得していくぞ。
じつは、この絶対値を含む方程式の解き方は厄介。なぜなら、
の2つの解き方のタイプが存在していくからな。
お察しの通り、ぶっちゃけ、そう、
場合分けしないほうが楽に決まっている!!
でもな、世は世知辛くて、
全部が全部、100%、場合分けしない、ってわけにもいかないんだ。
それじゃあ、どんな時に、場合分けをしないで絶対値記号をふくむ方程式を解くことができるのか。
それは、方程式が次の形になっている時だ。
│文字式│ = 文字以外の項
例えば、
$$│x− 2│ = 6$$
だな。このタイプの方程式は、場合分けしなくてもとけるんだ。
早速、場合分けしないで済む解き方を紹介していくぞ。
解き方は次の3ステップだ。
まずは絶対値記号を外していくぞ。
このタイプの方程式なら、次の法則が使えるんだ。
$a>0のとき、$
$│x│=a の解は x=±a$
これは数直線を書いてみるとわかりやすいよな。

$x$の絶対値が$a$ってことは、絶対記号の中にある$x$は
の可能性がある。
例題に戻ってみよう。
$$│x− 2│ = 6$$
絶対記号の中身$x− 2$はプラスバージョンの$6$なのか、もしくは、マイナスバージョンの$-6$のどちらかになるはずだよな。
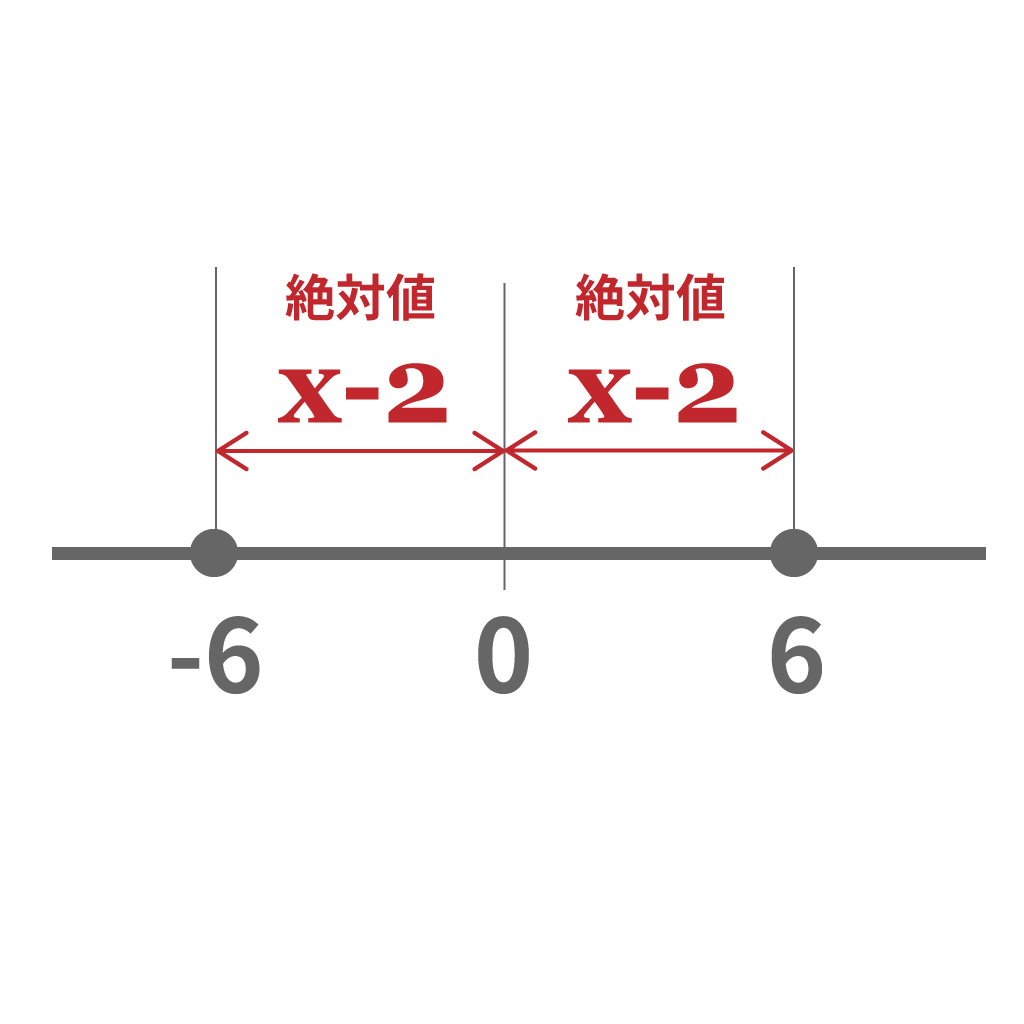
だから、
$$│x− 2│ = 6$$
$$x− 2 = ±6$$
となる。
今回みたいに、絶対値記号の中が文字の項1つだけじゃなくても問題ない。
なぜなら、その中身を何か別の文字を変えてやればいいからな。
例えば、$x− 2$を$A$とすれば、
$$│x− 2│ = 6$$
$$│A│ = 6$$
こうなって、さっきの法則、
$a>0のとき、$
$│x│=a の解は x=±a$
がつかえるんだ。
絶対記号が外れたら、移項して方程式を解いていくぞ。
解き方は中学数学の解き方と同じだ。
(文字の項)=(文字以外の項)
に変形してやればいいんだ。
例題では左サイドの$-2$を右に持っていこう。
$$x− 2 = ±6$$
$$x = 2±6$$
後は方程式の解を求めるだけだ。
$$x = 2±6$$
って事は、
の2パターン解があるってことだ。
それぞれ計算してやると、
になるはずだ。
これがこの方程式の解なるわけだな。
以上、場合分けなしの絶対記号をふくむ方程式の解き方だ。

それじゃあ!

前回「連立不等式の解き方」を見てきたよな。
今日はもう1歩踏み込んで、
連立不等式の文章題
を解いてみよう。
例えば次の問題だ。
あるところに所持金が1500円の男がいました。その男はマスターから買い物を頼まれ、リンゴとレモンを調達せねばなりません。
近所のスーパーではリンゴが150円、レモンが100円でした。
マスターは合計で10個のリンゴとレモンが欲しいようです。そして「リンゴの方が好きなのでリンゴの方が多く買ってきてほしい」という要望もありました。さてこの男性はリンゴを何個買えばいいでしょうか。

それじゃあ早速この文章問題解いていくぞ。
連立等式の文章題の解き方は次の3ステップだ。
まず最初に、
文章内で求めたいものを文字($x$)でおこう。
この鉄則は、一次方程式の文章題でも、連立方程式の文章題でも、二次方程式の文章題でも同じだ。
例の文章題をみると、最後の方に
さてこの男性はリンゴを何個買えばいいでしょうか
って書いてある。つまり、
男が買わねばならないリンゴ数
を求めなきゃいけないな。
ってことで、
男が買わねばならないリンゴ数 = $x$個
としてみよう。
求めたいものを文字に置いたら、次は不等式を作っていくぞ。
連立不等式は、2つの不等式を用意すれば解けるな。
不等式とは、
2つの等しくない数の関係を表すもの
だった。
だから、文章から「2つの等しくない数量」を探すんだ。
1つ目は、合計金額について。
リンゴとレモンを買った合計金額は所持金の1500円より小さくないと買えないよな。
つまり、
(リンゴとレモンを買った合計金額)<(所持金の1500円)
という不等式が成り立つ。
2つ目の大小関係はリンゴとレモンの個数だ。
リンゴとレモン10個合計で必要なんだけど「リンゴのほうが多く」買わないといけないんだ。
つまり、
(リンゴの数)>(レモンの数)
という不等式になりそうだ。
って感じで、不等式を2つ立てていくぞ。
すると、次のような連立不等式になる。
$$\begin{cases} 150x+100(10-x)<1500 & \\ x>10-x & \end{cases}$$
あとは不等式の基本的な解き方に基づいてとくだけ。
連立不等式では、
複数の不等式の解の共通範囲を求めればよかったな。
例題で作った2つの不等式を解いてみると、次のようになる。
(1つ目)
$$150x+100(10-x)<1500$$
$$150x+1000-100x<1500$$
$$50x<500$$
$$x<10$$
(2つ目)
$$x>10-x$$
$$2x>10$$
$$x>5$$
つまり、連立不等式はこうなる。
$$\begin{cases} x<10 & \\ x>5 & \end{cases}$$
んで、共通範囲を視覚的にあぶりだすために数直線を書く。
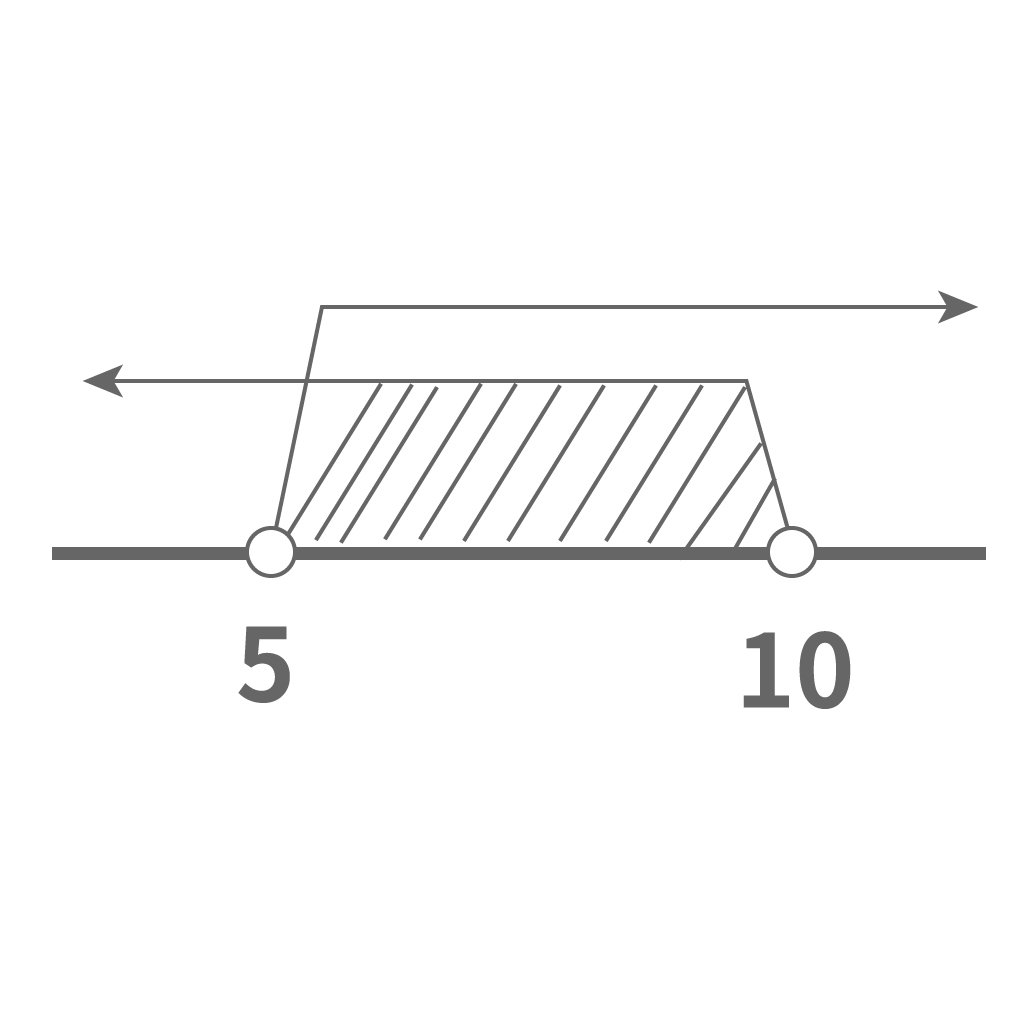
うん、つまり2つの不等式の共通範囲は次のようになる。
$$5<x<10$$
$x$はリンゴの個数だったな。
リンゴの個数は小数と分数とかでもない、正の整数だ。
つまり、リンゴの個数は6〜9個のいずれかでオッケーってわけだ。
こんな感じで、連立不等式の文章題だろうが、文章題攻略の基本は変わらねえ。
「求めたいものを文字でおく」という基本さえ間違えなければ、こっちのもんさ。

それじゃあな!

ここまでで基本的な不等式の解き方をマスターしたよな。
でもな、これで許してくれないのが数学ってもんよ。
次は、
連立不等式(れんりつふとうしき)
が登場するぜ。
連立不等式とは、
2つ以上の不等式が1つのグループになったものだ。
例えば次のような感じ。
$$\begin{cases} 2x+1<x-3 & \\ -5x+7≧-8 & \end{cases}$$
複数の不等式が共通で満たす解の範囲を求めることを、
連立不等式の解
と人間界では呼んでいて、その解を求めることを
連立方程式を解く
って言うぞ。
この連立不等式の解き方は次の3ステップだ。
それじゃ3ステップ踏んでいくぞ。さっきの例題を一緒に解いてみよう。
$$\begin{cases} 2x+1>x-3 & \\ -5x+7≧-8 & \end{cases}$$
まずは組になっているそれぞれの不等式を1つずつ解いていくんだ。
このステップでは、2つの不等式の関係は一切無視!
一つ一つにしっかり向き合ってくぜ。
$$\begin{cases} 2x+1>x-3 & \\ -5x+7≧-8 & \end{cases}$$
をバラしてやって、
$$2x+1>x-3$$
と
$$-5x+7≧-8$$
をそれぞれとこう。
すると、次のように2つの不等式の解が出てくるよな。
$$x>-4$$
$$x≦3$$
ここで出てくるのが数直線だ。
数直線とは、
数の大小関係を直線上に表したもの
だったな。
これは中学数学でも出てきた内容だから思い出してくれ。
数直線は書かなくてもゲームオーバーにならないが、書いたほうがわかりやすいからオススメだ。
数直線を書いた方が、
複数の不等式の解の共通範囲がわかりやすいんだな。
数直線で不等式の解の範囲を表すときに1つ注意してくれ。
それは、
不等式の解の境界だ。つまり、領域の端っこのことな。
境界を含む時は「●」で塗りつぶし、境界を含まないんだったら「○」にしてやろう。
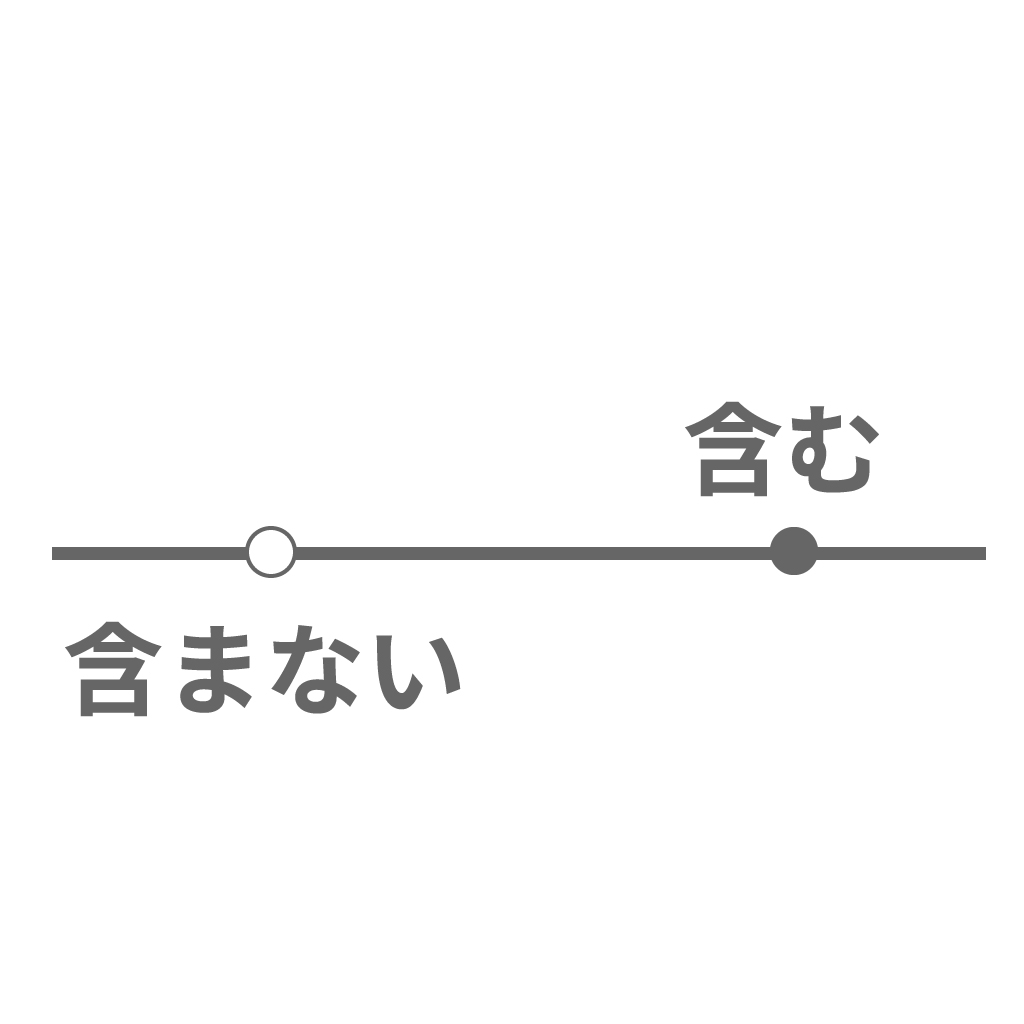
不等式は「境界を含むか含まないか」が大事だ。ここをミスっちまうとどんなに善良な人間だろうが不正解になっちまうおそろしい世界だ。
で、
例題の不等式の解を数直線を書いてみると次のようになる。
$$x>-4$$
$$x≦3$$
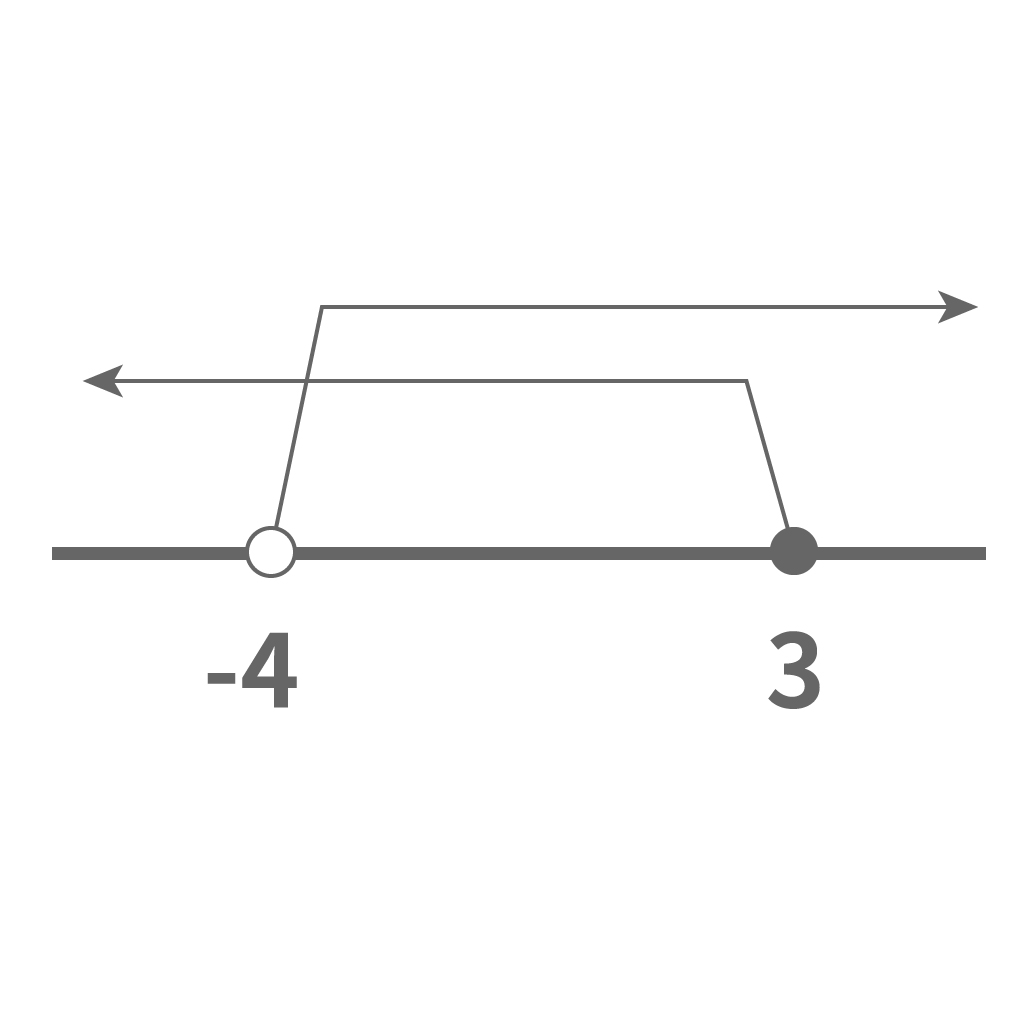
最後に、数直線から2つの不等式の解の共通範囲を求めよう。
2つの不等式の解の範囲がかぶっている範囲
を探せばいいんだな。
数直線で書いてみて、被っている領域を発見したら、斜線を引いたり、塗りつぶしてやったりして、視覚的にわかりやすくするといいな。
さっきの例では、ここが共通範囲。
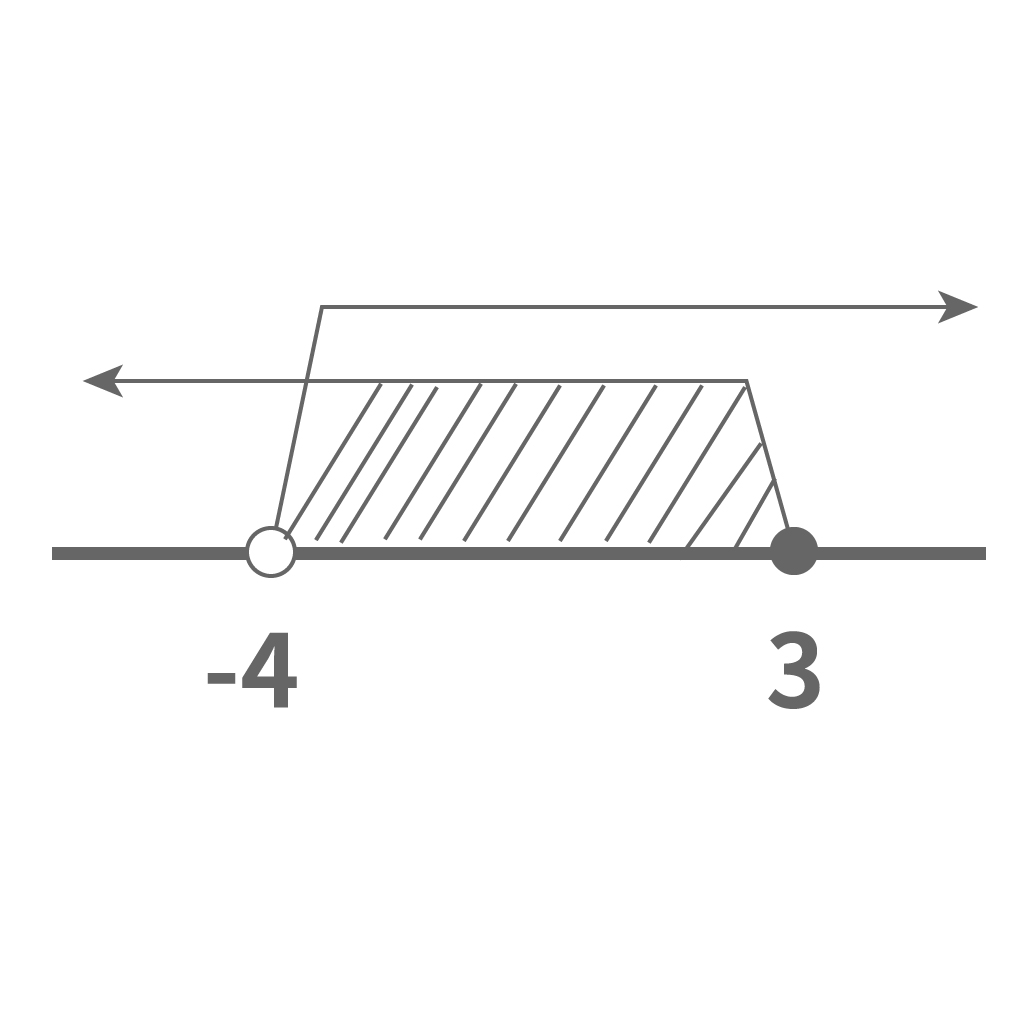
したがって、この斜線の範囲が連立不等式の解になる。
この被り領域を不等号で表すと次のようになるな。
$$-4<x≦3$$
これが連立不等式の解だ!
でもな、たまに { でつながっていない連立不等式もあるんだ。
例えば次のようなやつだな。
$$2x+1<x-3<-5x+7$$
1直線上に不等号が連なっていてるパターン。
一見奇妙に見えるが、これも連立方程式の一種だ。
この場合、
最初に2組の不等式に分けてやるんだ。
一直線になってる連立方程式は、次のように2つの不等式に分けられるからな。
$A < B < C$
だったら
に分けられるんだ。
つまり、
$$2x+1<x-3<-5x+7$$
は
$$\begin{cases} 2x+1<x-3 & \\ x-3<-5x+7 & \end{cases}$$
になる、と。
2組の不等式にわけたら、それぞれ解いてやって、解の共通範囲を求めてやれば万事OKさ。

それじゃあな!

この前は一次不等式の解き方を勉強してきたな。
今日はワンステップのぼって、
分数を含む一次不等式の解き方
を勉強していこう。
例えば次のような$x$についての不等式だ。
$$\frac{x-5}{4}+5>\frac{2}{3}x$$
分数が含まれて臆することはないぞ。
分数を含む一次方程式の解き方や分数を含む連立方程式の解き方と同じだ。
そう、
最初に分母を払えばいい
んだ。
つまり、不等式から分数を消し去ってやるのさ。
分数を掃除できたら、いつも通り不等式をとくんだ。
それじゃあさっきの例題を解いてみよう。
$$\frac{x-5}{4}+5>\frac{2}{3}x$$
まずは分数を消し去っていくぞ。
分数を含む項に注目して、その分母の最小公倍数を不等式の両辺にかければいいんだ。
分母の数を何倍かしたら、2つともそれぞれ同じになる
ような数を探せばいいんだ。
例題では分母が「4」と「6」だよな。
$$\frac{x-5}{4}+5>\frac{2}{3}x$$
この4と6の公倍数はたくさんあるけど、1番小さいのは「12」だ。
4と3をかけたら12になるし、6と2をかけても12になるからな。
この最小公倍数「12」を両辺にかけると、次のように不等式を変形できるぞ。
$$\frac{x-5}{4}+5>\frac{2}{3}x$$
$$12×\frac{x-5}{4}+12×5>12×\frac{2}{3}x$$
$$3(x-5)+60>8x$$
最小公倍数がよくわからない??
そんな時は、
すべての分母の数をかけ算したものを両辺にかける
という荒業もあるぞ。
たとえば次の例だと、分母の「4」と「6」をかけた「24」を不等式の両辺にかけてもいいわけだ。
$$\frac{3x-1}{4}+10>\frac{7}{6}x$$
$$24×\frac{3x-1}{4}+24×10>24×\frac{7}{6}x$$
ぶっちゃけ、この「24」は分母の4と6の公倍数だけれども、最小公倍数ではない。
でも、計算には支障ないからこれでもいいんだ。
不等式の両辺に分母の最小公倍数をかけたほうが、いい。
なぜなら、変形した後に文字の係数が小くて計算しやすい、っていうメリットがあるからな。
でも、別に公倍数なら何をかけてもいい、ってことも頭に入れておこう。
不等式を次のように変形するぞ。
文字(不等号)文字以外
項の移動には移項という技を使うんだ。
移項するときは符号に注意してくれよな。
逆サイドに項を運ぶとき、その項の符号を逆転させればいいんだ。
さっきの例の不等式は次のように変形できるな。
$$3(x-5)+60>8x$$
$$3x-15+60>8x$$
$$3x-8x>-45$$
$$-5x>-45$$
最後は文字の項の前についている数(係数)で不等式の両辺をわるぞ。
最後の最後に文字の項をツルツルにすればいいんだ。
ここで注意したいのは、係数の符号がマイナスの場合だ。
不等式の性質でやったように、
0より小さい数を不等式の両辺にかけたり割ったりすると、不等号が逆転する
という現象が起きるんだ。
つまり、このフェーズでも、もし係数が負の数だったら不等号が逆転しまうぜ。
そして例題ではなんと偶然にも、$x$の係数が負の数$-5$だ。
$$-5x>-45$$
だから、両辺を$x$の係数でわるときは不等号を逆転させて、次のようになるぞ。
$$-5x>-45$$
$$-5x÷(-5)<-45÷(-5)$$
$$x<9$$
以上が分数を含む一次不等式の解き方だ。
注意点は最後のステップだな。
文字の係数で両辺をわるとき、その係数がマイナスだった場合は不等号を逆転させるってことを忘れないようにしよう。

次は連立不等式の解き方を勉強していこう。
それじゃあ!

不等式とは何かわかったところで、いよいよ不等式を解いていくぞ。
高校数学 I で勉強する不等式の1つに、
一次不等式
ってものがある。これはマックスの次数が1の不等式だ。
例えば$x$についての不等式、
$$5x− 1 <9$$
があったとする。$x$がついている項$5x$に注目してみると、$x$が1回しかかけられてないよな。
式$5x− 1 <9$における最大の次数はこいつがマックスで「$1$」ってことになる。
だから、これは一次不等式なんだ。
ここではこの一次不等式の解き方を解説していくぞ。
一次不等式の解き方は次の3ステップだ。
まずは移項から始めよう。
(文字)不等号 (文字以外)
となるよう、一次不等式を変形するんだ。
文字の項が文字以外の項と仲良くしてたら、そいつらを引き離さなきゃいけないんだ。
例えば、不等式の左側で「文字の項」と「数字の項」が一緒になっていたら、そいつはいけねえ。
すかさず数字の項を右側に移項するんだ。
もし、不等式の右側に文字の項がいたら、そいつを左側に持ってくりゃいい。
移項のやり方は方程式と同じだ。
つまり、逆サイドに項を運ぶ時は符号を逆転させればいいんだ。
プラスのやつを逆に運ぶならマイナスをつけるぞ。
なぜ移項が不等式でも使えるのか??
それは、不等式の性質の、
不等式の両辺に同じ数をたしたり引いたりしても、2つの数の大小関係は変わらない
を使っているからなんだ。
例題の
$$-5x− 1 <9$$
に戻るぞ。
左側に
が同居しちゃってるよな。これはまずい。
数字の項 $− 1$を右に移項するぞ。
$$-5x− 1 <9$$
$$-5x <9+1$$
$$-5x <10$$
これで、
(文字)不等号 (文字以外)
という形に変化できた。
次は$x$の前についてる数字($x$の係数)で不等式の両辺をわるんだ。
さっきの例題を見てみる。
$$-5x <10$$
$x$の前についてる数字はどっからどう見ても$-5$だよな?
だから、不等式の両辺を$-5$でわるんだ。
ここでの注意点は割る数の符号な。
割る数がマイナスだったら、不等号を逆にしなきゃいけないんだ。
例題ではなんという偶然か、$x$の前についてるのは負の数だ。
$− 5$で不等式の両辺を割るときは不等号の「$<$」を逆転させて、
$$-5x <10$$
$$-5x÷(-5) >10÷(-5)$$
$$x> − 2$$
となる。
このように、不等式の左サイドを文字1つだけにできたらゴール。これが一次不等式の解なんだ。
基本的な一次不等式の解き方はマスターしたな。
でもな、たまーに、
かっこががついている一次不等式があるんだ。
例えば次のような問題。
$$2(x− 1) <10x+1$$
かっこがいても動ずることなかれ。
分配法則でかっこを外してから、さっきのステップを踏むんだ。
試しにやってみるぞ。
$$2(x− 1) <10x+6$$
$$2x− 2 < 10x+6$$
$$-8x < 8$$
$$x > -1$$

次は分数を含む一次不等式の解き方に挑戦していこう。
それじゃな!

2つの等しくない数の関係を不等号で表した式
だったな。
例えば、
$$5>3$$
とか
$$100000<1000000000000$$
とかが不等式だ。
でもな、たまに文字が含まれている不等式があるんだ。
例えば、$x$についての不等式、
$$5x− 1 > 9$$
があったとしよう。
不等式の左右の数の関係を崩さないような文字の値、
これを、
不等式の解
と人間界では呼んでいるんだ。
例えば、さっきの不等式を見てくれ。
$$5x− 1 > 9$$
$x$に入っても問題ないのは、$3$とか$4$とか$50$でも$100$でも良さそうだ。
こいつら$x$にぶっ込んでも不等式は変わらないよな。
このように、不等式の解はたくさんある。
方程式みたいに1個とか2個とか、そういう次元のレベルじゃない、ってことをまずはおさえようぜ。
そして、不等式の文字に入るたくさんの値を「すべて求める」こと。
これを、
不等式を解く
というんだ。
さっきの不等式の例に戻るぞ。
$$5x− 1 > 9$$
$x$に入れても問題ない$3$とか$4$とか$50$でも$100$、っつうのはすべてこの「不等式の解」に当たるんだ。
でもな、こうやってたくさんの解を列挙するのはとんでもなくつれえよな。
だから、不等式の解はコンパクトに、
不等号で表す!
例えばさっきの不等式 $5x− 1 > 9$ を見てくれ。
$2$より大きいなら、$x$に何を入れても不等号の関係は変わらねぇよな。
だからこの不等式の解は「$x$が$2$より大きいですよ」と表した不等式、
$$x > 2$$
になる。
$3$とか$4$とか$50$とか$100$とか、そういったすべての解をひっくるめて、不等号で表せるんだ。

それじゃあ!

等しくない2つの数の関係を不等号で表した式
だったな。
例えば、
$$x> 1$$
とか
$$x+1 <3$$
が不等式だ。
実はこの不等式には次の2つの性質があるんだ。
$$(1)a<bのとき, a+c < b+c, a-c<b-c$$
$$(2)a<bのとき, c > 0 ならば ac < bc, \frac{a}{c}<\frac{b}{c}, c < 0 ならば ac > bc, \frac{a}{c}>\frac{b}{c}, $$
それぞれ順番に見ていくぞ。
$$(1)a<bのとき, a+c < b+c, a-c<b-c$$
不等式の両辺に同じ数をたしたり引いたりしても、2つの数の大小関係は変わらない、と言っているんだな。
例えば、
$$3 > 1$$
という不等式があったとする。
この両辺に$2$をたしてみるぞ。
$$3+2 > 1+2$$
こいつを計算すると、次のようになる。
$$5 > 3$$
両辺に$2$をたしても大小関係は変わらず、左の方が右よりも大きいよな。
今回は足した場合だけど、引いた場合でも同じさ。
この不等式の性質を使えば、
不等式でも移項できる
ということになる。
移項とは、中学数学の方程式で習ったやつだ。
イコールマークを飛び越えて、逆サイドに項を移動するときに符号を変える技
だったよな。忘れちまったら復習よろしく!
なぜ 不等式も方程式と同じように移項できるのか。
その理由は、この不等式にはこの1つ目の性質があるからだ。
移項したい項を不等式の両辺から引いてやるんだ。
すると、あたかもその数が移項しているように見えるカラクリだ。
例えば、
$$x+1 < y$$
の$1$を右に移項してみる。
そのとき、この$1$を両辺から引いてるんだ。そうすると次のようになる。
$$x+1 < y$$
$$x+1-1 < y-1$$
$$x < y-1$$
$1$が左から右に移動した際、符号が変わってマイナスがついたように見えるな。
このように、方程式と同じように不等式でも移項できるってことも押さえておこう。
$$(2)a<bのとき, c > 0 ならば ac < bc, \frac{a}{c}<\frac{b}{c}, c < 0 ならば ac > bc, \frac{a}{c}>\frac{b}{c}, $$
次の性質はちょっと厄介だぞ。
これは、不等式の両辺にある数をかけたり割ったりしたときの性質を表している。
そのかける数がプラスかマイナスかによってその性質が異なるんだ。
正の数をかけたり両辺にかけたり割ったりした場合、不等式の大小関係は変わらない。
そのまま不等号を維持できるぞ。
例えば、
$$5 > 3$$
という不等式があったとして、そいつの両辺に$2$をかけてみる。
$$5×2 > 3×2$$
$$10 > 6$$
うん、左と右の大小関係わからないよな。
次に、負の数をかけたり割ったりしたときの性質を見てみよう。
その場合、不等式の大小関係は維持されず、不等号が逆になるんだ!
例えば、
$$5 > 3$$
に負の数$-2$をかけるぞ。
$$5×(-2) > 3×(-2)$$
$$-10 > -6$$
あれ、おいおい!
左の$-10$のほうが右の$-6$よりちいせえじゃねえか!
こりゃあ、不等式の不等号がおかしいから、不等号を逆転させればいいのさ。
$$-10 < -6$$
上の検証でわかるように、マイナスの数を不等式の両辺にかけたり割ったりしたら、大小関係を逆転するんだ。

出題者が大好きなトラップなのさ
次は不等式の性質を踏まえて、不等式の解について勉強していくぞ。
それじゃあな!

中学数学では方程式を習ってきたよな。
方程式とは、
2つの等しい数の関係を等号で表したもの
だ。
そう、2つの数を等号(=)、イコールで結んだことを思い出してくれ。
例えば、$A$と$B$と言う2つの数字の大きさが等しいことを表すときは、
$$A = B$$
という方程式を書いたはずだ。
それじゃあ、
2つの数が等しくない時はどうする?
2つの数の関係を数式で表現するのは諦めるしかないのか。
そこで登場するのが、
不等式
だ。
不等式とは、
2つの数の大きさが等しくないことを不等号で表したもの
なんだ。
「不等号」とは2つの数の大小関係を表せる符号で、次の4種類あったよな。
忘れちまったやつは復習しといてくれ。
例えば、
$$3 > 2$$
っていうのも不等式の1種だ。
不等号の口が向いている数のほうが大きいことを表しているから、これは正しい不等式だ。
さらに次のように文字 $x$が混じっていても不等式だ。
$$x+1 > 0$$
こいつは、不等号の口が向いている$x+1$が、その逆側の$0$より大きい、ってことを表してるぜ。
$x+1$は$0$じゃないんだけど、$0$よりも大きいぞ、ってことを意味しているのさ。
うん、これが不等式だ。
繰り返しになるが、不等式とは、
2つの数の大きさが等しくないことを不等号で表したもの
ってことを肝に銘じておこうぜ。

次は「不等式の性質」を勉強していこう。
それじゃな!