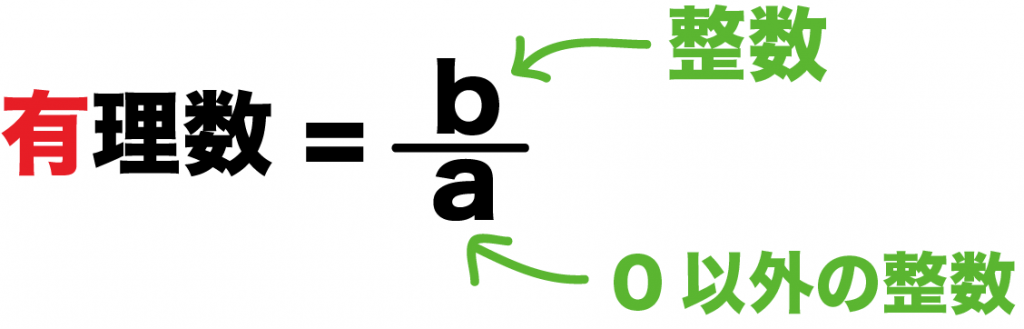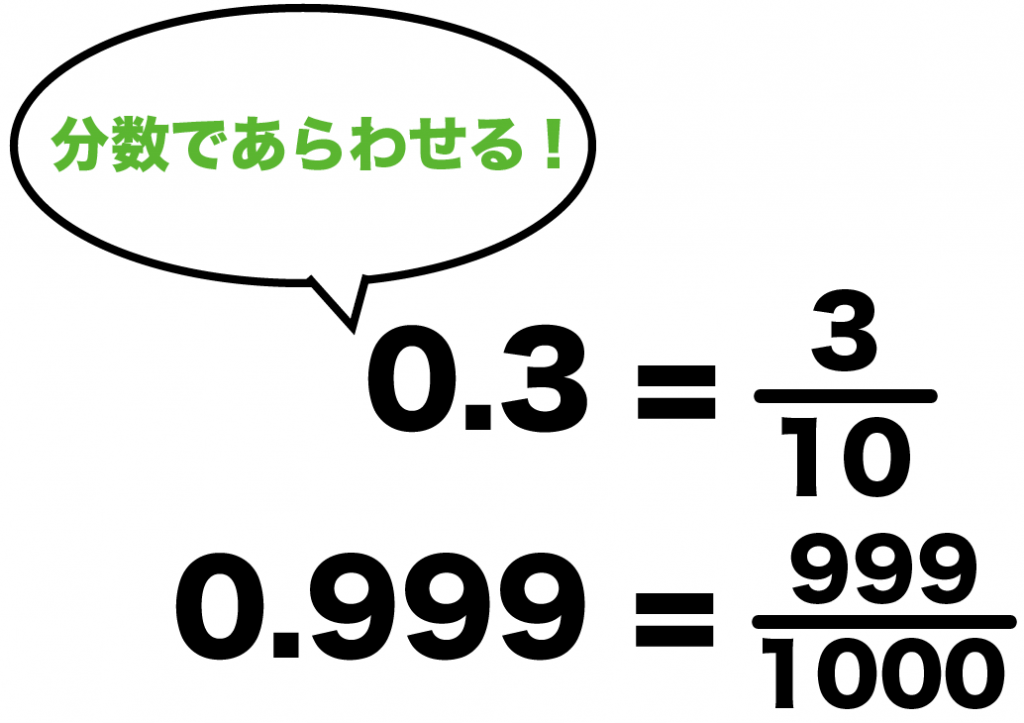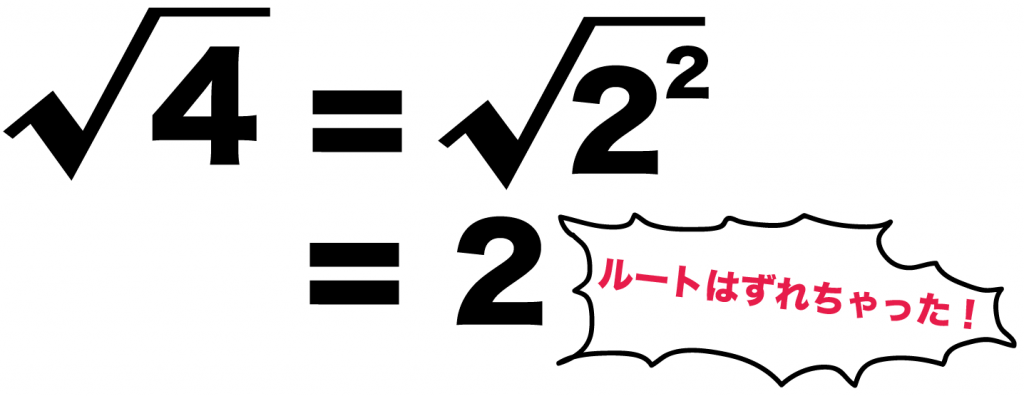【中3数学】有理数と無理数とはなんだろう??
有理数と無理数とはなんだろう??
中3数学では、
有理数と無理数
を勉強していくよ。
小学校ではならなってなかった新しい概念だね。
有理数
と
無理数
って1文字しか変わらないから間違いやすい。
非常にややこいね。
そこで今日は、
有理数と無理数とはなにか??
をわかりやすく解説していくよ。
= もくじ =
- 有理数とはなんだろう??
- 無理数とはなんだろう??
有理数とはなにものなの?!?
まずは、
有理数とはなにか??
を振り返ってみよう。
有理数とはずばり、
分数であらわせる数だ。
整数をa, bとすると、
分数 a分のb
であらわせるってことさ。
ただし、分母は「0」じゃないっていう条件あるけどね。
だって、どんな数も0で割ることはできない
っていうルールがあるからね。
せっかくだから、有理数の具体例をみていこう!
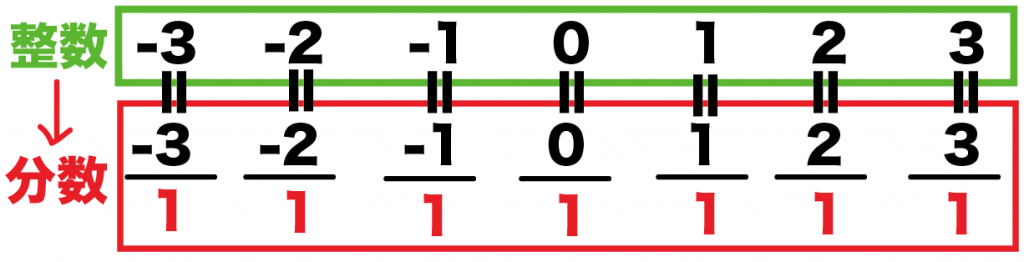
有理数の例1. 「整数」
まず、有理数の例としてあげられるのが、
整数
だ。
整数ってたとえば、
1, 2, 3, 4, 5….
って1以上の整数だったり、
0
だったりするやつ。
もちろん、符号がマイナスでも大丈夫。
-1, -2, -3, -4, -5….
とかね。
こいつらが有理数なのはあきらか。
なぜなら、
整数は分母を1とした分数であらわせるからね。
たとえば、
- 5 =「1分の5」
- 1234 = 「1分の1234」
だ。
分母を1にすれば分数であらわせる。
だから、整数は有理数なんだ。
有理数の例2. 「有限小数」
2つめの有理数の例は、
有限小数
ってやつだ。
有限小数とはずばり、
小数の位が無限に続かないやつね。
たとえば、
0.3
とか、
0.999
とか。
こいつらって、
小数の位が無限に続いてないじゃん??
0.3だったら小数第1位でおわってるし、
0.99999だったら、小数第5位でとまってる。
こんな感じで、
ケタが続かない小数を「有限小数」ってよんでるのさ。
んで、
有限小数は有理数だよ。
なぜなら、分数であらわせるからね!
有限小数は、
(小数の位)÷(10の「小数の位の数」乗)
ですぐに分数にできちゃう。
たとえば、
- 0.3 ⇒ 10分の3
- 0.999 ⇒ 1000分の999
みたいにね。
有限小数は「有理数」っておぼえておこう!
有理数の例3. 「循環小数」
3つめの有理数の例は、
ってやつだ。
これは無限に小数の位がつづく無限小数のなかでも、
小数の位の続き方に規則性があるやつ
なんだ。
たとえば、
0.33333333333…..
とか、
0.123412341234….
とかね!
こいつらはじつは、分数であらわすことができるんだ。
⇒詳しくは循環小数を分数に変換する方法をよんでみて
さっきの例でいうと、
- 0.33333…. = 3分の1
- 0.12341234…. = 9999分の1234
になるね!
よって、循環小数も分数にできる。
つまり、有理数ってことだね!
じゃあ無理数とはなんだろう!?!
それじゃあ、
無理数とはなんなんだろう!??
ちょっと気になるよね。
無理数とはずばり、
分数であらわせない数
のことだよ。
「有理数では無い数」=「無理数」
ならおぼえやすいかな。
えっ。
分数であらわせない数字なんてあるのかって?!
じつはね、おおありなんだ。
具体的にいうと、
循環しない無限小数が無理数だよ。
つまり、
小数の位が続いているけど、続き方に規則がない小数のこと
だ。
そうは言っても、無理数にピンとこないね??
無理数の具体例をみていこう!
無理数の例1. 「π(円周率)」
中学数学ででくる無理数の例は、
π(パイ)
だね。
直径と円周の比の円周率のことだったよね??
じつは、これ、
無限に続いてる小数で(無限小数)、
しかも、
その続き方に規則性がまったくないんだ。
試しに、円周率を100ケタぐらいみても、
3.141592653589793238462643383279502884197169399375105820974944 5923078164 062862089986280348253421170679…
・・・・っダメだ。。
規則性もクソもねえ!ランダムにケタが続いているよね。
こういうやつが、
無限小数で、しかも、循環しない小数
つまり、無理数ってわけ。
無理数の例2. 「平方根(ルート)」
中3数学でならった
「平方根」
も無理数だよ。ルートとよばれてるやつだ。
ルートがついているやつはたいてい無理数だね。
たとえば、良く登場してくる、
ルート2
は圧倒的に無理数だね。
なぜなら、
無限につづく小数で、しかも規則性がないからね。
こっちも試しにルート2の小数のケタをかきなぐってみると、
1.4142135623 7309504880 1688724209 6980785696….
まじムリっ!
ぜんぜんケタの繰り返しに規則性がみつけられないじゃん!?
だから、
ルート2は無理数
といえそうだ。
でもね、ルート2が平方根だからといって、
√(ルート)がついている数字はぜんぶ無理数ってわけじゃない。
たとえば、ルート4をみてみよう。
こいつには一見、無理数の香りがする。
ルートがついてるし。
だけどね、こいつは無理数じゃない。
なぜなら、
ルート(√)がはずせちゃうからね。
√の中身の4は「2の2乗」。
ってことは、√4の根号ははずせちゃうね。
√をはずしてみると、
√4 = 2
になる。
つまり、√4の正体は整数の2ってことなのさ。
整数は有理数だったね??
ってことは、
√4も有理数なのさ。
√がついてるからといって、無理数と決めつけないようにしよう!
ルートがはずれるか確認してみてね。
まとめ:有理数と無理数の違いは分数であらわせるかどうか!
有理数と無理数の違いはピンときたかな?
こいつらの違いは、
- 有理数:分数であらわせる数
- 無理数:分数であらわせない数
っておぼえておけば大丈夫。
有理数と無理数を見分けられるようにしよう!
そんじゃねー