ここまでで絶対値の記号をふくむ方程式の解き方を2種類やってきたよな。
お察しのようにこの世界には、
絶対値記号がふくまれる不等式
も存在しているぜ。
ありがたいことに、この不等式の場合にも次の2種類の解き方があるんだ。
- 場合分けしない
- 場合分けあり
今日はそのうちの「場合分けしない」簡単な解き方を紹介していくぞ。
場合分けをしない版！絶対値記号をふくむ不等式の解き方
残念ながら、不等式の事情は方程式と同じだ。
例外中の例外をのぞけば、場合わけが必要だぜ。
で、その例外中の例外ってやつは、次のタイプの不等式だ。
│文字式│ 不等号 文字以外の項
絶対値記号に文字が挟まっていて、さらに不等号の逆サイドには文字がない問題ってわけな。
このタイプの問題では次の公式を使える。
公式
$a>0のとき、$
$│x│<aの解は -a<x<a$
$│x│>aの解は x<-a, a<x$
なぜこの公式が使えるのか？
それは数直線を書いてみるとわかるぞ。
絶対値とは
原点0からの距離
だったよな。
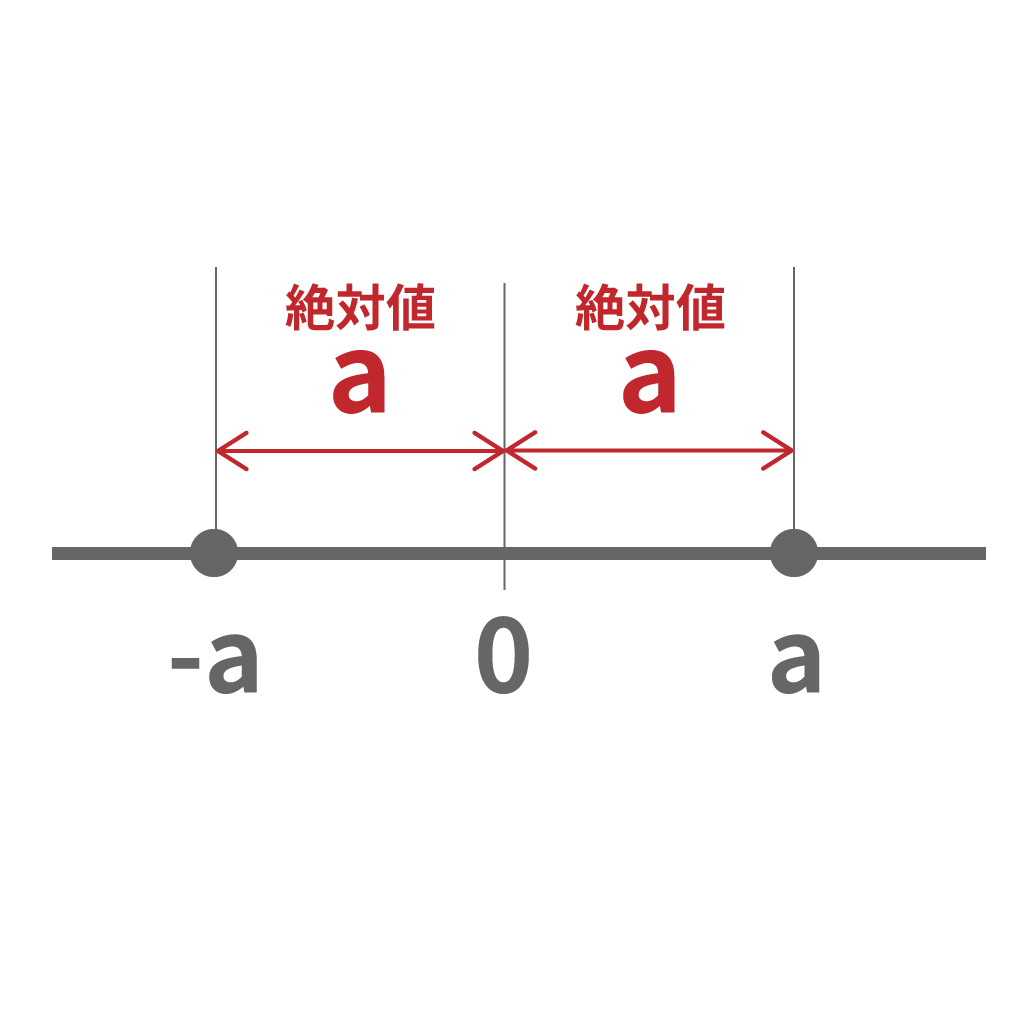
「絶対値がある数より大きい」っていうシチュエーションだったら、次の2つの可能性がある。
- プラスの方向に突き抜けてでかい
- マイナスの方向に突き抜けてでかい
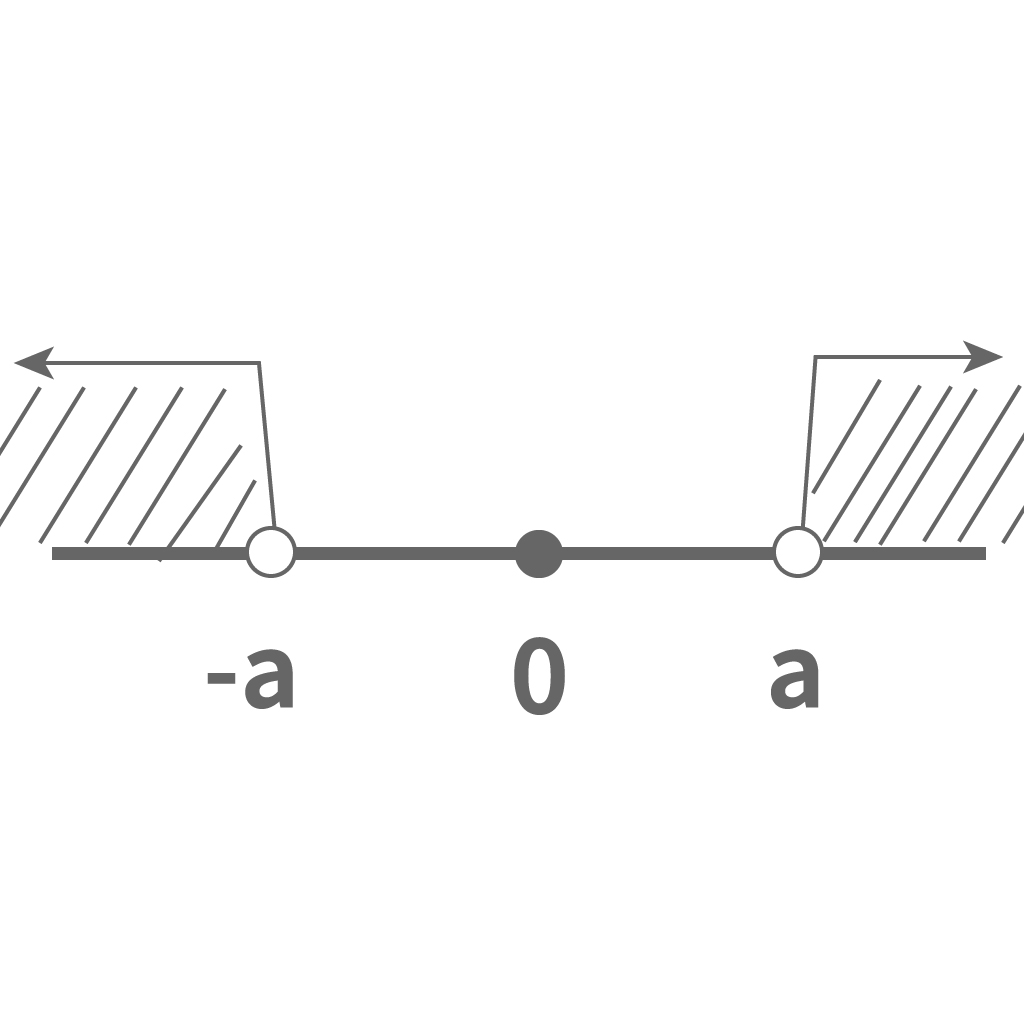
絶対値が小さい場合でも同じように考えればいいんだ。
絶対値がある数より小さいってことは
- ある数のプラスバージョン
- ある数のマイナスバージョン
の間の範囲になる。
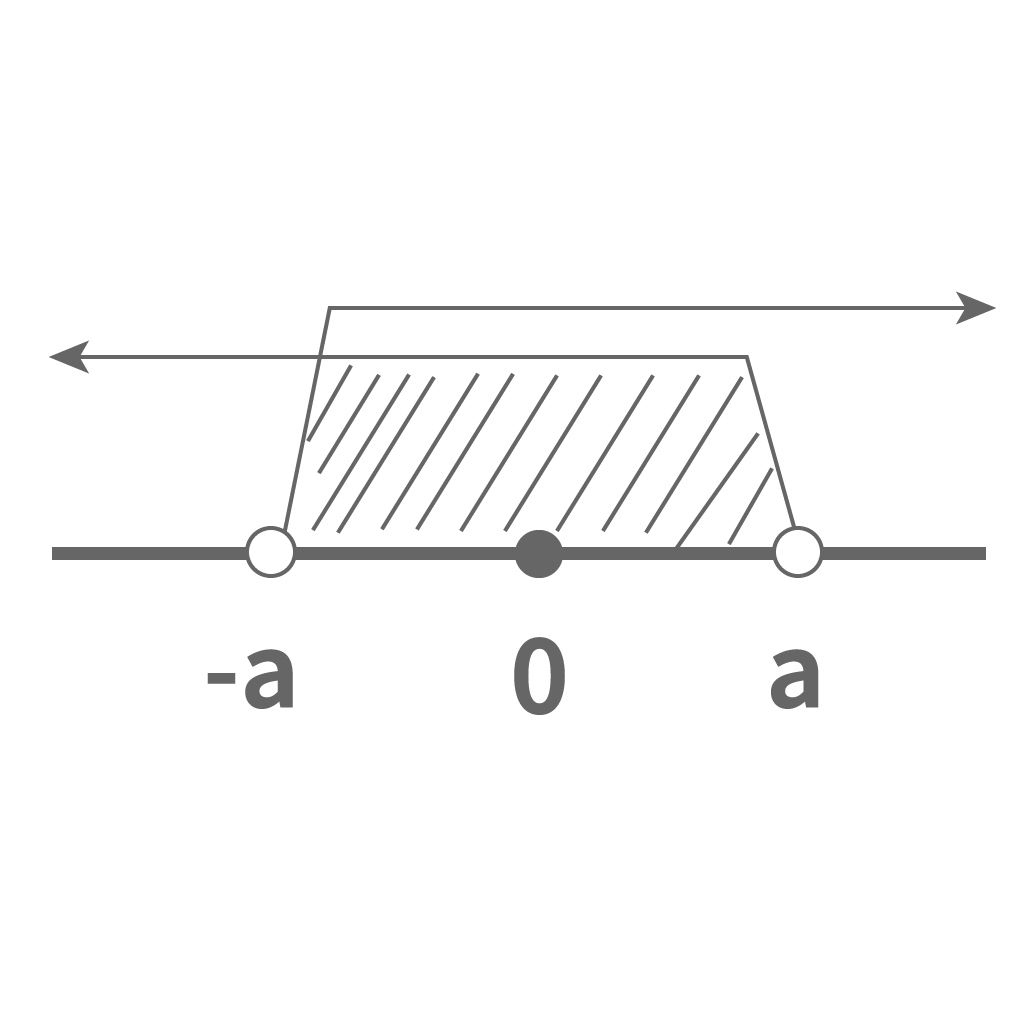
うん、この公式は便利そうだ。
でも、なぜ全てが場合しない方法で解けないのか気になるよな。
それはな、不等式の領域の境界に文字が入っていると、文字が変化したら不等式の領域もグラグラしちまうよな。
例えば、不等式の境界に$x$文字が含まれていたら、$x$が変化するとこの領域の境界も変化しちまう。
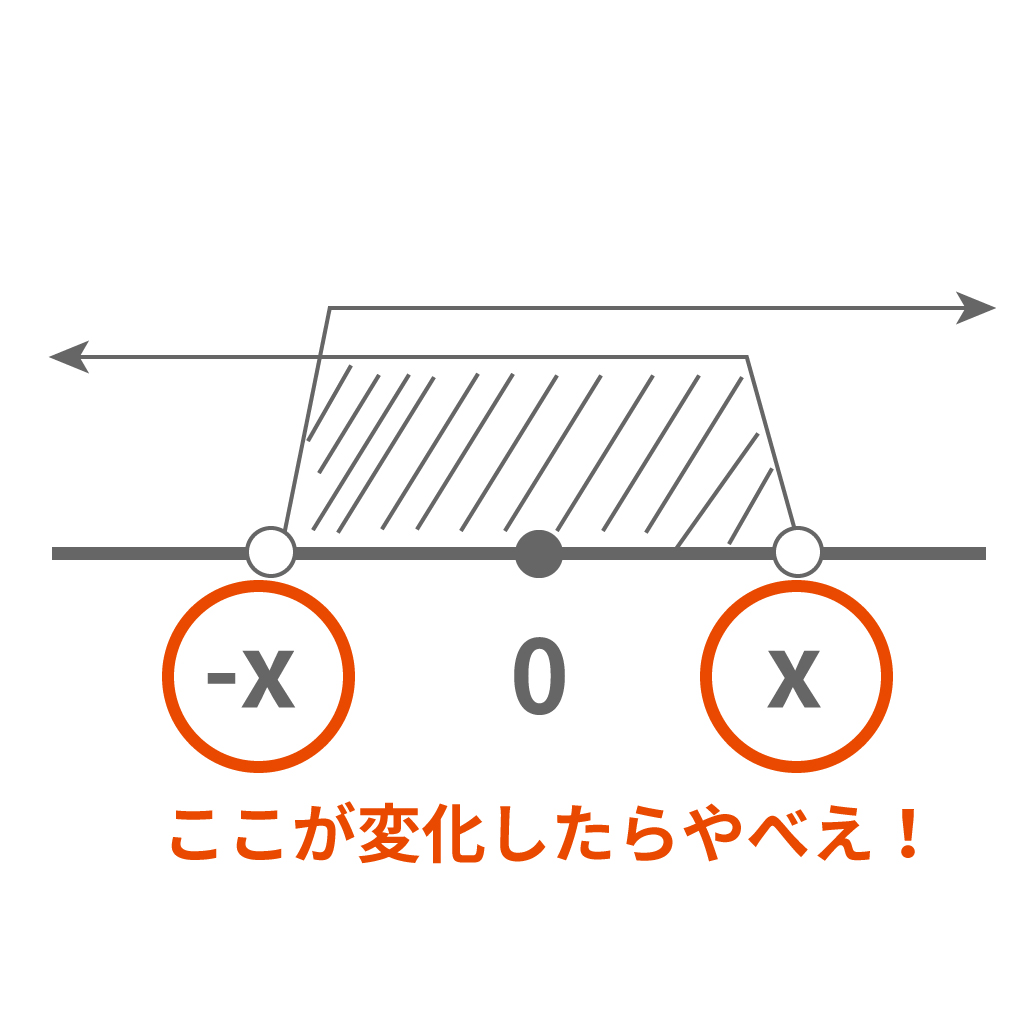
だから、この例外中の例外を除いて、俺たちは絶対値記号をふくむ不等式を見たら場合分けしなきゃいけないんだ。
絶対値記号をふくむ不等式の解き方の例題
それじゃあ早速実戦だ。
次の絶対値記号をふくむ不等式を解いてみよう。
$$│x│>2$$
オッケー、こいつぁ、うまい具合に
│文字式│ 不等号 文字以外の項
の形になってる不等式だな。
ってことで、場合分けしないでもいい。
だから、最初に見てきた公式のうちの次のものが使えるはずだ。
$a>0のとき、$
$│x│>aの解は x<-a, a<x$
今回は$a$が$2$ってわけだから、この絶対値記号をふくむ不等式は次のようになる。
$│x│>2$
$x<-2, 2<x$
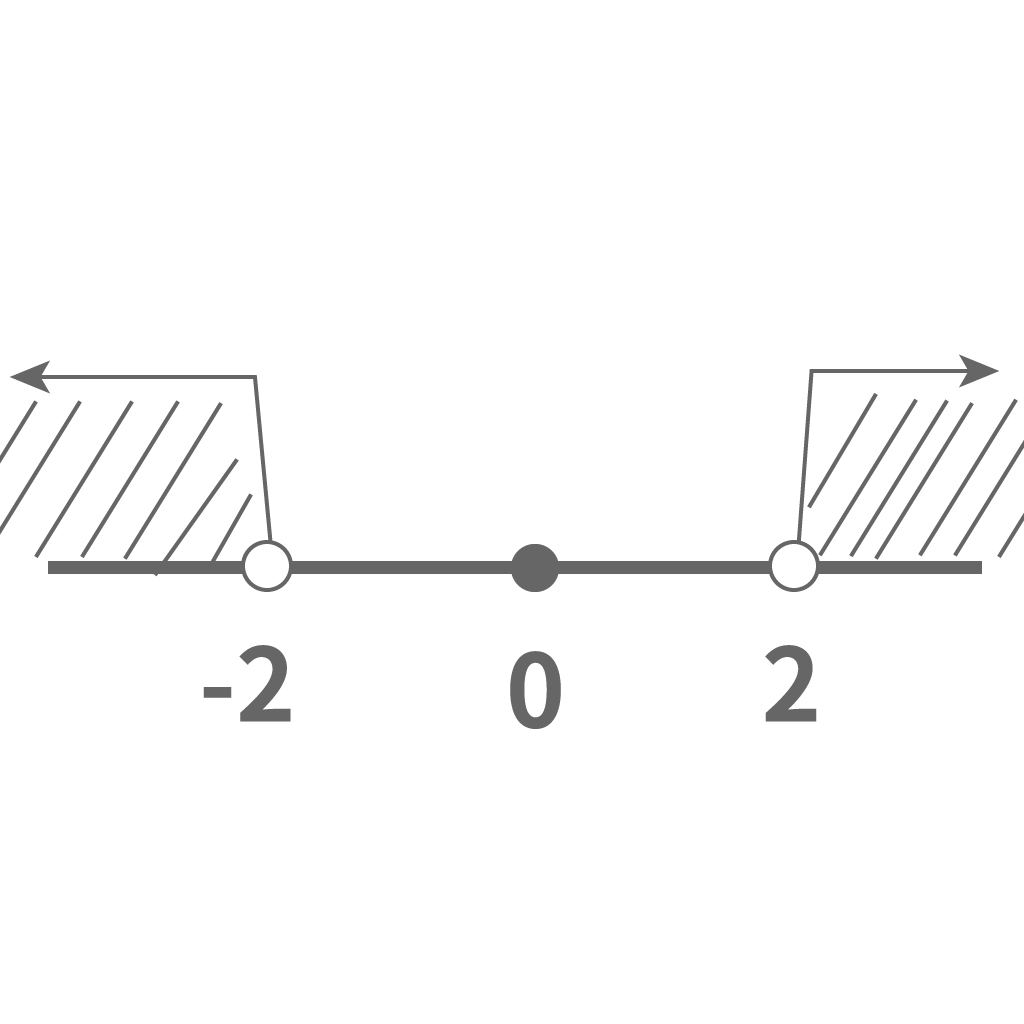
これに限るな。焦らずゆっくり着実に不等式を解いていこう。
次は「場合分けありの不等式の解き方」を勉強していこう。
そんじゃ！
