こんにちは!この記事を書いているKenだよ。指、鳴らしてるね。
マグマが冷えて固まってできる岩を火成岩といって、その火成岩には、
の2種類あるってこれまで勉強してきたよね。

で、それぞれの岩には具体的な岩の種類があって、火山岩には、
の3種類があったね。
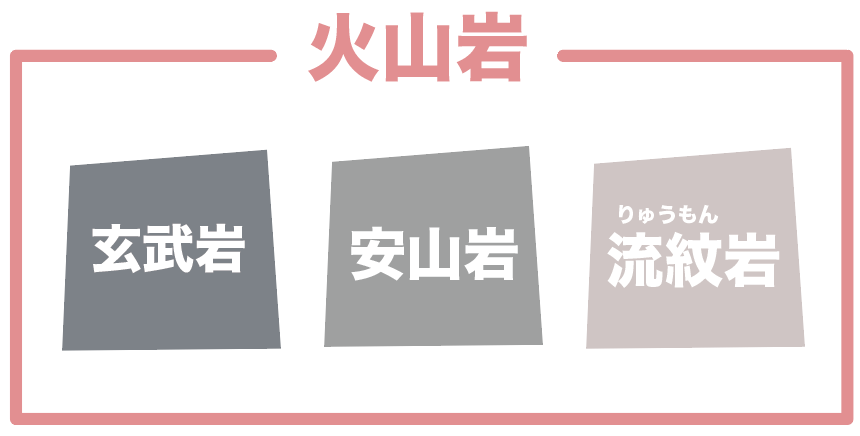
火山岩の種類はテストに出やすくて覚えなきゃいけないから少々厄介。
同じ火成岩の一種の「深成岩の種類」とごっちゃ混ぜにしちゃいやすいからね。
そこで今日はテスト前に使える、
火山岩の種類の覚え方
を特別に伝授していこう。
中学理科で勉強する火山岩の種類は、
の3種類。
この火山岩の種類を覚えるための語呂はこれだ↓↓
ゲッ、ぜんぶ暗算で解きやがった!さすが母さん流だもんね!
えっ。全然火山岩の種類と結びつかないだって!???
そういう時はひらがなにしてみるとよくわかるはずだ。
ゲッ、ぜんぶ暗算で解きやがった!さすが母さん流だもんね!
げっ ぜんぶあんざんでときやがった!さすがかあさんりゅうだもんね!

そう。
御察しの通り、
| げ んぶ | 玄武岩 |
|---|---|
| あんざん | 安山岩 |
| か さん | 火山岩 |
| りゅう もん | 流紋岩 |
という風に火山岩の種類を表しているのさ。

この語呂のシチュエーションとしては、母さんに宿題の計算問題を解いてもらってる場面を想像してくれ。

一旦、解いてもらうと、
母さんはぜんぶの問題を暗算で瞬殺してしまったんだ。

すごい。はやい。
そこで、宿題の計算問題を解いてもらったきみが、
「さすが母さん流だもんね」
と満足気にうなずくってわけ。

実際には母さんに宿題を解いてもらったらダメだけど、火山岩の種類を覚えるためだったらこのシチュエーションはありだ。
火山岩の種類はテストにも何気に出やすいからよーく復習しておこう。
「そもそも火山岩と深成岩の違いを忘れちゃったよ!」
って言うときは「火山岩と深成岩の違い」でもう一度基礎を復習してみてね。
そんじゃねー
Ken
こんにちは!この記事を書いてるKenだよ。リズム、乗ってきたね。
マグマが固まってできる火成岩には、
の2種類があるって勉強してきたよね??

んで、地表の深いところでマグマが時間をかけてゆっくり固まってできる岩たちを「深成岩」というんだけど、この深成岩には、
の3種類があるんだ。

この深成岩の種類はテストでも狙われやすいから、テスト前に種類を暗記することになるわけだ。
今日はそんなテストに出やすい深成岩の種類の覚え方を今日は伝授していくよ。
それじゃあ早速、深成岩の種類の覚え方をみていこう。
ズバリ、深成岩の種類の覚え方の語呂は、
阪神が下降気味の選手を戦力外通告した
だ。
えっ。なんで、この頃で深成岩の種類が覚えられるのかって?!?
実はこの語呂をひらがなに直してみると、深成岩の種類が隠れていることがわかるね。
阪神が下降気味の選手を戦力外通告した
(はんしんがかこうぎみのせんしゅをせんりょくがいつうこくした)

そう。
というわけだね。
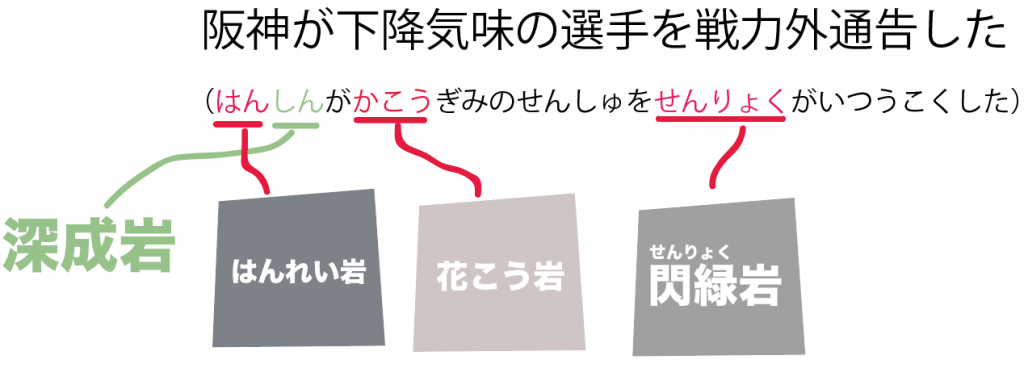
比較的、この語呂はとても現実的でイメージしやすい。
みんなも知っている阪神タイガースという野球チームが、
最近不調で下降気味の選手を戦力外通告してしまったんだ。

残念なことだけれども、多分野球という弱肉強食の世界では日々起きていることだし、うん、それが勝負の世界だ。
戦力外通告されてしまった無念を感じている野球選手の姿を思い浮かべながら、深成岩の種類を覚えていこう。
深成岩の種類を覚えたら次は「火山岩の種類」を覚えていこう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。椅子が、あるね。
中学理科の大地の変化ではいろんなことを暗記しないと攻略できないようになってる。
中でも難しいのが、
鉱物の種類の暗記
だ。
鉱物とは、
火山から出てきたもの(火山噴出物)の中で結晶になったもののこと
だったね。
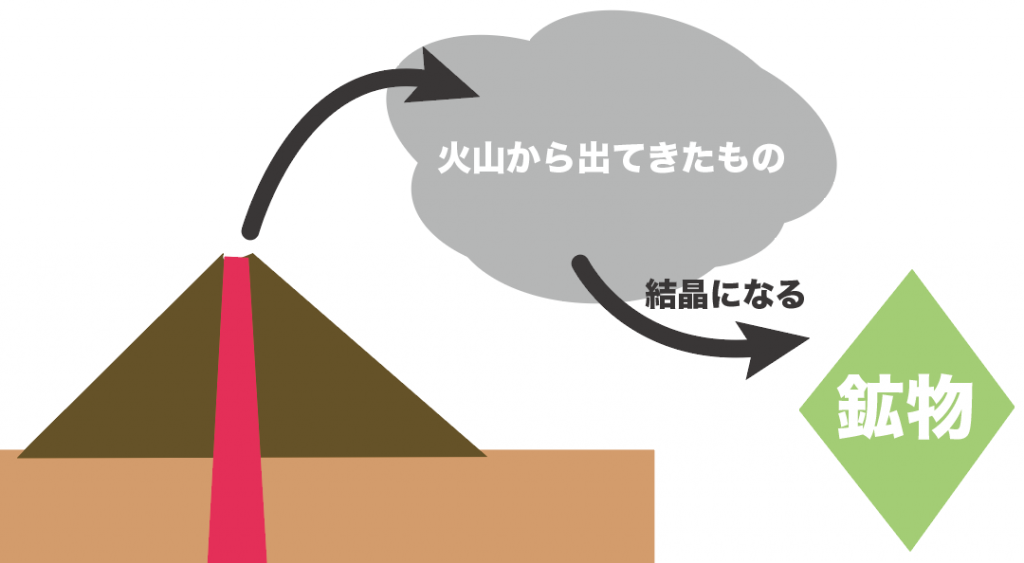
中学で習う鉱物の種類は全部で、
の7種類。
名前を覚えるだけじゃなくて、
でさらに分類して覚えないといけないから超厄介なんだ。
この鉱物の種類をまとめたのが次の表になるよ↓
| 無色鉱物 | 有色鉱物 | |||||
|---|---|---|---|---|---|---|
| 石英 | 長石 | 黒雲母 | 角閃石 | 輝石 | カンラン石 | 磁鉄鉱 |
とてもじゃないけど普通に生活してたんじゃ鉱物の種類が覚えられなさそうだから、
語呂を使った鉱物の覚え方
を考えてみたよ。覚えにくくてむしゃくしゃしてる時に参考にしてみてね。
まずは色が付いてない鉱物の「無色鉱物」の覚え方だ。
無色鉱物には、
の2種類があったよね。
この無色鉱物の覚え方は次のやつだ。
席8番だよ!無職の村長の席は!
(セキエイトだよ! ムショクのソンチョウノセキハ!)

次のシチュエーションを想像してみて。
ある日、とあるところに、村長のポジションを解雇された村長がいたんだ。
いわゆる、無職の村長だ。

そんな村長が村の夕食会に招かれていつもの村長の席につこうとしたんだけど、そこには現職の村長が座ってたんだよね。
だから、夕食会の支配人が無職の村長にこういうんだ。
「席8番だよ!無職の村長の席は!」
ってね。

この語呂のポイントは席の番号の8を「エイト」と英語読みすることかな。
っていう感じで鉱物の種類と、そいつらが無色鉱物であると覚えられるようになってるよ。
間違って「はちばん」と普通に読んでしまうと、石英が埋もれてしまうので要注意だ。
続いて、色がついている「有色鉱物」の覚え方だ。
有色鉱物には、
の5種類があったよね??
この有色鉱物の覚え方はコレだ↓
黒い雲出てきたから、各先生の席(かくせんせいのせき)、夕食(ゆうしょく)分取らないと!
観覧席(かんらんせき)で奇跡(キセキ)おこせるとでも?じれってえんだよ高校生(こうこうせい)!

さあ、この語呂のシチュエーションを想像するのは難しいぞ。
とある日、先生たちの夕食分の席を取ることを命じられた高校生がいたんだ。
球場の観覧席にね。

でも正直言ってめんどくさいから、
「後ででいいかな」
と、このミッションをものすごく放置していたんだ。
でも、外には黒い雲が出てきて雨降りそうで嵐になりそうで予約どころじゃなくなりそう。。。

それをみかねた先輩が、
「先生の席を夕食分取れ!」
と喝を入れたんだけど、高校生は動かない。

夕食の席が自動的に取れるという奇跡を観覧席で願ってるだけだったんだ。
その態度に周囲の大人たちがキレて、
「観覧席で奇跡おこせるとでも?じれってえんだよ高校生!」
ってまたこの高校生に喝を入れたって話ね。

この高校生にメンドくさがり屋の野球少年を当てはめてやればしっくりくるはずだ。
ゴロを覚えてやると、
って感じで、鉱物の種類の名前、さらに有色であることを覚えられるわけだ。
以上が鉱物の種類の覚え方だったね。
最後にもう一度復習しよう。
鉱物とは「火山から飛び出してきたものの中で結晶になったやつのこと」で、
の7種類もある。
しかも、色の有無で、
の2種類に分類して覚えないといけない。
無色鉱物の覚え方は、
席8番だよ!無職の村長の席は!
(セキエイトだよ! ムショクのソンチョウノセキハ!)

有色鉱物の覚え方は、
黒い雲出てきたから、各先生の席(かくせんせいのせき)、夕食(ゆうしょく)分取らないと!
観覧席(かんらんせき)で奇跡(キセキ)おこせるとでも?じれってえんだよ高校生(こうこうせい)!

だ。
テスト前にもう一度念仏を唱えてみよう。
鉱物の種類が覚えられたら次は深成岩の種類の暗記にチャレンジしてみよう!
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。ケバブ、思い出したね。
中1理科の大地の変化では、
火山の形
を勉強していくよ。
火山の形はずばり、
火山の元になる「マグマ」の粘り気によって違うんだ。
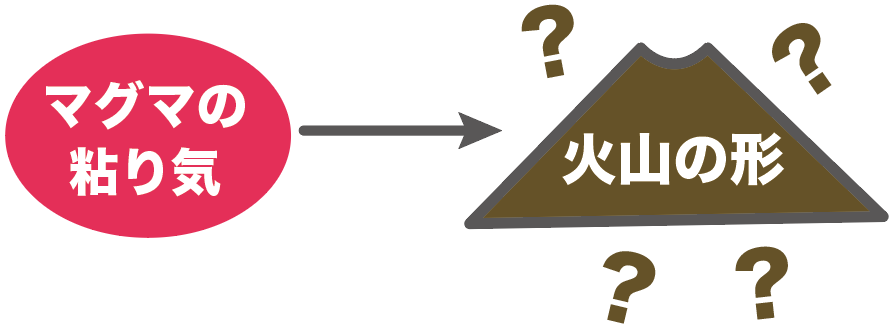
「火山・マグマとは」の記事で、
火山はマグマが冷えて固まったもの
って習ったよね?
火山の元の材料はマグマであるわけだから、マグマがどんな性質なのかによって火山の形が違ってくるのさ。
今日は、その火山の形を3つ勉強していこう。
中学理科で勉強する火山の形は全部で次の3つ。

まずは傾斜がゆるやかな火山ね。
こいつは巷では、
たて状火山
と呼ばれているよ。

火山の形が「盾を上向きに置いた時みたいな形」しているからね。

なぜこの火山の形がゆるやかで盾みたいな形をしているのかというと、
火山の元になったマグマの粘り気が弱いからなんだ。
地球の内部から吹き出したマグマの粘り気が弱かったから、地表に出たマグマたちは山盛りになりにくく、外へ外へドロドロ流れちゃったわけよ。
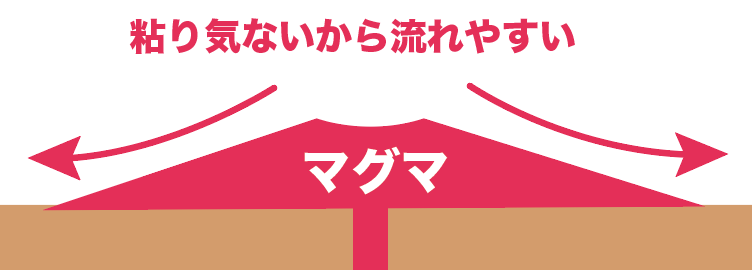
この「たて状火山」には次の性質があるよ。
たとえばこのたて状火山に当てはまるのは、
などなどだね。
2つ目の火山の形は円すいみたいな形をしているよ。
このタイプの火山の形を巷では「成層火山」と呼んでいるんだ。

火山の元になったマグマの粘り気は中程度。さっきのたて状火山のマグマと比べると粘り気が強いんだ。
粘り気がまあまああるマグマだから、地表に出てもそれほど外へ外へ広がらなかったわけね。

この成層火山には次の2つの性質があるよ。
たとえば、富士山や桜島なんかがこの円錐形の成層火山だね。
最後の火山の形はおわんをひっくり返したような形だ。

これを鐘状火山と呼んでいるよ。お寺の鐘をひっくり返したような形してるからだね。

御察しの通り、この火山の元になったマグマたちの粘り気は強かった、とんでもなく。
地球の内部からマグマが噴出しても、マグマはそう簡単に外へ外へ流れていかなかったのね。

だから、マグマが飛び出た位置から広がる前に固まっちゃったから、お椀のように盛り上がったような火山の形になったわけだ。
この鐘状火山は、
という特徴があるよ。
たとえば、
などがこのタイプの火山に当たるね。
以上が中学理科で習う火山の形だよ。
最後にせっかくだからもう一度復習してみよう。
火山の形は、火山の材料となった「マグマの粘り気」で決まって、

粘り気の違いごとに、
の3つの火山の形に分類できて、

それぞれの火山にはマグマの粘り気と形以外にも、
に違いがみられるんだったね。
最後に火山の形で勉強したことを表にまとめておくよ。
| マグマの粘り気 | 火山の形 | 火山の色 | 噴火の様子 | 具体例 |
|---|---|---|---|---|
| 弱 | ゆるやかな傾斜(たて状火山)
|
黒 | 弱 | 伊豆大島火山、キラウエア山 |
| 中 | 円すい形(成層火山)
|
灰 | 中 | 富士山、桜島 |
| 強 | おわん型(鐘状火山)
|
白 | 強 | 昭和新山、雲仙普賢岳 |
火山の形をマスターしたら次は火山灰に含まれる鉱物の種類を勉強していこう!
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。ブラックサンダーで復活だね。
中1理科の大地の変化という章では、
おもに火山とかマグマとか鉱物の種類
とかについて勉強していくよ。
その中でも特にややこしいのが、
という3種類の岩石の名前たちだ。
ぶっちゃけどれも3文字の名前だし、「火」がついている岩石が2つあるし、「成」っていう感じも2つの岩石についている。
テスト前になって理科の用語を暗記しようとすると混乱しちゃうよね。
そこで今日は、
火成岩・火山岩・深成岩の違い
をわかりやすくまとめてみたよ。
まず一番最初の「火成岩(かせいがん)」からみていこう。
火成岩とはズバリ、
マグマが冷えて固まった岩石のこと
だね。マグマが元になっている岩石ならどれでも火成岩というわけだ。
火成岩の覚え方としては、
火よりも熱いマグマが冷えて生成された岩石
と覚えてみよう。
んで、じつはこれから紹介する、
はこの「火成岩」の一種なんだ。

火成岩という大きなグループの中に、火山岩、深成岩という種類があるってわけね。
これは例えるなら、野菜とにんじんとキャベツの関係に似てるね。
にんじんとキャベツは、野菜っていうグループの中の1種類だよね?

にんじんは野菜だし、キャベツも野菜だ。
だけど、野菜はにんじんじゃないよね? 野菜といえばナスだってそうだし、ネギだって野菜だもん。
その関係と火成岩・火山岩・深成岩の関係は同じってこと。
続いて、火山岩(かざんがん)。
こちらは、
地表に出てきたマグマたちが固まってできた火成岩のことだ。

地表に出てきてしまったマグマたちだから、冷えて固まるための時間がすこぶる短いことが特徴だね。
火山岩の覚え方としては、
火山の地表まで出てきて急に短い時間で固まってしまった岩石
がいいかな。
続いて、火山岩のつくりをみてみよう。
火山岩を拡大してのぞいてみると、次のような感じのつくりになってるね。

火山岩の特徴としては、
があるよ。
この「形がわからない鉱物の部分」のことを「石基(せっき)」、大きな粒の鉱物のことを「斑晶(はんしょう)」というんだ。
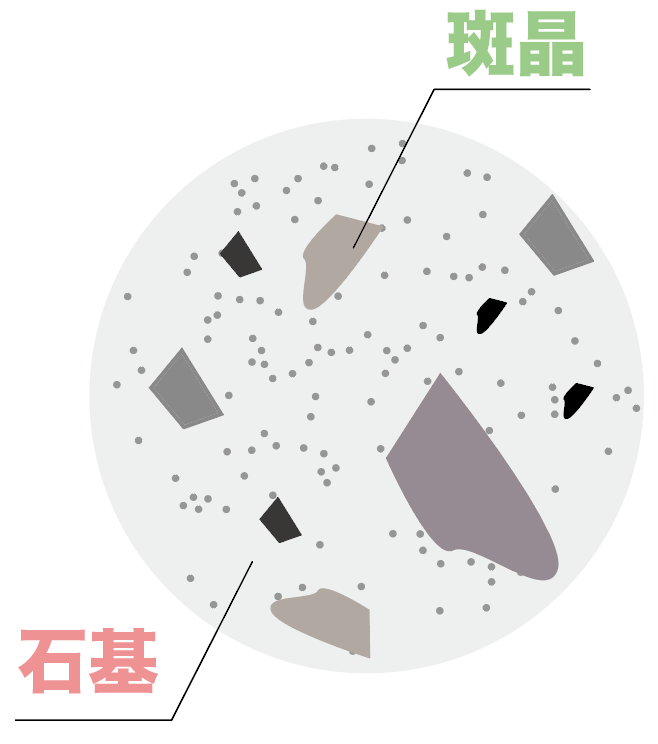
このように、
斑晶(はんしょう)という比較的大きな粒の鉱物がちょくちょくと石基(せっき)の中に広がっている状態のつくりのことを、
斑状組織(はんじょうそしき)
というよ。
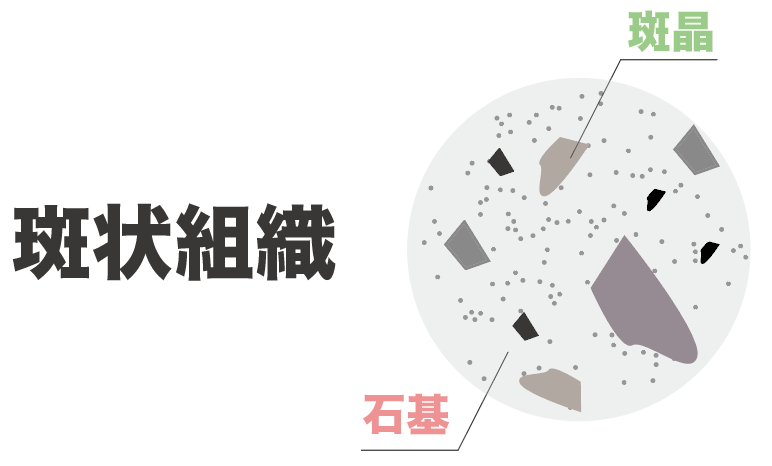
ってことで、火山岩のつくりは斑状組織(はんじょうそしき)ってことは頭の片隅においておこう。
火山岩このこのつくりになるには理由がある。
それは、
マグマの冷え方が急で短時間だからだよ。冷え方が急すぎてマグマに含まれる鉱物が結晶になりにくいわけ。
中学理科でよく出てくる火山岩の種類は次の3つ。
この火山岩の種類の覚え方を考えてみたから参考にしてみてね。
続いては、深成岩(しんせいがん)だ。
深成岩とは、
マグマが地表に出ずに地下にいたまま長い時間をかけて固まった岩石のこと
だね。
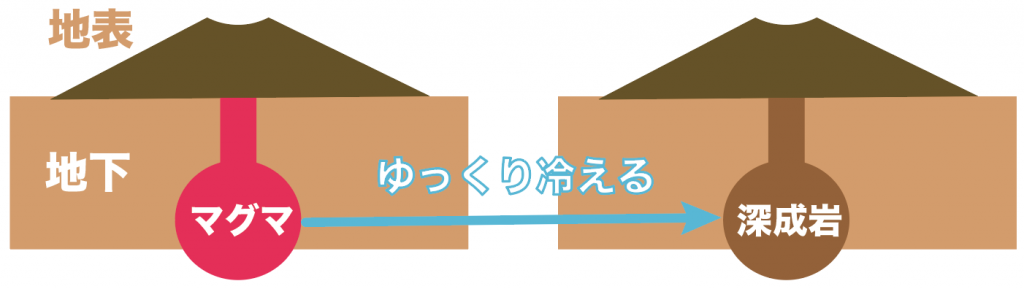
地下の深くで固まったあと、火山が水の流れで削られたり、大地の運動で大地が上昇したりすると地表に出てくるのさ。
深成岩の意味の覚え方としては、
地下の深くで固まって生成されて、山が削られると地表に現れる岩石
だね。
うまく状況をイメージできたかな??
ってことで引き続き、火山岩と同様に深成岩のつくりもみていこう。
深成岩を拡大してみてみると、次のようなつくりになってるはずだ。

深成岩のつくりの特徴としては、
同じぐらいの大きさの鉱物の粒が集まってる
ってこと。鉱物の大きさがまばらだった火山岩とは違うつくりだね。
この深成岩のように、
等しい大きさの粒が集まってできた状態のつくりのことを、
等粒状組織(とうりゅうじょうそしき)
というんだ。
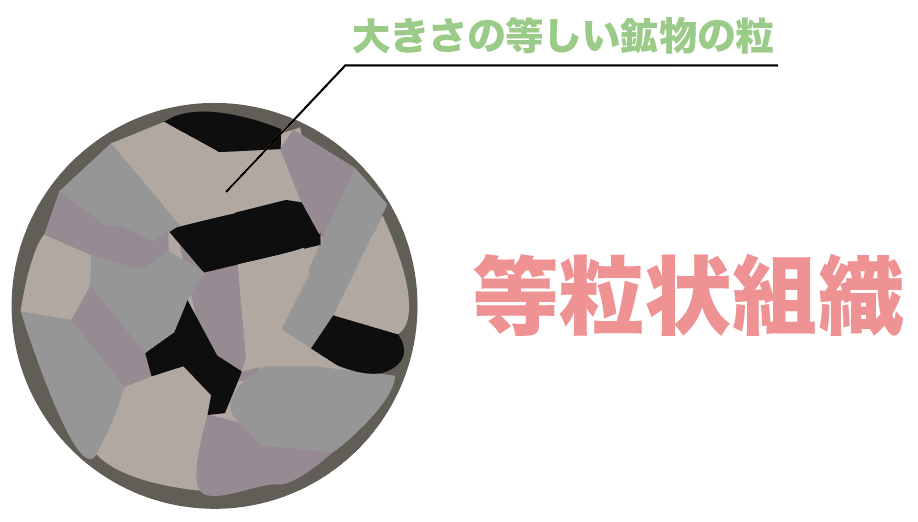
なぜ、深成岩がこのようなつくりになるかというと、
マグマがゆっくり冷えて岩石になるから、マグマに含まれる鉱物が結晶になりやすいんだ。だから大きい粒の鉱物がわんさか混じってるわけ。
中学理科で勉強する深成岩の種類は次の3つ。
深成岩の種類を覚えるのは大変だから次の「深成岩の種類の覚え方」を参考にしてみてね。
以上が火成岩・火山岩・深成岩の違いだったね。
せっかくだから最後にもう一度復習しておこう。
火成岩は「マグマが冷えて固まってできた岩石のこと」で、

火山岩と深成岩はそのうちの一種。

火山岩は「地表に出てきたマグマが急激に冷えた固まってできた岩石のこと」で、

深成岩は「地下の深いところでマグマが固まってできた岩石で、火山が削れたり、大地が上昇すると姿を表すんだったね。

火成岩・火山岩・深成岩の違いを表にまとめてみたよ↓
| 火成岩 | ||
|---|---|---|
| 火山岩 | 深成岩 | |
| 概要 | 地表に出てきたマグマが急激に冷えた固まってできた岩石 | 地下の深いところでマグマが固まってできた岩石 |
| つくり | 斑状組織 | 等粒状組織 |
| 冷えるまでの時間 | 短い | 長い |
| 種類 | 玄武岩 安山岩 流紋岩 | はんれい岩 閃緑岩 花こう岩 |
火成岩・火山岩・深成岩の種類が整理できたら次は「火山の形」もマスターしていこう!
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。トイレ、空いてたね。
中学1年生の理科もいよいよ大詰め。今日から「大地の変化」という単元を勉強していくよ。
山とか石とか岩とかについて習うんだけど、その基礎の基礎として、
というキーワードがものすごく重要になってくる。
今日は、この3つの言葉の意味をさらっと押さえちゃおうね。
まずマグマだ。
マグマとは、
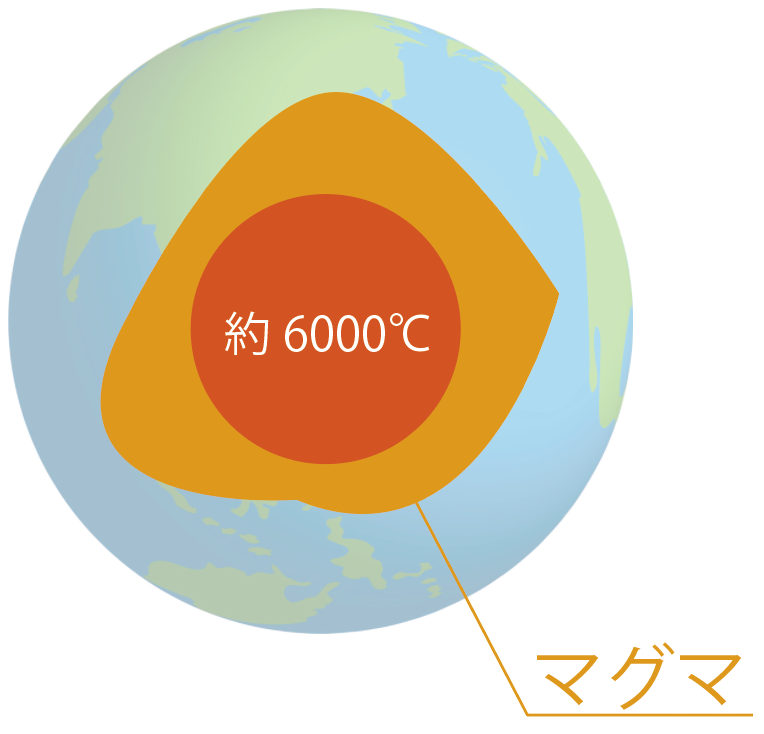
地球内部の熱によって地下の岩とかが溶けたものなんだ。
地球の内部に行ったことないからわからないかもしれないけど、ものすごく熱いらしい。その地球の中心温度はだいたい、
約6,000℃
らしいんだ。

だから、地球の内部の中心に近い岩石たちは熱すぎてもはや固体ではいられず、ドロドロの液体になっちゃってるわけ。

この岩石がドロドロに溶けちゃったものを「マグマ」っていうわけね。
この地球の内部の岩石がドロドロに溶けたマグマたち。
正直行って、行き場はない。
時間が経つにつれて、自分たち以外のマグマたちがどんどん増えて来て、自分の居場所がなくなっていっちゃうね。

ついに、マグマの居場所がなさすぎて耐えきれなくるなると、今度は地球の地表を目指してせり上がってくるようになるよ。
最終的に地表付近の岩石を吹っ飛ばして、地表に水蒸気やマグマ、火山灰などいろんなものを地球の中から外に出すことになる。
この現象を「噴火」というわけね。

噴火すると、地球内部にたまっていたマグマが地表に吹き出してくる。

地球内部から出たマグマが地表にどんどん飛び出して来て、ちょっと山みたいに盛り上がるよね?
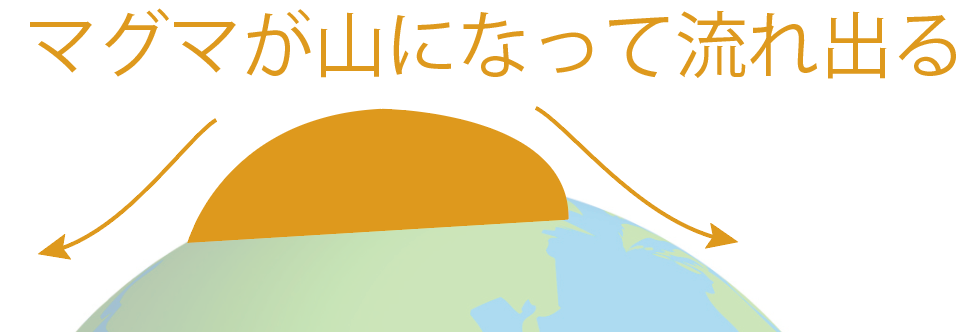
このマグマの山が冷えて固まったものを「火山」というんだ。

以上がマグマ・噴火・火山の基礎だったね。
最後に復習しておこう。
地球内部が熱すぎるから、中の岩石が溶けてドロドロになったものを「マグマ」といい、

マグマが地球内部から耐えきれず地表に吹き出しちゃうことを「噴火」、

地表に出たマグマたちが固まってできてたものを「火山」というんだったね。

これらのマグマの基礎をおさえたら、次は「火山岩・火成岩・深成岩の違い」を勉強してみよう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。ポスト、最高。
中学理科ではいろんな力を勉強していくよね?
水の中ではたらく力とか、バネにはたらく弾性力とか、物体に働く重力とかがあったはずだ。
今日は、もう一歩踏み込んで、
空気中ではたらく力
について勉強していこう。
中でも、
大気圧(たいきあつ)
ってやつを詳しくみていくよ。
まず大気圧とは何かをみていこう。
大気圧とは、
空気中ではたらく圧力のこと
だ。
じつは、空気中にある全ての物体は、空気によって四方八方から圧力を受けているんだ。
空気中にあるものすべてに働いている圧力だから、机の上の消しゴムも大気圧を受けてるし、
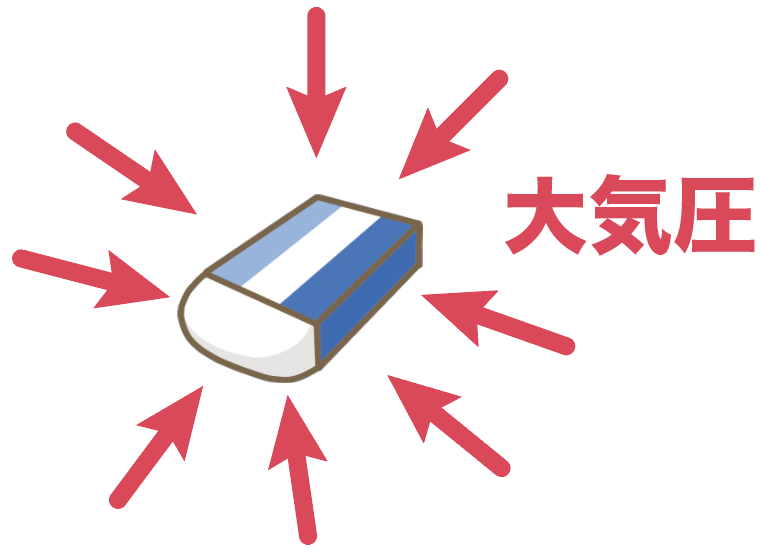
もちろん、この記事を読んでいる君の顔も大気圧を受けているわけだ。

たとえばわかりやすい例として、ここに1つの缶ジュースがあったとしよう。
もちろん、この缶ジュースも空気中にある限り、大気圧を受けてるはず。
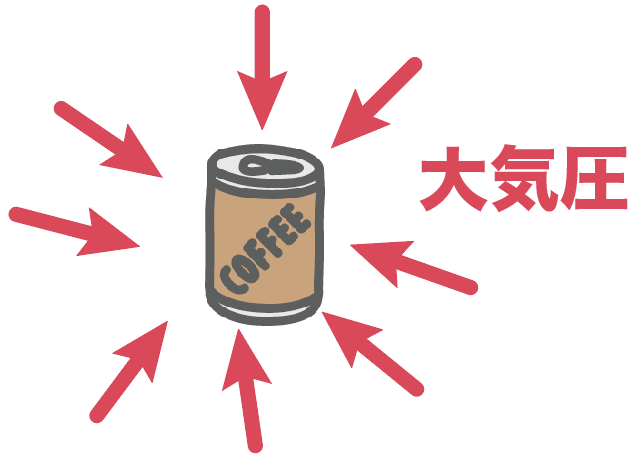
で、この缶ジュースから一気に中身の空気を抜いてしまったとしよう。
このとき、この缶ジュースは大気圧によって潰されてしまうんだ。
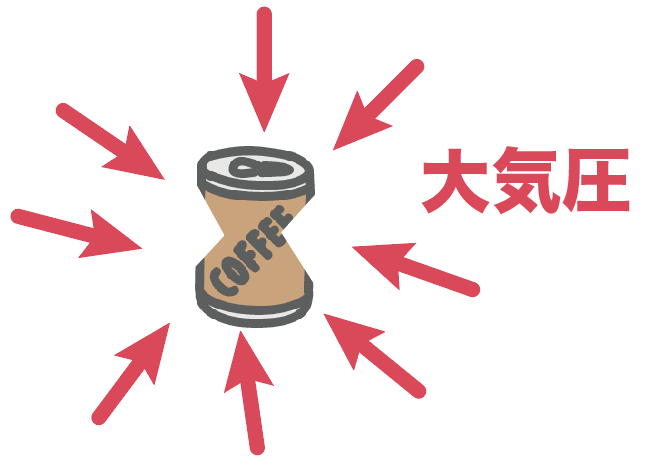
なぜなら、缶ジュースを中から支えていた空気がなくなっちゃって大気圧が0になる。すると、缶の外の空気による大気圧が釣り合わなくなっちゃうわけさ。
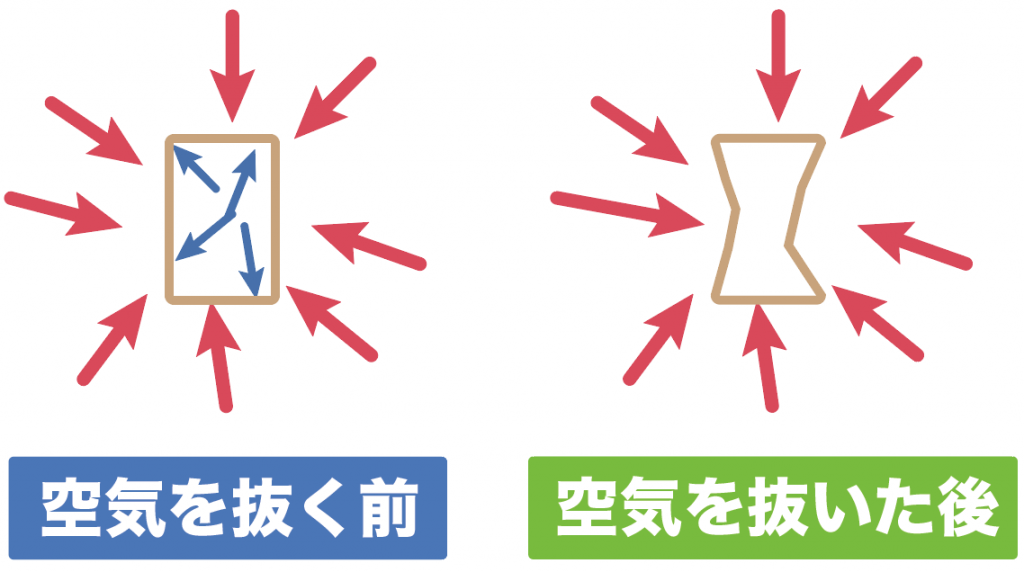
大気圧っていうのは普段は意識しづらいけど、確かに空気中にある全てのものにはたらいている圧力なんだ。
じゃあ大気圧はなぜあるんだろう??
その理由は、
空気の重さにあるよ。
空気は目に見えなくて重さなんてないように見えるけど、じつはちゃんと質量を持ってるんだ。
地球の大気を、海面から上空の空気があるところまで全部足してみよう。
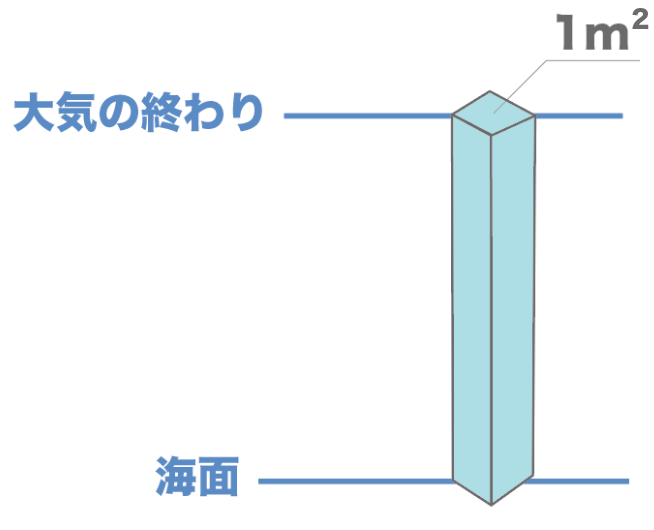
この足した部分の面積を1m²だとすると、その全部足したと時の重さはなんと、
約100,000N(正式には101,325N)
になるんだ。
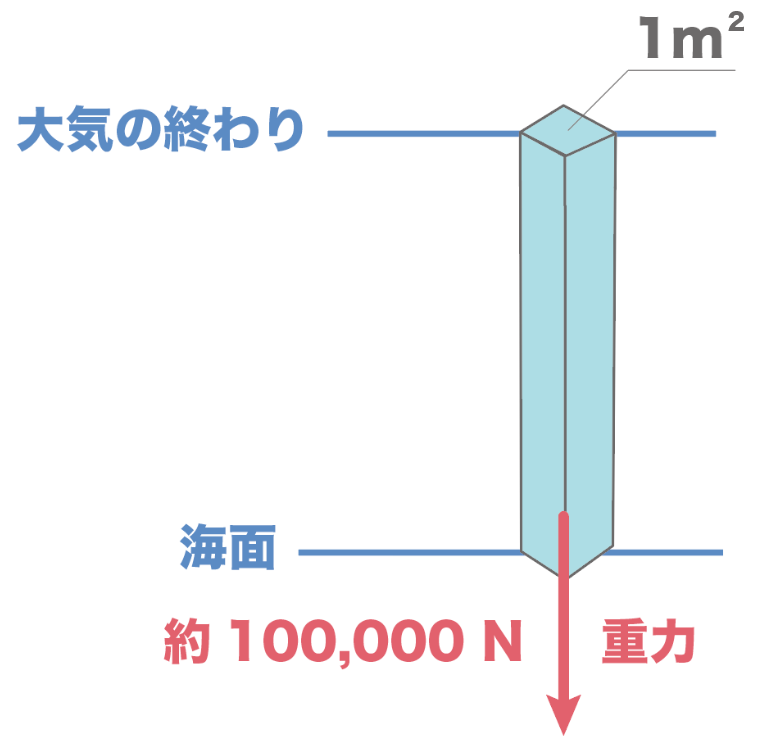
1N(ニュートン)は100gの物体に働く重力と等しかったから、実質、
1m²あたり10,000,000gの物体の重力と同じぐらい力がかかってるはずなんだ。
10,000,000gは10,000kgのことで、さらに上の単位で現すと、
10トン
ってことになる。
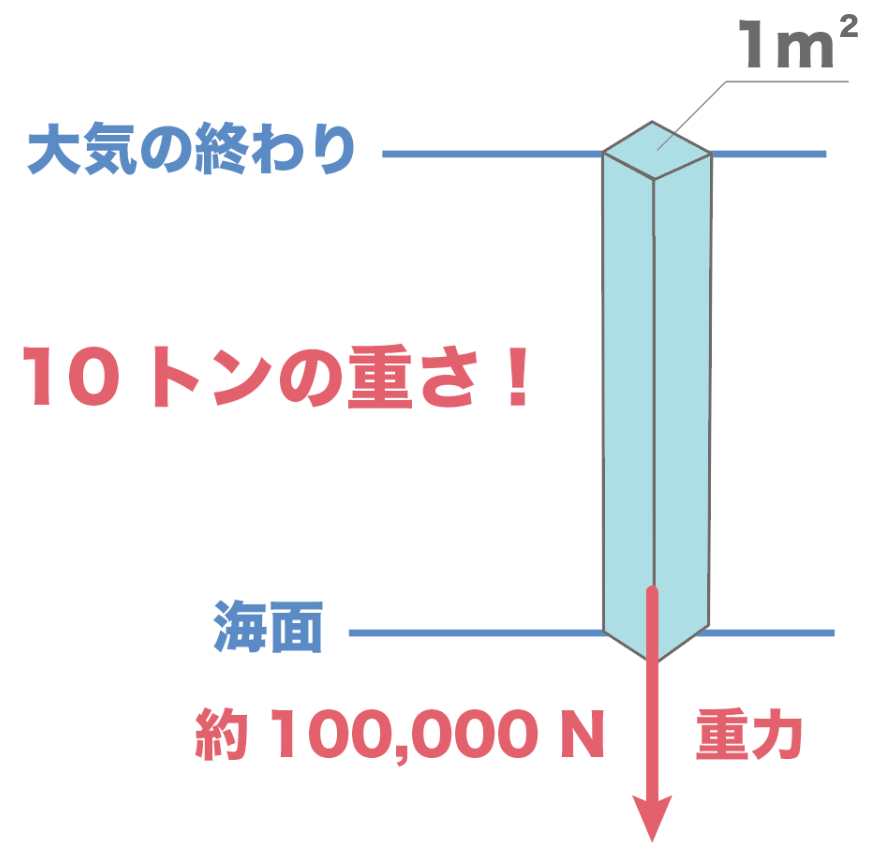
1m²あたり10トンの物体がのっているのと同じ力が大気の重さにあるなんて信じられないぜ!
大気圧は空気の重さが原因ってことがわかった。
上に行けば行くほど、のしかかってくる空気の量が少なくなるから、大気圧が小さくなるんだ。
たとえば、海で泳いでいる時に受ける大気圧と、富士山に登った時の大気圧を比べると、圧倒的に富士山に登った方が大気圧は小さい。
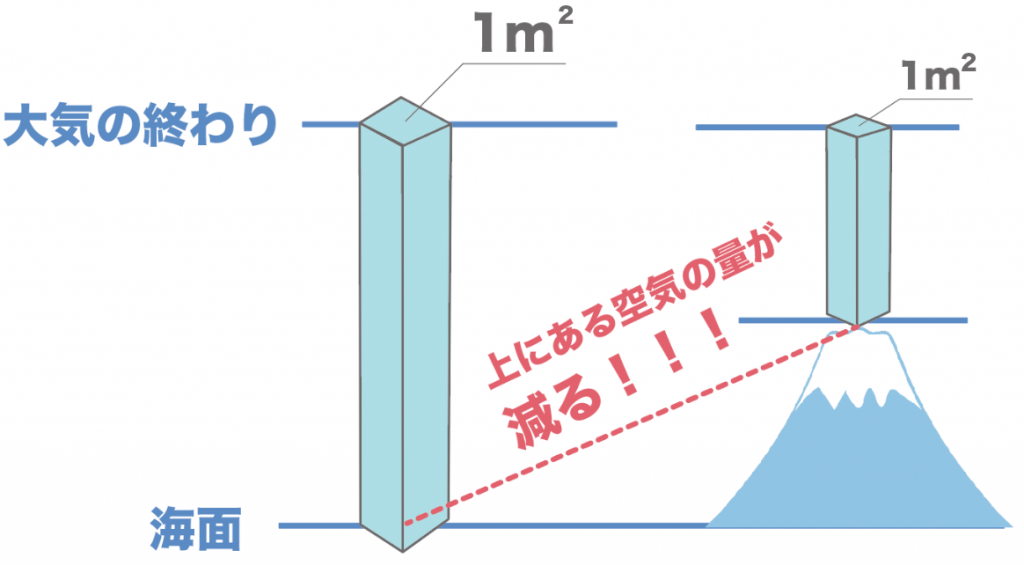
なぜなら、富士山の高度は高いから、上にある空気の量が少なくなるからね。
富士山に地上で購入したポテトチップスを持って行くと、袋が膨らんでしまうのはこのためだ。

ポテトチップスの袋の中の空気(地上のもの)の大気圧の方が、富士山頂上の大気圧より大きいからね。
1大気圧は、1m²あたり約100,000N(正式には101,325N)の力がかかってるんだったよね?
これを圧力の単位に直してやると、
100,000 [Pa(パスカル)]
になるね。
「パスカル」という単位をちょっと復習しておくと、
1パスカルは1m²あたりにはたらく1Nのこと
だったね。
※ 圧力を忘れかけているときは「圧力の求め方」を読んでみてね。
でも天気予報をきいてると、大気圧の単位は、
ヘクトパスカル [hPa]
であることに気づかない?
たとえば台風のニュースなんかで、
中心の気圧は970ヘクトパスカル 最大風速は30メートル、 最大瞬間風速は40メートルが予想されます。
なんて感じで登場しているよね。
これはどういう単位なのかというと、
1hPa(ヘクトパスカル)= 100Pa
のこと。100パスカルが集まれば1ヘクトパスカルに進化できるわけだ。
じゃあなぜ気象情報でヘクトパスカルを使うようになったのか??
これはちょっと話が長くなるけどまとめておこう。
昔々、気象業界では大気圧の単位でバール(bar)というものを用いていて、
1大気圧= 1 bar
という単位だったんだ。
ただ、気象情報で使う大気圧としてはbarだとデカすぎるから、それを1000分の1をしたミリバール[mbar]というものを使っていた。
ただ、1990年ぐらいになると、この大気圧の単位を世界で共通している単位(SI単位系)に統一しようとしたわけ。
もともと大気圧の単位で使っていたbarの代わりに、世界共通のPa(パスカル)を使うことにしたんだ。
パスカルの場合、
1大気圧=100,000 [Pa(パスカル)]
だったね。
でも、パスカルを使い始めると、もともと大気圧の単位でミリバールに慣れていた人々が混乱しちゃう。
だから、1ミリバールの単位と同じ数値感で大気圧を語れるように、ヘクトパスカルを使い始めたのさ。
1大気圧=1,000mbar
だったから、ヘクトパスカルを使えばパスカルでもちょうど、
1気圧=1,000hPa
という感じで、ミリバールに単位の大きさをうまく合わせることができたんだ。
ということで、もともと使っていたミリバールという単位に数値感を合わせるために、ヘクトパスカルを使うようになったんだとさ。
以上が中学理科で習う大気圧だったね。
最後に復習しておこう。
大気圧とは、
空気中のすべての物体にはたらく圧力のこと
で、

大気圧は空気の重さが要因となって生じているんだ。

大気圧の単位はパスカルを使うけど、特に気象業界ではヘクトパスカル(100パスカルのこと)を使う慣習があるよ。
テスト前によーく復習しておこう。
以上で中1理科の力の単元は終了。
次はマグマとか岩石について勉強して行こう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。四分音符、だね。
中1理科ではいろんな力を勉強してきたよね??
その中でも今日は、
水中ではたらく力
を勉強していこう。
中学理科のテストに出やすいキーワードは、
の2つ。
まずは水圧だ。
水圧とは、
水中ではたらく圧力のこと
で、水中にある全ての物体はこの水圧というやつをうけているんだ。
たとえば、もし柔らかい風船を水中に深く沈めたとすると、風船はただじゃ帰らせてもらえない。
水圧という圧力を受けてしまうことになり、
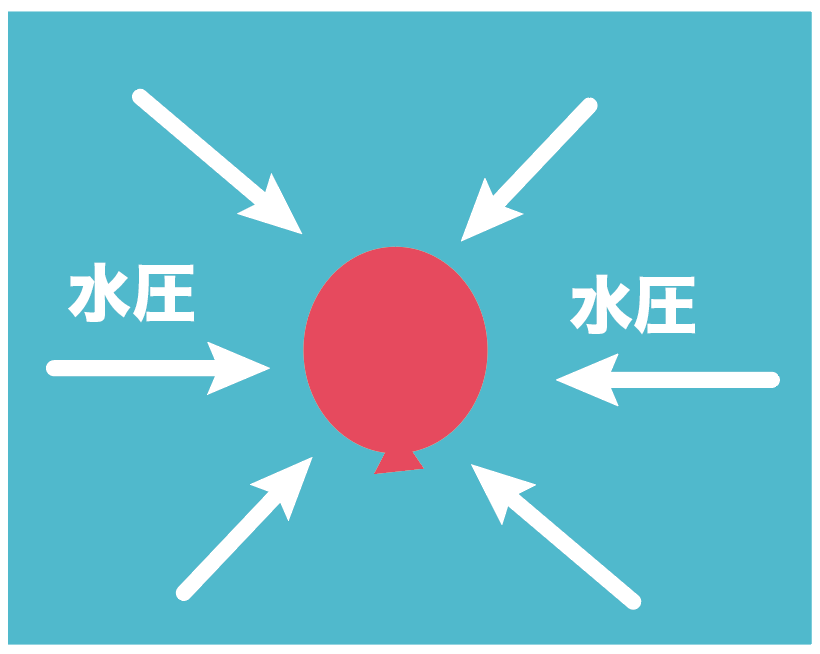
もしかしたら割れてしまうかもしれない。
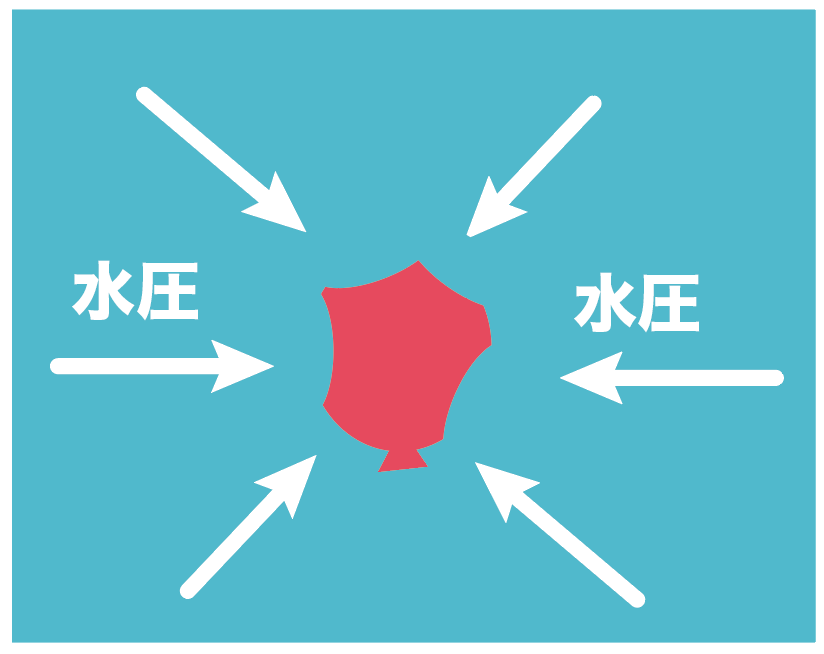
この水圧について押さえておくべきなのは次の4つのポイントだ。
まず、
なぜ水圧が発生するのか??
ということを押さえておこう。
水圧というやつは、
水の中にある物体より上にある水の重力が原因で発生しているんだ。
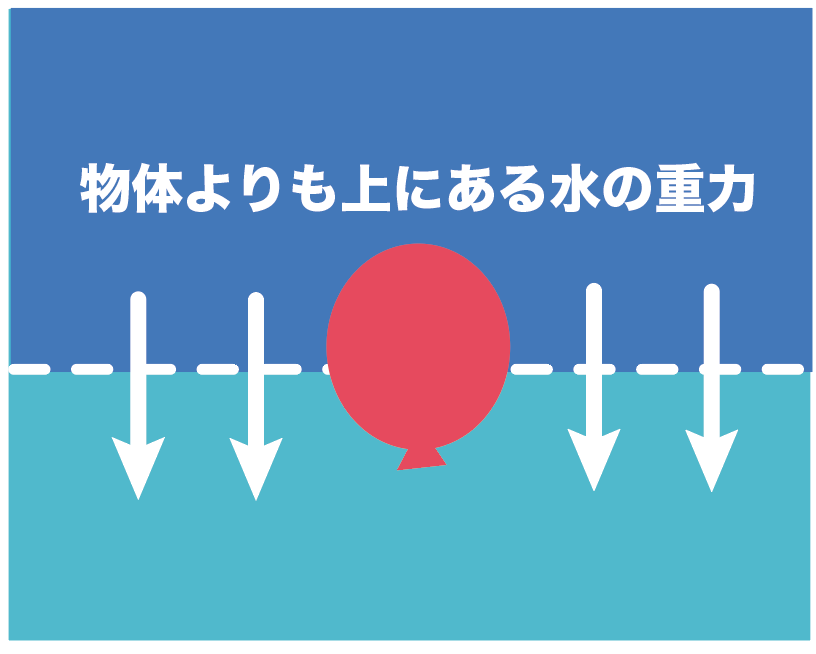
水圧の要因は、水中の物体よりも上にある水の重力ということがわかった。
それがゆえに、
物体が深くにあればあるほど水圧が大きくなるんだ。
なぜなら、物体よりも上にある水の量が増えるからね。
たとえば、水深10mよりも、50mにある物体の方が受けている水圧が大きいってことね。
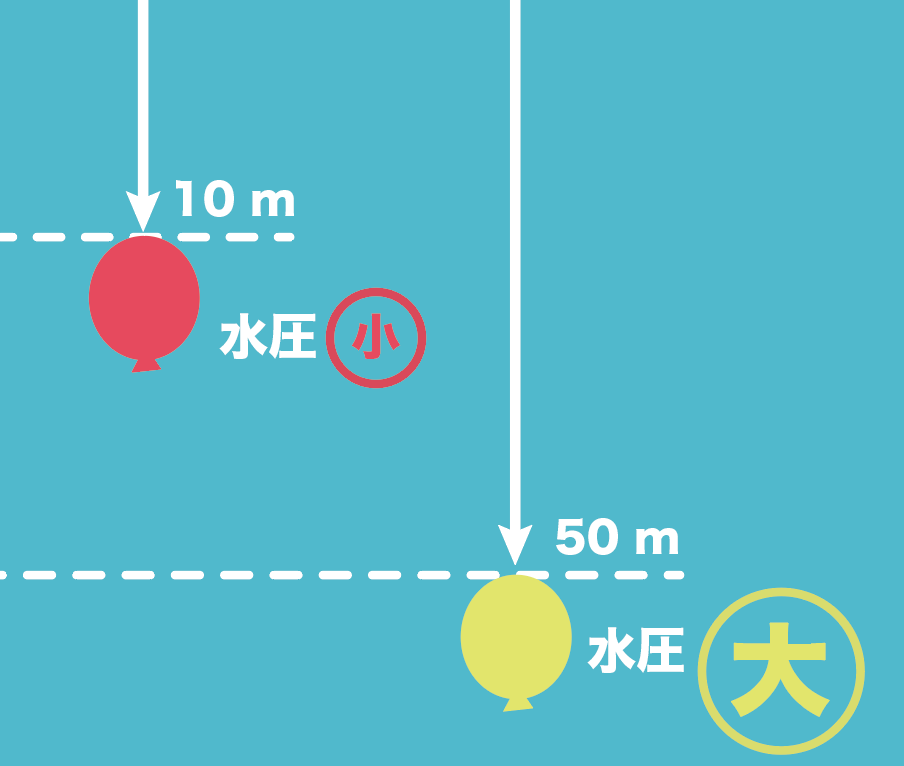
しかも、水圧は1方向から受ける圧力じゃない。
物体はあらゆる方向から圧力を受けることになるんだ。

右も左も上も下も右斜め上も、左下斜めも・・・ね。
深ければ深いほど水圧は大きくなるんだったよね??
ってことは、
物体の上面よりも下面の方が大きい水圧を受けていることになるはずだ。
なぜなら、
物体の上面よりも下面の方が深いところにあるからね。
たとえば、缶ジュースを水の中に沈めたとしたよう。
この時、缶底の方が、プルタブとかある飲み口よりも水圧を受けていることになるわけね。
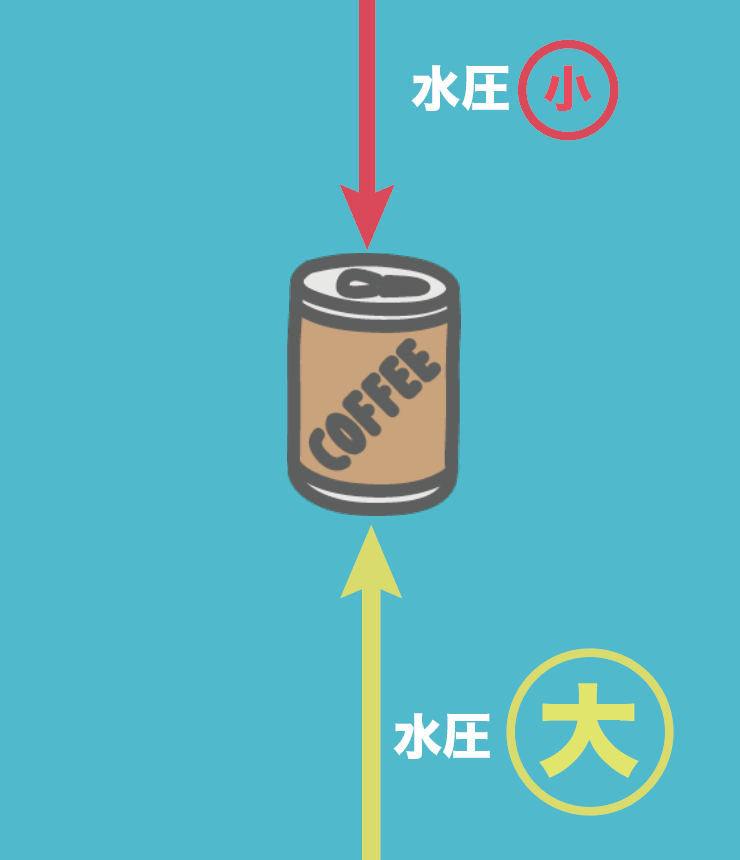
続いては「浮力」だ。
浮力とは、
水中にある物体が上向きに受ける力のこと
だね。
たとえば、ピンポン球を沈めたシチュエーションを想像してみて。

ピンポン球はずっと水中にいられなくて、水上に浮上してきちゃうでしょ??
これはピンポン球が浮力を受けているからなんだ。
それじゃあ、この浮力というやつはなぜ発生するんだろうね?
これはズバリ、
水中の物体に働く上面と下面の水圧の差
だ。
さっき水圧を勉強した時に、
物体の上面よりも下面の方が大きな水圧を受けている
って習ったよね。
つまり、水中の物体には、上からの水圧が押し負けるような下からの水圧が働いているわけだ。

この水中の物体の水圧の差が浮力の正体だね。
ってことは、浮力は物体の形とか大きさによって異なるはず。
たとえば、横にむちゃくちゃ長い物体だったら、水圧の差が働く面積が広くなるから、その分、水圧の差の合計の浮力も大きくなるはず。

また、縦にむちゃくちゃ長い物体だったら、そもそも上面と下面の深さの差が大きくなるから、水圧の差が大きくなるはず。よって浮力も大きくなる。
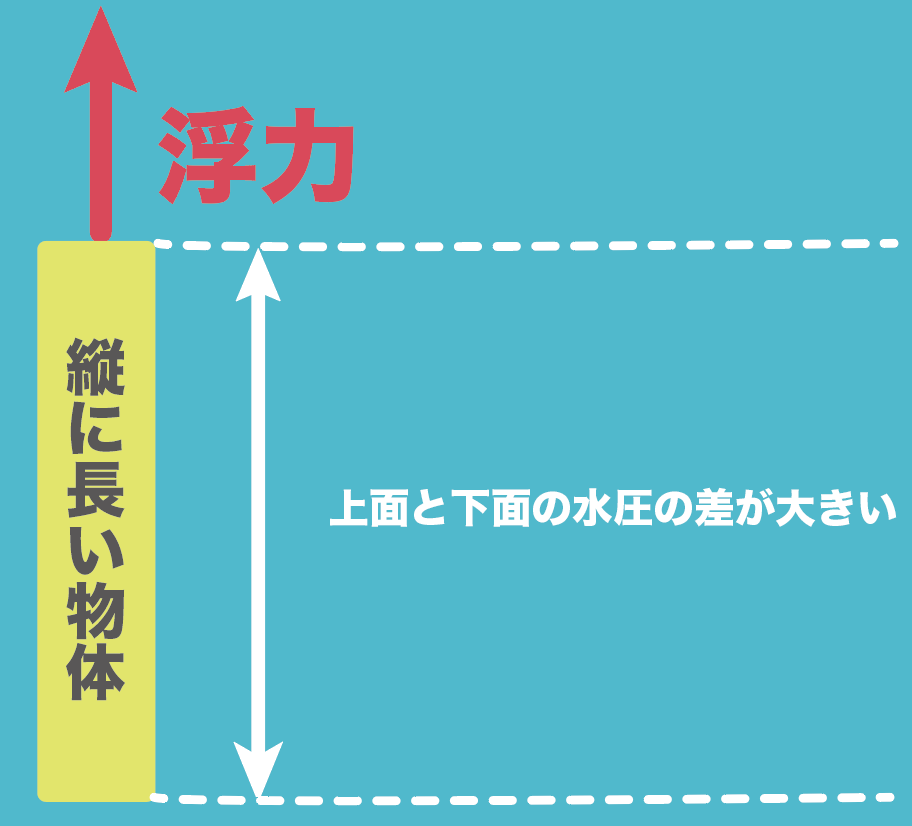
これらのことをまとめると、
物体の体積が大きくなればなるほど浮力が大きくなる
ってことになるね。
じゃあ浮力の大きさはどれくらいなんだろうね??
これはアルキメデスという人がだいぶ昔に発見して知られているアルキメデスの定理というやつなんだけど、
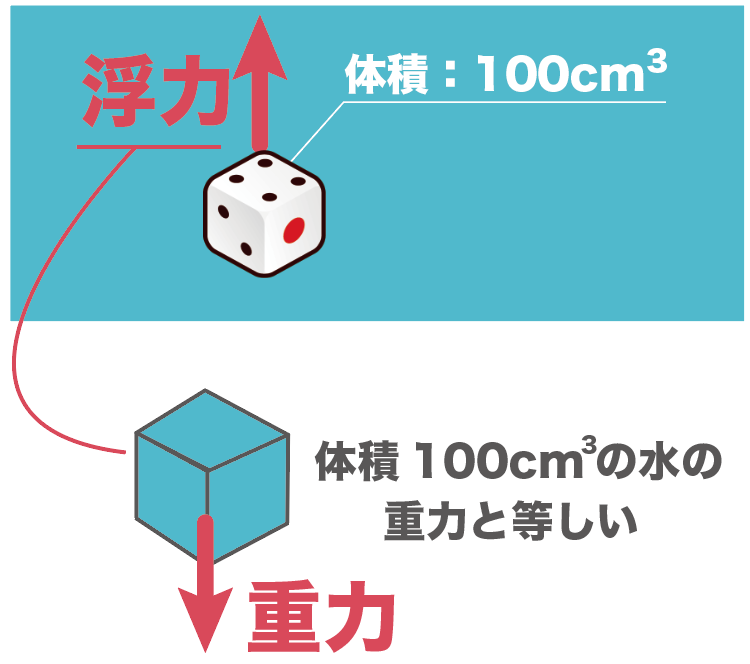
浮力の大きさは、水中の物体が押しのけている水の重力
なんだ。
たとえば、100cm³のサイコロを水に沈めたとしよう。
このサイコロが受ける浮力は、サイコロが押しのけてしまった100cm³の水に働く重力に等しいってことだね。
経験でなんとなくわかってると思うけど、
水中の物体は浮かんでくる奴もいれば、沈む奴もいるよね?
たとえば、ピンポン球を水中に沈めてもうかんできちゃう。

だけど、鉄の玉を水中に沈めたら浮かび上がってことない。

二つとも浮力を受けているはずなのにこれはどうしてなんだろうね??
じつは、浮かび上がるか上がらないかは、
水中の物体に働く重力が浮力よりも大きいかどうか
によって決まってくるんだ。
もし、物体に働く重力が浮力よりも小さいときは、浮かび上がってきちゃう。

逆に、物体に働く重力が浮力よりも大きいときは、沈みっぱなしだ。
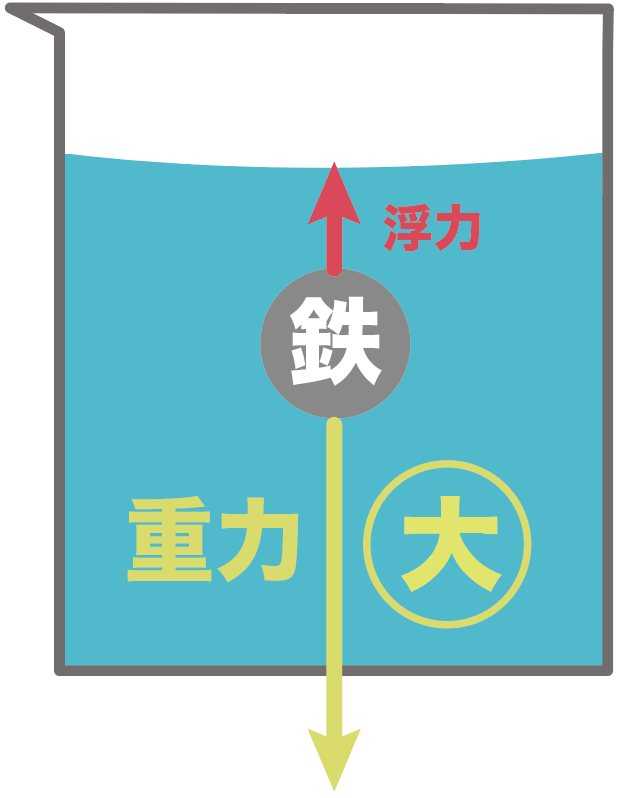
つまり、
水の密度よりも小さい密度を持つ物体は浮力で浮かんできちゃって、
水の密度よりも大きい密度を持つ物体は沈みっぱなしなんだ。
同じ体積で見た時に、水の方が重ければ(水の密度よりも小さい)、浮力が大きくて浮かび上がって、その逆はまあそういうことなのだ。
密度を忘れちゃったら密度の求め方を復習してみてね。
以上が水圧と浮力についての基礎だったね。
最後に忘れないうちに復習しておこう。
水圧とは、
水中ではたらく圧力のこと
で、水中の物体は四方八方から水圧を受けていて、深ければ深い位置にある物体ほど水圧が大きい。

浮力とは、
水中にある物体の上面と下面にかかる水圧の差によって生じる力のことで、
水中の物体の体積が大きければ大きいほど浮力は大きいんだ。

水圧・圧力をマスターしたら今度は空気中ではたらく「大気圧」を勉強していこう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。ハンバーグ、うまいね。
中1理科の「身のまわりの現象」で力について勉強してきたよね?
今日はちょっと心を入れ替えて「バネ」に注目してみよう。
バネに働く力と、バネの伸びの関係を表した法則に、
フックの法則
というものがあるんだ。
これは、
バネの伸びは、バネを引く力の大きさに比例する
という法則だよ。
数学で勉強した「比例」を思い出してほしいんだけど、バネの伸びと引く力の関係が比例ってことは、
バネに2倍の力が働いたら、バネの伸びも2倍になるし、
バネに10倍の力が働いたら伸びも10倍になるってことなんだ。
バネの働く力を横軸、バネの伸びをy軸にとったグラフを書いてみると、こんな感じで原点を直線になるはずね。
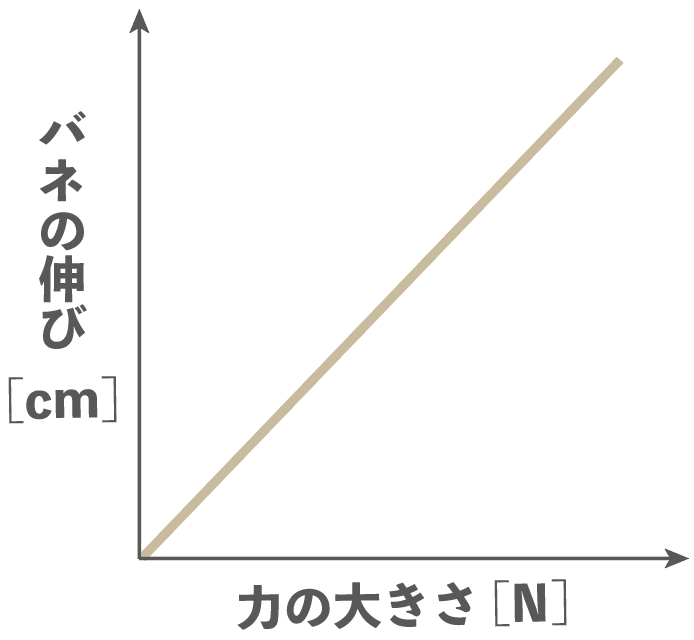
「比例のグラフのかきかたを忘れたぜ?」
って時はQikeruの記事で復習してみよう。
ウンウン。だいたいフックの法則はわかった。
だけどさ、
一体、このフックの法則はどういう風に役立つんだろう??
「何でこんな法則を中学理科で勉強しないといけないんだよ!?」
ってキレそうになってるやつもいるかもしれない。
じつはこのフックの法則がすごいところは、
バネの伸びから、バネにはたらいている力の大きさがわかるようになったことだ。
例えば、こんな感じでバネに力を加えたとしよう。
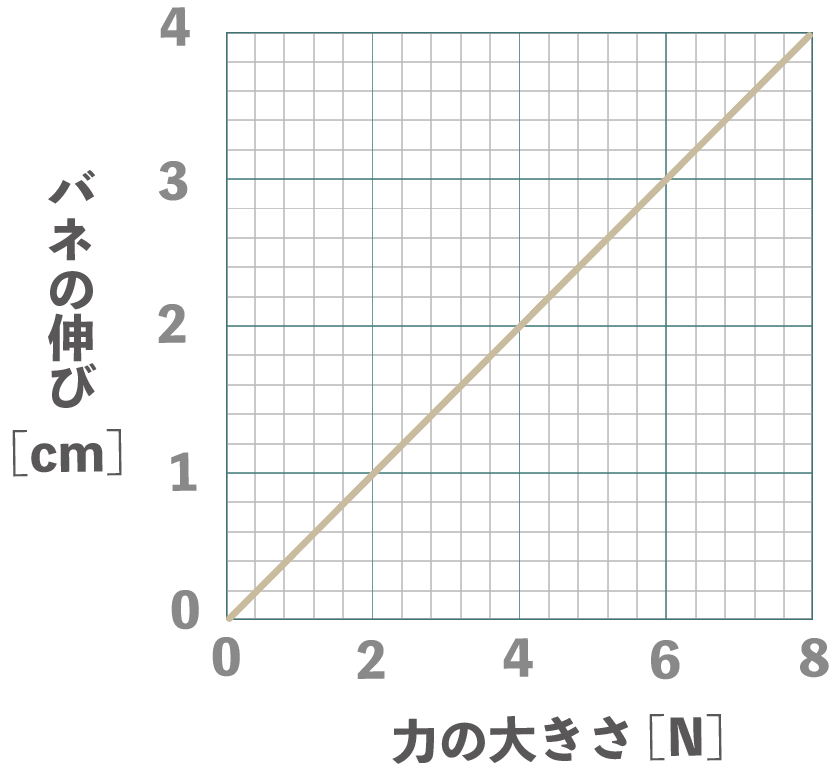
もし、バネの伸びが2cmになったら、このバネにどれくらいの力が加わってるんだろうね??
この時、バネの伸び2cmに当たる力をグラフから読み取ると・・・・
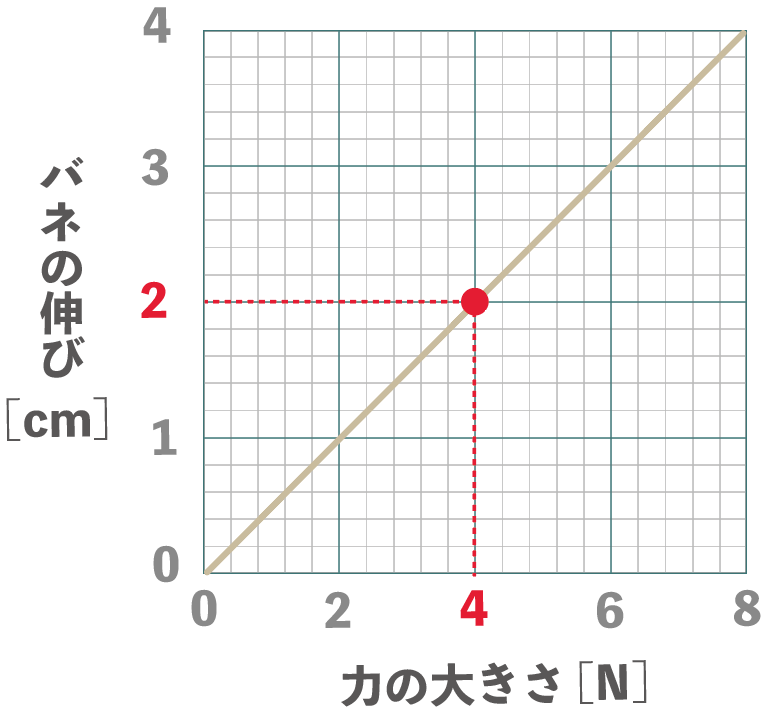
ほら!
4N
がはたらいてるってわかるでしょ?
これを応用したのが「バネばかり」というアイテムだ。

バネの先に重さを測りたいものを吊るしてみると、バネばかりにはたらいた力がわかるんだ。
その力は、バネに吊るした物体の重力のこと。
ここから逆算して物体の重さがわかるってわけ。
ここまででフックの法則の基本と、その応用例まで完璧だね。
この記事の最後に、中学理科の定期テストに出やすいフックの法則に関する問題を解いてみよう。
2つのバネAとBにそれぞれ重りをつるしてみた。この時、バネAとBにかかった力とバネの伸びの関係は次の表のようになりました。
| バネA | 伸び [cm] | 2 | 4 |
|---|---|---|---|
| 力の大きさ[N] | 2 | 4 | |
| バネB | 伸び [cm] | 1 | 2 |
| 力の大きさ [N] | 2 | 4 |
まずはバネの伸びと力の表から、グラフをかいてみよう。
書き方は簡単。
たとえば、バネAなら、力の大きさが2Nのとき、バネの伸びは2cm、
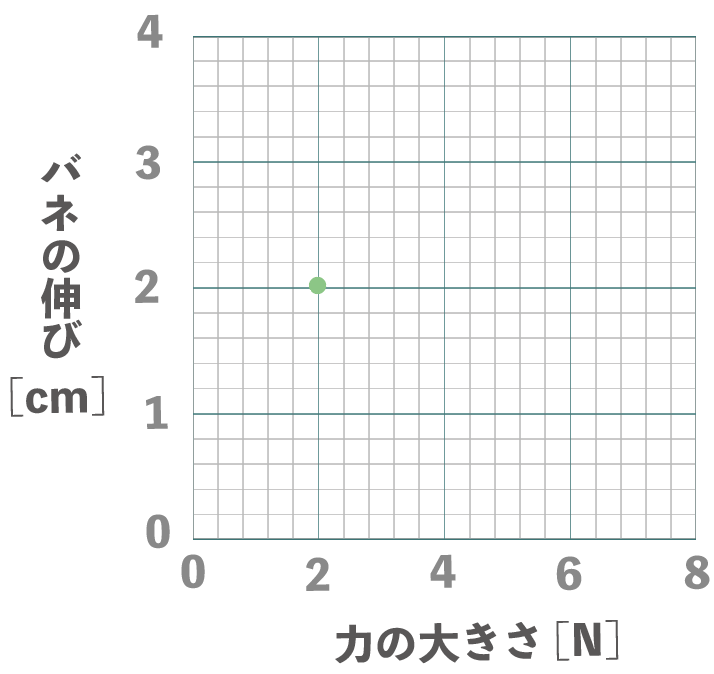
力の大きさが4Nのとき、バネの伸びは4cmだ。
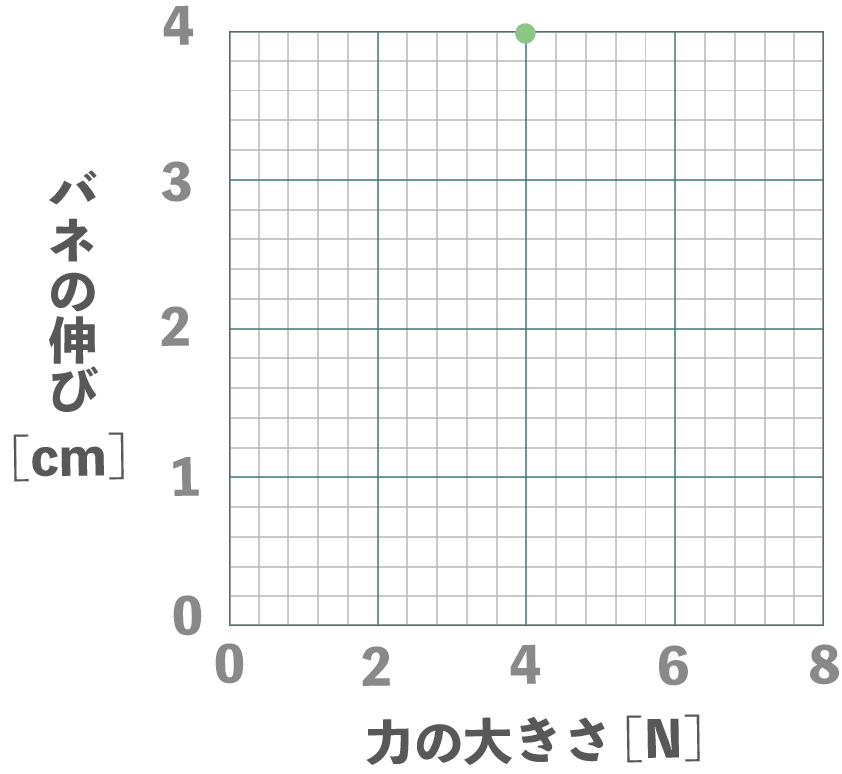
こんな感じで最低でも2つの点を打てればオッケー。あとはこの2点を直線で結んであげよう。
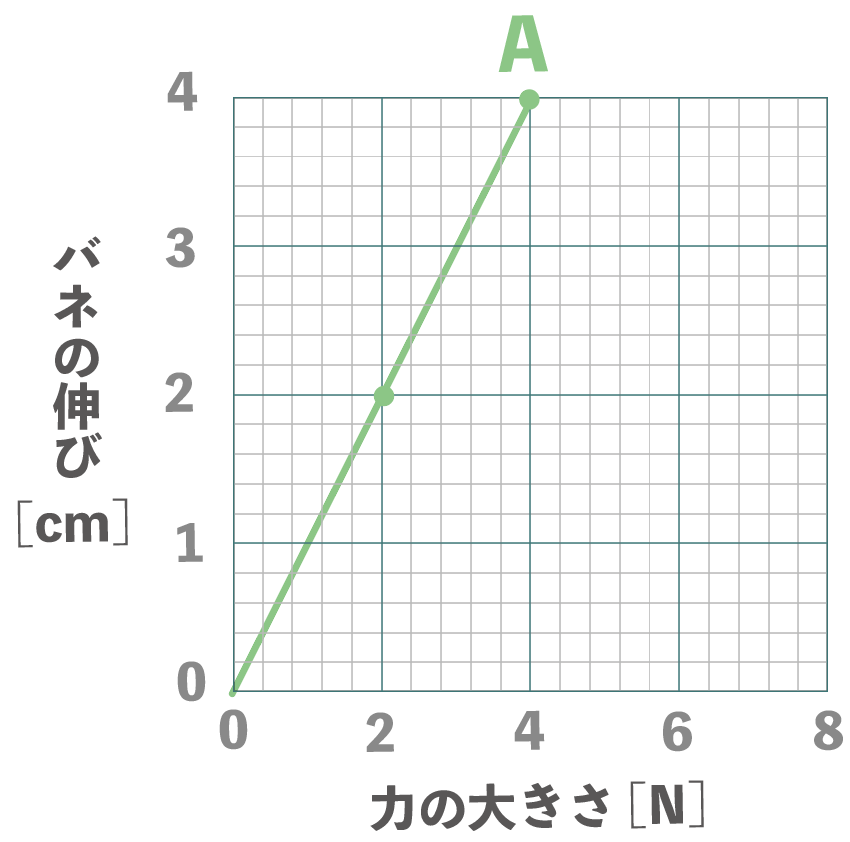
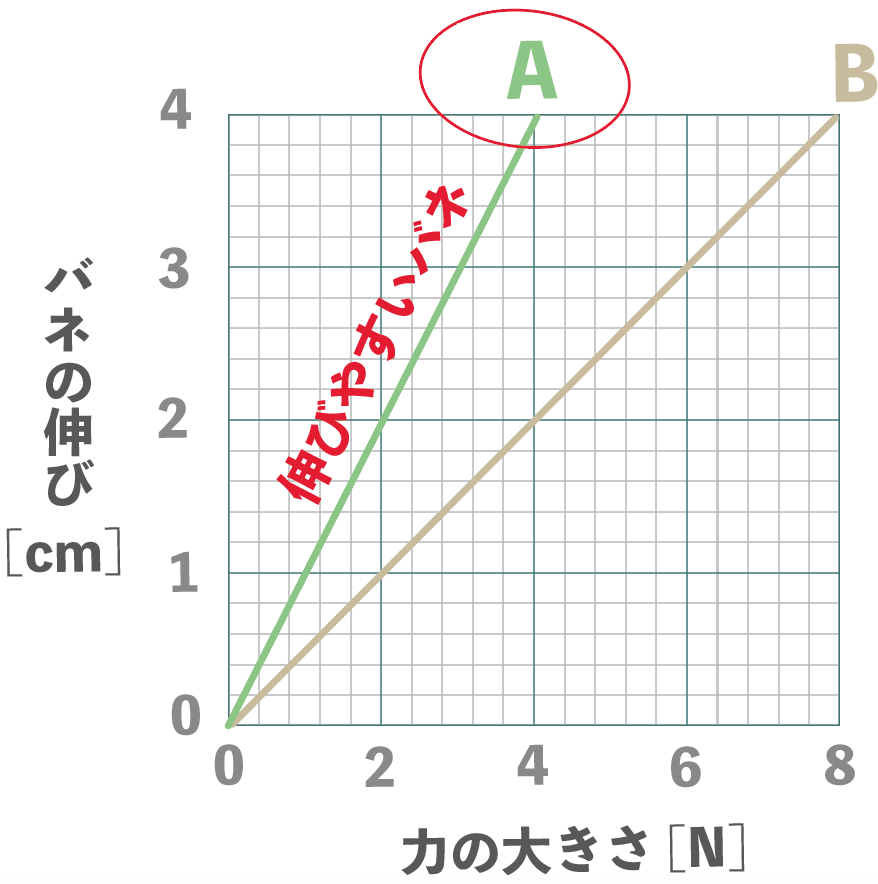
バネBも同じようにグラフを作ってやると、最終的にこんな感じになるはずだね↓↓
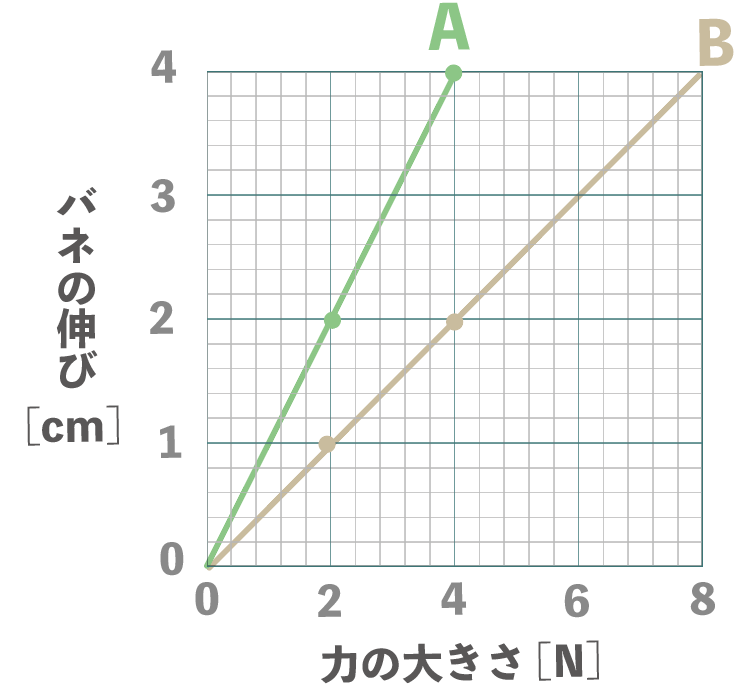
バネの伸びは、バネに働く力が大きくなればなるほど大きくなってるね。
しかも、バネに働く力が2倍になれば、伸びも2倍になってる。
こういう関係のことを数学では、
比例(ひれい)
と呼んでいたね。
このバネの伸びと力の関係を理科では「フックの法則」と呼んでいるんだ。
3つ目の問いできかれているのは、
バネBに8Nの力を加えた時にどれくらいの伸びるのかってことだ。
つまり、バネに働く力の大きさから、バネの伸びを計算しろと言ってるね。
この手の問題は、最初に作ったグラフを見てやればいいね。
横軸のバネに働く力が8Nの時、縦軸がどうなってるのか追ってみると、
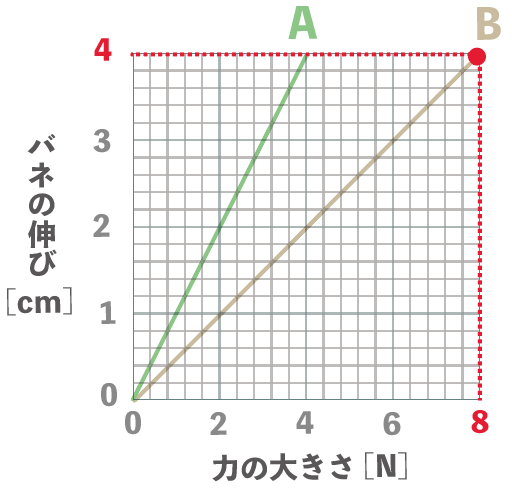
うん。
4cm
になってるね。
ってことで、バネBに8Nの力を加えた時には4cm伸びるんだ。
今度は問3の逆。バネの伸びからバネに働いている力を求めればいいんだ。
この問題もグラフを使って読み取っていくよ。
問いでは、
バネAを3cmのばすときの力
がきかれてるから、バネAのグラフの縦軸のバネの伸びが3cmの点を見つけてあげて、その時の横軸の値を確認してあげる。
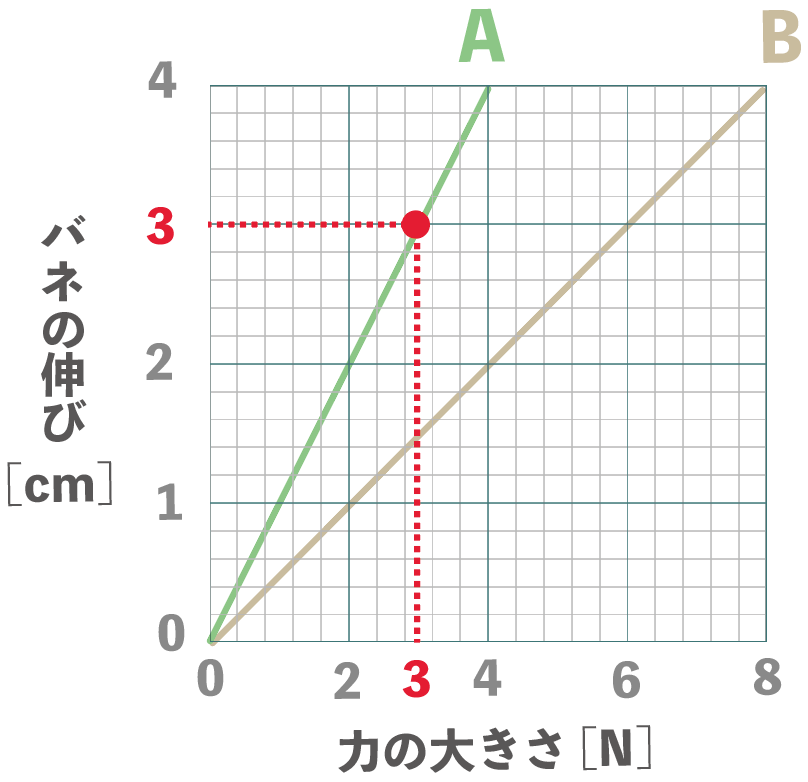
すると、うん、
3N
になってるね。
最後に、バネの伸びやすさについて。
伸びやすいバネのグラフは急になってるはずだ。
なぜなら、グラフが急になっていると、バネの力が増えた時に、同時に伸びが大きくなりやすいってことだからね。これはつまり、伸びやすいバネってこと。
練習問題でいうと、ばねA のグラフの方が急だから、伸びやすいのバネAだ。
以上がフックの法則の基礎と問題の解き方だったね。
最後にもう一度復習しておこう。
フックの法則とは、
の関係を表したもので、この2つは比例の関係にあるんだ。
フックの法則を使うと何が便利かっていうと、
バネの伸びから、そのバネに働く力の大きさがわかるってことだったね。
フックの法則をマスターしたら、水の中で働く力の、
水圧・浮力について勉強していこう。
そんじゃねー
Ken
こんにちは!この記事を書いてるKenだよ。布団、強いね。
中1理科の身のまわりの現象では「力」について勉強してきたよね。
などなど。
ただ、実際のテストには、
「物体に働く力を作図しなさい!」
って問題がよく出てくるから、今日はその作図問題で役に立つ、
力の表し方
を勉強していこう。
理科の世界では力を「矢印」を使って表していくよ。

力を矢印で表すとき、次の3つのポイントさえ押さえておけばいいんだ。
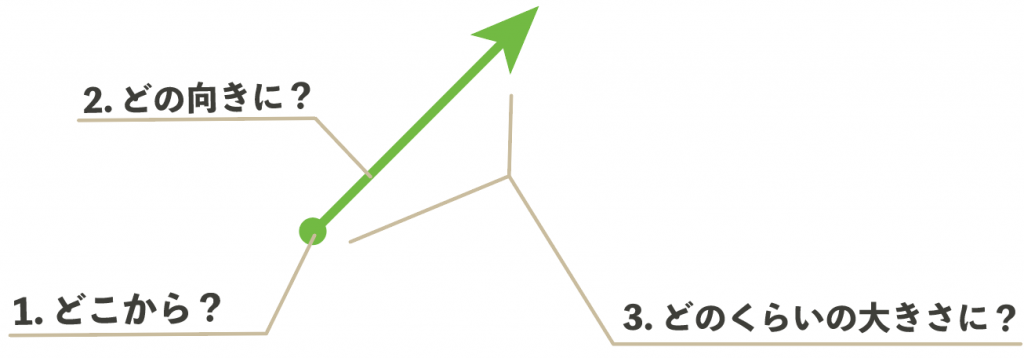
つまり、力の矢印をどこからかいて、
どの向きにむけ、
どのくらい伸ばすかがポイントってわけさ。
力の表し方のうち最も基本的な、
力のはたらく点
だね。
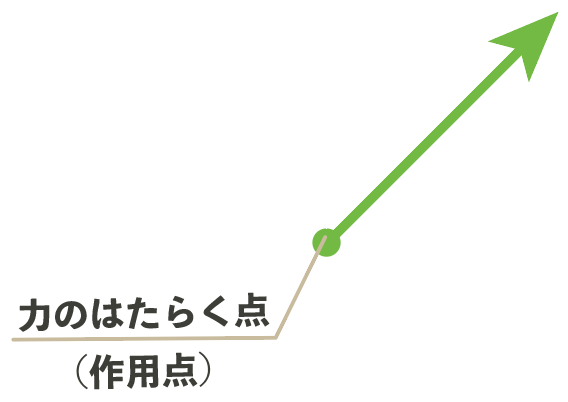
巷ではこれを「作用点(さようてん)」とも呼んでいるね。
つまり「力の矢印をどこからかくのか」って話だ。
たとえば、机の上の消しゴムを指で押したシチュエーションを考えてみよう。

左から消しゴムを押すと、消しゴムと指が接してるとこから力が始まるはずだね?
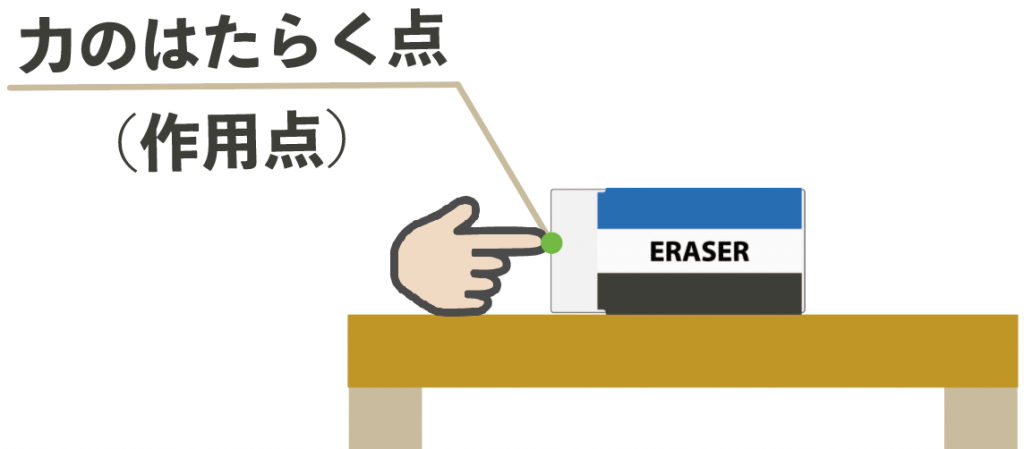
逆に右からだったら右側、
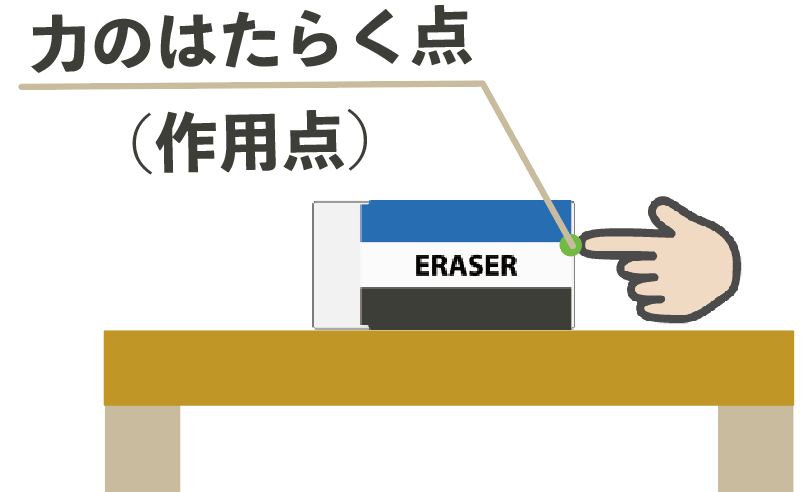
上からだったら上から力が始まるはずだ。
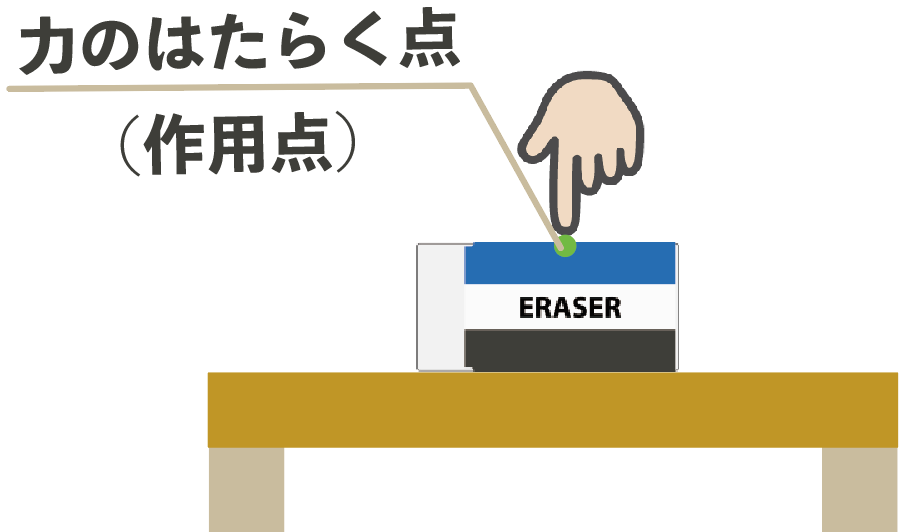
じゃあ一旦、消しゴムの左サイドから力を加えることにしたとしよう。
つぎは、
力をどの向きに働かせるのか?
が重要になってくるよ。
たとえば、机の面に平行にゆっくりとおしたとすると、こんな感じになるし、

消しゴムを下から突き上げるように、力を働かせてやると、こんな感じの力の向きになるはずだね。
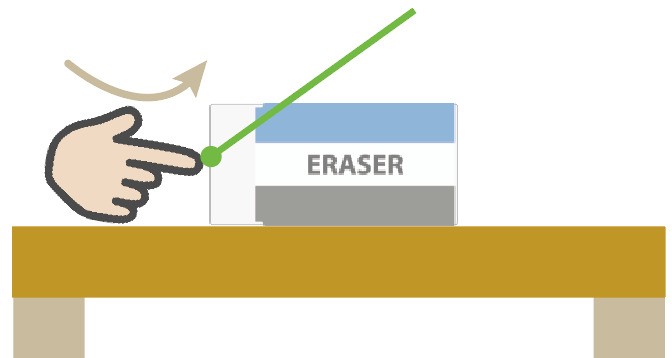
最後は力の大きさだ。
力の表し方の矢印でいうと、
どれくらい矢印を伸ばしてやるのか?
ってことになる。
たとえば、消しゴムをそこらへんの小学生がデコピンしたとしたら、このくらいの力の大きさかもしれないけど、
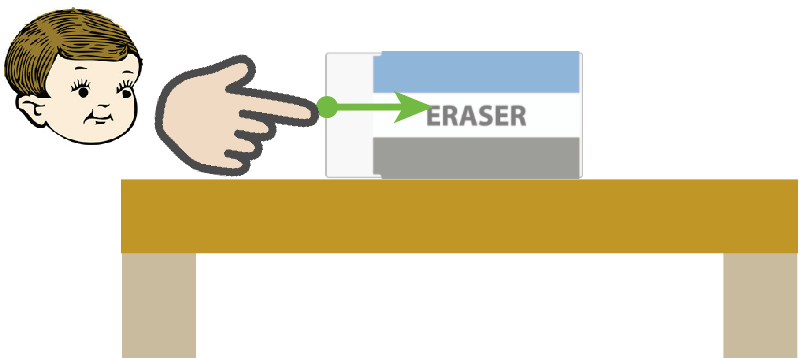
じゃあ力士がデコピンしたらどうなる?

そう。そうだよ。
小学生よりも大きな力で消しゴムに力を及ぼしているはずだ。
力の大きさは「矢印の長さ」で表すから、力士の時はこれぐらいに力の矢印の長さが長くなるはず。

以上が力の表し方のポイントだよ。
の3つのポイントを押さえて、力を矢印で表現していくんだ。

力の始まりに点をうって、

力の向き決めて、

最後に大きさを矢印の長さで表現するっと。

これで力の表し方もマスターしたね。
次は力の作図問題と同じくらい狙われやすい「フックの法則の問題」にチャレンジしてみよう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。目頭、あついね。
ここまで力の種類とか力のはたらきとかをみてきたんだけど、もっと重要な
力の単位
について今日は勉強していこう。
重さの単位はg(グラム)、距離の単位はm(メートル)っていう感じでそれぞれに大きさを把握するための単位があると思うんだよね。
力の単位は、
ニュートン(N)
というものを用いるよ。
今日はこの力の単位の正体を一緒に暴いていこう。
教科書のニュートン(N)の説明を見てみると、
100gの物体にはたらく重力の大きさにほぼ等しい
って書いてあるね。
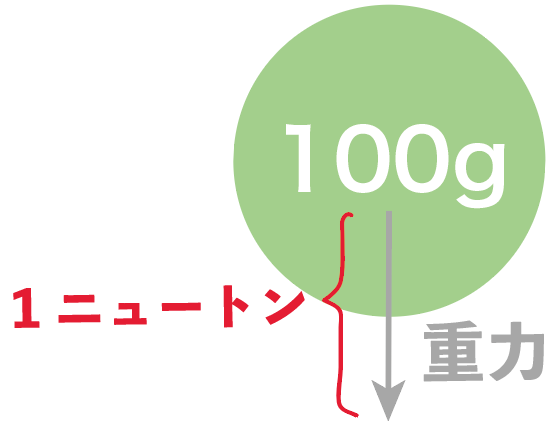
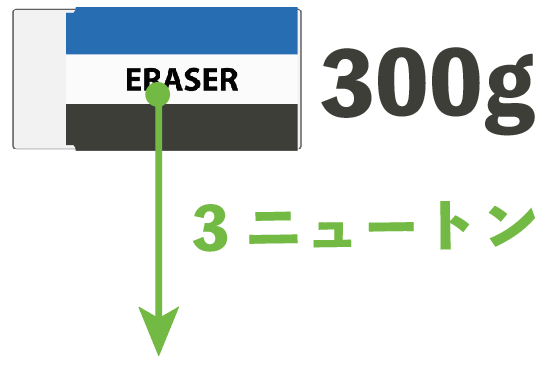
たとえば、300gの消しゴムがあったら3Nの重力が働いていることになるし、
10,000g ( =10kg) の机があったら、この机に働く重力は100Nってわけだね。
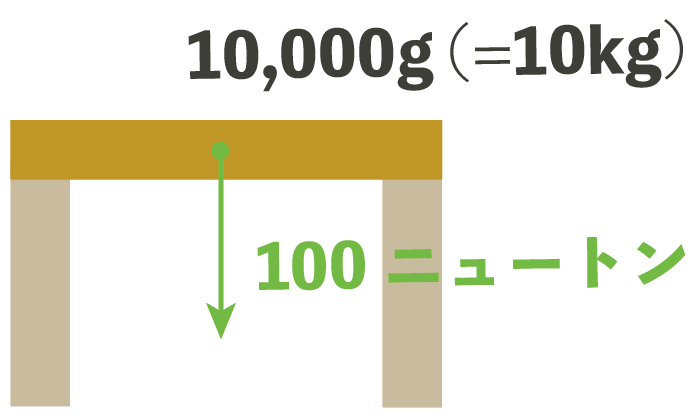
物体に働く重力のニュートンを求めたい場合は、質量を100で割ると計算できるってわけだ。
がしかし、だね。
なぜ、100gの物体に働く重力が1ニュートン(N)になるんだろうね??
教科書にはくわしく書いてないし、はぐらかされてる感がする。
そこで今日はこれがなぜなのかを少しばかり暴いていこう。
まず、正確にニュートンとはどういう単位なのか?
を見ていこう。
Wikipediaによると、
1キログラムの物質に1m/s² の加速度を生じさせる力
とあるね。
つまり、質量1kgの物体に力を加えると、
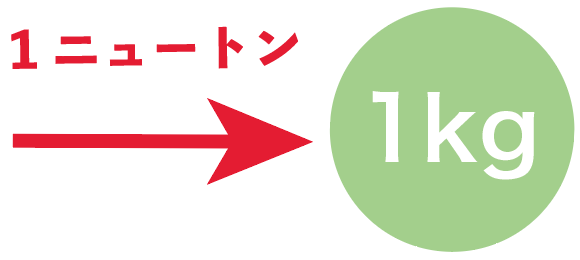
1秒間に毎秒1mの速さずつ加速するような力
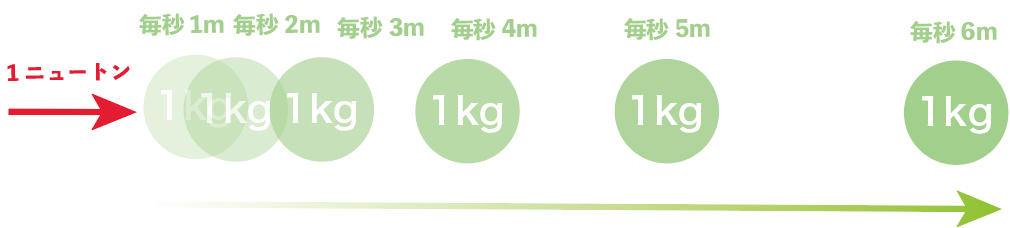
ってことさ。
ちなみに、この力・質量・加速度の関係をニュートンの第一法則と呼ぶよ。
ここで、物体に働く重力が、物体にどれくらいの力を及ぼしているのかを見てみよう。
重力は、地球上にあるものたちに、1秒間に、
9.80665 m / s
の速さずつ加速させるような力をおよぼしてるよ。
これは約、
10 m / s2
だ。
つまり、地球の中心に向かって1秒間あたり、毎秒10mの速さずつ速くなるってことさ。
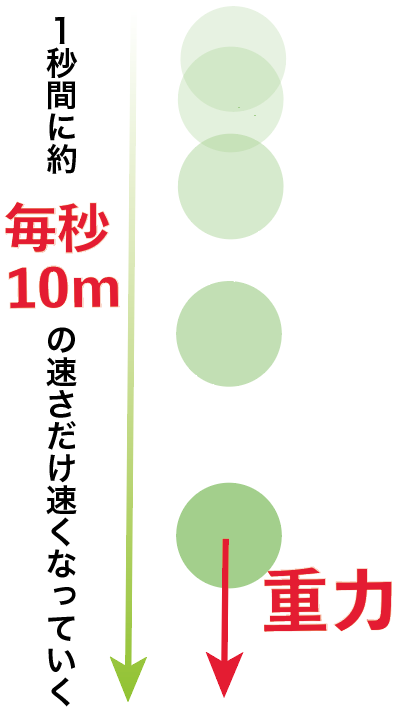
ここで力の単位ニュートンの定義に戻ろう。
ニュートンは、
1kgの物体に1m/s²の加速度を与える力
だったよね。
重力の場合、地球上にあるものは約10m/s²の加速度を生じさせているから、
1kgの物体の重力は10Nになるね。
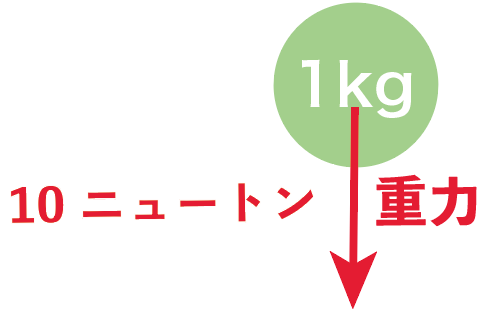
だから、質量を10分の1の0.1kg(=100g)にしてやれば、力もその10分の1の「1N」になるのさ。
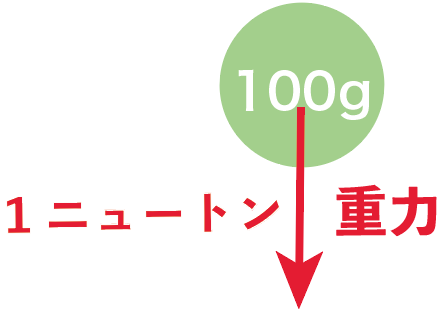
したがって、
1ニュートンは「100gの物体に働く重力と等しい」ということができるんだ。
以上が力の単位ニュートンだね。
色々グダグダ言ってきたけど、中学理科では、
100gの物体に働く重力の大きさが1ニュートン
と覚えておけば大抵の問題を計算できるはずだ。
物体の質量[g]を100で割れば力の大きさ[N]が計算できるってわけね。

基本を押さえて、かつ、なぜそう言えるのかまで押さえておけば完璧だね。
力の単位をマスターしたら次は力の表し方を勉強してみよう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。タイカレーで復活だね。
中学理科では力について勉強していくんだけど、まず覚えなきゃいけないのが、
力の種類
だ。
「身のまわりにはどんな力の種類があってどのようなはたらきをしているのか?」
これを押さえておけばテストでビビることはないね。
中学理科で勉強する力の種類は次の6つだ。
まずは垂直抗力(すいちょくこうりょく)という力だ。
これはどういう力かというと、
静止している物体が、接している面から受ける垂直で上向きの力のこと
だね。
たとえば、消しゴムが机の上で静止していたとしよう。

この消しゴムは、机を垂直に上から押しているよね?
こんな感じで力が働いてるはずだ。
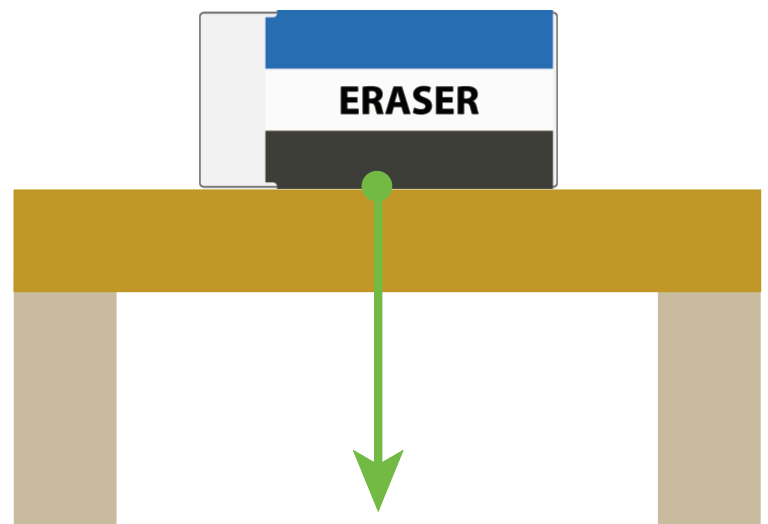
しかし、だよ?
こんなに消しゴムから机に対して押す力が働いているのに、机は変形しないし、沈まないし、くぼまない。
なぜなら、
消しゴムの力に対して逆向きで大きさが同じ力が働いているからなんだ。
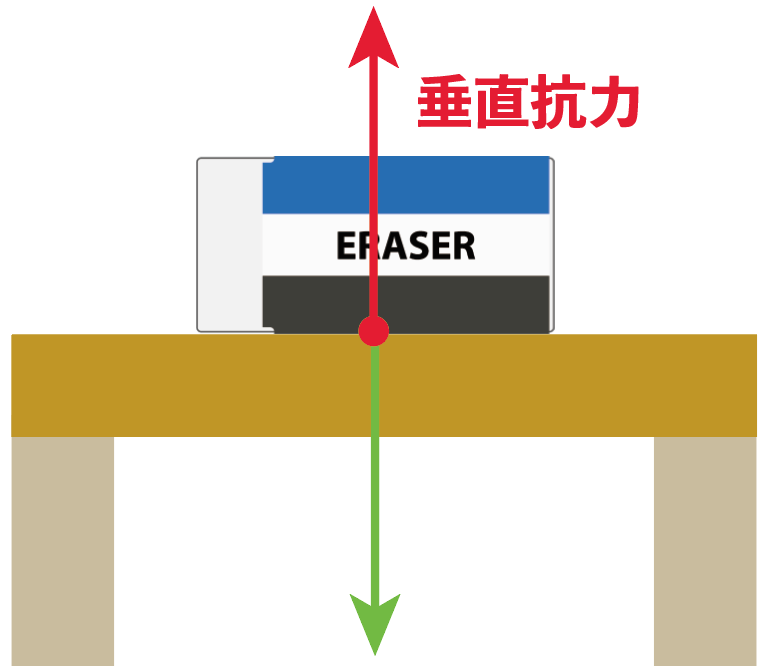
この机が消しゴムを押し返す力のことを「垂直抗力」と呼んでいるよ。
2つ目の力は「重力(じゅうりょく)」だ。
重力とは、地球に乗っかってる全てのものが地球から受ける力のことで、地球の中心に向かって力が働いているんだ。
丸い地球の上にのっかっっていても、地球の上に立っていられるのが重力のおかげ。地球がぼくらを真ん中に引っ張ってくれているわけさ。
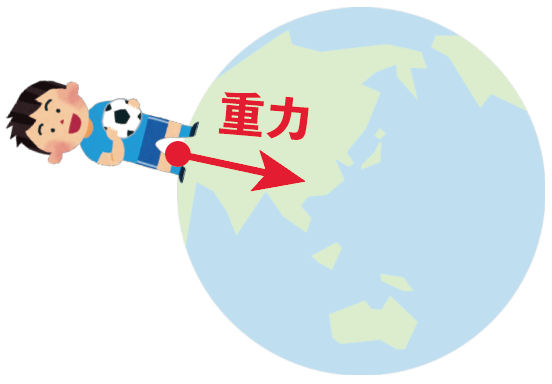
ボールを放したら地面に落ちるのも重力の仕業で、地面が地球の中心方向にボールを引っ張ってるからなのさ。
3つ目の力は「弾性力(だんせいりょく)」だ。
これは、
変形した物体が元の形に戻ろうとするときに働く力だね。
たとえば、バネ、あるでしょ?

あれを引っ張ってやると、引っ張った方向に伸びるよね?
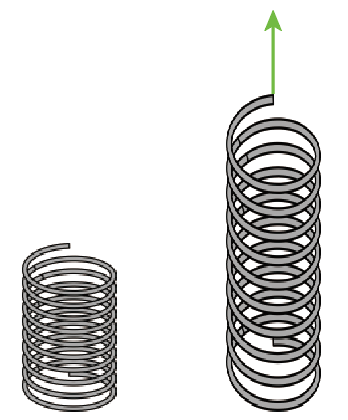
しかし、このときバネも黙っちゃいない。
引っ張った向きとは逆向きにバネから引っ張られるはずなんだ。
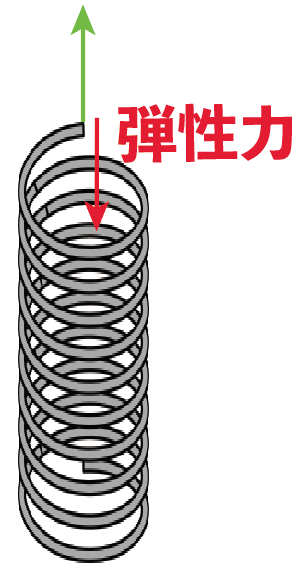
このバネが元に戻ろうとする力のことを「弾性力」というよ。
お次は摩擦力(まさつりょく)だ。
これは2つの物体が接している時、接触している面に働く平行な力のことだね。
たとえば、机に乗っかってる消しゴムを動かしてやると、動かした逆向きに摩擦力が働くよ。
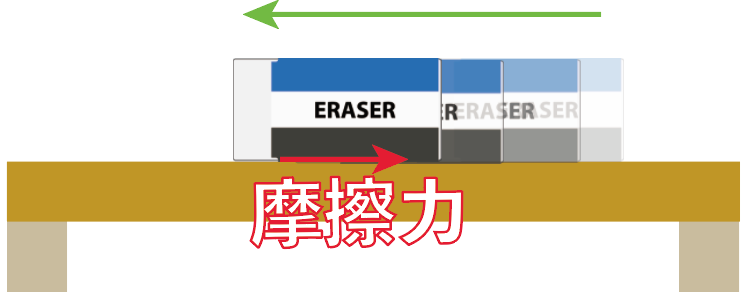
摩擦力は物体の滑らかさとかの環境によって大きさが異なるよ。
ツルツルの机で消しゴムを移動させれば摩擦力が小さいし、ゴリゴリの机でやれば摩擦力が大きい。
ちなみに、摩擦力は止まっているものを動かす時の摩擦力と、動いているものが受ける摩擦力の2種類があるんだけど、大きさでいうと、止まっているものを動かす時の摩擦力の方が大きいんだ。
だから、重たいものを押して運ぶときは動き始めが一番きついってわけね。
磁石にも力が働いているよ。
磁石にはN極とS極の2種類があったよね?

同じ種類の極同士を近づけると、反発し合う力が働いて、
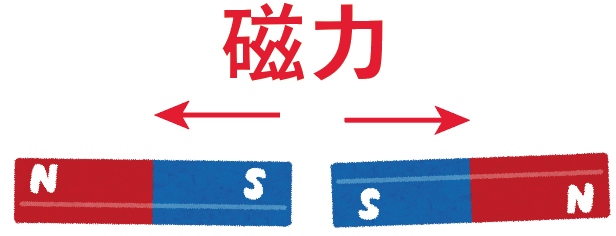
違う種類の極同士を近づけると、引き合う力が働くんだ。
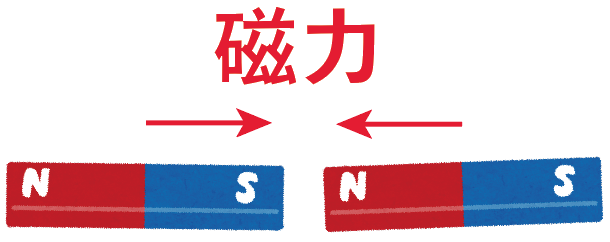
これを磁石の力(磁力)と呼んでいるよ。
じつは、電気にも力があるよ。
電気には、磁石と同じように、
という2種類いるんだ。

そう。御察しの通り、
同じ種類の電気だと反発し合う力が働いて、

違う種類の電気だと引き付け合う力が働くのさ。

以上が中学理科で勉強する力の種類だよ。
の6つを覚えておけば、なんとかなるんじゃないかな。
覚えるときに大切なのはその力を身近な具体例と結びつけること。
イラストと一緒に覚えてみよう!
「力の種類がしっくりきた!」
ってなったら次は力の単位(ニュートン)を勉強してみよう。
そんじゃねー
Ken