中学理科で勉強するフックの法則とは何者?
こんにちは!この記事を書いているKenだよ。ハンバーグ、うまいね。
中1理科の「身のまわりの現象」で力について勉強してきたよね?
今日はちょっと心を入れ替えて「バネ」に注目してみよう。
バネに働く力と、バネの伸びの関係を表した法則に、
フックの法則
というものがあるんだ。
これは、
バネの伸びは、バネを引く力の大きさに比例する
という法則だよ。
数学で勉強した「比例」を思い出してほしいんだけど、バネの伸びと引く力の関係が比例ってことは、
バネに2倍の力が働いたら、バネの伸びも2倍になるし、
バネに10倍の力が働いたら伸びも10倍になるってことなんだ。
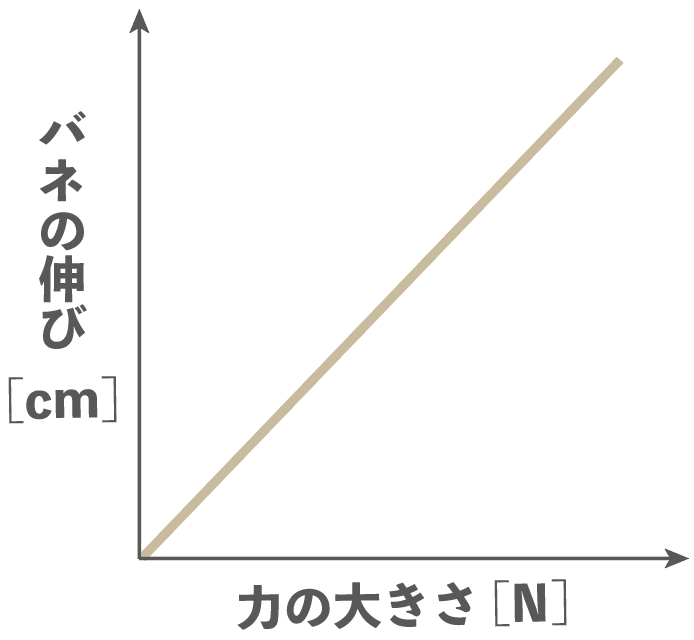
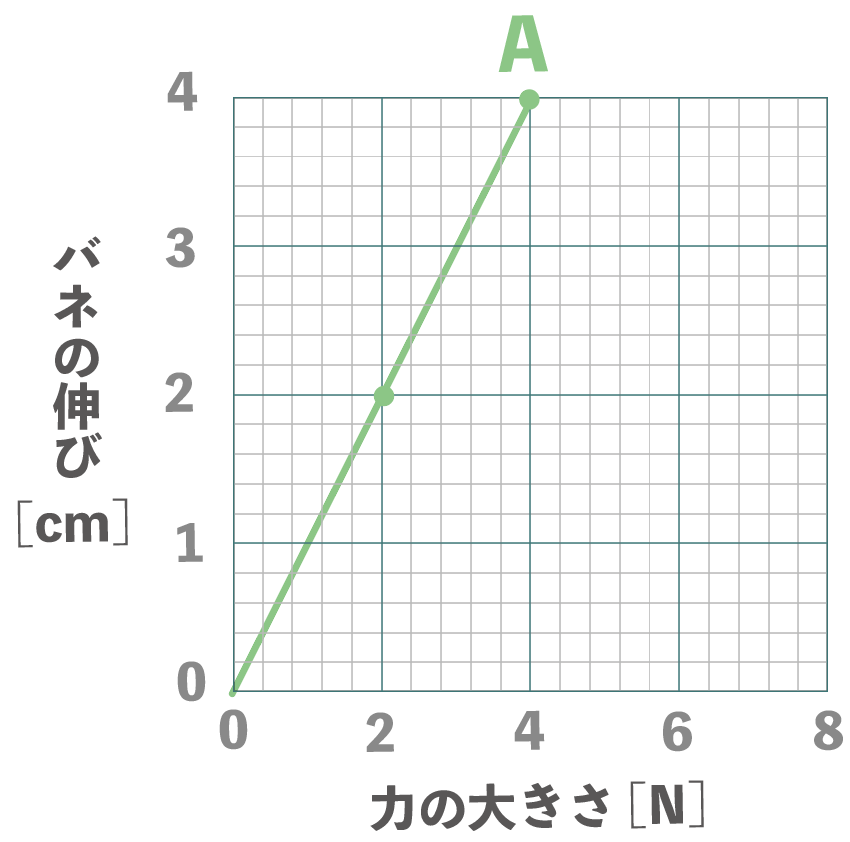
バネの働く力を横軸、バネの伸びをy軸にとったグラフを書いてみると、こんな感じで原点を直線になるはずね。
「比例のグラフのかきかたを忘れたぜ?」
って時はQikeruの記事で復習してみよう。
フックの法則は何の役に立つのか?
ウンウン。だいたいフックの法則はわかった。
だけどさ、
一体、このフックの法則はどういう風に役立つんだろう??
「何でこんな法則を中学理科で勉強しないといけないんだよ!?」
ってキレそうになってるやつもいるかもしれない。
じつはこのフックの法則がすごいところは、
バネの伸びから、バネにはたらいている力の大きさがわかるようになったことだ。
例えば、こんな感じでバネに力を加えたとしよう。
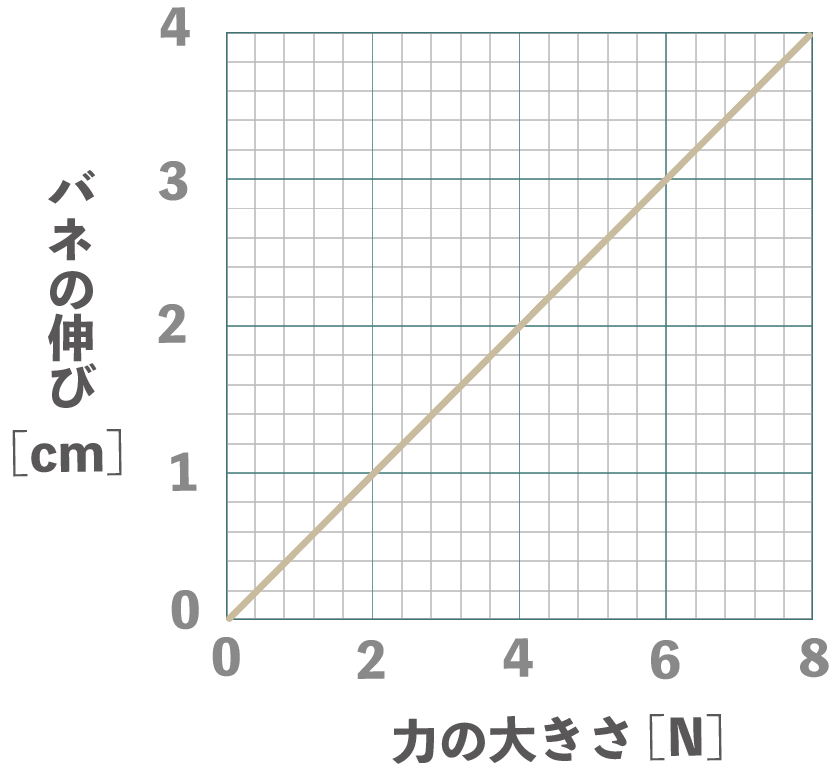
もし、バネの伸びが2cmになったら、このバネにどれくらいの力が加わってるんだろうね??
この時、バネの伸び2cmに当たる力をグラフから読み取ると・・・・
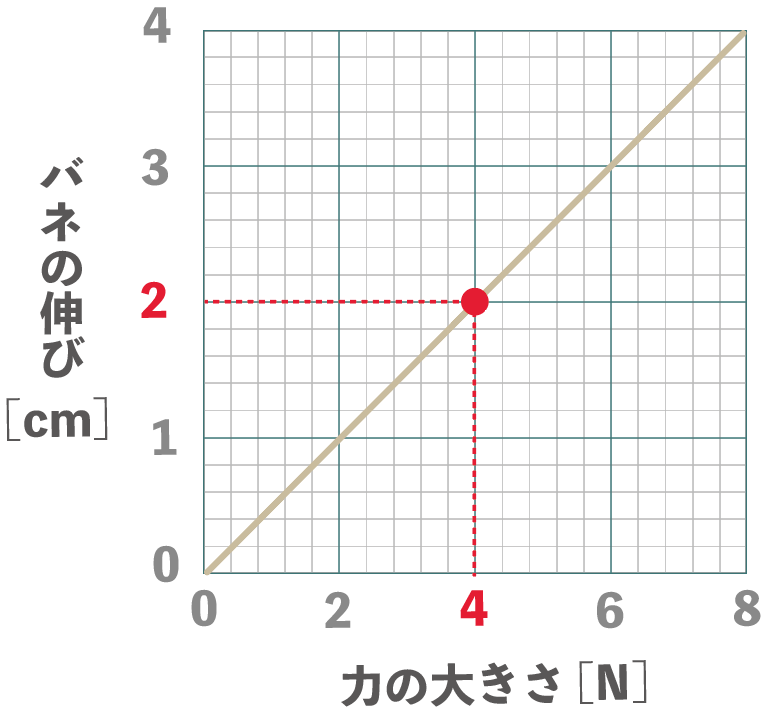
ほら!
4N
がはたらいてるってわかるでしょ?
これを応用したのが「バネばかり」というアイテムだ。

バネの先に重さを測りたいものを吊るしてみると、バネばかりにはたらいた力がわかるんだ。
その力は、バネに吊るした物体の重力のこと。
ここから逆算して物体の重さがわかるってわけ。
中学理科のテストに出やすいフックの法則の問題
ここまででフックの法則の基本と、その応用例まで完璧だね。
この記事の最後に、中学理科の定期テストに出やすいフックの法則に関する問題を解いてみよう。
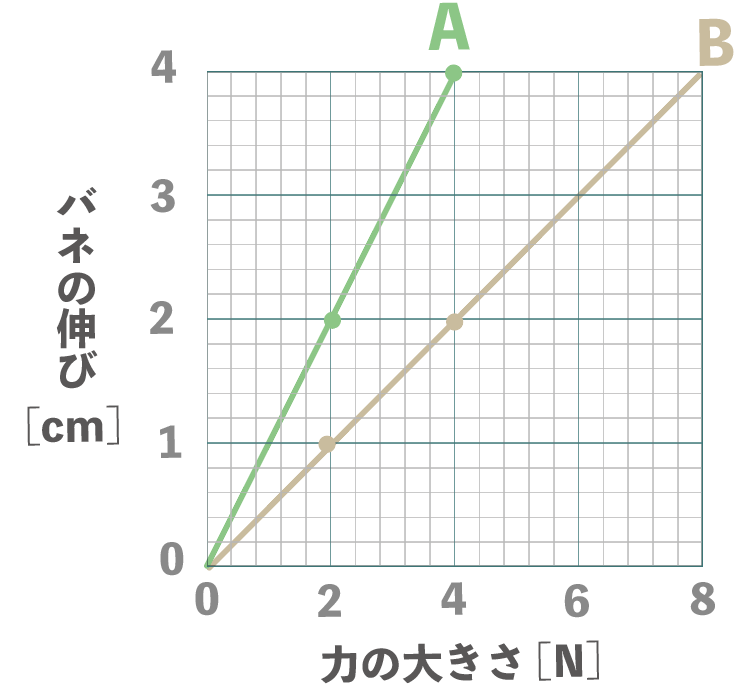
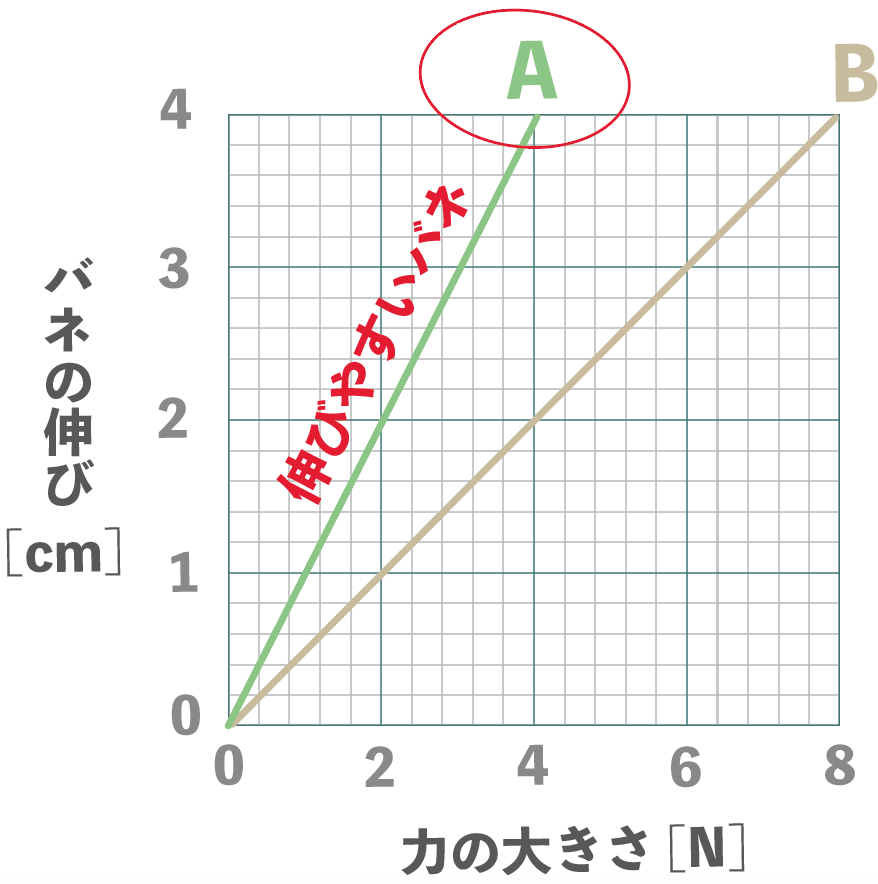
2つのバネAとBにそれぞれ重りをつるしてみた。この時、バネAとBにかかった力とバネの伸びの関係は次の表のようになりました。
| バネA | 伸び [cm] | 2 | 4 |
|---|---|---|---|
| 力の大きさ[N] | 2 | 4 | |
| バネB | 伸び [cm] | 1 | 2 |
| 力の大きさ [N] | 2 | 4 |
- バネAとBの力の大きさとバネの伸びの関係のグラフをかいてください。横軸に力の大きさ(N)、縦軸にバネの伸び(cm)です。
- バネの働く力とバネの伸びの関係はどうなってるのか?また、この関係を表した法則は?
- バネBを8Nの力で引くと何cm伸びますか?
- バネAを3cmのばすには何Nの力が必要か?
- バネAとBではどちらの方が伸びやすくなってますか?
問1. グラフをかく
まずはバネの伸びと力の表から、グラフをかいてみよう。
書き方は簡単。
たとえば、バネAなら、力の大きさが2Nのとき、バネの伸びは2cm、
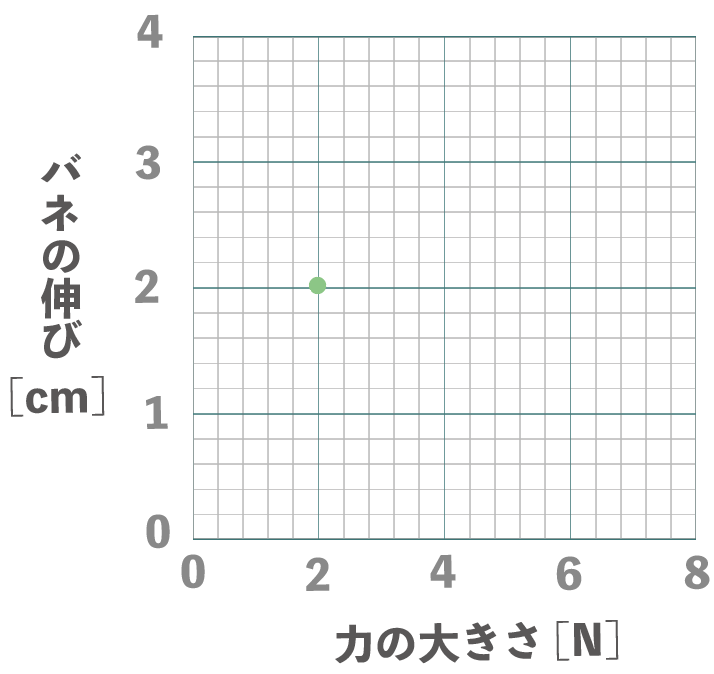
力の大きさが4Nのとき、バネの伸びは4cmだ。
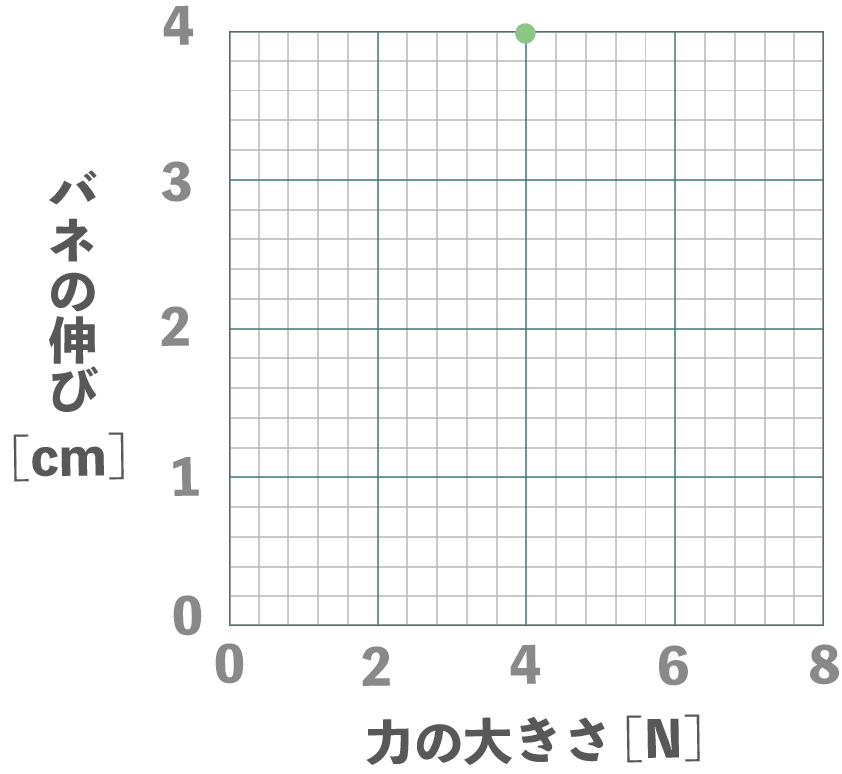
こんな感じで最低でも2つの点を打てればオッケー。あとはこの2点を直線で結んであげよう。
バネBも同じようにグラフを作ってやると、最終的にこんな感じになるはずだね↓↓
問2. バネの伸びと力の関係は?
バネの伸びは、バネに働く力が大きくなればなるほど大きくなってるね。
しかも、バネに働く力が2倍になれば、伸びも2倍になってる。
こういう関係のことを数学では、
比例(ひれい)
と呼んでいたね。
このバネの伸びと力の関係を理科では「フックの法則」と呼んでいるんだ。
問3. バネに働く力から伸びを求める
3つ目の問いできかれているのは、
バネBに8Nの力を加えた時にどれくらいの伸びるのかってことだ。
つまり、バネに働く力の大きさから、バネの伸びを計算しろと言ってるね。
この手の問題は、最初に作ったグラフを見てやればいいね。
横軸のバネに働く力が8Nの時、縦軸がどうなってるのか追ってみると、
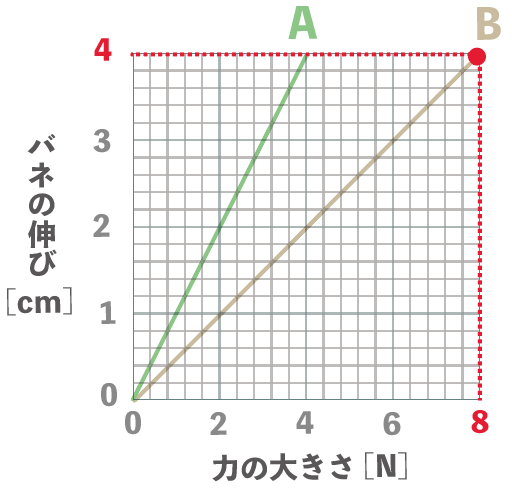
うん。
4cm
になってるね。
ってことで、バネBに8Nの力を加えた時には4cm伸びるんだ。
問4. バネの伸びから力を求める
今度は問3の逆。バネの伸びからバネに働いている力を求めればいいんだ。
この問題もグラフを使って読み取っていくよ。
問いでは、
バネAを3cmのばすときの力
がきかれてるから、バネAのグラフの縦軸のバネの伸びが3cmの点を見つけてあげて、その時の横軸の値を確認してあげる。
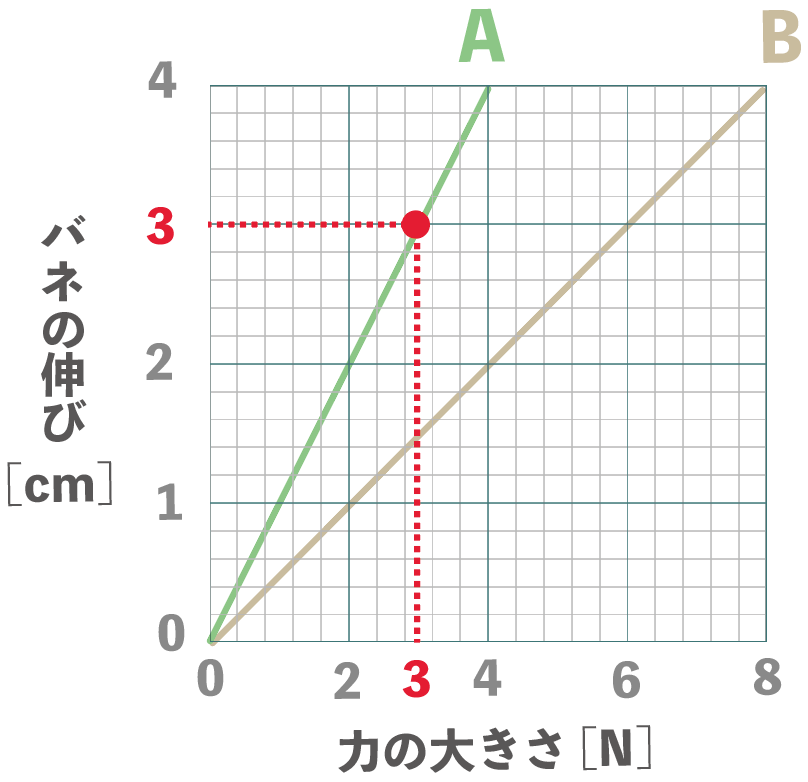
すると、うん、
3N
になってるね。
問5. 伸びやすいバネはどっち?
最後に、バネの伸びやすさについて。
伸びやすいバネのグラフは急になってるはずだ。
なぜなら、グラフが急になっていると、バネの力が増えた時に、同時に伸びが大きくなりやすいってことだからね。これはつまり、伸びやすいバネってこと。
練習問題でいうと、ばねA のグラフの方が急だから、伸びやすいのバネAだ。
フックの法則の完璧!あとは慣れ!
以上がフックの法則の基礎と問題の解き方だったね。
最後にもう一度復習しておこう。
フックの法則とは、
- バネの伸び
- バネに働く力
の関係を表したもので、この2つは比例の関係にあるんだ。
フックの法則を使うと何が便利かっていうと、
バネの伸びから、そのバネに働く力の大きさがわかるってことだったね。
フックの法則をマスターしたら、水の中で働く力の、
水圧・浮力について勉強していこう。
そんじゃねー
Ken











