こんにちは！この記事をかいているKenだよ。もやしは安いね。
確率でたまーに、
「少なくとも」
がつく問題でてくるよね？？？
たとえば、つぎのようなやつだ↓↓
例題
4枚のコインをなげて少なくとも1枚が表になる確率を求めなさい。
こんな感じで、「少なくとも」がついている問題は、
ふつうに解くとメンドイ。
楽な計算方法をつかってみよう！
そこで今日は、
「少なくとも」がついた確率の求め方
を3ステップで解説していくよ。
よかったら参考にしてみて。
「少なくとも」がつく確率の問題。
世の中にはたくさんある。
今回紹介するのは、
少なくとも1枚/回がAになる確率
を求める問題の解き方だよ。
この手の問題は3ステップで計算できちゃうんだ。
さっきの例題を解説していくよー
例題
4枚のコインをなげて少なくとも1枚が表になる確率を求めなさい。
まずは、
ぜんぶAにならないこと
をみつけよう。
例題では、
少なくとも1枚表になる確率
を求めるんだったよね？？
Aにあたるのは、
表になる
ってこと。
つまり、「ぜんぶAにならないこと」は、
ぜんぶ表にならないこと
だね。
これが第1ステップだ！
つぎは、さっきの、
ぜんぶAにならないこと
の確率を計算してみよう！
例題でいうと、
コインを4回なげて、ぜんぶ表にならない確率
ってことだね。
これは、
コインを4回なげてぜんぶ裏になる確率
ってこと！
コインを4枚なげると、表裏の組みあわせはぜんぶで16通り。
ぜんぶ裏になる場合の数は1通りしかない。
よって、ぜんぶ裏になる確率は、
16分の1
になるはず！
＞＞コインの確率の求め方はこちら
最後に、その確率を1からひいてみよう。
つまり、
1 – （ぜんぶAにならない確率）
を計算すればいい。
例題では、「ぜんぶAにならない確率」は、
16分の1
だったよね？？
よって、
1 – (ぜんぶAにならない確率)
= 1- (16分の1)
= 16分の15
になるんだ。
おめでとう。
「少なくとも」の確率問題も攻略だね！！
でもさ、
なぜメンドイ方法で計算するんだろう？？
って思うない？？
ふつうに確率の求めればいいじゃない！？
って切れてるヤツもいるかもしれない。
この解き方を使う理由は、
「少なくとも1枚（回）がAになる」場合の数が多すぎるからなんだ。
ふつうに計算すると、場合の数をかぞえるときに苦戦する。
だから、ストレートに確率を計算するんじゃない。
「ぜんぶAにならない場合の数」を数えて確率をだすんだ。
「少なくともAにならない確率」と、
「ぜんぶAにならない確率」を足したら1になるはずだね？？
だって、どちらかは絶対に起きるからね。
つまり、足したら1、100%起きる確率になるのさ。
だから、
ゼッタイに起きる確率の「1」から「ぜんぶAにならない確率」
をひいてやると、
「少なくともAにならない確率」
を計算できちゃうんだ。
どう？？スッキリしたかな？？
「少なくとも」がつく確率の問題は、
1から「ぜんぶAにならない確率」をひいてみよう！
これで計算が早くなるはず。;
じょじょに慣れていこうね！
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。布団、気持ちいね。
確率の問題には色んなタイプがある。
たとえば、
サイコロとか、コインとか、玉とか・・・・
もう、いろいろね。
そんな中、よくでてくるのが、
トランプの確率の問題
だ。
今日はこのタイプの問題を攻略するために
トランプの確率の基本をおさえておこう！
基本を押さえると、トランプの確率を計算しやすくなるよ。
トランプの数字には、
1~13まである。
と名前をかえてることに注意。
英語になっているけど、数字としてとらえちゃおう。
1つの数字につき4つのマークがあるよ。
の4種さ。
1~13の13枚のカードはそれぞれ4種類あるってわけ。
ってことは、トランプは全部で、
13 × 4 = 52枚
あることになるね。
トランプには「赤」か「黒」の2色があるよ。
「スペード」と「クローバー」は黒。
「ハート」と「ダイヤモンド」は赤になっているんだ。
だから、52枚のトランプカードの中には、
入っていることになる。
実際にトランプの確率を計算してみよう。
52枚のトランプから1枚ひいたとするね。
1枚ひいてエースがでる確率を求めてみよう。
トランプはぜんぶで52枚ある。
だから、52通りのひき方があるはず。
1つの数字につきマーク違いの4枚がある。
エースだって4枚あるはずだね。
つまり、4通りのひき方がある。
だから、トランプから1枚ひいてエースをひく確率は、
（エースをひく場合の数）÷（ぜんぶの場合の数）
= 4 ÷ 52
= 13分の1
になるね！
1枚ひいて「黒」がでる確率を計算しよう。
黒いカードはぜんぶで「26枚」あったよね？
ってことは26通りのひき方があるわけだ。
黒いカードをひく確率は、
(黒いカードをひく場合の数)÷（すべての場合の数）
= 26÷52
= 2分の1
になるよ。
最後はクローバーをひく確率だ。
1つのマークはぜんぶで13枚ある。
ってことは、クローバーには13通りのひき方があるってわけ。
1枚ひいてクローバーをひく確率は、
（クローバーの場合の数）÷（ぜんぶの場合の数）
= 13 ÷ 52
= 4分の1
になるよ。
トランプの確率の問題は基本をおさえれば大丈夫。
基本がわかったらガンガン問題をといていこう！
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。みかんを5つ買ったね。
玉を取り出すときの確率の問題。
けっこうでてくるよね。
たとえば、
赤玉が2個、白玉が4個入った袋から1回だけ玉を取り出す問題
とかね。
今日はこのタイプの、
玉の確率の問題でつかえる公式
を紹介していくよ。
よかったら参考にしてみてー
さっそく公式を紹介するね。
1回玉を取り出したとき、ある色の玉がでる確率は、
（その色の残りの玉数）÷（全部の残りの玉数）
で計算できちゃうよ。
たとえば、つぎの例題をといてみよう。
例題1
赤玉が2個、白玉が4個入った袋から1回だけ玉を取り出すとき、赤玉をひく確率を求めてください。
このとき、
だね？
公式をつかうと、
（赤玉の残りの数）÷（ぜんぶの玉の残数）
= 2÷6
= 3分の1
になるんだ。
どう？？簡単でしょ？
えっ。
玉を1回だけじゃなくて、2回以上取り出したい？！？
2回以上取り出す時は、くじ引きの確率と一緒。
（1回目の玉の確率）× （2回目の玉の確率）×（3回目の玉の確率）・・・
みたいに、
玉をひくごとの確率をかけていけばいいんだ。
たとえば、つぎの例題をといてみよう。
例題2.
赤玉が2個、白玉が4個入った袋から連続で2回玉を取り出すとき、すべて赤玉をひく確率を求めてください。
さっきの計算式で確率をだせちゃうね。
つまり、
（1回目の玉の確率）× （2回目の玉の確率）
ってわけ。
1回めに赤玉をひく確率は、
（赤玉の残数）÷（全玉数）
= 2 ÷ 6
= 3分の1
になるね。
2回目は赤玉が1つなくなった袋から玉をひくよね？？
だから、2回目も赤玉をひく確率は、
（赤玉の残数）÷（全玉数）
= 1 ÷ 5
= 5分の1
になるわけだ。
よって、2回連続で赤玉を引く確率は、
（1回目の確率）×（2回目の確率）
= （3分の1） × （5分の1）
= 15分の1
になる。
おめでとう！
これで玉の確率を計算できるね。
玉の確率は一見むずかしい。
だけど、
（ある色の残り数）÷（ぜんぶの残り数）
さえ計算すれば大丈夫。
あとは問題をたくさんといてみよう！
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。グレープフルーツは常備だね。
当たりくじをひく確率って、
（当たりくじの本数 ）÷（残りの本数）
だったよね？？
たとえば、5本中1本当たりのくじがあったとしよう。
当たりくじがでる確率は、
（当たりくじの本数：1）÷（残りのくじ本数：5）
= 5分の1
になるんだ。
だけどさ、
この公式って、
くじを1回しか引かない問題でしか使えないよね？？
これじゃあ、2回以上ひく問題はとけないね！
そこで今日は、
2回以上くじを引くときの確率の求め方を解説していくよ。
よかったら参考にしてみて。
確率の求め方はつぎの公式だよ。
（1回目のくじ引きの確率）×（2回目のくじ引きの確率）×（3回目のくじ引きの確率）・・・
たとえば、「当たりくじを連続でひく確率」だったら、
（当たりくじの残り本数）÷（残りくじ本数）
をかけていけばいいね！
たとえば、つぎの例題をといてみよう。
例題
10本中3本が当たりくじのくじ引きがある。3回ひいて連続で当たりがでる確率を計算してください。
こいつは2ステップでとけちゃうんだ。
1回目は、
のくじが箱にはいってるよね？？
だから、
（当たりくじ数）÷（残りのくじ数）
= 3÷10
= 10分の3
になるよ！
2回目は、当たりくじを1本ひいたあとだ。
1本当たりくじが消えているはず。
だから、箱の中には、
が残ってるよね？？
このとき、当たりくじをひく確率は、
（残当たりくじ数）÷（残りの全くじ数）
= 2÷9
= 9分の2
になるんだ。
おなじように考えると、3回めに当たりくじをひく確率は、
が箱にのこっている。
だから、3回目に当たりをひく確率は、
（残当たりくじ数）÷（残すべてのくじ数）
= 1÷8
= 8分の1
になる。
あとは公式通りに、
（1回目のくじ引きの確率）×（2回目のくじ引きの確率）×（3回目のくじ引きの確率）
を計算するだけ。
になったから、
（3回連続で当たりくじを引く確率）
=（1回目のくじ引きの確率）×（2回目のくじ引きの確率）×（3回目のくじ引きの確率）
= (10分の3)×（9分の2）×（8分の1）
= 120分の1
になるよ！
おめでとう！
これで2回以上くじを引く問題も攻略だね。
くじ引きの確率問題はどうだったかな？？
2回でも3回でもくじ引きをひいても大丈夫。
あとは公式になれていこう。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。すた丼くいたいね。
ある日。
くじ引きに参加したとしよう。
一等賞はディズニーリゾートのペアチケット。
チャレンジャーはAさん、Bさん、キミの3人だ。
当たりくじは10本中1本。
しかも、1人1回しかくじを引けないんだ。
当たりをひくのはむずそうだね・・・・・
そんな状況にいたとしよう。
そこでキミは、
どの順番なら当たりくじをひきやすいのか？？
って思うよね？
最初にくじをひいたほうがお得なの？？
それとも、
ライバルにはずれを引かせてやるのがいいのか。。
むちゃ迷うね。。。
だけど、残念ながら、
どの順番で引いてもおなじ確率になるんだ。
だから、くじ引きの順番を争っても意味がない。
順番はゆずっても大丈夫。;
なぜ、くじ引きに順番は関係ないんだろう？？
もやもやするね。
順番ごとに確率を計算してみよう。
もし、1番目にくじをひいたときを考えよう。
1番目にひくとき、
が箱にはいってるはず。
くじ引きを1回ひいたときの確率の求め方で計算してみよう。
だから、当たりじをひく確率は、
（当たりくじの本数）÷（残りのくじ本数）
= 1÷10
=10分の1
になる。
つぎは2番目にくじを引いたときの確率。
当たりくじの確率ってどれくらいなんだろう？？
2番目にくじをひくときは、
を計算してみて。
一人目がはずれくじを引く確率は、
（はずれくじの残本数）÷（すべてのくじの残本数）
= 9÷10
= 10分の9
だね。
そして、2人目のキミが当たりくじを引く確率は、
（当たりくじの残本数）÷（すべてのくじの残本数）
= 1÷9
= 9分の1
になるんだ。
よって、1人目がハズレで2人目が当たりくじをひく確率は、
（一人目がはずれくじを引く確率）×（2人目が当たりくじを引く確率）
= （10分の9 ）×（9分の1）
= 10分の1
になるね。
これはさっきの確率といっしょ！
くじを最後にひく確率を求めよう。
計算方法は、
2回以上くじをひいた場合の計算方法をつかえばいいんだ。
（一人目がはずれくじを引く確率）×（2人目もはずれくじを引く確率）×（3人目で当たりくじをひく確率）
を計算していくよ。
一人目がはずれくじを引く確率は、
（はずれくじの残本数）÷（すべてのくじの残本数）
= 9÷10
= 10分の9
二人目がはずれくじを引く確率は、
（はずれくじの残本数）÷（すべてのくじの残本数）
= 8÷9
= 9分の8
3人目のキミが当たりくじを引く確率は、
（当たりくじの残本数）÷（すべてのくじの残本数）
= 1÷8
= 8分の1
になる。
よって、
1~2人目がハズレで3人目で当たりくじをひく確率は、
（1人目がはずれくじを引く確率）×（2人目がはずれくじを引く確率）×（3人目で当たりくじを引く確率）
= （10分の9 ）×（9分の8）×（8分の1）
= 10分の1
になるね。
こいつもさっきと同じ確率だね！
つまり、
どの順番でも確率はおなじってことだ。
どう？？しっくりきたかな？？
くじ引きの確率は順番なんて関係ない。
これを知っているとかなり便利。
くじ引きに冷静に参加できるからね。
中学数学でもたまにでてくるから、しっかりおさえておこう。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。オレンジは目覚めにいいね。
中学数学の確率でたまーに、
くじ引きの問題
ってあるよね？？
たとえば、
6本のうち当たりくじが4本あるとき、当たりくじをひく確率を求めなさい。
っていう感じで。
こういう問題はむずかしそう。
だけど、公式をつかえば5秒で確率を計算できるんだ。
つぎの公式で計算できるよ。
（当たりor はずれを引く確率）
＝（当たりorはずれの本数）÷（残りのくじ本数）
あ、くじを1回引く場合だけどね。
たとえば、6本のうち2本が当たりくじだとする。
くじを1回ひいて「当たりくじ」がでる確率を求めてみよう。
だよね。
公式をつかってやると、
（当たりくじを引く確率）
＝（当たりくじの本数）÷（ぜんぶのくじ数）
＝ 2 ÷ 6
= 3分の1
になるんだ。
「当たりくじの数」を「残りのくじ数」でわるだけ。
簡単でしょ！？
でもさ、なんで公式が使えるんだろう？？
ちょっと怪しいよね。。
この公式がつかえる理由は、
1つ1つのくじ引きを区別しているから
なんだ。
「当たりくじ」たちはすごく似ている。
ぶっちゃけ、どれも同じ。
だけど、確率を計算するときは同じじゃだめなんだ。
こいつらを区別しないといけない。
たとえば、
みたいな感じでね。
当たりくじだけじゃなくて、はずれでも同じ。
見た目は同じだけど、別ものとしてあつかってやろう。
だから、「当たりくじのひき方」だったら、
の2通りがあるはず。
ぜんぶのくじ引きは、6通りのひきかたがある。
だから、確率の公式をつかってやれば、
（当たりくじの場合の数）÷（すべてのくじ引きの場合の数）
= 2÷6
=3分の1
になるんだ。
おめでとう！
くじ引きの確率もマスターだね。
くじ引きの確率の問題？？
おそれることはない。
ただ、公式で計算すればいいんだ。
くじの1つ1つが区別されるっておぼえておこう。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。コイン、ほしいね。
コインの確率の問題ってでてくるよね？？
具体的にいうと、
〜枚のコインを投げて○○が△△回でる確率を求めなさい
ってやつだ。
コインの確率がわかると便利。
勝負やゲームに強くなる。
テストの点数もあがる。
いいとこづくしなんだ。
今日はコインの確率を一瞬で計算できる公式を紹介していくよ。
よかったら参考にしてみて。
コインの枚数をn、求めたいコインの場合の数をaとしよう。
このときのコインの確率は、
a÷2^n
で計算できるんだ。
「コインの枚数」と「ある場合の数」さえわかればいいってことだね。
たとえば、つぎの例題をといてみよう。
例題
3枚のコインをなげてすべて表になる確率を計算しなさい。
3ステップで確率を計算できちゃうよ。
まず樹形図をかこう。
出る目は「表」か「裏」のどちらかだよね？？
だから樹形図はこうなるはず↓↓
※ 樹形図の書き方を参考にしてみてね。
求めたい場合の数をしらべてみよう。
例題では、
3枚のコインがすべて表になる確率
を計算したかったんだよね？？
さっきの樹形図をみてみよう。
「3枚すべてのコインが表になる場合の数」は、
1通りしかないね。
うん、どうみても1つだ。
公式をつかおう。
例題では、
コインの枚数が「3」、表になる場合の数は「1」。
だから、コインの確率公式をつかってやると、
（すべて表になる場合の数）÷（2のコインの枚数乗）
＝ 1÷2^3
＝ 1/8
になるね。
おめでとう！
これでコインの確率もマスターだね。
コインの確率は簡単。
の2つさえわかればいいからね。
あとは公式で計算してみよう。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。コーヒー豆買いたいね。
中学数学の確率で、
サイコロの問題
ってけっこうでてくる。
たとえば、サイコロを2つふって目の和が4になる確率を求めよ！とかね。
たまに3つサイコロなげるときもある。
サイコロの確率ってめんどくさいから、
公式があったらいいのになあ・・・・・・
とか思ってない？？
今日はそんなキミのために、
中学数学でつかえるサイコロの確率問題の公式
をわかりやすく解説していくよ。
よかったら参考にしてみて。
サイコロをn個ふったときの確率の公式は、
(あるできごとの場合の数)÷（6のn乗）
で計算できちゃうよ。
たとえば、サイコロを2つふって、目の和が8になる確率を求めよう。
2つのサイコロの確率の場合の数は
「表」をかいて求めるんだったね？？
「目の和が8になる」場合の数をかぞえてみると、
5通りであることがわかる。
また、サイコロは2つ振っているね。
公式をつかってみると、
（目の和が8になる場合の数）÷（6の2乗）
＝ 36分の5
になるね！
サイコロの数nを代入して、場合の数を数えるだけ。
すぐに確率を計算できちゃう。
だけどさ、
なんでこの公式つかえちゃうんだろう？？
簡単すぎてちょっと怖いよね。
じつはこれ、確率の求め方の公式をつかっているんだ。
を代入してるだけ。
えっ。
なぜ6^n通りになるのかって？！？
じつは、1つのサイコロに目が6つあるからなんだ。
だから、n個のサイコロをふったときには、
6をn回かけた場合の数があるんだ。
どう？？スッキリしたかな？？
サイコロの確率の公式はどうだったかな？？
サイコロの数を数えて、
樹形図や表で場合の数をゲットするだけ。
実践問題で公式をつかっていこう。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。焼き肉は週一でいいね。
サイコロを2個以上投げたとしよう。
このとき、「ぜんぶ同じ目になること」を「ゾロ目がでる」ってよんでいるよ。
たとえば、サイコロを4つふったとしよう。
ぜんぶの目が4になったら「ゾロ目」がでたっていうんだ。
ゾロ目をだすといいことばかりだ。
ボーナスがもらえたり、ワープできたりと、かなりお得。
それだけめずらしくてラッキーってことなんだ。
だからこそ、
サイコロでゾロ目がでる確率
ってむちゃくちゃ気になるよね？
今日は、
サイコロをふってゾロ目がでる確率を3秒で計算できる公式
を紹介していくよ。
よかったら参考にしてみて。
サイコロの数をnとしよう。
ゾロ目になる確率は、
6/6^n
になるよ。
ただし、nは2以上にかぎるけどね！
たとえば、サイコロ4つのゾロ目の確率を計算してみよう！
サイコロの数は4だから、
「n」 に「4」を代入すればいいわけだ。
すると、
（4つのサイコロでゾロ目がでる確率）
＝ 6 ÷ 6^4 ＝ 1/ 216
になるはず。
つまり、
1/216っていう確率で、
「3の目」が4つでるかもしれないし、
「1の目」が4つでるかもしれないんだ。
どう？？簡単な公式でしょ？？
でもさ、
なぜゾロ目の確率が計算できるんだろう？？
nに「サイコロの数」をいれるだけ。
簡単すぎる。
ぜったいあやしいよね？？。
だから、
なぜゾロ目の確率公式がつかえるのか？？？
っていうことを確認していこう。
サイコロを何個ふっても、
「ゾロ目がでる場合の数」って「6」なんだ。
なぜなら、
サイコロの目が同じになる場合の数は1~6で1つずつだからね。
だから、1000個サイコロをふろうが、1万個サイコロをなげようが、
ゾロ目になる場合の数は6通りになるんだ。
あとは分母の、
すべての場合の数を求めるだけ！
6のn乗
だったね？？
なぜなら、1個のサイコロは6通りの目をもっているからね。
n個のときは6をn回かけると場合の数になるんだ。
だから、n個のサイコロをふったときにゾロ目がでる確率は、
6/6^n
になるよ。
どう？スッキリしたかな！？
サイコロでゾロ目がでる確率の公式は簡単。
n個サイコロをふったとすれば、
6/6^n
の公式で計算できちゃうんだ。
じゃんじゃん計算していこう。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。散歩は大事だね。
中学数学の確率で重要なのは、
場合の数の調べ方
だ。
「場合の数」さえ数えられれば大丈夫。
あとは確率の公式にいれるだけだからね。
「場合の数の調べ方」さえおぼえれば、
確率マスターになれるわけさ。
今日はそんな確率で大切な、
場合の数の調べ方を2つ紹介するよ。
よかったら参考にしてみて。
中学数学ではおもに、
樹形図で場合の数を調べていくよ。
調べ方はつぎの2つさ。
つぎの例題をときながら解説していくよ。
例題
3・4・8がかかれたカードが3枚ある。こいつらを並べて3ケタの数字をつくるとき、偶数になる確率を求めよ。
このとき、樹形図はつぎのようになるね。
※詳しくは「樹形図の書き方」をよんでみてー！
まずは「すべての場合の数」をしらべよう。
これは確率の計算で分母にくるやつだね。
調べ方はとっても簡単。
樹形図のいちばん右をぜんぶ数えればいいんだ。
例題でいうと、いちばん右には6つの実がなっているよね？？
だから、
すべての場合の数は「6通り」になるんだ。
樹形図のいちばん右をかぞえると「すべての場合の数」になる
って覚えておこう。
今度は「あるできごと」の「場合の数の調べ方」だね。
これは確率の公式の分子にくるやつだ。
この調べ方はちょっとむずかしい。
なぜなら、あてはまる場合の数を樹形図から選ばないといけないからね。
たとえば、さくらんぼが腐ってる場合の数をしらべたいとき。
このとき、樹形図をばーーってみてみよう。
さくらんぼが腐ってそうな場合の数をみつけるんだ。
ざっと見た結果、
緑でかこった1通りしかないね。
こんな感じで場合の数を数えればいいんだよ。
例題をみてみよう。
例題で求めたいのは、
3ケタの数字が偶数になる確率
だったよね？？
樹形図でかぞえてみると、
4通りある！
よって、
（3ケタの数字が偶数になる確率）
＝ （偶数になる場合の数）÷（すべての場合の数）
＝ 4÷6 = 2/3
になるね。
おめでとう！
これで場合の数の調べ方をマスターしたね。
中学数学では基本的に、
樹形図で場合の数をしらべていくよ。
の2つさえ調べられればこっちのもの。
あとは、公式で確率を計算するだけだね。
じゃんじゃん調べていこう！
そんじゃねー
Ken
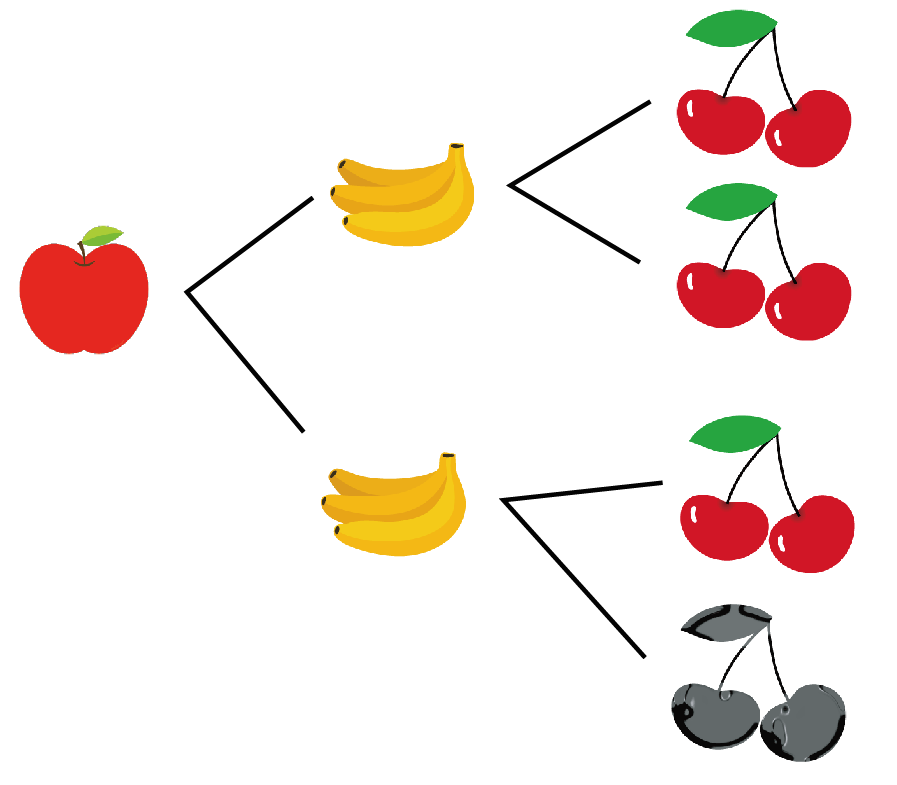
こんにちは！この記事をかいているKenだよ。小腹がすいたね。
中学数学の確率で便利なのは、
樹形図
というアイテムだ。
樹形図とは文字通り、
樹の形みたいに枝分かれしている図のことだよ。
ちょうど下みたいな図だね↓↓
どう？？樹の枝みたいでしょ？？
中学生が勉強する確率では、
「樹形図」をつかって場合の数をかぞえていくんだ。
確率では樹形図がむちゃ重要ってわけ。
さっそく樹形図をかいていこう。
3ステップでかけちゃうんだ。
つぎの例題をときながら解説していくよ。
例題
3・4・8がかかれたカードを3枚ならべてできる整数の場合の数を求めなさい。
まずは何回挑戦できるかかいてみよう。
つまり、
トライアル数ってわけ。
コインを3回なげるんなら「3」、
くじ引きを2回ひけるなら「2」がトライアル数だね。
例題のトライアル数は「3」。
なぜなら、
カードを3枚並べられるからさ。
もちろん、カードを4枚ならべるなら「4」、
120枚並べるなら「120」がトライアル数だ。
このトライアル数をヨコにずらーっと書いてみよう！
まずは一回目のトライアルでどうなるか考えてみよう。
コインだったら表か裏か。
くじ引きだったら当たりか・はずれだね。
例題で1枚目になるのは、
のいずれかのカードだね？？
つまり、
1枚目は3枚のどれかってわけ。
だから、「1枚」の下に「3」「4」「8」の3通りをかいてあげよう。
つぎは、前回のトライアルの結果をふまえてどうなるか？？
ってことを考えてみよう。
1回目が終わったら、1回目をふまえて2回目。
2回目が終わったら、1・2回目をふまえて3回目
の結果を予想するんだ。
例題でいうと、
1回目のトライアルの後、残されたカードは2枚。
1枚目に4がくると、
つぎは「3」か「8」の結果になる。
おなじように「3」と「8」がきている場合を考えると、
こんな樹形図になるはず↓↓
同じように、3回目の結果も予想してみよう。
2枚カード並べたら残り1枚だね。
つまり、残っているカードを並べるだけってことだ。
だから、3枚目も加味するとこうなるはず↓↓
おめでとう！これで樹形図は完成だね。
すべてのカードの並び方は6通りってわけ！
樹形図の書き方はどうだったかな？？
ポイントは、
前のトライアルの結果をふまえること。
これにつきるね。
1回目のトライアルが終わったら2回目はどうなるのか。
これをイメージしてみよう。
そんじゃねー
Ken
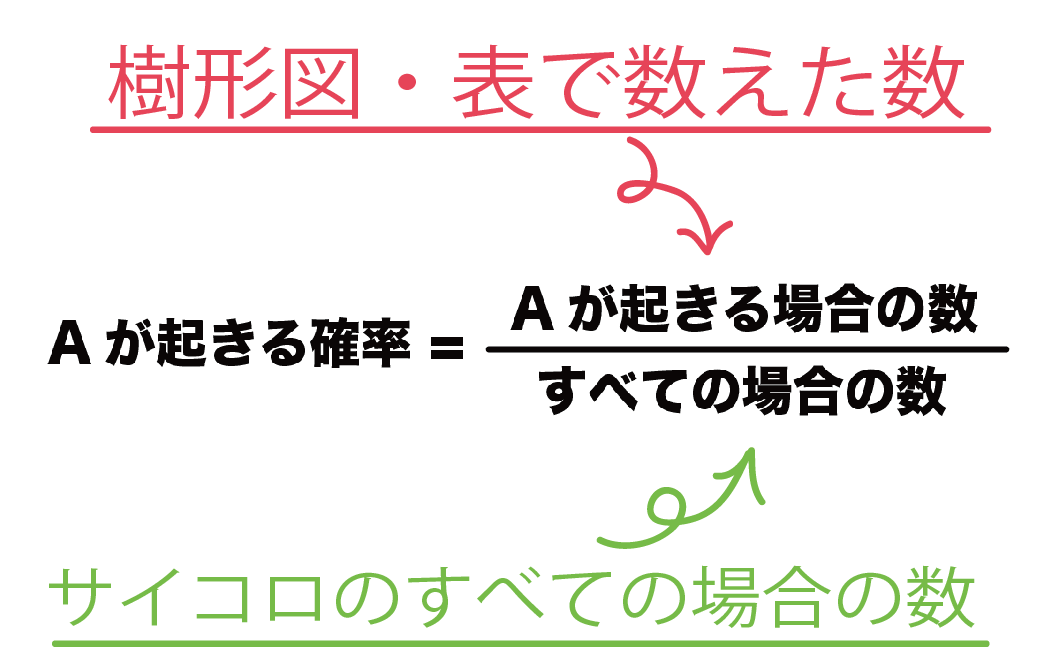
こんにちは！この記事をかいているKenだよ。3Dメガネを2つ買ったね。
確率の公式・計算式は正直、たくさんある。
だけど、中学数学ではたった1つの公式で大丈夫。
どんな確率問題もとけるようになるんだ。
あることがら「A」がおきる確率の求め方は、
つぎの公式で計算できちゃうよ。
（Aが起きる場合の確率） = （ことがらAが起きる場合の数）÷（すべての場合の数）
だ。
もうちょっと公式っぽくしたい。
そんなときは、
としよう。
すると、
P(A) = a/n
ともあらわせるね！
さっそく公式をつかおう。
たとえば、コインを3回なげたとする。
このとき、3回とも表になる確率を計算してみよう。
3回コインをなげたときの場合の数をもとめよう。
表・裏のパターンはぜんぶで何通りあるかな？？
ってことを数えていくんだ。
樹形図をかいてみよう。
1枚目が「表」だったら、つぎは「表」か「裏」。
2枚目も「表」がでたら、そのつぎも「表」か「裏」・・・・
というように考えていくよ。
すると、こんな感じの樹形図がかけるはず！
コインを3回なげたときの数は右のやつをかぞえてね。
すると、
8通り
あることがわかるはず。
つまり、確率の求め方の公式の「n」が「8」になるってことだね。
その8通りの中で、
「すべて表」になっているのは何通りなんだろう？？
今度はこれを数えていくよ。
樹形図をみると、すべて表なのは1通りだね。
だから、確率の求め方の計算式の「a」は「1」になるね。
あとは公式で計算するだけ。
だから、
（3回表になる確率）
＝（3回表になる場合の数）÷ （3回コインをなげた場合の数）
＝ 8分の1
になるってわけだ。
おめでとう！
これで確率の求め方の公式がわかったね。
中学で勉強する確率の公式は1つ。
P (A) = （ことがらAが起きる場合の数）÷（すべての場合の数）
だけ。
あとは、樹形図で場合の数を正確に数えるだけだ。
問題といて確率になれていこう！
そんじゃねー
Ken
