中学理科の「電流と磁界」で知っておきたいのが、
の3つ。
こいつらを知っておくと、「電気と磁石」の内容がスーッと頭に入ってきやすいよ。
まずそもそも押さえておきたいのが
磁石とはなんなのか?
ってこと。
磁石は生活に溶け込んでいて、日常生活でも見かける機会があるよね。
でもまあ、こいつは何者なんだって話から入ろう。
磁石とは、
古代ギリシャ時代に発見された不思議な石
と思っておけばいい。
どうやら、ある羊飼いが鉄の杖を地面についたところ、杖が地面にくっついてしまった事件が起こった。
この偶然のハプニングから、磁石が発見されたらしいんだ。

普通の石ころとは違って、「不思議な力が働いている石」が磁石というわけ。
続いては磁力だね。
磁力とはズバリ、
磁石に働く力のこと
だね。

さっき磁石とは「不思議な石」と言ったけど、何が不思議かっていうと、
この石には「ある力」が働いているからなんだ。
具体的にどういう力かというと、
を持っているよ。
中1理科の「力の種類」でちょっと勉強したけど、磁石には N 極と S 極があって、
という性質があるね。

こんな感じで、磁石に働く力を「磁力」と呼んでいるんだ。
磁界とは、
磁力が働く状態になっている空間のこと
を言うよ。
例えば、ここに磁石がポンと置いてあるとしよう。
そして、その磁石の磁力がこの範囲に働いている。
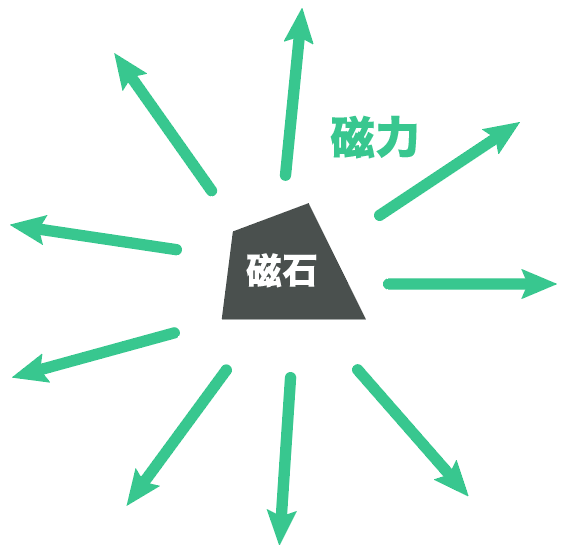
この時、磁力が働いている範囲を「磁界」と呼んでいるんだね。
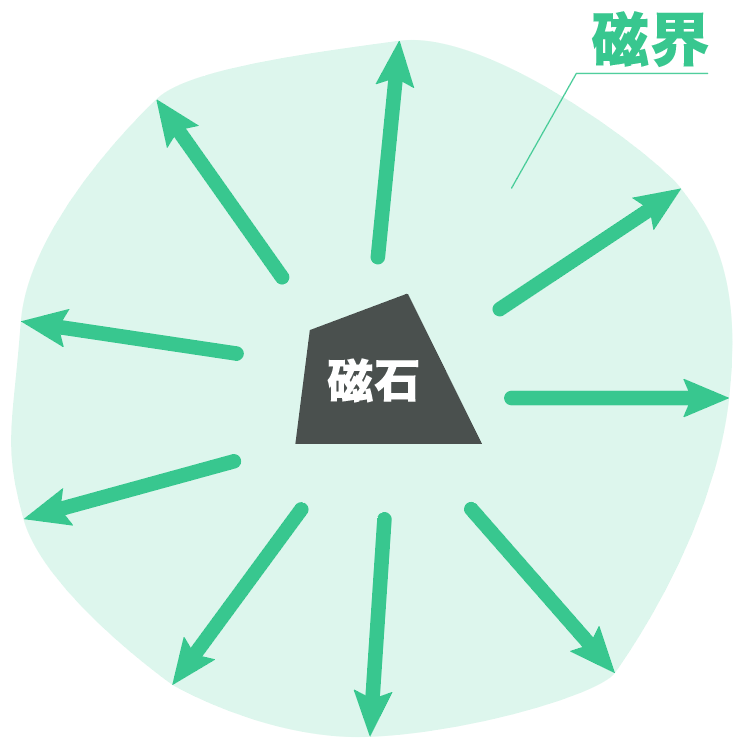
さっき紹介した「磁界」には「ある方向性」があることが発見されたんだ。
それは、
N 極から S 極に向かう
というもの。

例えば、ある磁界の中に、方位磁針を置くと 「ある方向」を指し示すことになる。
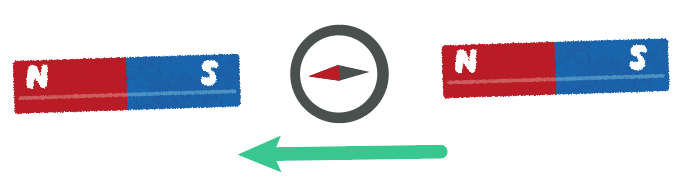
なぜなら、方位磁針の針は磁石になっていて、Nの部分にN極、反対側はS極になってるからだ。
だから、方位磁針の針のN極はS極がある方を向くはず。
このN極からS極への方向性を「磁界の向き」というよ。
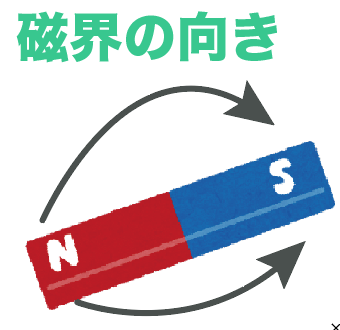
で、「磁界の向き」を線で表したものを「磁力線」と呼んでいるんだ。
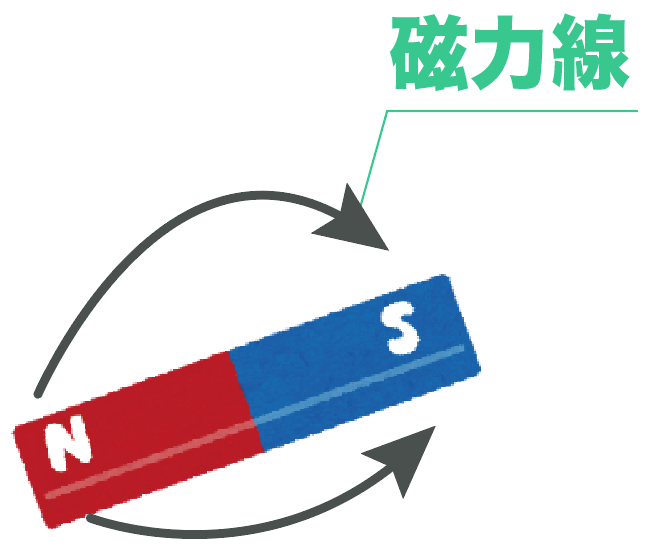
磁力線をかきたいときは、磁界の中に方位磁針を置いて、 N 極が示す方向を線で結んでやるといいぜ。

という感じで、
というキーワードをまずは押さえていこう!
次はいよいよ「右ねじの法則の使い方」を見ていくよ。
そんじゃねー
Ken
中2理科の電気の単元で、
とか見てきたけど、もう1個、中学理科で覚えておく公式があるんだ。
それは、
電力量の計算公式
だ。
電力量とは、ズバリ
電流が流れたときに生じる電気エネルギーの総量のこと
だね。
単位は熱量と同じジュール [J] を使うよ。
計算公式も熱量と同じで、
(電力量) = (電力) × (電流を流した時間)
なんだ。

例えば、300 W の電化製品を100秒使った場合を考えてみよう。
この場合、電力量を求める公式を使って、
電力量 = 電力×電流を流した時間
= 300 × 100
= 30,000 [J]
という電力量になるね。
ここまで電力量の計算方法わかった。
それに加えて知っておきたいのが、
Wh
という新しい単位だね。
これはどういうやつなのかというと、
1Wの電力を1時間消費したときの電力量のこと
だ。
1時間が3600秒だから、
1Wh = 1W × 3600
= 3600 [J]
のことを表しているよ。
ちなみにWhはだけでなく kWh というものも使われていて、これはWhに「キロ」をつけただけ。
1[kWh] は [Wh] の1000倍。
1 [kWh] = 1000 [Wh] になるね。
以上が電力量の紹介だったね。
実はこの「電力量」は僕らの生活に身近なもの。
電気代を支払う時には「電力量」を基準として、お金を払うことになってるんだ。
試しに、僕が平成31年2月に使用した電力量をさらしてみよう。
請求書を見てたところ、
103kWh
だったよ。
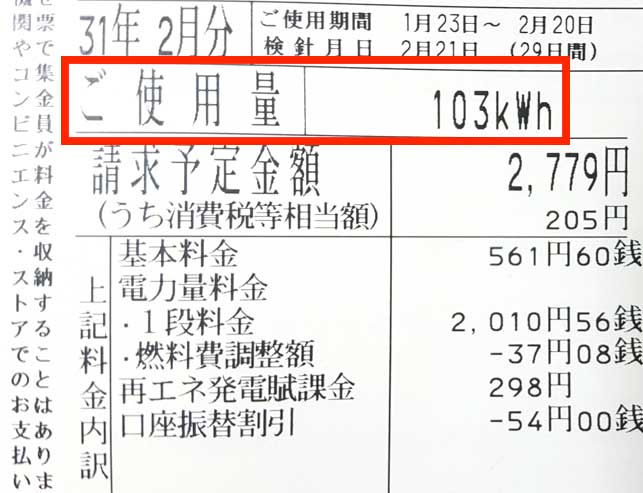
このkWhをジュールの単位に直してやると、
103×1000×3600
=370,800,000 [J]
の電気エネルギーを消費してしまっていたことになる。
これを電力使用日数の29で割ると、
370,800,000 [J] ÷ 29
= 12,786,206[J]
を1日あたり使っていたことになる。
これはどれくらいの消費電力なのか?
具体的な例に落とし込んでみると、
1200 W のドライヤーを10,655秒使っている
ぐらいの電力量。

この10,655秒を時間に直してやると、
約3時間!
ドライヤーを3時間ぶっ続けで使ってるぐらい、僕は平成31年の2月に電力を消費してしまっていたんだ。
いやあ、環境破壊しちゃてるね。
このように自分が使った電力量を確認してみると、理解が深まるから領収書をチェックしてみてね。
そんじゃねー
中学2年生の電気ではいろんな公式でできて大変!
ここまで
を勉強してきたけど、もう一つ勉強しなきゃいけないのが
熱量を求める計算公式
だ。
電気の分野でいう「熱量」とは、
電流を流したときに発生する熱量のこと。
単位はジュール [J]を使っていくよ。
で、この熱量の計算公式は次の式で表せるんだ。
熱量 = 電力×時間
だね。

熱量をJ、電力をW、電流が流れた時間をsとすると、
J=Ws
になる。
それもそのはず。
「電力」は1秒あたりに生じる電気エネルギーのことだったね?
この電力に「電流が流れた秒数」をかけてやれば、「電気エネルギーの大きさ」を計算できるわけだ。
例えば、1000ワットの電熱線に5秒電流を流したときに生じる熱量を考えてみよう。
さっきの公式を使えば、
熱量=電力×時間= 1000 × 5
= 5000 [J]
という感じで、
5000ジュールの熱量が発生するとわかる!!!
「熱量」というやつは、僕らの生活で身近に使われているよ。
例えば、食品の裏側の成分表示。
エネルギーの欄にカロリー表記がされているよね?

実はこの「カロリー」は熱量の単位のこと。
ジュールではなくカロリーという単位を使っているだけで、言ってることは同じなんだ。
「カロリー」という単位は
水1gの温度を1度上げるために必要な熱量のこと。
1カロリーをジュールで表してあげると、
約4.2 J
に相当するものなんだ。

だから、単位をジュールからカロリーに変えたいときは、
ジュールを4.2で割ればカロリーになるね。
例えば、5000 [J] は何カロリーなのか調べてみよう。
ジュールをカロリーに直すためには4.2で割ればいいから、
5000÷4.2
=1190 cal
という感じで「1190 cal」になるね。
ちなみに食品の栄養表示のカロリーはただのカロリーではなく、
キロカロリー(kcal)
で表示されることが多い。
キロカロリー(kcal)はカロリーを1000倍した単位になっているよ。
メートルとキロメートルの関係と同じで、mからkmに直したいときは1000分の一すればいいね。
例えば、さっきの1190カロリーは、1000分の1してキロカロリーに直すと、
1190÷1000
= 1.19 kcal
になる。
次は「電力量の計算公式」を勉強していこう!
そんじゃねー
Ken

中2理科で新しく出てくるのが「電力」という言葉。
電力とはズバリ、
1秒あたりに使われる電気エネルギーの大きさのこと
だ。
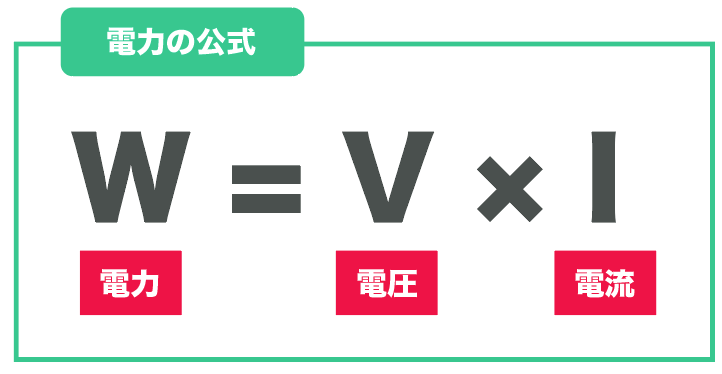
この電力を計算できる公式は
電力[W] = 電圧×電流
電圧をV、電流をI、電力をWとしてアルファベット表記で表すと
W = VI
になるね。
例えば、電源電圧が10 Vで、抵抗に0.2Aの電流が流れたとしよう。
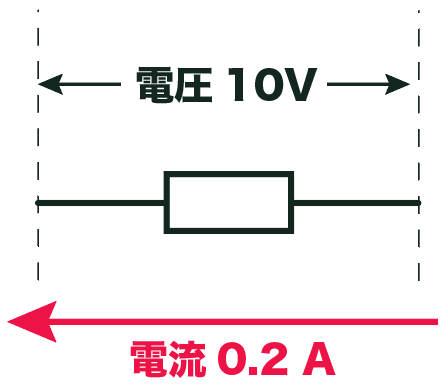
この抵抗に発生している電力は「電圧」と「電流」をかけて
電力[W] = 電圧×電流
=10×0.2
= 2 [W]
になるわけだ。
電力の計算の公式は簡単。なにせ、
電圧に電流をかけるだけ
だからね。
だがしかし、テストまでに公式を忘れないか心配だよね。
そんな時のために、電力の公式の語呂合わせを考えてみたよ。
WにVサイン
だ。
アルファベット表記で電力の計算公式を表していて、
を表しているんだね。

語呂のシチュエーションとしては、
カメラの前で W の形に V サインしてるやつを想像してみてほしい。

2つでVサインをしてWを作っているわけね。
あと、電力の公式で知っておきたいのは、
オームの法則を使えば「W=VI」以外の公式に変化する
ってことかな。
前回勉強したオームの法則の公式を使うと、公式の表現の幅が広がってくるんだ。
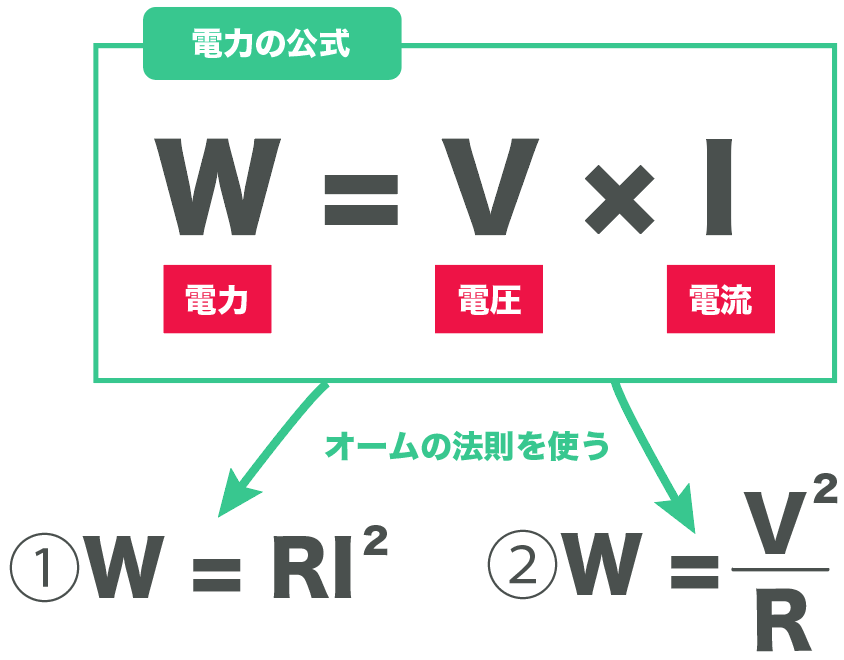
例えば先ほどの
W=VI
のVに、オームの法則の「V = RI」を代入してやると、
W = VI
W = RI²
になるね。つまり、電力は抵抗と電流で表すと、
電力=抵抗値×電流²
になるんだ。
同じことが、オームの法則の電流の公式(I = R分のV)でもできる。
電力の公式を「抵抗」と「電圧」だけで表すと、
W = VI
W = R分のV²
になる。つまり、電力は電圧と抵抗値で表すと、
電力=電圧² ÷ 抵抗値
でもあらわせるんだ。
このように、電力の公式はオームの法則を絡めると力が倍増。

そんじゃねー
前回、オームの法則の基本的な問題の解き方を見てきたね。
今日はもう一歩踏み込んで、
ちょっと難しい応用問題にチャレンジしていこう。
オームの法則の応用問題はだいたい次の3つのパターンだよ。
まずは直列回路なんだけど、抵抗の数が2つ以上の問題ね。
例えばこんな感じ↓
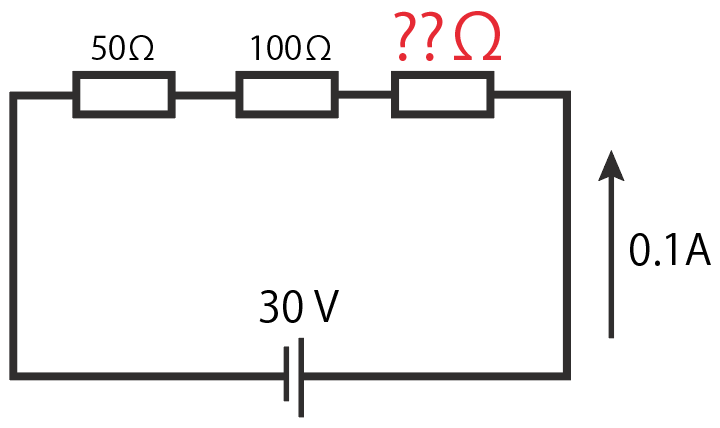
それぞれの抵抗にかかる電圧の大きさを求めていけばいいね。
一番左の抵抗値には0.1Aの電流が流れていて、しかも抵抗値が50Ω。
こいつでオームの法則を使ってやると、
$$V = RI$$
$$= 50 × 0.1$$
$$= 5 [V]$$
となって、5ボルトの電圧がかかっていることになる。
そして、その隣の100Ωの抵抗でも同じように0.1 Aの電流が流れているね。
なぜなら、直列回路では全体に流れる電流の大きさが等しいからさ。
で、こいつでも同じようにオームの法則を使ってやると、
$$V = RI$$
$$= 100 × 0.1$$
$$= 10 [V]$$
になる。
電源電圧の30Vからそれぞれの抵抗に5Vと10 V がかかっているから、最後の一番右の抵抗にかかっている電圧は
$$30-5-10$$
$$= 15 [V]$$
がかかっていることになる。
この抵抗でオームの法則を使ってやると、
$$R = \frac{V}{I}$$
$$= \frac{15}{0.1}$$
$$= 150 [Ω]$$
になるね。
今度は並列回路で抵抗の数が増えるパターンだね。
例えば次のような問題。
3つの抵抗が並列につながっている回路で、抵抗値がそれぞれ20Ω、50Ω、100Ωだとしよう。電源電圧が10 [V]のとき、回路全体に流れる電流の大きさを求めよ
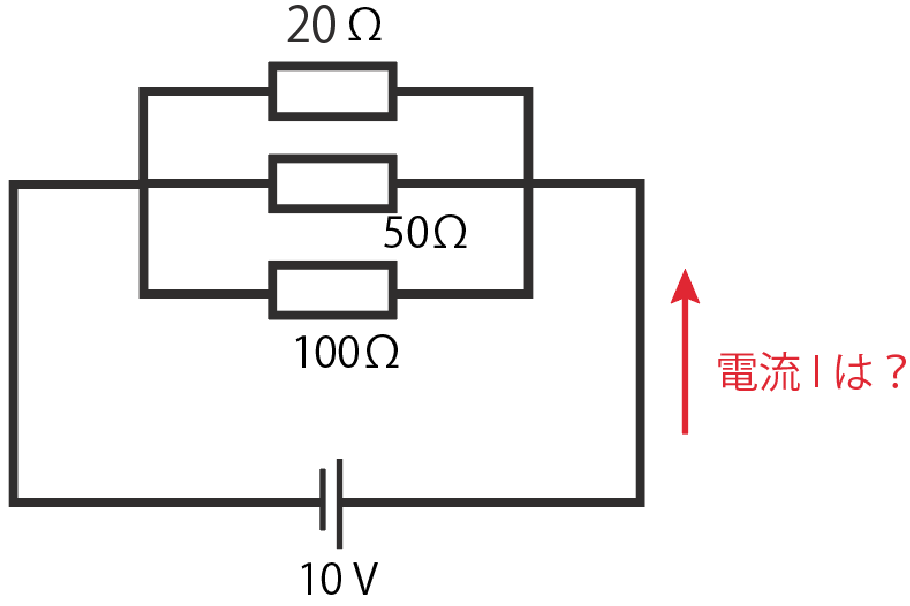
この問題の解き方は、
で回路全体の電流の大きさが求められるね。
並列回路では全ての抵抗に等しく電源電圧がかかる。
一番上の20Ωの抵抗でオームの法則を使うと、
$$I =\frac{V}{R}$$
$$= \frac{10}{20}$$
$$= 0.5 [A]$$
その下の50Ωの抵抗では
$$I =\frac{V}{R}$$
$$I =\frac{10}{50}$$
$$= 0.2 [A]$$
一番下の100Ωの抵抗では、
$$I =\frac{V}{R}$$
$$I =\frac{10}{100}$$
$$= 0.1 [A]$$
になる。
で、これら3つの枝分かれ後の電流を全て足したやつが「回路全体に流れる電流の大きさ」になるから、
$$0.5 + 0.2 + 0.1$$
$$= 0.8 [A]$$
が正解だ!
最後の問題は直列回路と並列回路が混合している問題だね。
例えば次のような感じ。
電源電圧が10 V、全体に流れる電流の大きさが0.2A。左の直列回路の抵抗値が30Ωだとしよう。並列回路の下の抵抗値が25Ωの時、残りの上の抵抗値を求めよ
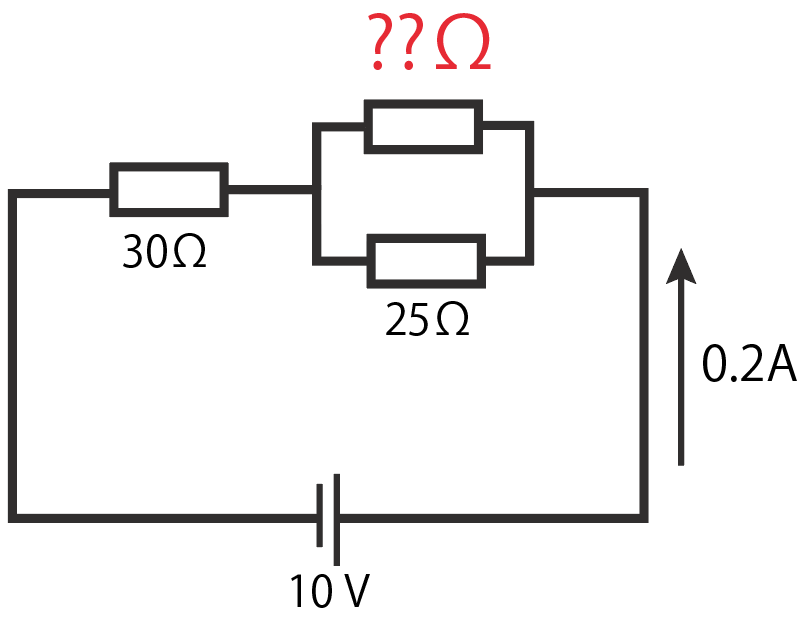
まず直列回路になっている左の抵抗にかかる電圧の大きさを求めてやろう。
この抵抗は30Ωで0.2Aの電流が流れているから、オームの法則を使うと、
$$V=RI$$
$$= 30×0.2$$
$$= 6 [V]$$
になるね。
電源電圧が10 V だったから、右の並列回路には残りの4Vがかかっていることになる。
回路全体に流れる電流は0.2Aだったから、この並列回路全体の合成抵抗は、
$$電圧÷電流$$
$$= 4 ÷ 0.2$$
$$= 20 [Ω]$$
になる。
次は右の並列回路の合成抵抗から上の抵抗の値を求めていこう。
詳しくは「並列回路の電圧・電流・抵抗の求め方」を読んでほしいんだけど、
全体の抵抗の逆数は各抵抗にかかる抵抗の逆数を足したものに等しい
だったね?
上の抵抗をRとしてやると、この右の並列回路の合成抵抗R’は
R’分の1 = R分の1 + 25分の1
になるはず。
で、さっき合成抵抗R’は20Ωってわかったから、
20分の1 = R分の1 + 25分の1
というRについての方程式ができるね。
分数を含む一次方程式の解き方でといてやると、
$$\frac{1}{20} = \frac{1}{R} + \frac{1}{25}$$
$$5R = 100 + 4R$$
$$R = 100 [Ω]$$
になる。
ふう、長かったぜ。
オームの法則の応用問題はこんな感じかな!
やっぱ応用問題を解くためには基礎が大事で、
を理解している必要があるね。
問題を解いていてあやふやだったら復習してみて。
そんじゃねー
Ken

中学2年生の電気の分野で重要なのは「オームの法則」だったね。
前回はオームの法則の覚え方を見てきたけど、今日はもう一歩踏み込んで、
オームの法則を使った実践的な練習問題
にチャレンジしていこう。
オームの法則の問題では、
の2種類の回路で、それぞれ電流・電圧・抵抗を計算する問題が出題されるよ。
ということで、この記事では、
直列・並列回路における電流・電圧・抵抗をオームの法則で求める問題を一緒に解いていこう。
直列回路の問題から。
まずは直列回路の電流を求めるパターンだね。
例えば次のような問題。
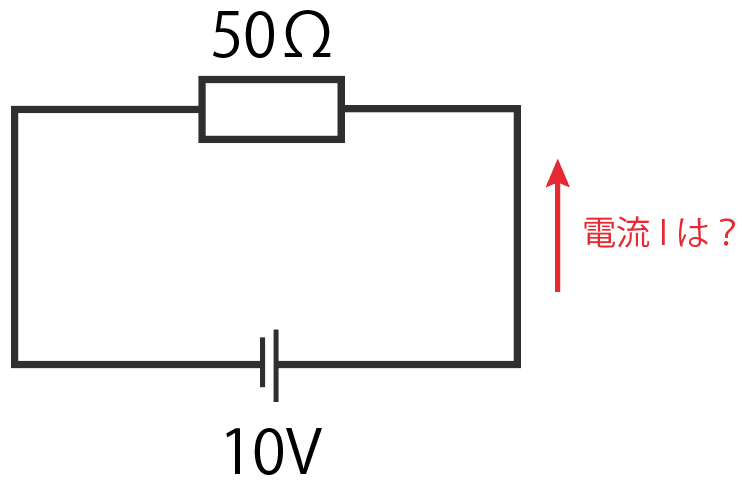
これは抵抗にかかる電流をオームの法則で求めてあげればOK。
電流を求めるオームの法則は、
I = R分のV
だったね?
こいつに抵抗R= 50Ω、電圧V =10Vを代入してやると、
I = R分のV
I = 50分の10
I = 0.2
と出てくるから、電流は0.2Aだ!
次は電圧だ。
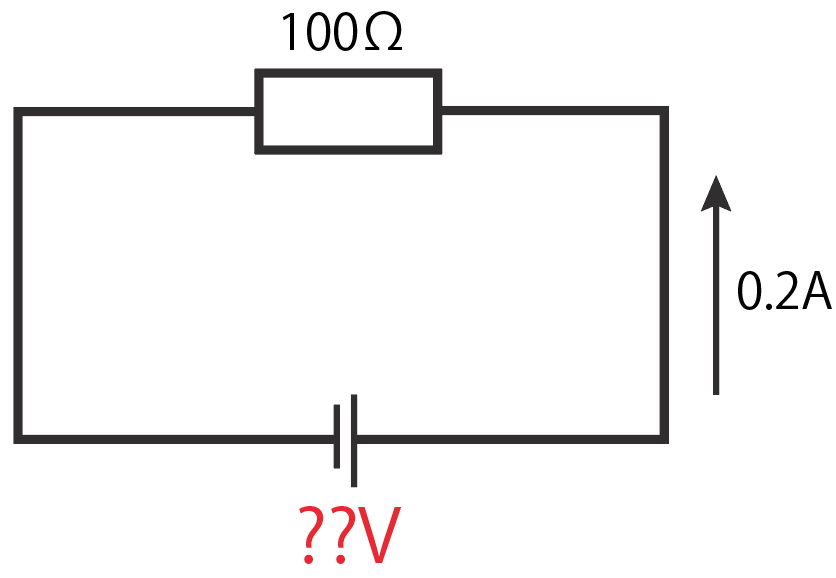
この問題もオームの法則を使えば一発で計算できる。
電圧を求めるオームの法則は、
V=RI
だったね。
こいつに抵抗R=100Ω、電流I=0.2Aを代入してやると、
V = RI
V = 100×0.2
V = 20[V]
ということで、20 [V]が電源の電圧だ!
最後に直列回路の抵抗値を求めていこう!
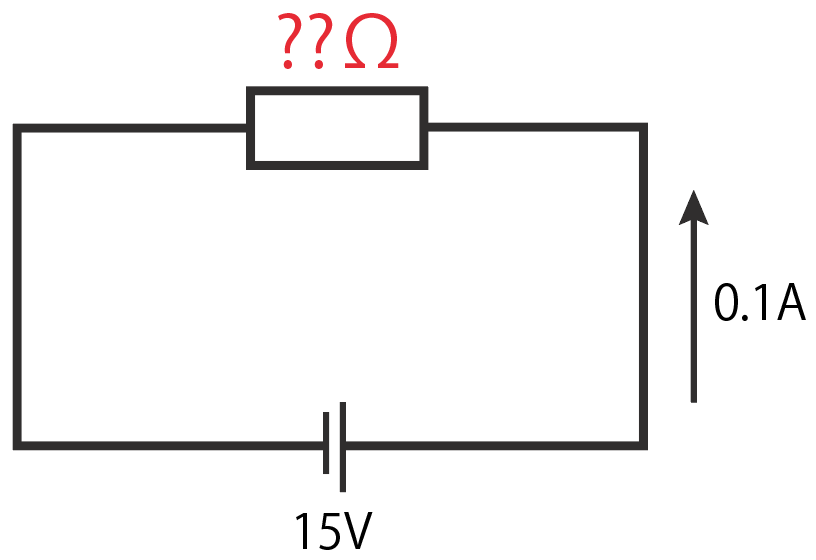
抵抗を求めるオームの法則は
R=I分のV
オームの法則に電源電圧15V、流れる電流の大きさ0.1Aを代入して、
R=I分のV
R=0.1分の15
R= 150 [Ω]
になるから、この抵抗値は150Ωというのが正解だ!
次は並列回路のオームの法則の問題。
電圧・電流・抵抗の3つの値を求める問題をそれぞれといていこう。
例えば次のような問題かな。
電源電圧がわからなくて、並列回路の抵抗値がそれぞれ50Ωと100Ω。枝分かれする前の電流が0.3アンペアだとしよう。この時の電源電圧を求めよ
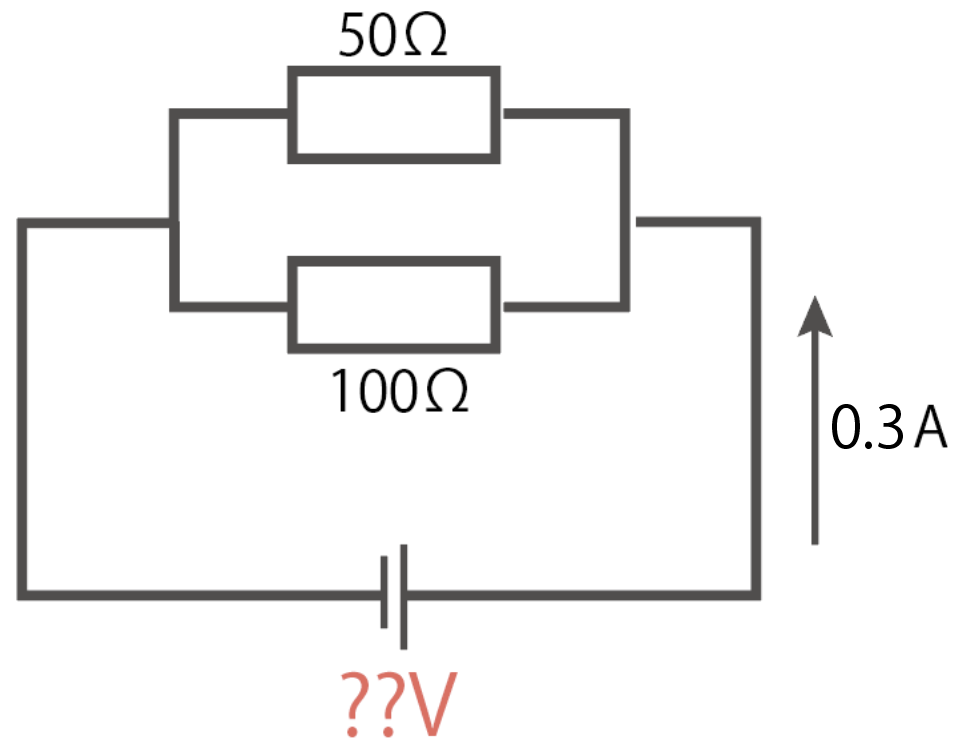
これは並列回路の性質である
抵抗にかかる電圧はすべて等しい
という性質を使おう。
枝分かれした抵抗に流れる電流を計算して、そいつを足すと0.3Aになるという方程式を作ればオッケー。
今回使うのはオームの法則の電流バージョンの
I = R分のV
だ。
電源電圧をVとすると、それぞれの抵抗に流れる電流は
になる。こいつらを足すと枝分かれ前の電流0.3Aになるから、
これを分数が含まれる一次方程式の解き方で解いてやろう。
両辺に100をかけて
V + 2V = 30
3V = 30
V = 10
と出てくる。つまり、電源電圧は10 [V]ってわけ。
続いては、並列回路の電流を求める問題だ。
抵抗値がそれぞれ200Ω、100Ωの抵抗が並列につながっていて、電源電圧が20 V だとしよう。この時の回路全体に流れる電流を求めよ
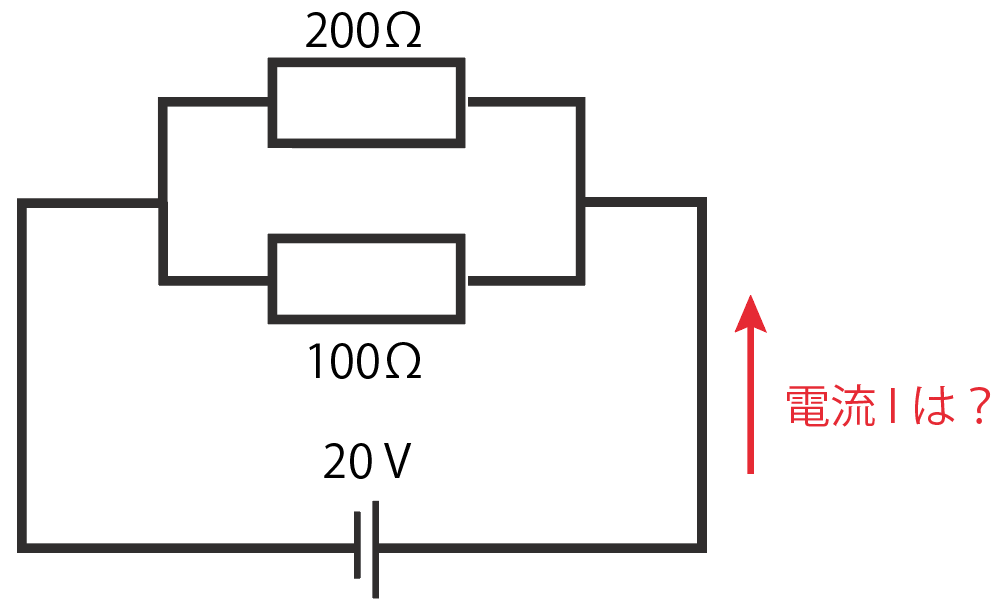
この問題は、
という2ステップで解けるね。
一番上の100オームの抵抗に流れる電流は、オームの法則を使うと、
I = R分のV
= 100分の20
= 0.2 [A]
さらに2つ目の下の200オームの抵抗に流れる電流は
I = R分のV
= 200分の20
= 0.1 [A]
回路全体に流れる電流はそいつらを足したやつだから
0.2+0.1
= 0.3 [A]
が正解だ。
次は抵抗を求めてみよう。
電源電圧が10 V、 枝分かれ前の回路全体に流れる電流が0.3アンペアという並列回路があったとしよう。片方の抵抗値が100Ωの時、もう一方の抵抗値を求めよ

まず抵抗値がわかっている下の抵抗に流れる電流の大きさを計算してみよう。
オームの法則を使ってやると、
I = R分のV
= 100分の10
= 0.1 [A]
という電流が100Ωの抵抗には流れていることになる。
で、問題文によると回路全体には0.3 [A]流れているから、そいつからさっきの0.1 [A]を引いてやれば、もう片方の抵抗に流れている電流の大きさがわかるね。
つまり、
0.3 – 0.1
= 0.2 [A]
だ。
あとは、電流0.2 [A]が流れている抵抗の抵抗値を求めるだけだね。
並列回路の電圧は全ての抵抗で等しいから、この抵抗にも10Vかかってるはず。
この抵抗でもオームの法則を使ってやれば、
R = I分のV
= 0.2分の10
= 50 [Ω]
が正解。
以上がオームの法則の基本的な計算問題だったよ。
この他にも応用問題として例えば、
が出てくるね。

そんじゃねー
中2理科の電気の分野で狙われやすいのがオームの法則。
詳しくは前回の「オームの法則とは?」を参考にしてほしいんだけど、
なにせ、この法則は、
覚えづらい!!
「V = RI?」
「電圧=抵抗×電流?」
知るかよ?そんなん。
ただ、幸か不幸かこのオームの法則はむちゃくちゃテストに出やすいから、
語呂合わせ・指隠し
という2つの方法で覚えていこう。
まずは語呂合わせから。
オームの法則の表し方の
の3パターンで見ていこう。
オームの法則で一番出てきやすいのが
アルファベット表記の公式。
電圧をV、抵抗をR、電流をIとすると、
V=RI
になる公式だったよね。
この英語表記のオームの法則の覚え方で使える語呂合わせは次のものだ。
部室にアライグマ
シチュエーションは部活動の拠点である「部室」を想像してほしい。
なんとね、その部室に「アライグマ」が紛れ込んでしまったんだ。
アライグマ。
たぶん、この学校は山の中にあったらんだろうね。
なぜこの語呂でオームの法則を覚えられるんだろう?
じつはそれは全部カタカナにしてやるとわかりやすいよ。
ブ(V)シツ二(=)アライ(RI)グマ
そう。
という感じで、オームの法則アルファベット標識の全てを網羅しているんだ。
ポイントはカタカナの「二」をイコールの「=」として捉えられるかだね。
ここさえクリアしてやればオームの法則ももらったも同然。
オームの法則を忘れそうになった時は、
部室に紛れ込んでしまったアライグマをイメージしよう。

きっとオームの法則を思い出せるはずだ。
が、しかしだよ?
オームの法則は英語表記だけでなく、日本語で
電圧 = 抵抗×電流
と表す時もあるよね。
じつは、この日本語表記のオームの法則は、
圧力に抵抗して流される
という簡単な語呂で覚えられる。
これはそうだな、生徒会で異を唱えた1人の生徒を想像してくれ。
そいつ以外は満場一致で制服の自由化が決定していて、周囲には反対意見が出せない圧力がありありだった。
だけど、そいつは勇気を出して圧力に抵抗した。

でも、最終的には折れちゃったんだよ。流されちゃったんだ。

勇気ある一人の生徒が圧力に抵抗しだけど、虚しく周囲に流されてしまったシーンをイメージしてもらえれば大丈夫。
この語呂合わせを使えば、
圧(電圧)力に(=)抵抗(抵抗)して流(電流)される
という感じで、
となって、オームの法則の日本語表記である
電圧 = 抵抗×電流
も覚えられたはず。
最後にオームの法則を単位で表した法則の覚え方も伝授しておこう。
単位を見てみると、
ボルト(電圧)=抵抗(オーム)×電流(アンペア)
だったよね。
これらの単位を抜き出してみると、
ボルト=オーム×アンペア
になるよね。
この覚え方としては、
ボルトに青
という語呂だ。

シチュエーションとしては、何かの機械の部品のボルトがあるんだけど、ボルトに色を塗っていた時に、誰かが間違えた。
ボルトの色を黒にするところを青になってしまったんだ。
そこで担当者が一言。
「ボルトに青・・・・」
と思わずつぶやいてしまったシーンを想像してみよう。
この語呂合わせを覚えておけば、
というように、単位でオームの法則を覚えられちゃうな。
また、語呂合わせと同じくらい覚え方でメジャーなのが、
指で隠して覚える方法だ。
このように丸の絵の中に一番上に V、 その左下にR、その右横にIを書いてやる。

そして、上のVとの境界線に÷、下の横の2つの境界線には×付け足してみる。

そうすると、求めたいものを指で隠すだけでオームの法則を思い出せるという仕組みになっているよ。
例えば、電流を求めたい時は電流Iを隠す。
すると、こうなる。
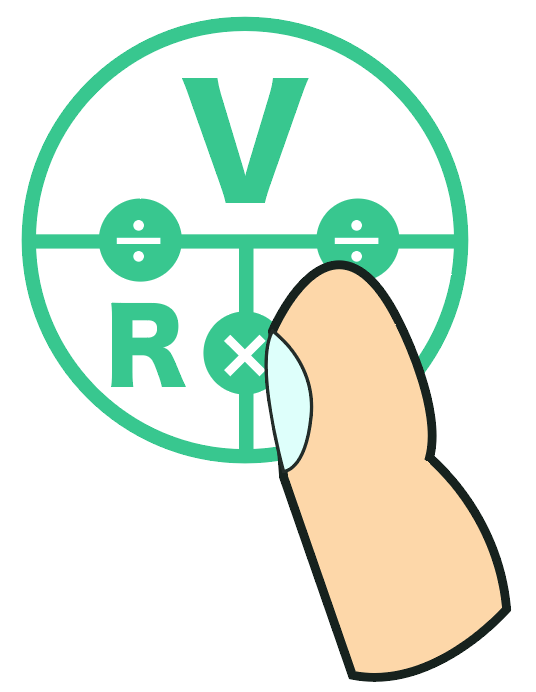
この時、見えているように計算すればいい。
つまり、
電圧÷電流
で抵抗を計算できるわけだね。
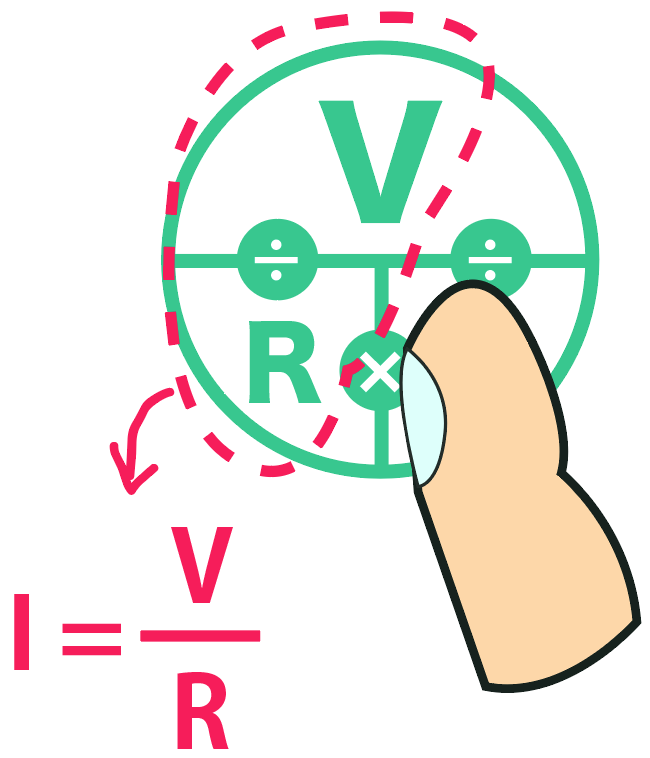
この指隠しを使えば簡単にオームの法則を思い出せるからめちゃくちゃ便利なんだけど、問題は、
丸の中に V・R・Iのどこにどれを配置するか?
ということだ。
この配置を忘れたら指隠しもありゃしない。
この指隠しのポジションの覚え方は、
仮面ライダーだ。

仮面ライダーみたいに、この指隠しの頭の部分にはV がきていて、ツノが生えてるんだ。
これはまるで仮面ライダーの仮面。
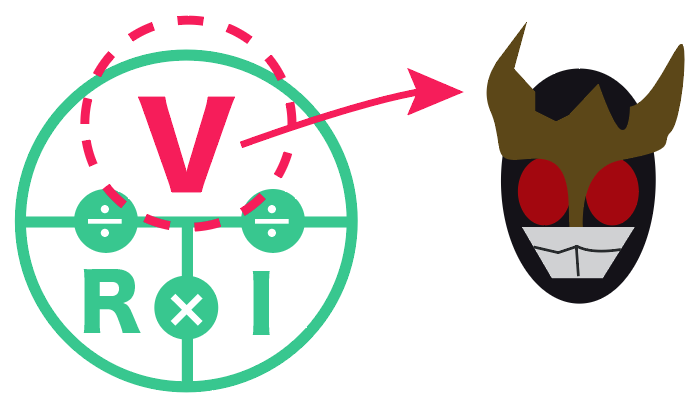
仮面のVをつけたら、あとはその下にあると「R」と「I」をくっつけてあげりゃいいね。
ということで、今日紹介した
の2つの覚え方を使ってオームの法則を頭に刻んでいこう〜!
法則を覚えられたら「オームの法則を使った計算問題」にチャレンジしてみよう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。カーペット、2分割だね。
電気の分野で重要になってくるのが、
オームの法則。
オームの法則とは簡単に言ってしまうと、
ある抵抗にかかる電圧・抵抗値・電流の関係を示した公式
のことだよ。
電圧・抵抗値・電流のどれか2つがわかっていれば、残りの1つがわかっちゃう、という魔法のような法則なんだ。
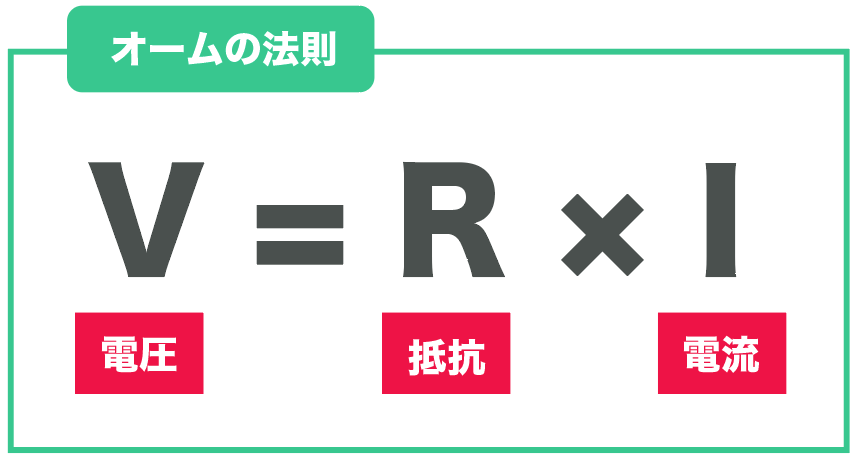
具体的にいうと、オームの法則の公式は
電圧 = 電流 × 抵抗
で、アルファベットで表すと(電圧をV、抵抗をR、電流をI)、
V = RI
になるね。
テストにオームの法則はめちゃくちゃでやすいから、まずは
オームの法則は一体何者なのか?
を説明していくよ。
オームの法則とは、
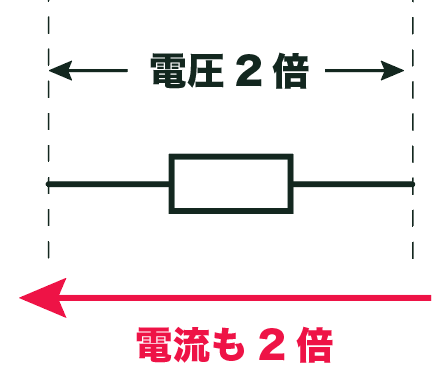
抵抗器に流れる電流の大きさは両端にかかる電圧の大きさに比例する
という法則のこと。
つまり、ある抵抗に電圧を2倍かけたら、抵抗に流れる電流も2倍になるってわけ。
100倍の電圧をかけたら電流も100倍になるし、1000倍の電圧なら1000倍の電流が流れるのね。
オームの法則の何が凄いかって言うと、
物体ごとに電流の流れやすさが違うってことが発見されたことかな。
例えば、3ボルトの電圧をかけた時、1アンペアの電流が流れる物体もあるし、
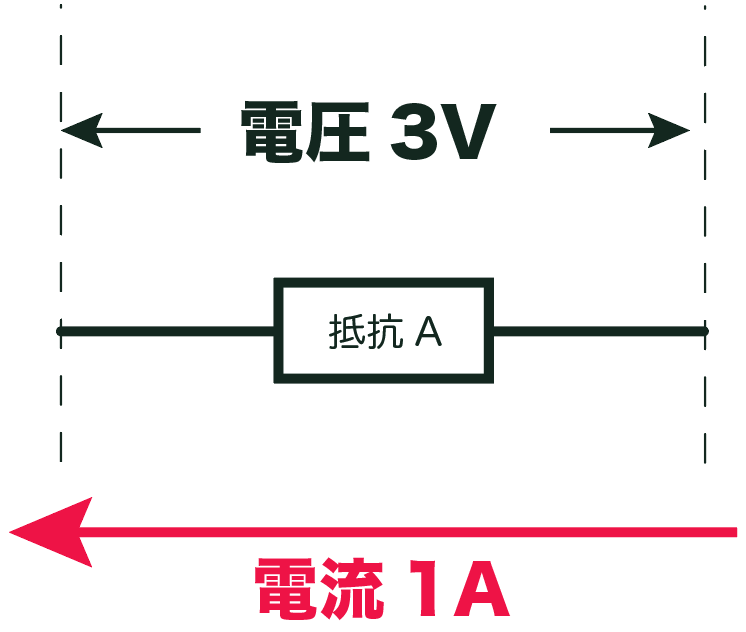
同じ3ボルトをかけても2アンペア流れる物体もあるってわけだ。
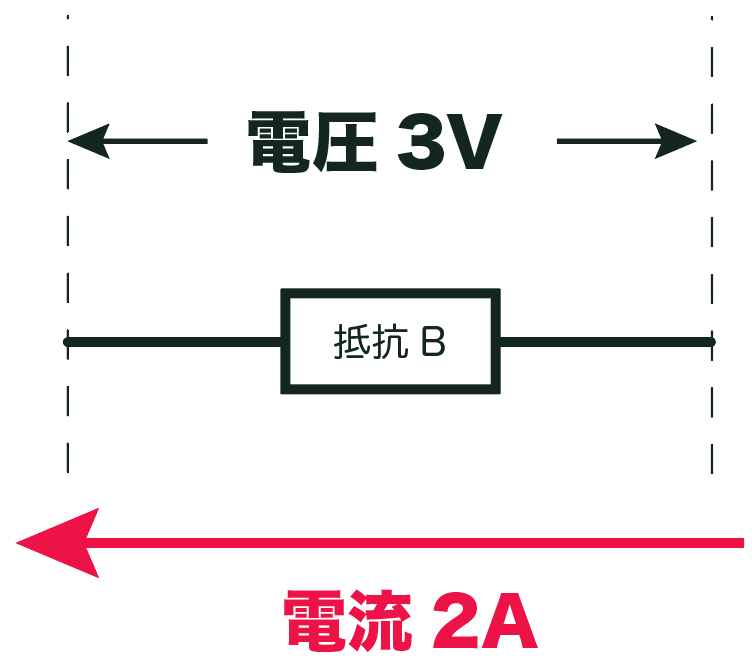
この流れる電流の違いは何なのか??
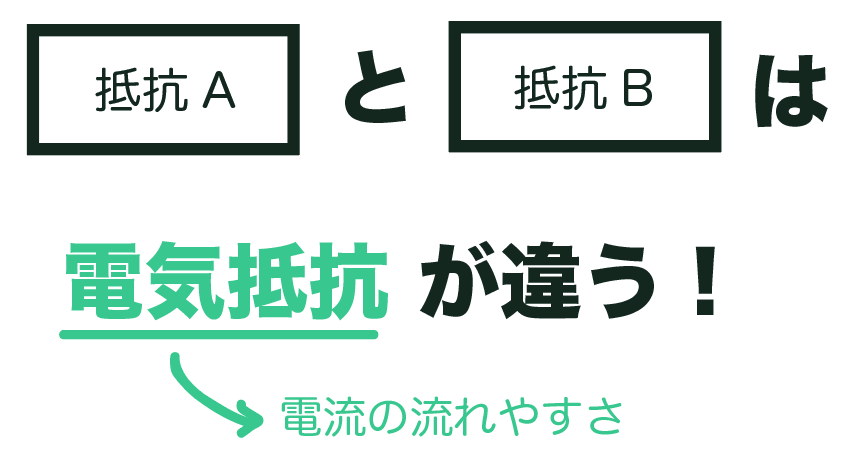
実はこれは、
物体ごとに電気抵抗という「電流の流れやすさが違う」からなんだ。
これを発見したのがオームの法則の最大の功績とも言えるね。
この法則を発見したのはオームの法則の名前にもなっている「ゲオルク・オーム」っていうドイツの人。

https://upload.wikimedia.org/wikipedia/commons/d/dc/Ohm3.gifより
この物理学者が1826年に発見した法則なんだ。
彼は抵抗に電圧をかけていって、その時に流れる電流を計測してみたんだけど、
「電流が電圧の大きさに比例してるやん!」
って気づいてしまったんだね。
電圧と電流は比例関係にあるから、
y = ax
という比例の式で表せる。
xは電圧、yは電流のこと。グラフで書くとこんな感じになるよ↓
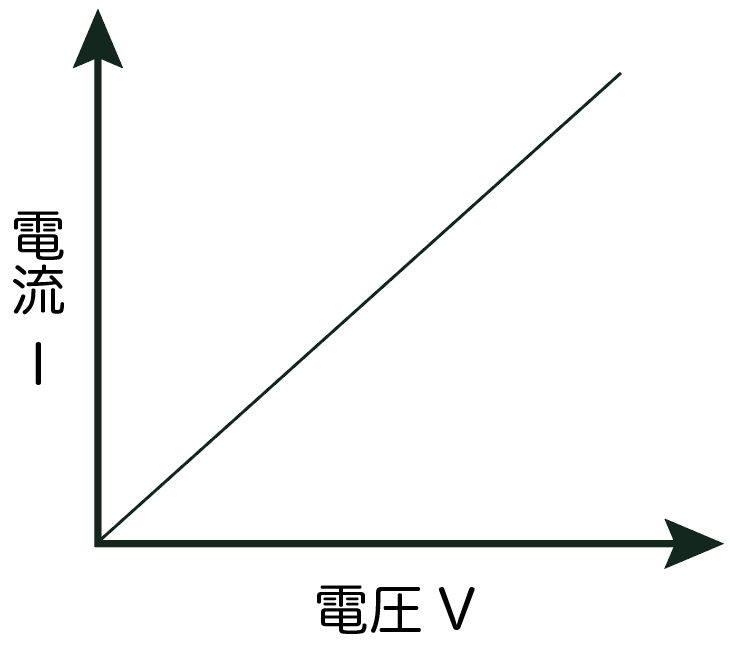
比例だから原点(0, 0)を通っているし、直線のグラフになるはずだね。
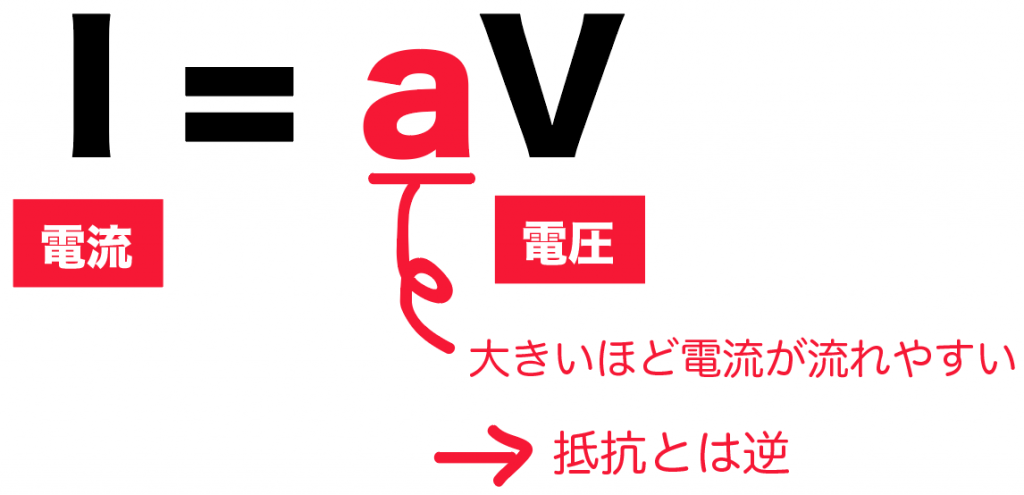
比例定数をaとしてあげれば、
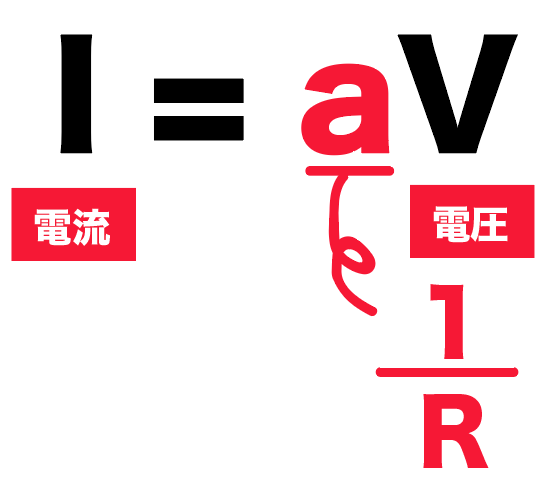
電流 = 比例定数a × 電圧
I = a V
という式が成り立つよ。
※電圧をV、電流をIとする

ここで、比例定数に注目。
こいつが大きければ大きいほど電流が流しやすく、小さければ小さいほど電流が流れにくくなるよね?
つまり、これは「電流の流れやすさ」を表しているんだ。
さっき紹介した電気抵抗とは逆のことだよね。
抵抗は大きければ大きいほど電流が流れにくくなるから、じつはこの比例定数aを逆数にした
a分の1
が抵抗Rのことになる。
つまり、
a = R分の1
だから、これをさっきの
電流 = 比例定数a × 電圧
に代入してあげると、
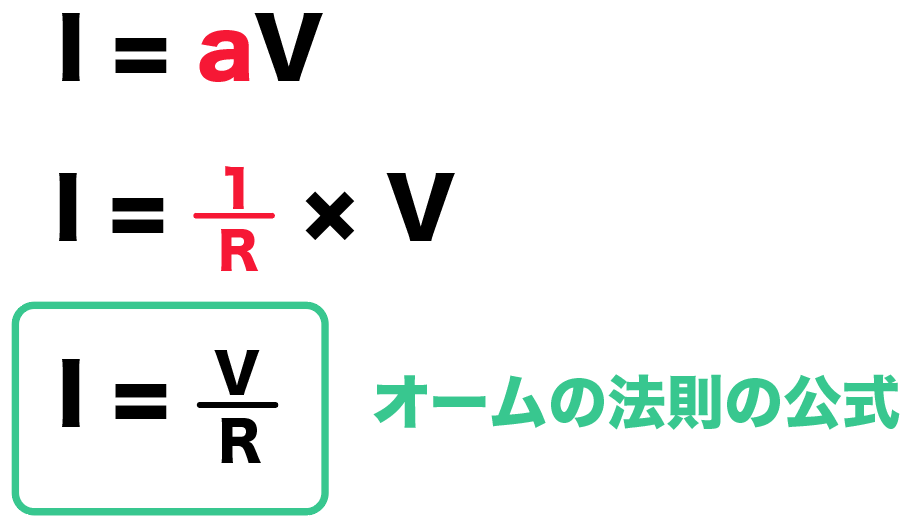
電流 = 比例定数a × 電圧
I = R分の1 × V
※ 抵抗をRとする
これをVについて等式変形してやると、
V = RI
という最初に紹介したオームの法則の公式になるわけだ。
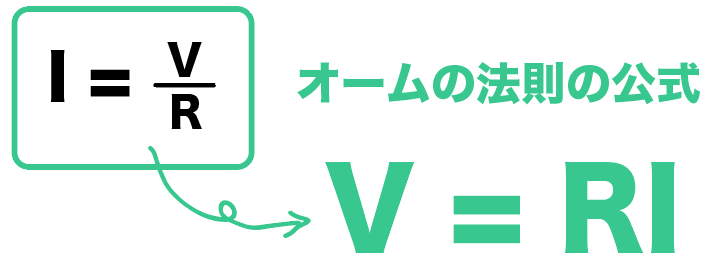
これがオームの法則の概要だね。

V = RI
公式を覚えるの大変かもしれないけど、本質さえ押さえておけば公式を忘れても大丈夫。
そんじゃねー
Ken
こんにちは!この記事を書いてるKenだよ。ペッパーランチ、注入だね。
今日は中2理科の電気の単元で重要になってくる、
電気抵抗とは何か?
を勉強していこう。
電気抵抗とはズバリ、
電流の流れにくさを表した数値のこと
なんだ。単位はオーム(Ω)ね。
こいつが大きければ大きいほど、その物体には電流が流れにくくなるってことね。
例えば、
の電気抵抗を持っている2つの物体があったとしたら、抵抗値の大きい物体Bの方が電流が流れにくいってことね。
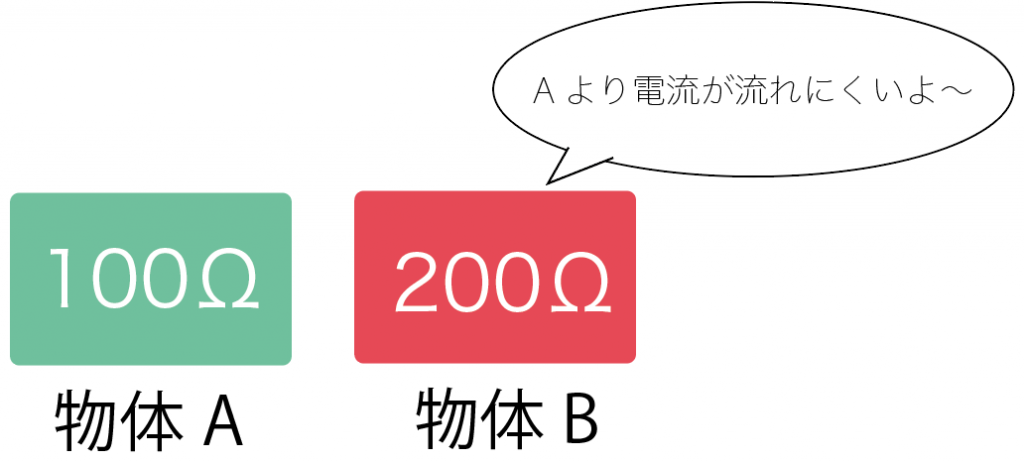
これが電気抵抗の基本だ。
で、この電気抵抗(Rとする)というやつは、その物体にかかる電圧Vと電流Iを使うと、次の式で表すことができるよ。
R= V/I

これは今後むちゃくちゃ頻繁に使うことになるオームの法則ってやつね。
この式からわかるのは、
電圧(V)が一定の時に、分母の 電流(I )が大きければ大きいほど、抵抗値が小さくなるってこと。
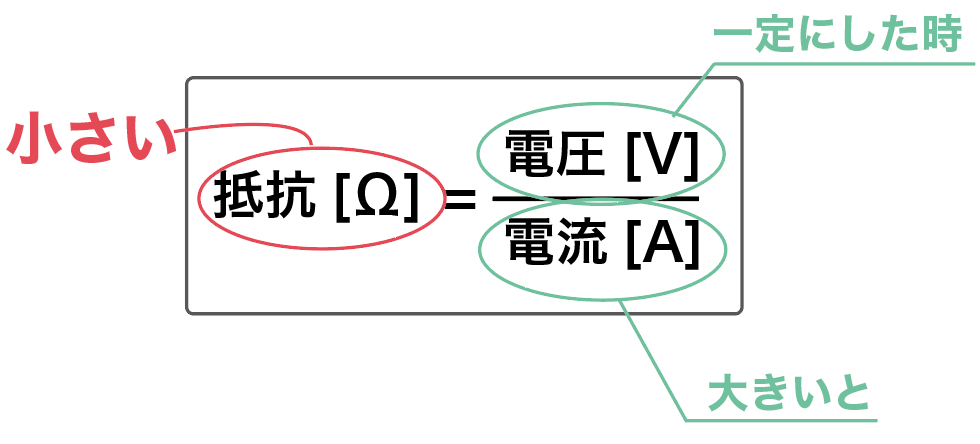
つまり、電圧が同じの時、
大きい電流が流れる物質ほど電気抵抗は小さいってことね。
その逆もまた然りで、電流が小さい場合は分母が小さくなるから抵抗値は大きくなる。
流れる電流が小さいほど電気抵抗は大きいってことになる。
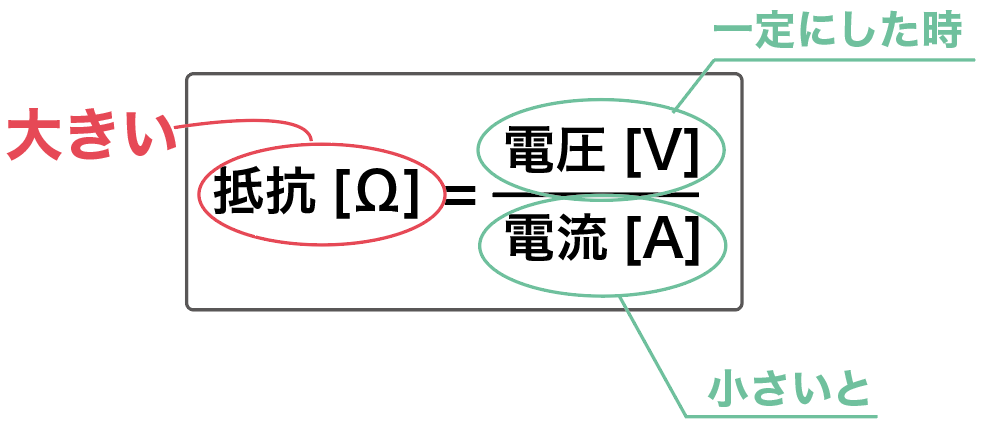
ここまででだいたいの電気抵抗とは何かが見えてきたね。
と、ここで疑問に思うのが、
「抵抗値は何によって決まるのか?」
ってことだよね。
抵抗値が100Ωの物体Aと、200Ωの物体Bは何が違うんだろうって思うはず。
じつは、物体の抵抗値というやつは次の4つの要素によって変化していくんだ。
まず物質の種類によってだね。
そいつが何でできているかによって抵抗値が違ってくるんだ。
なぜなら、物質によって電流の流れやすが異なるからだ。
電流とは電子の流れのことだったよね?
電流の流れは、
物体を構成する原子がどうなっているのか?
によって変化するんだ。
原子がむちゃくちゃ詰まっている構造の物質のなのか?

はたまた、スカスカの構造の物質のなのか?
それによって、電子の通りやすさが変化するから、電流の流れやすさが違ってくるというわけね。
次に物体の温度も抵抗値に影響してくるよ。
温度が高くなるほど抵抗値は大きくなるんだ。
物質の温度が変化すると、物質中の原子は振動動きが大きく、そして速くなる。
そうなると、物質の中の電子は激しく振動している原子に邪魔されて通りにくくなるから、温度が高くなると電流が流れにくくなるんだ。
これはマリオでいうと、ドッスンの落下頻度が高まってしまった状態と同じ。
あれが頻繁に落ちたり上がったりしていたら、いくら熟練のマリオでもくぐり抜けにくくなるはず。
物体の長さによっても抵抗値というのは変わってくるよ。
物体が長ければ長いほど、電気抵抗は大きくなるんだ。

物体が長いと、電子が通らなければならない道のりが増えるよね?
その分、物質の中の原子に邪魔されやすくなっちゃう。
だから、物体が長いと抵抗値も大きくなるってことね。
断面積が大きければ大きいほど抵抗値は小さくなるよ。
断面積っていうのは、物体を切ったときの断面の面積のことだね?
つまり、道路でいう道幅みたいなもんだ。
この断面積が大きくなると当然、電子が通る道幅も大きくなるから電子は通りやすくなる。
つまり、電流は通りやすくなるから抵抗値は小さくなるんだ。
以上が電気抵抗の基本だよ。
最後に復習しておくと、
電気抵抗とは電流の流れにくさのことで、単位はオーム(Ω)を使っていくよ。
で、この電気抵抗ってやつは
によって変化するって覚えておこう。
次はオームの法則を勉強していくよ。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。冷やしおしぼり、最高。
中学理科で電気の単元を勉強していると、
電圧計の使い方
を学んでいくよね?
電圧計とは文字通り、
ある区間にかかる電圧の大きさを計測するもの。
電圧計の使い方はテストに出やすいだけでなく、覚えていれば実験でも活躍できる特典付きだ。
今日はその電圧計の使い方における注意点を2つに絞ってまとめてみたよ。
次の2つの注意点を抑えておこう。
今回は具体例として、
電池に電球をつないだ簡単な回路で、電球にかかる電圧を計測したいケースを考えてみよう。
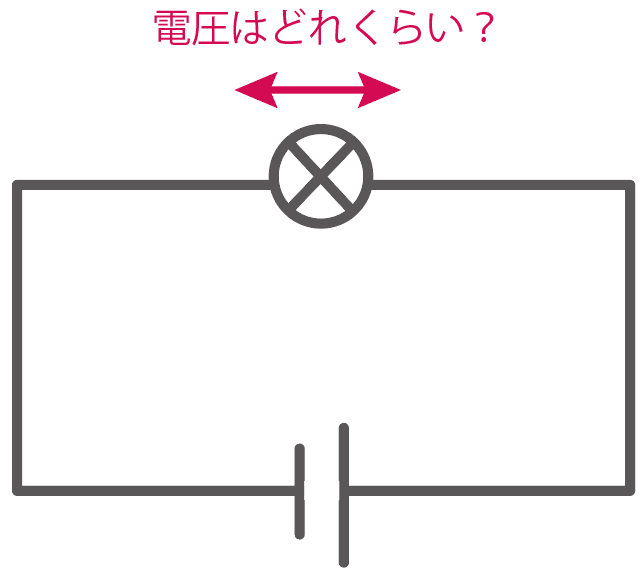
まず知っておきたいのは、
電圧計は並列で回路につなぐってことだ。
電球にかかる電圧を計測したい場合、電球と並列になるように電圧計をつないで、次のようになるはず。
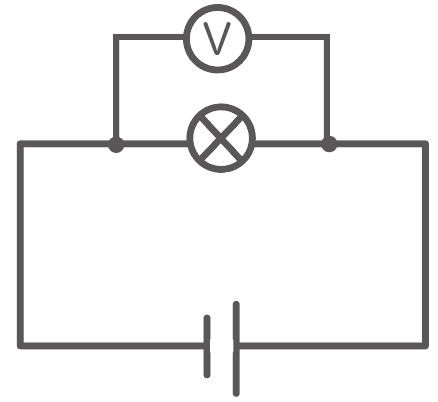
うん。ようは電圧を計測したい区間を
![]()
で、はさめばいいってわけね。
ふむふむ。
えっ。なんで電圧計は並列つなぎじゃないといけないのかって!?
電流計は直列つなぎだったから疑問に思っちゃうよね。
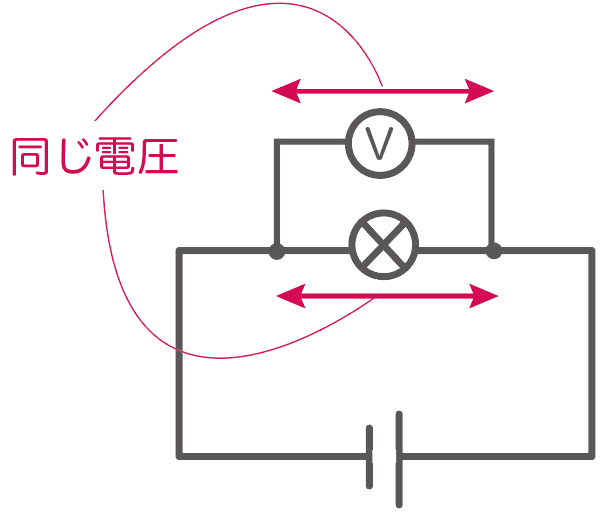
じつはこれ、並列回路には
回路にかかる電圧は全て等しい
という性質があるからなんだ。
さっきの例でいうと、電球と電圧計は並列につながってるから電圧が同じ。
電圧計にかかる電圧を読み取ってやれば、それすなわち電球にかかる電圧ってことになる。
じゃあ逆に、電圧計を直列でつないでしまうとどうなるのか?
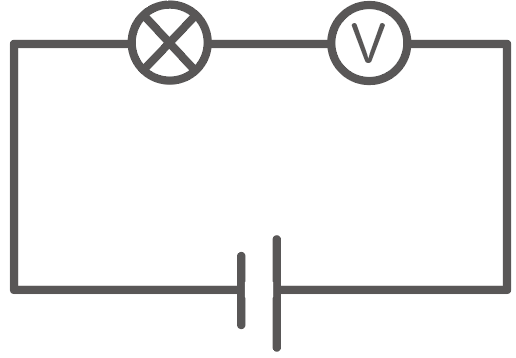
直列回路では電圧は抵抗ごとに異なる
って勉強してきたよね?
つまり、抵抗の大きさによってかかってくる電圧が違うってことね。
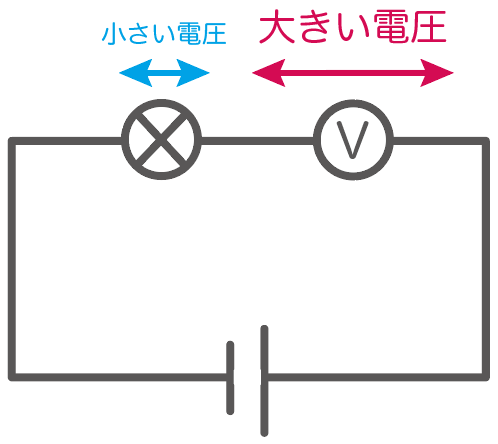
で、電圧計は幸か不幸か、
むちゃくちゃ抵抗が大きい機械
なんだ。
だから、電圧計を直列につないでしまうとさあ大変。
電圧計に大きな電圧がかかってしまい、電圧計は壊れるかもしれないし、電圧を計測したかった区間に電圧がほとんどかからなくなってしまうのね。
電圧計は並列つなぎにすべきってことはわかった。
あとは、電圧計を回路につなぐだけ。
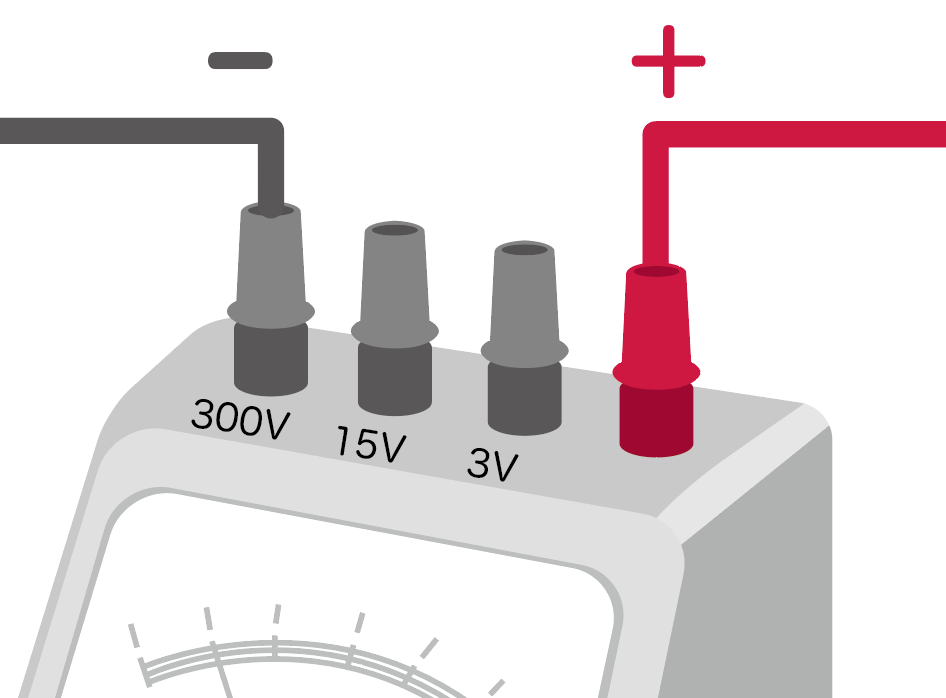
このときに注意したいのが、
電圧計をつなぐときは、電流が流れてくる方向に+端子、その逆側に-端子をつないでいくよ。
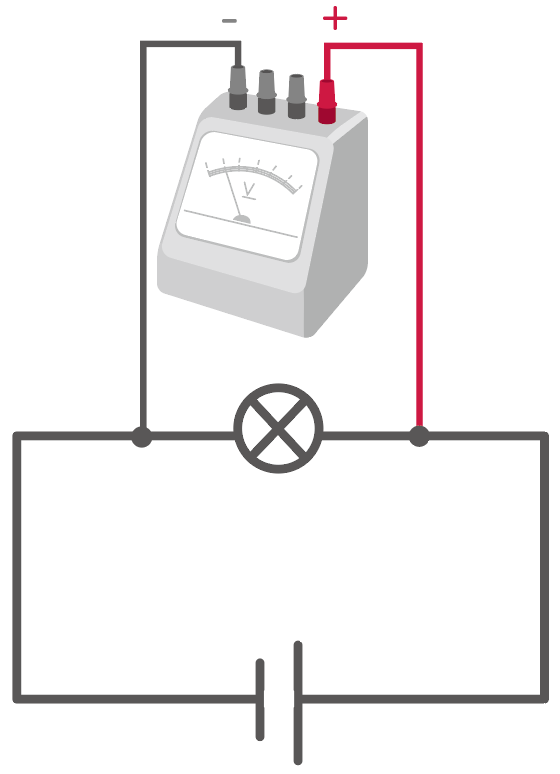
で、ポイントはマイナス端子のつなぎ方。
電圧計にはマイナスの端子が計測できるマックスの電圧の単位ごとに、
の3種類がある。
そのうちのどれかに繋げばいいんだけど、順番としては、
単位が大きいマイナス端子からつなぐ
というのが鉄則だ。
つまり、一番大きい
300V
のマイナス端子からだね。
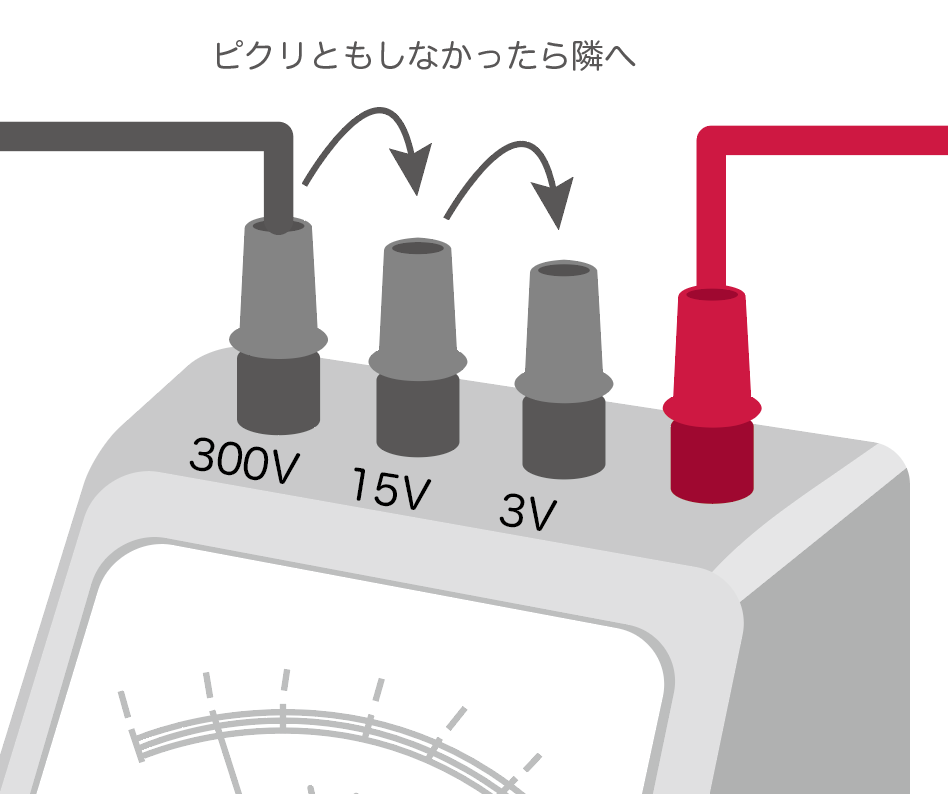
その理由としては、
予想外に大きな電圧が出ても、電圧計が振り切らないようにするためだね。
ぶっちゃけ、電圧計を使うまでどのくらいの電圧が流れているかはわからない。
だから電圧計で電圧を計測するときは、一番単位が大きい端子から始めるのがいいね。
これなら電圧が200Vでも耐えられるし、100Vでも耐えられる。
もし、300Vで針が振れなかったときは、端子を3V、もしくは15Vというように変更していこう。
電圧計の使い方をマスターしたら、次は「電気抵抗とは何か」を勉強していこう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。お湯、汲んできたね。
中学理科の電気で狙われやすいのが、並列回路の電圧・電流・抵抗の求め方。
前回勉強してきた「直列回路の電圧・電流・抵抗の求め方」とは異なるから、並列回路は並列回路のルールを覚えなきゃいけないんだ。
今日はそのテストにも出やすい並列回路の電圧・電流・抵抗の求め方をわかりやすく解説してみたよ。
まず電圧からだね。
並列回路の電圧のルールはすこぶる簡単。
それは、
全体の電圧は各抵抗にかかる電圧に等しい
ってやつだ。
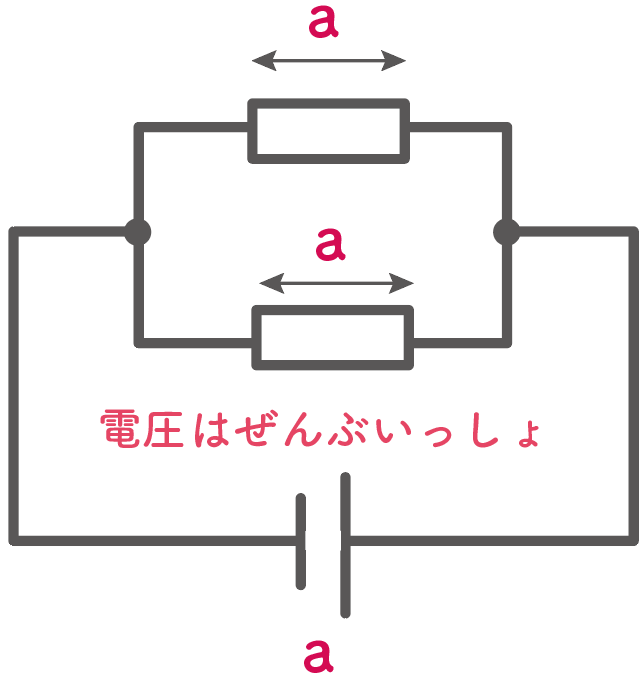
どの抵抗だろうが電球だろうが、並列に繋がっているなら、そこにかかる電圧は同じってことね。
例えば、 3Vの電源に2つの抵抗A・Bを並列につなげているところを想像してみて。
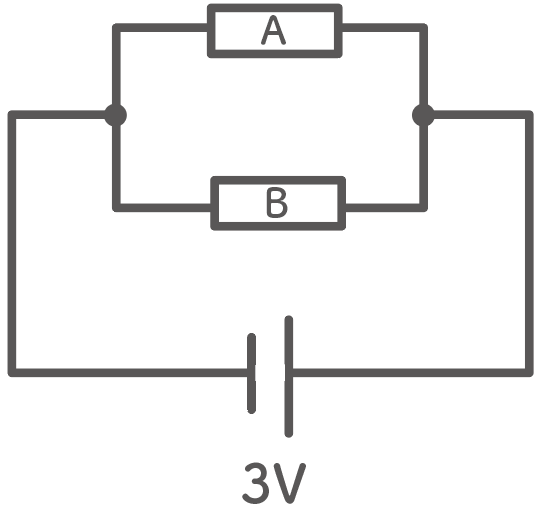
このとき抵抗 A・ B 、それぞれにかかる電圧はなんと。
3V!!
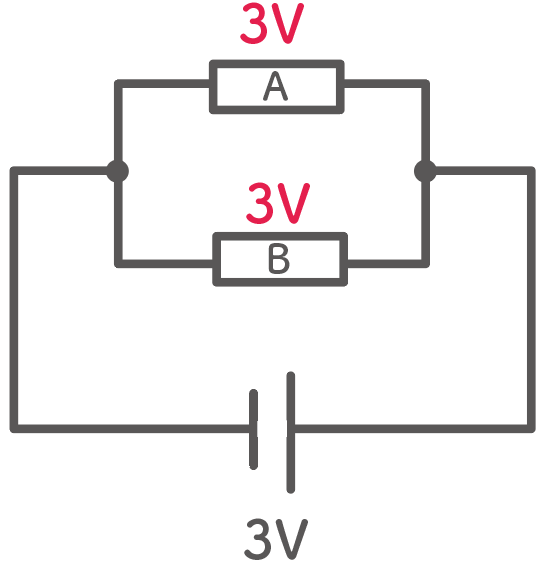
電源の電圧と全く同じってことなんだ。らくしょ〜
次は電流だね。
並列回路の電流は次のルールを覚えておけばいいよ。
枝分かれして電流を足すと全体に流れる電流になる
ってやつ。
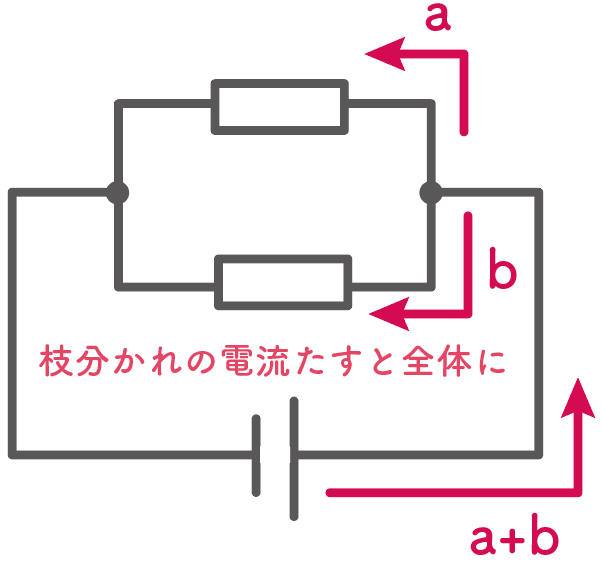
どういうことか具体的に説明していくね。
例えば、全体の枝分かれする前の電流の大きさが3[A]だとしよう。
この時、抵抗Aに流れる電流が2[A]だったとしたら抵抗Bに流れる電流はいくらになるだろうか???
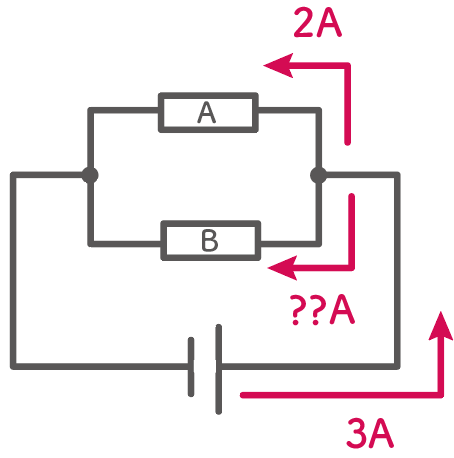
そう、そうだよ。
全体の電流3 [A]から抵抗に流れる電流の2 [A]を引いて1 [A] 流れるというのが正解だ。
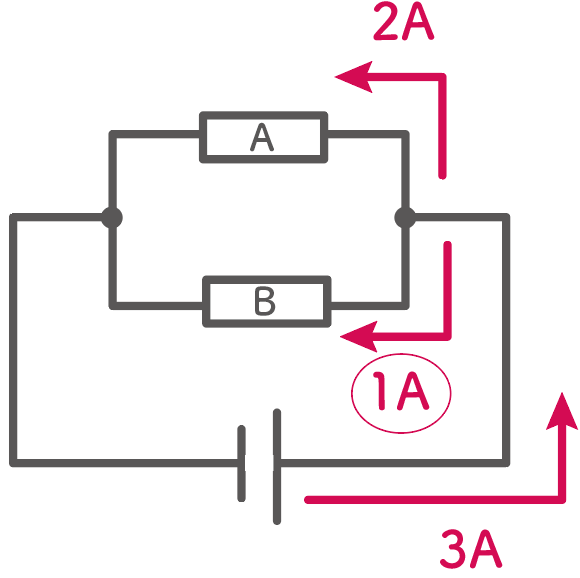
枝分かれの電流を足したら、全体の電流になると覚えておけばいいね。
最後に並列回路の抵抗の求め方だね。
これは若干トリッキーなので注意が必要。並列回路のルールは次のものになるよ↓
全体の抵抗の逆数は各抵抗にかかる抵抗の逆数を足したものに等しい
だ。
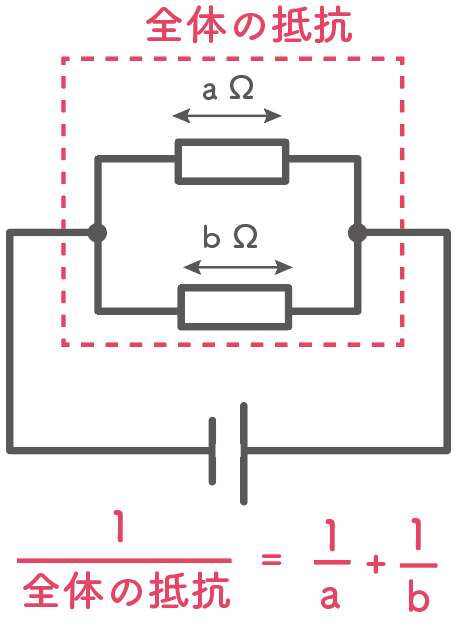
ちょっとわかりづらいから具体例で見てみよう。
例えば、2つの抵抗が並列回路で繋がっていて、抵抗Aが200Ω、抵抗Bが100Ωだとする。
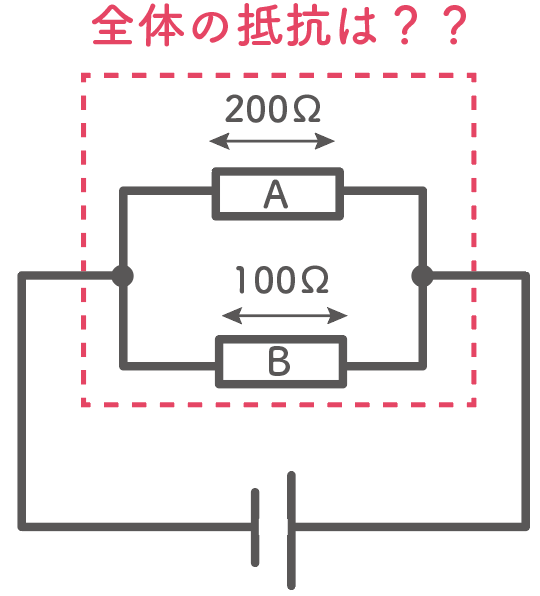
この時、2つの抵抗を合わせた全体の抵抗値を求めるとしよう。
さっきの並列回路の抵抗のルールを適用すると、2つの抵抗の逆数を足したものになるから、
(Aの抵抗値)分の1 +(Bの抵抗値)分の1 = (全体の抵抗値)分の1
となるわけだね。
これをさっきの電気回路に当てはめて全体の抵抗を求めてみるよ。
(Aの抵抗値)分の1 +(Bの抵抗値)分の1 = (全体の抵抗値)分の1
200分の1 + 100分の1 = (全体の抵抗値)分の1
200分の3 = (全体の抵抗値)分の1
(全体の抵抗値)= 3分の200 ≒ 66.6666Ω
になるね。
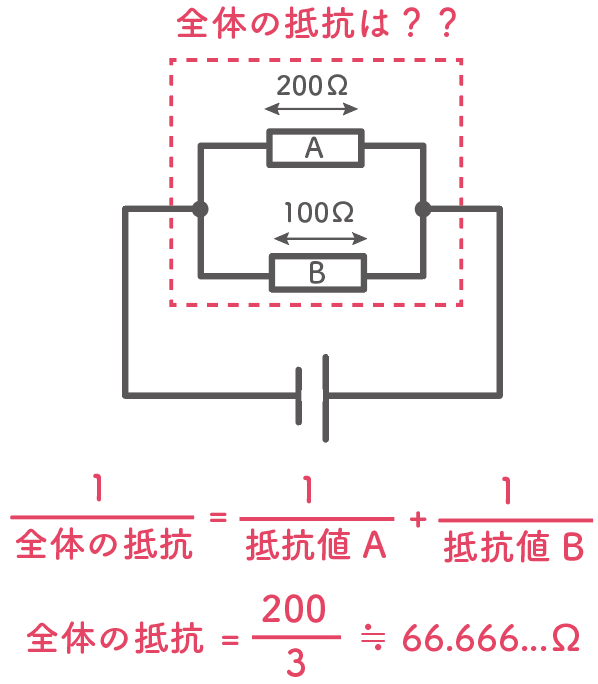
このことから分かるのは、
全体の抵抗はそれぞれの抵抗よりも小さくなるってことだ。
66.66という抵抗値はもちろんAの抵抗値200Ωよりも小さいし、もう一個のBの抵抗値の100Ω よりも小さいよね。
んな感じで、全体の抵抗を求めると小さくなってしまうのが、並列回路の抵抗なんだ。
以上が並列回路の電圧・電流・抵抗の求め方だったよ。
最後におさらいしておこう。
並列回路の電圧は電源の電圧と同じでどこでも電圧は等しいね。

電流は枝分かれを足したものが全体の流れる電流になって、

全体の抵抗の逆数は、各抵抗にかかる抵抗の逆数を足したものに等しい
と覚えておこう。

次は「電圧計の使い方」を勉強していこう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。ニラ、摂取したね。
電気の回路には、
の2種類あるって勉強してきたよね??
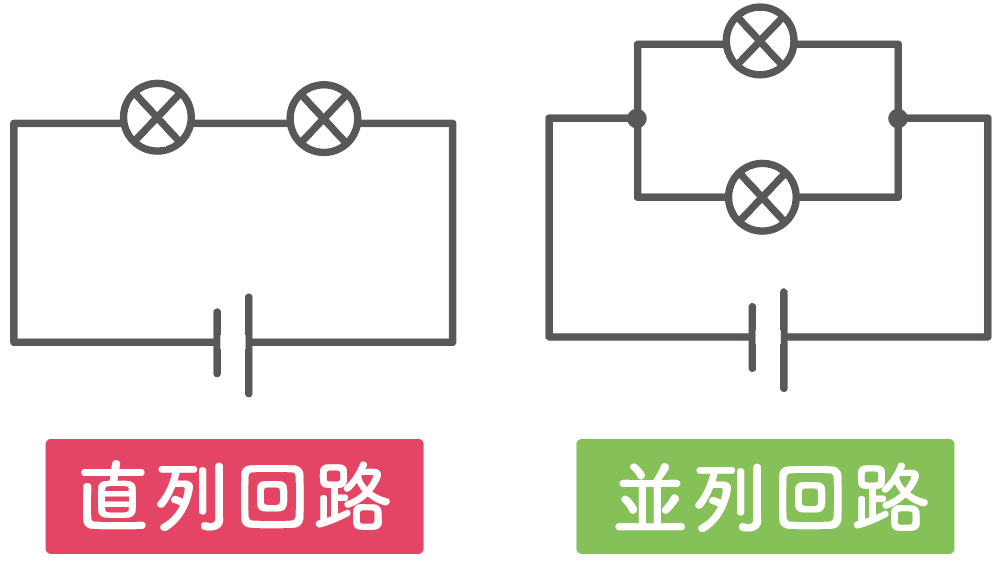
今日はその中でも
直列回路
に目を向けてみよう。
「直列回路」とは、
導線の道筋が1本になっている回路のこと
で、一筆書きできる回路が直列だ。
この直列回路に関して覚えておきたいのが、
の3つの求め方。
むちゃくちゃテストに出やすいからマスターしておくに越したことはないね。
今日はこの直列回路の電圧・電流・抵抗の求め方をわかりやすくまとめてみたよ。
直列回路の電流はむちゃくちゃわかりやすくて、
回路のどこでも電流の大きさは同じになっているんだ。
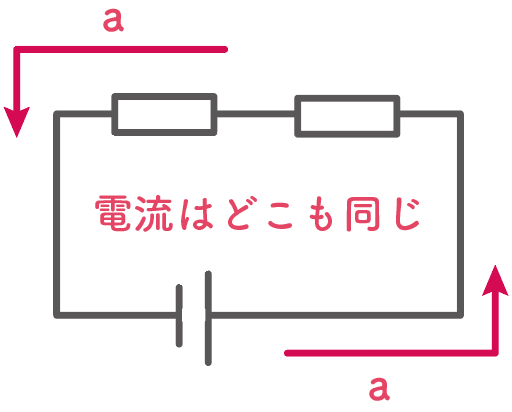
たとえば、このA地点で50mAの電流が流れていたとすると、
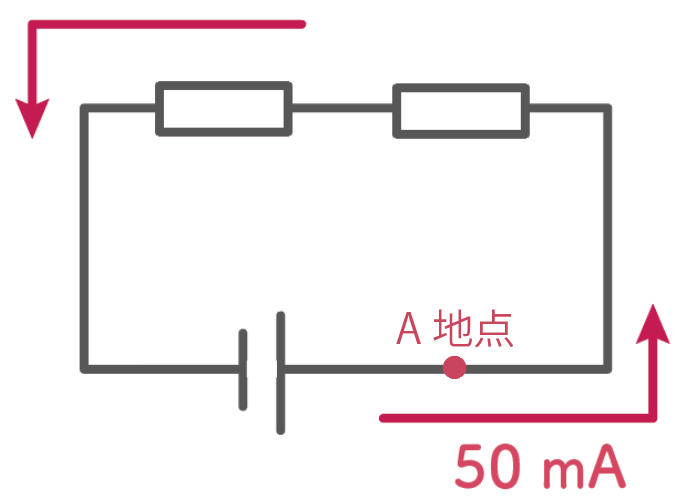
他のB・C地点でも同じ一定の50mAの電流が流れていることになるのさ。

だが、直列回路の電圧の求め方はちょっとやっかい。
電圧は、
抵抗にかかる電圧の和が電源の電圧に等しい
というルールがあるよ。
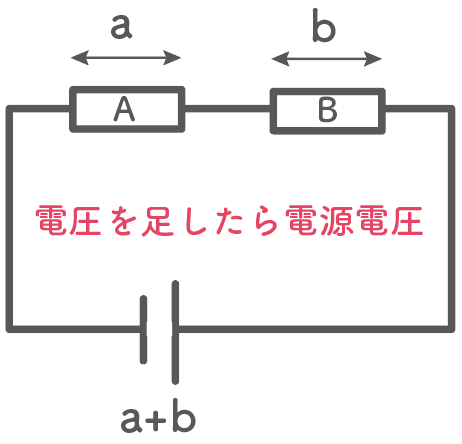
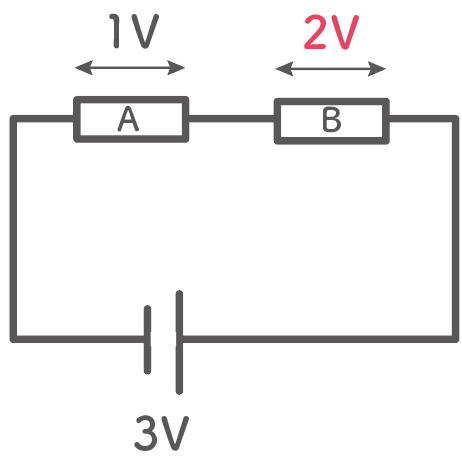
たとえば、3Vの電池があったとしよう。
こいつに2つの抵抗をつなげて、抵抗Aにかかる電圧が1Vだったとしよう。
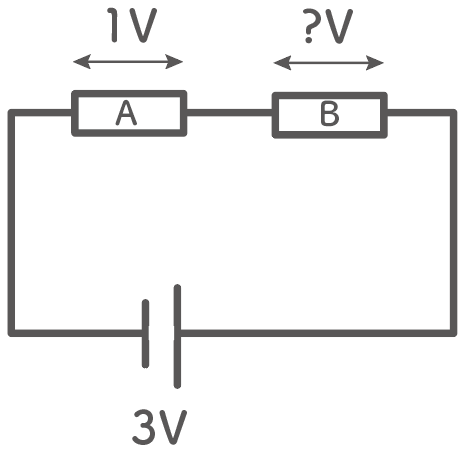
このとき、もう1つの抵抗にかかる電圧は2Vになるんだ。
なぜなら、抵抗AとBの電圧を足したら電源電圧3Vになるはずだからね。
最後に直列回路の抵抗の求め方だね。
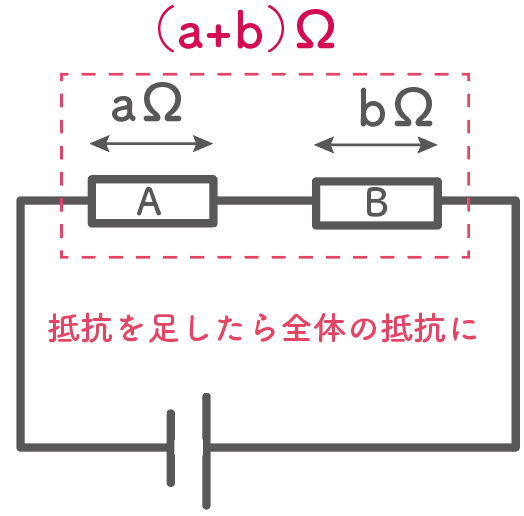
こいつは、
回路全体の抵抗は、それぞれの抵抗を足したものに等しい
というルールがあるよ。
たとえば、抵抗Aが100Ω、抵抗Bが200Ωだったとしよう。
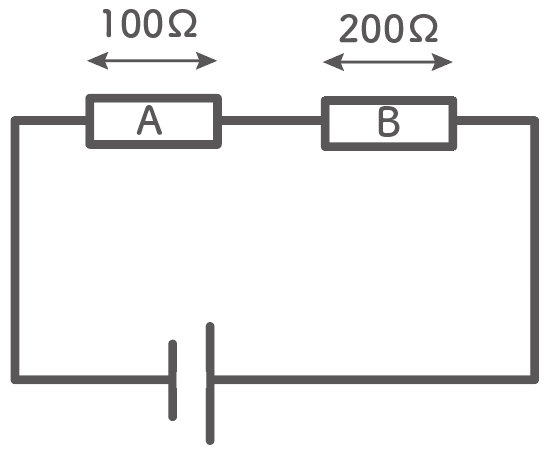
このとき、回路全体の抵抗は、その2つの抵抗を足した、
100 + 200
= 300Ω
になるんだ。
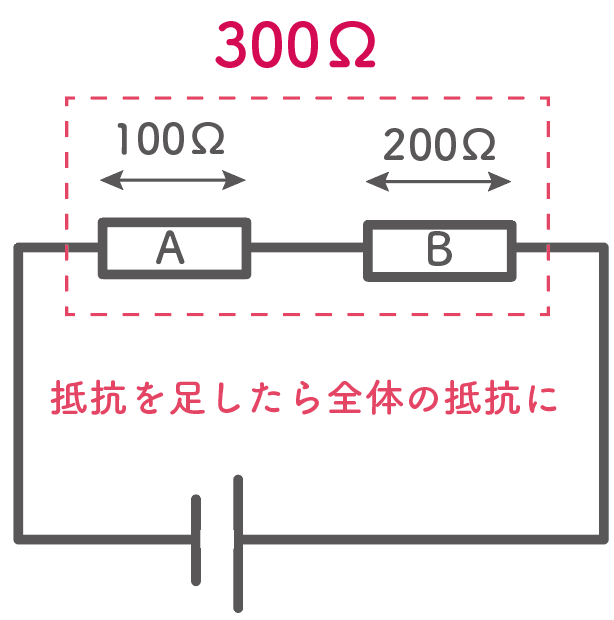
直列回路だったら抵抗値をたすだけで全体の抵抗が出ちゃうから楽チンね。
以上が直列回路の電流、電圧、抵抗の求め方だね。
最後に忘れないように復習しておくと、
直列回路の電流はどこでも同じで、

それぞれの抵抗にかかる電圧を足したら、電源の電圧になって、

全体の抵抗は各抵抗値を足したものに等しいんだったね。

次は「並列回路の電圧・電流・抵抗の大きさの求め方」を勉強していこう。
そんじゃねー
Ken