テストに出やすい!オームの法則の応用問題まとめ3選
オームの法則の応用問題を解いてみたい!
前回、オームの法則の基本的な問題の解き方を見てきたね。
今日はもう一歩踏み込んで、
ちょっと難しい応用問題にチャレンジしていこう。
オームの法則の応用問題はだいたい次の3つのパターンだよ。
- 直列回路で抵抗の数が増えたパターン
- 並列回路で抵抗の数が増えたパターン
- 直列回路と並列回路が混同しているパターン
直列回路で抵抗の数が増えるパターン
まずは直列回路なんだけど、抵抗の数が2つ以上の問題ね。
例えばこんな感じ↓
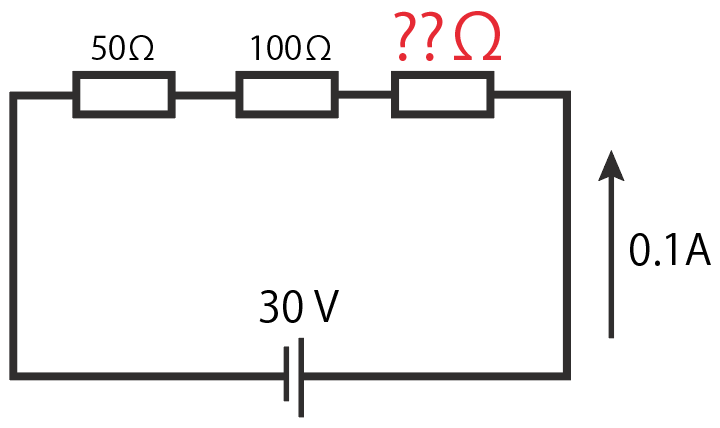
それぞれの抵抗にかかる電圧の大きさを求めていけばいいね。
一番左の抵抗値には0.1Aの電流が流れていて、しかも抵抗値が50Ω。
こいつでオームの法則を使ってやると、
$$V = RI$$
$$= 50 × 0.1$$
$$= 5 [V]$$
となって、5ボルトの電圧がかかっていることになる。
そして、その隣の100Ωの抵抗でも同じように0.1 Aの電流が流れているね。
なぜなら、直列回路では全体に流れる電流の大きさが等しいからさ。
で、こいつでも同じようにオームの法則を使ってやると、
$$V = RI$$
$$= 100 × 0.1$$
$$= 10 [V]$$
になる。
電源電圧の30Vからそれぞれの抵抗に5Vと10 V がかかっているから、最後の一番右の抵抗にかかっている電圧は
$$30-5-10$$
$$= 15 [V]$$
がかかっていることになる。
この抵抗でオームの法則を使ってやると、
$$R = \frac{V}{I}$$
$$= \frac{15}{0.1}$$
$$= 150 [Ω]$$
になるね。
並列回路で抵抗の数が増えるパターン
今度は並列回路で抵抗の数が増えるパターンだね。
例えば次のような問題。
3つの抵抗が並列につながっている回路で、抵抗値がそれぞれ20Ω、50Ω、100Ωだとしよう。電源電圧が10 [V]のとき、回路全体に流れる電流の大きさを求めよ
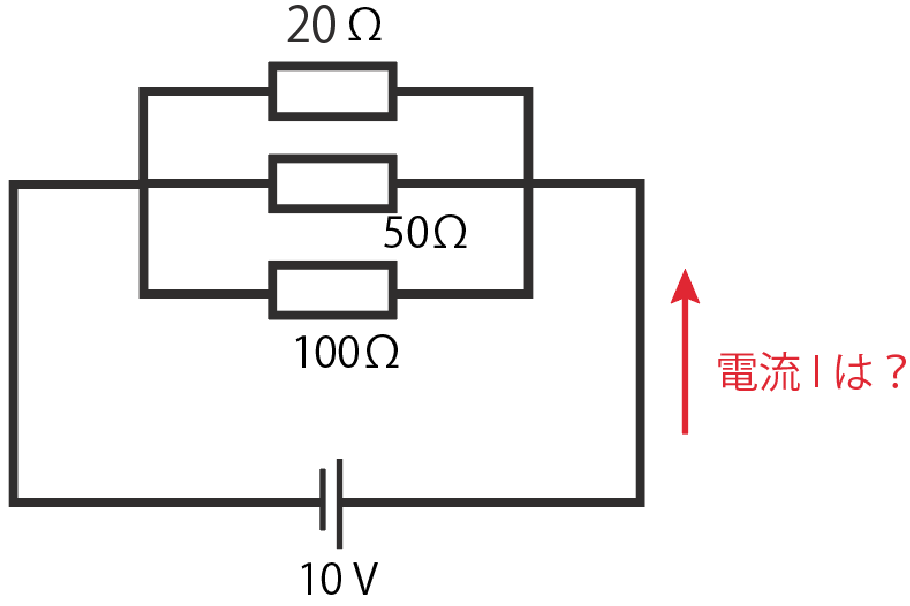
この問題の解き方は、
- 枝分かれした電流の大きさを求める
- そいつらを全部足す
で回路全体の電流の大きさが求められるね。
並列回路では全ての抵抗に等しく電源電圧がかかる。
一番上の20Ωの抵抗でオームの法則を使うと、
$$I =\frac{V}{R}$$
$$= \frac{10}{20}$$
$$= 0.5 [A]$$
その下の50Ωの抵抗では
$$I =\frac{V}{R}$$
$$I =\frac{10}{50}$$
$$= 0.2 [A]$$
一番下の100Ωの抵抗では、
$$I =\frac{V}{R}$$
$$I =\frac{10}{100}$$
$$= 0.1 [A]$$
になる。
で、これら3つの枝分かれ後の電流を全て足したやつが「回路全体に流れる電流の大きさ」になるから、
$$0.5 + 0.2 + 0.1$$
$$= 0.8 [A]$$
が正解だ!
直列と並列回路が混同しているパターン
最後の問題は直列回路と並列回路が混合している問題だね。
例えば次のような感じ。
電源電圧が10 V、全体に流れる電流の大きさが0.2A。左の直列回路の抵抗値が30Ωだとしよう。並列回路の下の抵抗値が25Ωの時、残りの上の抵抗値を求めよ
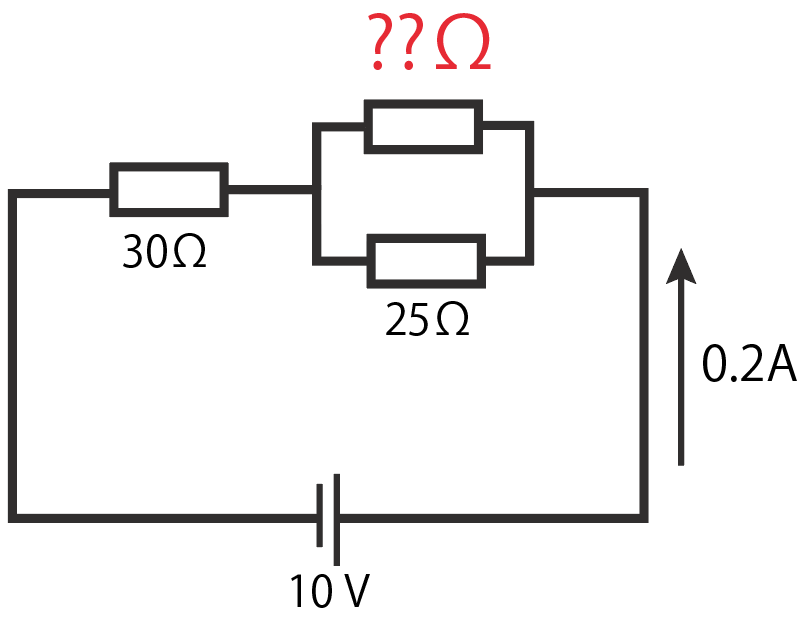
まず直列回路になっている左の抵抗にかかる電圧の大きさを求めてやろう。
この抵抗は30Ωで0.2Aの電流が流れているから、オームの法則を使うと、
$$V=RI$$
$$= 30×0.2$$
$$= 6 [V]$$
になるね。
電源電圧が10 V だったから、右の並列回路には残りの4Vがかかっていることになる。
回路全体に流れる電流は0.2Aだったから、この並列回路全体の合成抵抗は、
$$電圧÷電流$$
$$= 4 ÷ 0.2$$
$$= 20 [Ω]$$
になる。
次は右の並列回路の合成抵抗から上の抵抗の値を求めていこう。
詳しくは「並列回路の電圧・電流・抵抗の求め方」を読んでほしいんだけど、
全体の抵抗の逆数は各抵抗にかかる抵抗の逆数を足したものに等しい
だったね?
上の抵抗をRとしてやると、この右の並列回路の合成抵抗R’は
R’分の1 = R分の1 + 25分の1
になるはず。
で、さっき合成抵抗R’は20Ωってわかったから、
20分の1 = R分の1 + 25分の1
というRについての方程式ができるね。
分数を含む一次方程式の解き方でといてやると、
$$\frac{1}{20} = \frac{1}{R} + \frac{1}{25}$$
$$5R = 100 + 4R$$
$$R = 100 [Ω]$$
になる。
ふう、長かったぜ。
オームの法則の応用問題でも基本が命
オームの法則の応用問題はこんな感じかな!
やっぱ応用問題を解くためには基礎が大事で、
を理解している必要があるね。
問題を解いていてあやふやだったら復習してみて。
そんじゃねー
Ken



