中学理科の天気の単元では、
天気図の記号
を勉強していくね。
天気図記号とは、天気図で使われる記号たちのことで、この天気図の記号を見れば、
観測地点の天気・風向・風力がわかるようになるんだ。
たとえば、こんな奴が天気図の記号かな↓
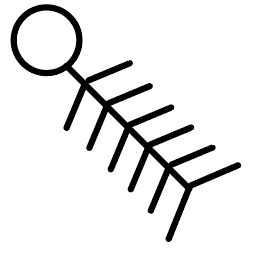
まあ、なんか、遺跡とかに書いてありそうだけど、これだけで天気・風向・風力を表しちゃってるすごいやつなんだ。
今日はその天気の基本である、
天気図の記号の書き方
をマスターしていこう。
次の3ステップでOK。
まずやらなきゃいけないのが、
天気記号をかく
つまり、
観測地点の天気がどうなっているのか?を記号で表すことになるんだ。
たとえば、天気図の天気記号は次のような種類があるよ。

めちゃくちゃいっぱいあって覚えづらいけど、ようは
丸をかいて、中に何か書けばいいね。
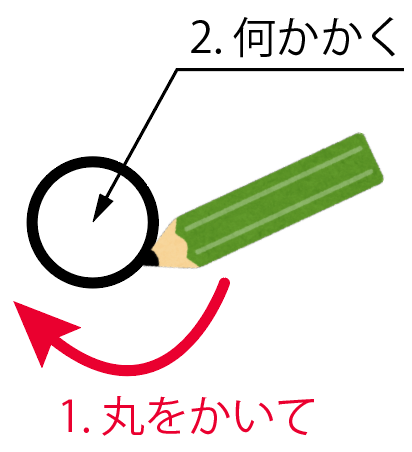
これだけで天気を表せるなんて最強だ。
ただ、天気図でちょっと難しいのは、
快晴・晴れ・曇りの区別
かな。
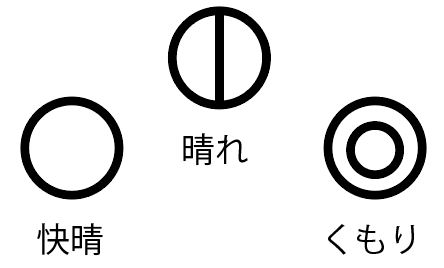
これら3つの天気は
「雲量」という雲の量で判断するよ。
空全体を10とした時、雲が覆っている割合のことを「雲量」というんだけど、それが0から1の場合は快晴。
2から8の場合は晴れ。雲量が9から10の時はくもりになるね。
まあ、ぶっちゃけここら辺は感覚的なものになるから、微妙な判断は個人に任せることになるね。
たとえば、こんな感じの空の日があったとしよう。

ぼくの感覚だと、これは空10に対して、まあ、そうだな、雲は2ぐらいあるな。
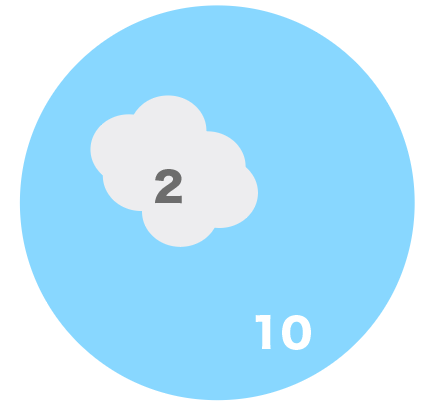
というわけで雲量は「2」で、天気は「晴れ」ということになる。
続いては、風向を書いていこう。
風向とは、
風が吹いてくる方角のこと。
例えば、東から風がふいてくれば、風向は「東」になるね。
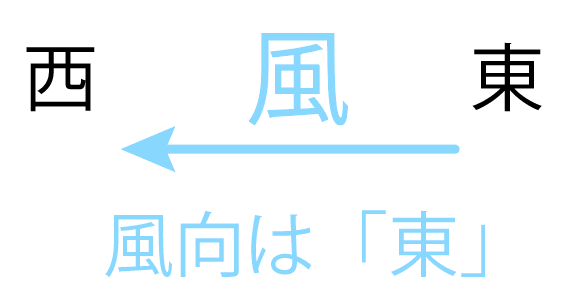
天気図の記号では、
風向の向きに棒をつけて風向を表すんだ。
しかも厄介なのが、その方角は「16方位」を使わなきゃいけないこと。
いやあ、細かい。
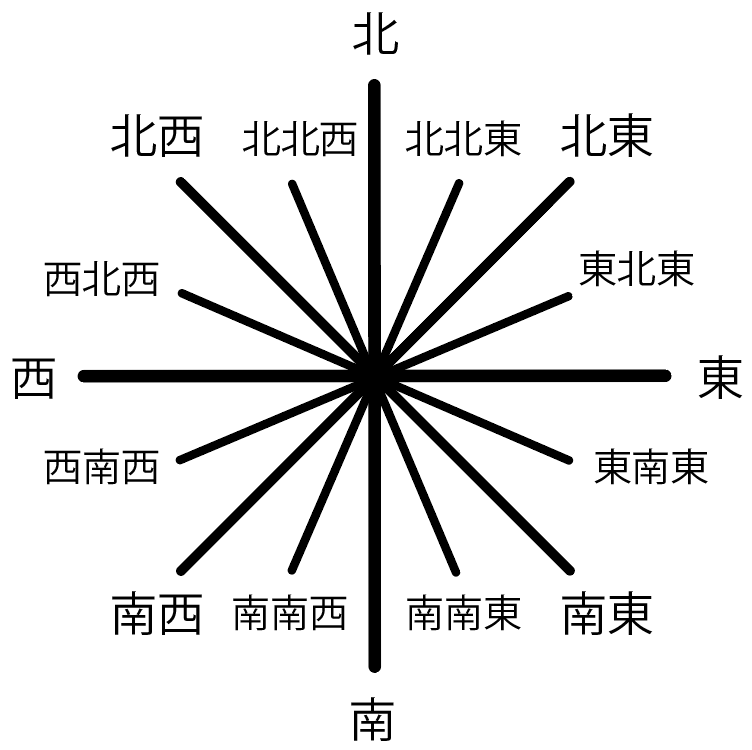
例えば、南東から風が吹いている場合、南東の向きに棒をかけばいいよ。

最後に、風の強さを表す「風力」を記入していこう。
風力は、
0〜12の13段階で表すんだ。
どうやって強さを判断するのかというと、
風力階級表という表を参考にするよ。
この表では、ある風速に当てはまる風力が書かれているから、風速を測って、それに当てはまる風力を割り当てていくんだ。
風力がゼロの場合は、天気記号に何もかからなくて大丈夫。

風力が1から6の時は、棒のツノの右側にどんどん線を手前から足していくよ。

7から12の時は左側に線を奥からつけたしていって、12でマックスの風力になるのね。

ということで、最初に見た謎の天気号の正体は、
を表した天気図の記号だったわけだ。

こんな感じで、天気図の記号も、
を書き込めば大丈夫。
天気図記号の基本をマスターしたら、今度は「凝結・露点とは何か」を勉強していこう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。ランチパック、3連続だね。
天気予報でよく出てくるのが、
湿度
という数値だ。
これはズバリ、
空気の湿り具合を数値で表したもの
で、もっと具体的に言うと、
ある温度の1m³の空気に含まれる水蒸気の質量が、その温度の飽和水蒸気量に対してどれくらいなのか?を百分率で表したもの
なんだ。
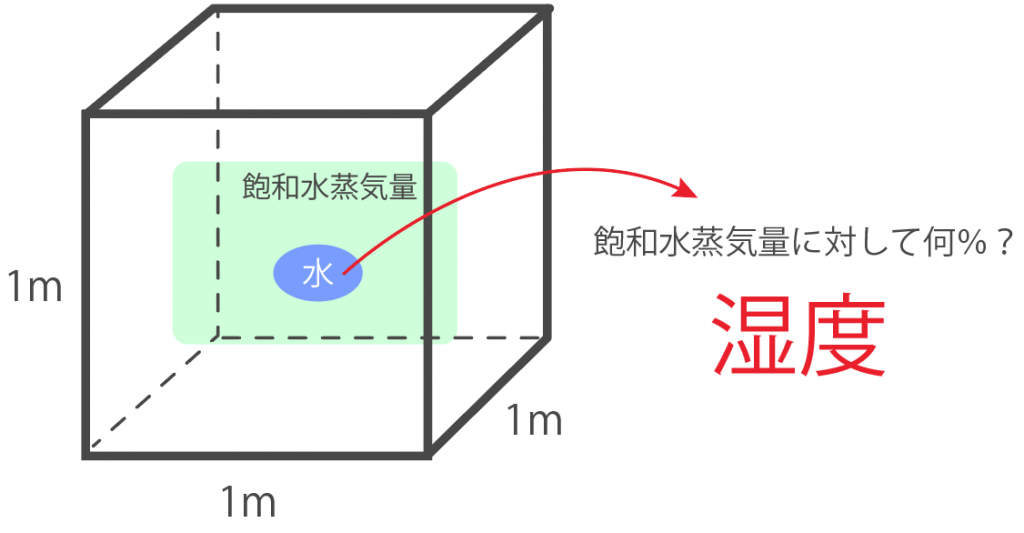
湿度の計算式はこんな感じ↓
湿度 [%] = (1m³の空気に含まれる水蒸気の質量)÷(その空気の温度の飽和水蒸気量)× 100

この式を見ればわかるけど、
「1m³の空気に含まれる水蒸気の質量」と「その空気の温度の飽和水蒸気量」が等しかったら湿度は100%になるね。
湿度100%という状態は、限界まで水蒸気がパンパンに詰まっているわけだ。
この事態は全然あり得ることだから、部屋の湿度計が100%で動じることなかれね。
例えば、水蒸気が1m³あたり10g含まれている空気があったとしよう。
飽和水蒸気量が50 g だった場合、湿度は
湿度 [%] = (1m³の空気に含まれる水蒸気の質量)÷(その空気の温度の飽和水蒸気量)× 100
= 10 ÷ 50 × 100
= 20%
になるんだ。
こんな感じで、湿度の計算では
がわかっていれば計算できるね。
テストでは単純に湿度を計算するだけじゃなくて、
湿度から水蒸気の質量を求める問題
も出てくるよ。
例えば、次のような問題↓
こういう問題は、
湿度の計算公式を変形させりゃいいね。
湿度の公式は
湿度 [%] = (1m³の空気に含まれる水蒸気の質量)÷(その空気の温度の飽和水蒸気量)× 100
だったから、これを「1m³の空気に含まれる水蒸気の質量」について等式変形してやると、
(1m³の空気に含まれる水蒸気の質量)= 湿度 ×(その空気の温度の飽和水蒸気量)÷ 100
になるはず。
この式で「1m³の空気に含まれる水蒸気の質量」を計算してやると、
(1m³の空気に含まれる水蒸気の質量)= 湿度 ×(その空気の温度の飽和水蒸気量)÷ 100
= 40 × 30 ÷100
= 12 [g]
になるね。
つまり、1m³ に12 [g] の水蒸気が入っていたことになる。
というわけで、ここまでの湿度の練習問題が解ければ完璧。
次は「天気図の書き方」を勉強していこう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。マット、買ったね。
世の中には2種類の電流が存在してるって知ってた?
それは、
の2つ。
今日はこいつらの違いを説明していこう。
まず「直流電流」からだね。
これは、
一定の向きに流れる電流のこと
だ。
例えば、「電池の電流」が直流だよ。
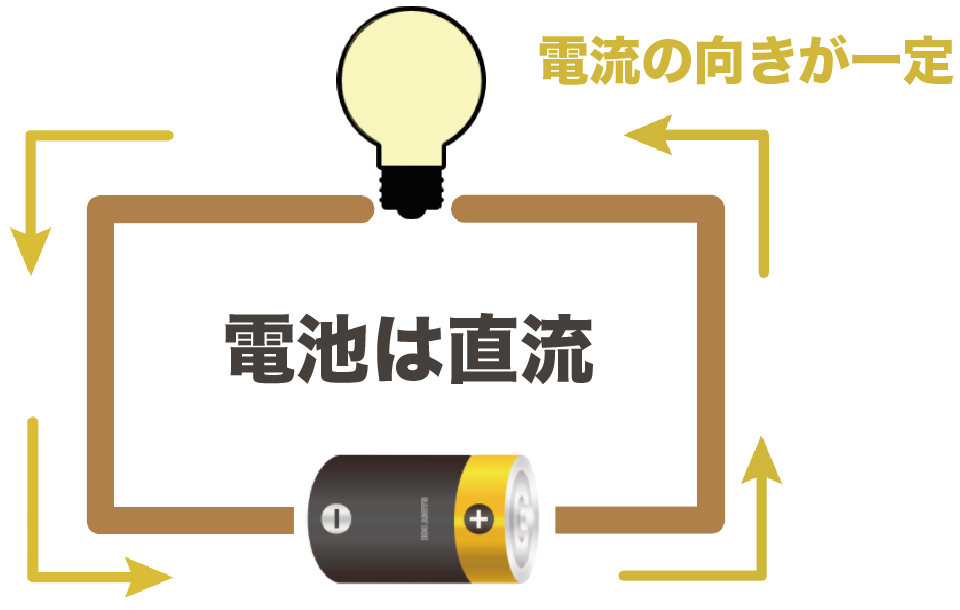
電池のプラスからマイナス方向に流れるようになっていて、紛れもなく一方向の電流。
電流の大きさも一定だね。
横軸に「時間」、縦軸に「電圧」のグラフを描くとこんな感じになる ↓
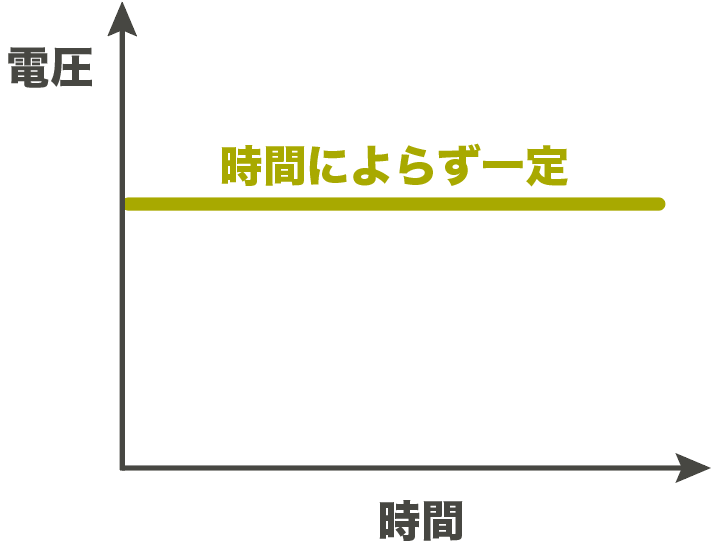
常に電流の大きさも向きも同じになってるのね。
一方、交流電流とは、
電流の向きと大きさが周期的に変化している電流
なんだ。
例えば、家庭用のコンセントの電流は「交流」。

電流の大きさ・向きが時間によって絶えず変化しているのが特徴だね。
さっきと同じように、時間と電圧のグラフをかいてみると、このように波のようなグラフになるんだ↓

でも、このままだと電流の大きさとか向きが一定じゃなくて使い物にならないから、ACアダプタという装置を通すんだ。
みんなが使っているスマホも充電するときにACアダプタの充電器を使っているはず。
そうすると、交流が直流に変換されて、電化製品には直流が流れるようになるのね。
ここで疑問になってくるのが、
「ぜんぶ直流でよくね?」
ということ。
交流の電流も、最後の最後で直流に変換するなら、最初からぜーーーんぶ直流でいいんじゃないかと思っちゃうよね。
それじゃあ、
なぜ、家庭用のコンセントは交流電流なのか?
実はその答えは、
家庭用の電気をつくる発電機の仕組み
によるんだ。
発電機の仕組みを簡単に言ってしまうと、
コイルと磁石を使って発電しているよ。

「電磁誘導」という現象を利用しているんだ。
コイルに磁石を近づけたり離したりして、磁界を変化させる。
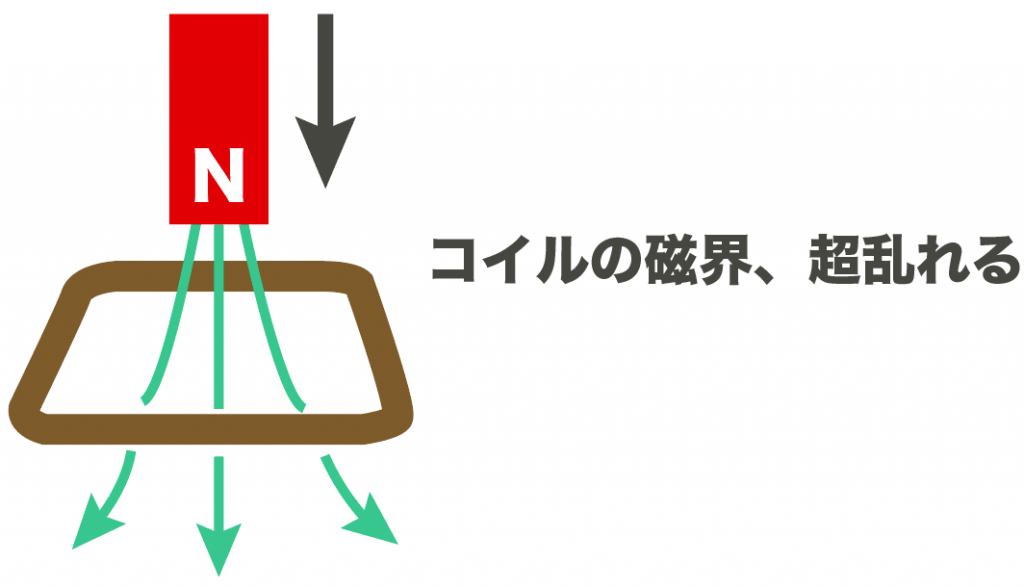
その結果、コイルに誘導電流が流れて、そのゲットした電流を各家庭に送っているわけだ。簡単にいうと。
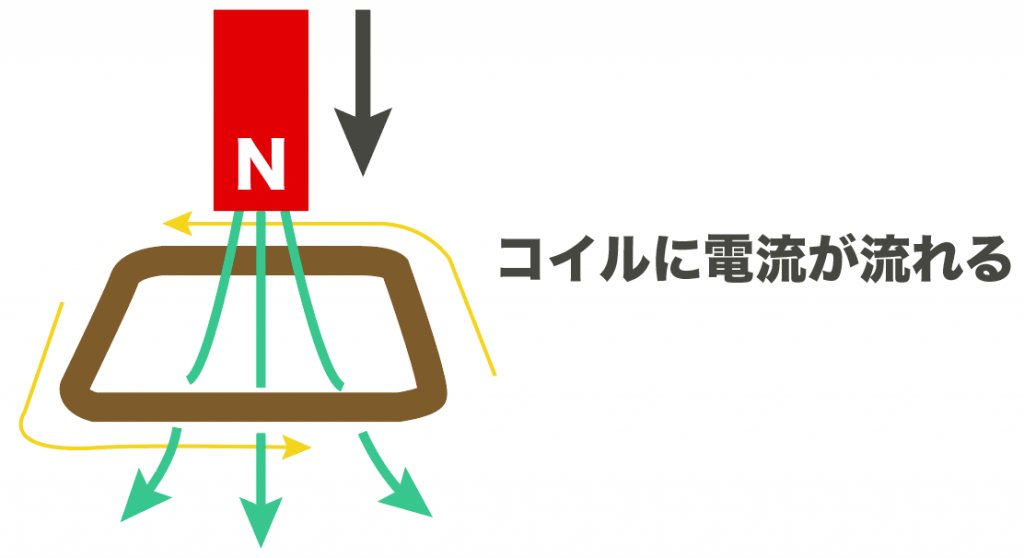
つまり、発電機の中身を見てみると、コイルの近くを磁石が上下に動いたりしていることになる。
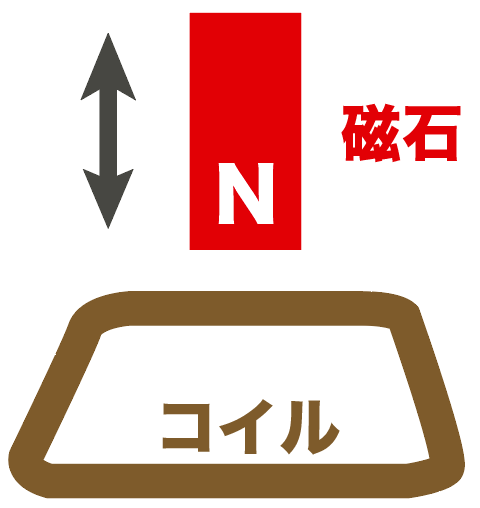
レンツの法則でシミュレーションしてみればわかるけど、
磁石を出したり入れたりすると、電流の大きさ・向きが時間によって変化するんだ。
N極の磁石をコイルに突っ込む時は反時計回りに流れるし、

引っ込めると、逆向きの電流が流れることになる。
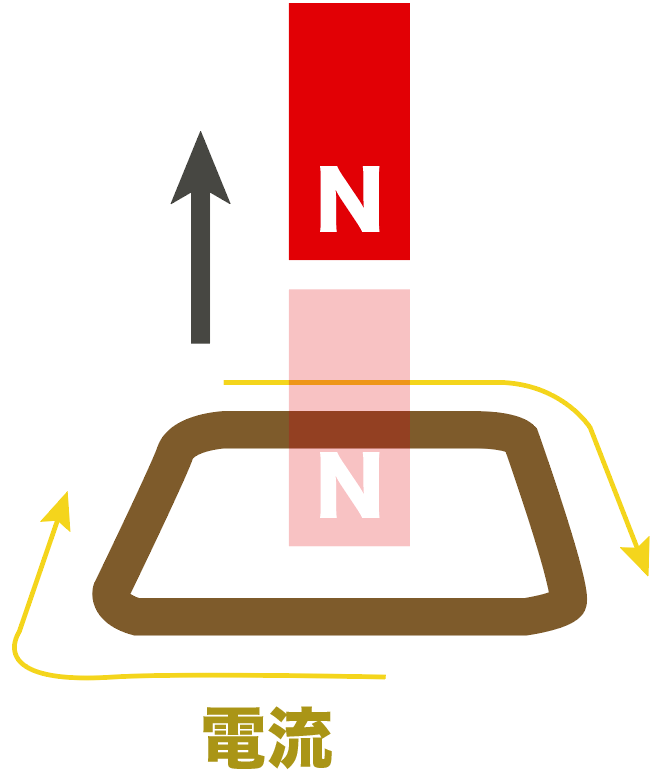
つまり、磁石の動きによって電流の向きが変化するわけだね。
だから、発電機によって作られる家庭用のコンセントは「交流」になっているんだ。
発電機の中身はもっと複雑なんだろうけど、シンプルにいってしまうとこんな感じ。
「直流」と「交流」の違いは理科の勉強だけじゃなく、一生お世話になるから納得しておこう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。いも、買いすぎたね。
今日は電気と磁石の単元で重要になってくる、
を勉強していこう。
まず電磁誘導とは、
コイルの近くで磁石を動かしたら、コイルに電流が流れる現象のこと
だ。
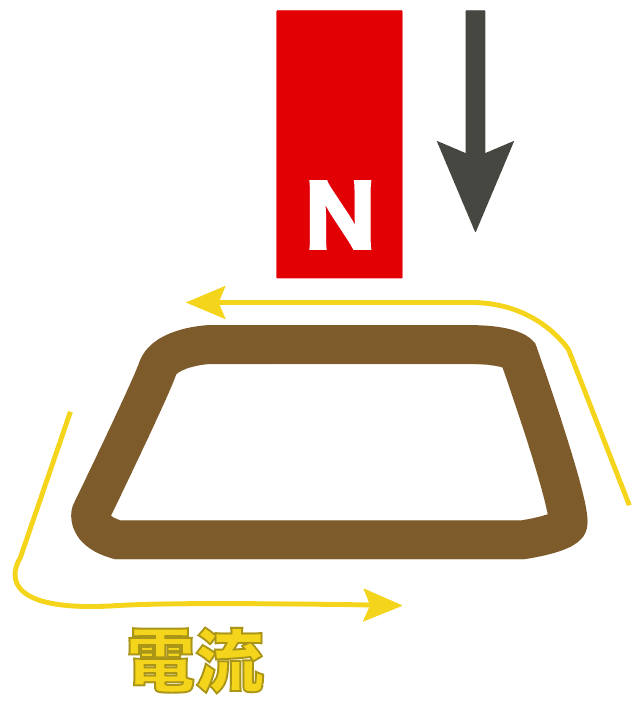
磁石をコイルに近づけたり遠ざけたりすることで、今まで平和だったコイル内の磁界が大乱れ。

その乱れが原因となって、コイルに電流が流れるってわけ。

いやあ、摩訶不思議すぎるぜ。
そして、この「電磁誘導が起きた時に流れる電流のこと」を
誘導電流
と呼んでいるんだ。
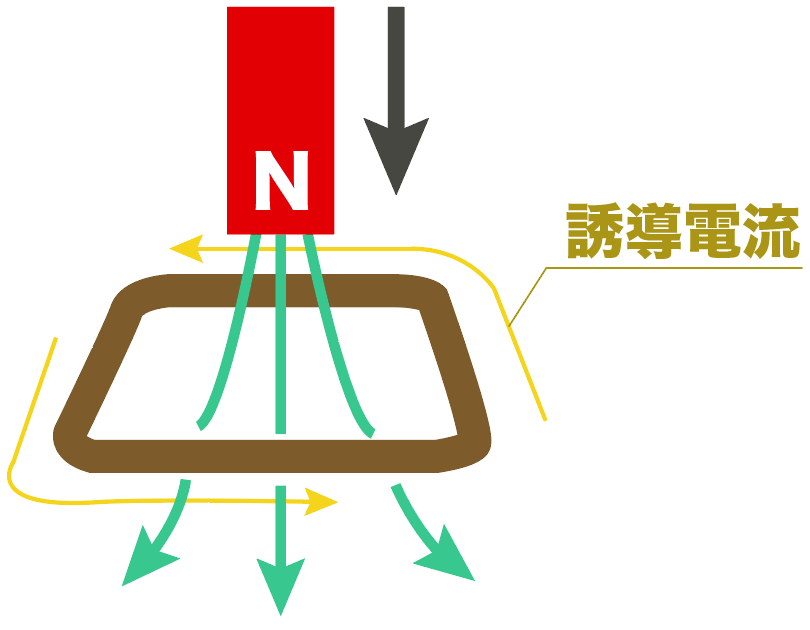
この誘導電流というやつは、
という性質を持っているよ。
クソ巻き数が多いコイルを使えば誘導電流がデカくなる。
磁力の強い磁石を使っても誘導電流がデカくなる。
素早く磁石を動かしても誘導電流がビッグになるわけだ。
いやあ、誘導電流も摩訶不思議だぜ。
最後にレンツの法則だ。
これは1800年代のロシア人のレンツさんが発見した法則のことね。
このレンツの法則は、
誘導電流の向きに関する法則なんだ。
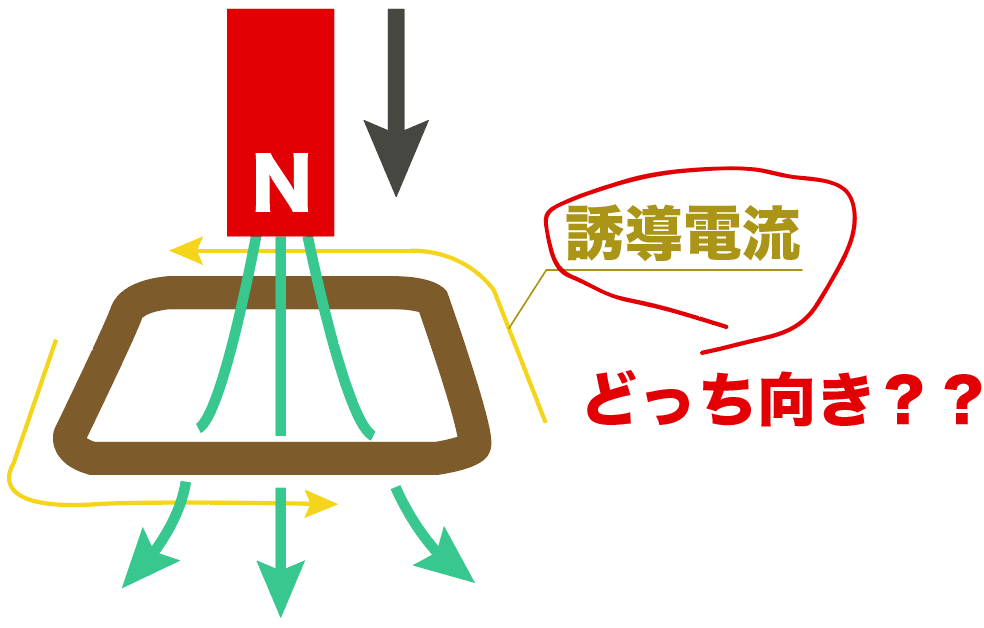
実は、
誘導電流は「磁界の変化を妨げる向き」に磁界が発生するように流れる
というルールになっているんだ。
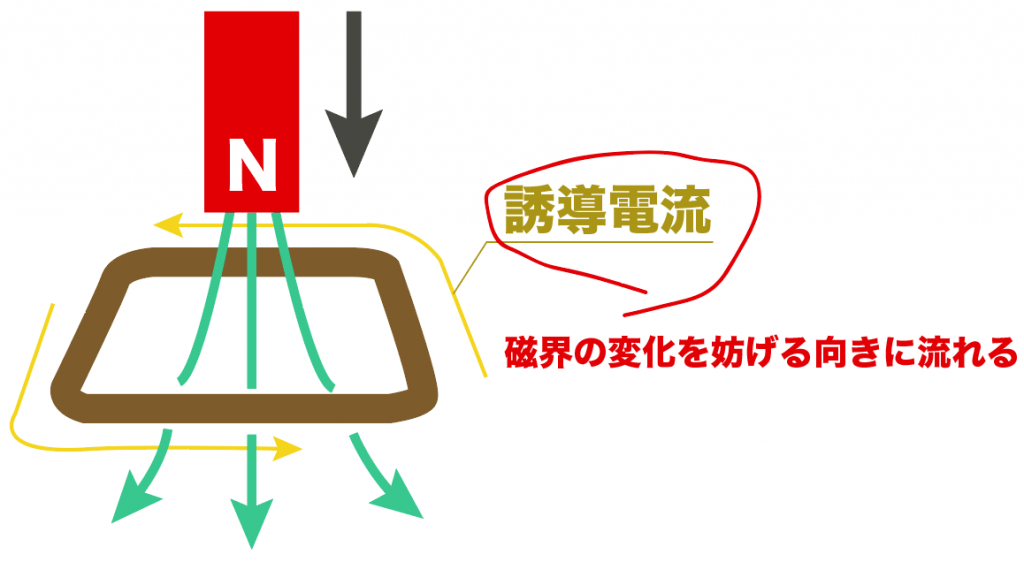
例えば、このようにコイルに 磁石のN極を近づけたとしよう。
この時、コイルの内部の磁界は上から下への磁界が増えているね?
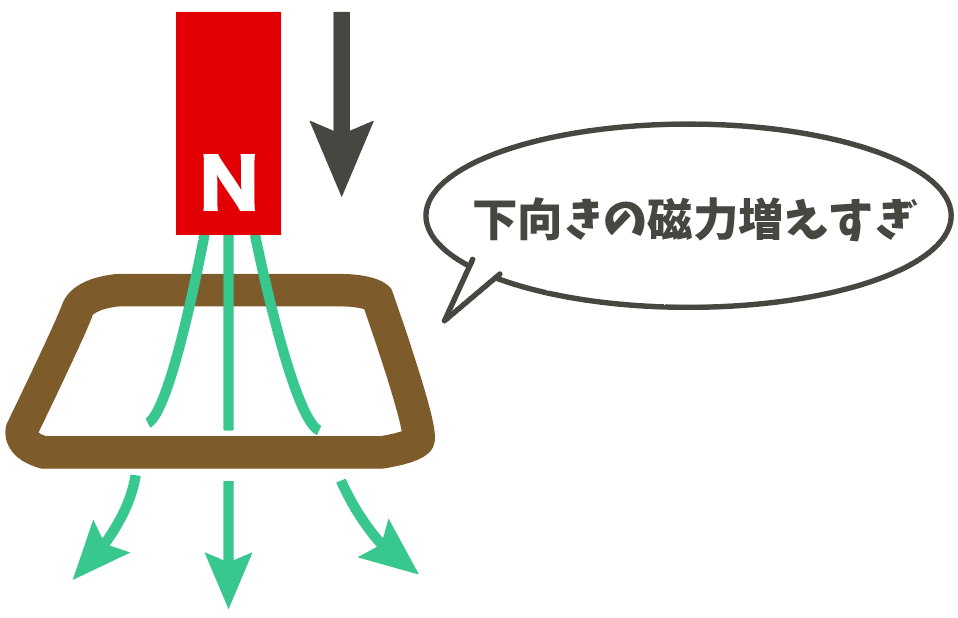
でも、コイルはこの変化を好かんわけだ。
増えちまった磁力を打ち消すような磁界を自ら作ろうとするんだ。
だから、このような向きの磁界がコイルに発生する。
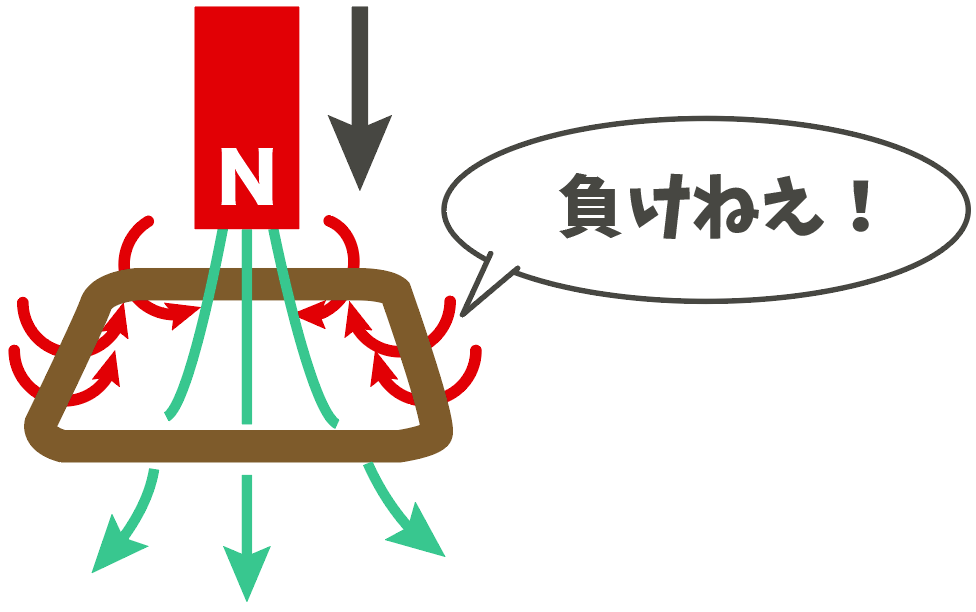
そして、ここで使うのが右ねじの法則。
電流の向きに対して右回りに磁界ができるんだったね?
だから、このように磁界が誕生するということは、コイルに反時計回りに電流が流れていることになる。
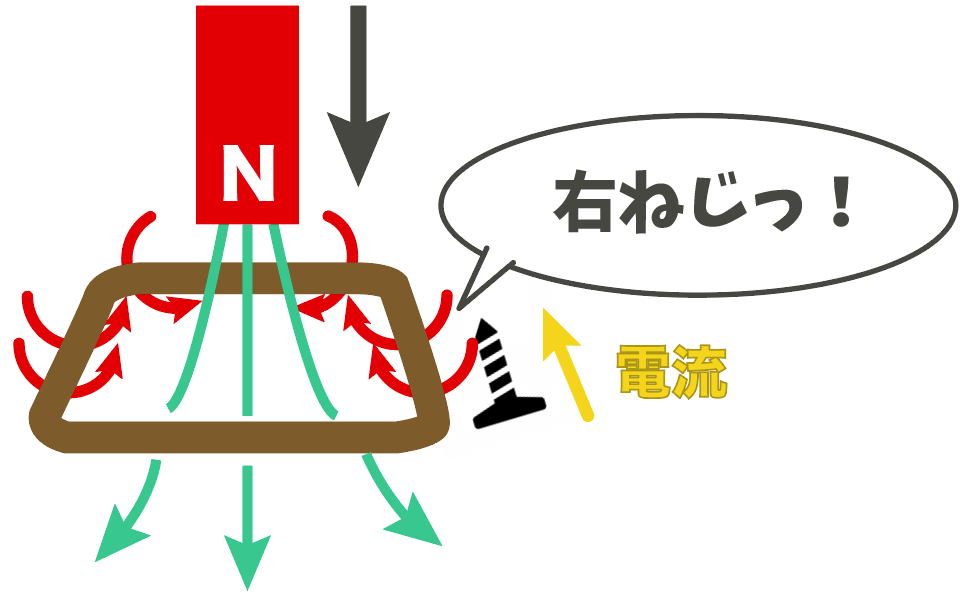
いやあ、という感じでちょっとむずいけど、
という3ステップで考えれば大丈夫。
レンツの法則の問題は出てきやすいからテスト前に練習しておこう。
次は「直流と交流の違い」を勉強していくよ。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。柱が、黒いね。
導線を磁界の中にセットして、電流を流すと「ある現象」が起きる。
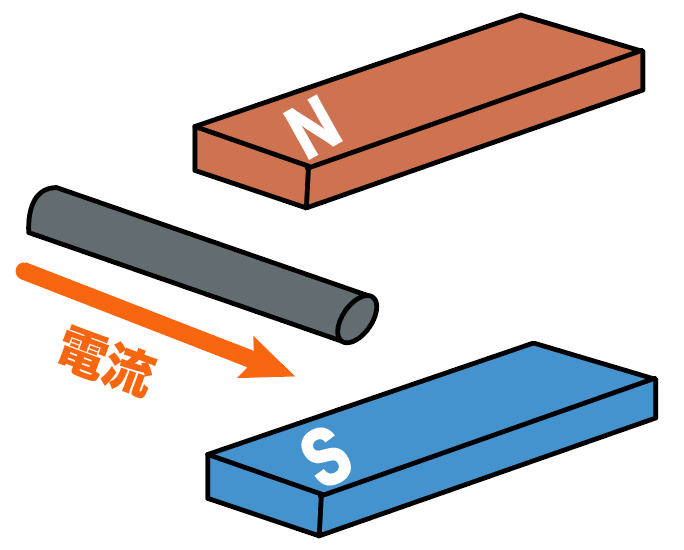
それは、
導線が動く
ってやつ。
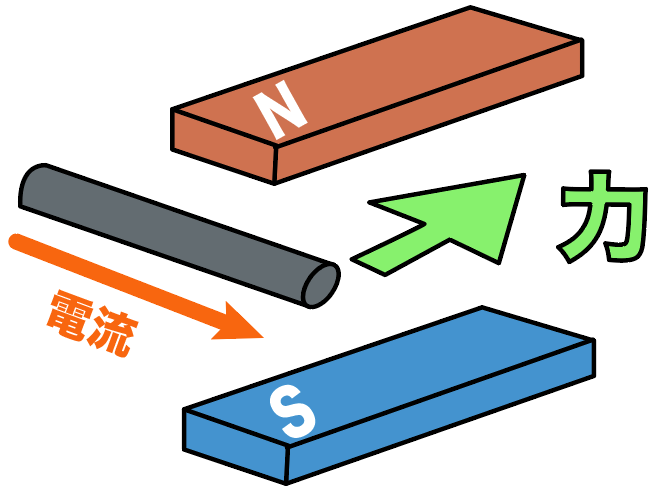
しかも、電流を大きくすると、より大きく動く、というおまけつきだ。
実は、このコイルが「磁界から受ける力の向き」というものは、
の2つによって決まるんだ。
そんな導線が受ける力の向きを知るために使えるのが、
フレミングの左手の法則
だ。
使い方はいたって簡単。
まず左手を出してみよう。
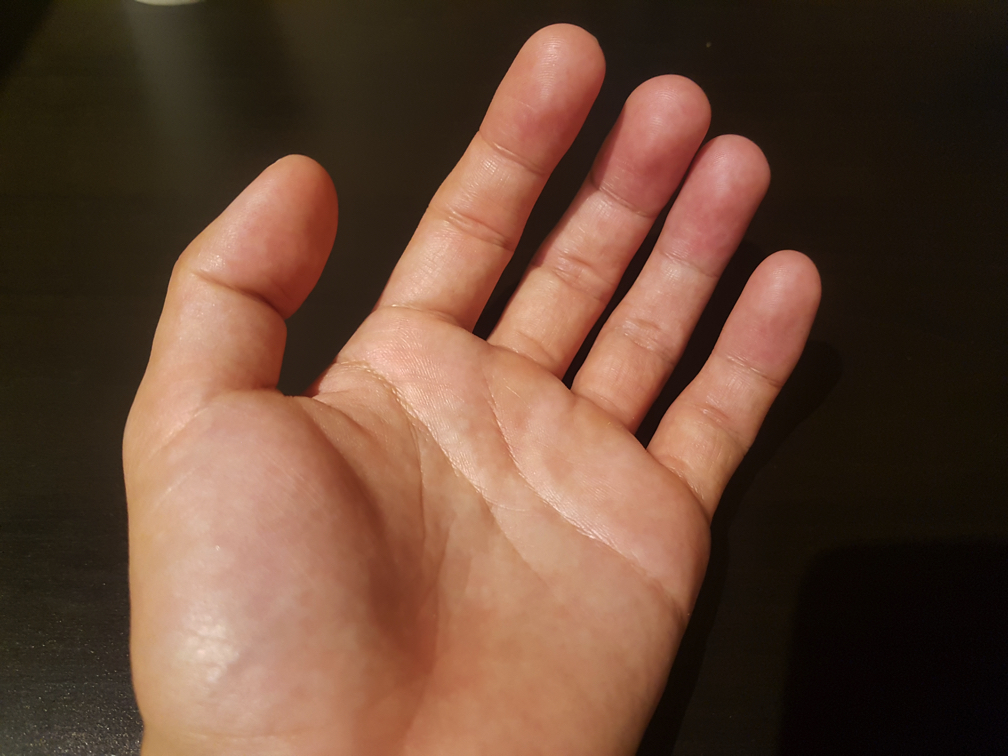
薬指と小指をしまってみる。

すると、
の3本が残るよね。
その状態で、人差し指を真上に、中指を右に、親指を顔の方に向けてみよう。

これがフレミングの法則の基本ポジションだから、この指の形をマスターしようぜ。
じつはそれぞれの指には役割があって、
| 親指 | コイルが磁界から受ける「力の向き」 |
|---|---|
| 人差し指 | 磁界の向き |
| 中指 | 電流の向き |
になっているよ。

フレミングの左手の法則の使い方を見ていこう。
まず中指の向きを「電流の向き」に合わせて、
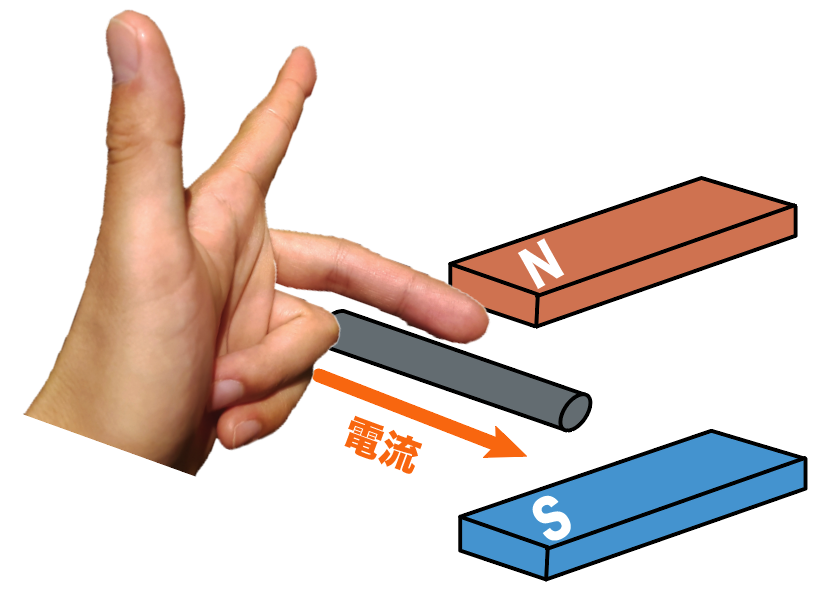
次に人差し指を「磁界の向き」に合わせる。
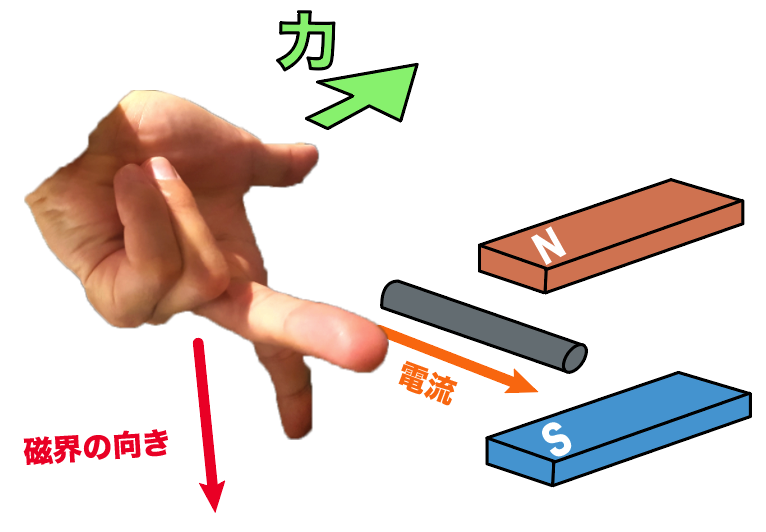
残った親指が、コイルが「磁界から受ける力の向き」になるんだ。
だから、フレミングの左手の法則の使い方は、
という3ステップになるね。
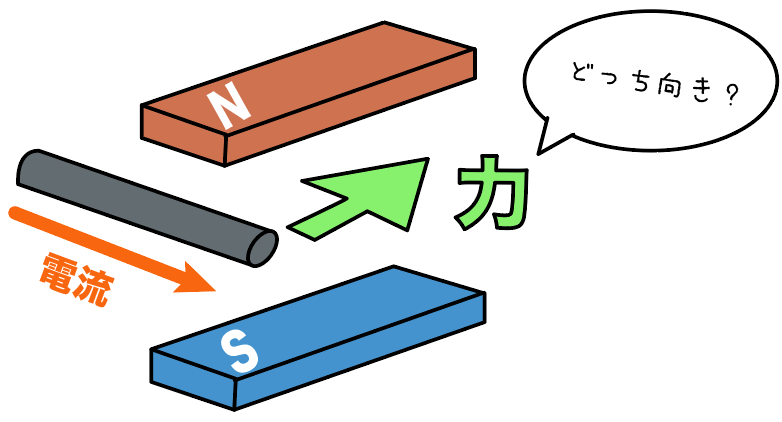
例えば、上に N 極、下に S 極の磁石があるシチュエーションを想像してみよう。
この時、導線に左から右に電流が流れたとする。
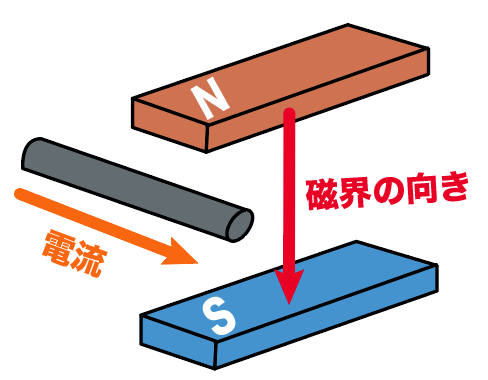
この導線に働く力を求めてみよう。
まずは左手の中指を電流の向きに向ける。

そして、磁界の向きに人差し指を向ければいいから、左手はこんな感じ。

で、残った左手の親指の向きが「導線が磁界から受ける力の向き」になるから、導線は緑の矢印の向きに動くね。

ここまでフレミングの左手の法則の使い方はわかったけど、
じゃあ一体どうやって覚えるんだろう?
すぐに忘れちゃいそうだよね。
覚え方でおすすめなのが、
「でん、じ、りょく」
と唱えながら指を触っていく方法。
フレミングの左手の法則の基本ポジションを作って、右手の人差し指で、左手の中指を触りながら「でん」、

人差し指を触りながら「じ」、

親指を触りながら「りょく」と。

左手の指たちを触りながら、
「どの部分がどの役割を担っているか?」を口ずさみながら全身で覚えていく。
これがオススメの覚え方かな。
次は「レンツの法則」を勉強していこう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。サングラス、救出したね。
前回の「右ねじの法則」で、
導線に電流を流すと磁界ができる
という現象を勉強してきたね?
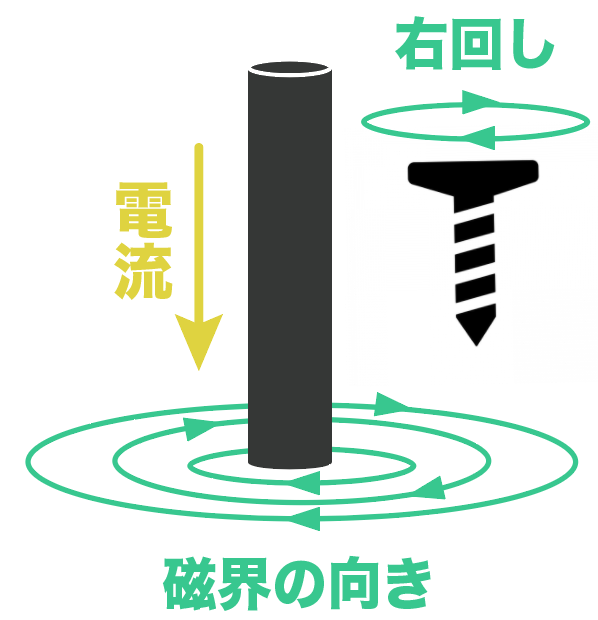
詳しくは「右ねじの法則」を読んでほしいんだけど、この性質を踏まえると、
円形に巻いたコイルに電流を流すと磁界ができる
はずなんだ。
例えば、銅線を円形状に巻いたコイルがあったとしよう。

そこに電流を流すと、導線に生じる磁界の向きは「右ねじの法則」により、このようになっているはず↓
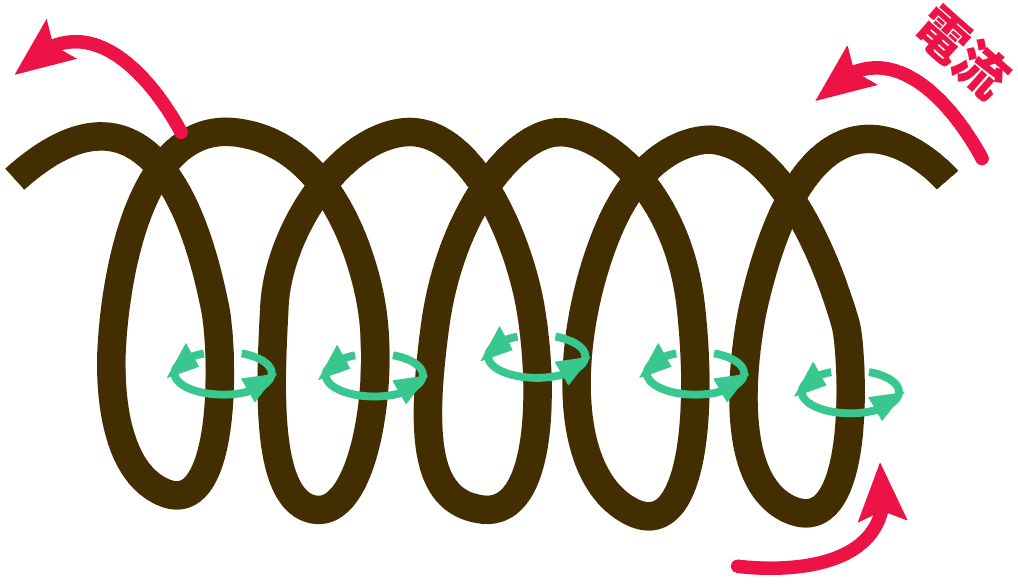
1つ1つの導線に生じる磁界の向きを合わせてやると、コイル全体では、
右から左に流れるような磁界が生じているんだ。
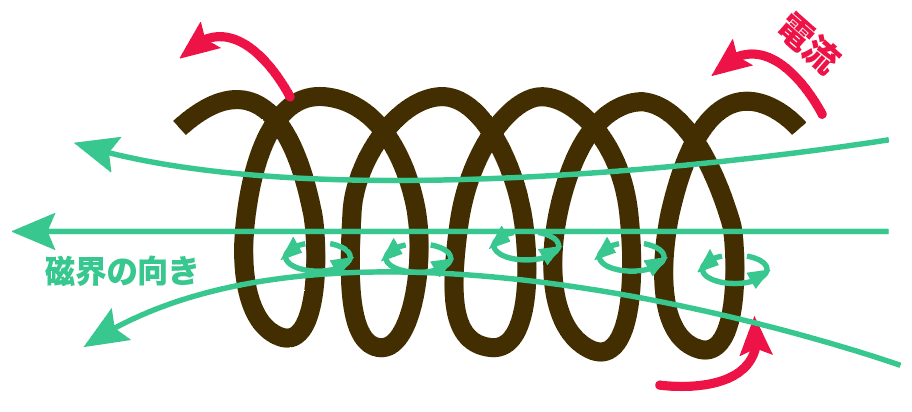
このコイルの磁界の向きを覚えるために使うのが
右手の法則
になってくるわけだ。
ってことで、「右手の法則」の使い方を解説していこう。
その名の通り「右手」を使う法則だ。

右の「小指〜人差し指」がコイルに流れる電流の向き、親指の向きが磁界の向きを表しているんだ。

電流の向きに「人差し指から小指」の4本の向きを合わせてやる。
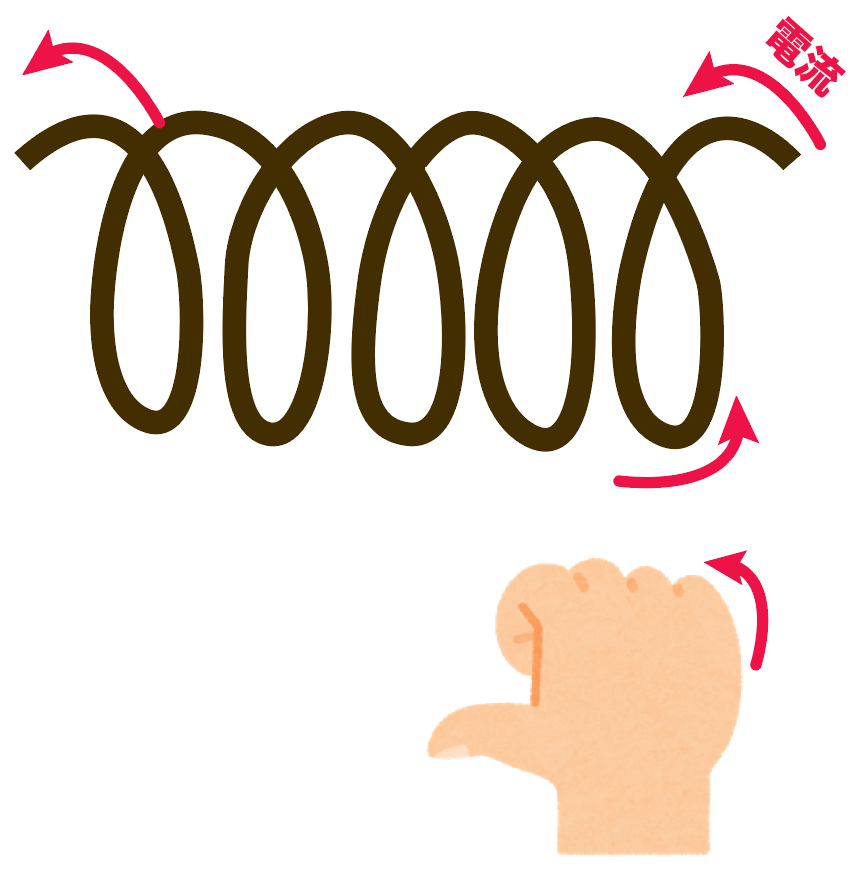
このとき、残りの「親指」の方向に磁界が発生する。
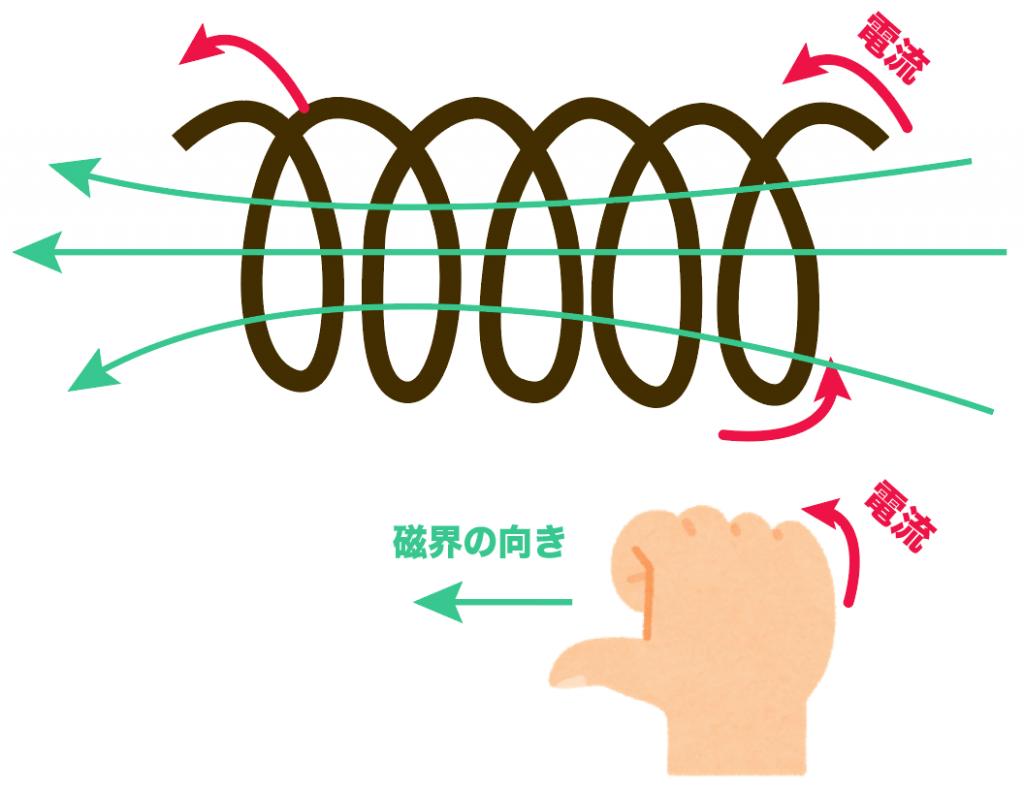
これが右手の法則。
こいつを使ってやれば、
コイルに電流を流したら生じる磁界の向きをいつでも思い出せるってわけ。
例えば、このようにコイルに電流が流れている場合を考えてみよう。
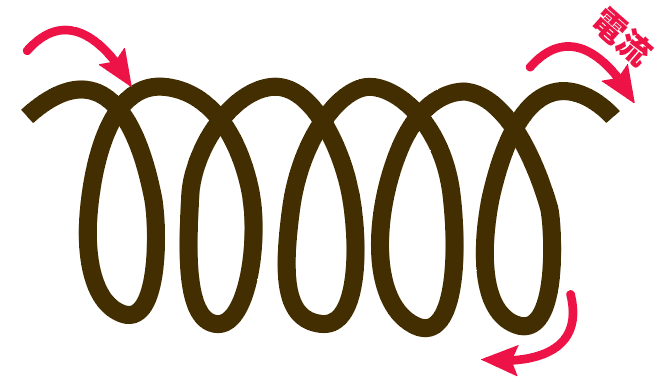
右手の「人差し指〜小指」を電流の向きに合わせればいいから、右手をくるっと回すことになる。
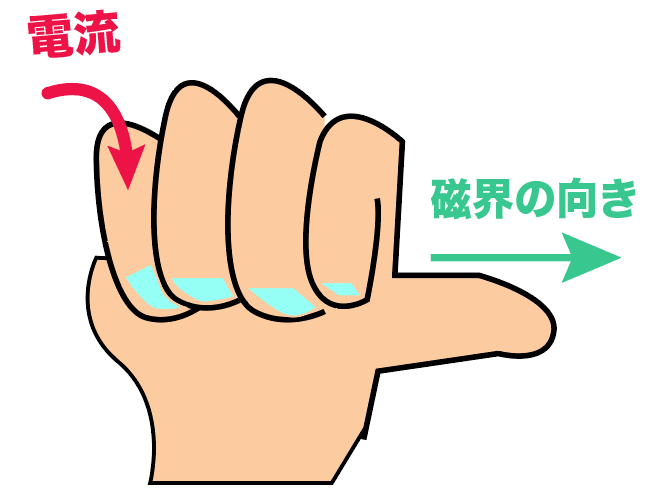
あとは右手の親指の向きに注目。
親指は右に向いているから、コイルの中を通る磁界の向きは
左から右
になるね。
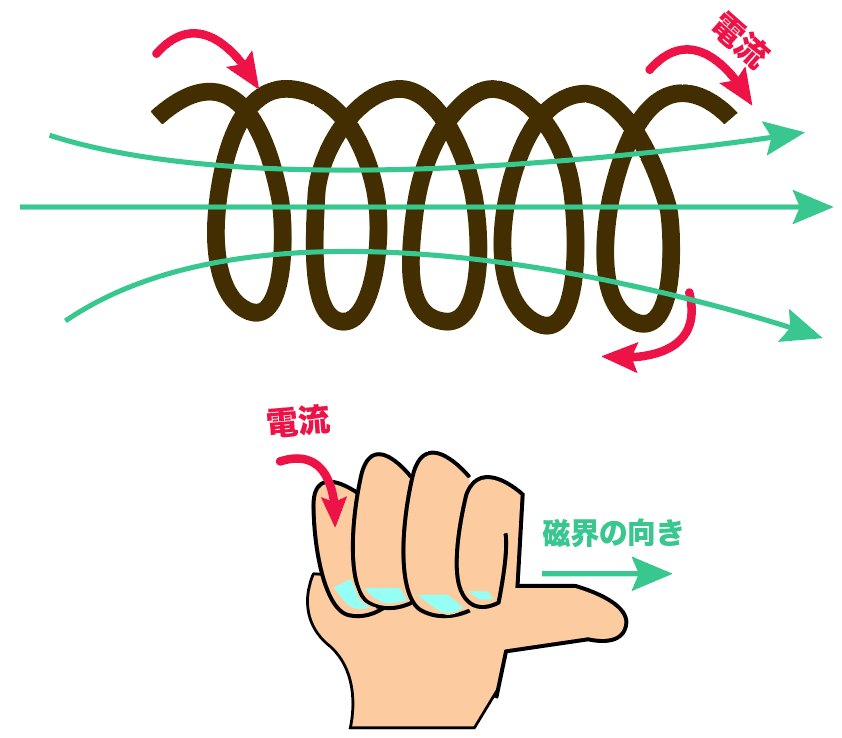
こんな感じで、右手の法則は大活躍。
えっ、右手の法則を忘れた時はどうすればいいのかって?!
そういう時は、右ねじの法則を使ってみよう。
1つの1つのコイルの部分に注目して、右ねじの法則を使っていけば、コイルの中の磁界の向きがわかるはずだ。
ちょっとめんどくさいけど、右手の法則なら2秒ぐらいで磁界の向きがわかるから使っていこう!

そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。ナイス、トライ。
実は不思議なことに、
導線に電流を流すと周りに磁界ができる
って知ってた??
ある導線に電流を流してやると「進行方向に対して右回り」に磁界ができるんだ。
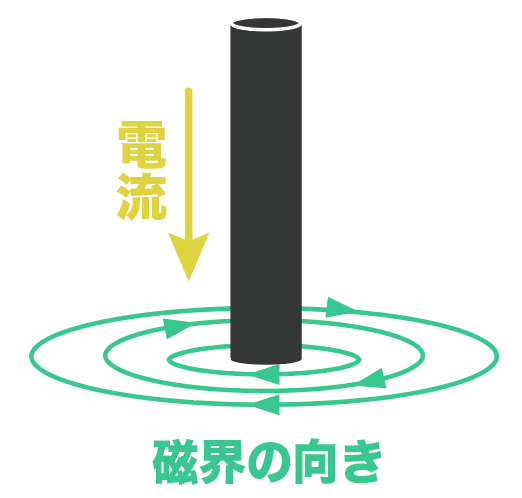
逆方向に電流を流せば、磁界の向きも逆回りになるはず。
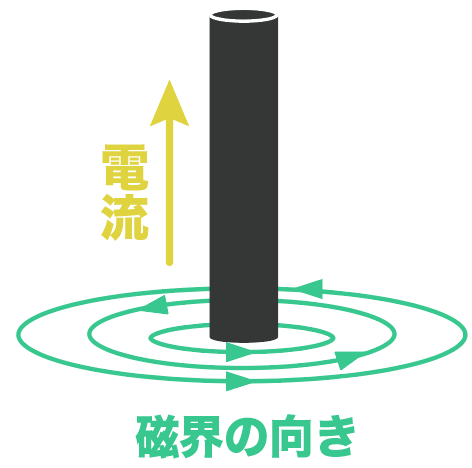
いやあ、摩訶不思議だね。じつに。
電流を流したら磁界ができる
という単純なルールだから、覚えやすいかなと思うかもしれない。
だが、しかし、この現象で暗記が難しいのが
電流・磁界の向き
だ。
電流の向きで磁界の向きが変わるからややこしいのさ。
そんな、電流の向きから磁界の向きを導けるのが、
右ねじの法則
というものだ。
今日はこの「右ねじの法則」の使い方をみていこう。
右ねじの法則うんぬんの前に、
ねじ
を詳しく見ていこう。

実はこの「ねじ」、
(頭から見て)右に回すと、ねじが進む
っていう性質がある。
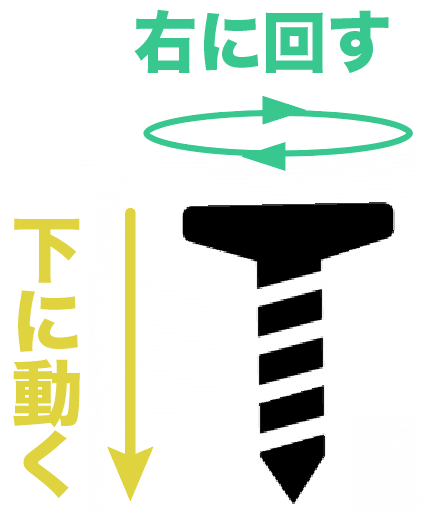
逆にねじを立てて右に回せば(頭から)、逆向きにねじが進むことになる。
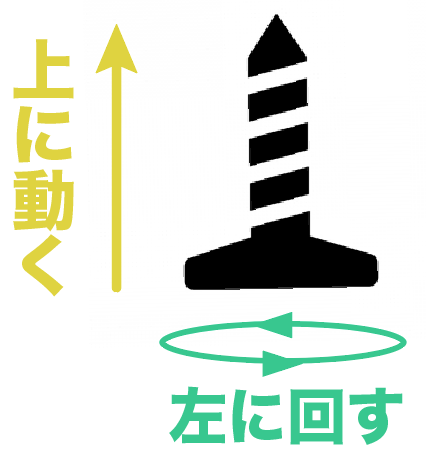
これが「ねじの基本」だ。
いよいよ右ねじの法則とは何か見ていこう。
ズバリ、
ねじの動きを使って、電流と磁界の向きを覚えやすくるためのツール
だ。
ねじが進む向きを「電流の向き」、ねじが回る向きを「磁界の向き」としてやる。
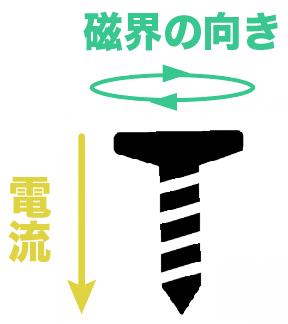
すると、電流の向きにねじの向きを合わせてやれば、その導線に生じている磁界の向きがわかるんだ。
例えば、このように導線に電流が流れていたとしよう。

まず、進行方向にねじの先を置く。

そして、どっちに回すとねじが前に進むかを考えてみよう。
ねじは右に回すと前に進むから、このように右回りになるはず。
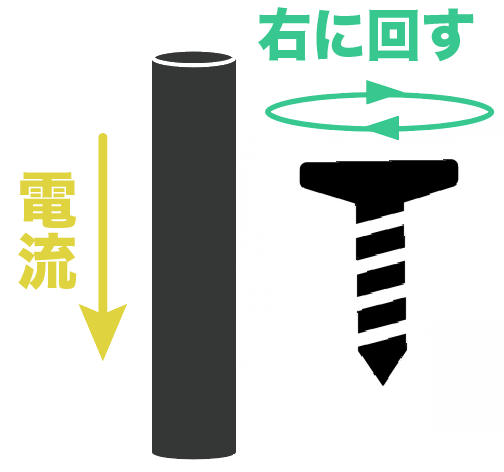
このねじを回す向きが磁界の向きだ!

いやあ、すげえな、ねじ。
右ねじの法則はだいたいわかったかな?
今度は右ねじの法則を使って問題を解いてみよう。
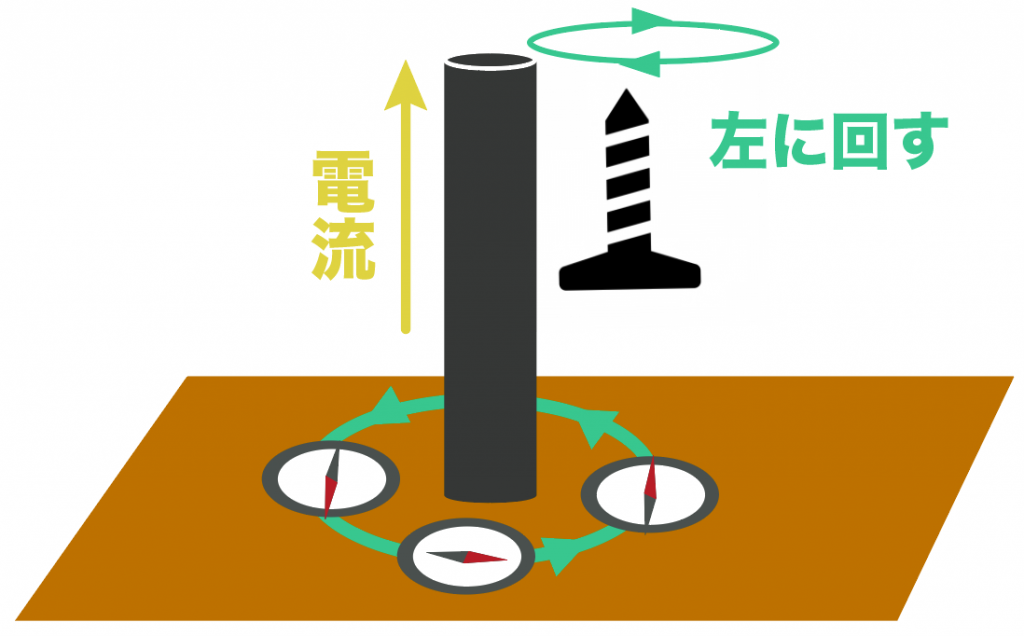
次のように導線に電流が流れているとき、導線の周りの方位磁針はどのようになるでしょうか。
方位磁針の向きの絵をかいてね
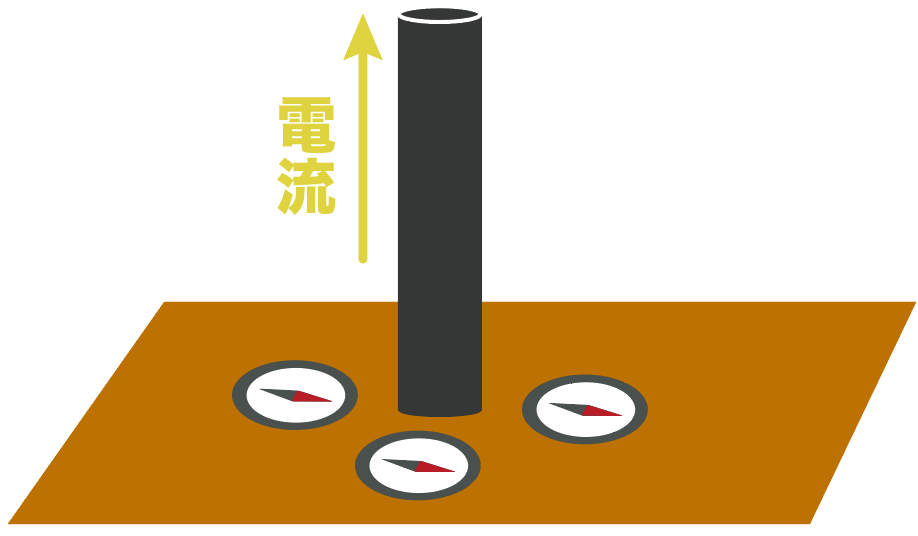
この問題では、右ねじの法則を使ってやればいい。
右ねじの法則使って、電流の進行方向にねじの先端を置く。
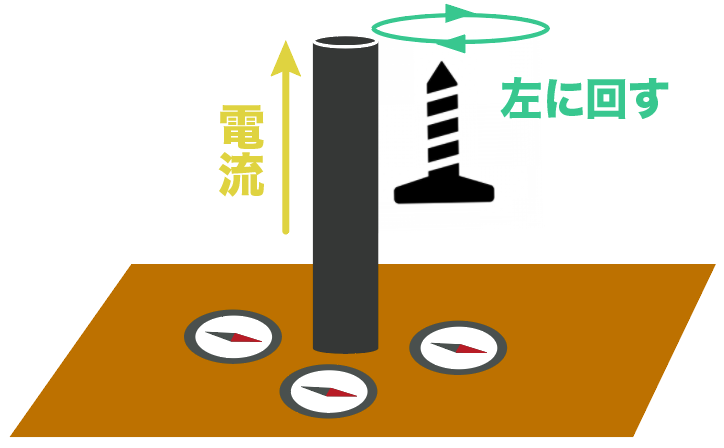
その向きに進むように、ねじを回してやればいいから、上から見たら左回りの磁界が発生するはず。
で、方位磁針のN 極は、磁界の向きを向くはずだから、こんな感じで右回りに方位磁針のN 極が向くようになる。
右ねじの法則の問題が解けたら完璧。
次はこいつを応用した「右手の法則」を見ていこう。
そんじゃねー
Ken
中学理科の「電流と磁界」で知っておきたいのが、
の3つ。
こいつらを知っておくと、「電気と磁石」の内容がスーッと頭に入ってきやすいよ。
まずそもそも押さえておきたいのが
磁石とはなんなのか?
ってこと。
磁石は生活に溶け込んでいて、日常生活でも見かける機会があるよね。
でもまあ、こいつは何者なんだって話から入ろう。
磁石とは、
古代ギリシャ時代に発見された不思議な石
と思っておけばいい。
どうやら、ある羊飼いが鉄の杖を地面についたところ、杖が地面にくっついてしまった事件が起こった。
この偶然のハプニングから、磁石が発見されたらしいんだ。

普通の石ころとは違って、「不思議な力が働いている石」が磁石というわけ。
続いては磁力だね。
磁力とはズバリ、
磁石に働く力のこと
だね。

さっき磁石とは「不思議な石」と言ったけど、何が不思議かっていうと、
この石には「ある力」が働いているからなんだ。
具体的にどういう力かというと、
を持っているよ。
中1理科の「力の種類」でちょっと勉強したけど、磁石には N 極と S 極があって、
という性質があるね。

こんな感じで、磁石に働く力を「磁力」と呼んでいるんだ。
磁界とは、
磁力が働く状態になっている空間のこと
を言うよ。
例えば、ここに磁石がポンと置いてあるとしよう。
そして、その磁石の磁力がこの範囲に働いている。
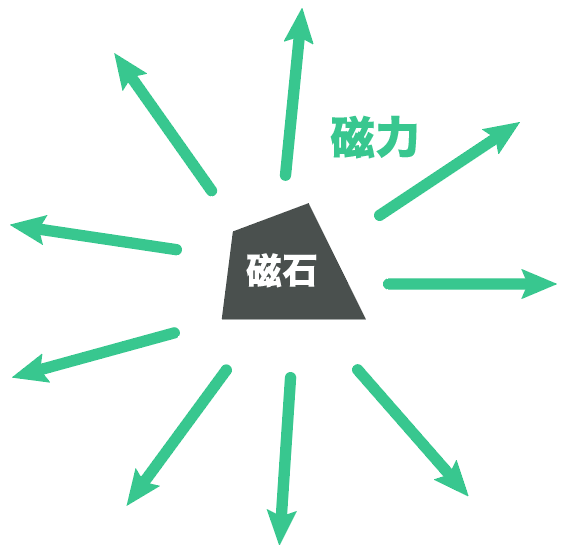
この時、磁力が働いている範囲を「磁界」と呼んでいるんだね。
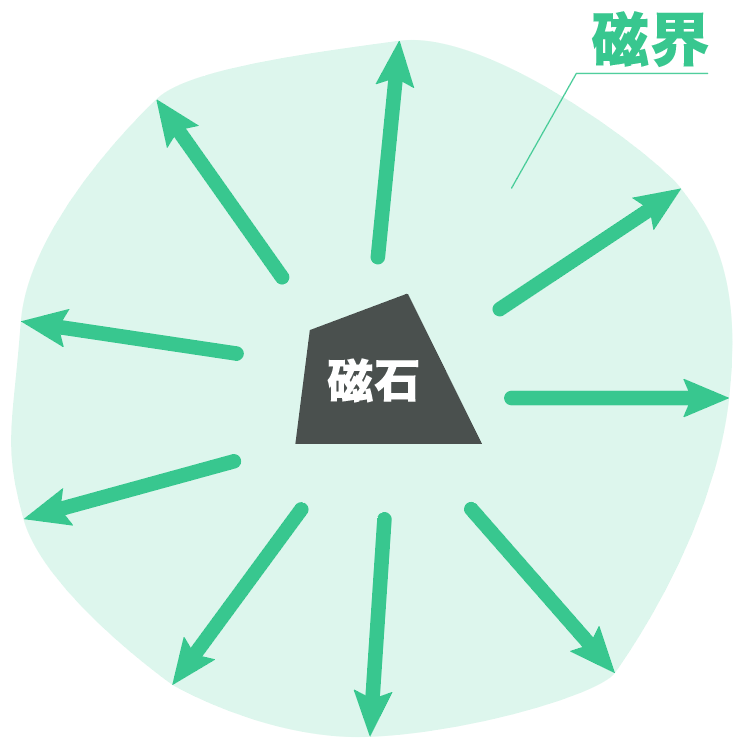
さっき紹介した「磁界」には「ある方向性」があることが発見されたんだ。
それは、
N 極から S 極に向かう
というもの。

例えば、ある磁界の中に、方位磁針を置くと 「ある方向」を指し示すことになる。
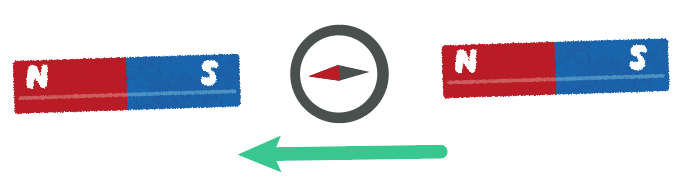
なぜなら、方位磁針の針は磁石になっていて、Nの部分にN極、反対側はS極になってるからだ。
だから、方位磁針の針のN極はS極がある方を向くはず。
このN極からS極への方向性を「磁界の向き」というよ。
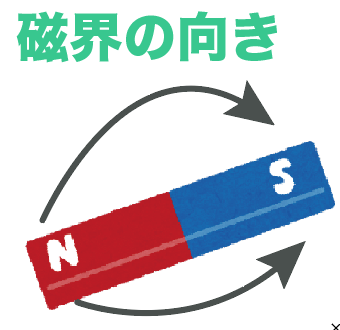
で、「磁界の向き」を線で表したものを「磁力線」と呼んでいるんだ。
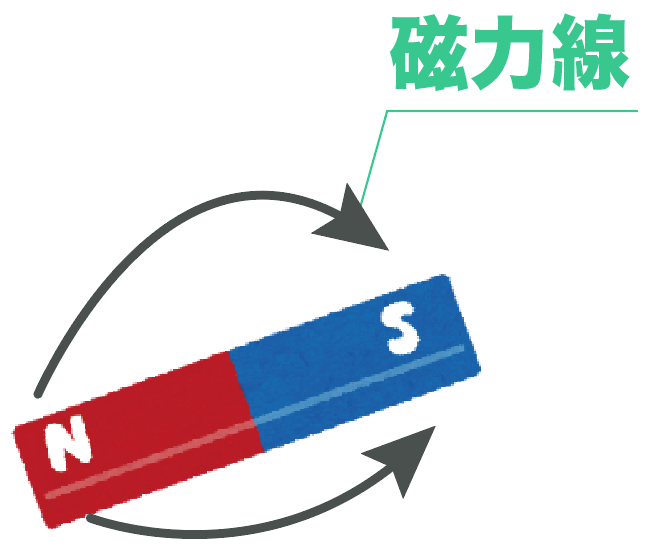
磁力線をかきたいときは、磁界の中に方位磁針を置いて、 N 極が示す方向を線で結んでやるといいぜ。

という感じで、
というキーワードをまずは押さえていこう!
次はいよいよ「右ねじの法則の使い方」を見ていくよ。
そんじゃねー
Ken
中2理科の電気の単元で、
とか見てきたけど、もう1個、中学理科で覚えておく公式があるんだ。
それは、
電力量の計算公式
だ。
電力量とは、ズバリ
電流が流れたときに生じる電気エネルギーの総量のこと
だね。
単位は熱量と同じジュール [J] を使うよ。
計算公式も熱量と同じで、
(電力量) = (電力) × (電流を流した時間)
なんだ。

例えば、300 W の電化製品を100秒使った場合を考えてみよう。
この場合、電力量を求める公式を使って、
電力量 = 電力×電流を流した時間
= 300 × 100
= 30,000 [J]
という電力量になるね。
ここまで電力量の計算方法わかった。
それに加えて知っておきたいのが、
Wh
という新しい単位だね。
これはどういうやつなのかというと、
1Wの電力を1時間消費したときの電力量のこと
だ。
1時間が3600秒だから、
1Wh = 1W × 3600
= 3600 [J]
のことを表しているよ。
ちなみにWhはだけでなく kWh というものも使われていて、これはWhに「キロ」をつけただけ。
1[kWh] は [Wh] の1000倍。
1 [kWh] = 1000 [Wh] になるね。
以上が電力量の紹介だったね。
実はこの「電力量」は僕らの生活に身近なもの。
電気代を支払う時には「電力量」を基準として、お金を払うことになってるんだ。
試しに、僕が平成31年2月に使用した電力量をさらしてみよう。
請求書を見てたところ、
103kWh
だったよ。
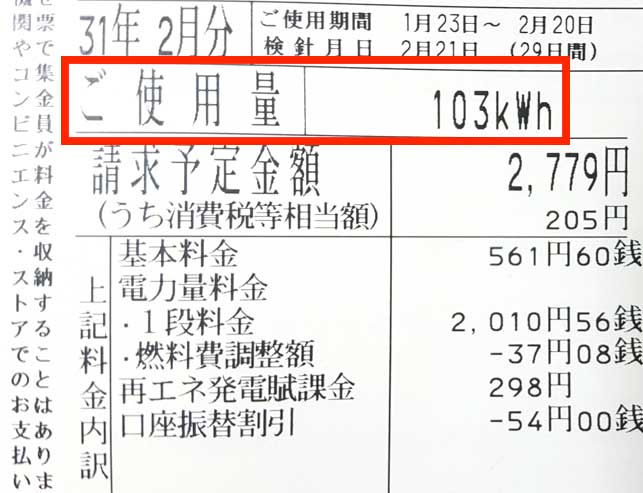
このkWhをジュールの単位に直してやると、
103×1000×3600
=370,800,000 [J]
の電気エネルギーを消費してしまっていたことになる。
これを電力使用日数の29で割ると、
370,800,000 [J] ÷ 29
= 12,786,206[J]
を1日あたり使っていたことになる。
これはどれくらいの消費電力なのか?
具体的な例に落とし込んでみると、
1200 W のドライヤーを10,655秒使っている
ぐらいの電力量。

この10,655秒を時間に直してやると、
約3時間!
ドライヤーを3時間ぶっ続けで使ってるぐらい、僕は平成31年の2月に電力を消費してしまっていたんだ。
いやあ、環境破壊しちゃてるね。
このように自分が使った電力量を確認してみると、理解が深まるから領収書をチェックしてみてね。
そんじゃねー
中学2年生の電気ではいろんな公式でできて大変!
ここまで
を勉強してきたけど、もう一つ勉強しなきゃいけないのが
熱量を求める計算公式
だ。
電気の分野でいう「熱量」とは、
電流を流したときに発生する熱量のこと。
単位はジュール [J]を使っていくよ。
で、この熱量の計算公式は次の式で表せるんだ。
熱量 = 電力×時間
だね。

熱量をJ、電力をW、電流が流れた時間をsとすると、
J=Ws
になる。
それもそのはず。
「電力」は1秒あたりに生じる電気エネルギーのことだったね?
この電力に「電流が流れた秒数」をかけてやれば、「電気エネルギーの大きさ」を計算できるわけだ。
例えば、1000ワットの電熱線に5秒電流を流したときに生じる熱量を考えてみよう。
さっきの公式を使えば、
熱量=電力×時間= 1000 × 5
= 5000 [J]
という感じで、
5000ジュールの熱量が発生するとわかる!!!
「熱量」というやつは、僕らの生活で身近に使われているよ。
例えば、食品の裏側の成分表示。
エネルギーの欄にカロリー表記がされているよね?

実はこの「カロリー」は熱量の単位のこと。
ジュールではなくカロリーという単位を使っているだけで、言ってることは同じなんだ。
「カロリー」という単位は
水1gの温度を1度上げるために必要な熱量のこと。
1カロリーをジュールで表してあげると、
約4.2 J
に相当するものなんだ。

だから、単位をジュールからカロリーに変えたいときは、
ジュールを4.2で割ればカロリーになるね。
例えば、5000 [J] は何カロリーなのか調べてみよう。
ジュールをカロリーに直すためには4.2で割ればいいから、
5000÷4.2
=1190 cal
という感じで「1190 cal」になるね。
ちなみに食品の栄養表示のカロリーはただのカロリーではなく、
キロカロリー(kcal)
で表示されることが多い。
キロカロリー(kcal)はカロリーを1000倍した単位になっているよ。
メートルとキロメートルの関係と同じで、mからkmに直したいときは1000分の一すればいいね。
例えば、さっきの1190カロリーは、1000分の1してキロカロリーに直すと、
1190÷1000
= 1.19 kcal
になる。
次は「電力量の計算公式」を勉強していこう!
そんじゃねー
Ken

中2理科で新しく出てくるのが「電力」という言葉。
電力とはズバリ、
1秒あたりに使われる電気エネルギーの大きさのこと
だ。
この電力を計算できる公式は
電力[W] = 電圧×電流
電圧をV、電流をI、電力をWとしてアルファベット表記で表すと
W = VI
になるね。
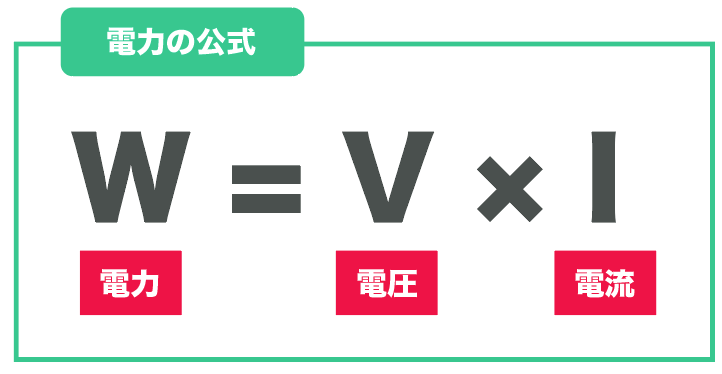
例えば、電源電圧が10 Vで、抵抗に0.2Aの電流が流れたとしよう。
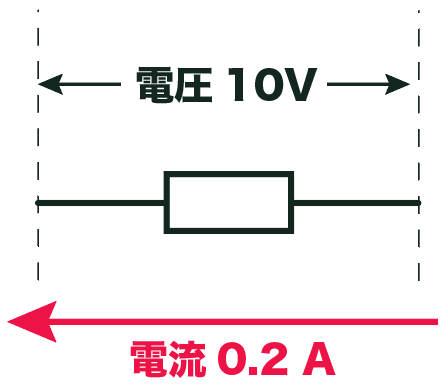
この抵抗に発生している電力は「電圧」と「電流」をかけて
電力[W] = 電圧×電流
=10×0.2
= 2 [W]
になるわけだ。
電力の計算の公式は簡単。なにせ、
電圧に電流をかけるだけ
だからね。
だがしかし、テストまでに公式を忘れないか心配だよね。
そんな時のために、電力の公式の語呂合わせを考えてみたよ。
WにVサイン
だ。
アルファベット表記で電力の計算公式を表していて、
を表しているんだね。

語呂のシチュエーションとしては、
カメラの前で W の形に V サインしてるやつを想像してみてほしい。

2つでVサインをしてWを作っているわけね。
あと、電力の公式で知っておきたいのは、
オームの法則を使えば「W=VI」以外の公式に変化する
ってことかな。
前回勉強したオームの法則の公式を使うと、公式の表現の幅が広がってくるんだ。
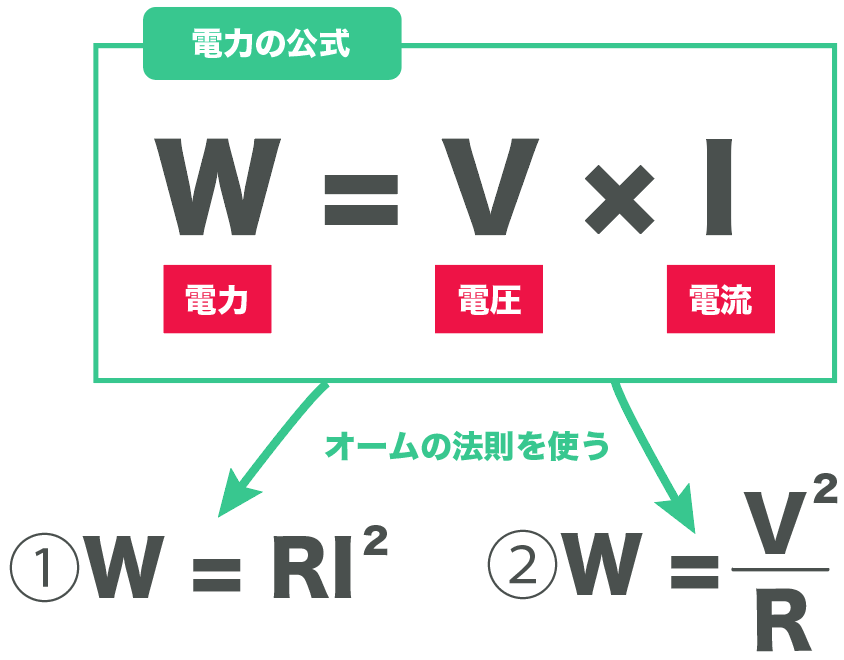
例えば先ほどの
W=VI
のVに、オームの法則の「V = RI」を代入してやると、
W = VI
W = RI²
になるね。つまり、電力は抵抗と電流で表すと、
電力=抵抗値×電流²
になるんだ。
同じことが、オームの法則の電流の公式(I = R分のV)でもできる。
電力の公式を「抵抗」と「電圧」だけで表すと、
W = VI
W = R分のV²
になる。つまり、電力は電圧と抵抗値で表すと、
電力=電圧² ÷ 抵抗値
でもあらわせるんだ。
このように、電力の公式はオームの法則を絡めると力が倍増。

そんじゃねー
前回、オームの法則の基本的な問題の解き方を見てきたね。
今日はもう一歩踏み込んで、
ちょっと難しい応用問題にチャレンジしていこう。
オームの法則の応用問題はだいたい次の3つのパターンだよ。
まずは直列回路なんだけど、抵抗の数が2つ以上の問題ね。
例えばこんな感じ↓
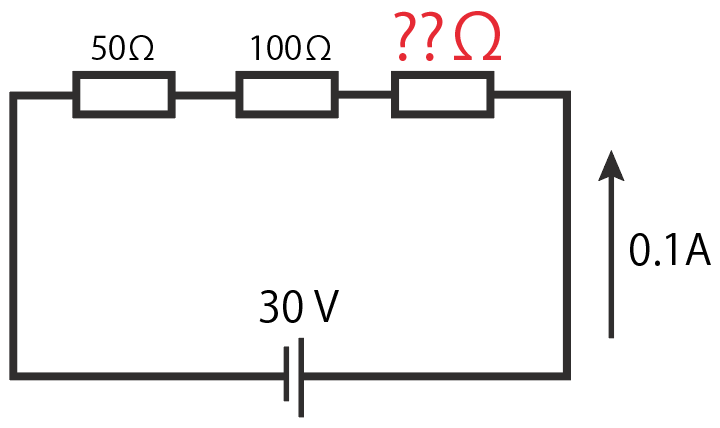
それぞれの抵抗にかかる電圧の大きさを求めていけばいいね。
一番左の抵抗値には0.1Aの電流が流れていて、しかも抵抗値が50Ω。
こいつでオームの法則を使ってやると、
$$V = RI$$
$$= 50 × 0.1$$
$$= 5 [V]$$
となって、5ボルトの電圧がかかっていることになる。
そして、その隣の100Ωの抵抗でも同じように0.1 Aの電流が流れているね。
なぜなら、直列回路では全体に流れる電流の大きさが等しいからさ。
で、こいつでも同じようにオームの法則を使ってやると、
$$V = RI$$
$$= 100 × 0.1$$
$$= 10 [V]$$
になる。
電源電圧の30Vからそれぞれの抵抗に5Vと10 V がかかっているから、最後の一番右の抵抗にかかっている電圧は
$$30-5-10$$
$$= 15 [V]$$
がかかっていることになる。
この抵抗でオームの法則を使ってやると、
$$R = \frac{V}{I}$$
$$= \frac{15}{0.1}$$
$$= 150 [Ω]$$
になるね。
今度は並列回路で抵抗の数が増えるパターンだね。
例えば次のような問題。
3つの抵抗が並列につながっている回路で、抵抗値がそれぞれ20Ω、50Ω、100Ωだとしよう。電源電圧が10 [V]のとき、回路全体に流れる電流の大きさを求めよ
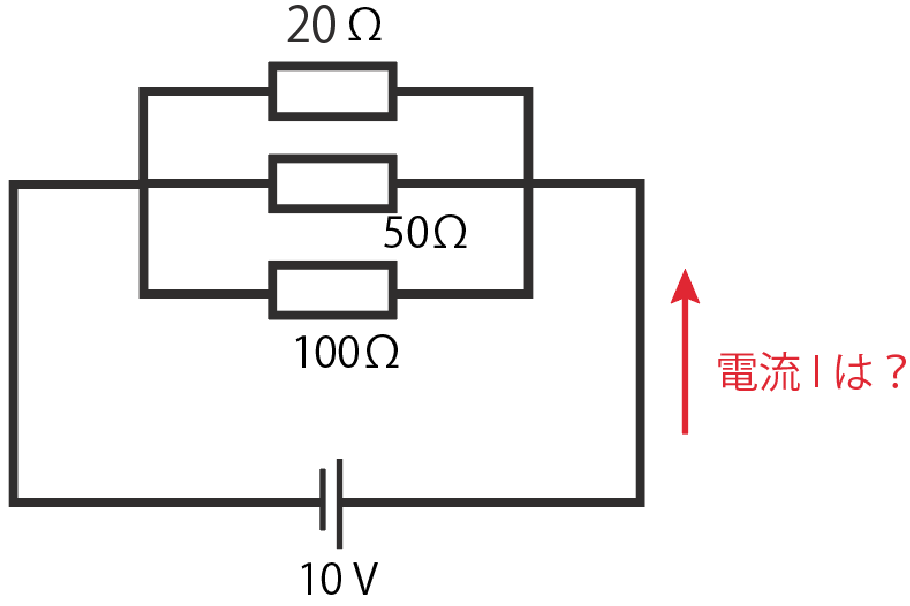
この問題の解き方は、
で回路全体の電流の大きさが求められるね。
並列回路では全ての抵抗に等しく電源電圧がかかる。
一番上の20Ωの抵抗でオームの法則を使うと、
$$I =\frac{V}{R}$$
$$= \frac{10}{20}$$
$$= 0.5 [A]$$
その下の50Ωの抵抗では
$$I =\frac{V}{R}$$
$$I =\frac{10}{50}$$
$$= 0.2 [A]$$
一番下の100Ωの抵抗では、
$$I =\frac{V}{R}$$
$$I =\frac{10}{100}$$
$$= 0.1 [A]$$
になる。
で、これら3つの枝分かれ後の電流を全て足したやつが「回路全体に流れる電流の大きさ」になるから、
$$0.5 + 0.2 + 0.1$$
$$= 0.8 [A]$$
が正解だ!
最後の問題は直列回路と並列回路が混合している問題だね。
例えば次のような感じ。
電源電圧が10 V、全体に流れる電流の大きさが0.2A。左の直列回路の抵抗値が30Ωだとしよう。並列回路の下の抵抗値が25Ωの時、残りの上の抵抗値を求めよ
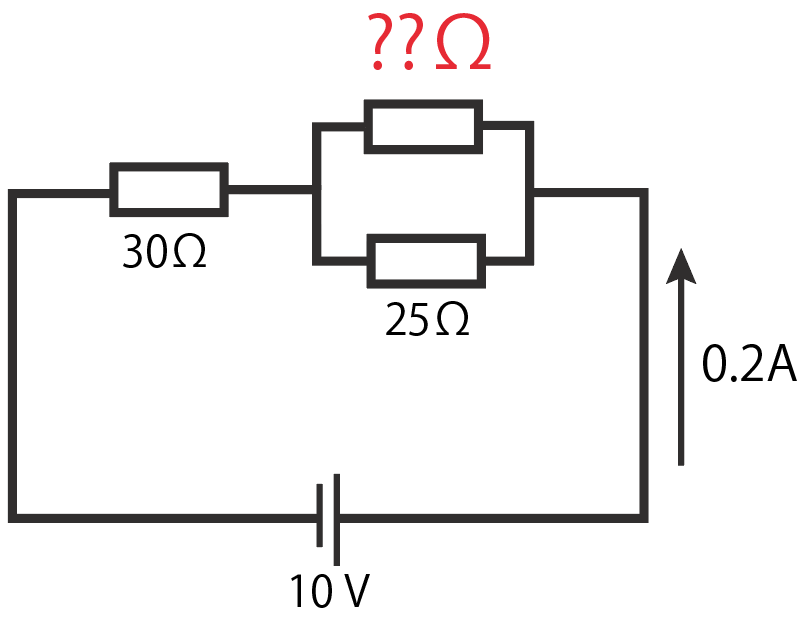
まず直列回路になっている左の抵抗にかかる電圧の大きさを求めてやろう。
この抵抗は30Ωで0.2Aの電流が流れているから、オームの法則を使うと、
$$V=RI$$
$$= 30×0.2$$
$$= 6 [V]$$
になるね。
電源電圧が10 V だったから、右の並列回路には残りの4Vがかかっていることになる。
回路全体に流れる電流は0.2Aだったから、この並列回路全体の合成抵抗は、
$$電圧÷電流$$
$$= 4 ÷ 0.2$$
$$= 20 [Ω]$$
になる。
次は右の並列回路の合成抵抗から上の抵抗の値を求めていこう。
詳しくは「並列回路の電圧・電流・抵抗の求め方」を読んでほしいんだけど、
全体の抵抗の逆数は各抵抗にかかる抵抗の逆数を足したものに等しい
だったね?
上の抵抗をRとしてやると、この右の並列回路の合成抵抗R’は
R’分の1 = R分の1 + 25分の1
になるはず。
で、さっき合成抵抗R’は20Ωってわかったから、
20分の1 = R分の1 + 25分の1
というRについての方程式ができるね。
分数を含む一次方程式の解き方でといてやると、
$$\frac{1}{20} = \frac{1}{R} + \frac{1}{25}$$
$$5R = 100 + 4R$$
$$R = 100 [Ω]$$
になる。
ふう、長かったぜ。
オームの法則の応用問題はこんな感じかな!
やっぱ応用問題を解くためには基礎が大事で、
を理解している必要があるね。
問題を解いていてあやふやだったら復習してみて。
そんじゃねー
Ken