こんにちは!この記事をかいてるKenだよ。肉摂取しすぎたね。
図形と相似の単元では、
相似の利用
を勉強していくよ。
相似を日常でもつかってみよう!
っていう単元。
なかでもよくでてくるのが、
校舎の高さを求める問題
だ。
今日は、この問題のパターンを2つ紹介するよ。
これならどんな校舎がきてもイチコロさ。
まずは、
影で校舎の高さを求める問題を解説していくよ。
つぎの練習問題をといていこう。
この問題は3ステップでとけちゃうよ。
相似な図形をさがしてみよう。
影をつかう問題では、
の2つが相似になってるよ。
なぜなら、三角形の相似条件の、
2つの角がそれぞれ等しい
にあてはまるからね。
人と校舎は地面に対して垂直にたってるね。
だから、地面と接してる角度は90°。
ある時刻における、
地面と太陽の角度、
つまり、太陽高度はおなじだから、
の2つが等しいはずだね。
だから、
が相似なんだね。
つぎは相似比を計算してみよう。
2つの三角形の「影の辺の長さ」に注目してみよう。
それぞれ、
だったね??
2つの三角形の相似比は、
(人の三角形):( 校舎の三角形) = 0.8 : 12.5
になるはず。
相似比から校舎の高さを計算してみよう。
校舎の高さをx m とすると、
1.6 : x = 0.8 : 12.5
0.8x = 1.6×12.5
x = 25
になるね。
おめでとう!
校舎の高さゲットできたね。
おつぎは、
縮図で校舎の高さを求める問題だよ。
これは作図しなきゃいけないから、
を用意してね。
つぎの練習問題をといてみよう。
身長1.6mの人間が校舎から20m離れたところから、校舎の頂点をみつめています。
ちょうど校舎のてっぺんが水平方向から42°のところにみえるとします。
このとき、400分の1の縮図で校舎の高さを計算しなさい。
この手の問題はつぎの3ステップでとけちゃうよ。
まずは、
「人の目」と「校舎」がつくる三角形
に注目しよう。
この三角形の縮図をかけばいいんだ。
問題文では、
400分の1の縮図をつかえ
っていう指示だったね。
「校舎までの距離20m」を400分の1にすると、
5cm。
角度が42°の直角三角形をかいて、その高さをだせばいいってことだね。
まず定規で5cmの直線をかいてあげて、
分度器で42°をはかって直線をひいてみる。
あとは、直角三角形の直角が必要だから垂線をかこう。
コンパスを持ち出す。
そして、5cmのところで半円をかく。
半円と辺の交点にコンパスの針をおき、チョビ円をかく。
逆側の交点にも針をおき、チョビ円をかく。
チョビ円どうしの交点とはじめの半円の中心をむすべば直角のできあがり!
⇒くわしくは垂線のかきかたをよんでね
こんなかんじで、
角度42°の直角三角形の縮図がかけたね。
おそるおそる、直角三角形の高さをはかってみると・・・・
ん!?
4. 5 cm
じゃないか!
直角三角形の高さは、
校舎の高さを400分の1に縮めたもの
だ。
400倍して校舎の高さにもどそうか。
実際の校舎の高さ
= 4.5 × 400
= 1800 [cm]
= 18 [m]
になるね。
・・・・おっとあぶねえ。
これは、
人の目線〜校舎のてっぺん
までの距離だ。
「地面」から「人の目線」までの距離
をたさないとね。。
ひとの目線の高さをたしてやると、
18 + 1.6
= 19.6 [m]
になる。
これが校舎の高さだ。
おめでとう!
これで縮図で校舎の高さを求められたね。
相似の利用の校舎の問題はどうだったかな??
校舎の高さを2つの方法で計算できれば大丈夫。
テストに校舎の高さの問題がでても、相似を利用してやればどうにかなるのさ。
そんじゃねー
Ken
ある日、数学が苦手なかなちゃんは、
二次関数の変域の問題に出会いました。

関数y=x²について、xの変域が -2≦x≦4 のとき、yの変域を求めなさい。

二次関数の変域・・・・?
変域って、
聞いたことあるな。。
でてきたもんね。
でも、
今回は2次関数。。
なんか違う気が・・・
おっ、
いいところに気づいた!
二次関数の変域のナゾ
を解き明かしていこう!
一次関数の変域って覚えてる?
わ、わすれた!!
二次関数の変域は違うの?
そう!
yの最大・最小値が
xの変域の端にならないことがある!!
へっ!?
なんで??
それは、
グラフの形に秘密がある。
たとえば、
この二次関数のグラフ
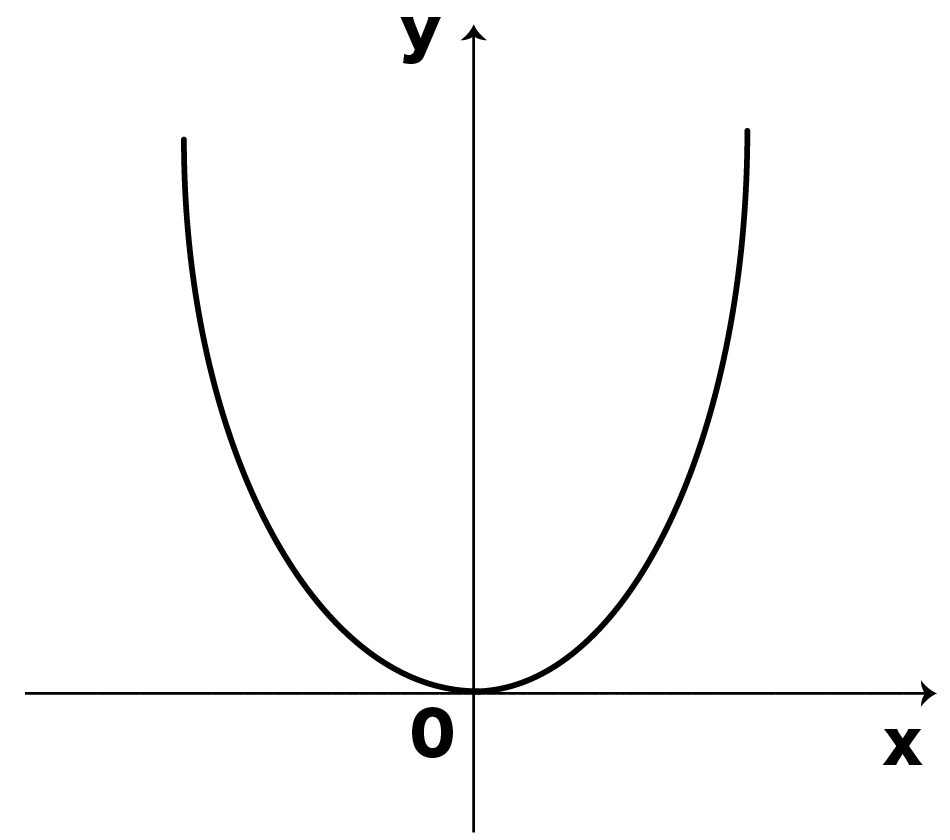
y軸に左右対称だ!
1次関数のグラフとの違い
分かったかな?
はい!
このグラフだと、
yが0より小さくなること
はないですよね!

そう!
じゃあ、
比例定数の正負が
グラフにどう影響あたえる??
一次関数だと、
比例定数の正負によって、
右上がり、
右下がりだった!
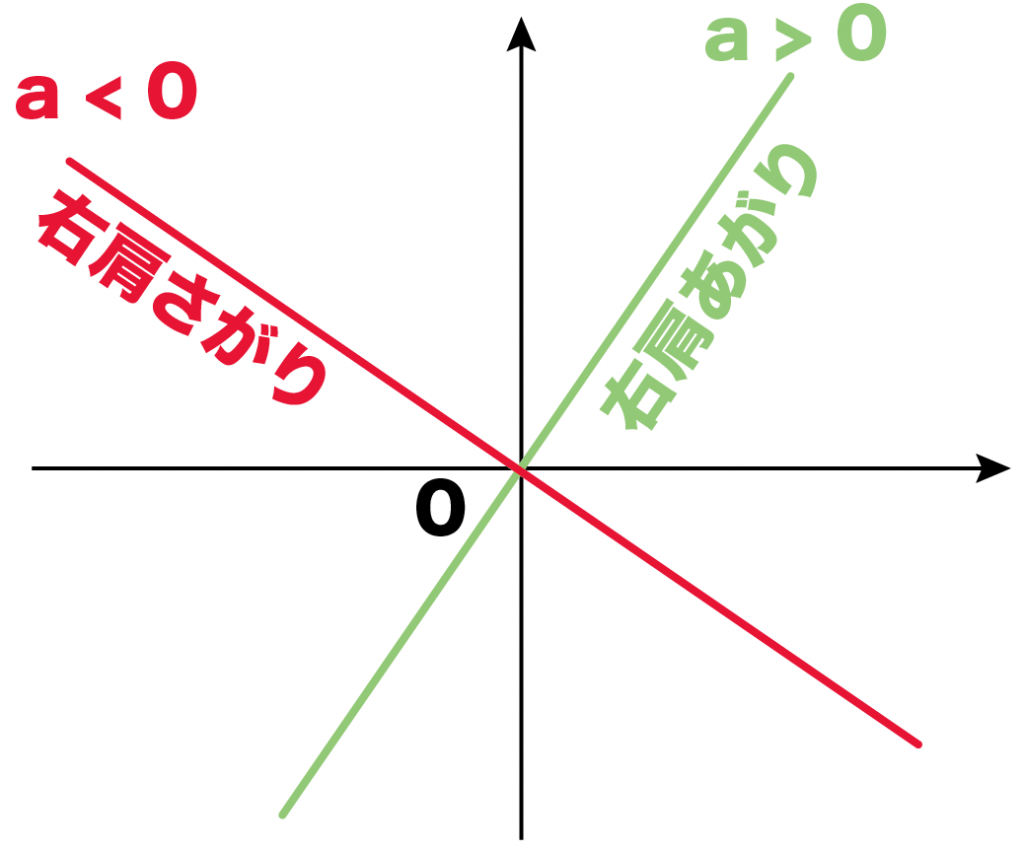
うん。
じゃあ、二次関数はというと、
↓を見比べてみて!!
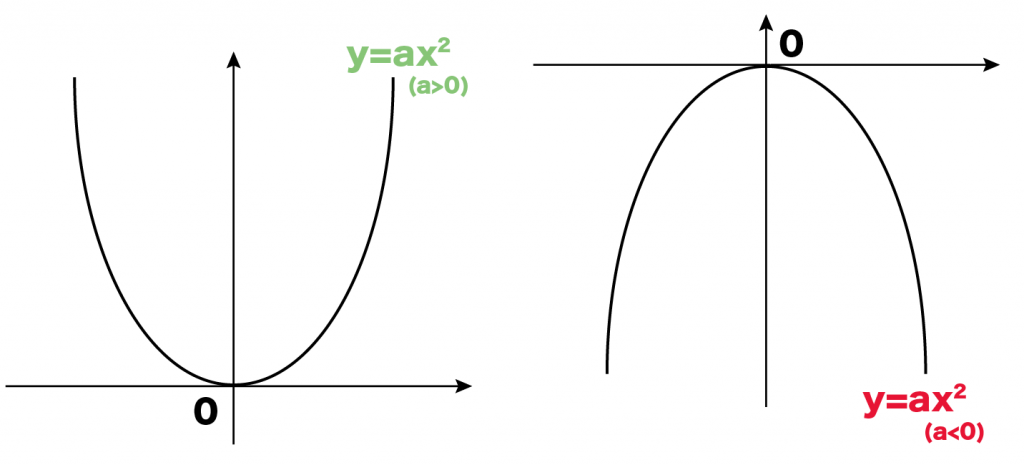
yの変域が特殊。
0で一番小さいときと、
0が一番大きいときがある!!
よく気が付いた!
こっから本番!
練習問題をといてみよう。
関数y=x²について、xの変域が -2≦x≦4 のときのyの変域を求めなさい。

y=x²
の定数aは正負どっち?
aは1!
ってことは、
「正」だ!
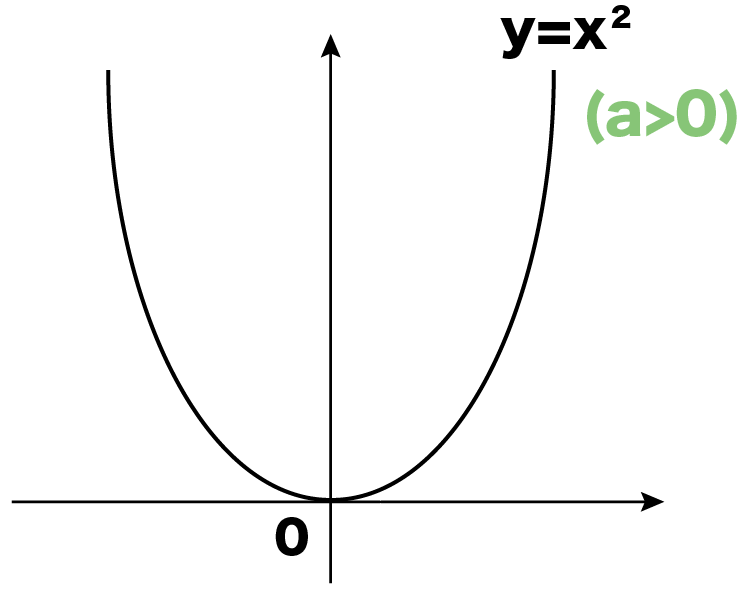
そう!
簡単でも確認は大事
xの変域に、
0が入るかどうか
を確認すること。
これ、大事!!
なんでかって、グラフを見て!
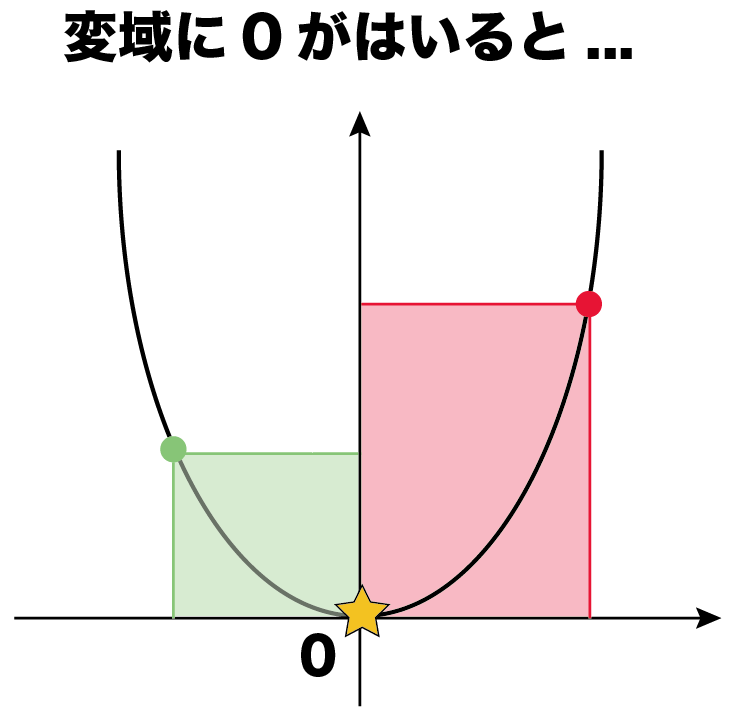
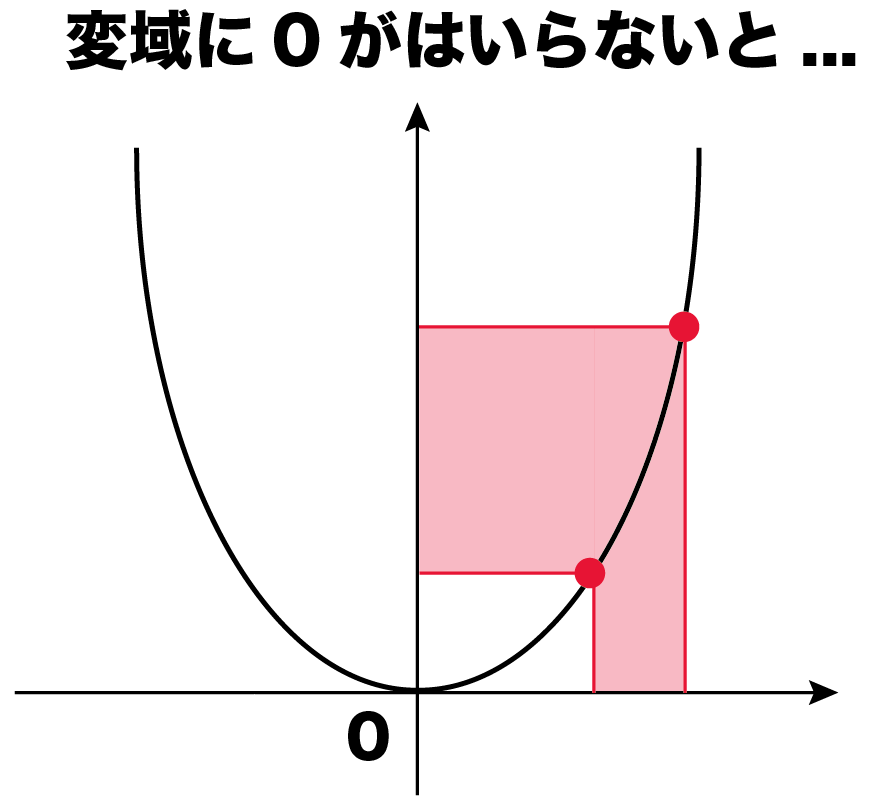
xの変域に0が入るとやばい。
yの変域の最小が0になる!
そう!
さっきの問題の変域、
「-2≦x≦4」
には0はいってる??
入ってる!
絶対値が大きいほう
だよ。
念のため確認。
-2と4、
絶対値が大きいのは?
どっちだっけ・・・・・・
絶対値は、
正負関係なく、数字が大きいほど大きい
よ!
ってことは、
4だ!
xの変域に0がふくまれるときは、
絶対値が大きいxを代入する
って覚えよう!
はい!!
さっそく代入してみます。
絶対値が大きいxは4。
y=x²に代入すると、
4×4=16になる。
yの変域は、
0≦y≦16かな!
二次関数の変域とけてるじゃん!
やっっったーあーーー!
二次関数の変域のポイントは、
グラフをかくこと。
これにつきるね。
グラフだと
わかりやすかった!!
でしょ??
ここまでをまとめるよ。
【定数aの正負】→【xの変域に0が入るか】→【代入は絶対値が大きいほう】
変域が求められるといいね!
が、がんばります!
練習問題つくったよ!
解いてみよう!
【1】y=2x²において、
【2】y=-x²で、
ありがとうございます!
ある日、数学が苦手なかなちゃんは、
放物線に出会いました。

二次関数y=ax2のグラフ。。。
放物線?
ほーぶつせん
ほーぶつせん
ほーぶつせん
・・・・・

2次関数で
『ほーぶつせん』
が出てきたんだけど、
よくわからなくて。
なるほど!
『放物線』のことだね。
ひらがなだとわかりづらい。
漢字を見てみよう。
放る、物、線?
そうそう!
『放った物の線』
何か、物を放るの??
そう!
例えば、
ボールを斜めに投げるとどう?
上がってから、降りてくる!
放ったボールみたいな曲線を
放物線
っていうんだよ。
身近でわかりやすい放物線っていうと、
『噴水』かな
あっ、先生!
あそこの噴水、
放物線に似てる!
放物線は身近にたくさんある!
放物線の特徴を見つけていこう!!
はい!!
曲線になってるとこ
だよ。
反比例のように分かれてもない!
二次関数の放物線は曲線になってるの!
じゃあ反比例と二次関数は一緒?
なるほど!
名前ついてるんだ!
2種類ある!
2種類しかないんだね
二次関数y=ax2の放物線は、
の2種類なんだよ。
なにがちがうんですかー?
ポイントは、
aの部分!
二次関数の比例定数だね。
aが0より小さいと噴水みたいになって、
噴水をひっくり返したみたいになるわけ。

じゃあ、次の特徴!
あっ、先生!
わたし、見つけた!!
ぬ!?
y軸を折り目にして折ってみると、
ほら……!
ピッタリ!
いいとこに気づいた!
y=ax²の式は、
y軸に対称になってるよ♪
他に放物線に特徴あるかな??
yが0以上しかならないときと、
0以下しか出てこない時がある!!
そう!
a>0だとyは0以上、
a<0だと0以下なんだ!
二次関数y=ax2の比例定数aをいじってみて。
いじる??
大きくしたり小さくしてみてよ。
符号かえずにね。
あっ、放物線が閉じたり開いたりしてる・・・!?
そう!よく気付けた!
aの絶対値が大きいほど閉じたグラフになる。
小さいほど、開いたグラフになるんだ。
あっ、ほんとだ!
これで、5つ見つけられたね。
じゃあ、まとめておこう!
ありがとうございます!
これだけじゃない!探せば他にもきっとある!
目指せ、二次関数マスター!!
その歩みが今始まったのだ!!
がんばります!
こんにちは!この記事をかいてるKenだよ。徒歩はこころにいいね。
中学数学で二次関数をたくさん勉強してきた。
グラフの書き方とか、
比例定数の求め方とか、
変域の問題とか、
ほんといろいろ。
今日は最後のとりでの、
二次関数の利用を勉強していこう。
とくにテストにでやすい、
図形を移動させる文章問題
をいっしょにといていこうね。
さっそく問題をといてみよう。
練習問題
1辺の長さが5cm、10cmの直角三角形ABCがあります。
こいつと合同な直角三角形DEFがちょっと先においてあります。
△ABCを毎秒1cmの速さで△DEFにむかって動かします。
点BがDからEまで動くとプログラムされてます。
点Bが点Dにきてからx秒後の三角形が重なった部分の面積をy[cm^2]とするとき、
yをxの式であらわしてください。
あと、グラフとxの変域とかも答えてくれ。
つぎの3ステップで解けちゃうよ。
三角形が重なる部分をイメージしよう。
この面積がyになるはず。
想像できないと関数の式つくれないよね?
実際にイメージしてみるために、
2つの三角形をぐいっと近づけてみよう。
すると、2つの三角形が重なる黄色い部分ができるじゃん??
イメージできれば第1ステップ終了。
三角形の面積は、
底辺×高さ÷2
だったよね??
ってことは、重なった三角形の面積をだすには、
の2つが必要になるわけ。
ってことで、まずは底辺。
練習問題の辺DBの長さを求めればいいんだね。
BがDにきてからx秒後のね。
点BがDにきたときのDBの長さは0だ。
ここから、1秒間に1cmの速さで三角形は右に動いていくから、
x秒後には、
DB = x cm
になってるはず。
つぎは三角形の高さをだしてみよう。
BCとDFの交点をGとすると、2つの三角形が重なってできる三角形の高さは、
DG
だよね??
この辺の長さは、
△ABCと△DBGが相似ってことをつかえば求められる。
なぜ、こいつらが相似な関係にあるのかというと、
っていうかんじで、
2つの角がそれぞれ等しい
っていう相似条件をみたしてるからなんだ。
AB:AC = 2:1でなおかつ、
△ABCと△DBGは相似だね。
よって、
AB:AC
= DB: DG = 2: 1
x : DG = 2:1
DG = 1/2 x
になるね。
三角形の「底辺」と「高さ」が求められたね。
あとは、
三角形の面積を計算するだけ。
重なった部分の三角形、つまり、
△DBGの面積は、
底辺×高さ÷2
= DB ×DG÷2
= x × 1/2 x ÷2
= 1/4 x^2
になるね。
重なった三角形の面積がyだったから、
y = 1/4 x^2
になるわけね。
重なった部分の面積ゲットーーー!おわたーーーー!
ってなるのははやい。
まだ、1つだけやることが残ってるんだ。
それは、
グラフをかくこと
だ。
まずは、
xの変域を求めてみよう。
今回の問題では、BがDに重なってからの秒数をxとしてたね??
ってことは、
xは負の数はありえない。
つまり、
x ≧ 0
だよね??
んで、BはEまでしか進めないことになってるから、
x ≦ 10
なはず。
よって、xの変域は、
0≦x≦10
になるね。
xの変域をもとにグラフかいてみようか。
x・y座標が整数になる点
をうてばいいね。
二次関数のグラフの書き方がわからんときは復習してね。
二次関数のグラフのかきかたの基本は、
座標をうちまくって雰囲気で放物線をかく
だったね???
1メモリが1の座標に点をうちこんでやるんなら、
の4点でいい。
この点をうって、それっぽい放物線をかいてやると、
こうなるはず↓↓
xが0より小さい場合は点をうったり線をかいたりしちゃダメだよ。
これで文章問題の問いにすべて答えることができたね。
おめでとう!
二次関数の利用の図形の問題はどうだったかな??
図形の公式通りに等式をたてればいいんだ。
あとはxの変域を間違えないようにね。
そんじゃねー
Ken
みんな、元気にしてる?そらだよ☆彡
今日は二次関数y = ax2 のグラフをかくんだ!
どちらかというと、今日は「絵を描く」感覚(^_-)-☆
え?絵を描くの苦手?
大丈夫だよ、グラフは絵とはべつものだし!
いっしょに二次関数y=ax2のグラフの書き方を勉強していこう!!
二次関数y=ax2のグラフの書き方はつぎの3ステップ。
グラフが通る点をたくさんゲットして、
雰囲気で放物線をかけばいいのさ。
「グラフ」はたくさんの値=「点」の集まりの「線」だよね。
ということは、まずは「値」を求めなきゃ、グラフは描けないよね。
そして今度は、点たちを座標に書き込むことができる。
点を描き込むことができれば、できたも同然!
あとは点と点を結んで「線」(放物線)を描けちゃうんだ。
今日はいっしょに、
y=1/2x^2
の二次関数のグラフをかいていこうか。
xとy データの「表」をつくるよ!
紙と鉛筆の用意はできたかな?
さっそく始めるよ!
まず、xの値の範囲を決めよう。
沢山あったほうがより正確なグラフがかける。
だけど、今はおおよその形がわかればいいから、
データは10程度あればいいかな。
ってことで、今回はxの変域を「-5 ≦ x ≦ 5」と範囲を決めよう。
そうすると、表はこんな感じになる。
つぎはxの値をいれたときのyを求めればいいね。
地道に計算してみると、こうなる↓↓
計算ばっかでやんなっちゃうけど、ここは我慢しようね。
あとは計算結果を表にうめるだけ。
できたー?
さっきの点データを座標にかきこんでいくよ。
今回グラフをかくのは、メモリの単位が1のの座標でかくんだ。
だから、座標の点はxとyが整数の点だけでいいね。
y=1/2x^2の点データでいうと、
の5つの点だね。
こいつを座標にうちこんでみると、
こうなるね。
最後に点と点を結んでいくよ!
フリーハンドでもいいし、ものさしを使ってもいいよ。
座標の点をもとに雰囲気と直感でかいていこう。
座標をうてないところは点データをもとに、
そこらへんを通るように調整しよう。
おーーーらっよっと、
全部頑張って描きあげたよ!
こんな感じになったかな?
二次関数y=ax2の書き方はどうだったかな??
きれいな二次関数の放物線のグラフをかくコツは、
たくさん点データを求めること。
これにつきるかな。
雰囲気の部分がすくなくなるからね。
あとは、いろんなグラフを描いてみよう。
またね(^_-)-☆
そら
こんにちは!この記事をかいているKenだよ。トイレが近いね。
中学で勉強する関数もいよいよ大詰め。
一年生のころから、
とかたくさん関数をみてきたね。
今日は、ほんとうに最後の最後。
新しい関数を1つ勉強するんだ。
その名も、
いろいろな関数
だ。
ぶっちゃけ、名前とかとくにないんだけど、
身近でとっつきやすいよ。
マイナーっちゃマイナーなんだけど、テストにたまにでてくるんだ。
記事をよんでマスターしておこう。
つぎの例題をといてみよう。
練習問題
つぎの表はSIMカードの1ヶ月分の料金体系をあらわしています。

データ使用量ごとに料金が決まっています。
データ使用量をx GB、月額料金をy円とするとき、つぎの4つの問に答えなさい。
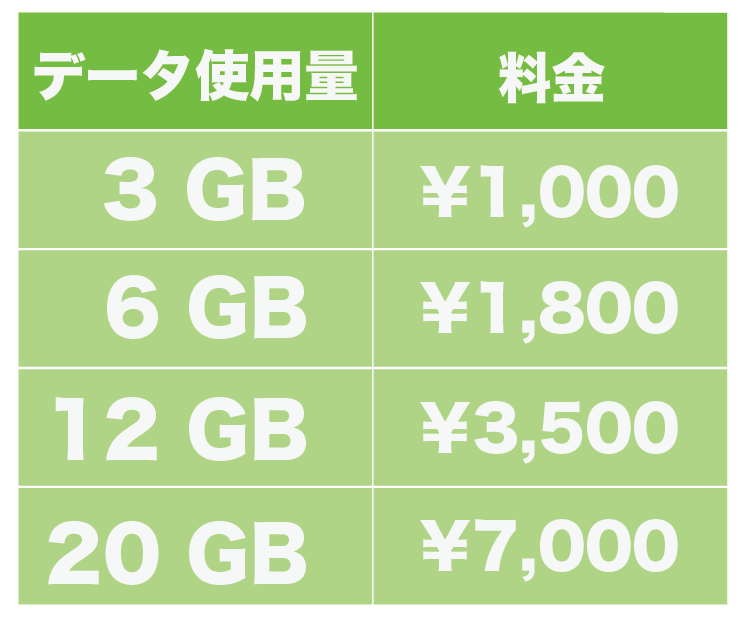
<データ使用量>
問1.
グラフをかきなさい。ただし、横軸を「データ使用量」、縦軸を「料金」とする
問2.
こいつは関数といえそうか
問3.
6GBつかうと月いくらか?
問4.
月々のおこづかいが3,000円のとき、何GBまでデータを使用できるか?
それじゃあさっそく、問1からといてみようか。
いろいろな関数のグラフをかいてみよう。
まず、x軸とy軸をひいてみるっと。
んで、この問題では、
だったね??
料金体系通りに関数のグラフをかいてみよう。
データ使用量が3GBまでのとき、
月額料金yは「1,000円」で一定だったね??
だから、このいろいろな関数のグラフは、
こうなるはずだ↓↓
こんなかんじで、
までの使用量の場合の様子をグラフにしてやると、
になるね。
あとは、境界をかいてやるだけ。
その境界をふくまないときは「○」、
ふくむときは「●」でぬりつぶしてやればいいのさ。
今回は「〜GBまで」っていう料金体系だったから、
上限の境界はふくむわけね。
不等号に=がついてるところが「●」、それ以外は「○」だよ。。
はい、グラフ完成〜
結論からいっちゃおう。
こいつは、まぎれもない関数なんだ。
なぜなら、
xが変化するごとにyの値が1つに決まるでしょ??
たとえば、
xが10のとき、yは3500に定まってるじゃん??
だから、こいつは関数なんだ。
もしも、こんなかんじにグラフがぶっこわれたら、こいつは関数じゃない。
なぜなら、
xが10のとき、yの値が3500と7000の2つあるからね。
ってことで、安心してね。こいつは関数だ。
つぎは、xが6のときのyの値を求めればいいね。
いろいろな関数のグラフをみてみると、
x = 6のうえには、
の2つがあるようにみえるよね??
だがしかし、境界に注目してほしいんだ。
棒のはしっこね。
境界のルールは、
だったよね??
ってことは、x = 6のときをふくんでるのは、
y = 1800のグラフ
だ。
つまり、
月額データ使用量が6GBのとき、料金は1800円ってわけね。
今度は逆だ。
yがある値以下になるときのxの変域を求めればいいのよ。
グラフをみてみると、3000円以内になるためには、
の2つなら月額3000円以内になりそうだ。
だから、
1ヶ月に6GBまでデータを使用できるね。
以上でいろいろな関数の問題は終了だよ。
どう?? なんだかいけそうな気がするでしょ?
ちょっと変わってる関数だけど、ポイントは1つ。
それは、
境界
だ。
グラフの端っこが含むか含まないのかに注意してね。
そんじゃねー
Ken
こんにちは!ぺーたーだよ。
中学3年生で習う相似。
「相似」ってふつうに生活してたら耳にしないよね??
最初はだれもが「ん、相似ってなんだ?」ってなる単元だ。
この単元でいちばん出てくるのは、
相似比を求めるタイプの問題
なんだ。
今日はテストで問題が解けるように、
相似比の求め方を解説していくよ。
よかったら参考にしてみて。
=もくじ=
相似比の求め方を勉強する前に、まず、
相似とはなにか??
を復習してみようか。
相似な図形とはずばり、
1つの図形の形を変えずに大きくしたり小さくした図形のことだよ。
たとえば、ある△ABCをビックライトでむちゃくちゃでかくした。
その結果、
△DEFができたとしよう。
このとき、△ABCと△DEFは相似な図形である
っていえるんだ。
なぜなら、2つの三角形は拡大・縮小の関係にあるからね。
んで、相似比っていうのは、
相似な図形の対応する辺の比
のことなんだよ。
たとえば、△ABCと△DEFの例だったら、
が相似比なんだ。
さあ、今回はこの相似比を求め方を解説していくよ。
相似比の求め方はつぎの3つのステップだよ。
練習問題をいっしょにといてみよう。
練習問題
下の2つの三角形は相似である。相似比を求めよ。
まず相似な図形の向きをそろえよう。
対応する頂点・辺がかさなるように回転させればいいんだよ。
練習問題をみてみよう。
このままだと対応する辺が見つけにくくない?
その理由は、三角形の向きが同じじゃないからだ。
だから、2つの三角形の向きを同じにしてあげよう!
△DEFを左にぐるっとまわしてやればいいのさ。
そうするとこうなるよ。
これで対応する辺がみつけやすくなったね。
つぎは、対応する辺の長さを確認してみて。
相似比は、
対応する辺の長さの比
だったよね??
だから、相似比を求めるためには、
2つの対応する辺の長さ
を知る必要があるわけ。
練習問題でいうと、
が対応する辺だね。
こいつらの長さはそれぞれ、
になってるね!
あとは相似比を求めるだけ。
相似比は、
対応する辺の長さの比
だったよね??
だから、もし、2つの相似な図形があったら、
対応する辺1 : 対応する辺2
の比を求めればいいわけ。
練習問題でいうと、△ABCと△DEFの相似比は、
AB : DE
を求めればいいね。
なぜなら、
この2つの辺が対応する辺同士だからね。
だったから、
AB : DE
= 5: 15
= 1: 3
になる。
これが2つの三角形の相似比なんだ。
答えるときは一番簡単な整数で答えるよ。
そこだけ注意してね!
他の辺で計算しても1:3になるから安心して。
図形の相似比を求めるには回転させるのがカギ!
頭の中で回転させるイメージ力が必要。
回転させたらノートの余白に描いちゃおうね。
目ですぐに確かめられるから、解く時間を減らすこともできるよ。
相似比は基本的なことだからやり方覚えておいてね。
じゃ、また今度!
ぺーたー
こんにちは!Drリードだよ。
二次方程式の解き方にはたくさん種類があったね。
今日はもう1つ解き方を勉強していくよ。
その名も、
平方完成をつかった二次方程式の解き方
だ。
この解き方は、
因数分解できなくて、
なおかつ、
解の公式を忘れたときに使える解き方なんだよ。
絶望的な状況をすくってくれるのが平方完成ってわけ。
つぎの2次方程式の問題をといていこうか。
平方完成をつかった二次方程式になれるためにね。
練習問題
つぎの二次方程式を解きなさい。
x^2 + 6x -5 = 0
xがついてない項を右に移項しちゃおう。
つまり、
数字の項を右によせちまえばいいわけ。
練習問題でいうと、
3つめの項の、
-5
がxがついてない項だ。
こいつを右に移項すると、
x^2 + 6x -5 = 0
x^2 + 6x = 5
になるね。
つぎは、どんな手をつかってもいいから、
左辺を「xをふくむ式」の2乗にしてみよう。
例題の式をみてみて。
x^2 + 6x = 5
左をxをふくむ式の2乗にするために、
両辺に同じ数をたしてみよう。
左側が ( )2 の形になるためには、「?」に何が入ったらいいと思う?
そう。
そうだよ、そうなんだ。
?には「9」がはいって、
x^2 + 6x + 9 = 5 + 9
になればいいね。
なぜなら、
左辺で因数分解の平方の公式の、
(a+b)^2 = a^2 + 2ab +b^2
がつかえるようになるからね。
さっそく因数分解してやると、
x^2 + 6x + 9 = 5 + 9
(x+3)^2 = 14
こんなかんじで、左辺に(xをふくむ式)の2乗をつくりたいときは、
xの係数の半分を2乗したやつを両辺にたせばいいね。
なっとくだ!
ここまできたら、平方根の解き方の形になったね。
左辺の2乗をとっぱらって、右辺を左辺の平方根にすればいい。
練習問題の、
(x+3)^2 = 14
もおなじように平方根の解き方をつかってみると、
x + 3 = ±√14
x = -3 ± √14
になるね。
おめでとう!
これで平方完成の解き方もマスターだ。
このめんどくさい解き方を、
平方完成で解く方法
っていうんだ。
因数分解できなくて、解の公式も忘れたら平方完成で解く
って、覚えといてくれよ。
心配なときは、つぎの練習問題もといてみてね。
レベルの高い解き方なんだから、練習あるのみだよ。
何回もね。へいへいほ~~♪
練習問題2. つぎの二次方程式を解きなさい。
x^2 + 3x + 1 = 0
⇒ 平方完成の二次方程式の問題の答えはこちら
平方完成は高校数学ですごく大切になるんだ。
平方完成を制するものは高校数学を制すといっても過言じゃあない。
いまのうちからマスターしておこう。
そいじゃねー
Dr.リード
こんにちは。けんいちだよ。
二次方程式では、便利な「解の公式」を勉強したね。
2次方程式「ax² + bx + c = 0」において、
解のxが、
x = {-b±√(b² -4ac)}÷2a
になる公式だったね。
じつはこの解の公式。
なんと、
bが偶数のときは解の公式が使いやすくなるんだ。
b’をxの係数(b)を半分にしたやつとすると、
x = {-b’ ± √(b’²-ac)}/a
たとえば、xの係数が偶数の二次方程式、
x² – 6x +1 = 0
があったとしよう。
このとき、xの係数の半分は-3。
こいつを偶数の公式のb’に代入してやると、
x = {-b’ ± √(b’²-ac)}/a
= {-(-3) ± √(-3)²-1)}/1
= 3± √8
= 3± 2√2
になるね。
ふつうの解の公式よりも簡単にとける。
まじ最高だ。
今日はせっかくだから、
なぜ偶数の解の公式がつかえるのか??
と
どういうふうに便利になのか??
をみていこうか。
=もくじ=
bが偶数のときの解の公式は便利ってわかった。
じゃあつぎは、
なぜ偶数のときの解の公式が使えるのか??
をみていこうか。
bは偶数だから、整数b’を使うと、
b=2b’
と表せる。
すると、二次方程式「ax² + bx + c = 0」 は、
ax² + 2b’x + c = 0
とかきなおせるね。
解の公式のなかの「b」を「2b’」におきかえればいいね。
すると、
x = {-2b’±√((2b’)² -4ac)}÷2a
= {-2b’±√(4b’² -4ac)}÷2a
になる。
つぎはルートの中身を簡単にするよ。
中身の、
4b’² – 4ac
を共通因数の4でくくると、
4( b’² – ac )
になるじゃんね。
4は2の2乗だから、ルートの外にだしてやると、
x = {-2b’±√4(b’² -ac)}÷2a
= {-2b’±2√(b’² -ac)}÷2a
になる。
最後に約分しよう。
分母と分子に共通の2っていう約数があるからね。
分母・分子を2でわると、
x = {-b’±√(b’² -ac)}/a
になる。
これでbが偶数の公式になったね。
実際に具体例で計算してみると、それがよく分かるよ。
例えば、2次方程式「3x^2 -8x +1 = 0」をふつうの解の公式で解いてみよう。
係数をそのまま当てはめると、
x = -(-8)±√{(-8)²-4×3×1}/2/3
= 8±2√13/6
= 4±√13/3
になるね。
でも、この二次方程式のbは「-8」で偶数。
さっきの偶数の解の公式もつかえるね。
偶数の解の公式にあてはめてみると、b’=-4だから、
x = -(-4)±√{(-4)²-3×1}/3
= 4±√13/3
ってなるね。
そうそう。
偶数の解の公式をつかってやると、
素因数分解や約分の手間がはぶけるんだ。
a=1のときは分数じゃなくなるからもっと簡単。
bが偶数の場合は絶対お得だよ!!!
二次方程式のbが偶数になってる??
迷わず偶数の解の公式をつかってみよう。
ふつうの解の公式よりはやく解けるからね。
問題をたくさんといてなれていこう。
そんじゃねー
けんいち
こんにちは!この記事をかいているKenだよ。日光にさらされてるね。
中3数学では、夏がすぎたころから、
関数y=ax2
を勉強していくね。
この単元では文字通り、「y=ax2」っていう関数を学んでいくよ。
教科書では、
xの2乗に比例する関数
ってよんでるね。
だけど、この単元を勉強していて思うのは、
ちょっと単元名かっこわるくね??
ってこと。
こんな名前にするんなら、二次関数っていう名前のほうがいいのにって思うはず。
実際、塾とか参考書とかでは、
「関数y=ax2」のことを「二次関数」とよんでるケースも多いね。
でも、中学数学の教科書のどこをさがしても、「二次関数」っていう単語がでてこないんだ。
こりゃ不思議!
どうして教科書が表記に気をつけているのかな・・・
そんな疑問を解消するために、
なんで中学教科書では「関数y=ax2」を二次関数と呼ばないの?
をかいてみたよ。
よかったら参考にしてみてね。
結論からいっちゃおう。
教科書で「関数y=ax2」を二次関数と呼ばないのは、
「関数y=ax2」は特殊な二次関数の1つにすぎないから
なんだ。
だから、関数y=ax2を二次関数って呼んじゃうと、他の大多数の二次関数たちが怒りだすわけさ。
宇宙にはかぞえきれないぐらいたくさん2次関数が存在していて、
その中の1つのある特殊な二次関数が、
関数y=ax2
ってわけ。
ちょっと変わった二次関数で周りから浮いてるんだけど、
二次関数っちゃ二次関数なんだ。
なぜなら、関数y=ax2の右辺は二次式だからね。
xの次数の2がいちばん大きな次数じゃん??
だから、二次関数とよんでも間違いじゃないんだ。
関数y=ax2が二次関数の特殊なやつの1つで、
二次関数ぜんたいをあらわさないとしたら、
二次関数はどういう式であらわされるんだろう・・・
って思うよね。
これは高校数学の範囲になるんだけど、
二次関数はつぎの式であらわされるんだ。
y = ax2 + bx + c
二次式ってことは、最大の次数が2。
ってことは、それより小さい次数の1とか0の項もいるかもしれない。
だから、xが2乗されてるax2だけじゃなくて、
xが1乗されてるbxとか、
xがついてないc とかが足されてるのさ。
んで、中3数学で勉強する「関数y=ax2」は、この二次関数の式で、
のときの二次関数をいってるわけ。
2つの係数が0なんて変わってる二次関数でしょ??
だから、こいつを二次関数と呼ばずに、「xの2乗に比例する関数」ってよんでるわけよ。
ごちゃごちゃいってきたけど、だいたい、その理由は、
中1数学で「比例」を「一次関数」とよばなかった理由とおなじだね。
「比例する関数」は、
y=ax
だったよね??
こいつは一次関数の一種。
なぜなら、一次関数y=ax+bでbが0のときの場合にすぎないからね。
xの2乗に比例する関数のあつかいも、
比例と一次関数の関係に似ていると思っておこう。
関数y=ax2を二次関数とよんでしまうのは、
ルフィをワンピースと呼んでしまうのと似てるね。
ルフィってワンピースの主人公であっても、ワンピースっていう漫画自体じゃないじゃん?
また、ブラック缶コーヒーだけが好きな人を、缶コーヒー好きと呼んでしまうことにも似てるね。
ブラック缶コーヒーは、缶コーヒーの中の1種にすぎないのにだよ?
ってことで、関数y=ax2はたしかに二次関数なのだけれども、
二次関数っていう大きなカテゴリーじゃないってことをおさえておこう。
学校のテストでは、
って名前でよんであげてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。ジンジャーは心にきくね。
中3数学では、
二次関数y=ax2を勉強していくよ。
ここではあろうことか、いろんな問題が出題される。
二次関数の比例定数を求める問題とか、
グラフをかく問題とか、
xとyの変域を求める問題とかね。
もう、ほんとたくさん。
そんな中でもとっつきやすいのが、
y=ax2のグラフから関数の式を読み取る問題
だ。
手頃でしれっと解けちゃうから、得点源になるはず。
この記事でしっかりマスターしておこう。
たとえばつぎのような問題だ。
この手の問題は3ステップでとけちゃうよ。
まず、
x・y座標が正確に読み取れる点
をさがしてみよう。
もし、座標のメモリの単位が「1」だとしたら、
x・y座標がともに整数になってる点をさがせばいいのさ。
例題のメモリの単位も「1」だよね??
ってことは、xとyの座標が整数の点をさがせばいい。
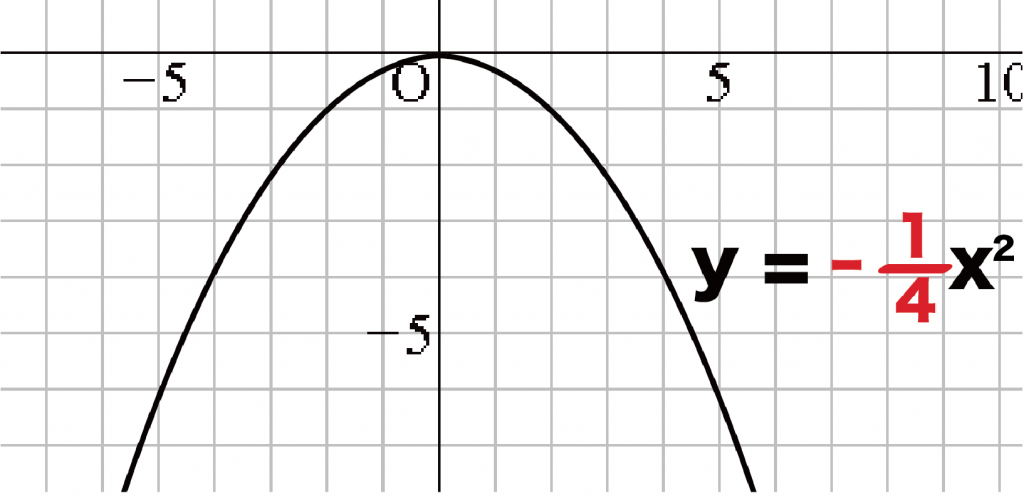
よーく目をこらしてみてみると、
・・・・・・・・・・・
はっ!
この放物線、
(2, -1)
とおってねえ?
こんなかんじで、xとyのメモリの交点を通っていて、
座標を読み取れる点をさがせばいいのさ。
さっき読み取ったx、y座標を二次関数y=ax2に代入しよう。
っていったかんじで代入してみて。
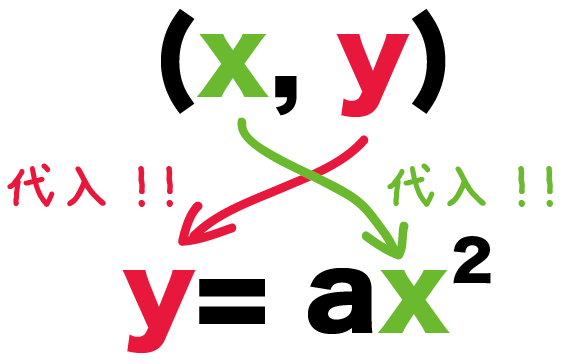
練習問題では、
になってたよね??
この座標たちをy= ax2に代入してみると、
-1 = a × (2)^2
-1 = 4a
になる。
あとは一次方程式を解くだけ。
xとyの座標を二次関数y=ax2に代入すると、
aに関する1次方程式ができるはず。
こいつを方程式の解き方通りにといてやればいいのよ。
練習問題でのこった一次方程式は、
-1 = 4a
だね??
こいつをaについて解いてやると、
a = -4分の1
になる。
よって、このグラフの二次関数y= ax2の式は、
y = -4分の1 x^2
になるね。
おめでとう!
これでy =ax2のグラフから式を読み取れたね。
二次関数y=ax2のグラフから式を読み取れるようになったかな??
解き方の最大のコツは、
座標を正確に読み取ること。
これにつきる。
ここで間違えると、一次方程式も意味をなさなくなっちゃうからね。
遠視の人はめがねをかけてでもいいから、
正確に座標をゲットしてみよう。
そんじゃねー
Ken
ある日、数学が苦手なかなちゃんは、
放物線に出会いました。
二次関数y=ax2のグラフ。。。
放物線わけわかんない泣
ゆうき先生だ!
いろいろな名前
があるの知ってたかな??
とか。
ちょうてん・・・・
じく・・・・・
漢字で覚えたほうがいいよ。
でも、聞き慣れない言葉だと、どうしても・・・・・・
じゃあ、『軸』はどう?
y軸とかx軸の仲間??
今まで、グラフで見てきたよね!
『頂点』は初めましてかな?
『頂点』って、どんな点だろう??
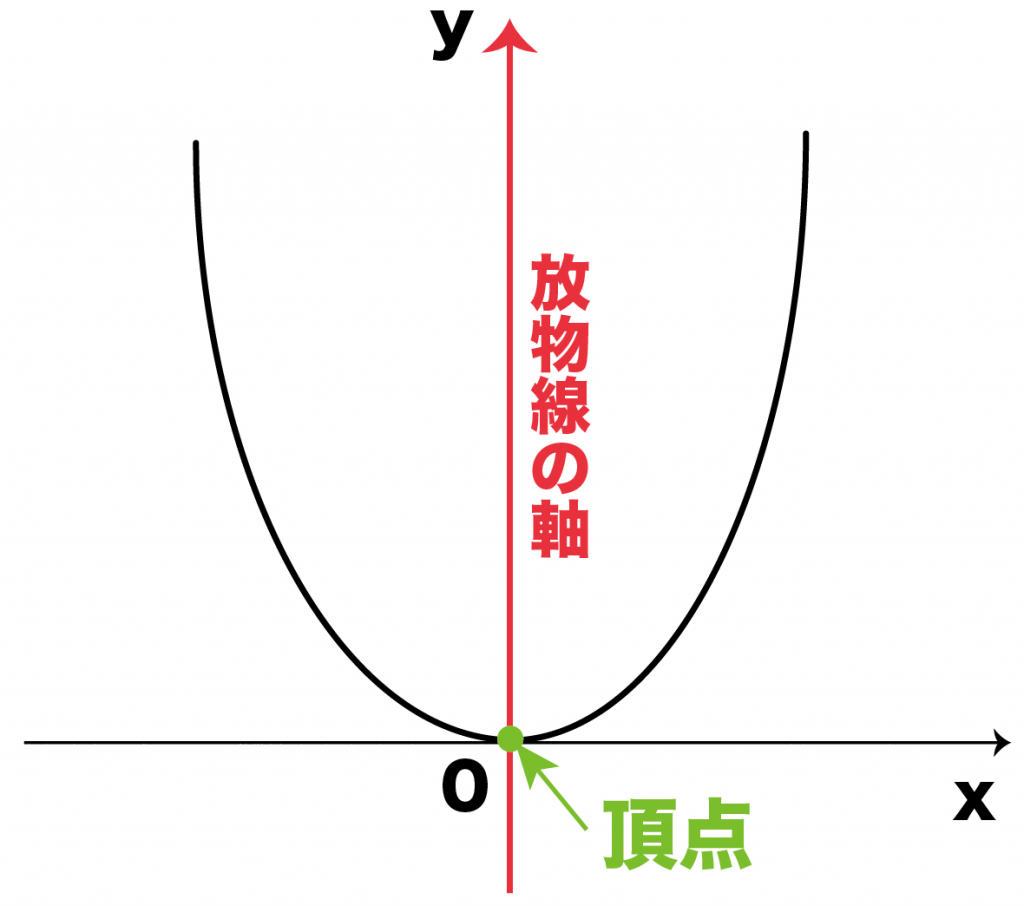
放物線の軸からみていこう。
放物線の対称軸のこと
なんだよ。
そのときの折り目を「対称軸」というの。

y軸
になってるね。
つぎは放物線の「頂点」。
放物線の頂点とは、
「放物線の軸」と「放物線」の交点のこと
をいうんだ。
よくわからんねーー
二次関数y=ax2だったら、
原点の(0, 0)
が頂点だね。
よくわからないときは、
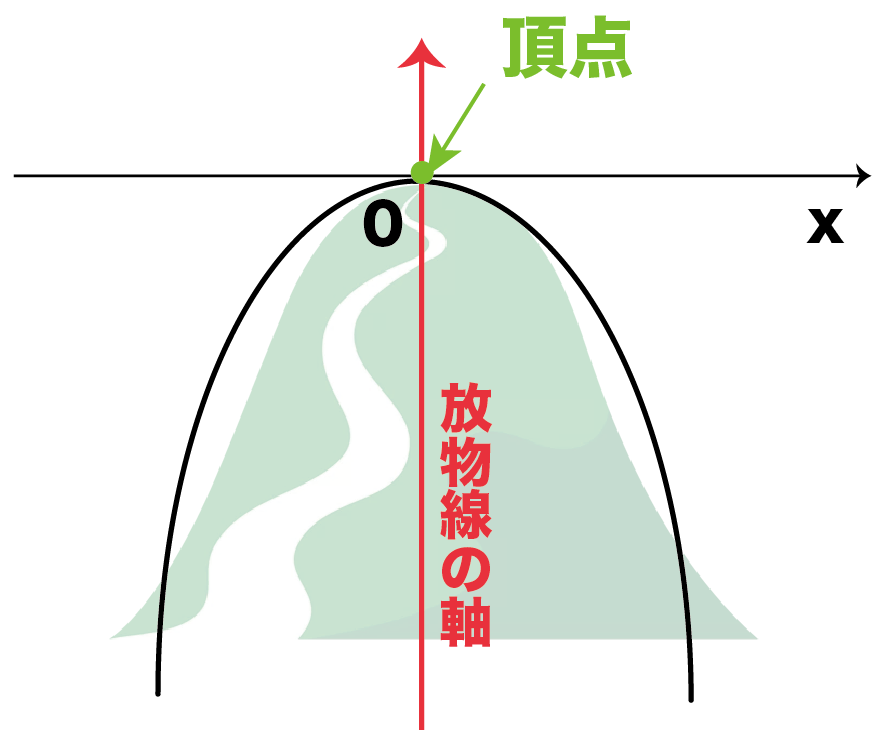
山の頂上をイメージして。
「山の頂点みたいに盛り上がってるところ」が頂点
っておぼえればいいの。
y = ax2で「aが0より小さいとき」は、
ほんとうの山みたいになるよ。
「y=ax^2」の放物線
をくわしくみていこうか。
この放物線には、
頂点と軸がいつだって同じ!
っていう特徴があるんだ。
いつも頂点が(0,0)で、
軸はy軸ってこと??
いろいろなグラフをイメージするといいよ。
たとえば、
比例定数aが正と負のときを考えてみよう。
こんなかんじで、
上下逆さまになるじゃん?
頂点も軸も一緒だ!
じゃあ、比例定数aを大きくしたり、
小さくしたりしてみてよ。
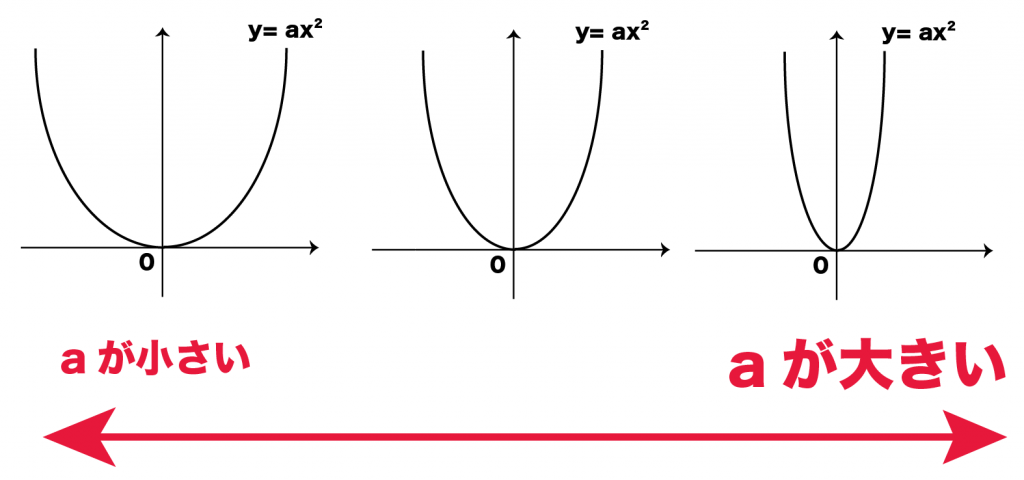
頂点と軸はいっしょだ!
そう!
二次関数y=ax2の頂点と軸はいつも同じなんだ。
頂点と軸に興味を持ってくれたから、
細かいこと話したいけど、
どう?
高校数学にどうつながってるんだろう・・・・・
高校でも変わらないよ♪
……
(納得いかない)
まだあるから!
高校に入ると、
色んなところに頂点や軸がある二次関数
が出てくる。
ちなみに、この二次関数の頂点と軸はわかるかな?
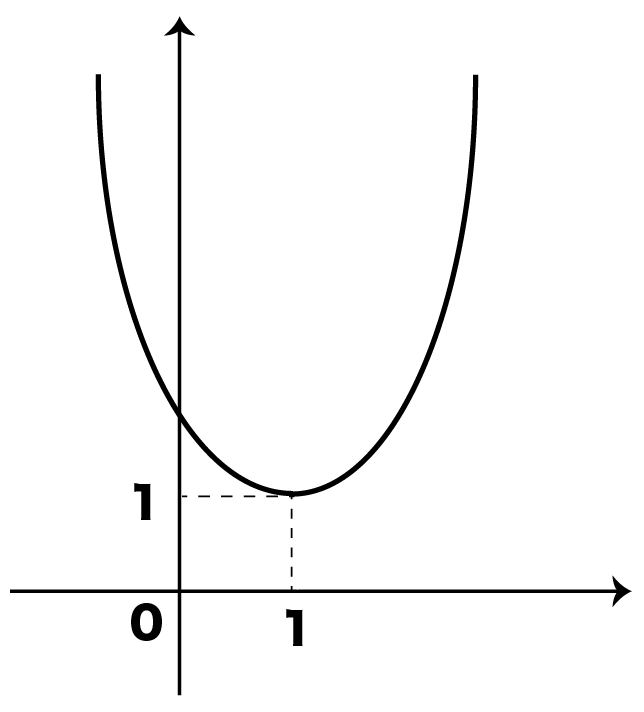
えっと、
頂点が(1,1)で、
軸がx=1
ってこと?
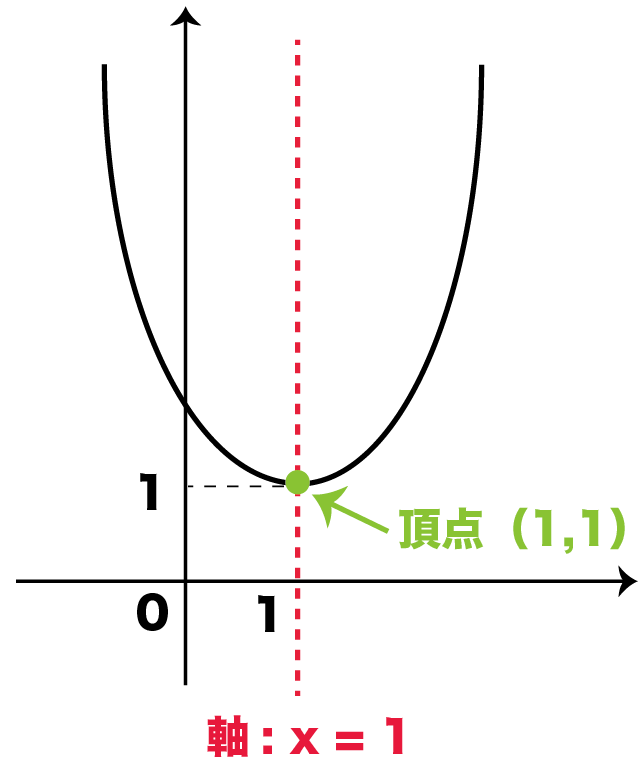
そう!
それが分かれば十分!
興味があって、高校まで待てないなら、
詳しく調べてね♪