こんにちは!この記事をかいているKenだよ。大根は干すとうまいね。
循環小数の問題でよくでてくるのは、
循環小数を分数に変換する問題
だ。
これは文字通り、
永遠につづく循環小数
を
分数
で表せって問題なんだ。
たとえば、こんな感じのやつね↓↓
例題
循環小数0.123412341234…..を分数で表しなさい。
求め方がわからんと苦戦する。
だけど、やり方はすごく簡単なんだ。
いっかいマスターすれば怖いものなしさ。
そこで今日は、
循環小数を分数になおす方法
をわかりやすく解説していくよ!
3ステップでいけちゃうね。
例題をいっしょに解いていこう!
例題
循環小数0.123412341234…..を分数で表しなさい。
まずは、
繰り返しになってる数をかぞえてみよう。
例題の循環小数をみてみて。
0.123412341234…
は、
1234の「4ケタ」が繰り返えされてるね??
だから、リピート数は「4」だ。
あ、ちなみに、この循環小数はこうやって表せるんだ。
⇒くわしくは「循環小数の表し方」をみてみてね
これが第1ステップ。
つぎは、方程式を2つたててみよう。
えっ。
そんなに方程式なんて立てられないって!??
そんなことはないよ。
じつは、
循環小数の方程式のたてかたはいつも同じなんだ。
もとの循環小数をx、繰り返しになってるケタ数をaとしよう。
このとき、
っていう2つの方程式をつくればいいのさ。
例題で繰り返しになっている数は、
4ケタ
だったよね??
だから、a = 4 、循環小数 = 0.123412341234…を
10^a X = 10^a × 循環小数
に代入してやると、
10^a X = 10^4 × 循環小数
10000X = 10^4 × 0.123412341234…
10000X = 1234.12341234…
になるね。
んで、もう一個の式は、
X = 循環小数
のまんま。
X = 0.123412341234…
になるね。
よって、例題ででてくる2つの方程式は、
だ!
つぎは、2つの方程式を引き算しよう。
「大きいほう」から「小さいほう」をひけばいいんだ。
つまり、
(Xに10のa乗をかけた方程式)-(Xの方程式)
っていう計算だ。
例題でも2つの方程式を引くと、
10000X = 1234.12341234…
– )X = 0.123412341234…
————————————–
10000X – X = 1234.1234… – 0.12341234…
9999X = 1234
になるね!
あとは方程式をとくだけ。
xだけの一次方程式だから簡単だね。
例題でも、
9999x = 1234
をといてみよう。
xの係数「9999」で両辺をわってやると、
9999x ÷ 9999 = 1234 ÷ 9999
x = 9999分の1234
になるね!
よって、循環小数0.12341234…は、
9999分の1234
って分数に変換できちゃうってわけ!
どう??
しっくりきたかな!?
循環小数を分数に変換できた??
使ってるのは、中1数学でならう、
一次方程式の解き方
だけだ。
やってること自体は簡単だから、計算問題をたくさんといてみよう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。電卓は手打ちにかぎるね。
世の中にはいろんな小数がある。
0.75
とか、
0.32432
とかさ。
もうね、数えきれないぐらいある。
そんな中、小数の1種類として、
無限小数
ってやつがいるんだ。
こいつは文字通り、
小数点以下が無限に続いている小数
のことだ。
たとえば、
0.5555…..
とか、
0.1413584325432…
とかね。
どこまでも小数点以下が続いてるわけさ。
で、さらに無限小数の中には、
あるパターンが繰り返してつづく小数
って種類がいるんだ。
たとえば、
0.333333….
だったら、「3」 っていうケタ数が繰り返し使われているよね??
もし、
0.12341234….
だったら「1234」っていうケタ数がリピートされてる。
こういうかんじで、
同じパターンが循環してあらわれる無限小数のことを
循環小数
っていうんだ。
でもさ、
循環小数って、どうやって表すんだろうね??
リピートしてる数はどう表現すりゃいいんだ・・・・・!?
ってなるよね。
そこで今日は、
循環小数の表し方をわかりやすく解説してみたよ。
よかったら参考にしてみてね。
さっそく、循環小数の表し方を紹介していこう。
4ステップでいけちゃうよ。
例として、3つの分数を循環小数であらわしてみよう。
まずは分数を小数になおしてみて!
分子÷分母
を計算すればいいね。
例題の分数も小数になおすと、
になるね!
こんな感じで、
できるだけ多くの小数点以下の数をかいてみよう。
小数点以下のケタで「繰り返しのパターン」をみつけよう。
何回もでてくる数字に注目すればいいんだ。
例題でいうと、
って感じで、パターンがみつかるね。
これが第2ステップ!
くり返されてる数の上に「•」を打とう!
でもね、ただ「•」を打つだけじゃない。
繰り返す数によって点の打ち方がちがうんだ。
ってやつだ。
最大で2つしか点は打てないんだ。
どんなに繰り返しが多くてもね。
例題の循環小数たちをみてみよう。
繰り返しになってる数はそれぞれ、
って感じになるね。
繰り返しのケタ数が2以下の、
に関しては、繰り返しのすべてに点をつければよし。
最後の「333分の107」は別格だ。
なぜなら、繰り返しが3つだからね。
繰り返し数が3以上のときは、
繰り返しになってる端と端の上
に点をうてばよかったね。
この例でいうと、
ってことだね!
これが第3ステップ!
いちばん右の点以下の数をけしちゃおう。
もちろん、実際には消えてなんかいない。
ただ、省略してるだけなんだ。
例題でもおなじ。
いちばん右の点以下の数をけしてやると、
こうなるね!
どんな循環小数でもあらわせそう。
循環小数の表し方はどうだったかな??
まず、繰り返しパターンをさがして、
数によって点の打ち方をかえればいいんだ。
ガンガン循環小数であらわしていこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。肉はつくねだね。
ルート3の値の覚え方って知ってる??
いちばん有名なのは、
ひとなみにおごれや(人並みにおごれや)
っていう語呂だ。
なぜルート3が覚えられるのかというと、
1(ひと)73(なみ)2(に)0(お)5(ご)08(れや)
になってるからなんだ。
おぼえちゃえば無敵。
ルート3の近似値をいつでも・どこでも思い出せるんだ。
えっ。
「人並みにおごれや」の意味がわからないって!?
たしかにね。
これはね、ぼくの推測でしかないけど、
一般人なみにおごってよ
っていうメッセージなのかもね。
噂によると、ルート3の覚え方にはつづきがあって、
人並みにおごれやおなご(1.730508075..)
らしいんだ。
つまり、女性に対してのメッセージで、
俺にもおごってよ・・・・
っていう男の愚痴なのかも。
この語呂っておぼえやすくて便利。
だけどさ、
ちょっと古くさいし、状況がハッピーじゃないよね??。
そこで今日は、
マイ勉オリジナルの「ルート3の覚え方」を2つ紹介するよ。
好きな語呂をおぼえていこう!
さっそく、ルート3の覚え方を紹介していくよ。
しっくりきたものを選んでみよう。
まず1つ目の覚え方は、
いい波に乗れ、ゴーヤ
だ。
この語呂をおぼえると、
1(いい)73(波)2(に)0(のれ)508(ゴーヤ)
って感じで、
ルート3の値を8ケタ覚えられるんだ!
えっ。語呂の意味がわからないだって?!?
そうだな。
イメージとしては、サーファーのゴーヤくんをイメージしてほしい。
ちょうどね、そこにね、いい波がきたんだ。
100年に一度くらいのね。
そんなとき、みんなこう叫ぶと思うんだ。
そう。
いい波に乗れ、ゴーヤ!!
ってね。
ゴーヤがいまにも波に乗ろうとしていて、応援するような語呂だ。
ルート3の値もばっちりだね。
つぎのルート3の覚え方は、
いい七味ふれ、ごまは・・・
だ。
この語呂により、
1(いい)73(しちみ)20(ふれ)50(ごま)8(は)
っていう感じで、ルート3の値を8ケタおさえられるんだ。
シチュエーションとしては、そうだな。
食卓を囲う家族
をイメージしてくれ。
キミがゴマに醤油をかけて食べようとしてたんだ。
いつも通りにね。
ただ今日はね、珍しく、父ちゃんがこう言い放ったんだ。
いい七味ふれ、ゴマは…
ってね。
どうやら、父ちゃんにとってはゴマには醤油じゃない。
断然、七味派っぽいんだ。
ぶっちゃけ好きにしてくれって話だけどねw
ルート3の値の覚え方をいろいろ考えてみた。
だけど、結局、やっぱり、
ひとなみにおごれや
がシンプルかもねw
でも、
ゴーヤとかゴマや七味をつかっても大丈夫。
ようは、
ルート3のだいたいの値を覚えてればいいって話なんだ。
ガンガン平方根を覚えていこう!
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。冷凍庫がうまってくね。
平方根の覚え方ってきになるよね??
とくに、
ルート2の覚え方。
平方根の計算でよくでてくるしさ。
近似値をおぼえると計算が楽になるんだ。
ルート2の覚え方でいちばん有名なのは、
ひとよにひとみごろ(一夜一夜に人見頃 )
ってやつだ。
この語呂合わせは、
1(ひと)4(よ)1(ひと)4(よ)2(に)1(ひと)3(み)56(ごろ)
になっていて覚えやすいんだ。
これなら、
√2の9ケタの数字をおぼえられるわけだ。
すごいね。
えっ。
「ひとよひとよにひとみごろ」の意味がわからないって!??
たしかにね。
21世紀で使わないような文章だよね。
ぶっちゃけ、イメージしずらい。
たぶん、おそらく、推測だけど、
一晩一晩、人にはちがった見頃があるねー
って意味だと思うんだ。
つまり、なんだろうな、
あうたびにキレイになってる女性をうたった詩っぽいね。
詳しくは知らんけど。
正直、この覚え方はふるくさいし、
シチュエーションを理解しずらい。
そこで今日は、
「ひとよひとよにひとみごろ」以外のルート2の覚え方
を3つ紹介するよ。
いろいろな覚え方で近似値をおぼえよう!
覚え方を3つ紹介するよ。
しっくりきたやつでおぼえよう!
1つめの語呂合わせは、
いよいよ兄さん、ゴロ打ったかあ
だ。
この語呂合わせでは、
14(いよ)14(いよ)213(兄さん)、56(ゴロ)打ったかあ
っていう感じで、
ルート2の9ケタをおぼえられるんだ。
シチュエーションとしては、そうだなあ、
少年野球団に所属する兄弟を想像してくれ。
むちゃくちゃエースの兄さんがいて、毎打席ホームランを打ってたんだ。
だけどね、ゲームを重ねていくにつれて兄さんがスランプに。
スランプになりすぎてゴロしか打てなくなっちゃったんだ。
そんな兄さんをみかねて弟が、
いよいよ兄さん、ゴロ打ったかあ
とつぶやいてるわけ。
なんか寂しいシーンだね。
諸行無常を感じるね、もはや。
野球好きならこの語呂で覚えよう!
つぎの覚え方はちょっと長い。
位置について、よーいドンでしじみをゴム手袋でとってきて
だ。
1(いち)41(よーい)4213(しじみ)56(ゴム)
になってるからルート2を覚えられるってわけ。
ぶっちゃけ、かなり特殊なシチュエーションだ。
浜辺に住む家族を想像してほしい。
母ちゃんが息子たちにこういったんだ。
ヨーイドンでしじみをゴム手袋でとってきて
ってね。
つまり、なんだろうな、おつかいみたいなもんだ。
砂浜でしじみをみつけてほしいらしい。
たぶん、夕飯のみそ汁に使いたいんだろう。
つぎは会話パターンじゃない語呂だね。
なぜ、ルート2がおぼえられるかというと、
14(いし)14(いし)2(に)13(いさん)56(ゴム)
になってるからなんだ。
この語呂でもルート2の9ケタまで覚えられるってわけ。
状況としては、
自分に残された遺産を、石と石にはさんで、ゴムでとめちゃってるシーンなんだ。
ぜんぜん日常的じゃないねw
まず、遺産なんてないし、石と石を輪ゴムしたりしないからね。
うーん、まず遺産がほしい。
ルート2の覚え方はたくさんある。
王道の中の王道の、
ひとよひとよにひとみごろ
で覚えてもよし。
はたまた、トリッキーな語呂で覚えてもよしだ。
ルート2の近似値を頭にいれておこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。血糖値は高いね。
平方根をみていると、
どれくらいの大きさなんだろうな・・?
って思うことあるよね。
ルート!ルート!
っていわれてもデカさわからんし。
たとえば、ある少年に、
19万円ほしい
っていわれたら、大きい金額であるし、慎重になるじゃん??
でもさ、
ルート19万円ほしい
っていわれてもピンとこないよね??。
高いのか低いのか検討もつかん。
今日はそんな事態に備えて、
平方根のだいたいの値の求め方を勉強していこう。
この「だいたいの値」のことを、
数学では「近似値」とよんでいるんだ。
平方根の近似値を求め方では、
大きな数であてをつけて、じょじょに範囲をせばめていく
っていう手法をつかうよ。
だから、まずは、
その平方根がどの整数の範囲におさまっているのか??
を調べる必要があるんだ。
さっきでてきた、
√19万円
がだいたい何万円になっているのか??
を調べていこう!
まずは、
平方根がどの整数と整数の間にあるのか??
のあてをつけよう。
あての付け方としては、
2乗をしたときに√の中身をこえてしまう整数
と
ギリギリこえない整数
をだせばいいんだ。
√19で考えてみよう。
整数を1から順番に2乗してみると、
・・・・・・・
になるね。
どうやら、「19」は、
のあいだにありそうだね。
よって、√19は、
4 < √19 < 5
の範囲におさまってるはず!
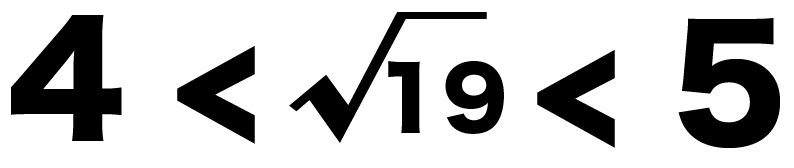
つまり、
√19の1の位は「4」ってわけだね。
ふう!
近似値の1の位はわかったね??
おなじことを小数第1位でもやろう。
「√19」の1の位は4だったね??
今度は、小数第一位の数字を1から順番に大きくしていこう。
んで、
2乗して19をこえるポイントをみつければいいんだ。
・・・・
ぬぬ!
19は、どうやら、
のあいだにありそうだね。

ってことは、√19の範囲は、
4.3 < √19 < 4.4
になるはずだ。
だから、√19の小数第1位は「3」になるはずだね。
最後もやり方はおなじ。
小数第2位を1から順番に増やして2乗。
ルートの中身を超えるポイントをみつければいいんだ。
√19でも小数第2位のあてをつけよう!
小数第1位は「3」だったよね??
だから、調べるのは4.31からだ。
0.01ずつたして、そいつらを2乗していこう!
おっと!
4.36の2乗で19をこえちゃったね。
ってことは、19は、
の間にあるはずなんだ。
つまり、
4.35 <√19 < 4.36
になってるね!
ってことは、
√19の小数第2位は「5」になるはず!
やったね!
この「4.35」が√19の小数第2位の近似値だよ。
あの少年は4.35万円、つまり、4万3500円ぐらいを請求していただわけだね。
まったく、可愛いけど憎いやつだ。
こんな感じで、
1の位からじょじょに範囲をせばめていこう!
平方根の近似値があってるか確認してみて。
計算機の√ボタンをおしてやれば・・・・ほら!
一発で平方根の近似値がだせるんだ。
たくさんのケタ数をね。
うん!
たしかにあってる!
√19の小数第2位は「5」だもんね。
計算機で確認できるから便利だ。
平方根の近似値の求め方はシンプル。
1の位からじょじょに範囲をせばめればいいんだ。
池の魚をおいつめるみたいだね。
計算は大変だけど、気合と根性でせばめていこう!
そんじゃねー
Ken
こんにちは!この記事をかいてるKenです。レモンは皮がうまいね。
ルートの問題でよくでてくるのは、
平方根の大小
の問題だ。
ようは、
整数や平方根をみくらべて、どっちのほうがデカいのか??
をあてる問題だ。
はじめてだと大小をくらべるのはムズいよね。
わかるよ、その気持ち。
でもじつは、
平方根の大小の問題はシンプルなんだ。
なぜなら、問題の種類をたった2タイプにわけられるからね。
この2つさえマスターすればこっちのもの。
今日は、この2つの問題をくわしくみていこう!!
まずは、
平方根と平方根の大小をくらべる問題
だ。
たとえば、つぎのような問題だね↓↓
例題
つぎの2つの平方根の大小を不等号をつかってあらわしなさい。

解き方はちょー簡単。
ルートをとっぱらって大小をくらべればいい
のさ。
さっきの例題をみてみて。
をくらべるのはむずいね??
だから、思い切って√をとって、中身の、
の大小をくらべるんだ。
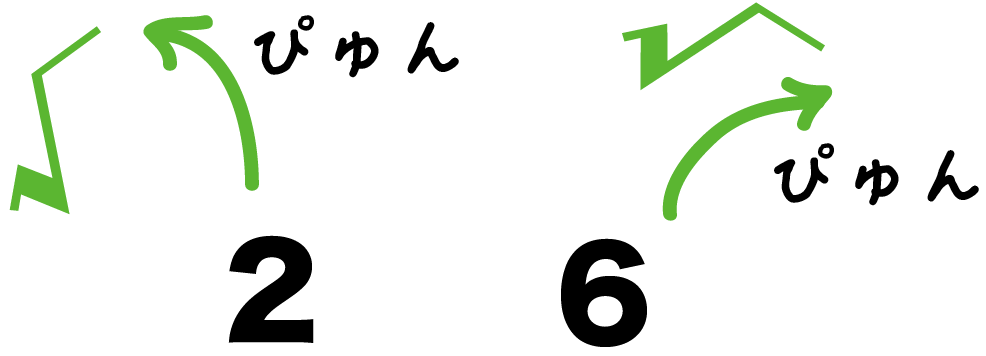
2と6をくらべると、
あきらかに6が大きいよね??
だから、√をつけても√6のほうが大きいのさ。
えっ。なぜこんなことがまかり通るのかって!??
じつは、平方根には、
√の中身が大きいほど絶対値が大きくなる
っていう性質があるからなんだ。
だから、√2よりも√6が大きいし、
√10なんてもっと大きい。
逆に負の平方根でいうと、
-√2より-√6のほうが小さいし、-√10なんてもっと小さい。
なぜなら、
負の数では絶対値が大きいほど小さくなるからね。
こんな感じで、平方根同士の大小をくらべるときは、
√の中身と符号で判断しよう!
つぎは「整数」と「平方根」をくらべる問題。
たとえば、つぎみたいなヤツだね ↓↓
例題
つぎの4つの数字の大小を不等号をつかってあらわしなさい。
このタイプの問題は、さっきよりもヤッカイ。
なぜなら、
整数を平方根になおす
必要があるからね。
整数と平方根同士をくらべるのはむずい。
だから、
整数を平方根にしてやって、
平方根同士をくらべる路線にもっていくんだ。
例題で整数なのは、
の2つ。
こいつらを平方根であらわしてみよう!
えっ。平方根になおす方法がわからないだって?!?
やり方は簡単。
あえて2乗してルートのなかにぶちこめばいいんだ。
だから、
はそれぞれ、
の平方根に置き換えられるわけさ。
こんな感じで、ぜーんぶ平方根になおせば一件落着。
さっきの「平方根同士の大小の解き方」でとけちゃうよね。
小さい順にならべてみると、
-√16, -√10, √5, √9
になるね。
んで、
さっき平方根にした整数をもとにもどすと、
-4, -√10, √5, 3
になるはずだ!
ついでに不等号であらわすと、
-4 < -√10 < √5 < 3
になるね。
おめでとう!
どんな大小でもバッチコイだ!
平方根の大小の問題??
やばそうにきこえるけど、意外に簡単。
の2種類しかないからね。
平方根同士だったらルートを無視。
整数は平方根になおしてみよう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。スタミナを補給したね。
平方根の求め方にはいろいろある。
小数の平方根の求め方、
分数の平方根の出し方、
平方根を簡単にする方法・・・・
などなど。
まさに多種多様。
混乱しちゃうかもしれないね。
そこで今日は、
超基本的な平方根の求め方を解説していくよ。
いちばん簡単な求め方だから、
ガッツリおさえちゃおう!
平方根の出し方を紹介するよ。
3ステップで求められちゃうんだ。
つぎの問題をといてみよう!
例題
つぎの数の平方根を求めなさい。
7, 9
元の数にルートをかぶせよう。
そう、
√
をね。
ぱさっとね、上からかければいいんだ。
さっきの例題では、
の平方根を求めるんだったね??
だから、こいつらの上に「√」をかぶせればいいのさ。
帽子みたいにね。
そうすると、
になるはずだ!!
つぎは、
±(プラスマイナス)
をつけてやろう。
文字通り、
プラスとマイナスが合体した記号
だ。
平方根にはプラスとマイナスのものがあって、
どちらも絶対値が等しい。
だから、
プラスマイナスで1つにまとめられるんだ。
※くわしくは平方根の性質をよんでみてね。
例題でも、さっきルートをつけた、
に±(プラスマイナス)をつけよう。
付け方はくそ簡単。
ふつーに左にチョコっとくっつけるんだ。
そうすると、
になるよね。
せっかくルートをつけたんだけど、
ルートをもう一回はずせるかチャレンジしてみよう。
ルートをはずせる条件は1つ。
それは、
ルートの中身が「○○の2乗」になっていればいいんだ。
条件にあてはまるなら、
2乗とルートをとっていいんだ。
たとえば、±ルートaの2乗だったら、±aになるってわけさ!
例題を振り返ってみよう。
まず、±√7だ。
ルートの中身は7だね。
この中身の7は・・・・うーん、どうやっても、○○の2乗の形になおせない。
だって、2回かけて7になる整数なんてないし・・・!
だから、
±√7は±√7でいいわけだ。
あともう1つの±√9。
こいつはルートをはずせそうだ。
なぜなら、
ルートの中身の「9」が「3の2乗」になってるからね!
√をとってやると、
±√9 = ±3
になるってわけさ。
よって、
7と9の平方根は、
の2つだ。
これで平方根の求め方もマスターだ!^-^
平方根の求め方はむちゃくちゃ簡単。
ルートをかぶせて、±を左にくっつける。
最後にルートをはずせるかトライするだけ。
ガンガン平方根を求めていこう!
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。窒素より酸素だね。
平方根の正体はなんとなくわかった。
じゃあつぎは、
平方根にはどんな性質があるのか??
をみていこう!
性質までおさえればこっちのもんさ。
平方根の性質には2つあるよ。
ある正の数の平方根は、
ってやつさ。
ちょっとよくわからないから、くわしくみていこう。
ある正の数の平方根には、
「プラス」と「マイナス」のやつ
が1つずつ存在してるんだ。

だから、2つの平方根が「プラス」ってわけでもないし、
平方根が「3つ」できたりもしない。
あくまでも、
「符号違い」
で、
平方根が「2つ」でてくる
ってことを覚えておこう!
たとえば、49の平方根を考えてみて。
「しちしちしじゅうく」だから、49の平方根は7になりそうだね。
あとは、7にマイナスをつけた「-7」も平方根だ。
なぜなら、負の数は2回かけるとプラスになるからね。
だから、「-7」も49の平方根になる。
こんな感じで、
プラスとマイナスの平方根がある
っておぼえておこう!
つぎは、平方根の絶対値に注目してみて。
ある正の数の平方根には、
絶対値が等しい
っていう性質があるよ。
49の平方根は、
の2つだったね??
さっきみたように、あきらかに符号がちがうね??
だけど、それと同時に、
絶対値がおなじ
ともいえるね。
なぜなら、2つの平方根の絶対値はそれぞれ、
だからね。
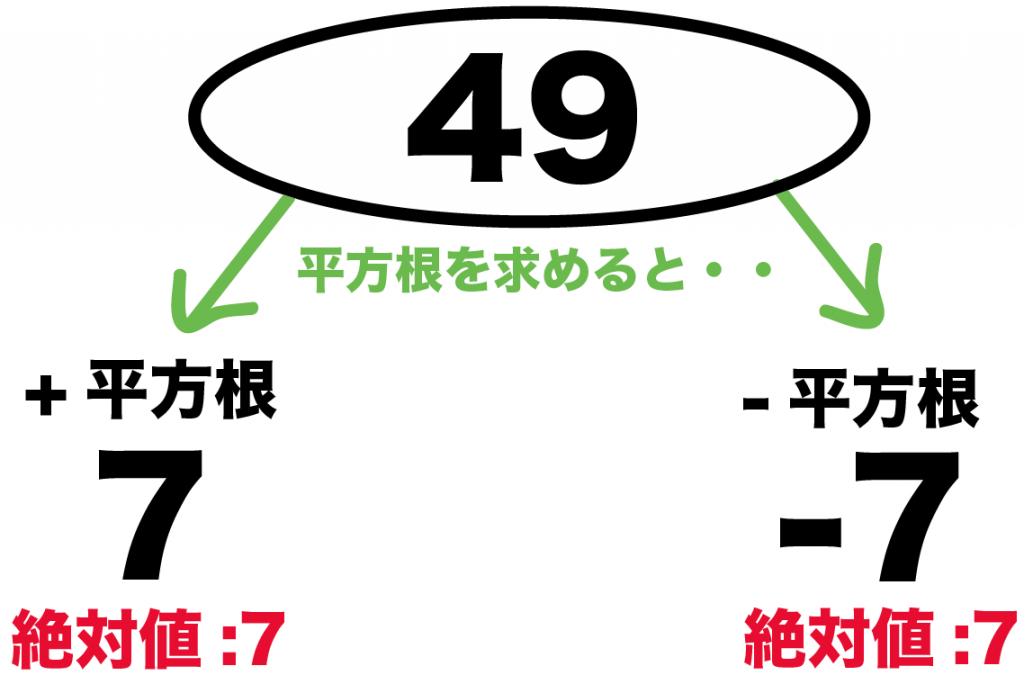
これが2つめの平方根の性質だ。
ある正の数の平方根には、
っていう性質がある。
こいつらをうまくつかうと、
2つの平方根を1つで表せるんだ。
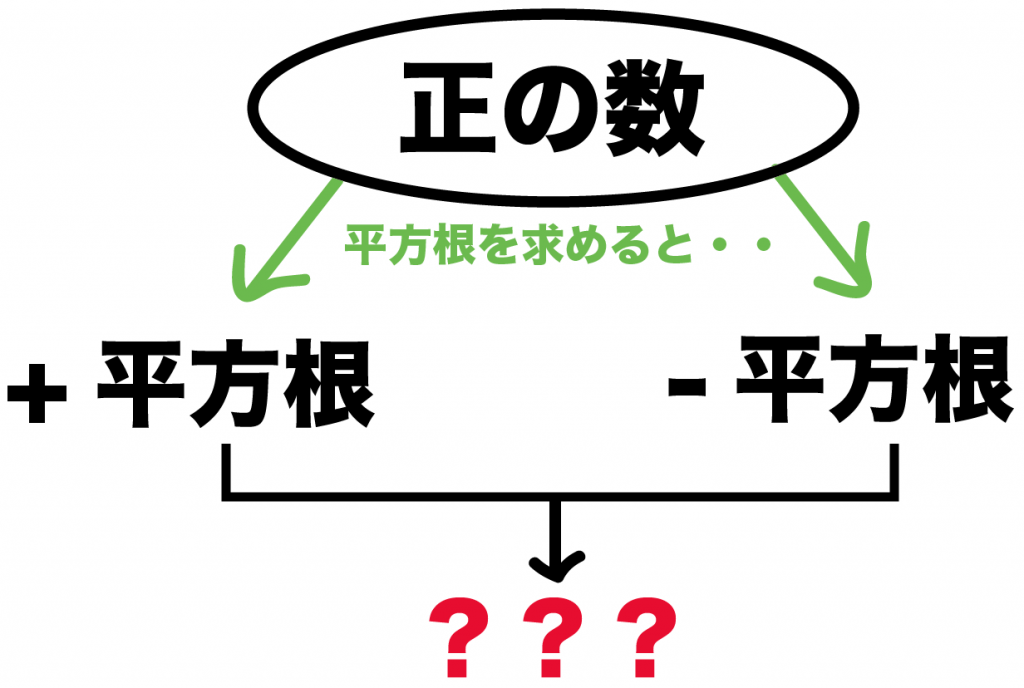
2つの平方根を1つの平方根であらわすには、
±(プラスマイナス)
っていう符号をつかうよ。

これはむちゃくちゃシンプルな記号。
上に「 +」、下に「-」がついてるから、正負の2パターンを同時に表現できるんだ。
プラスマイナスで平方根をあらわしてみると、
±平方根
になる。
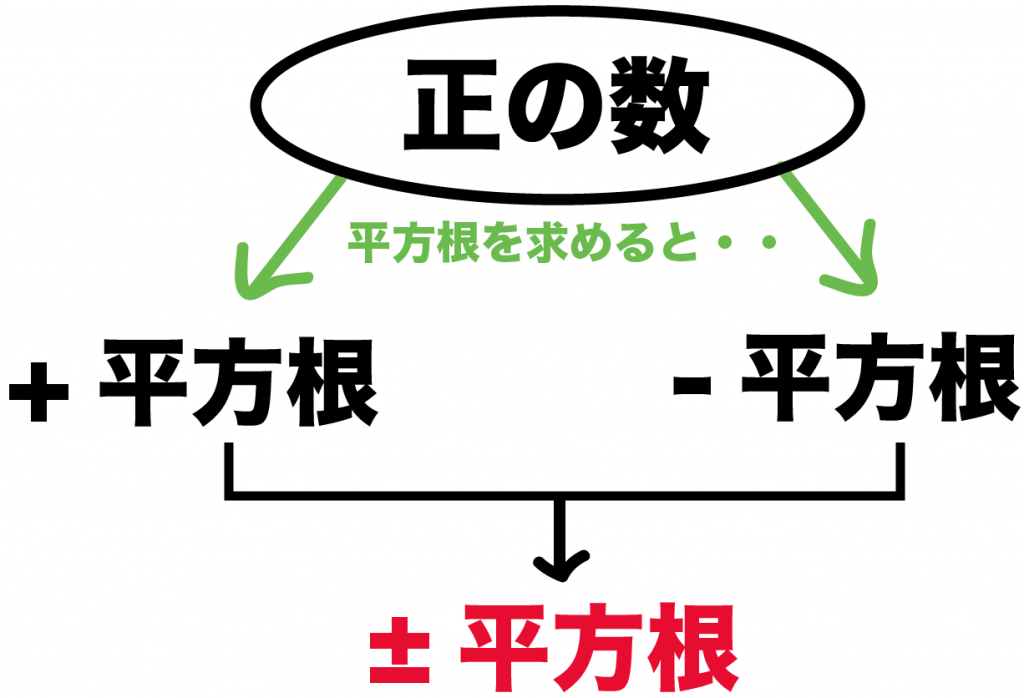
たとえば、49の平方根は、
の2つだったね??
こいつらをプラスマイナスで1つにすると、
±7
になるわけさ。
どう??
平方根の性質もしっくりしたかな??
平方根の性質には、
ってやつがある。
んで、
プラスマイナスをつかえば一気にあらわせるんだ。
これから平方根を勉強していくから、しっかり基本をおさえておこう。
そんじゃねー
Ken
こんにちは!この記事かいているKenだよ。鮭はたれが決め手だね。
中3数学になると、いきなり、突然、
√
っていう記号が出現するね。
はじめてみたときは、まじ意味不明。
ほかにも、わけのわからない、
平方根、ルート、根号・・・
みたいな用語がでてくる。
数学が苦手だったら、逃げ出したくなるね。
うん。まちがいない。
今日は苦手克服のためにも、
平方根・ルート(√)の意味とは???
を振り返ってみよう!
= もくじ =
まずは、
平方根(へいほうこん)の意味
だ。
漢字をちら見すると、
「根」
っていう漢字がみえるね。
漢字から推測しちゃうと、
大根や人参みたいな根菜の一種かと思うかもしれない。
だけどね、これは野菜、じゃない。
ある一種の数字のことなんだ。
えっ。もったいぶらずに早く言えだって??
そうだね。
じつは、平方根の意味とは、
2乗したら「ある数」になる数のこと
なんだ。
この数を「ある数」の平方根とよんでいるんだ。
たとえば、25の平方根を考えてみよう。
平方根を考えるときは、
なにを2乗したらその数になるんだっけ??
って考えてみればいいのさ。
えっと、、、、
2乗にしたら25になる数字かああー
うーん、ぬーん、
・・・・・
は!
5
だ!
だって、ごごにじゅうごだもんね。
5を2回かけたら25になるじゃん!!?
だから、25の平方根は5のはずだ!!
・・・・・・
ってかんじで平方根をみつけてみようw
あと、じつはね。
平方根にはプラスとマイナスの2パターンあるんだ。
だから、25の平方根は5のほかにも、
-5
があるよ。
なぜなら、-5を2回かけても25になるからね。

こんな感じで、
ある数の平方根は「+」と「-」の2通りある
っておぼえておこう。
⇒ 詳しくは平方根の性質をよんでみて
数学界には便利な記号がある。
それは、
√
ってやつだ。
名は、
根号(こんごう)
というんだ。英語っぽく読んでやると、
ルート
と発音するよ。
どっちかっていうと、
「ルート」って読むヤツの方が多いね。
ぶっちゃけ、
「根号」とよむやつはマイノリティ。
じゃあいったい、根号・ルートってなんなんだろうね??
こいつらは、
数字や文字にかぶせるだけで、平方根をつくれる記号
なんだ。
ちょっと特殊なマジックハットだと思ってもらえばいい。
ハリーポッターでいうと組み分け帽子みたいなもんだ。
たとえば、「正の数a」の平方根を√(ルート)であらわすと、
√a
と
-√a
になる。
なぜなら、
「√a」を2乗したらaになるし、
「-√a」を2乗してもaになるからね。
たとえば、さっきの例の25の平方根だったら、
の2つになるはず!
2回かけて25になる数は、
の2つだったよね??
つまり、
ってわけさ。
どう??
ルートってむちゃ便利でしょ!!?
かぶせるだけで平方根をつくれちゃうんだもん。
平方根は、
2乗したらある数になる数のこと
だったね??
んで、
かぶせるだけで平方根に変身させちゃう魔法のツールが、
ルート(根号)
ってわけだ。
平方根とかルートはたくさん登場してくる。
しっかり基礎をおさえておこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。にんじんはゆでたいね。
中3数学では、
式の計算の利用
って単元を勉強していくよ。
因数分解の公式をふつうの計算問に使ってみたり、
いろいろな証明にチャレンジしたりするんだ。
そんな中でも、よく質問をうけるのが、
図形の証明問題
だ。
たとえば、つぎのような証明問題だね。
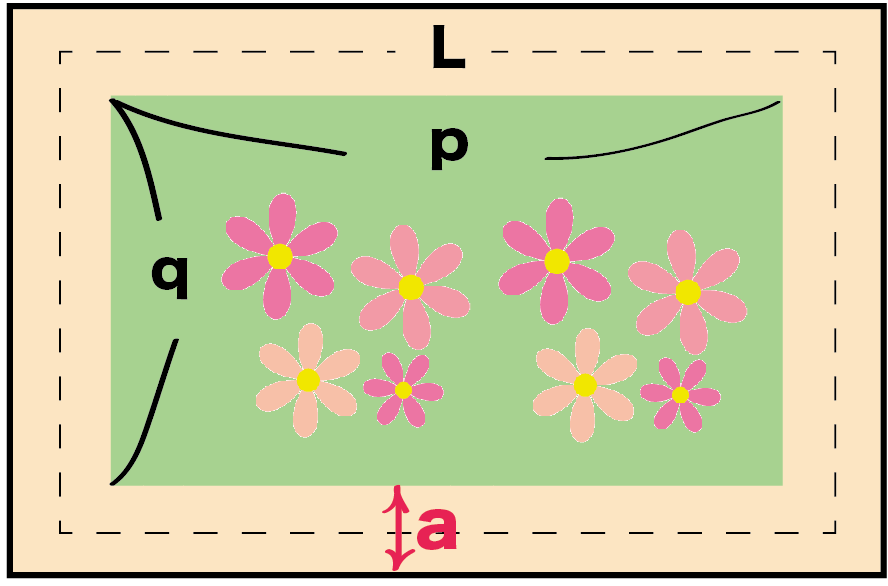
例題
タテの長さがp、横の長さがqの長方形の花壇がある。道幅をa、道のちょうど真ん中をとおる線の長さをLとする。道の面積をSとするとき、
S = aL
となることを証明しなさい。
今日はこのタイプの問題を攻略するために、
式の計算の利用の図形証明問題の解き方
を4ステップで解説していくよ。
よかったら参考にしてみてね。
4ステップでとけちゃうよ。
例題をいっしょにといてみよう!
例題
タテの長さがp、横の長さがqの長方形の花壇がある。道幅をa、道のちょうど真ん中をとおる線の長さをlとする。道の面積をSとするとき、
S = al
となることを証明しなさい。

道幅の面積Sを計算してみて。
S以外の文字で面積をあらわせばいいんだ。
道幅の面積は、
(「花壇+道」の面積)- (花壇の面積)
で求められるよ。
「全体の面積」から「花壇の面積」をひいちまえばいいってわけ。
例題でもまずは、
を計算してみよう。
まず、(花壇+道)の面積だね。
タテ・横の長さは、
になってる。
だから、この長方形の面積は、
たて×よこ
= (2a+p)(2a+q)
= 4a^2 + 2a(p+q)+pq
になるんだ。
うまく乗法の公式で展開してね。
つぎは花壇の面積。
花壇は、
の長方形だね。だから、こいつの面積は、
(花壇の面積)
= たて×よこ
= pq
になるね。
よって、道幅の面積Sは、
S = (花壇+道の面積)- (花壇の面積)
= 4a^2 + 2a(p+q)+pq – pq
= 4a^2 + 2a(p+q)
になる!
つぎは「道の真ん中を通ってる線」の長さだ。
例題では、
2×(道の真ん中のタテ+道の真ん中のよこ)
で求められるよ。
になってるから、
道の真ん中の線のぜんぶの長さLは、
L =2×(道の真ん中のタテ+道の真ん中のよこ)
= 2×(a+q+a+p)
= 2 (2a + p + q)
になるね。
道幅の面積Sを因数分解してみよう。
共通因数でくくってもいいし、
因数分解の公式をつかってもいいよ。
例題の道幅の面積Sは、
S = 4a^2 + 2a(p+q)
だったよね??
こいつを共通因数2aで()くくってやると、
S = 2a(2a+p+q)
になるはず。
これで因数分解は終了さ。
「道幅の面積S」に「道の真ん中を通る線L」を代入しよう。
Step2で求めたLは、
L = 2 (2a + p + q)
だったよね??
じつは、この、2a+p+qに注目してほしいんだ。
これ、Sを因数分解してできた文字といっしょだね。
だから、もし、
Lの式を(2a + p + q)についてとければSに代入できそうだね。
さっそく、Lの式を(2a+p+q)についてとくと、
2a + p + q = L÷2
になるね。
これを道幅面積Sの式に代入すると、
S = 2a(2a+p+q)
= 2a × L÷2
= aL
になるね!
これで「S = aL」を証明できちゃったね!
式の計算の利用??
花壇とか道幅とかめんどそう??
だけどね、使ってるのはシンプルにこの2つなんだ。
基本をおさえて証明を撃破していこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。公園をふらっとしたね。
中3数学ではたくさんの計算問題をとかされるよ。
その中の問題の1つに、
式の値の計算
ってやつがあるんだ。
これはぶっちゃけいうと、
文字式のなかの文字に数字を入れたらどうります??
っていう問題だ。

たとえば、つぎのような問題だね。
例題
x = 10, y = 2のとき、つぎの式の値を求めなさい。
(2x+3y)(2x-3y) – (x-2y)(x-5y) + 10
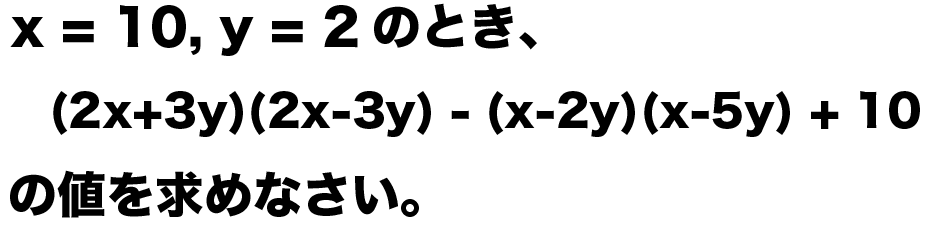
今日はこのタイプの、
式の値の計算の問題
を3ステップで解説していくよ。
解き方がわからないときに参考にしてみてね。
さっきの例題をいっしょにといていこう。
例題
x = 10, y = 2のとき、つぎの式の値を求めなさい。
(2x+3y)(2x-3y) + (x-2y)(x-5y) + 10
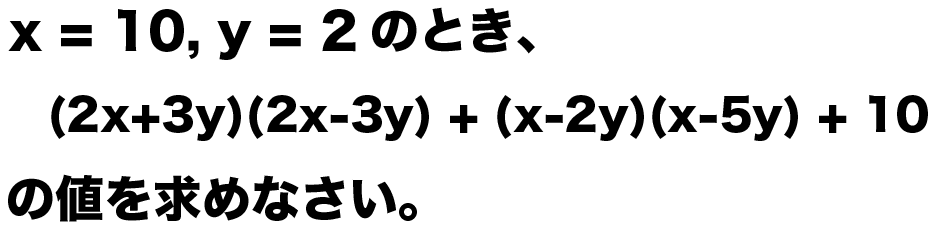
この手の問題はつぎの3ステップでとけちゃうよ。
とりあえず、与えられた文字式を展開しちゃおう。
展開には乗法公式をつかってあげると便利だよ。てか計算がはやくなるね。
例題の文字式は、
(2x+3y)(2x-3y) – (x-2y)(x-5y) + 10
だったよね??
この文字式にたいしては、
の2つがつかえそうだ。

さっそく乗法の公式で計算してみると、
(2x+3y)(2x-3y) + (x-2y)(x-5y) + 10
= 4x² – 9y² +(x² -7y +10y² ) +10
になるね!
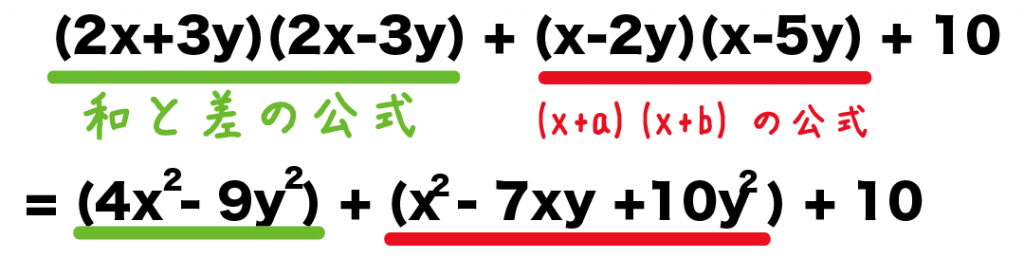
これが第1ステップさ。
つぎは展開したやつらのなかで同類項をまとめてみよう。
つまり、
文字と次数がおなじ項同士の足し算引き算をしてあげるってことさ。
例題でも、同類項をまとめてやると、
(2x+3y)(2x-3y) + (x-2y)(x-5y) + 10
= 4x² – 9y² +(x² -7y +10y² ) +10
= 5x² + y² – 7xy + 10
になるね!
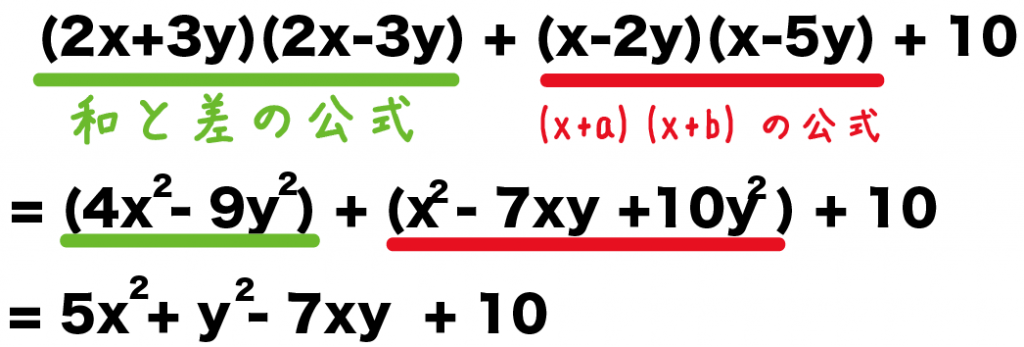
最後に数字を文字に代入してみよう。
xならxに、yならyに、値をぶちこんでやればいいんだ。
例題では、
だったね??
こいつらを同類項をまとめたあとの式に代入してやると、
5x² + y² – 7xy + 10
= 5×(10)² + (2)² – 7×10×2 + 10
= 374
になるね。
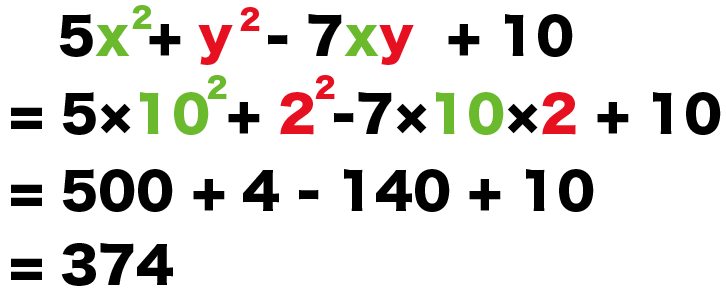
おめでとう!
これで式の計算の値も求めることができたね!
式の計算の値の問題はシンプル。
というか、
展開の公式さえおぼえていればどうにかなるね。
だって、
展開してきれいにととのえて文字を代入するだけだからね。
問題をといて代入になれていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。砂糖、最高。
因数分解の解き方はわかった。
もう、怖いものなしだね!
あと、この基本にくわえておぼえておきたいのが、
因数分解の利用の解き方
だ。
因数分解の利用ってなに??
って思うかもね。
ようは、
整数の計算でも因数分解や展開の公式をつかっちゃおう
っていう問題なんだ。
この解き方をマスターすると、
ムズい計算問題を簡単にとけちゃうんだよ。
この問題にはつぎの2種類あるよ。
それぞれ解き方をみていこう!
まず一つ目は、
因数分解の「和と差の公式」をつかう問題だ。
たとえば、つぎのような問題だね。
例題1
因数分解を利用して、つぎの計算をしてみてください。
39^2 – 31^2
3ステップでとけちゃうよ。
まずは、計算式を因数分解しよう。
因数分解の利用でつかう公式は、十中八九、
和と差の公式
だ。
a^2 – b^2 = (a+b)(a-b)
ってやつだね。
※因数分解の公式はここから復習しよう!
例題でもこの公式をつかってみよう。
39^2 – 31^2
では、aにあたるのが「39」、bにあたるのが「31」だね。
よって、
39^2 – 31^2
= (39+31) (39-31)
になるはず!!
因数分解してみたね??
今度は、()の中を計算しちゃおう!!
例題の()のなかには、
の2つの計算式がはいってるね。
こいつらを計算してやると、
になるね!
最後はかけ算しちゃおう。
最初の計算式よりもクソシンプルになったね。
例題でいうと、
39^2 – 31^2
= (39+31) (39-31)
=70×8
= 560
になるね!
これで因数分解の利用完了だ。
むちゃ簡単になったね!。
つぎは展開の公式をつかうパターンだ。
展開の公式を利用する問題では、
の2つをつかうのがほとんど。
※展開の公式を忘れちゃったら復習してみよう!
つぎの例題をいっしょにといていくよ。
例題2
展開を利用してつぎの計算をしなさい。
(1) 29^2 (2) 99 × 101
こいつは3ステップでとけちゃうよ。
計算式をきりのよい数字であらわしてみよう。
えっ。
「きりのいい」とかよくわからないって?!?
たしかにね。
そうだな、たとえば、
99だったら100、 19だったら20ってかんじで、
1の位が0になるような数であらわせばいいんだ。
例題では、
っていう中途半端な数字がでてきてるね??
こいつらの1の位が0の数字であらわすと、
になるはずだ。
これで計算式を書き直すと、
になるね!
つぎは展開公式をつかってみよう。
まず例題の1番に注目してみて。
こいつに平方の公式をつかってみよう。
(a+b)^2 = a^2 + 2ab + b^2
展開の公式で、
29^2 = (30-1)^2
を展開してやると、
29^2
= (30-1)^2
= 30^2 -2×30 +(-1)^2
になるね。
おつぎは2番目をみてみよう。
こいつは和と差の公式で展開できそうだね。
さっそく展開してみると、
99 × 101
= (100-1) (100+1)
= 100^2 -1^2
になるはずだ。
最後は力技。
公式で簡単にした計算をしてみよう。
まず例題の1からだ。
Step2までで、
29^2
= (30-1)^2
= 30^2 -2×30 +(-1)^2
ってなってたね。
こいつを最後まで計算してやると、
29^2
= (30-1)^2
= 30^2 -2×30 +(-1)^2
= 900 – 60 +1
= 841
になるね!
暗算でも計算できちゃう。
つづいて例題の(2)だ。
こいつも最後まで計算すると、
99 × 101
= (100-1) (100+1)
= 100^2 -1^2
= 10000-1
= 9999
になるね!
この計算もクソ楽になってる。
展開の公式サイコーだぜ。
因数分解の利用とか、正直、だるい。
だけどね、
公式をつかうとすごく便利なんだ。
電卓やそろばんを使わなくてもいいからね。
慣れるまで大変だけど、どんどんチャレンジしていこう!
そんじゃねー
Ken