こんにちは!この記事をかいているKenだよ。自然とふれあいたいね。
文字式の計算問題にはいろんな種類がある。
なかでも質問が多いのは、
文字式の割り算
だ。
たとえば、つぎのような問題だね ↓↓
例題
つぎの文字式を簡単にしなさい。
12a^2b^3 ÷ 9abc^2
割り算は足し算・引き算よりもむずそう。。
だけどね。
じつは、簡単な解き方があるんだ。
文字式の割り算のコツは、
数字と文字をべつべつに計算する!
だ。
数字と文字をいっきに考えちゃダメだ。パンクしそうになる。
だったら、
数と文字をわけて計算すればいいんだよ。
ってことで、つぎの3ステップで割り算してみよう!
例題をといてみよう。
例題
つぎの文字式を簡単にしなさい。
12a^2b^3 ÷ 9abc^2
まず、
数字の割り算
を計算しよう。
例題でも、数字の割り算だけしてみると、
12÷9
になるよね。
数字の割り算ならいける!はず!
12÷9をふつうに計算してやると、
12÷9
= 3分の4
になるね。
これが第1ステップ!
おつぎは文字の割り算。
文字式の割り算では、
「割る数」の指数を「割られる数」の指数からひけばいいんだ。
たとえば、x^100÷x^30を考えてみて。
割る数の「30」の指数を「割られる数」の100からひけばいいんだ。
だから、
x^(100-30)
= x^70
が答えになるね。
こんな感じで、例題も指数の引き算をしてみよう。
例題から文字の計算だけとりだすと、
a^2 b^3 ÷ abc^2
になるね。
÷の後ろの文字の指数を引き算してやると、
a^2 b^3 ÷ abc^2
= a^(2-1)b^(3-1)c^(-2)
= a^(1) b^2 c^(-2)
になるね。
マイナスの指数は分数の分母にまわしてやればいいから、
a^2 b^3 ÷ abc^2
= a^(1) b^2 c^(-2)
= ab^2/c^2
になるね。
これが第2ステップ!
最後は、
2つの割り算の結果をくっつけよう!
のりもボンドもいらない。
ただ、くっつけるだけでいいんだ。
例題の数字と文字の割り算はそれぞれ、
だったよね??
こいつらをこりっとつけてやると、
(4ab^2)
———-
3c ^2
になるね!
これで文字式の割り算もマスターだね。
文字式の割り算??
おそれることはない。
いったん、
数
と
文字
にわけて計算すればいいんだ。
文字式の基本だからしっかりマスターしておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。おしぼりは無敵だね。
文字式の利用で、
連続する3つの整数の和の問題
ってでてくるよね。
たとえば、つぎの問題 ↓↓
例題
連続する3つの整数の和が3の倍数になる訳を説明しなさい。ただし、整数は正の数とする。
日常生活では3つの整数の和なんて考えないよね??
だって、必要ないもん。
でもね、中2数学の問題ではよくでてくる証明なんだ。
今日はこの問題を攻略してみよう!
4ステップで証明できちゃうよ。
さっきの例題をといていこう!
例題
連続する3つの整数の和が3の倍数になる訳を説明しなさい。ただし、整数は正の数とする
ある正の整数を「n」としてみて。
nは「正の整数」だから、
1にもなるし、2にもなるし、10にだってなるんだ。
えっ。なぜ「n」を使わなきゃいけないんだって?!
えっ?
zを使いたい??
じつは、nは英語の「number (数字)」からきているんだ。
ぶっちゃけzとかqでもいいんだけどさ。
nをつかうとカッコいいじゃん?。
とりえあず正の整数を「n」とおこう!
連続する3つの整数をnであらわそう!
連続する3つの整数ってたとえば、
1, 2, 3
みたいに、1ずつ違う整数のことだ。
たとえば、
1, 4, 5
とかは連続してないね。
だって、1ずつ離れてないし。
nであらわすときは、
連続する3つの整数のうち、正の整数nを、
真ん中の整数
とおくといいよ。
そうすると、
をnで簡単にあらわせるからね。
連続する3つの整数は1ずつ離れてる。
よって、
になるはずだ!
つぎは、連続する3つの整数をたそう。
nであらわした、
をたせばいいんだ。
ぜんぶたしてみると、
(n-1)+n+(n+1)
= 3n
になるね!
最後に、和が「3の倍数」になる証拠をみつけよう。
証拠がみつかれば、
連続する3つの整数の和が「3の倍数」である
って証明できるからね。
例題でいうと、
連続する3つの整数の和は、
3n
になったね。
で、nは正の整数だったよね??
ってことは、
3n
は3の倍数になるんだ!
だって、「n」には1とか2とか6とかがはいるわけだからね。
そいつらが3倍されたら、
3の倍数になるじゃん??
だから、連続する3つの整数の和は3の倍数っていえるんだ!
この問題は、
の4ステップで証明できちゃう。どんどんチャレンジして行こう
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。チョキはすごいね。
等積変形の問題は大きく分けると、
の2つある。
どちらも等積変形をつかうのは同じ。
だけど、
びみょーに解き方がちがってくるんだ。
せっかく勉強するんなら、どちらの解き方もマスターしておきたいね。
そこで今日は、
等積変形の「三角形」の問題をいっしょにといてみよう!
等積変形の三角形の問題は、つぎのようなやつだね↓↓
三角形ABCのAC上にある点Pを通る直線のうち、三角形ABCの面積を二等分するものを作図しなさい。ただし、コンパスと定規しか使わないでね。
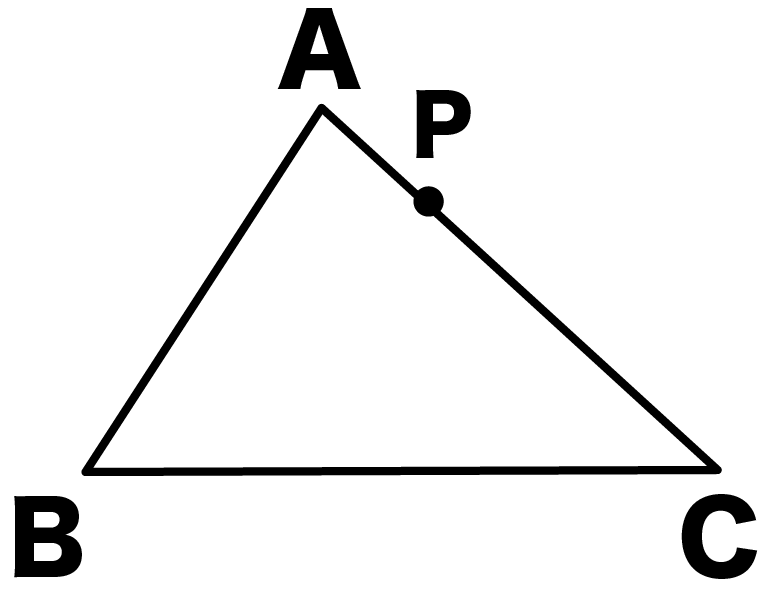
この手の問題の解き方はシンプル。
三角形を等積変形して、
そいつの面積を二等分する線をひけばいいんだ。
つぎの6ステップでとけるよ。
コンパスと定規で攻略していこう!!
三角形の底辺を延長しよう。
好きなだけ延長していいよ。とくべつにね。
できるかぎり左右にのばしてみて。
例題でいうと、底辺はBCだね。
こいつを横に延長してやると、こうなるね!
えっ。
かっこわるいって!?
そうだね。
でもここからが等積変形の面白いところなんだ。
「中点を通る点」と「対角」をむすんでやろう。
例題でいうと、点Pと点Bだね。
こいつらを定規ですーっと結んでやると、
こうなる!
頂角を通る平行な線をかいてみよう。
ここでも定規が活躍するよ。
例題でいうと、
点Aを通ってBPに平行な直線ってわけだ。
せっかくだから、
底辺との交点をDとしよう!
等積変形で「面積の等しい三角形」をつくっちゃうおう。
具体的にいうと、
新しくできた底辺との交点
と
二等分線が通る点
を結べばいいんだ。
例題でいうと、点DとPを結べばいいね。
えっ。どこが等積変形になってるのかッテ?!
じつは、これ、
△ABP = △DBP
になってるんだ。
なぜなら、
この2つの三角形は底辺BPを共有していて、
高さが同じだだからさ。
んで、もっといってやると、
△ABC=△DPC
になるんだ。
なぜなら、
でしかも、等積変形で、
△ABP = △DBP
ってわかってるからね。
だから、
△ABC = △PBC
になってるんだ。
等積変形についてもっと知りたいときは、
平行線と面積の記事をよんでみてね。
つぎは垂直二等分線をひいてみよう。
等積変形後でできた三角形の底辺で、垂直二等分線をかけばいいんだ。
えっ。
なぜ垂直二等分線をひくのかって?!
じつは、
三角形の底辺の中点を求めるのが目的なんだ。
例題でいうと、
△PDCの底辺DCの中点を求めるってことだね。
さっそく、垂直二等分線をかいてみよう。
コンパスの脚を適当にひらいて、
左の点Dに針をおく。
そして、半円を、かく。
つぎは、右端っこにある点Cに針をおいて、
こっちでも半円をかいてみよう。
んで、2つの半円の交点をむすんでやると、
ほれ!垂直二等分線のできあがりさ。
ついでだから、
垂直二等分線と底辺の交点をMとしよう。
この点Mは、辺DCの中点だね。
もし、点Pと点Mを結んでやると、
△PDCの面積を二等分していることになるんだ。
なぜなら、
△PMCの面積は△DPCの半分になっていて、しかも、
△DPC = △ABC
だからね。
つまり、△PMCは△ABCの面積の半分でもあるってわけだ。
どう??すっきりしたかな!??!
等積変形の三角形の問題!?
とりあえあず、コンパスと定規を準備。
そして、垂直二等分線をかいてやればいいのさ。
ガンガン等積変形していこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。汗かきたいね。
一次関数の変域の求め方の基礎はわかった。
だけど、ときどき、
変域の応用問題ってでてくるよね。
たとえば、つぎのような問題さ。
y=-2x+bのxの変域がc≦x≦4のとき、yの変域が-5≦y≦5である。bとcを求めなさい。
いっけん楽勝にみえる。
だけどじつは、うっかりミスを誘うトラップ問題なんだ。
今日はこの変域の問題の解き方を3ステップで解説していくよ。
よかったら参考にしてみてね。
例題をいっしょにといていこう。
y=-2x+bのxの変域がc≦x≦4のとき、yの変域が-5≦y≦5である。bとcを求めなさい。
この手の問題はつぎの3ステップでとけちゃうよ。
まずは問題で登場する、
一次関数の傾きの符号をチェックしよう!
傾きが+なのか??
それとも、とんでもなくマイナスなのか??
さらっと調べてみよう。
例題の関数の、
y = -2x + b
に注目してみて。
こいつの傾きは「-2」。
あきらかにマイナスがついちゃってるよね??
ってことで、例題の傾きは負の数だ。
つぎは、
xが大きくなるとyはどうなるか??
を考えてみよう。
もし、一次関数の傾きが+のとき、
xが大きければ大きいほどyも大きいね?
だから、xが最大値になるとき、yも最大値になるってわけ。
逆に、傾きが -のとき、
xが大きければ大きいほどyは小さくなっちゃう。
だから、xが最大値のときはyは最小値になるわけさ。
つまり、これをまとめるとつぎのようになる↓↓
例題をみてみよう。
一次関数の傾きは「マイナス」だったよね??
xとyの変域から最小値・最大値をだしてみると、
になってるね。
んで、一次関数の傾きがマイナスだから、
になるんだ!
つまり、
y = -2x + b は、
の2点を通るんだ。
こんな感じで、
xとyの組み合わせをみつけるのが第2ステップだよ。
最後は、2つの座標を式に代入してみよう。
例題の直線は、
の2点を通るはずだったね??
こいつを直線の式、
y = -2x + b
さっそく、y = -2x + bに(4, -5)を代入すると、
y = -2x + b
-5 = -2 × 4 + b
b = 3
になるね。
つぎは、bの値がわかった一次関数の、
y = -2x + 3
に(c, 5)を代入してcを求めてみよう。
すると、
y = – 2x + 3
5 = – 2c + 3
c = -1
になるよ。
これで文字の正体がわかったね。
おめでとう。
一次関数の変域の問題はよく、
グラフをかけば解ける
っていわれる。
だけどね、ぶっちゃけグラフなんていらん。
傾きの符号をみて、xとyの組み合わせを考えればいいんだ。
応用問題におそれず挑んでいこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。換気は大事だね。
一次関数の変域の問題ってよくでるよね。
たとえば、つぎのような問題さ。
例題
1次関数y = -3x+7について、xの変域が -1 ≦ x ≦ 9のとき、yの変域を求めなさい。
一次関数の変域とかあきらかにむずそうだけど、
基本をおさえればチョー簡単なんだ。
今日はこのタイプの問題を攻略するためにも、
一次関数の変域の求め方がわかる3ステップ
を紹介するよ。
よかったら参考にしてみて。
3ステップで変域を求められるよ。
例題をいっしょにといてみよう!
1次関数y = -3x+7について、xの変域が -1 ≦ x ≦ 9のとき、yの変域を求めなさい。
まず、変域の端と端を代入してやろう。
たとえば、xの変域が○ ≦ x ≦ □だとしたら、
を一次関数に代入すればいいんだ。
例題でわかっているのはxの変域の、
-1 ≦ x ≦ 9
だね。
この変域の端っこの、
を一次関数 y = -3x + 7 に代入すればいいんだ。
x = -1 を代入すると、
y = -3x + 7
= -3 × (-1) + 7
= 10
になる。
一方、x = 9を代入してやると、
y = -3x + 7
=-3 × 9 + 7
= – 20
になるね。
これが第1ステップ!
さっき計算した2つの値のどちらが大きいのか??
を比べてみよう。
そして、
大きい値を右に、小さい値を左にかくんだ。
例題では、
の2つをゲットできたね??
こいつらを比べてみると、
明らかに10のほうがでかい。
-20のほうが小さいね。
だから、10を右に、-20を左にかいてみて。
これが第2ステップ!
最後は不等号で結んでみよう。
使う不等号は、
問題でわかってる変域と同じものを使うよ。
例題でいうと、xの変域は「≦」を使ってるよね??
だからyの変域も「≦」を採用するのさ。
例題をみてみよう。
「大きい値」と「小さい値」の間に「y」をかく。
そして、
「小さい値」・「大きい値」と「y」を「≦」で結んでやるのさ。
-20≦y≦10
これでyの変域が求まったよ。
おめでとう。
でもさ、なんで変域が求められるんだろう??
話がうますぎるよね。
じつは、ここだけの話なんだけど、
一次関数がまっすぐだからなんだ。
xの変域の端っこと端っこのy座標が、
yの変域の端っこと端っこになっているよ。
これは傾きがマイナスでも同じだね。
もし、一次関数が波だっていたり、
ギザギザしていたら変域はこのやり方だと無理。
なぜなら、変域の端っこ以外に、
最大値とか最小値がいるかもしれないからね。
一次関数がまっすぐだからこそ、変域の端っこが最大値・最小値になる
ってことを覚えておこう!
一次関数の変域の求め方は簡単。
の3ステップでいいんだ。
問題をといて変域に慣れていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。本屋がよんでるね。
多角形の対角線の本数の求め方には公式があるよ。
n角形の対角線の本数は、
n(n-3)÷2
で計算できちゃうんだ。
つまり、
(頂点の数)×(頂点の数 – 3)÷ 2
ってことだね。
それじゃあ、
五角形の対角線の本数を求めてみよう。
公式のnに「5」を代入すればいいから、
n(n-3)÷2
= 5×(5-3)÷2
= 5
になるね。
た、たしかに対角線は5本ひけそう。。
す、すごいな。
この公式。
公式はめちゃ便利。
それはわかった。
だけれども、
なぜ多角形の対角線の本数を求められるんだろう??
話がうますぎるよね。
つぎの3ステップで考えると、
公式をつかえる理由がわかるよ。
1つの頂点から何本の対角線がひけるか
を考えてみよう。
まず、
隣りの2つの頂点
には対角線をむすべないよね。
むすぶと「辺」になっちゃう。
あと、自分には対角線ひけないよね??
対角線をひくためには、
2つの頂点が必要だからね。
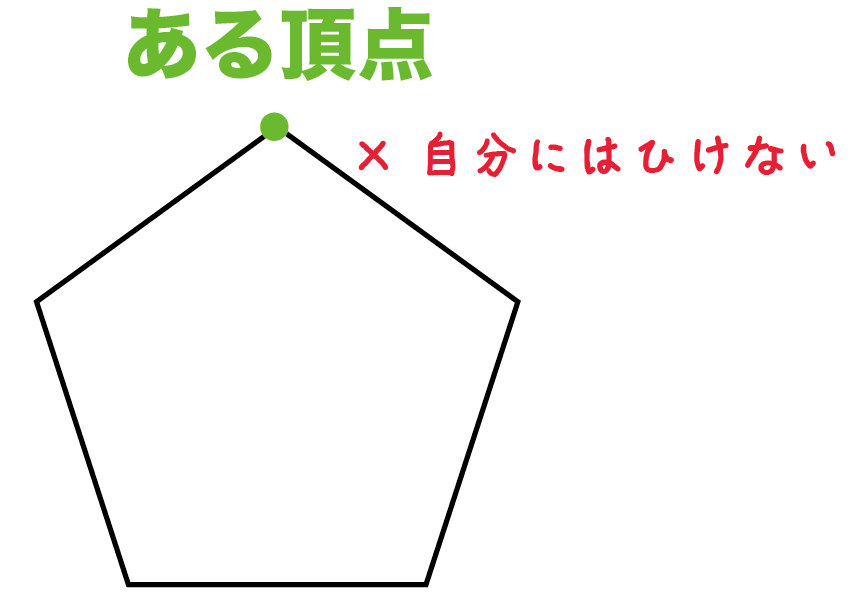
だから、
1つの頂点あたりn-3本の対角線
がひけることになるんだ。
だって、n個ある頂点のうち、
の3つにはひけないからね。
これが公式の「n-3」の意味だよ。
1つの頂点あたり、
「n-3」本の対角線がひける
ってわかったね??
それじゃあn角形ならどうなるかな??
n個の頂点があるから、
n(n-3)の対角線がひけそうだ。
だから、公式で(n-3)にnをかけているんだ。
最後はかぶりをはぶこう。
n角形のとき、
n(n-3)
の本数の対角線がひけそうってわかったね。
だけれども、
この本数にはかぶりがあるんだ。
なぜなら、
1つの対角線を2つの頂点でカウントしてるからね。
たとえば、五角形の対角線を考えてみよう。
下の緑の対角線をイメージしてほしい。
この対角線って、左の頂点1のときも数えているし、
右の頂点2のときもカウントしちゃっているんだ。
1本の対角線を2回ずつ数えていることになる。
だから最後に、
n(n-3)を2でわらなきゃいけないんだ。
どう??
納得いったかな??
多角形の対角線の本数??
そんなの簡単。
n(n-3)÷2
で計算してやろう。
公式をおぼえるのも大事だけど、
なぜ使えるのか??
までおさえておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。花粉に敏感だね。
3点を通る円の中心
を作図したいときってあるよね??
たとえば、つぎの問題が宿題にだされたときとかね ↓↓
例題
下の図のように、1直線上にない3点A, B, Cを通る円の中心を求めなさい。

見た目むちゃくちゃむずそう。。
だけど、基本をおさえちまえばサクっと作図できちゃうんだ。
今日はこの、
3点を通る円の中心の作図・書き方
を3ステップで解説していくよ。
よかったら参考にしてみて。
3ステップでかけちゃうよ。
作図につかうのは、
の2つだけだね。
例題をといていこう!
例題
下の図のように、1直線上にない3点A, B, Cを通る円の中心を求めなさい。

まず弦をかこう。
隣り合った2点を直線でむすべばいいんだ。
例題でいうと、
だね??
こいつらを直線でむすんでやると、こうなる↓↓
この直線たちが円の弦になるんだ。
2本ひけばステップ1完了!
つぎは弦の垂直二等分線を作図しよう。
垂直二等分線を2本かけばいいんだ。
えっ。垂直二等分線の作図方法わすれた??
そのときは垂直二等分線の書き方を復習してみて。
例題でいうと、
まず点Aにコンパスの針をおいて半円をかく。
コンパスの脚の幅をキープしたまま、
今度は点Bに針をおく。
そして、半円をかく。
2つの半円の交点をむすぶと、点A・Bの垂直二等分線のできあがり!
今度は弦BCの垂直二等分線。
てきとうにコンパスの脚をひらいて、点Bに針をおこう。
そして、半円をかく。
脚の幅をキープして点Cに針をおく。
そして、半円をかく。
おなじように半円の交点をむすべばいいのさ。
それが垂直二等分線になる。
どう??
垂直二等分線かけたかな??
最後は交点をうつだけ。
垂直二等分線がまじわっているところに、
ぽちっと点をうてばいいんだ。
その交点が「3点を通る円の中心」になるよ。
例題でもおなじ。
垂直二等分線の交点をうってやろう。
すると、こんな感じになる↓↓
おめでとう!
この交点が「3点を通る円の中心」だよ。
でもさ、
なんで「三点を通る円の中心」がかけちゃうんだろう???
都合よすぎるよね。
その理由はずばり、
「垂直二等分線上の点」と「端の点」同士の距離が等しいから
なんだ。
例題の円の中心をOとすると、
AO = BO = CO
になるってわけ。
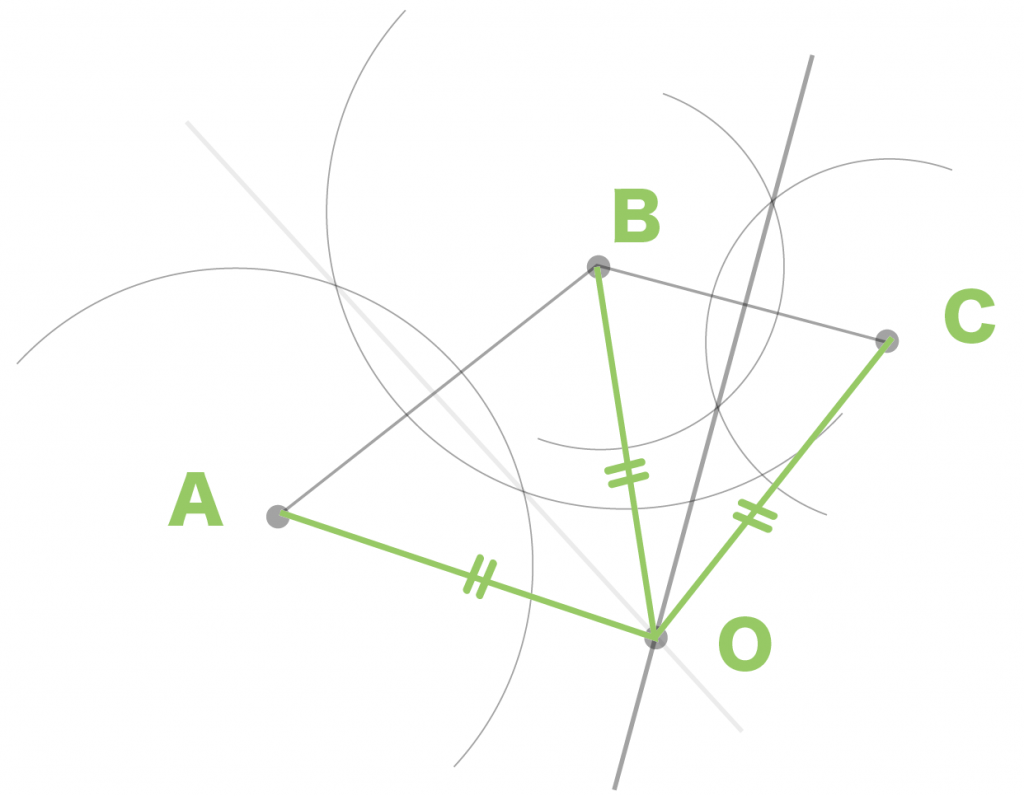
つまり、
点A, B, Cたちは点Oからの距離が等しいってことだね。
円の定義は「ある点から等しい距離にある点の集合」だから、
3点を通る円が点Oを中心にかけちゃうってわけ。
えっ。なぜ、
「垂直二等分線上の点」と「端の点」同士の距離が等しくなる
のかって?!?
それは、垂直二等分線をかいてみればわかる。
たとえば線分ABの垂直二等分線をかいて、二等分線上の点をOとしよう。
ABと垂直二等分線の交点をMとするよ。
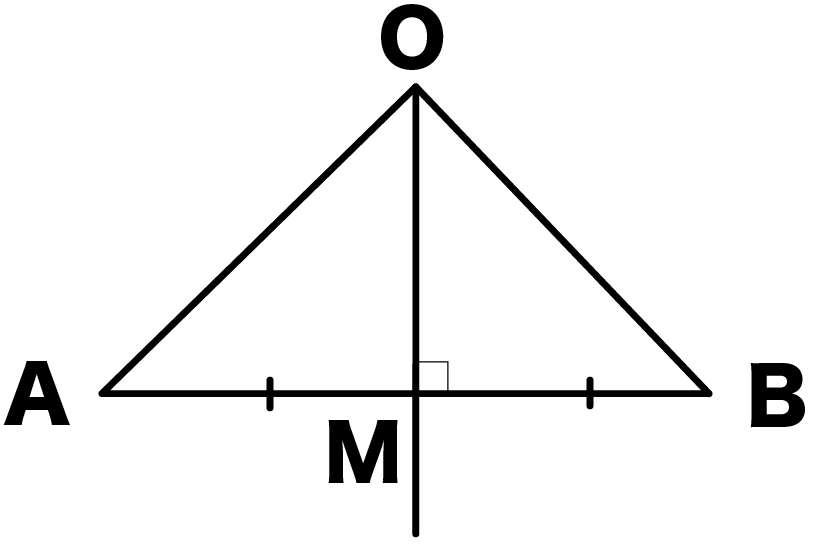
このとき、OMは垂直二等分線だから、
になる。
しかも、OMは共通だから、
2辺とのその間の角がそれぞれ等しい
という合同条件がつかえるね。
よって、
△AMO ≡ △BMO
になるわけだ。
対応する辺の大きさが等しいから、
AO = BO
になるんだ。
どう??納得いったかな??
三点を通る円の中心をかく
ってむちゃムズそう。
ただ、使うのは、
垂直二等分線だけ。
慣れてしまえば簡単なんだ。
テストまでに作図の練習をしてみよう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。カレーはグリーンに限るね。
中学数学の問題でたまーに、
コンパスと定規で正方形を作図しなさい
ってやつでてくるよね??
三角定規と分度器をつかえば楽勝。
正方形なんてかける。
だけど、
コンパスと定規だけしかダメ??
そりゃあ、ムズい作図になるね。
今日は、作図を攻略するために、
正方形の書き方・作図方法がわかる5ステップ
を紹介するよ。
よかったら参考にしてみてね。
正方形はつぎの5ステップでかけちゃうよ。
作図に用意するものは、
の2つだけ。
さあ、正方形をかいていくよー!
まず直線をかこう。
定規でまっすぐ線をかけばいいんだ。
これが第1ステップ!!
つぎは直線上で円をかいてみよう。
適当にコンパスの針を直線上におく。
まるっと円をかけばいいんだ。
これが第2ステップ!!
つぎはチョビ円を2つかくよ。
コンパスの脚をちょっと広げて、
円と直線の交点に針をおこう。
そんで、チョビっとだけ円をかく。
もう一個の交点でもおなじ。
チョビっと円をかいてね。
これで第3ステップ終了だね!
チョビ円の交点と、
円の中心を直線でむすんであげよう。
これは直線の垂線になっているね。
詳しくは「垂線の書き方」の記事をよんでみて。;
「円」と「直線」の交点をむすぼう。
むすんでできた図形が正方形になってるよ。
おめでとう!
正方形の書き方もマスターだね。
でもさ、
なんで正方形が作図できちゃうんだろう??
簡単すぎてこわいよね。
じつは、
4つの直角三角形が合同だからいえるんだ。
たとえば、角交点を下の図のように、
とおいてあげよう。
すると、
△ABO ≡ △BOC ≡ △COD ≡ △DOA
になるね。
んで、
合同な図形の対応する辺・角はそれぞれ等しいから、
がいえそう。
これは、正方形の定義の、
4つの辺がすべて等しく、4つの角がすべて等しい
をみたしているね。
だから、四角形ABCDは正方形になるんだ。
どう??納得したかな??
正方形の書き方はどうだったかな??
の5ステップだけでいいんだ。
コンパスと定規しか使わない。
なんだかいけそうな気がするでしょ??
練習して書き方になれていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。スパゲッティーは便利だね。
コンパスで正八角形の作図
ってできるんだっけ??
じつはね、
できるんだ。
正八角形の作図は宿題によくでるから、
書き方を知らないと困っちゃうね。
そこで今日は、宿題を瞬殺するために、
正八角形の書き方・作図方法を5ステップで解説していくよ。
よかったら参考にしてみてね。
5ステップで作図できちゃうよ。
作図に使うのは、
の2つだけ。
準備はできたかなー??
直線を1本ひこう。
定規でまっすぐ線をひけばいいんだ。
第1ステップ完了だね。
つぎは垂線をかくよ。
さっきの直線に垂線をかけばいいんだ。
垂線の書き方は簡単。
まず、コンパスの針を直線上において、
半円をかく。
今度は、半円と直線の交点に針をおこう。
コンパスの脚の長さはさっきより大きめにしてね。
そして、チョビっと円をかく。
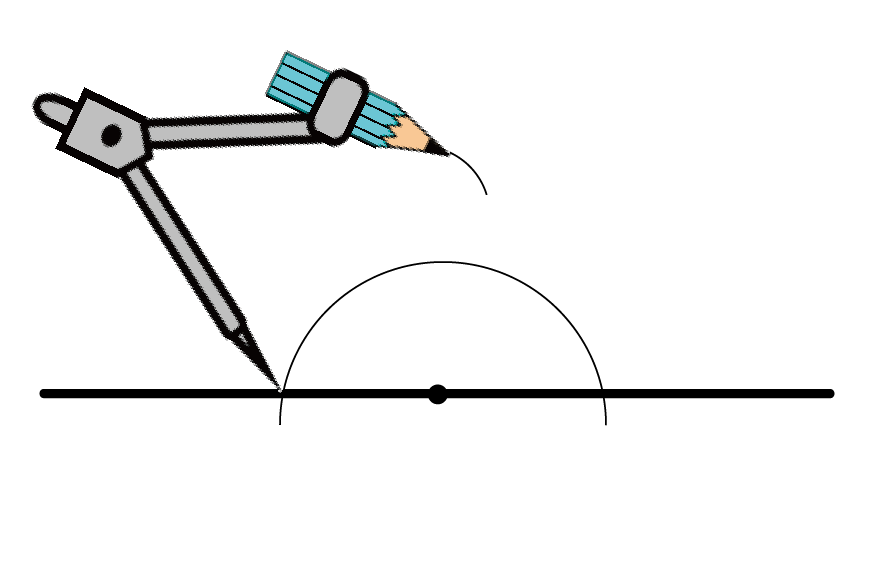
そして、そのコンパスの脚の長さをキープしたまま、
もう1個チョビ円をかいてやるんだ。
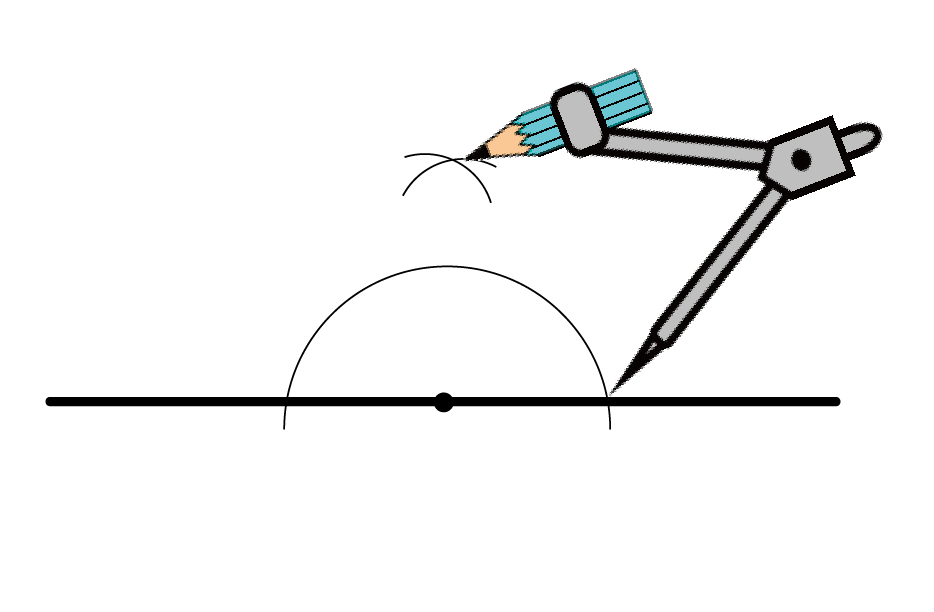
「チョビ円の交点」
と
「半円の中心」
を結んだ直線が「垂線」になるよ。
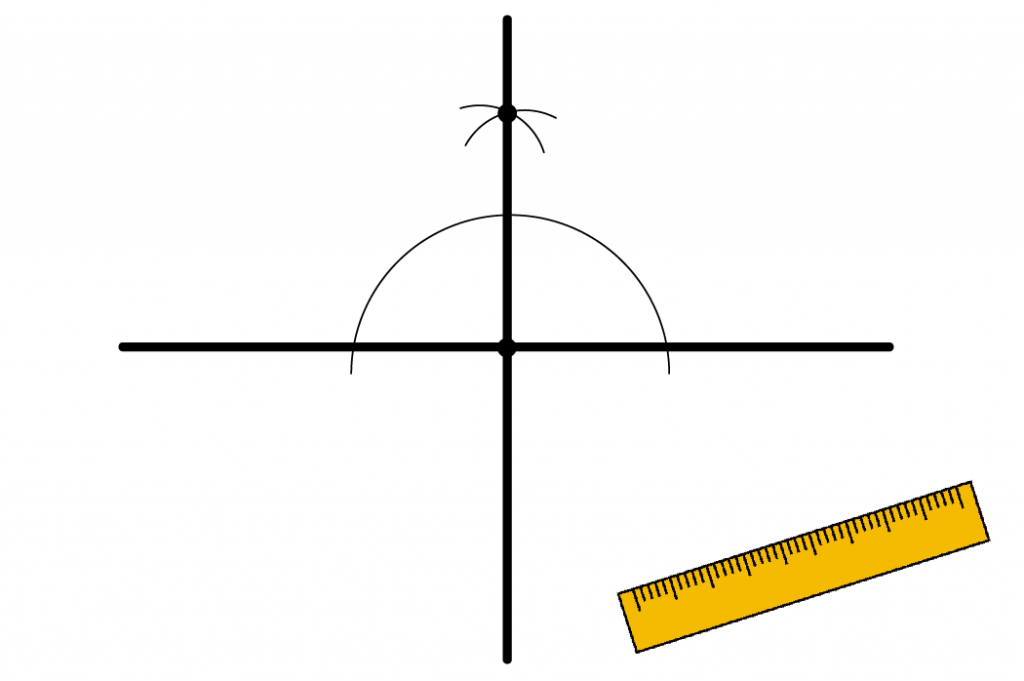
これが第2ステップ!
つぎは角の二等分線をかくよ。
「垂線」と「直線」の二等分線をかけばいいんだ。
つまり、
90°を45°にしてくれる二等分線だね。
まず交点にコンパスの針をおこう。
そして、テキトーに円を4分の1ぐらいかく。
今度は、
「直線」と「4分の1円」の交点にコンパスの針をおこう。
そして、適当な脚の長さでちょびっと円をかく。
つぎは「垂線」と「4分の1円」との交点に針をおく。
脚の長さをかえずに、
チョビ円をかいてみよう。
「チョビ円の交点」と「垂線と直線の交点」をむすぶ。
これが直角の二等分線だね。
あとおなじように、もう1本角の二等分線をかいてね。
これで第3ステップ!!
今度はまるっと1つの円をかくよ。
直線たちの交点にコンパスの針をおいてみて。
そして、テキトーな大きさの円をかけばいいんだ。
これが第4ステップ!
最後は、
円と直線たちの交点をむすべばいいんだ。
むすんでできた図形が正八角形になっているはず!
おめでとう。
これで正八角形を作図できたね!
正八角形の作図はムズい。
5ステップもあるからね。
ただ、この作図に必要なのは、
ってう基礎的なワザばかり。
復習にもなるから、一度作トライしてみよう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。ビビン丼は間違いないね。
中学数学の確率はぶっちゃけ、ムズい。
樹形図かかなきゃいけないし、
サイコロふらなきゃいけないし。
もう、つかれちゃうよね。
だけど、確率はテストで狙われやすい単元だ。
逃げるわけにはいかないね。
今日は、そんな確率の問題を倒すために、
確率を攻略できる5つのコツ
を伝授するよ。
確率のコツは5つあるよ。
問題のパターンに慣れよう。
いろんな種類があるからね。
問題の種類ごとにつかえる公式だったり、
確率の求め方がちがう。
パターンを知っておくだけで楽になるよ。
たとえば、
などなど。
いろんなタイプの問題をといてみよう。
できなかった問題の解き方をつぶしていくのがコツだよ。
中学数学の確率では、
が重要なんだ。
なぜなら、
場合の数を調べるときに樹形図をつかうからだ。
確率の求め方は、
(あるできごとの場合の数)÷(すべての場合の数)
だったよね??
場合の数がわからないと確率が計算できないってわけ。
つまり、「樹形図」をマスターしていないと確率が計算できないんだ。
樹形図の書き方はおぼえておこう!
>>詳しくは「樹形図の書き方」をみてね。
問題文に「少なくとも」がついてたら注意。
「少なくとも」がついている問題の解き方をつかってみよう!
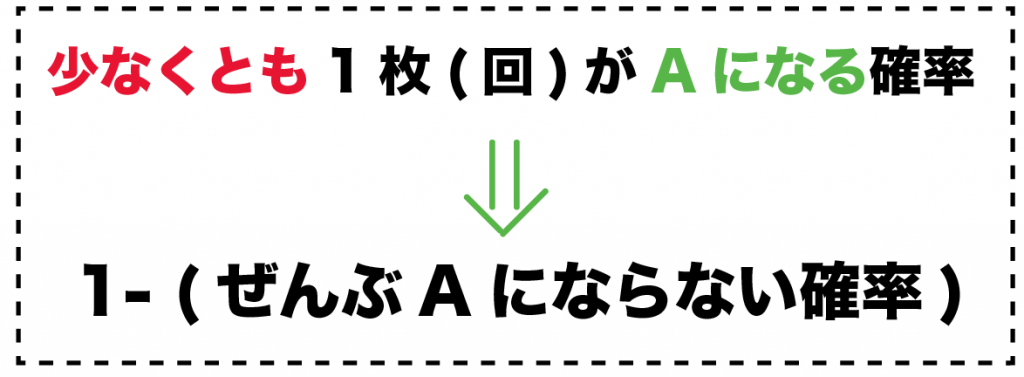
少なくとも1枚(回)がAになる確率
だったら、
1 – (ぜんぶAにならない確率)
を計算すればいいんだ。
えっ、なぜこんなメンドイ計算をするのかって!?
じつはその理由は、
場合の数が少なくて数えやすいからなんだ。
だから、確率の計算もしやすい。
詳しくは「少なくともがつく確率の解き方」の記事をよんでみね。
確率の問題では、
同じにみえるものを区別すること
が重要だよ。
たとえば、サイコロを2つ投げる問題だったら、
と区別するよ。
そっくりな当たりくじ同士でも、
って別々ものものとしてみるよ。
こんな感じで、
見た目が同じものを区別していこう!
計算した確率が、
0から1の間
におさまっているか確認しよう。
もし、計算できても、
確率が2とか、
300とか、
100000になってたら間違いだ。
なぜなら、
確率の範囲はゼッタイに「0から1」だからね。
確率が1だと100%ゼッタイにおこる確率になるし、
0だとゼッタイに起きない確率になる。
計算後にチェックしてみよう。
確率の問題は特殊。
方程式をといたり、
関数の交点を求めたりするのとは訳がちがう。
シンプルだけどむずい単元だ。
コツをおさえて問題になれていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。もやしは安いね。
確率でたまーに、
「少なくとも」
がつく問題でてくるよね???
たとえば、つぎのようなやつだ↓↓
例題
4枚のコインをなげて少なくとも1枚が表になる確率を求めなさい。
こんな感じで、「少なくとも」がついている問題は、
ふつうに解くとメンドイ。
楽な計算方法をつかってみよう!
そこで今日は、
「少なくとも」がついた確率の求め方
を3ステップで解説していくよ。
よかったら参考にしてみて。
「少なくとも」がつく確率の問題。
世の中にはたくさんある。
今回紹介するのは、
少なくとも1枚/回がAになる確率
を求める問題の解き方だよ。
この手の問題は3ステップで計算できちゃうんだ。
さっきの例題を解説していくよー
例題
4枚のコインをなげて少なくとも1枚が表になる確率を求めなさい。
まずは、
ぜんぶAにならないこと
をみつけよう。
例題では、
少なくとも1枚表になる確率
を求めるんだったよね??
Aにあたるのは、
表になる
ってこと。
つまり、「ぜんぶAにならないこと」は、
ぜんぶ表にならないこと
だね。
これが第1ステップだ!
つぎは、さっきの、
ぜんぶAにならないこと
の確率を計算してみよう!
例題でいうと、
コインを4回なげて、ぜんぶ表にならない確率
ってことだね。
これは、
コインを4回なげてぜんぶ裏になる確率
ってこと!
コインを4枚なげると、表裏の組みあわせはぜんぶで16通り。
ぜんぶ裏になる場合の数は1通りしかない。
よって、ぜんぶ裏になる確率は、
16分の1
になるはず!
>>コインの確率の求め方はこちら

最後に、その確率を1からひいてみよう。
つまり、
1 – (ぜんぶAにならない確率)
を計算すればいい。
例題では、「ぜんぶAにならない確率」は、
16分の1
だったよね??
よって、
1 – (ぜんぶAにならない確率)
= 1- (16分の1)
= 16分の15
になるんだ。
おめでとう。
「少なくとも」の確率問題も攻略だね!!
でもさ、
なぜメンドイ方法で計算するんだろう??
って思うない??
ふつうに確率の求めればいいじゃない!?
って切れてるヤツもいるかもしれない。
この解き方を使う理由は、
「少なくとも1枚(回)がAになる」場合の数が多すぎるからなんだ。
ふつうに計算すると、場合の数をかぞえるときに苦戦する。
だから、ストレートに確率を計算するんじゃない。
「ぜんぶAにならない場合の数」を数えて確率をだすんだ。
「少なくともAにならない確率」と、
「ぜんぶAにならない確率」を足したら1になるはずだね??
だって、どちらかは絶対に起きるからね。
つまり、足したら1、100%起きる確率になるのさ。
だから、
ゼッタイに起きる確率の「1」から「ぜんぶAにならない確率」
をひいてやると、
「少なくともAにならない確率」
を計算できちゃうんだ。
どう??スッキリしたかな??
「少なくとも」がつく確率の問題は、
1から「ぜんぶAにならない確率」をひいてみよう!
これで計算が早くなるはず。;
じょじょに慣れていこうね!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。布団、気持ちいね。
確率の問題には色んなタイプがある。
たとえば、
サイコロとか、コインとか、玉とか・・・・
もう、いろいろね。
そんな中、よくでてくるのが、
トランプの確率の問題
だ。
今日はこのタイプの問題を攻略するために
トランプの確率の基本をおさえておこう!
基本を押さえると、トランプの確率を計算しやすくなるよ。
トランプの数字には、
1~13まである。
と名前をかえてることに注意。
英語になっているけど、数字としてとらえちゃおう。
1つの数字につき4つのマークがあるよ。
の4種さ。
1~13の13枚のカードはそれぞれ4種類あるってわけ。
ってことは、トランプは全部で、
13 × 4 = 52枚
あることになるね。
トランプには「赤」か「黒」の2色があるよ。
「スペード」と「クローバー」は黒。
「ハート」と「ダイヤモンド」は赤になっているんだ。
だから、52枚のトランプカードの中には、
入っていることになる。
実際にトランプの確率を計算してみよう。
52枚のトランプから1枚ひいたとするね。
1枚ひいてエースがでる確率を求めてみよう。
トランプはぜんぶで52枚ある。
だから、52通りのひき方があるはず。
1つの数字につきマーク違いの4枚がある。
エースだって4枚あるはずだね。
つまり、4通りのひき方がある。
だから、トランプから1枚ひいてエースをひく確率は、
(エースをひく場合の数)÷(ぜんぶの場合の数)
= 4 ÷ 52
= 13分の1
になるね!
1枚ひいて「黒」がでる確率を計算しよう。
黒いカードはぜんぶで「26枚」あったよね?
ってことは26通りのひき方があるわけだ。
黒いカードをひく確率は、
(黒いカードをひく場合の数)÷(すべての場合の数)
= 26÷52
= 2分の1
になるよ。
最後はクローバーをひく確率だ。
1つのマークはぜんぶで13枚ある。
ってことは、クローバーには13通りのひき方があるってわけ。
1枚ひいてクローバーをひく確率は、
(クローバーの場合の数)÷(ぜんぶの場合の数)
= 13 ÷ 52
= 4分の1
になるよ。
トランプの確率の問題は基本をおさえれば大丈夫。
基本がわかったらガンガン問題をといていこう!
そんじゃねー
Ken