こんにちは、この記事をかいているKenだよ。トイレがいちばん落ち着くね。
三角形の作図って意外とむずかしいよね??
とくに、三角形の角度が正確にわからないとき、三角定規や分度器をつかってかくのはチョーむずかしい。

そこで、今日は、
どんな三角形でも「コンパス」と「定規」だけで作図できる書き方を紹介するよ。この作図方法はとってもシンプルで、3ステップでかけちゃうんだ。
正三角形でも二等辺三角形でもなんでもこいって感じさ!
さっそく三角形の作図方法をみていくよ。今日は、
ごくフツーのなんでもない三角形の作図
をマスターしちゃおう。
これができれば、正三角形や二等辺三角形でもなんでもかけるようになるよ。
例題として、つぎの三角形をかいていこう!
一辺が3、4、6cmの三角形をコンパスと定規で作図してちょ
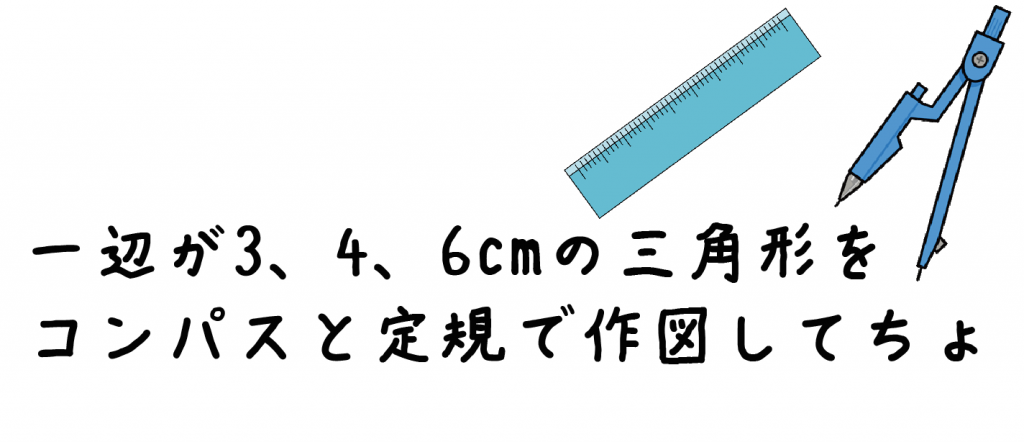
この三角形は3ステップでかけちゃうよ。
「三角形の1辺」をテキトーにピックアップしちゃおう。ピンときたものを選んでみてね。
例題では、4cmの辺を選んだよ。
手に持っている定規で、

ビシッと4cmの線分をかいてあげよう。

解説しやすくするために、線分の両端をA、Bとおいたよー
さっきの「線分の端」にコンパスの針をおこう。
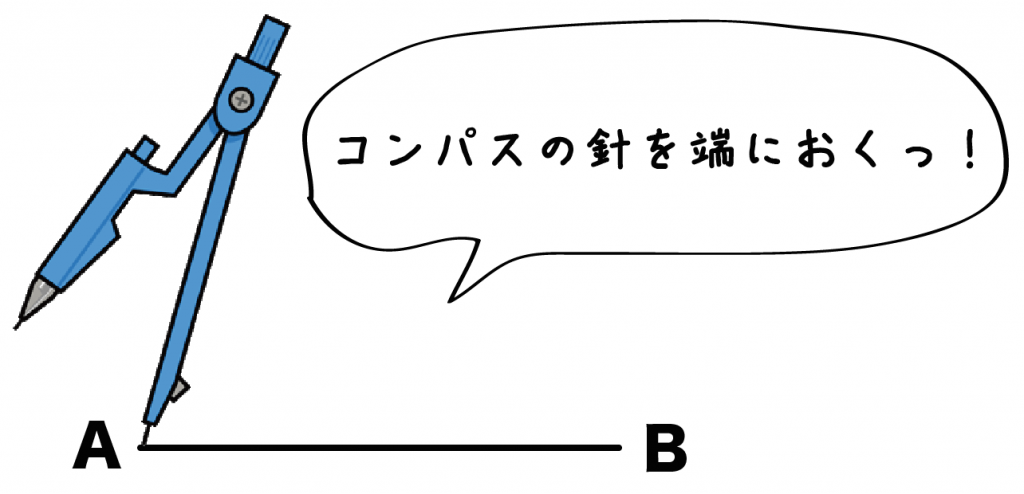
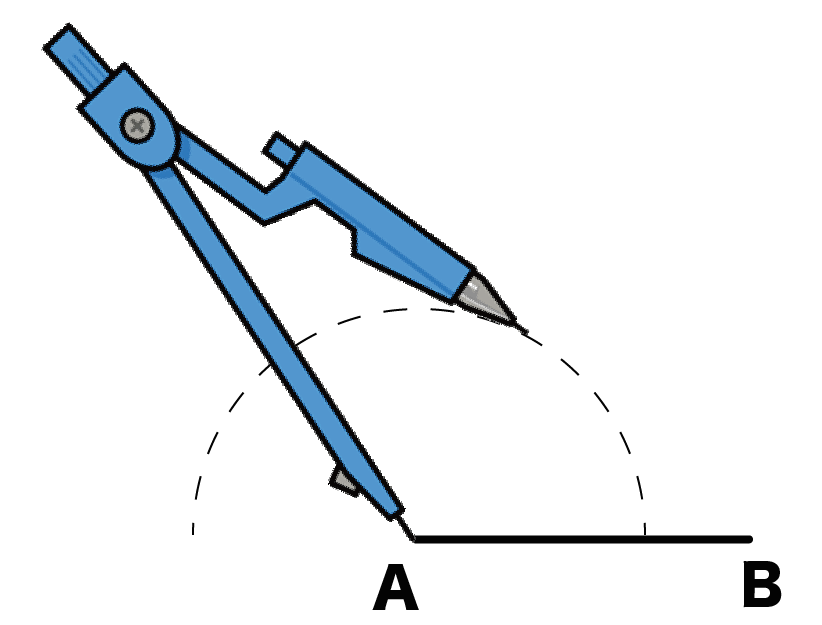
そして、「残りの辺の長さ」で「半円」をかいてあげるんだ。
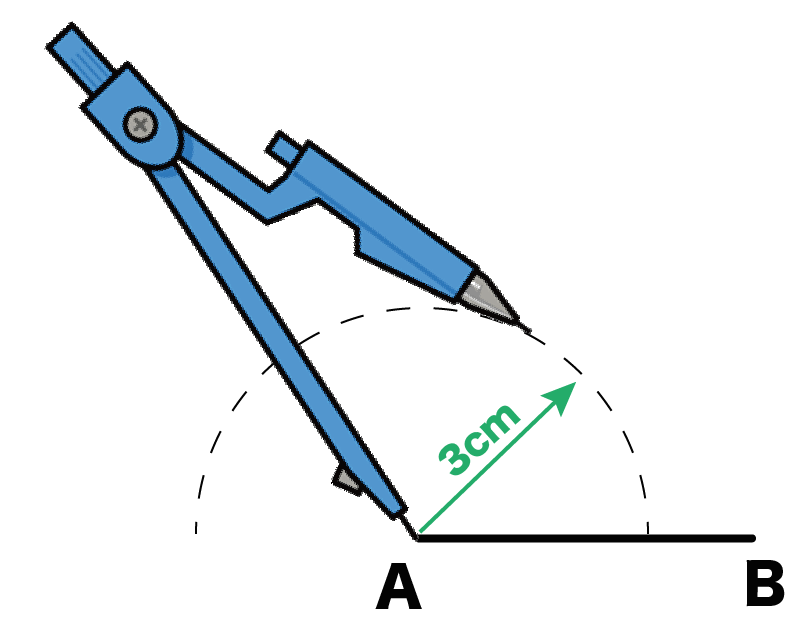
例題では、「3cm」の辺を選んでみたよ。だから、作図する円の半径は3cmってことになるね。
そんで、これを残りの辺でもやってみてね。
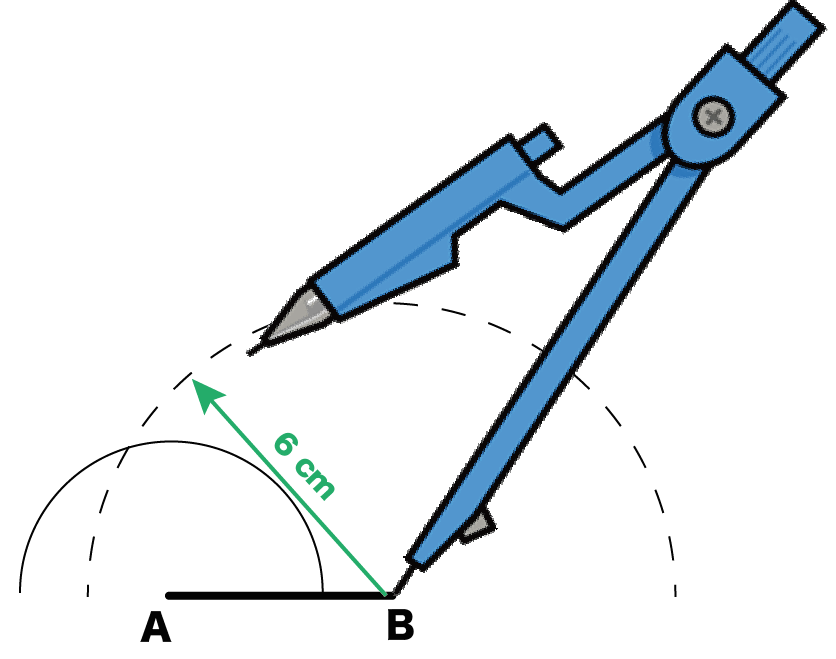
例題でいうと、
点Bにコンパスの針をおいて6cmの半円をかくってことだね!
いよいよ最後のステップ。
「2つの円の交点」と「線分の両端」を定規でむすんであげればいいんだ。
例題をみてみよう。
2つの円の交点をCとするよ。これが三角形の3つめの頂点ってことになる。
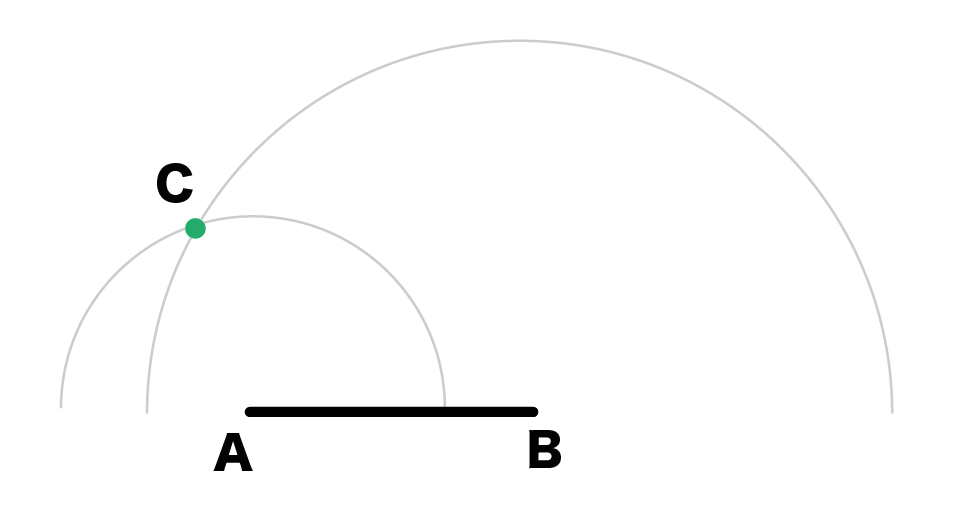
んで、
「頂点C」と「線分の両端(AとB)」を直線でむすんであげると、
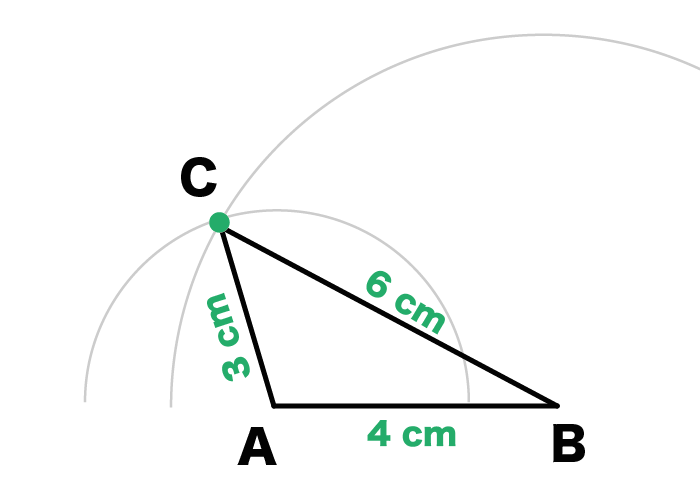
三角形ABCができちゃうんだ。
コンパスと定規があれば、三角形をどこでも作図できるようになったね。
正三角形も二等辺三角形もバッチコイさ。
三角形の書き方はシンプル。
だって、コンパスと定規さえあればいいからね。
いつでも三角形を作図できるようにコンパスをつねに携帯していよう。
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。犬のしつけに失敗したね。
立体の展開図の書き方をたくさんみてきた。
もう空間図形の展開図なんて飽きた! おれは平面がいい!!
なんて思うかもしれないね。 だけど、今日はもう一つ新しい「立体の展開図」を勉強していこう。

それは、
三角錐の展開図の書き方
だ。
まるで、とんがりコーンのような三角錐。
展開図の書き方は次の2種類あるんだ。
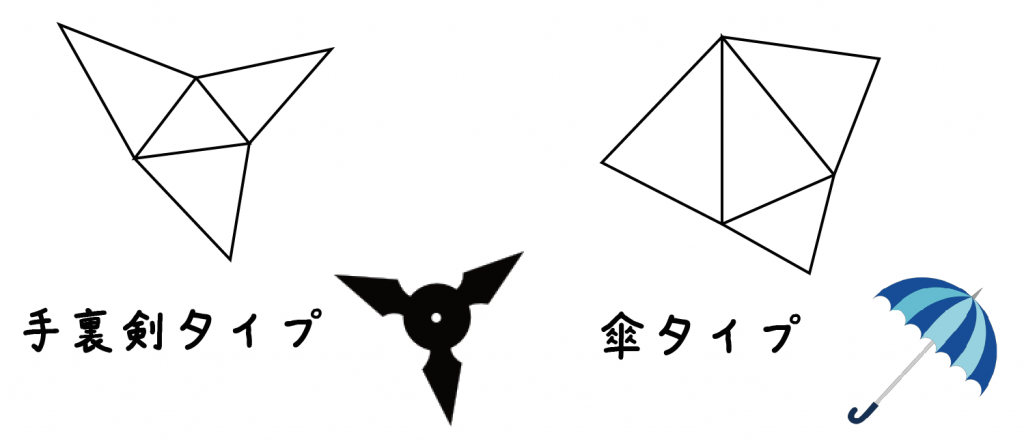
今日はせっかくだから、2つの作図法をマスターしちゃおう。
つぎの例題をときながらみていくよ。
例題
つぎの三角錐ABCDの展開図をかきなさい。そったら100点あげるよ。
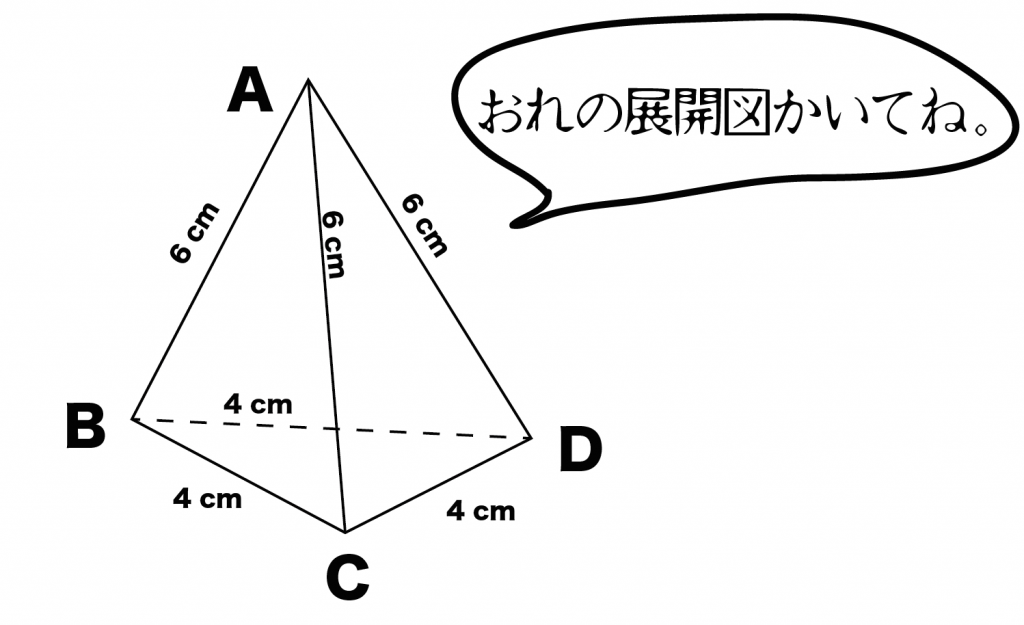
まずは1つ目の「手裏剣タイプ」の書き方をみていこう。

この書き方では、つぎの4ステップで作図できちゃうんだ。
底面の三角形をかいてみよう。気合で。
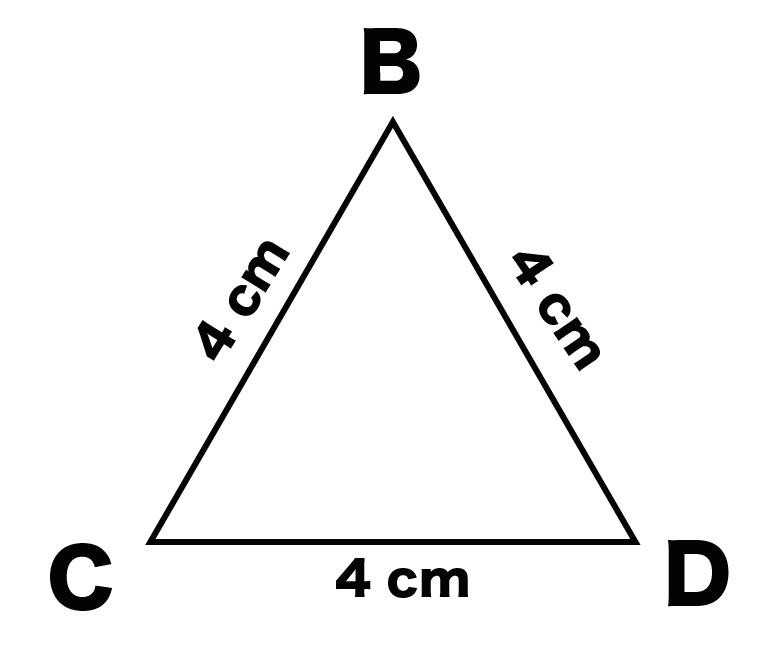
例題でいうと、三角形BCDだね。
コンパスや定規やをつかってみてね。
「ステップ1でかいた底面」に側面をつけたしてやろう!
各辺に対応するように側面をかいてあげるんだ。タケノコが生えるみたいにニョキニョキっとね。
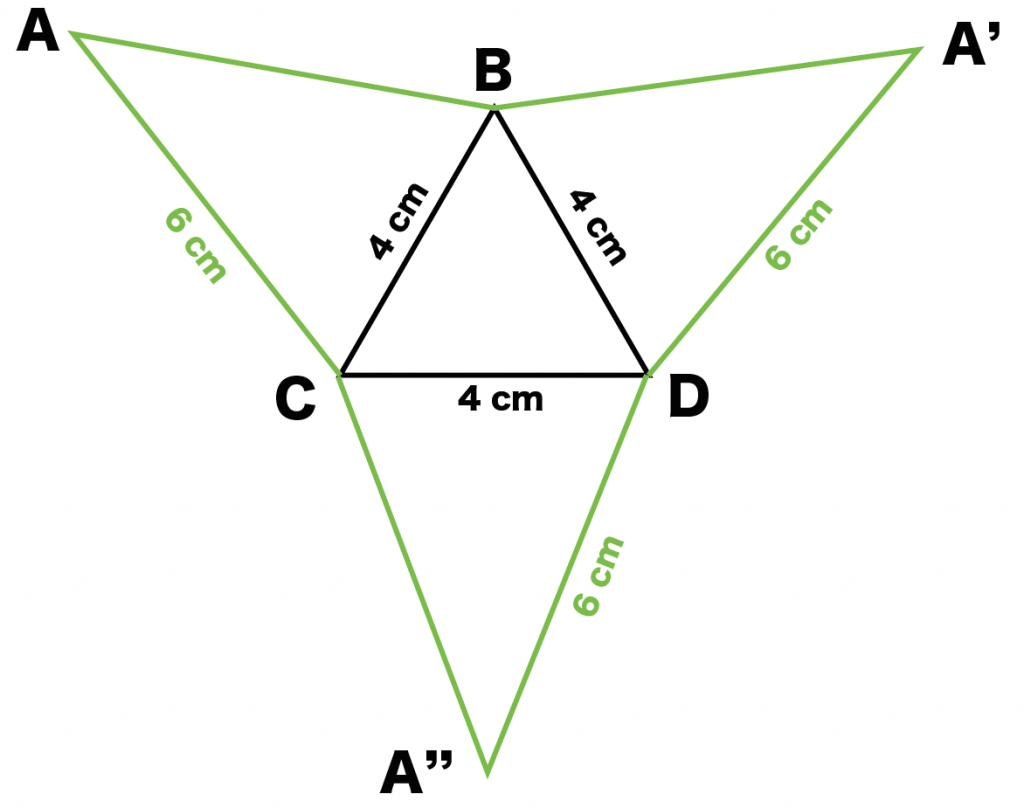
例題でいうと、
でつなげちゃおう!
最後に、展開図の折り目を「点線」にしてあげよう。展開図でいう「折り目」は展開図のうちがわの線のこと。
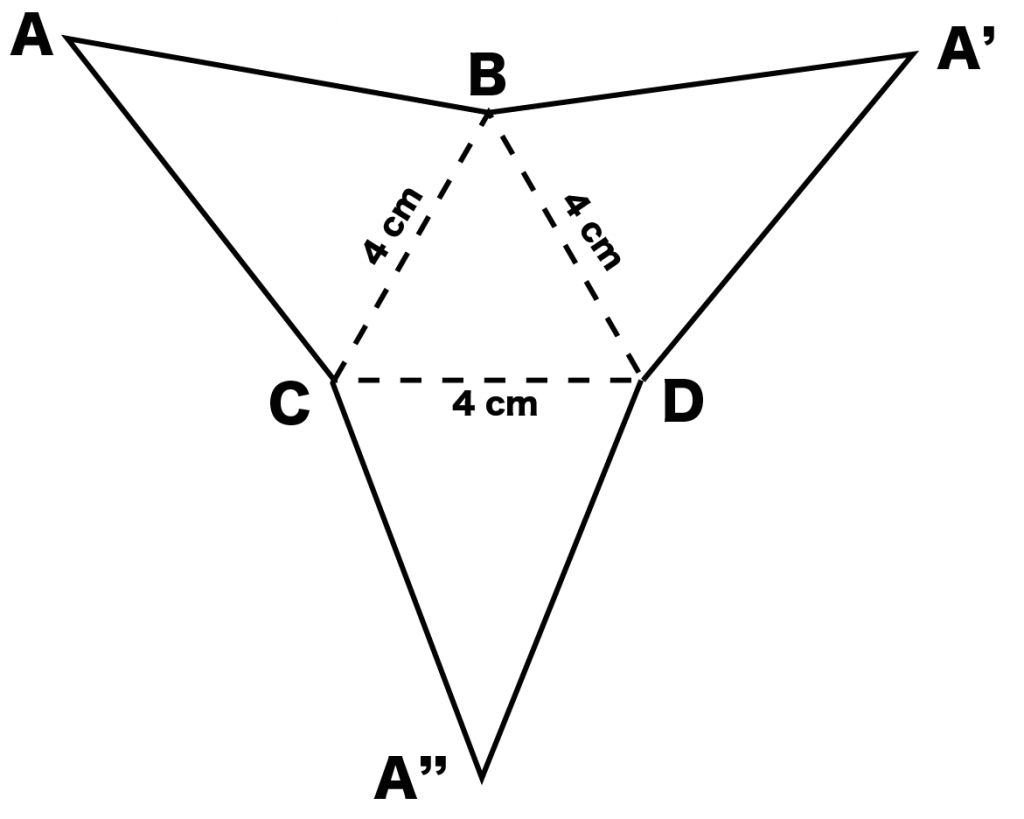
例題でいうと、
の内側の3辺がそれにあたるね。
これで三角錐の展開図は終了! やっぱ手裏剣に似てるっしょ??。
手裏剣タイプをマスターしたね?? そのつぎはなんと、傘。
そう、
よくダイソーとかに売っている傘のことだよ。

傘タイプの書き方はつぎの4ステップなんだ。
三角錐の側面を1つかいてあげよう。
側面は3つあるけど、もう、ほんっとどれもでもいい。好きな奴をピックアップしてみよう。
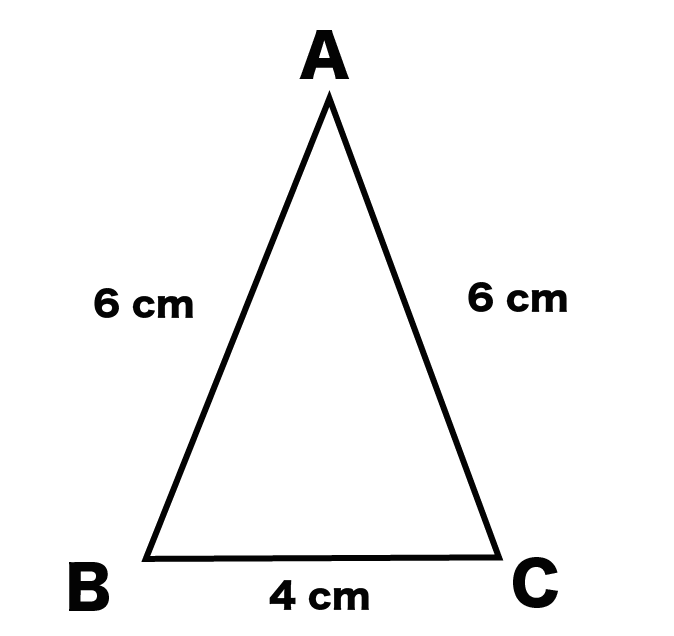
例題では、側面の三角形ABCをえらんでみたよ。
さっきかいた三角形の側面に、のこり2つの側面をつなげてあげよう。
対応する辺同士で合体させてやればいいんだ。
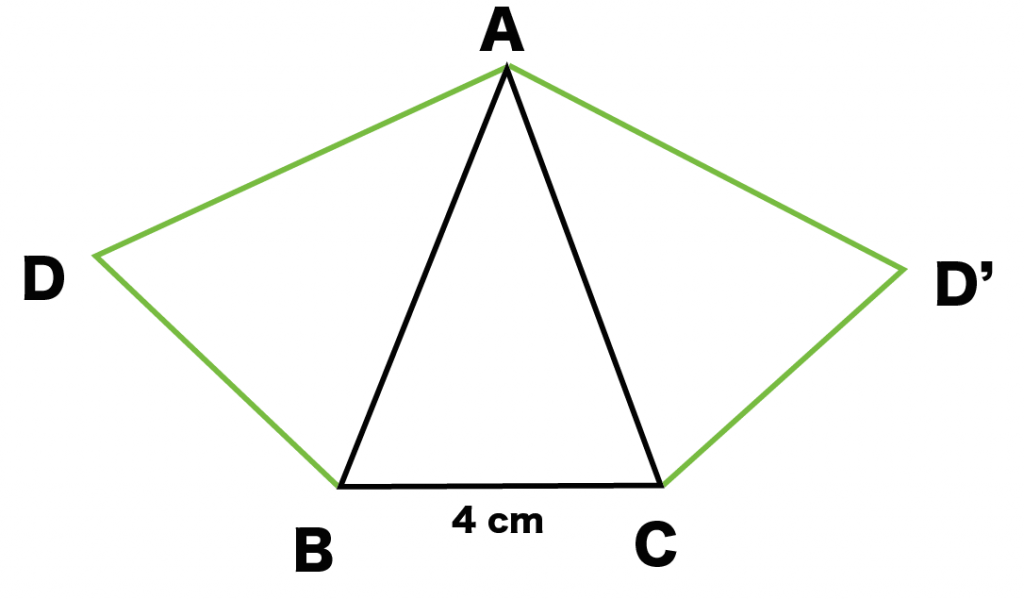
例題では、
三角形ABDを辺ABで合体させ、三角形ACDを辺ACでくっつけてみたよ。
センスみたいな形になればとりあえずオッケー!
底面の三角形もつなげてしまおう!
もちろん、対応する辺で合体させてね。
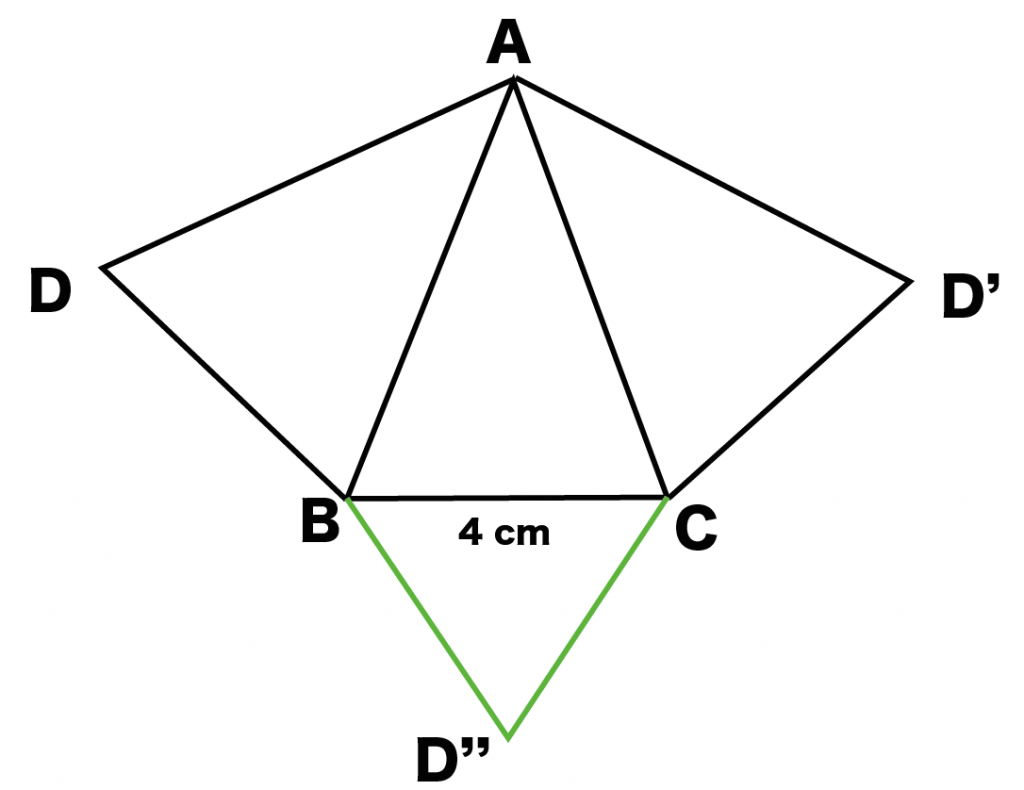
例題では、辺BCで底面の三角形BCDをくっつけているね。
コンパスと定規をつかって渾身の三角形をかいてくれ!
展開図の折り目を「点線」にするよ。
展開図の折り目って、
展開図の内側の線のことだったね??
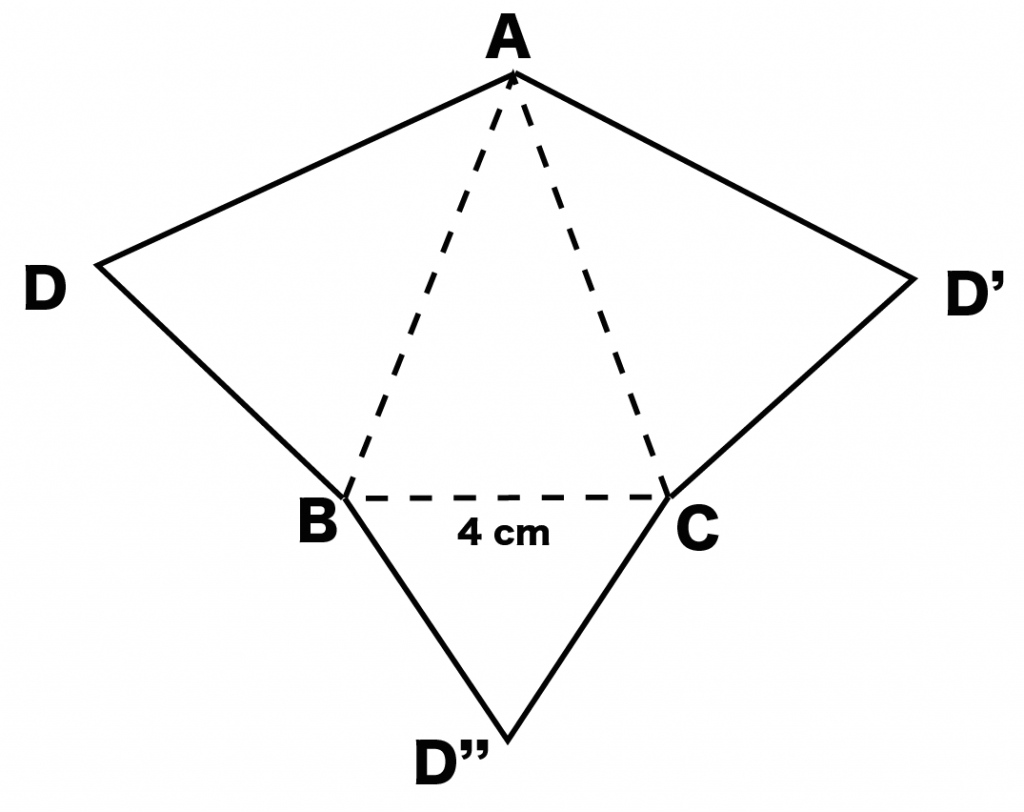
例題でいうと、三角形ABCの辺がすべて折り目になっているよ。だって、展開図のなかにあるからね。だから、
をすべて点線にしてあげよう。
これで三角錐の展開図のできあがりだね。傘にそっくりじゃない??。
おめでとう!!
三角錐の展開図の書き方って意外とシンプルだったでしょ??
書き方うんぬんよりも、三角形をいかに正確に作図できるか??っていうスキルを持っていることが大切かもしれないね。
三角形の書き方はこっちの記事を参考にしてみて。
この2つの方法でじゃんじゃん三角錐を展開していこう!!
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。フリスビーで遊びたいね。
「三角柱の展開図」ってヤッカイだよね??
展開しろっていわれても、なかなかイメージしずらいし、三角柱をみているとケーキみたいで腹がへってくる。
三角柱の展開図を瞬殺したい
って誰もが思っているはずだ。

そこで今日は、
三角柱の展開図の書き方・作図方法を2つだけ解説していくね。
困ったときに参考にしてみて。
~もくじ~
三角柱の展開図の書き方が42通りある、らしい。
だけれども、だいたい次の2つの書き方に分類することができるんだ。
それは、
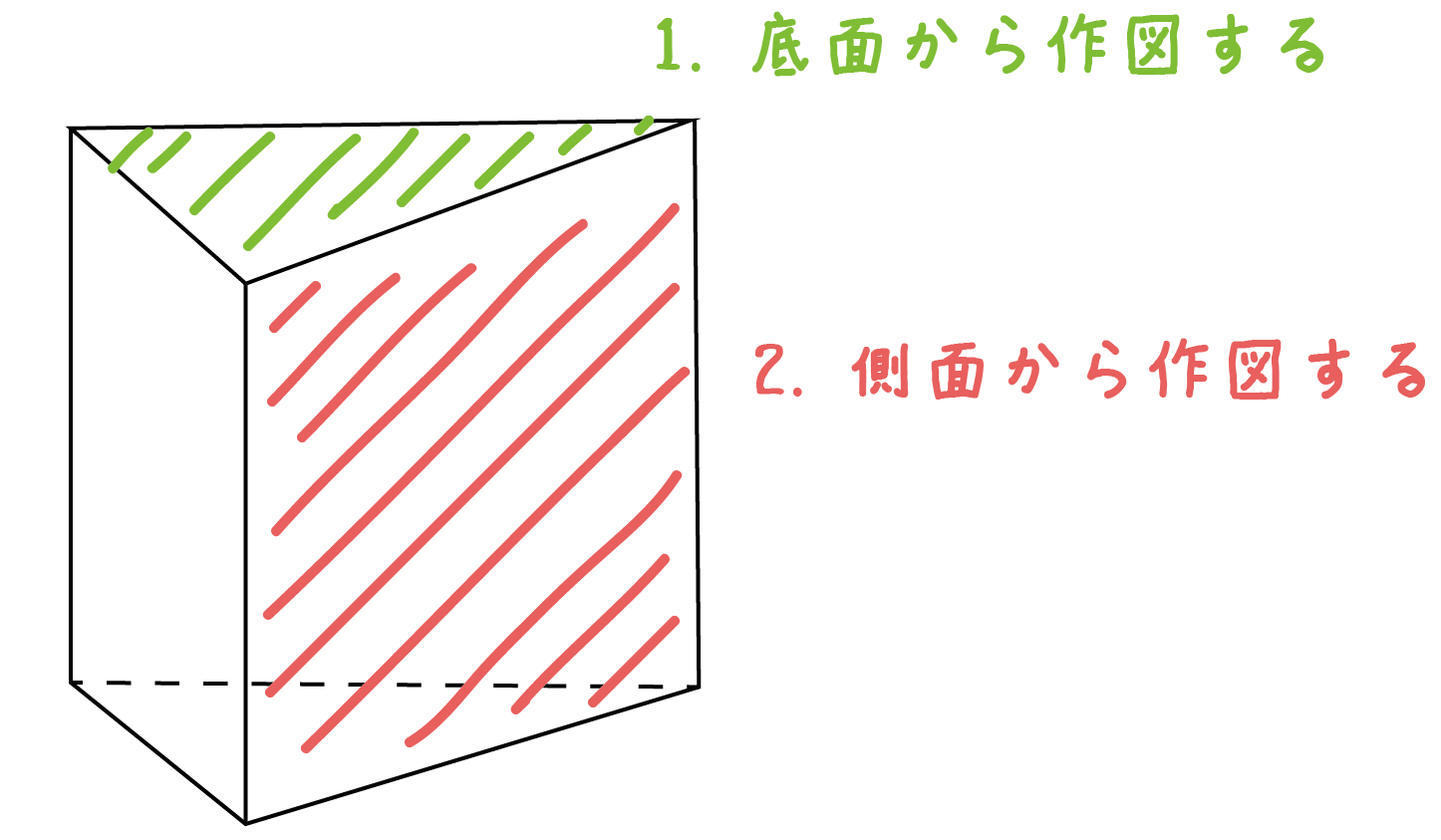
上の図でいえば、「赤い側面」から展開図をかいてもいいし、「緑の底面」から作図してもいいってことなのさ。
つぎの例題の「三角柱の展開図」をかいていくよ!
例題
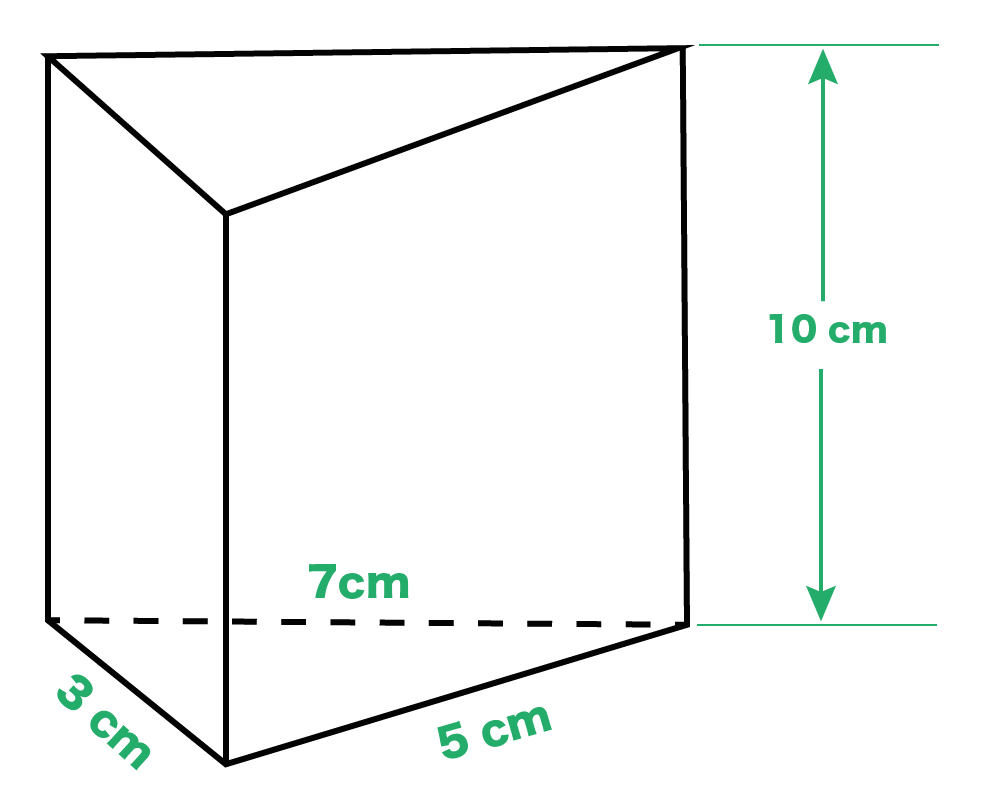
つぎの三角柱の展開図を作図してね。
底面の三角形の辺の長さ(3, 5, 7cm)、三角柱の高さ10 cm
もっとも人気のある、
側面から作図する書き方
をみていこう。
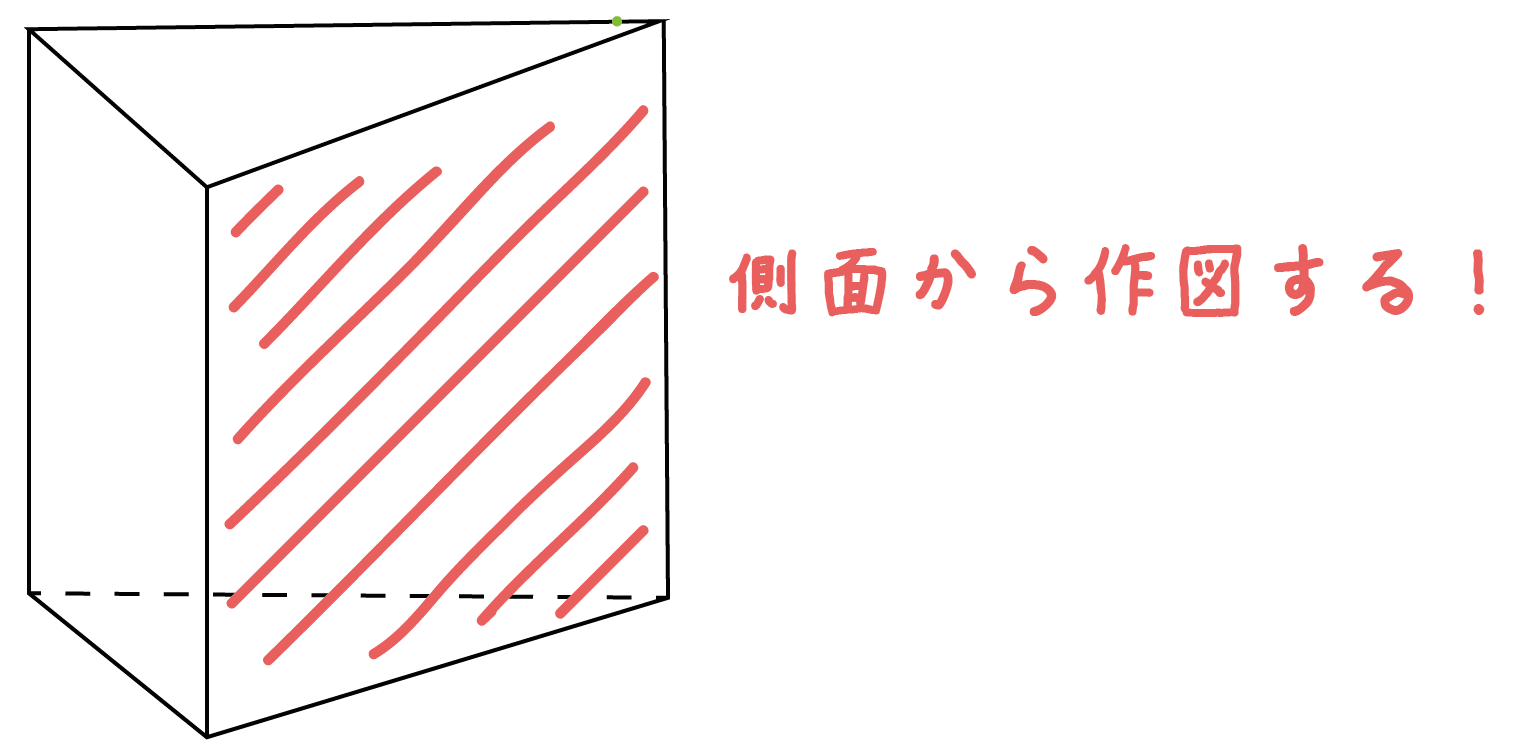
この書き方では、3つのステップで展開図を作図できちゃうんだ。
三角柱の側面は3つあるよね。
そのうち、1つの側面をかいてあげよう。
ようは、長方形を1つだけ作図するってこと。これなら楽勝さ。
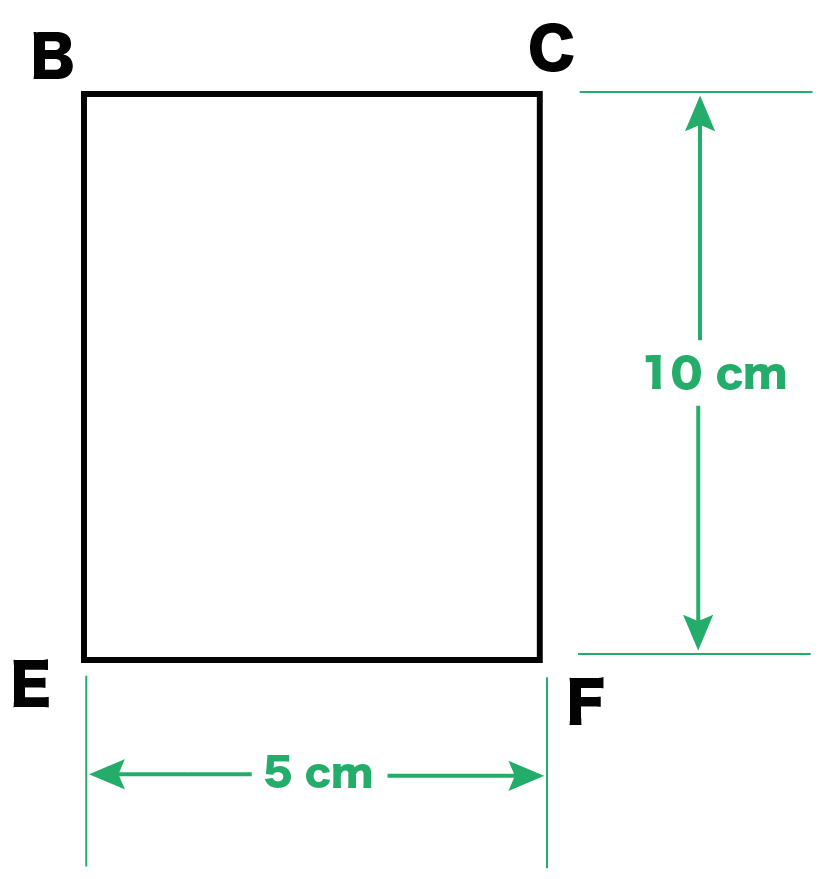
三角柱の頂点に適当に名前をつけてみよう。
A, B, C, D, E, Fといった感じで。
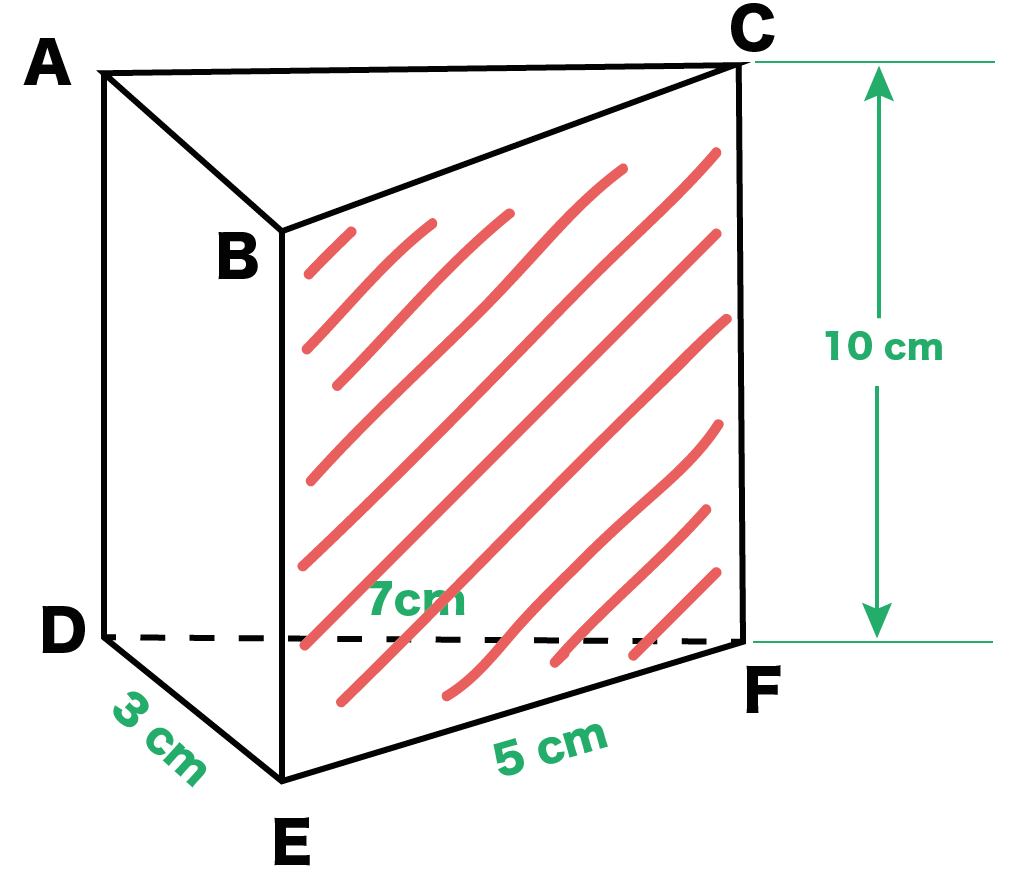
そんで、側面の1つである「長方形BCFE」をかいてみてね。
長方形を気合でかくと、こんな感じになるはずだ↓↓
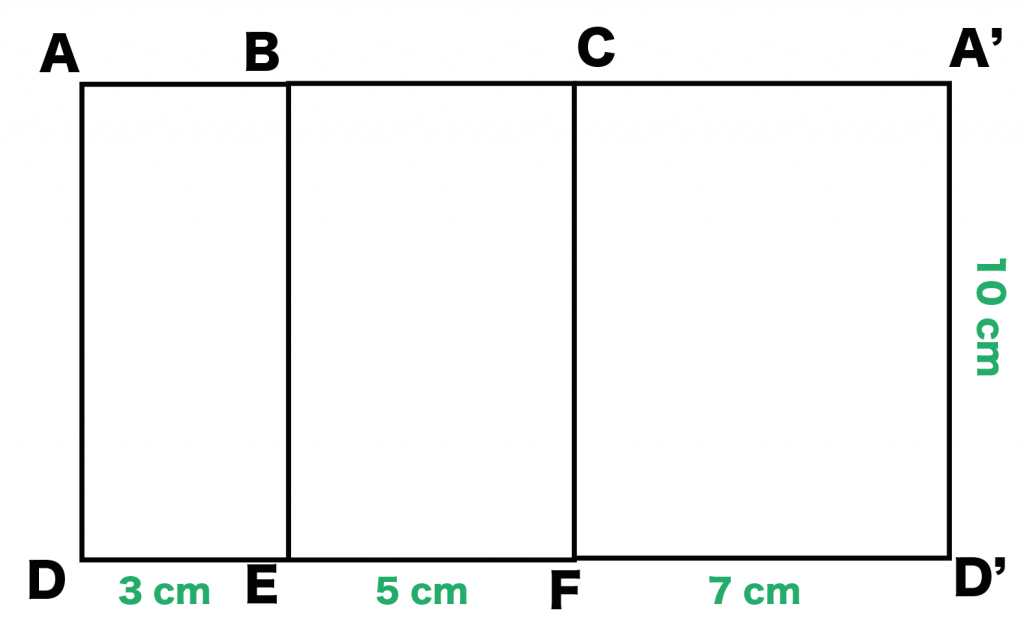
「もう2つの側面」を連結してあげよう!!
例題でいうと、
「長方形ABDE」と「長方形ACFD」だね。
こいつらをさっきの「長方形BCFE」と合体させてやるんだ。
合体の方法は、
「対応する同じ辺」をつなげてやるだけ! すると、こうなる↓↓
ただ、同じ頂点が2つでてきちゃうよね。
この例でいうと、AとDだ。
そういうときは、2つめの頂点に「’ (ダッシュ)」をつけてあげて目印をつけてやろう。こいつは2つめの点だぞ!ってね。
もし、3つめの同じ頂点ができそうだったら「”(ダッシュ)」を2つつけてみてー!
最後に残ったのは底面だね。
あとはコイツらを展開図につけるだけでいいんだ。
「ステップ1でかいた長方形」と「2つの三角形」を対応する辺で合体させてみよう!
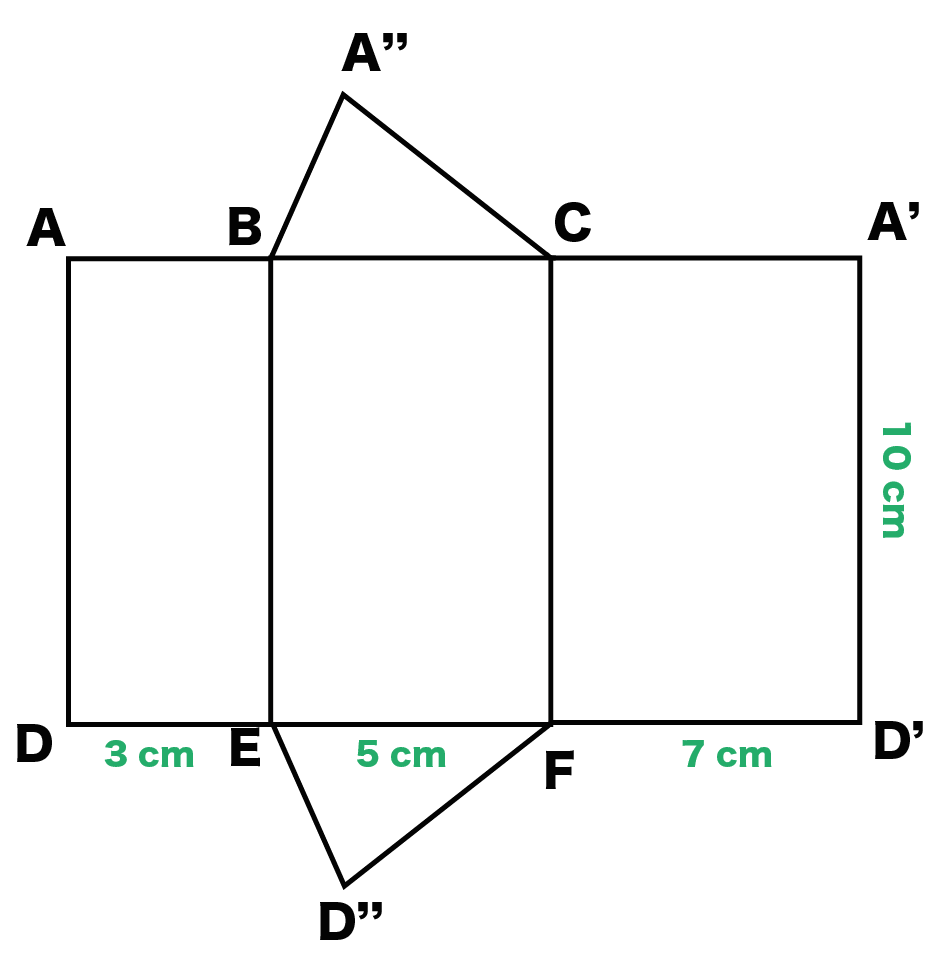
例題でいうと、
「三角形ABC」と「三角形DEF」を「長方形BCEF」と連結させるってことだね。
これで三角柱の展開図は終了だ!おめでとう!
つづいては、底面から作図する方法だ。
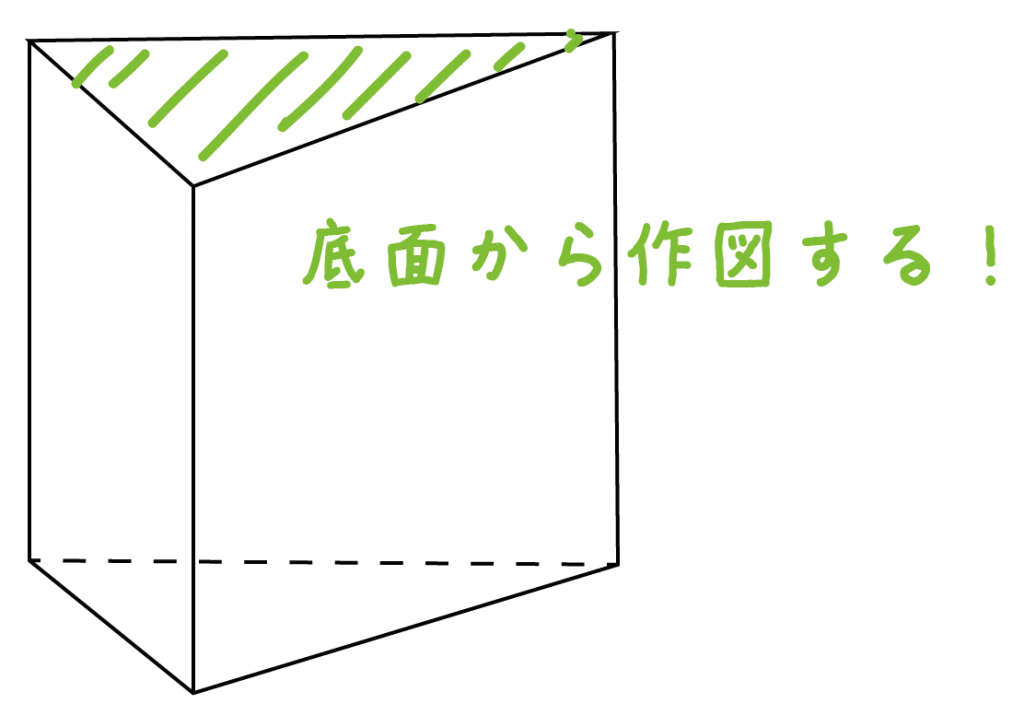
お腹いっぱいになってきたけど、もうちょっと頑張ってみよう。
上でも下でもどっちもいい。
三角柱の底面の「三角形」をかいてみよう。
例題でいうと、
三角形ABCをかくって感じ↓↓
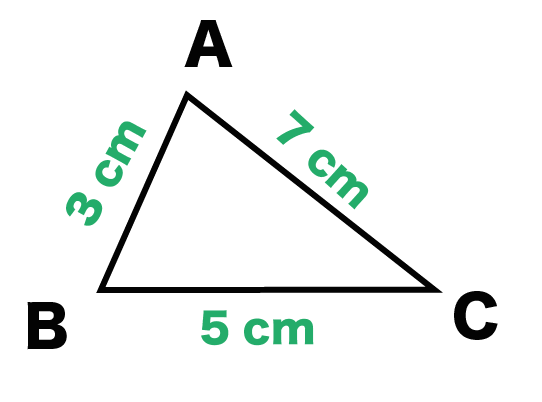
3つの長方形(側面)を合体させてみよう!
方法はいたって簡単。
対応する辺同士を連結させてやるだけさ。
例題だと、こんな感じになるよ↓↓
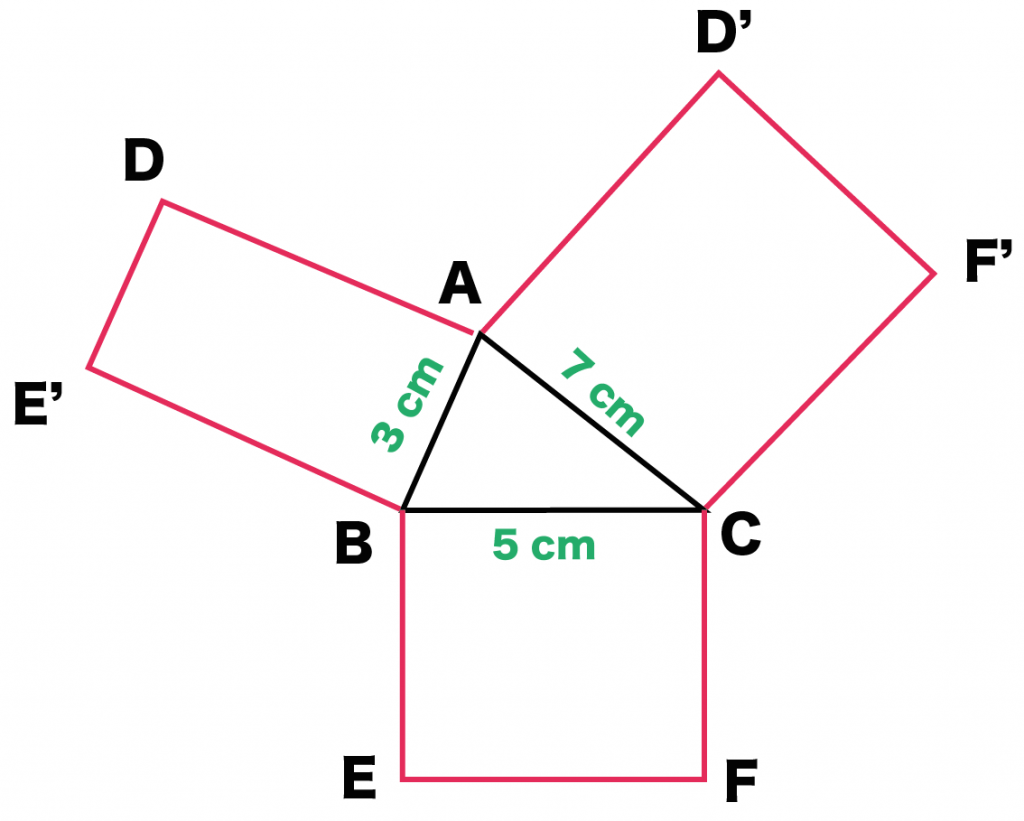
長方形を定規で3つかいてあげよう!!
残されたのはあと1つ。もう一方の底面だけさ。
あとはコイツを長方形のうえにのせてあげよう! 対応する辺同士をくっつけるればいいんだ。
例題でいうと、
「三角形DE”F’」を「長方形ACF’D」のうえにちょこんとのせているね。
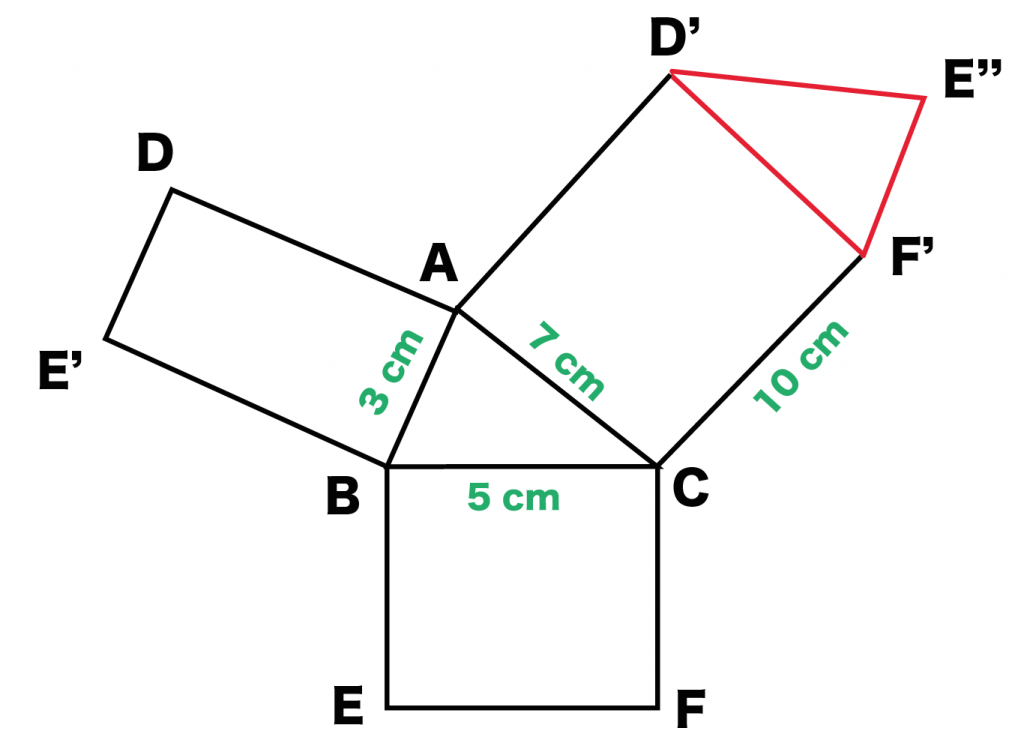
対応する辺は「DF」。一緒にくっつけることを忘れずに。
底面からでも展開図をかけたね!おめでとう!!
三角柱の展開図の作図はどうだった??
テストででても慌てずにゆっくりと作図してみてね。
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよー。緑ペンがほしいね。
円錐の表面積を求めなさいっ!
っていう問題はけっこうでる。先生はだしたくなる。
だけど、
円錐の表面積を求めるの
はけっこうムズい。できれば避けて通りたいね・・・・

このピンチを助けてくれるのが、
円錐の展開図を作図する
ということなんだ。
円錐を切り取ったら円錐はどんな紙切れになるのか??
円錐の展開図の書き方を知っていると、いとも簡単に表面積まで計算できちゃうんだ。
今日は、その、
円錐の展開図の書き方・作図法
をわかりやすく解説していくね。
さっそく、円錐の展開図の書き方をみていこう。だれでも簡単にかけるように4つのステップで作図していくよー
つぎの例題をみてみよう!
例題
つぎの円錐の展開図を作図してね!!(直径4cm、母線の長さ6cm)
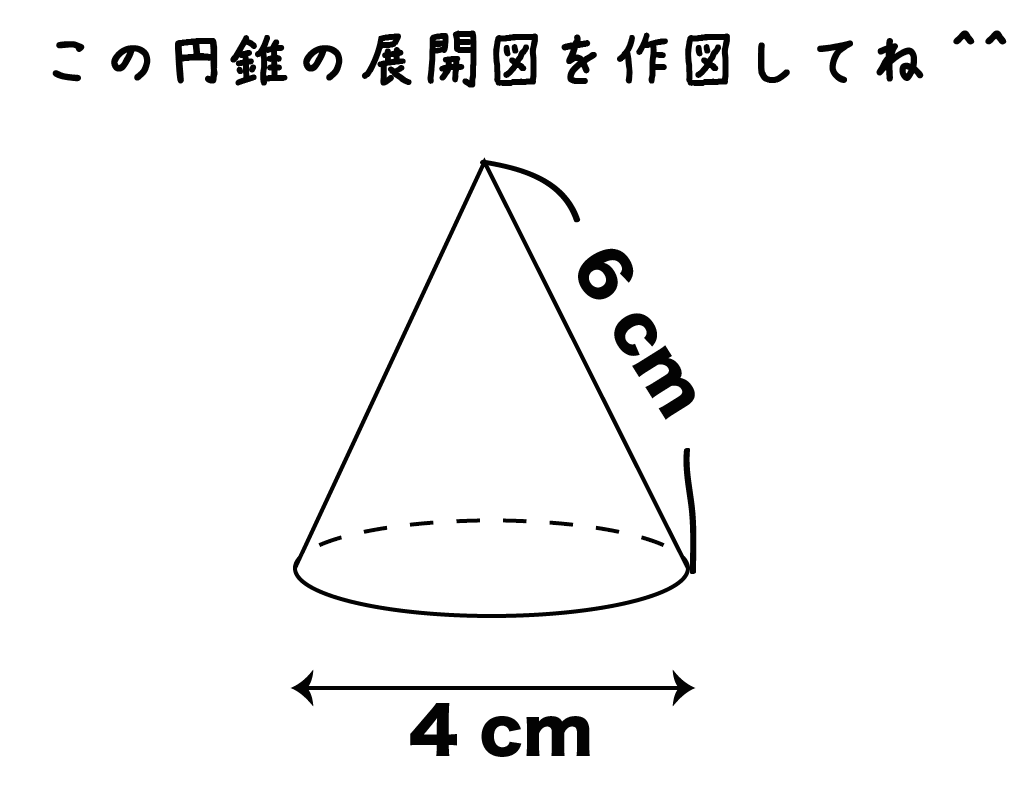
円錐の展開図の問題では、
だいたいこうなるっ!
ていう展開後をさきにイメージしておくとわかりやすいんだ。
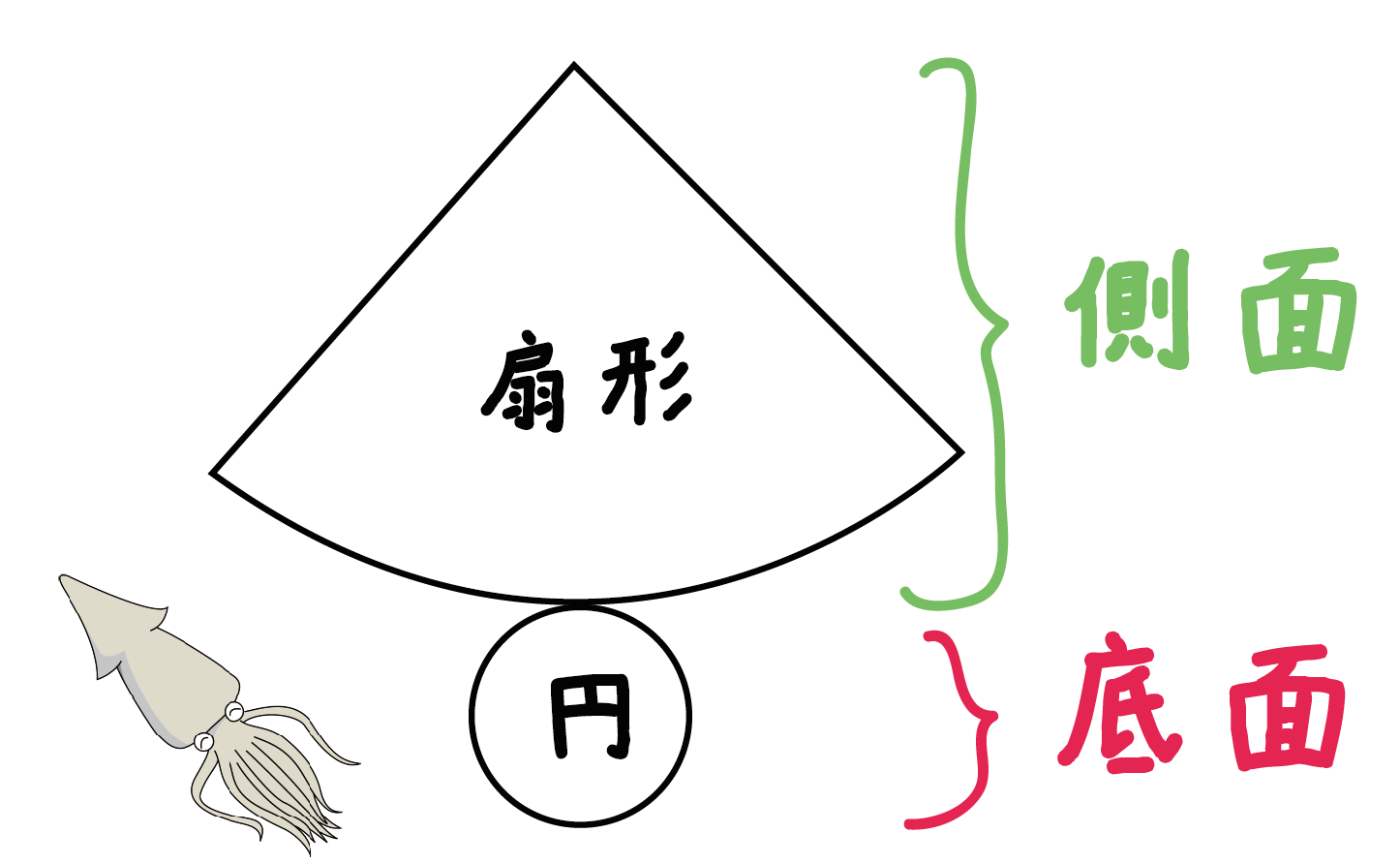
側面が扇形になって、底面の円がぴょこっとつくって展開図になるよ。
そこらへんのイカに似ているねw
それじゃあ、この展開図をぴしっとかいていこう!
まずは底面の円に注目しよう。
円周の長さを求めてあげるのが第一ステップだ。
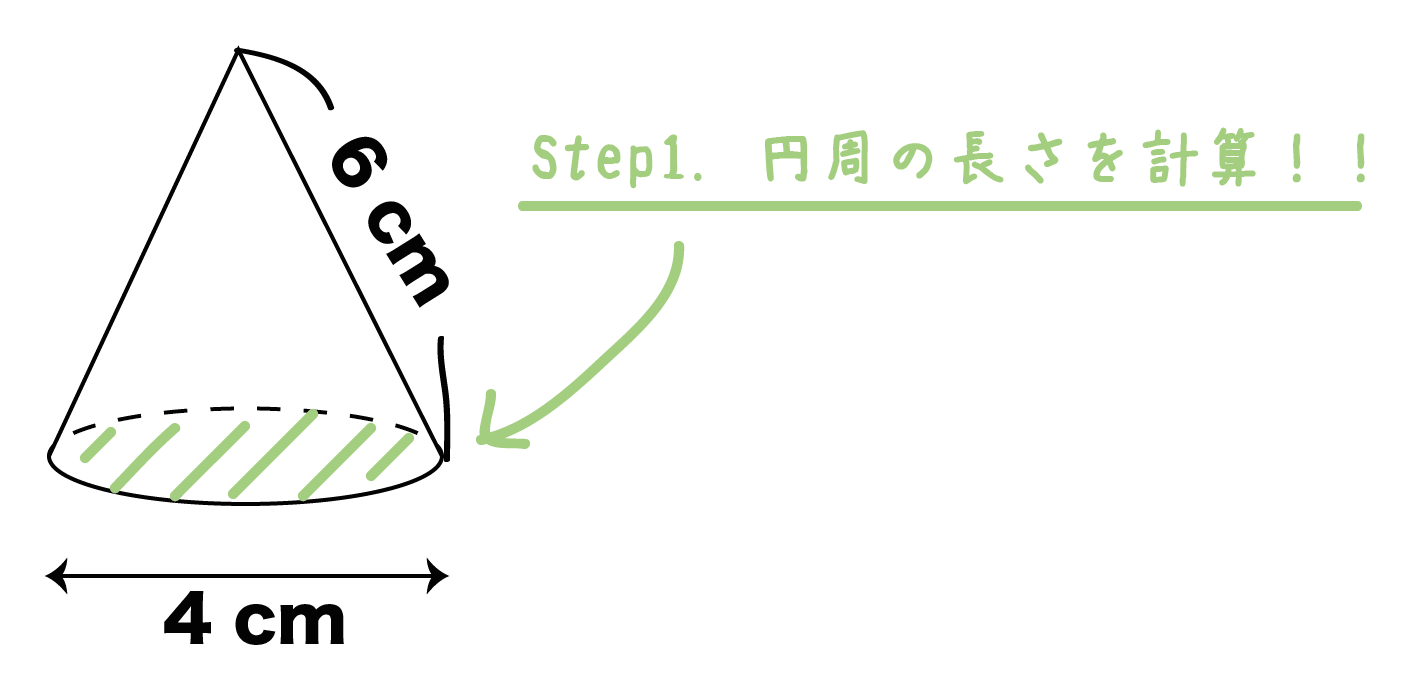
円周の長さは、
「直径×円周率」で求められたよね?? だから例題では、

円周の長さ = 4 π [cm]
になるよ。
つぎは円錐の側面の展開図をかくためのステップだ。
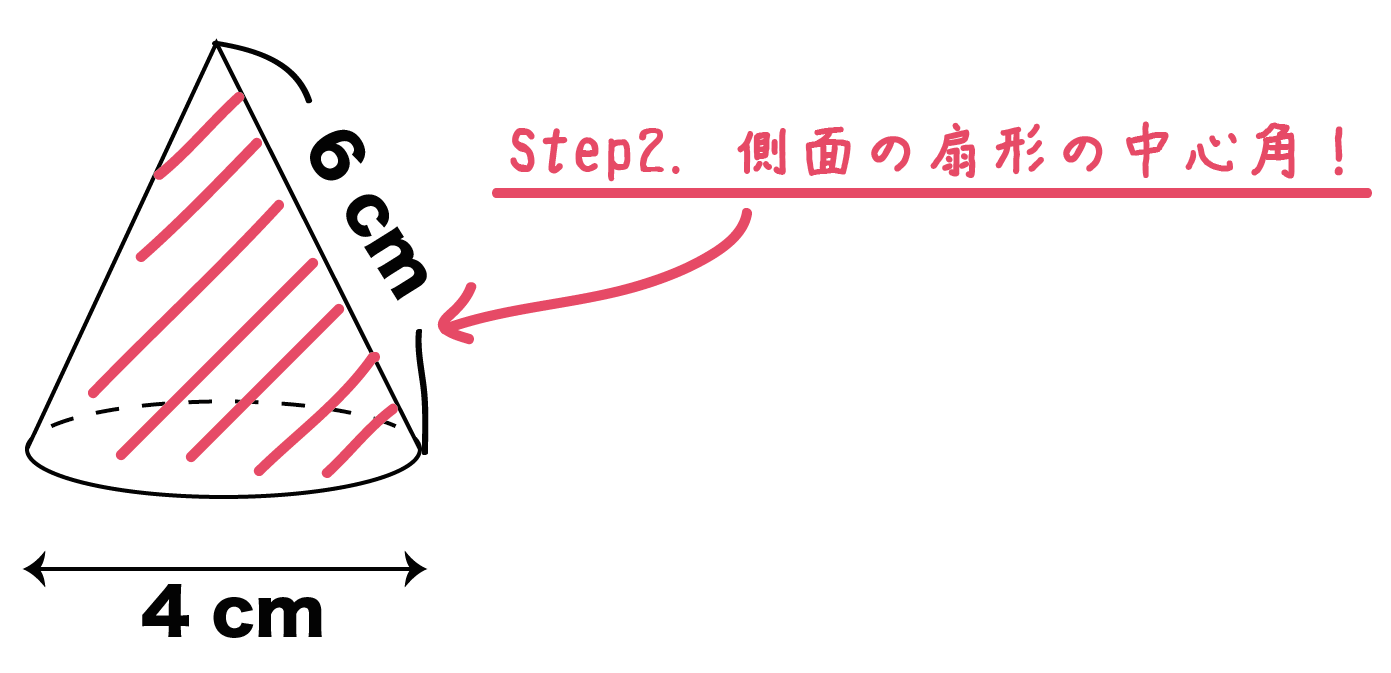
ここでは、円錐の側面を展開したときにできる「扇形の中心角」を求めるんだ!
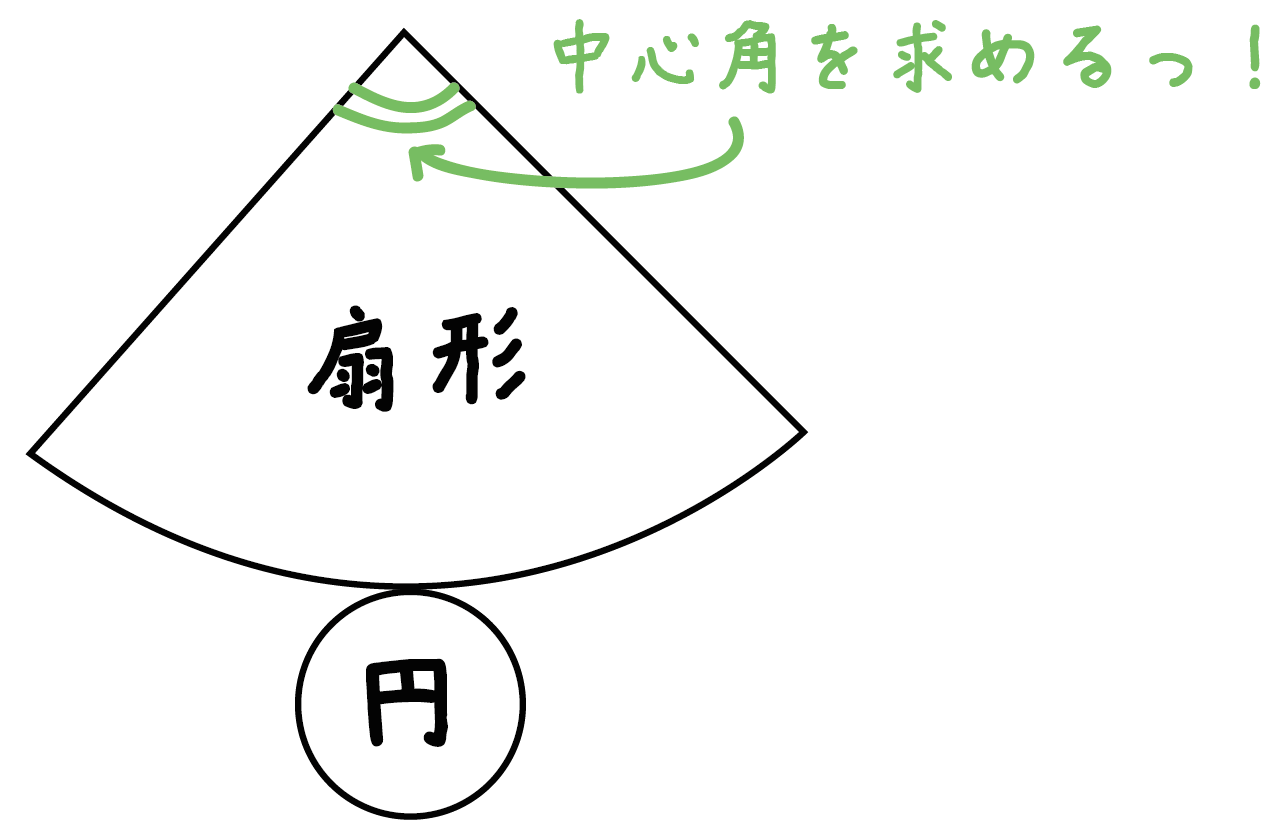
Step1で「底面の円周の長さ」を求めたよね??
じつは、円錐の展開図ではソレが「扇形の弧の長さ」になっているんだ。
扇形の中心角の求め方を参考に計算してやると、
x : 360 = 4π : 12π
x = 120°
になるね!
求めた中心角をもとに側面の扇形をかいてみよう。
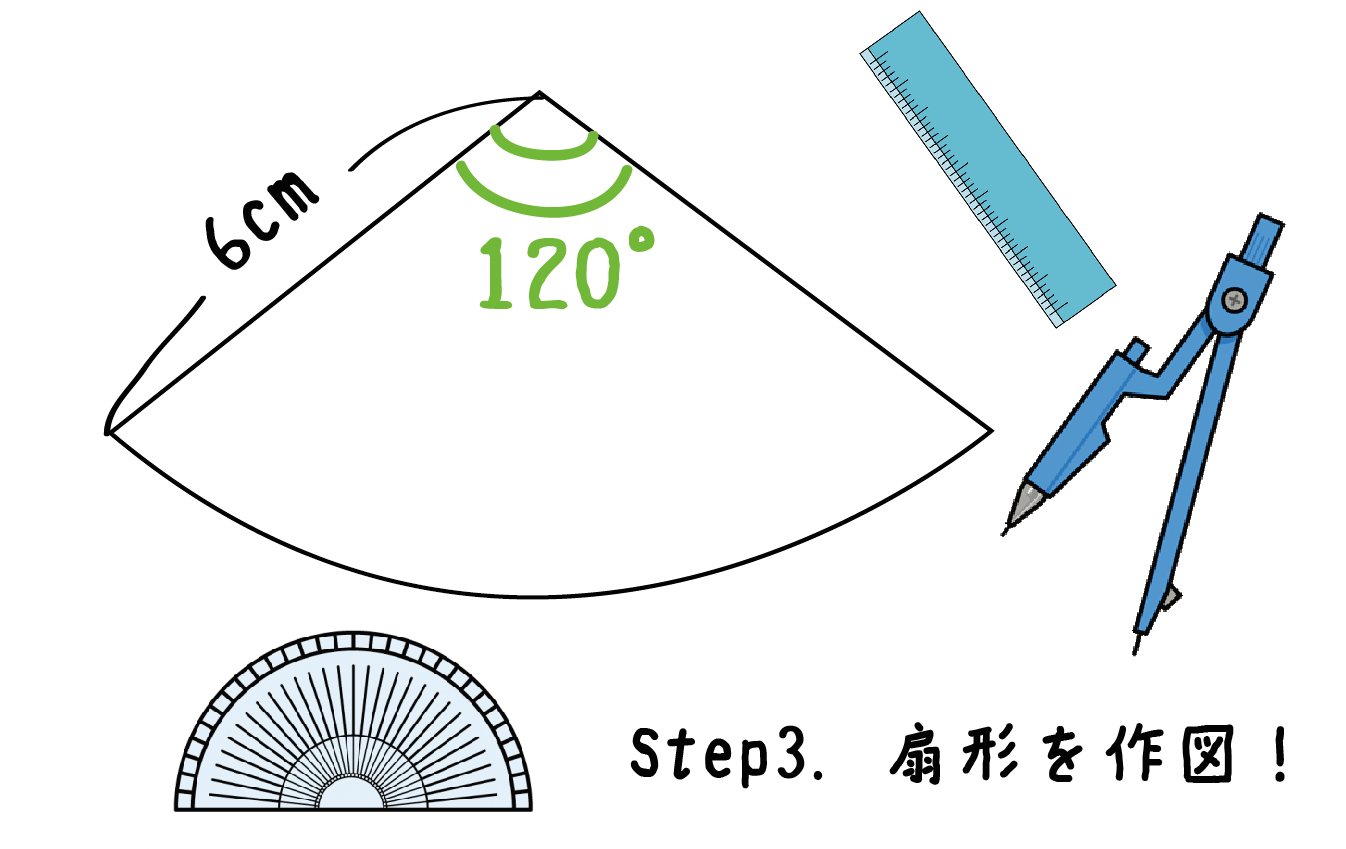
コンパスと定規、あわよくば分度器をつかってね。
例題でいうと、
中心角120°、半径6cmの扇形をかけばいいんだ。
いよいよ最後のステップだ。
さっきかいた扇形の展開図に、底面の円をのせてあげよう。 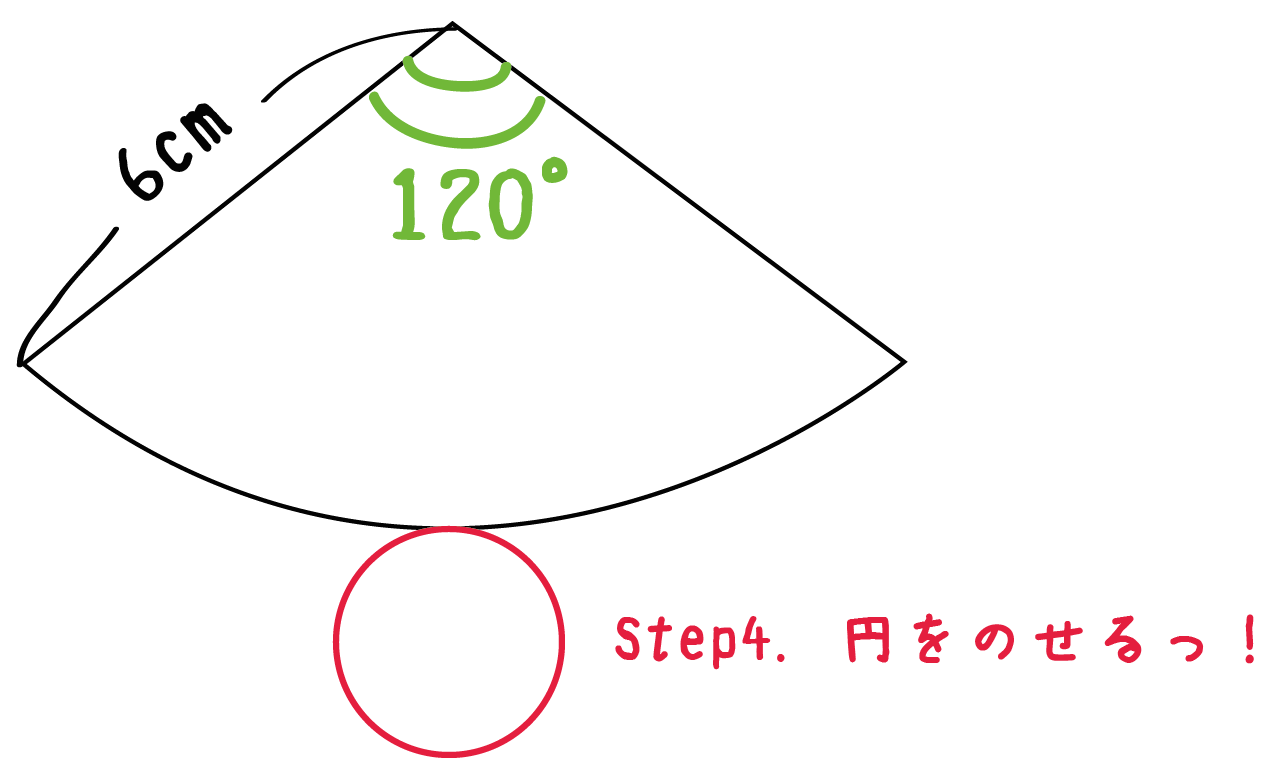
円をのせる位置は「扇形の弧の上」ならどこでもいい。ただ、美しい円錐の展開図を作図したかったら、
「扇形の中心の真下」に「円の中心」がくるようにする
といいよ。
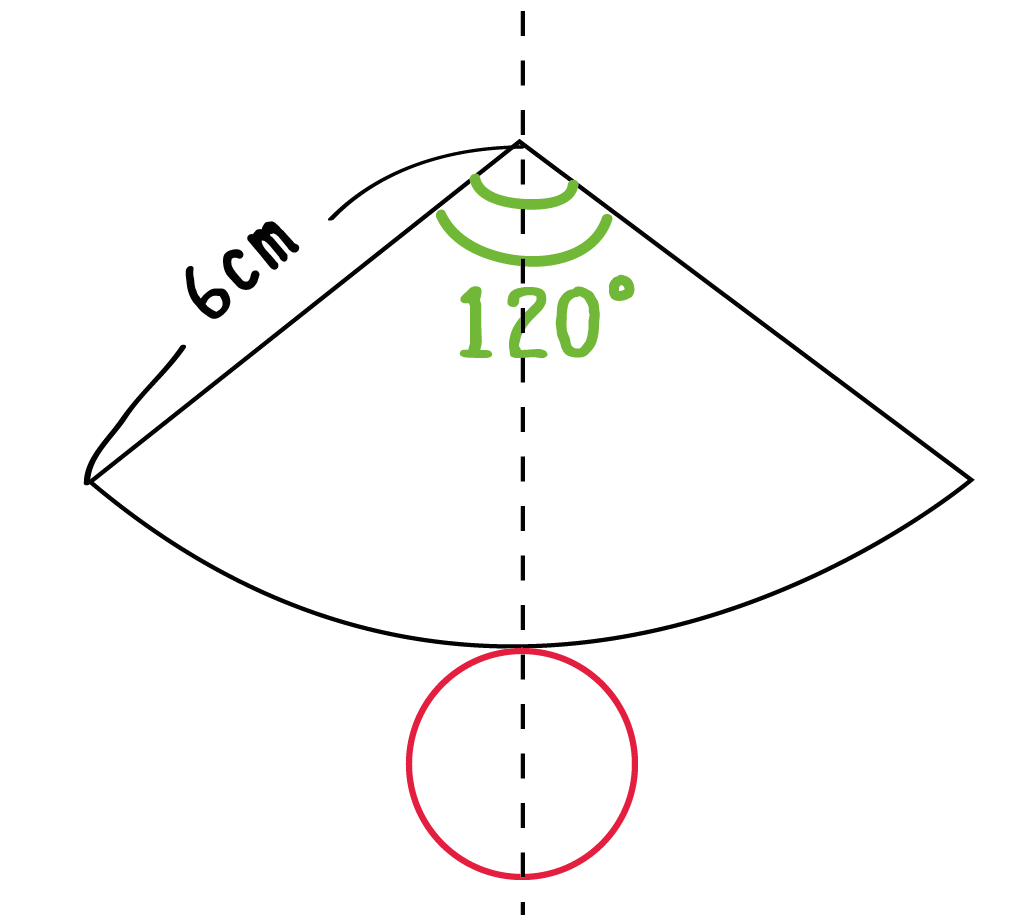
ただ、大切なのは位置よりも、
扇形と円が1点で接しているかどうか
ということ。
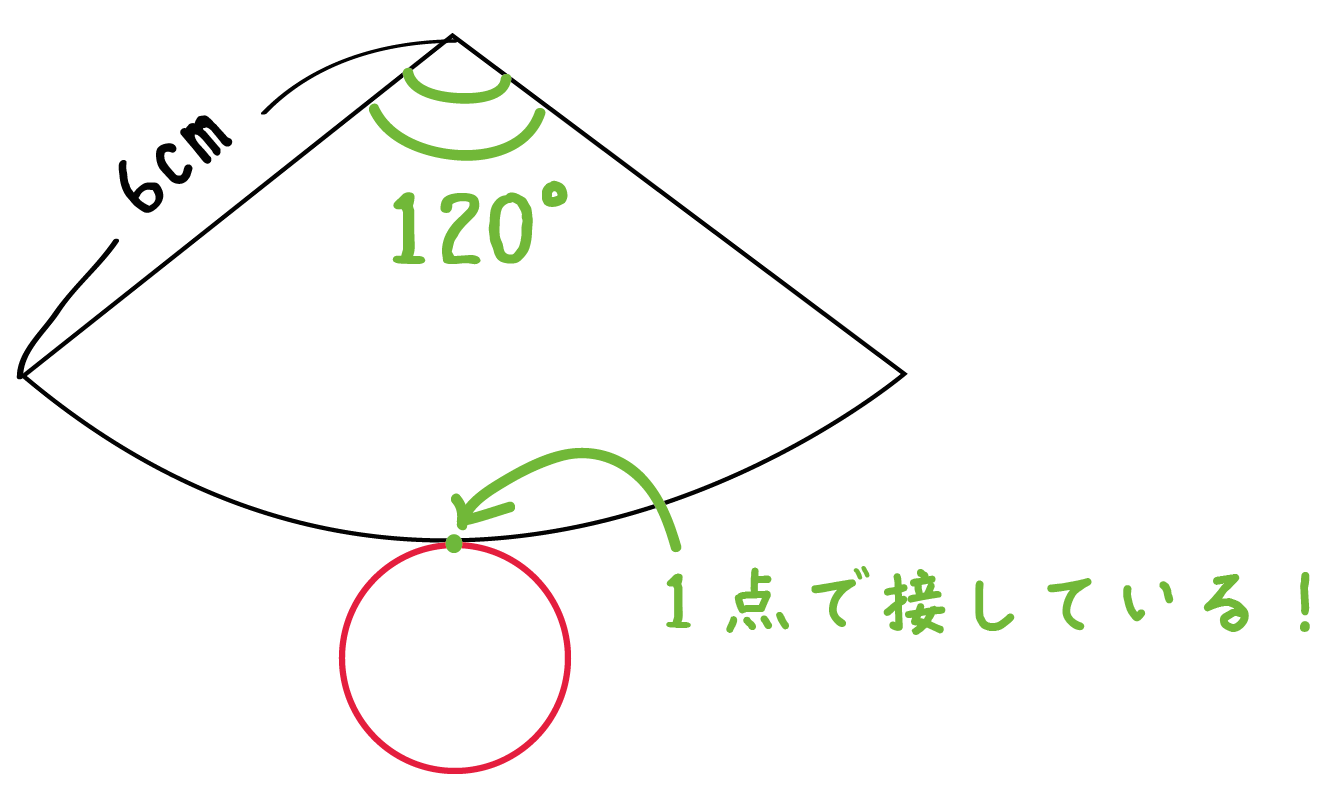
これは円柱の展開図の書き方でも触れたことだったね。
扇形に接している円になるようにしよう!
これで円錐の展開図は終了!
たったの4ステップでかけちゃったんだ。なかなかに簡単でしょ??
円錐の表面積を求める前に、展開図を作図できるようにしておこう!
そんじゃねー
Ken
こんにちは、この記事を書いてるKenだよー! 香港ケーキにはまってるよ。
立体の展開図の問題ってむずかしいよね??
立体をきりひらいた後、どうなるのか想像しないといけない。
これはマジで、ツラい。
展開図を作図するとチョコレートを食べたくなるねw

そこで、今日は、
3つのステップで「円柱の展開図の書き方」を解説していくよ。
円柱の展開図をかきたいときに参考にしてみてねー
円柱の展開図の書き方を紹介していくよ。
つぎの例題をみてみよう!
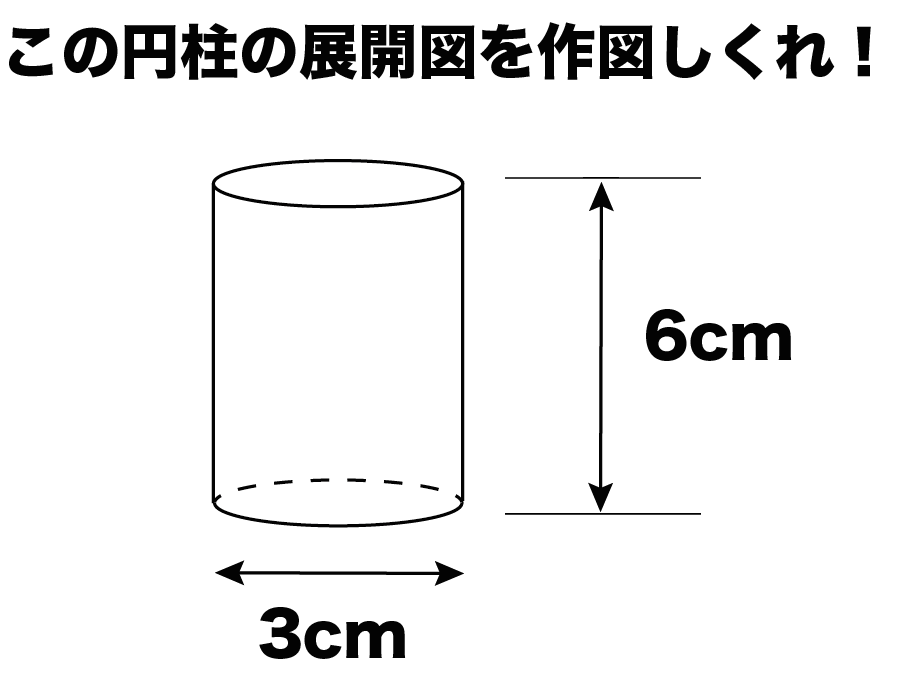
円柱の展開図は3ステップで作図できちゃうんだ。
円柱の底面は「円」だよね??
こいつの「円周の長さ」を計算しちゃおう!
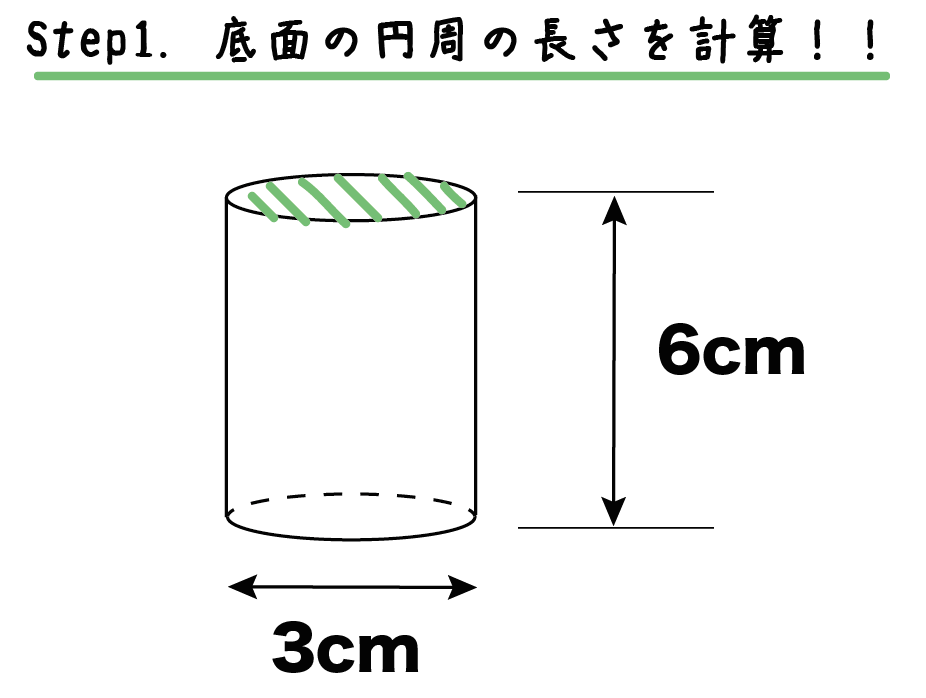
直径×円周率
だったよね?? だから、底面の「円周の長さ」は、

3π [cm]
になるよ!
つぎは、長方形をかいてあげよう。これは円柱の側面の展開図になるんだ。
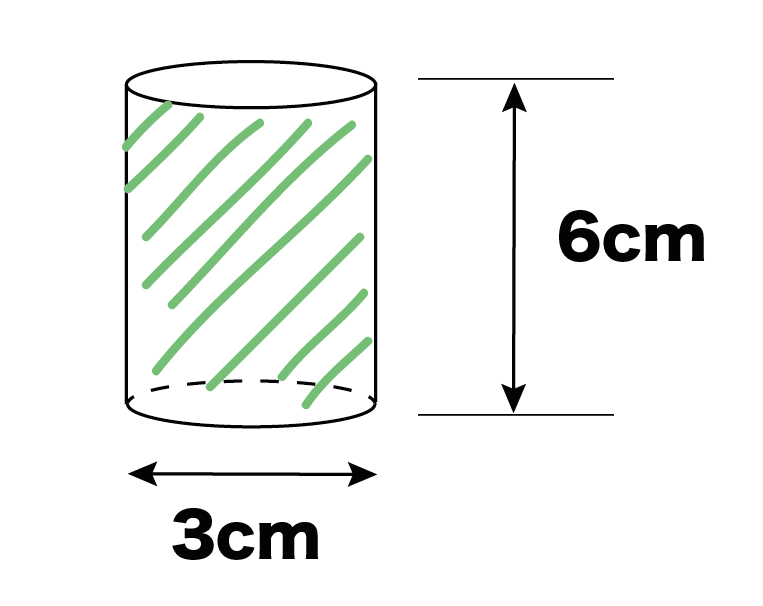
この長方形の横は「底面の円周の長さ」、縦の長さは「円柱の高さ」にしてあげよう。

さっきの例題でいえば、
円周の長さが「3π (≒9.42cm)」、円柱の高さが「6cm」だったね??

πを約3.14として作図してみるとこうなるよ。
あとは、長方形に円を2つ添えるだけ!
さっきの長方形のうえに、
ポンっと円を2つ上と下にかいてやればいいんだ。
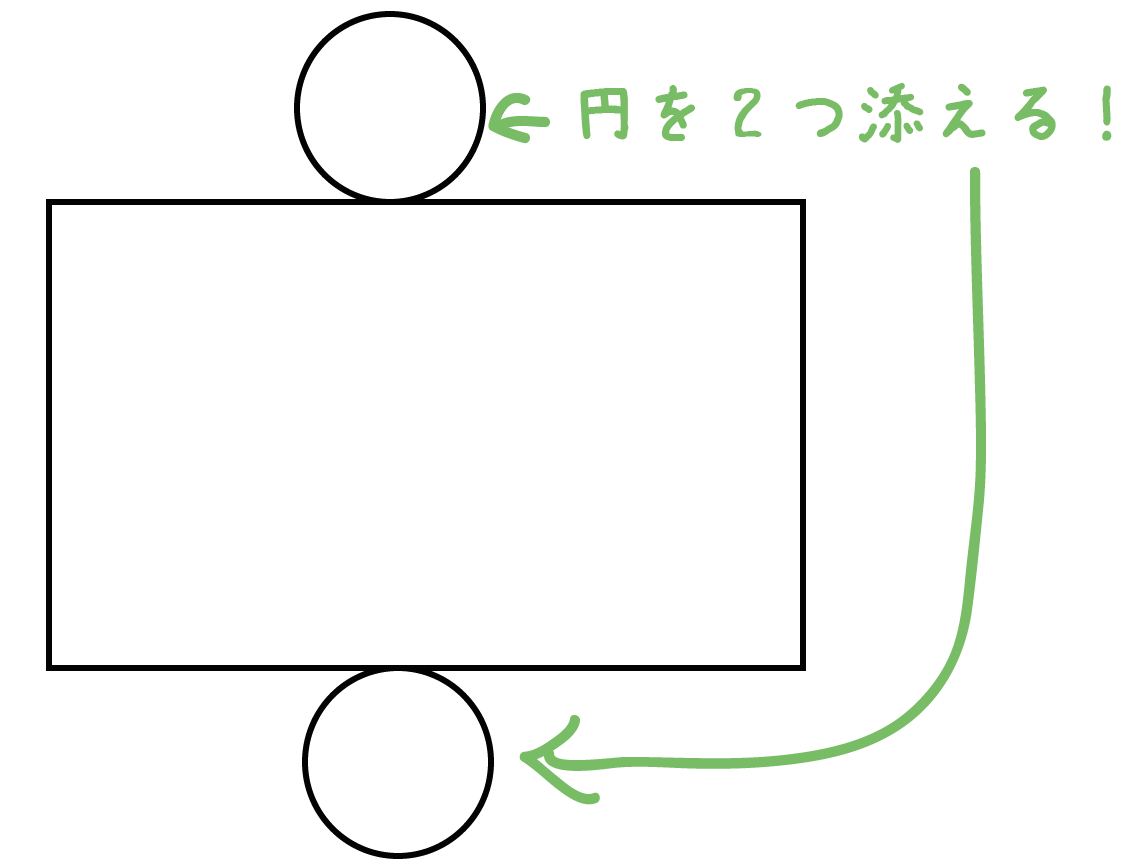
上の図みたいに、2つの円の位置が上下そろっていたほうがキレイ。
だけど、こんな感じで、ずらしも構わないし、
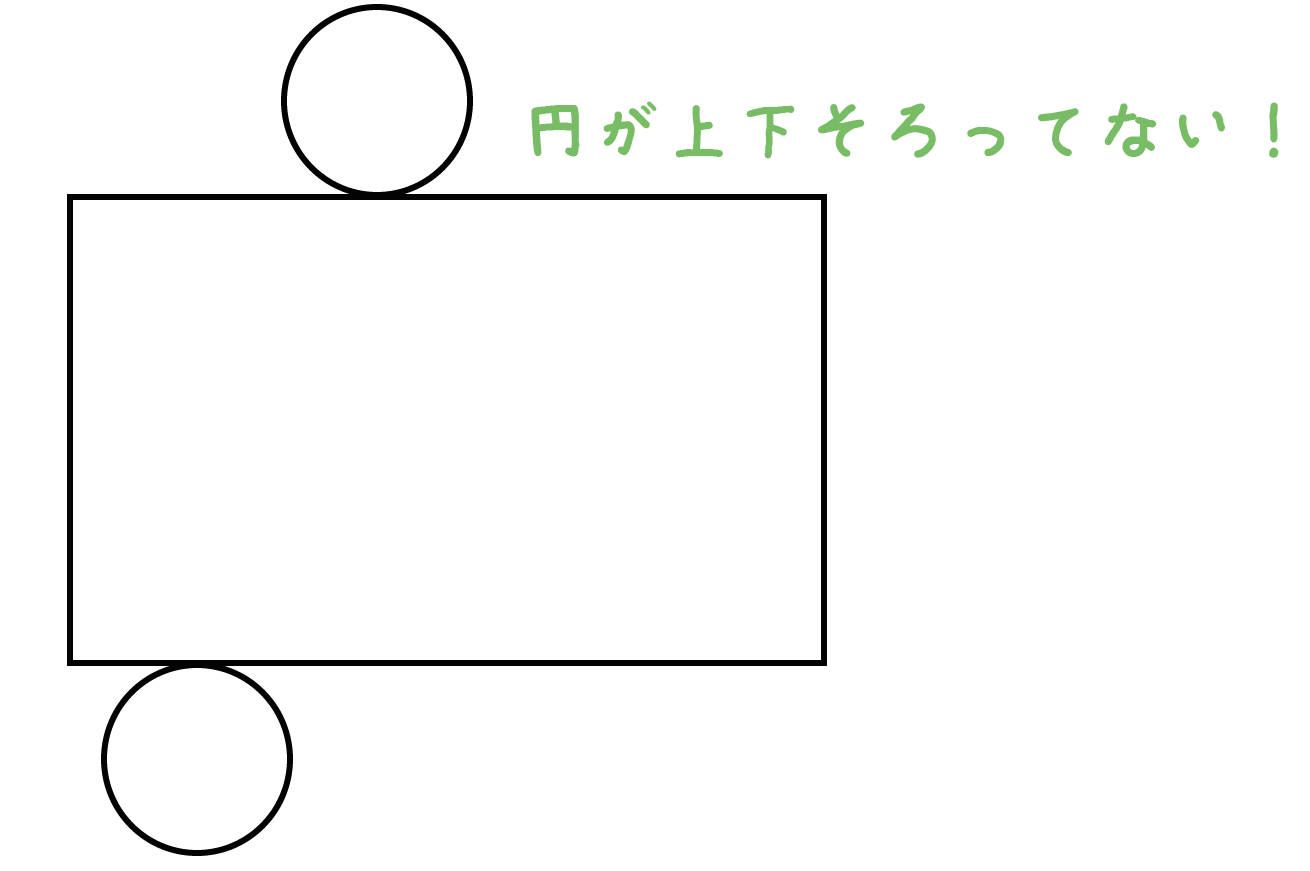
あえて両極端に円を配置してもいいんだ。
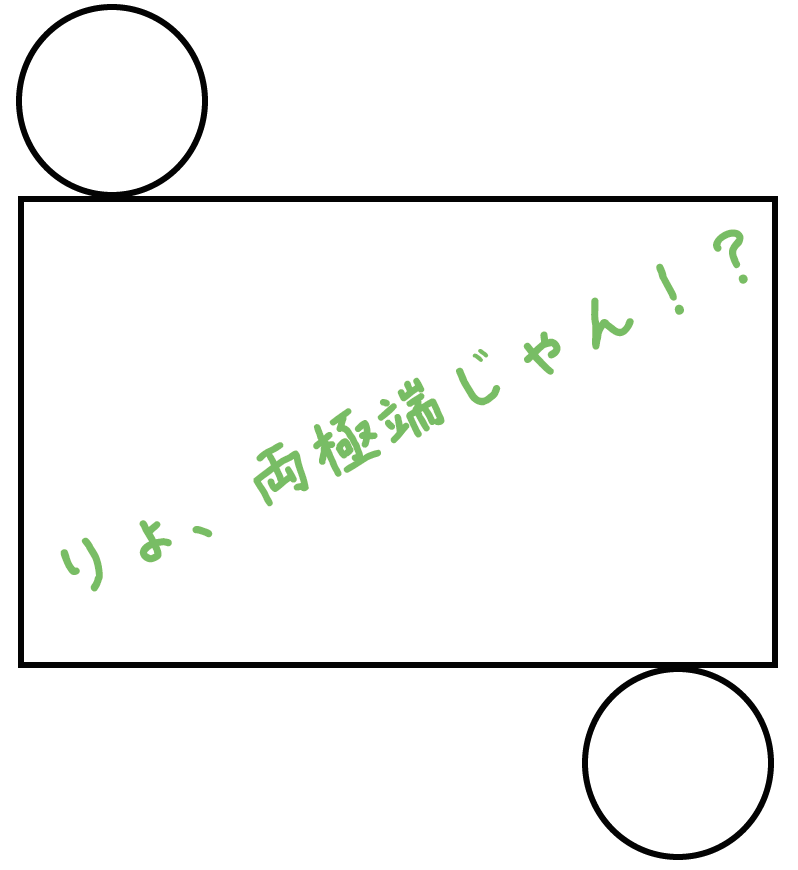
それより重要なのは、
「円」と「長方形の辺」が1点で「接している」ということなんだ。
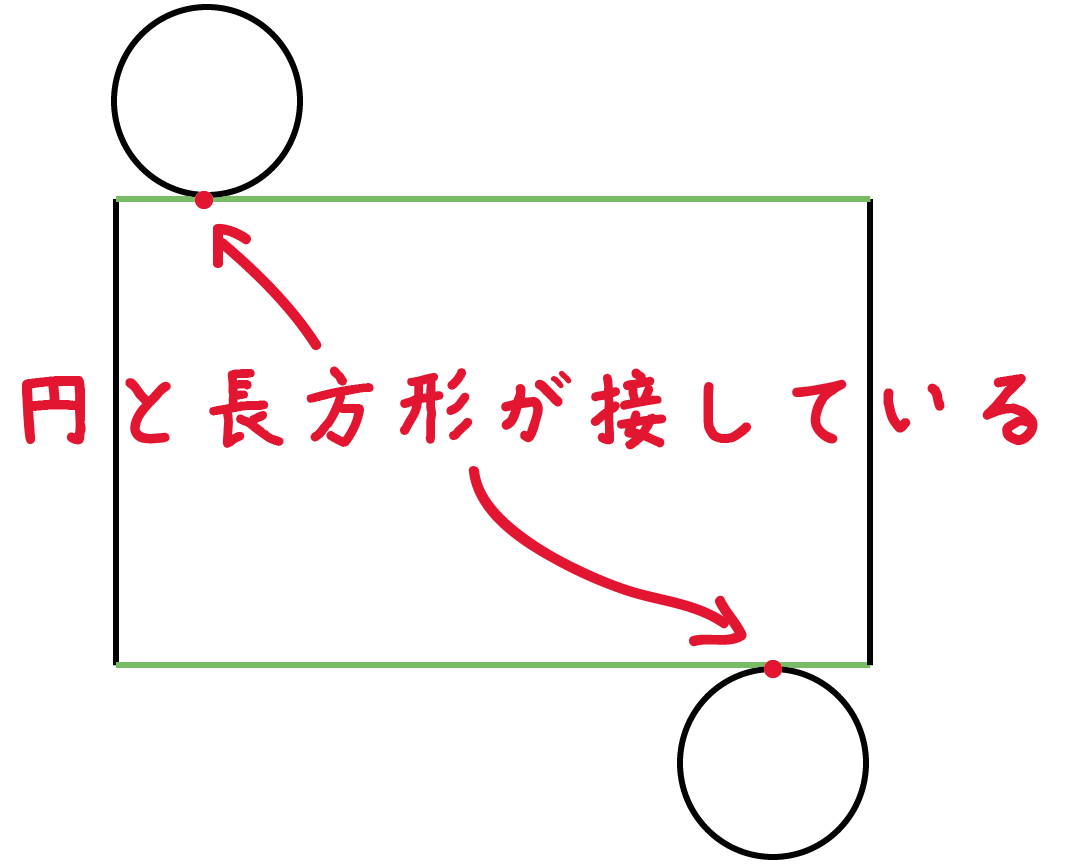
コンパスで接している円をかいてあげよう!
円柱の展開の書き方はオッケーかな??
の3ステップだったね。
展開図のかきかたをマスターしたら「円柱の表面積の求めかた」もついでに習得してみよう。
そんじゃねー
Ken
こんにちは、この記事をかいてるKenだよ。ベンチプレスにはまってるね。
中1数学の空間図形をいよいよ勉強していくよ。ここではおもに、
3次元の立体の図形
について学習していくんだ。
いままで二次元の図形とたたかってきたよね。これからは立体図形を相手にしていくんだ。
おっしゃああ!!
って気合いで教科書を読んでいると、
とにかく、
「立体図形の名前とか種類」が多すぎっ!!!
って思わない??

だから、今日は、
中1数学の「空間図形」に登場する立体の種類・名前10のまとめ
っていう記事をかいてみたよ。「立体の名前」を整理したいときに参考にしてみて。
〜もくじ〜
まず押さえておきたいのは、
球(きゅう)
という立体だ。

「球」とは算数用語集によると、
空間において,ある定点から等距離にある点の集まりを球といいます。
ってあるね。
つまり、球の中心から360°距離の等しい点をあつめまくった立体ってことだね。だから、中心から球の表面までの距離はすべて等しいよ。
ちょっと分けわかんないときは、「球」を丸いボールと思っちゃえばいい。

うん、そこらへんに転がっている「野球ボールみたいな立体」さ。
つづいては、
名前に「柱(はしら)」がつく空間図形だ。
通称、柱系の立体図形さ。
柱系の立体図形は、ただ単にそこらの「柱」と似ているってだけじゃない。
「2つの底面」が同じ形をしていて、なおかつ、「側面の図形」が四角形である立体のこと
なんだ。
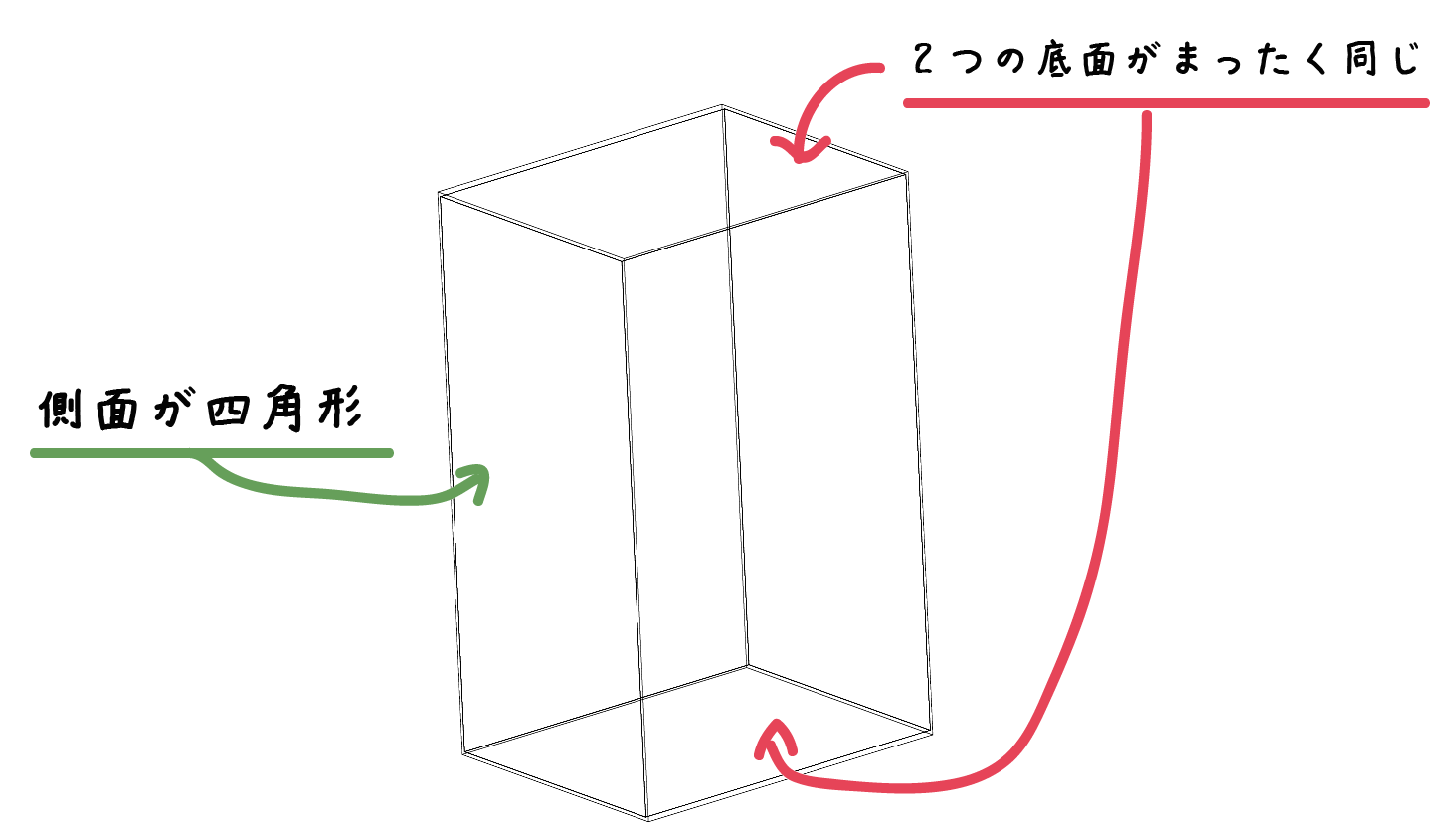
この種類の立体には、ゼッタイに、
柱(はしら)
っていう文字がついてる。
だけど、立体の名前では「チュウ」って読むから気をつけてね。
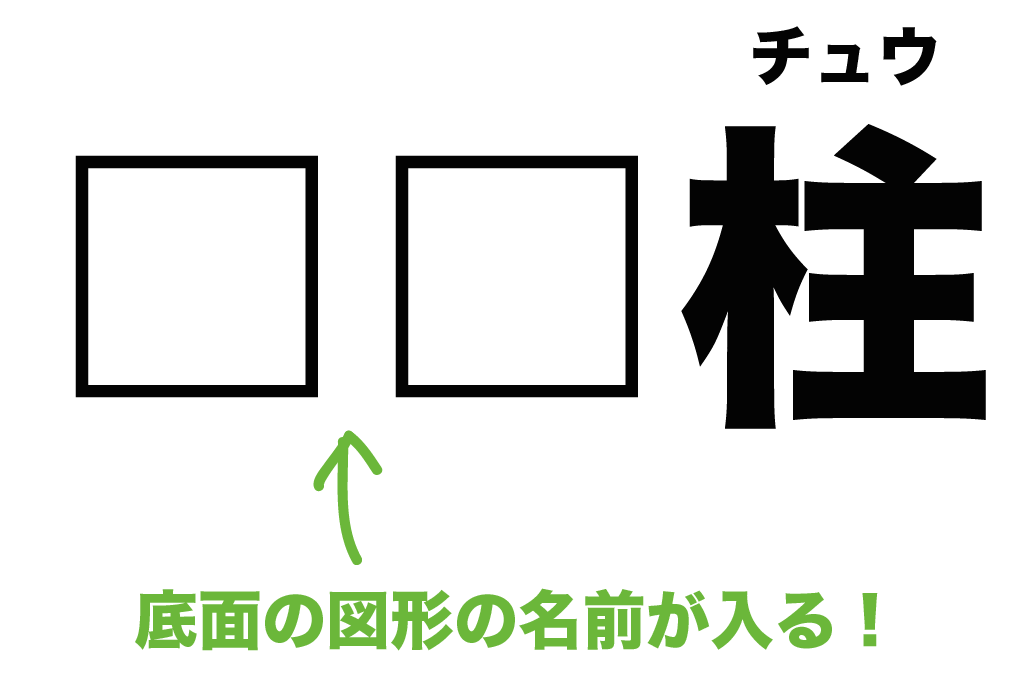
柱の前には「底面の図形」の名前が入るんだ。
底面の図形の種類によって、立体の名前が変わってくるってことだね。
そんで、「柱系の立体」には大きく分けてつぎの2つの種類の立体があるよ。
底面が多角形のもの
を「角柱」とよんでいるよ。
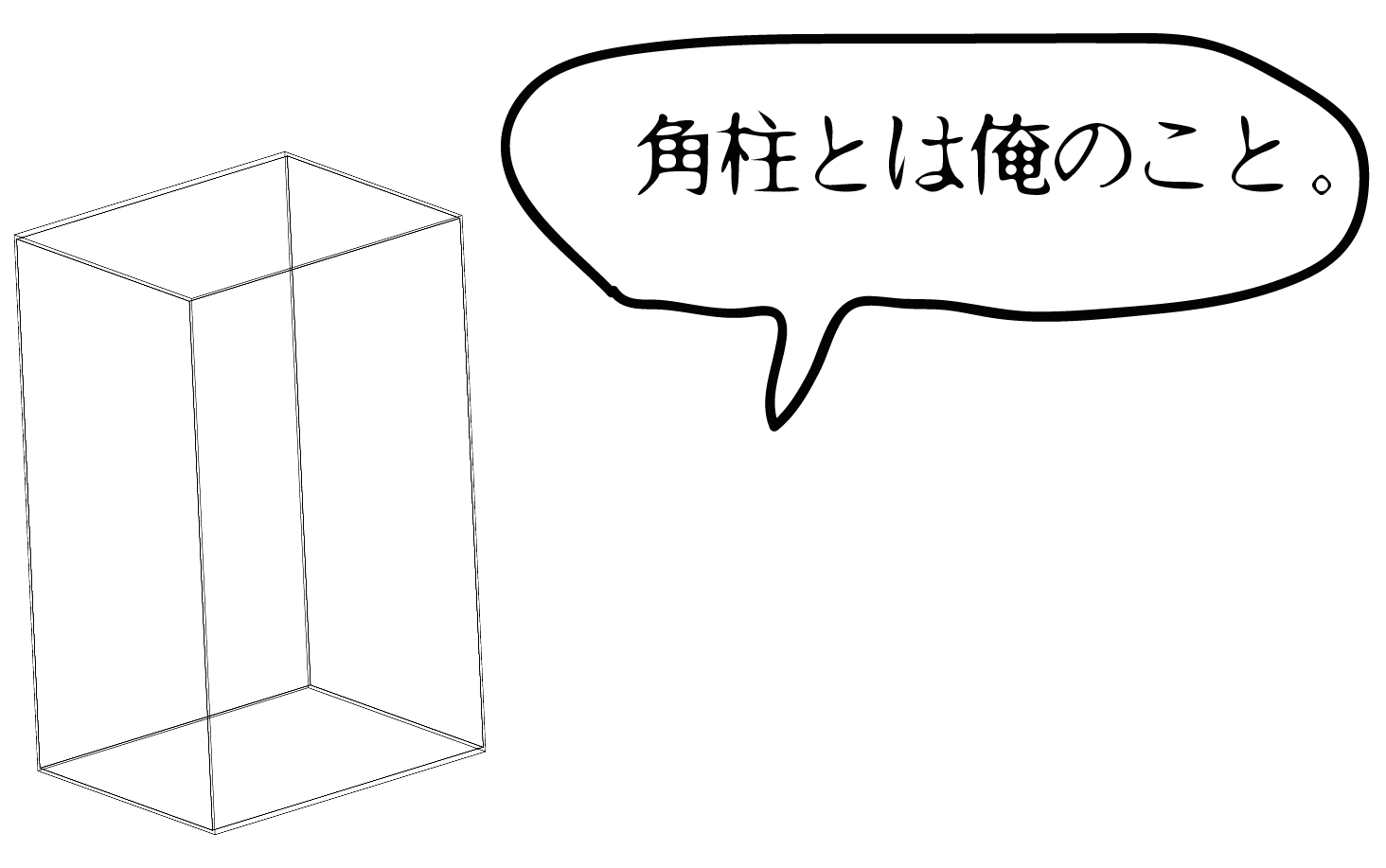
この「角柱」にもいろいろな種類のやつがいる。その角柱の名前は、
底面の多角形が「何角形になるか」で変わってくるんだ。
たとえば、
・・・・などなど。
そんで、もし、底面の辺の長さがすべて等しい場合、角柱の名前のまえに「正」がつくんだ。
たとえば、正三角形を底面とする角柱は、
「正三角柱」になるよ。
底面が「円」のときは「円柱(えんちゅう)」って呼ばれるんだ。

あれ?? 側面が四角形じゃなくない??
って思うかもしれないね。だけれど、こいつを切りひらいてやると、
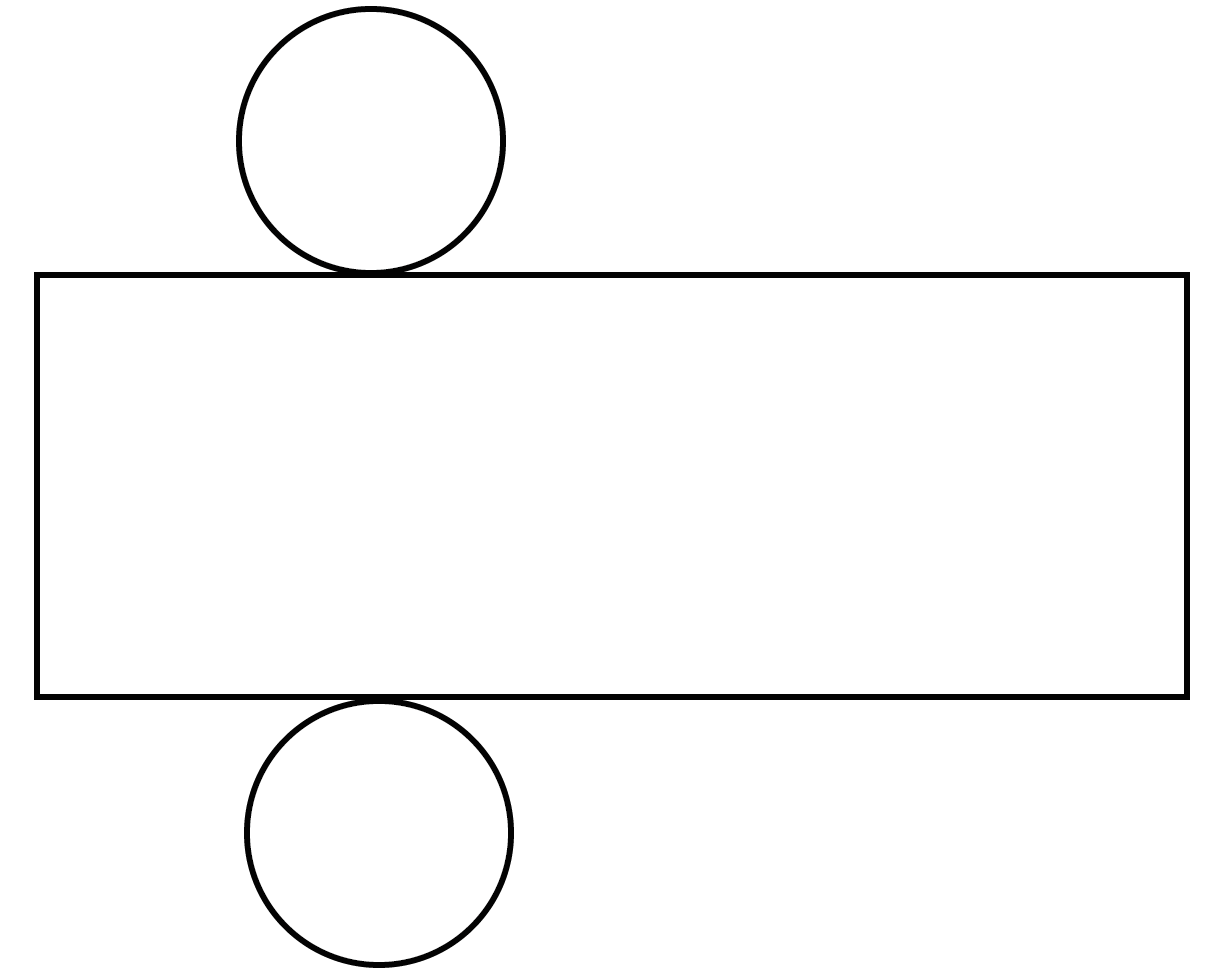
側面が長方形になっていることがわかる。
こいつはまぎれもない「柱系の空間図形」だ!
つづいては「錐系の立体図形」たちだ。
「錐(きり)」といえば、工具の一種。先端が尖っているアイツだね。

錐系の立体図形は、
底面が1つしかなく、底面の逆側は頂点の1点で交わっている立体
のことだ。
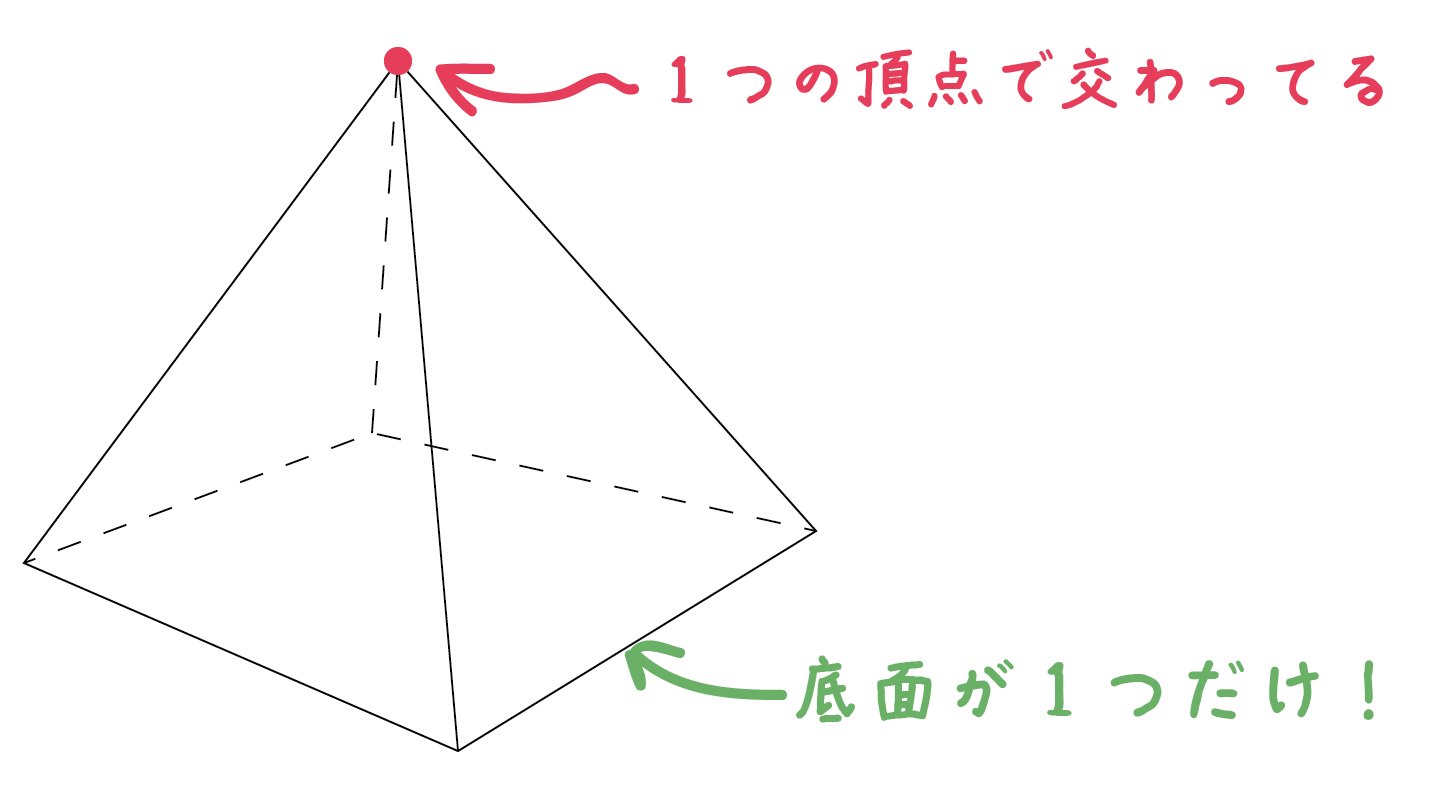
そして、「錐系の立体図形」の名前にはかならず「錐(すい)」が入ってるよ。
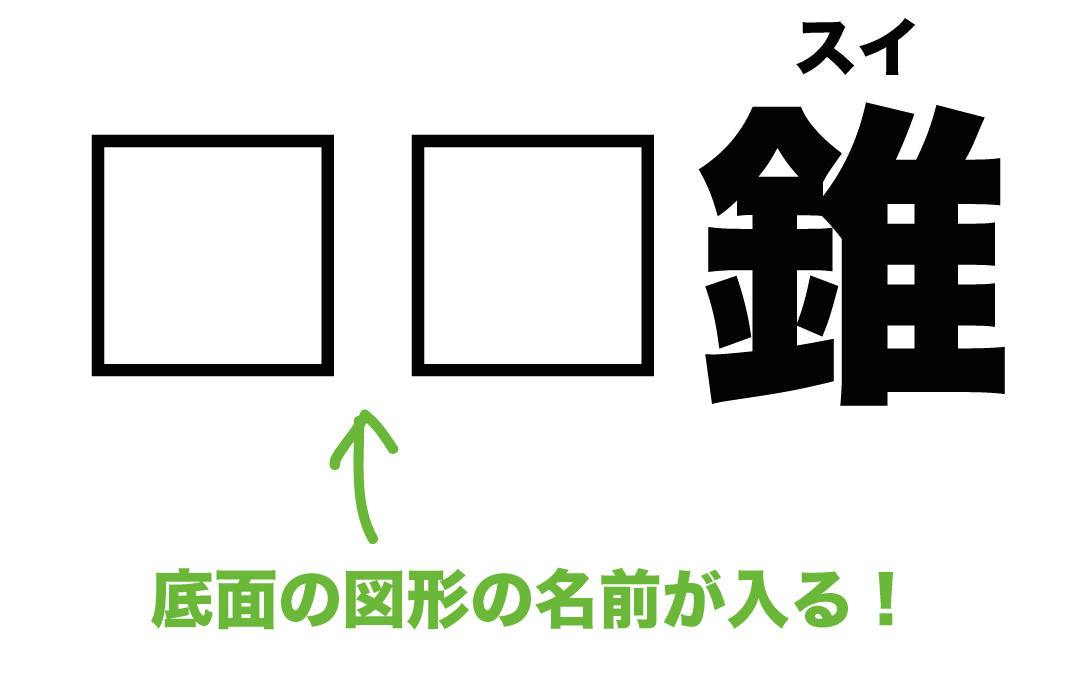
柱系の立体とおなじく、「錐」の前には「底面の図形の名前」をいれていくんだ。
これによって、立体の種類が変わってくるよー
それじゃあ、具体的な「立体の名前」をみていこう。
「底面が多角形になっている錐系の立体」を「角錐」っていうんだ。
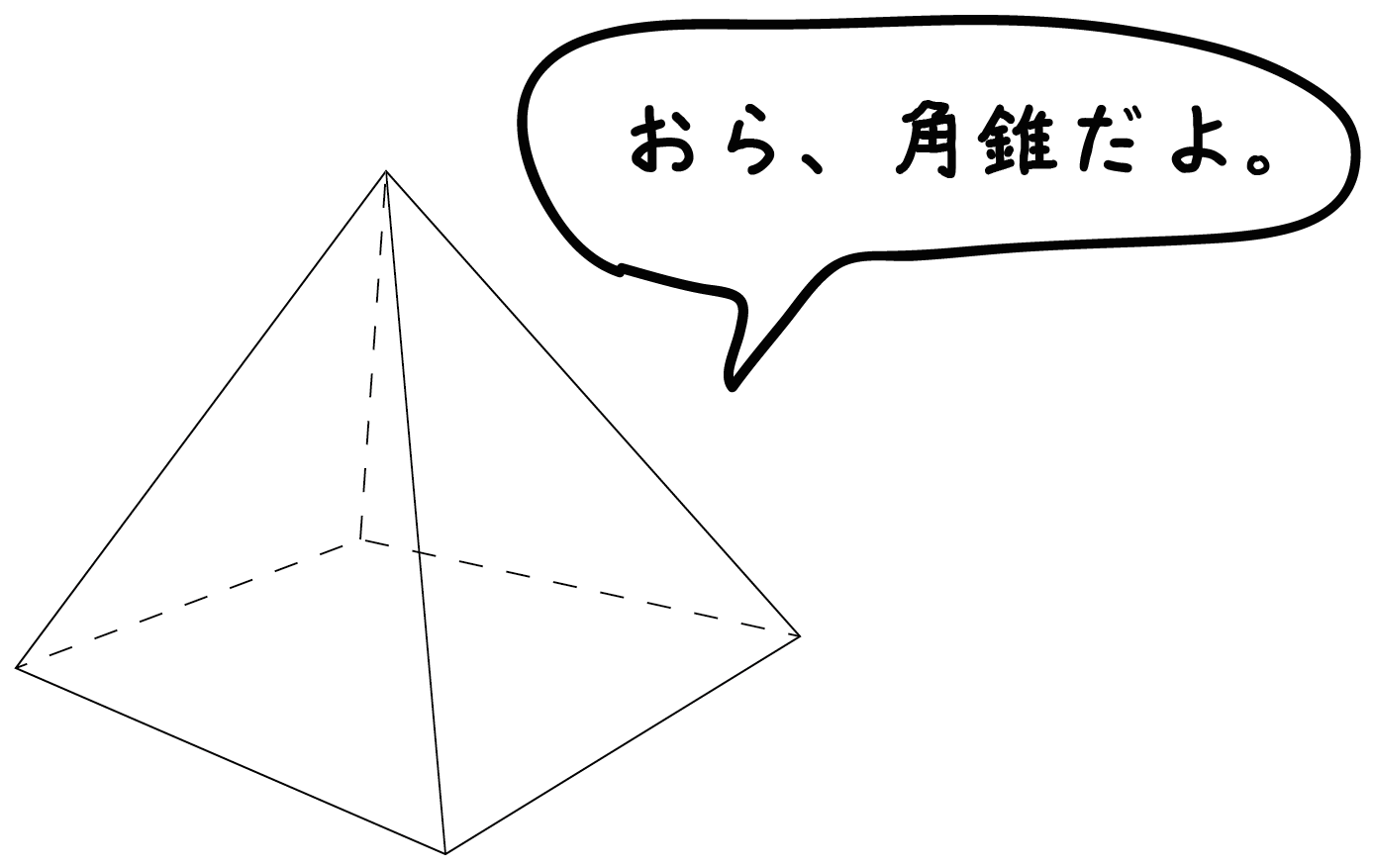
これは角柱と同じで、
といったように、底面の図形の名前が「錐」の前につくだけだよ。
それで、底面の辺の長さがすべて等しかったら、「正」という文字がつけられるんだ。
たとえば、「底面が正三角形の角錐」だったら「正三角錐」になるよー
円錐は「円」が底面になっている「錐系の立体」のことさ。

よく工事現場においてあるコーンなんかがそれにあたる。

この立体は表面積や体積をもとめる問題として狙われやすいよ。
十分に注意しておこう!
錐系の立体の「頂点」をスパッと切り落とした立体だ。
底面に平行にきってあげたあとに残る立体のことをさすんだ。これには、
の2種類がある。
角錐を底面に平行にスパッと切ったものを「角錐台」、円錐の場合は「円錐台」になるんだ。
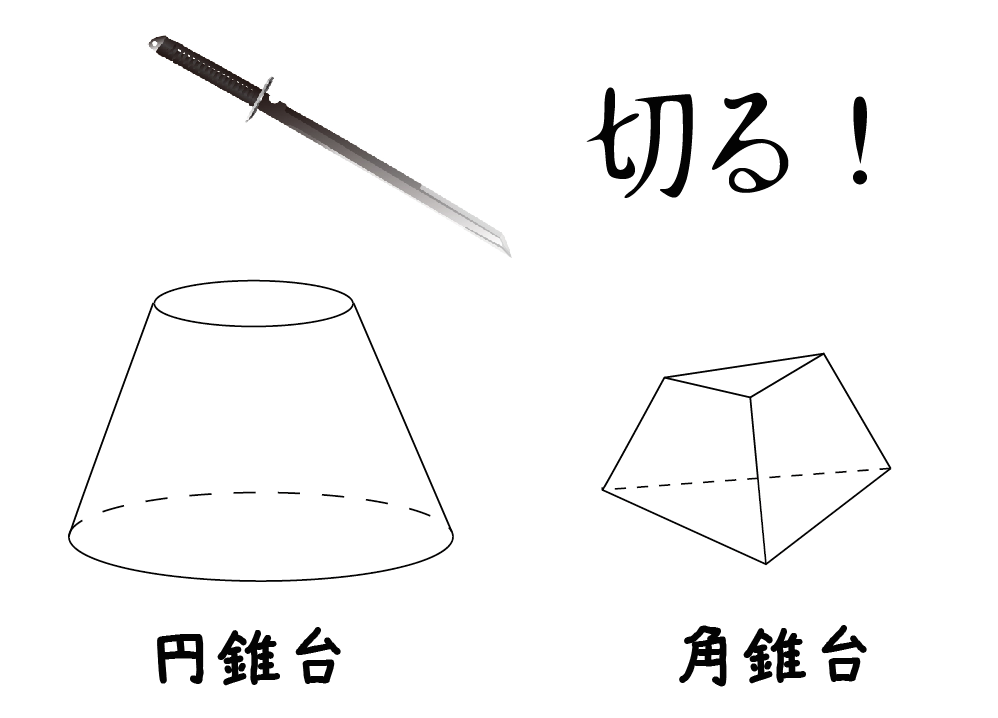
名前のうしろに「台」をつけるだけだね。
さて、最後の立体の種類「正多面体」の紹介だ。正多面体とはコトバンクによると、
各面がすべて合同な正多角形で、各頂点に同数の面が集まる多面体。
とあるね。
多面体とはすべて平面でできた立体のこと。その多面体をつくる「辺の長さがすべて等しい」ってわけだね。
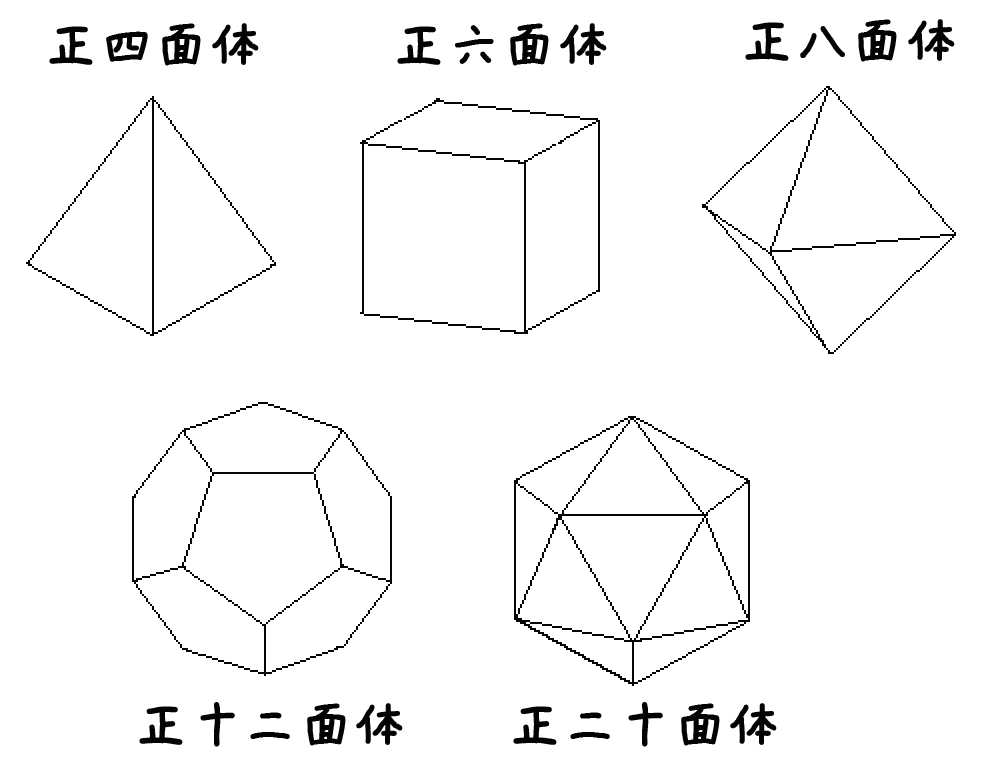
正多面体にはつぎの5種類しか存在していないんだ。
正多面体ネタはたまーにテストで狙われるよ。気をつけてっ!
ここまでみてきた立体の名前をぜんぶ覚えなくても大丈夫。
だいたいどんな立体の種類があったか、ってことをチラ見しておいてね。
さあ、これから空間図形を勉強していくよー!
そんじゃねー
Ken
こんにちは、この記事をかいてるKenだよー! ボタンを掛け違えてちまったね。
円の接線って知ってる??
「直線と円が一点で交わっていること」を「接する」っていって、
さらに、その直線のことを「接線」、直線と円がまじわっている点のことを「接点」とよぶんだったね。
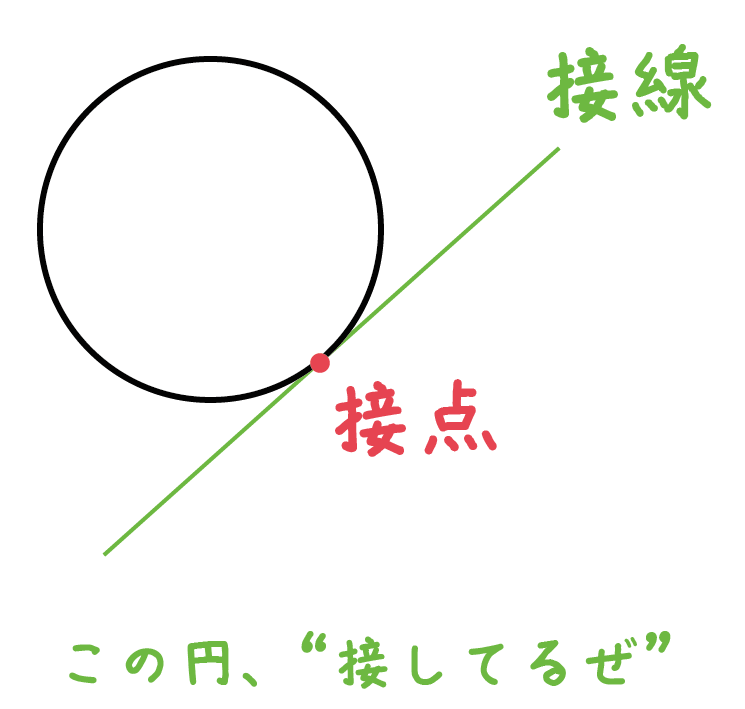
今日は、この「円の接線」の作図方法を解説していくよ。テスト前に確認してみてね。
~もくじ~
「円の接線の作図」ってヤッカイそうだよね???
だけど、コイツらは意外にシンプル。
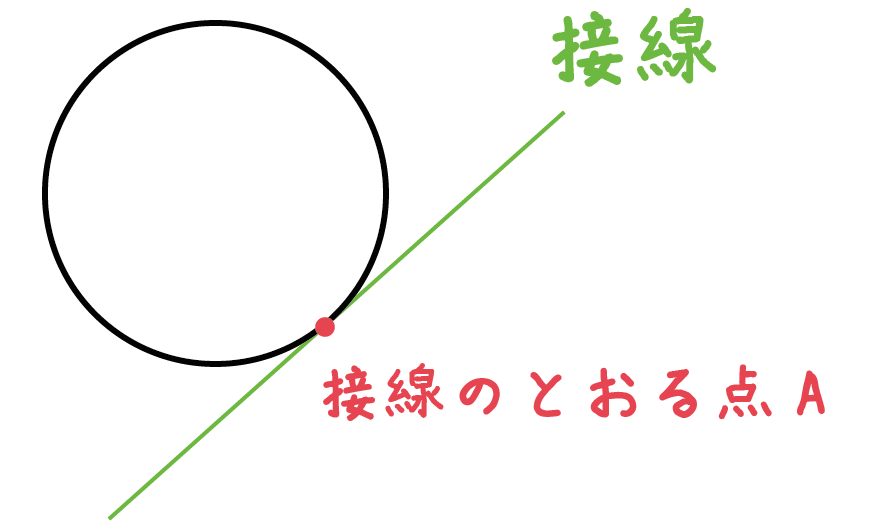
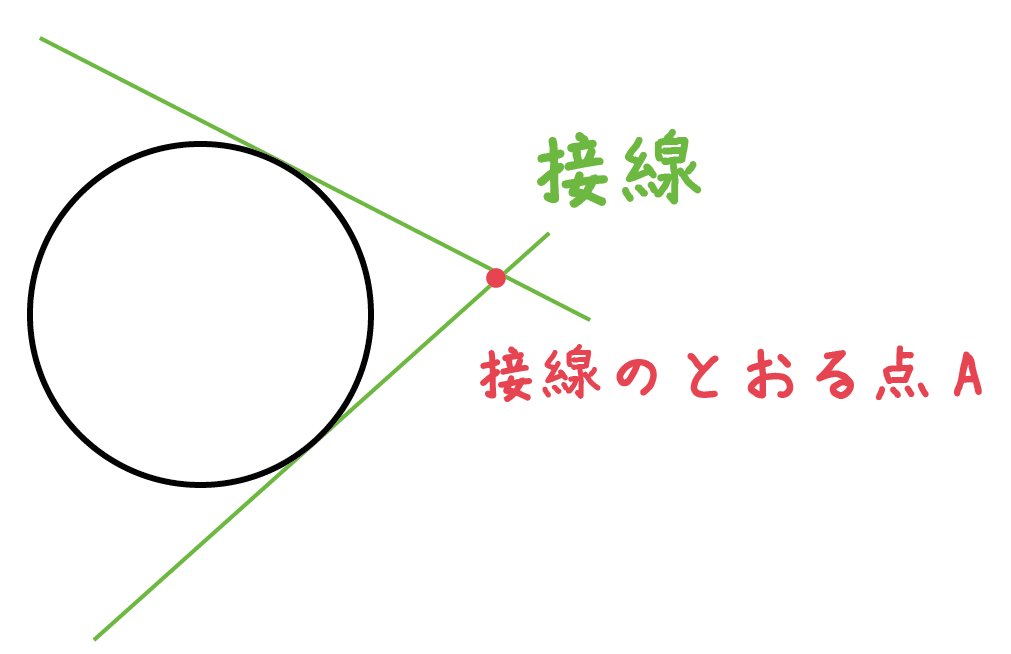
だいたい2つの種類にわけられるるんだ。「接線が通る点」の位置がちょっと違うだけさ。
「円周上の点」を通る接線の作図では1本の接線、
「外部の点」をとおる作図では2本の接線をひくことができるよ。
今日は2つの作図方法を確認していこう。作図のために必要なアイテムは、
だよ。準備はいいねー??
「円周上の1点をとおる」円の接線の作図からだね。
これは教科書にものっている基本の作図方法さ。
例題で作図をじっさいにしながら確認していこう。
例題。
点Aが接線となるように、この円の接線を作図しなさい。
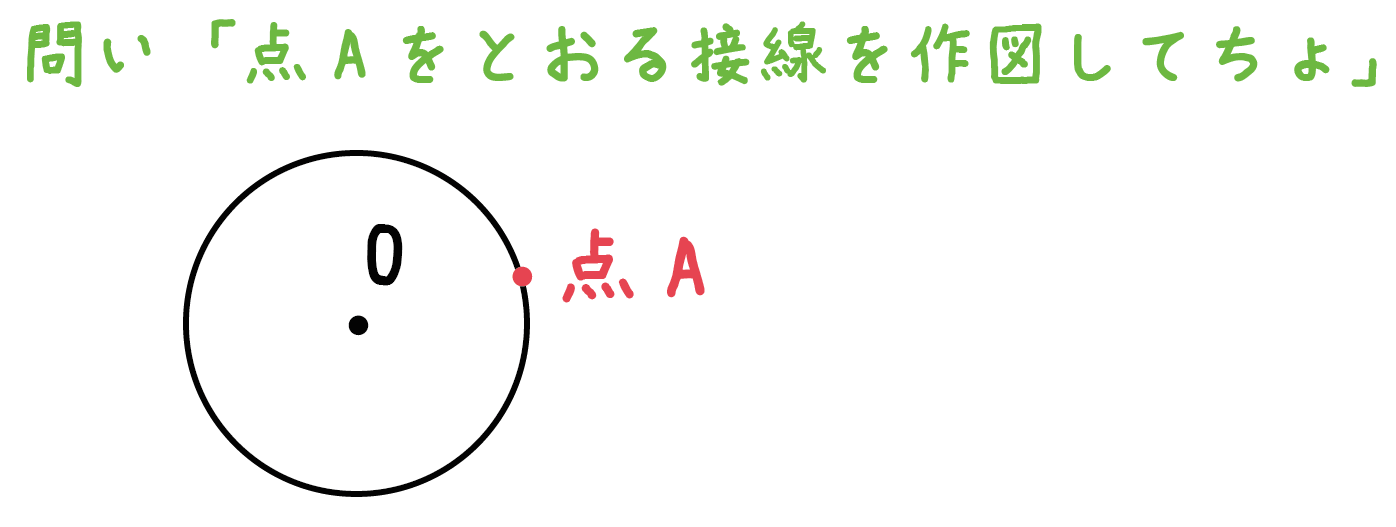
作図方法はたったの2ステップなんだ。
「円の中心」と「接線が通る線」で直線をかこう!
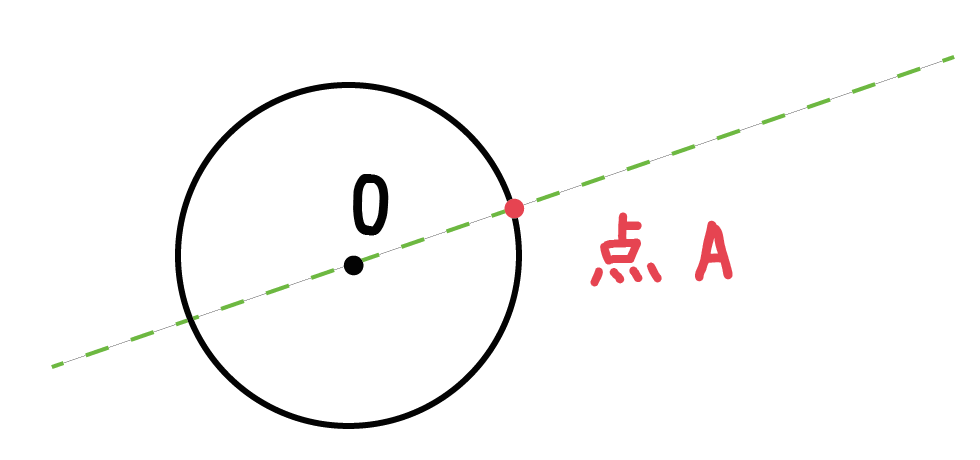
例題でいうと、「点O」と「点A」を定規でむすぶだけ。
線分じゃなくて直線でいいよー
さっきの直線の垂線を作図してみよう。
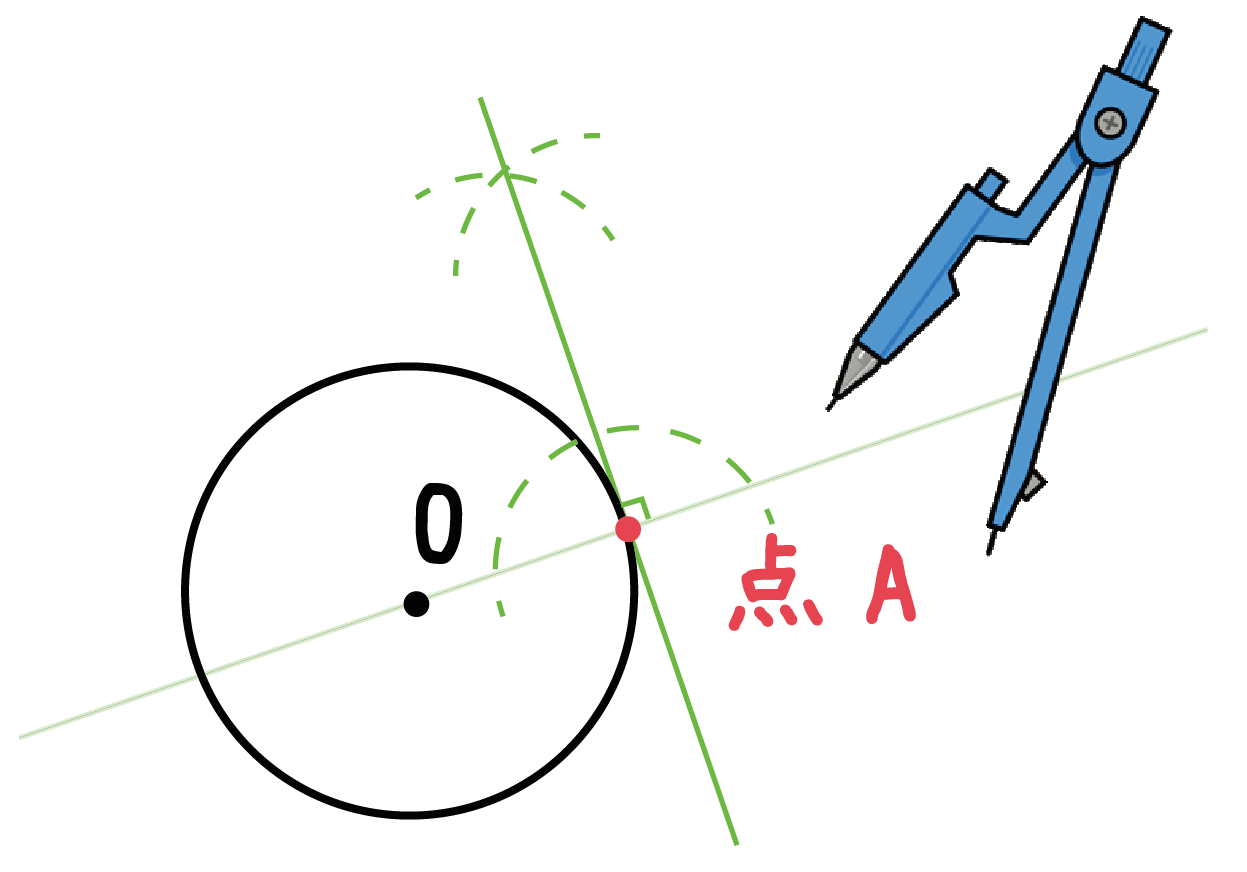
垂線の書き方を参考にして、「点Aをとおる直線OAの垂線」をかいてみよう。
コンパスをガンガン使っちゃってくれ。
この垂線が「円Oの接線」だよ!
ってことは作図終了だ!!おめでとう。
なぜ、垂線を作図するのかというと、
円の接線の性質のひとつに、
円の接線は、その接点を通る半径に垂直である
っていうものがあるからさ。
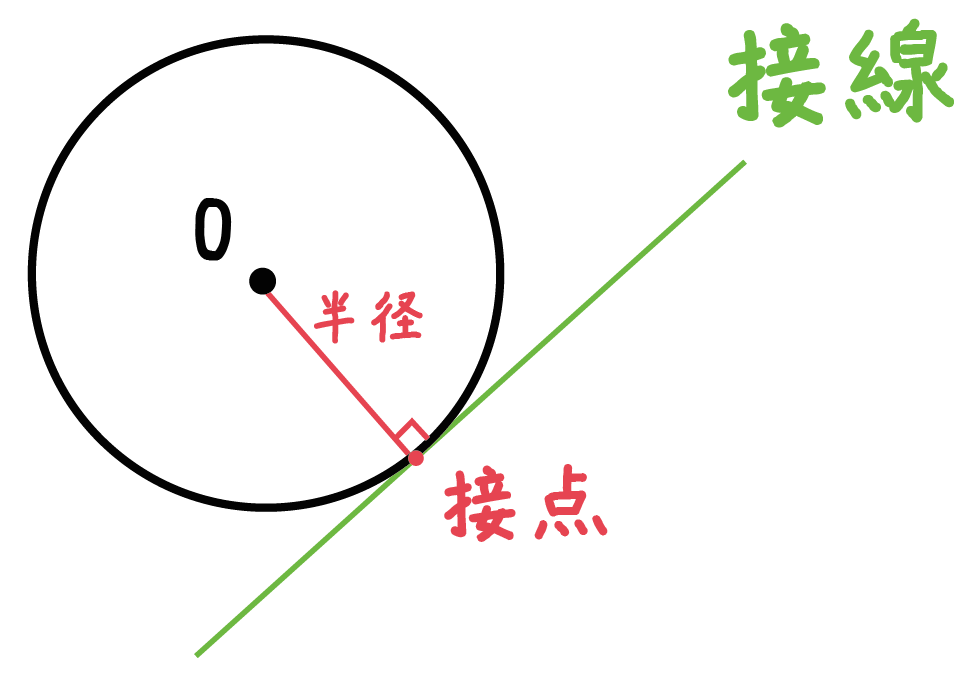
だから、円周上の点Aをとおる「線分OAの垂線」をひいてやれば、それは接線になるんだ。
つぎは2つ目の「外部の点をとおる作図方法」をみていこう。

例題をみながら解説していくよ。
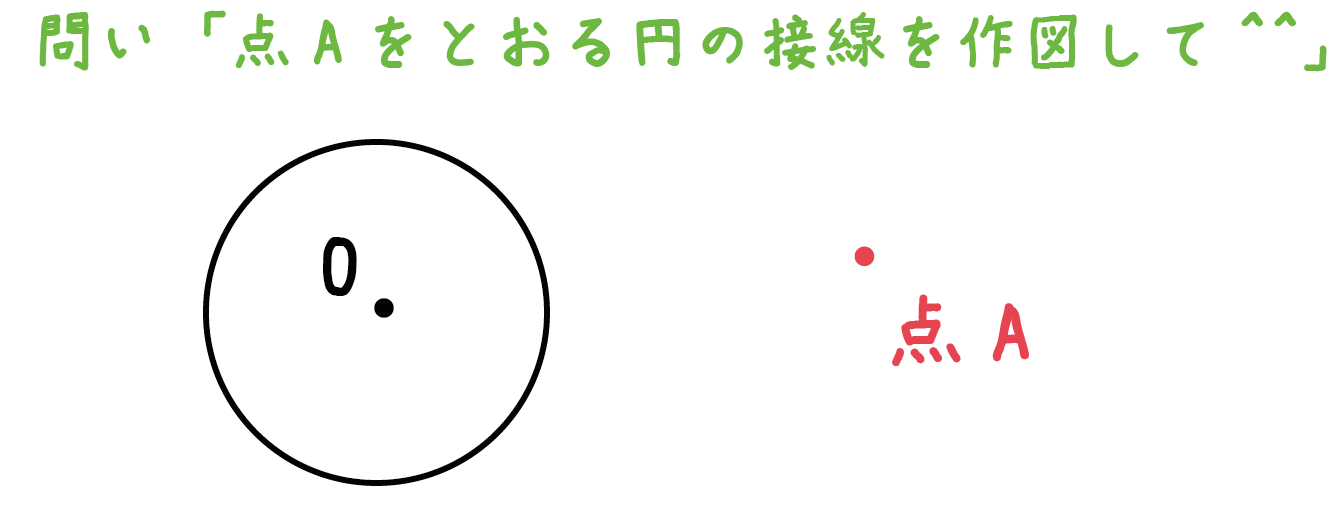
例題
点Aをとおる円Oの接線を作図してください。
つぎの5ステップで作図できるよー
「円の中心」と「外部の点」をむすんでみよう。
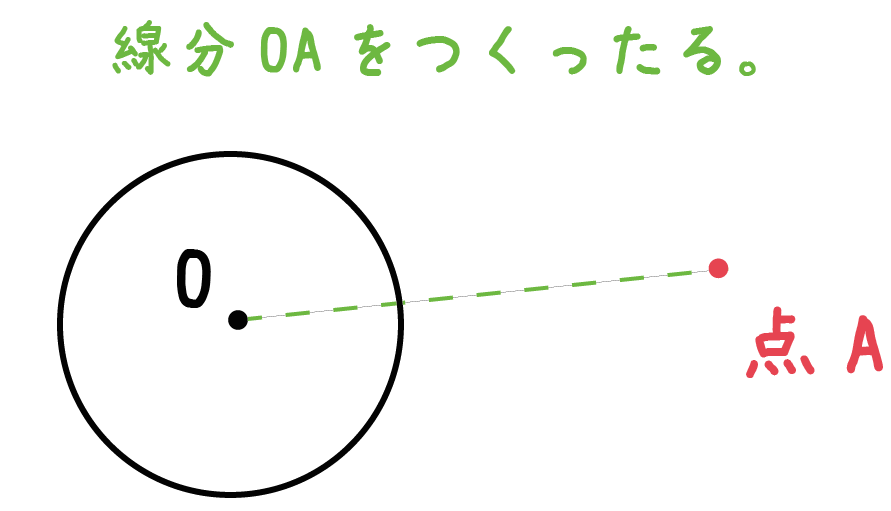
例題では、点Oと点Aだね。
こいつらを定規をつかってゴソっと結んでくれ!
「円の中心」と「外部の点」をむすんでできた線分があるでしょ??
今度はそいつの「垂直二等分線」をかいてあげよう。
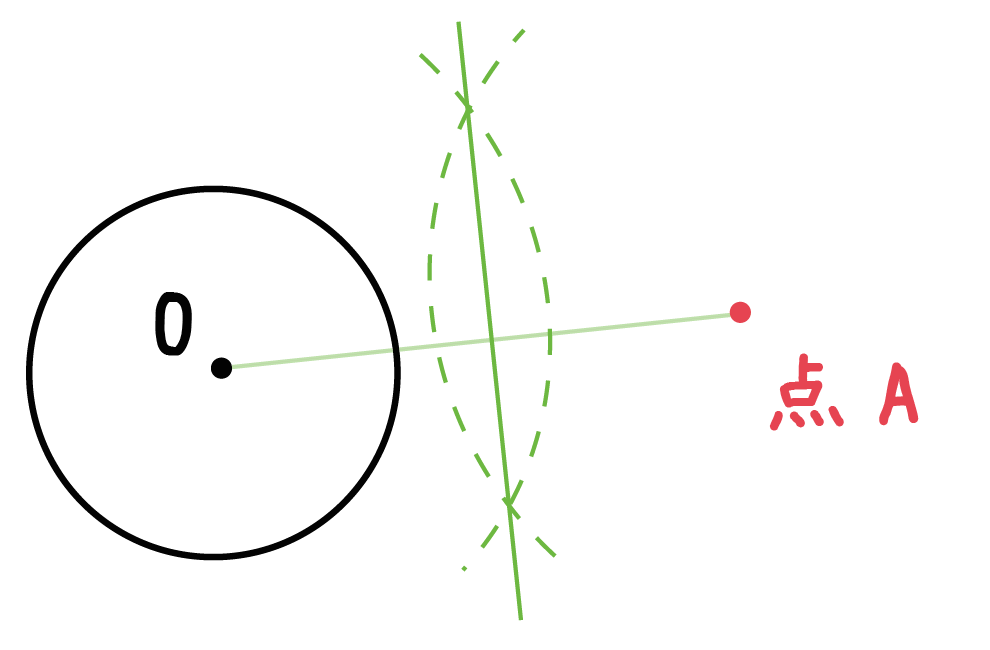
書き方を忘れたときは「垂直二等分線の作図」の記事を復習してみてね。
垂直二等分線をかいたのは、
線分の中点をうつためだったんだ。
垂直二等分線は、線分を「垂直」に「二等分」する線だったよね。
ってことは、線分との交点は「中点」だ。
せっかくだから、この中点に名前をつけよう。
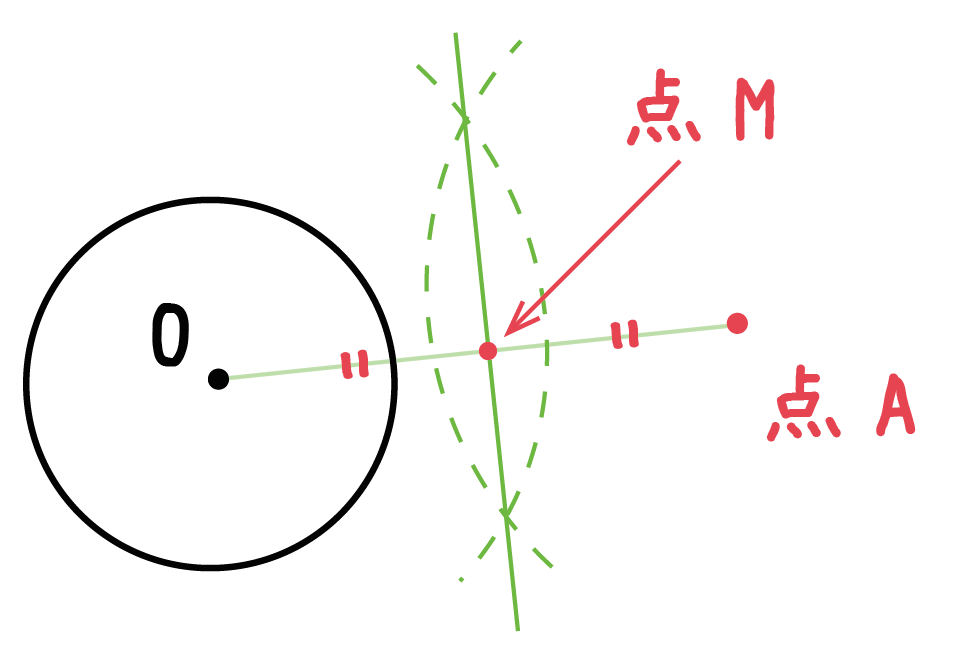
例題では「点M」とおてみたよ。
「線分の中点」を中心に円をかいてみよう。
例題でいうと、Mを中心に円をかくってことだね。
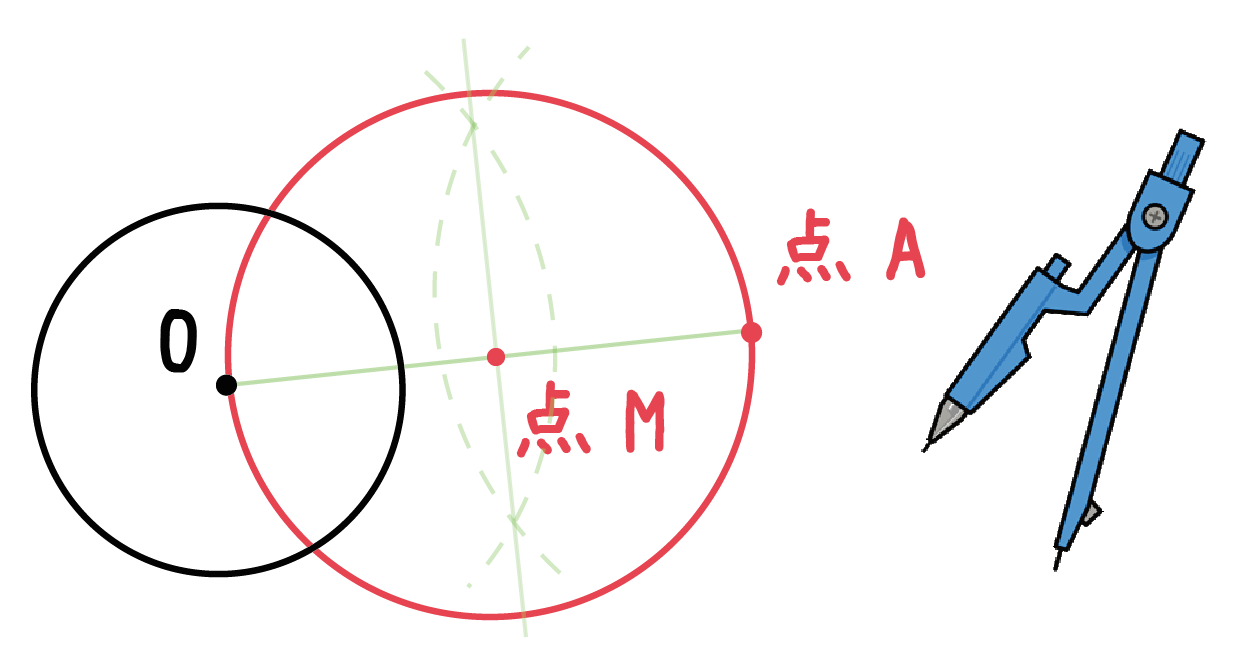
コンパスでキレイな円をかいてみてね。
「2つの円の交点」と「外部の点」をむすんであげよう。
それによって、できた直線が「円の接線」ってことになる。
例題をみてみよう。
円の交点を点P、Qとおこう。
そんで、こいつらを「外部の点A」とむすんであげればいいんだ。
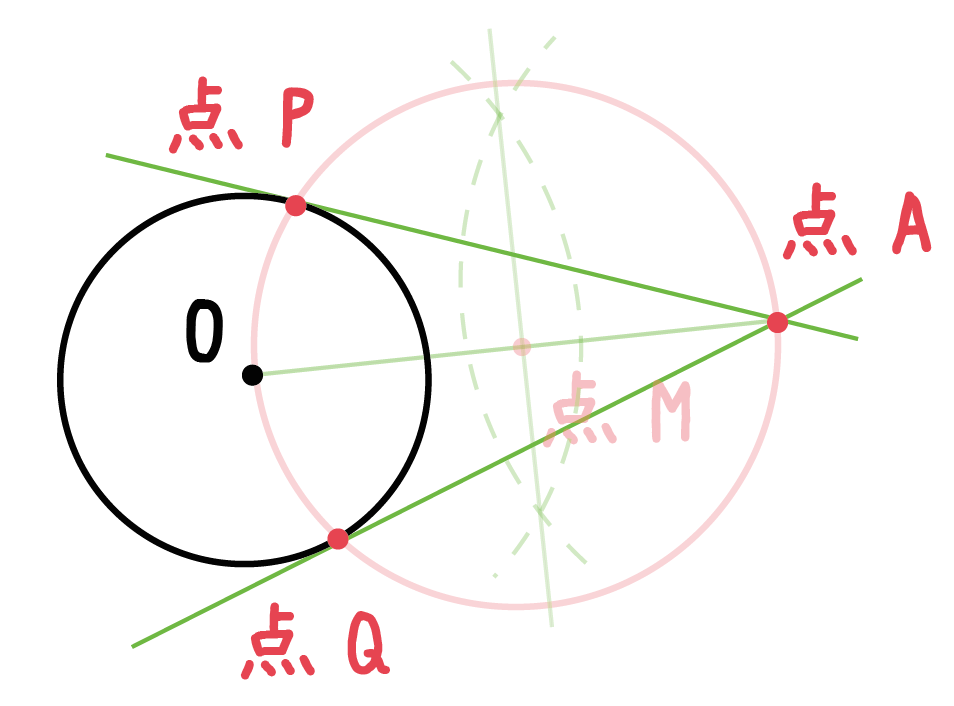
これによって、できた2つの「直線AP」と「AQ」が円Oの接線さ。
2本の接線が作図できることに注意してね。
それじゃあ、なんで「円の接線」かけっちゃったんだろう??
じつは、
直径に対する円周角は90°である
っていう円周角の性質を利用したからなんだ。
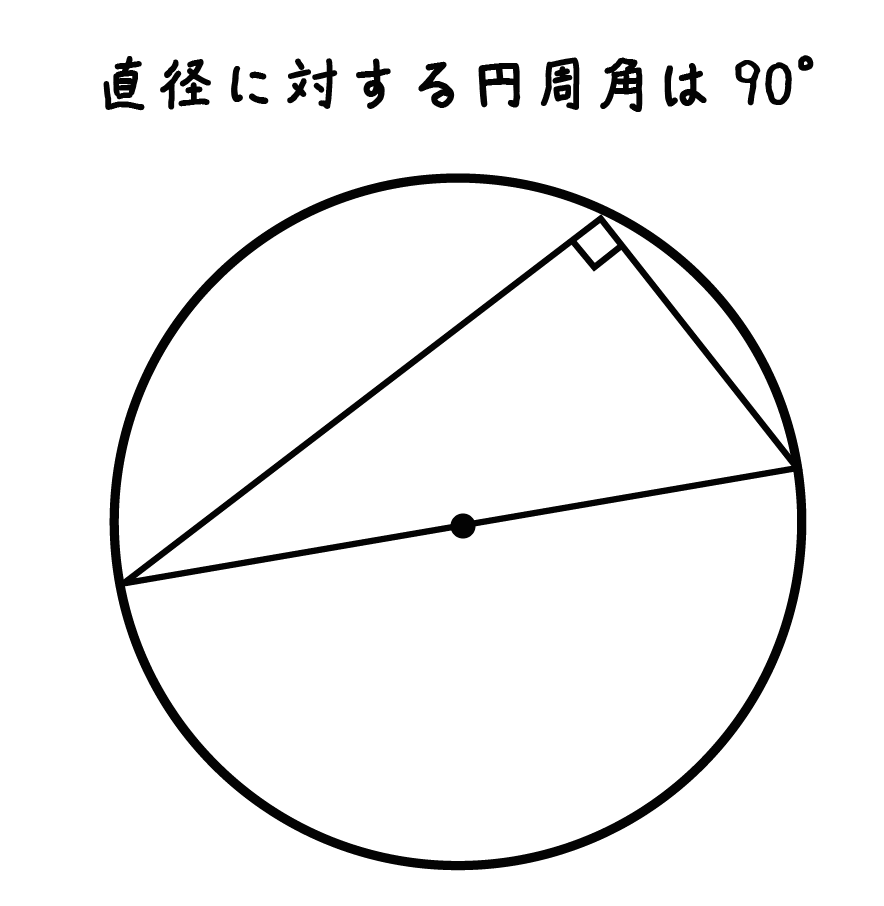
よって、
「角OPA」と「角OQA」が90°である
ってことが言えるんだ。
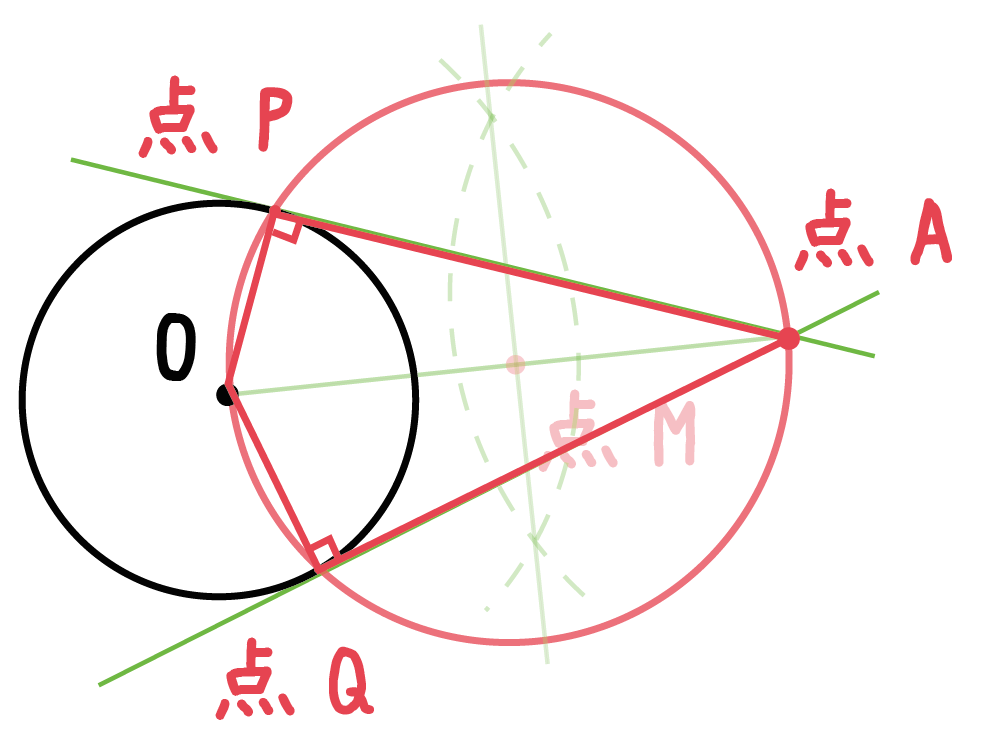
さっきの「円の接線の性質」、
円の接線は、その接点を通る半径に垂直である
をつかえば、線分PA、QAは円の接線ってことになるんだね。
これは中2数学でならう内容だから、今はまだわからなくても大丈夫だよー。
2つの「円の接線の作図パターン」をおさえれば大丈夫。
作図問題がいつ出されてもダメージをうけないように、テスト前に練習してみてね。
そんじゃねー
Ken

「扇形の中心角の求め方」の公式ってチョー便利。
教科書にはのっていない「知る人ぞ知る公式」なんだ。
扇形の中心角をx°、弧の長さをL、半径をrとすると、
x = 180L/πr
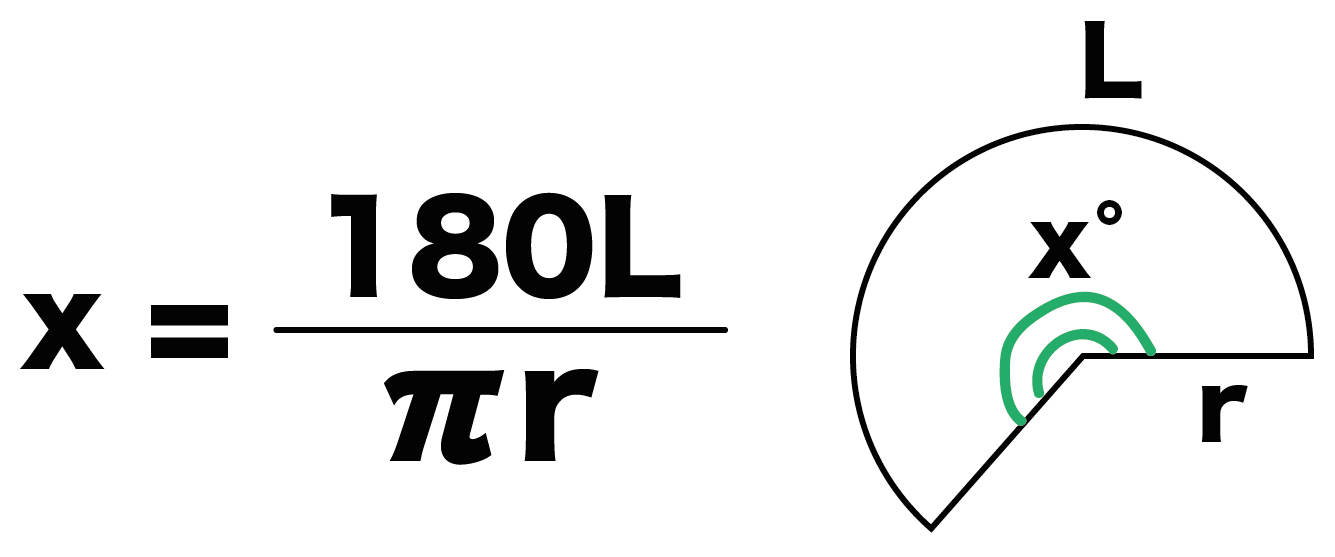
になるってやつさ。
つまり、扇形の「半径」と「弧の長さ」がわかれば「中心角」を求めることができるんだ。
たとえば、
半径 4 [cm]、弧の長さが 6π [cm]の扇形があったとしよう。
この「扇形の中心角」を求めたいときは公式をつかえば一発。
3秒ぐらいで中心角が求められるよ。
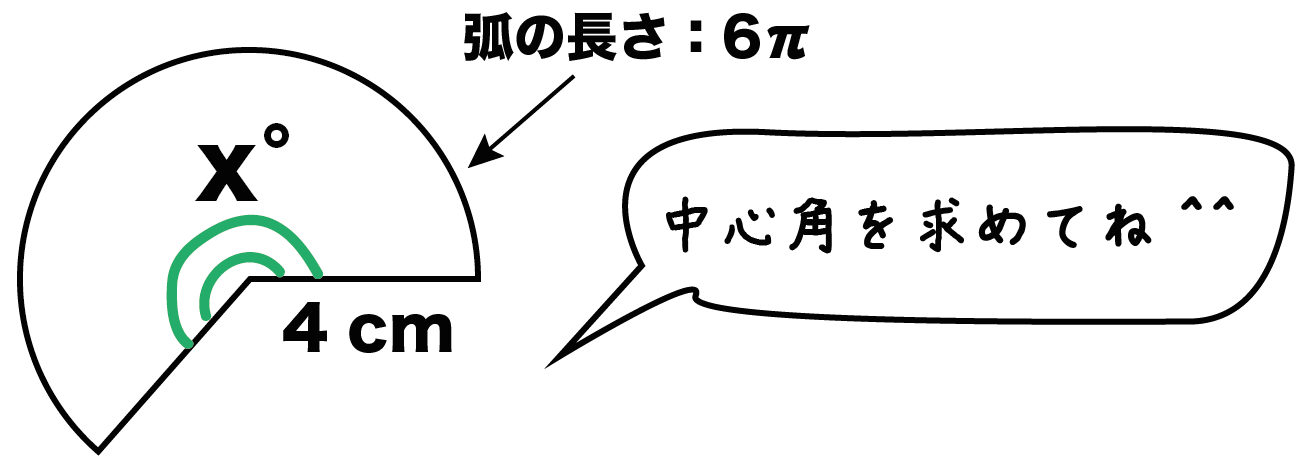
中心角の公式は、
x = 180L/πr
だったよね? これに半径r=4cm、弧の長さL= 6πを代入してやると、
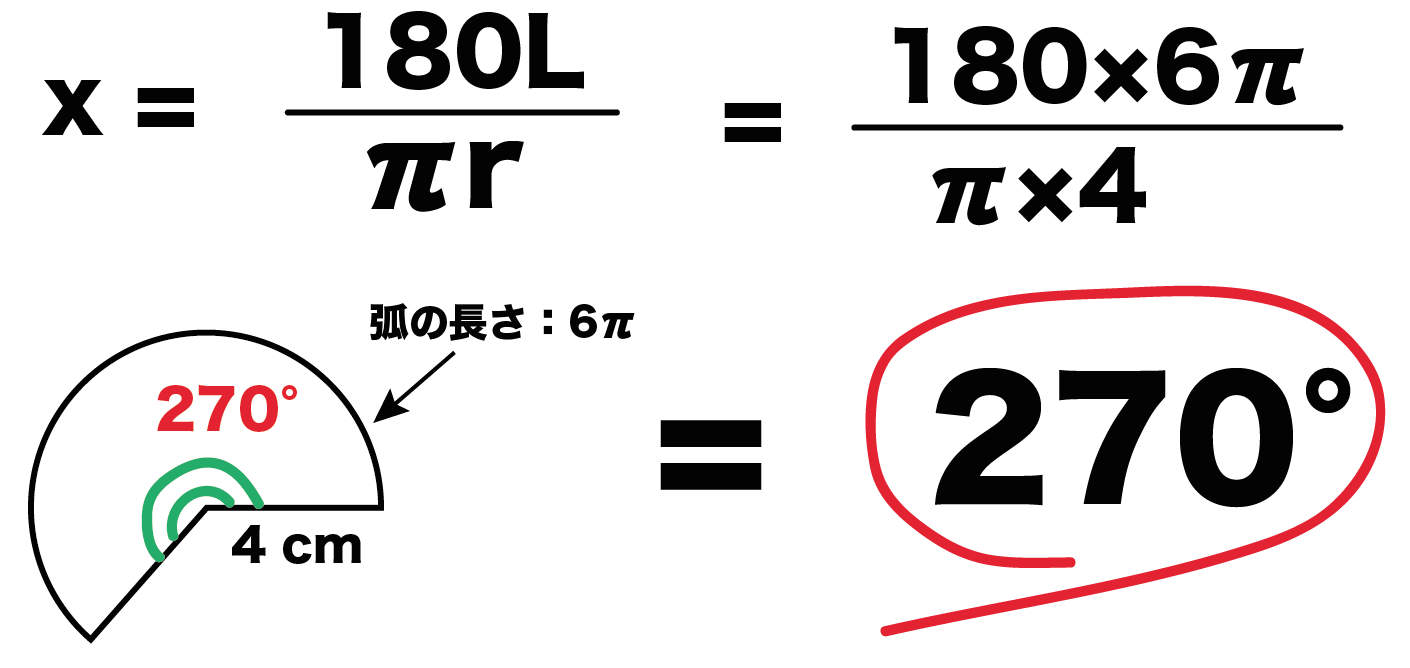
x = 270°
っていう答えがえられる。
これが中心角だよ。ものすごく簡単で便利でしょ??
それじゃあ、なぜこの公式で扇形の中心角が求められるのか??
ちょっと気になるよね??
じつは、扇形の中心角の公式は、
比例式をつかった中心角の求め方
から導きだしたものなんだ。
ってことは、「比例式から求める方法」を知っておけば公式を忘れても大丈夫ってことになる。
念のために、公式に頼らない「扇形の中心角の求め方」をみていこう。
さっきの「半径4cm、弧の長さ6π cmの扇形」の中心角を求めてみるよ。

中心角はつぎの3ステップで計算できるんだ。
まずは「扇形の中心角」を「x°」とおいてみよう。
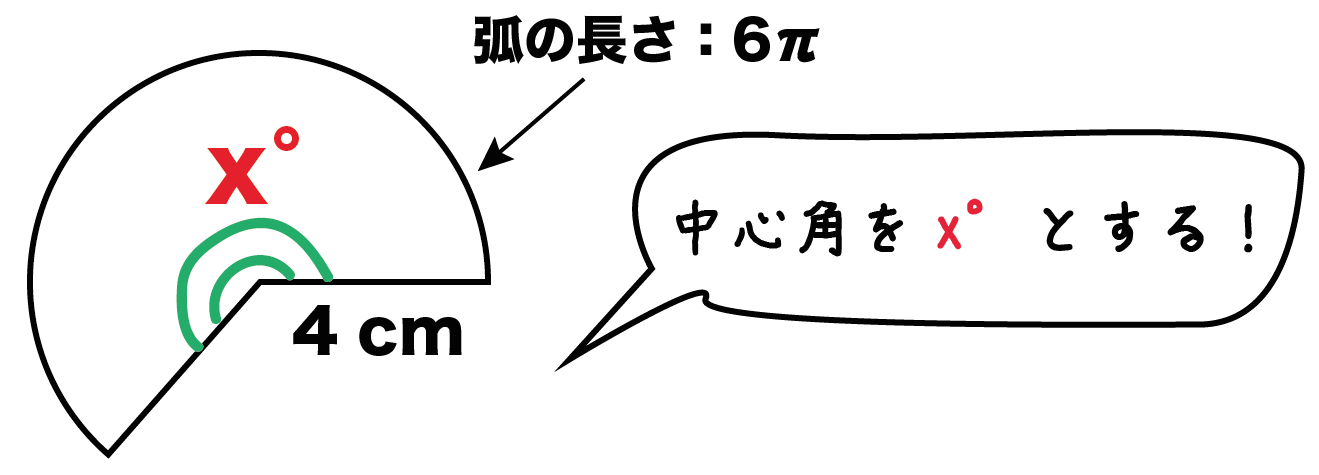
これは方程式の文章題と同じ。
「求める値」をxとするのが定石なんだ。
つぎはいよいよ比例式をたてるステップ。
「扇形の弧の長さ」は「中心角の大きさ」に比例する、
っていう性質をつかってあげよう。
すると、
円の「中心角」と「円周の長さ」、扇形の「中心角」と「弧の長さ」で
比例式をたてることができるよ。
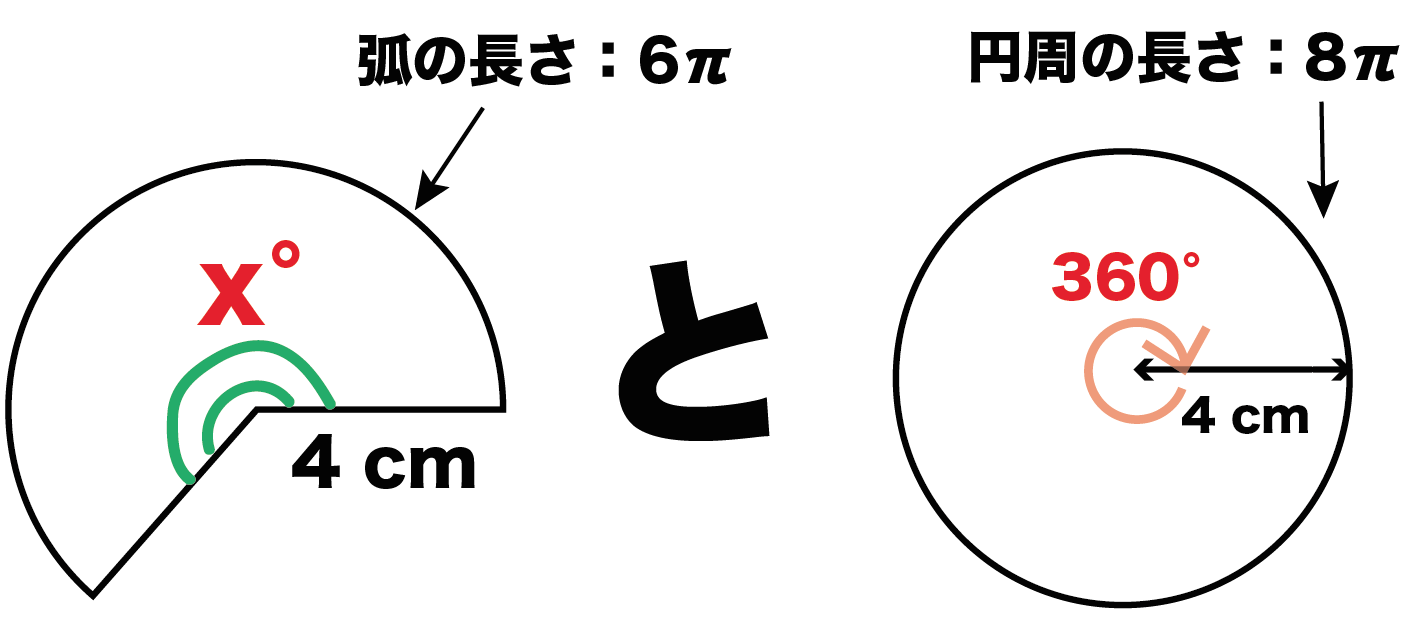
左辺を「中心角の比」、右辺を「弧の長さの比」で比例式をたててみよう。すると、
(扇形の中心角):(円の中心角) = (扇形の弧の長さ):(円周の長さ)
x : 360 = 6π : 8π
ってなるよー。
あとはこの比例式をといてやるだけ!
もし、比例式の解き方を忘れちゃったときは「【比例式の性質】3分でわかる!比例式の解き方」っていう記事を復習してみてね。
比例式は「内項・外項の積」で一発でとける。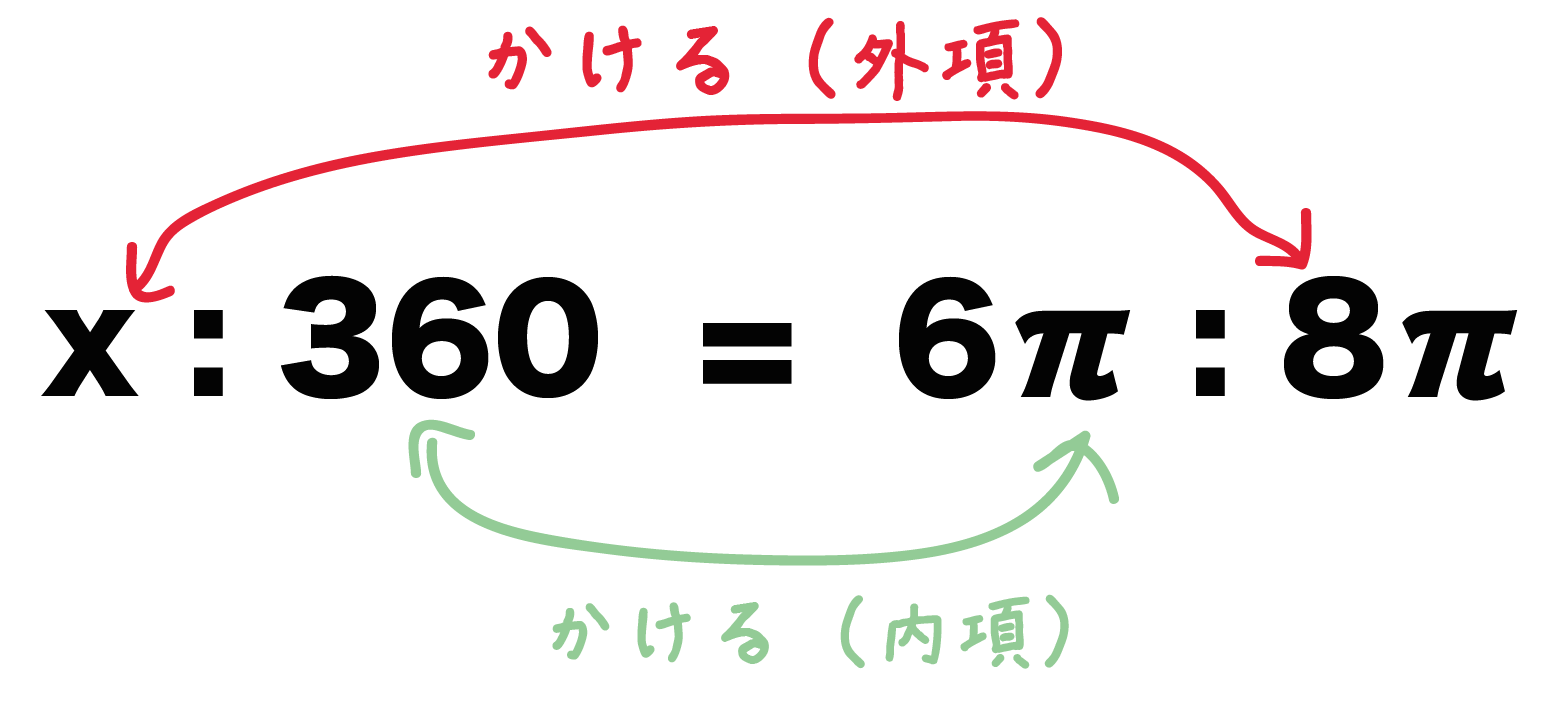
つまり、比の「外側同士をかけたもの(外項)」と「内側同士をかけたもの(内項)」を等式にしてやればいいんだ。
すると、
x × 8π = 6π × 360
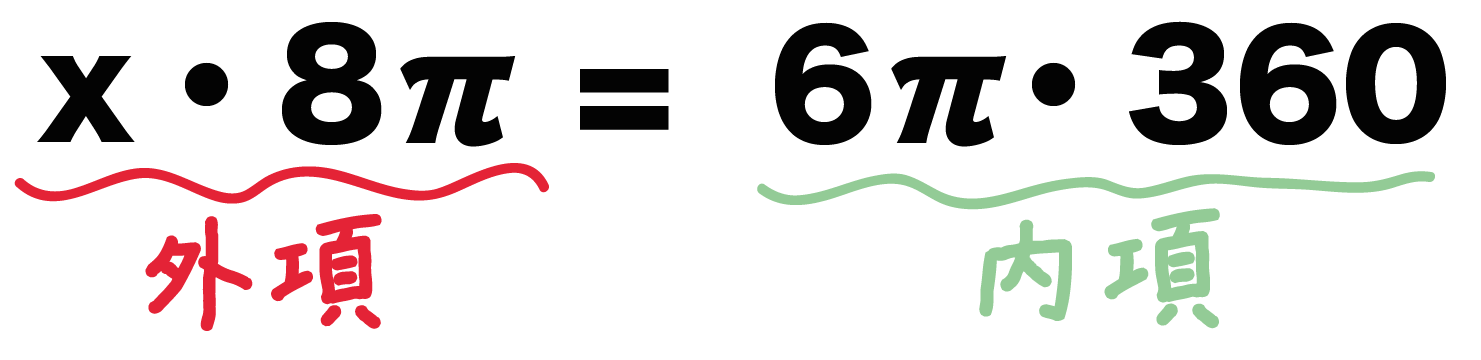
っていうxについての方程式ができるね。
こいつを解いてやると、
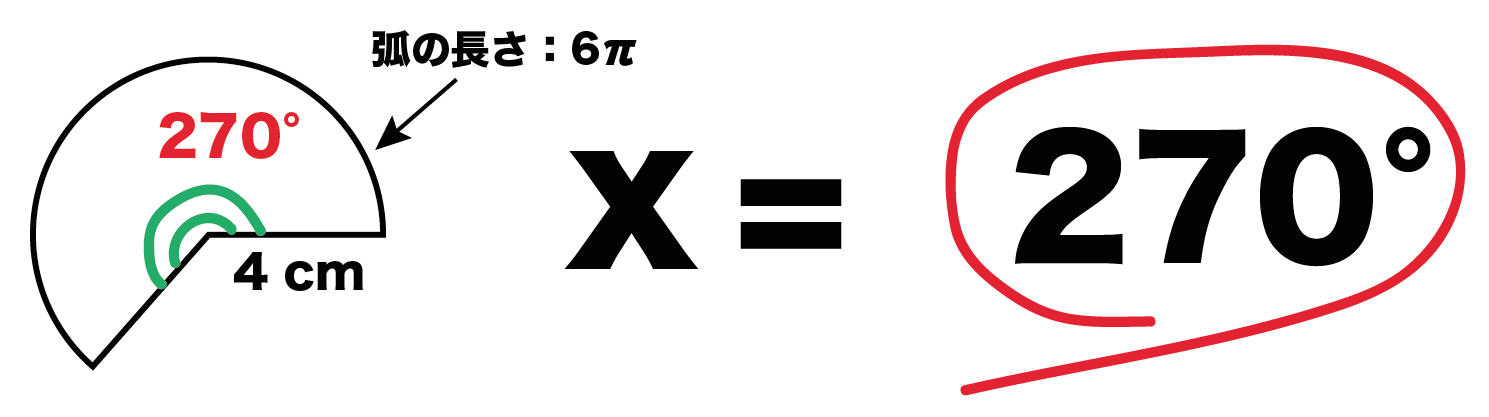
x = 270
っていう解がでてくる。このことから、
「半径4cm、弧の長さ6π cm」の扇形の中心角は270°になるってことがわかる!
めんどくさいときは公式で扇形の中心角を求めてもいいよ。
だけど、

なぜなら、公式は教科書にのってないからさ。
数学の先生たちは「扇形の中心角の求め方」の思考プロセスがみたいんだ。だから、計算式をかけよ!っていう問題にしてくるかもしれないぜ。
そんじゃねー
こんにちは、この記事をかいてるKenだよー!パンケーキはハチミツで食べるのがうまいね。
「扇形の弧の長さ」を求める公式ってわすれやすくない??
テストでたまーに狙われる分野だから、できれば公式をおぼえておきたいね。

今日は、テストで出されたときのために、
「扇形の弧の長さの求め方」の公式を振り返ってみよう!
~もくじ~
扇形の弧の長さを求めたい・・・・
そんなときにはどうすればいいのか。
電卓を使う?
ドラえもんに頼る??
ミュージックステーションをみる?
ノンノン。
ノン。
ちょっといい線までいってるけど、そのどれもが間違っている。
じつは、
扇形の弧の長さを求めるためには「ピザ」を思い浮かべるだけでいいんだ。

みんな大好き「ピザ」
ピザのカロリーを思い出して欲しい。
もし、1200kcalのホールピザを6等分すると、ひとつのピースには200kcalがふくまれているはずだ。
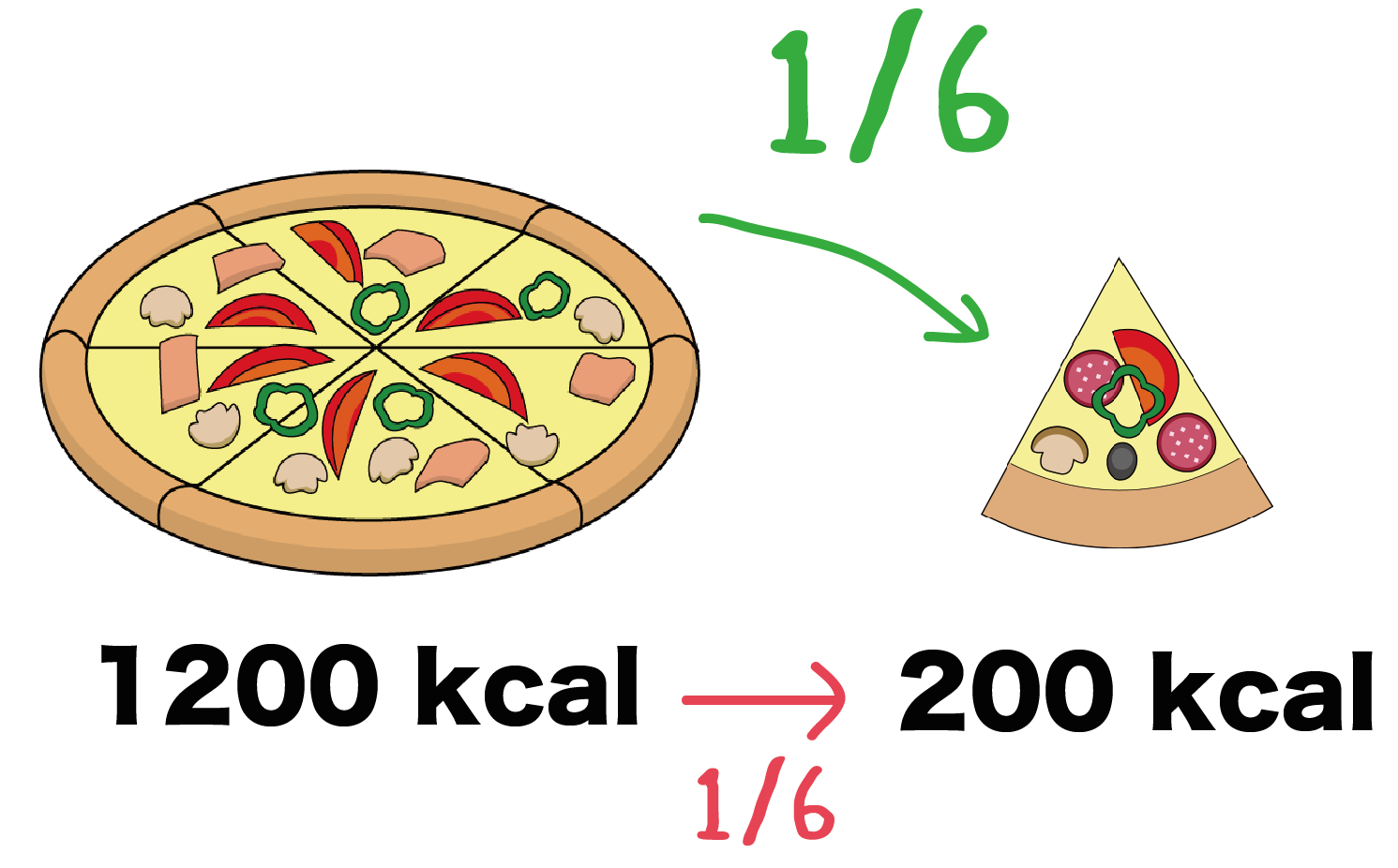
これはどうやって計算したのかというと、
「1つのピース」が「1枚のピザ」から何等分されているのか?
ということをヒントにして求めたんだ。
つまり、ピザの大きさを6等分すると含まれるカロリーまで6等分されるということさ。
これを「扇形の弧の長さ」に応用してあげよう。
扇形が「円の○○分の1」になっているという比を「円周の長さ」にかけてあげるんだ。
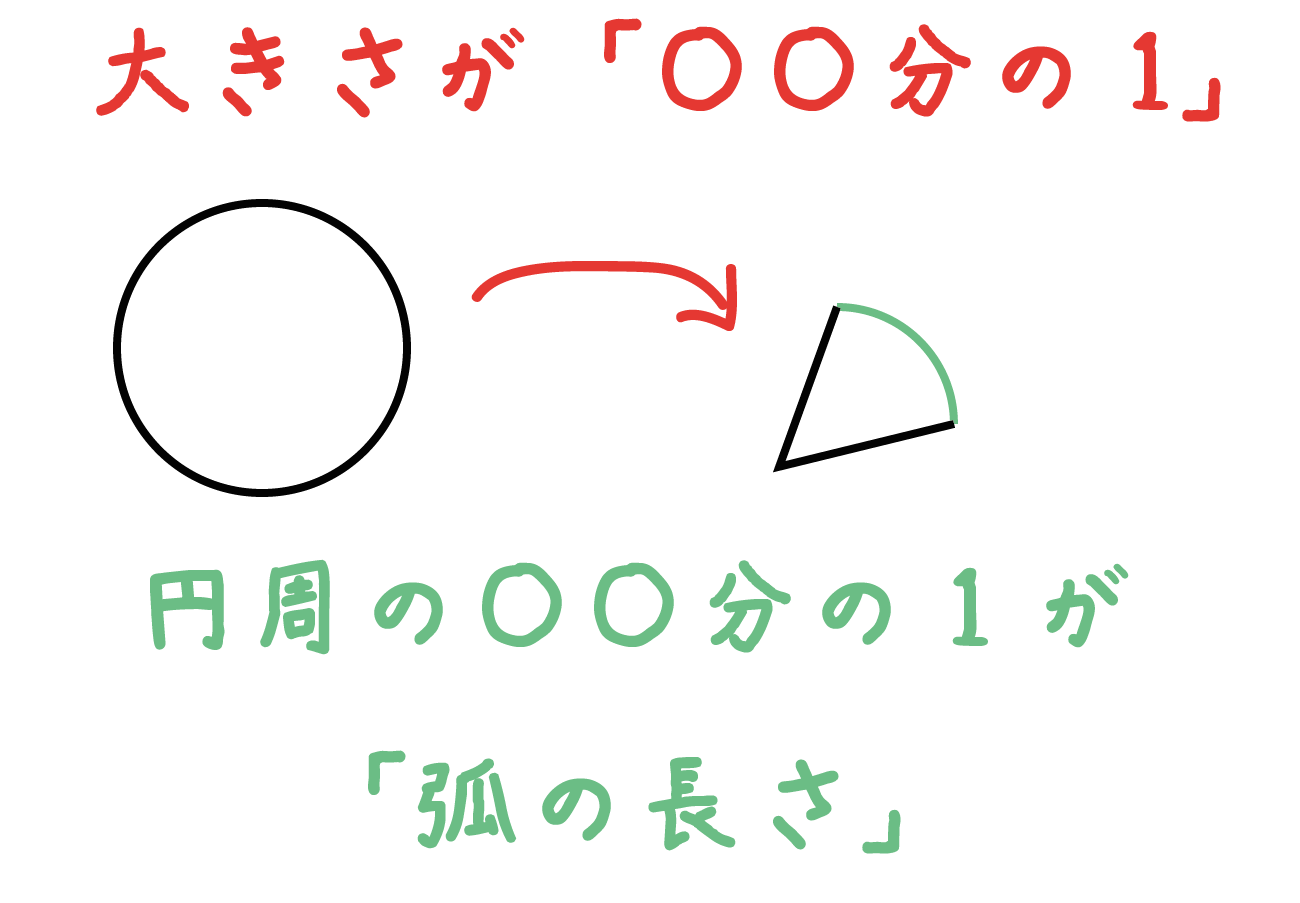
そうすれば、ピザでカロリーを計算したように、「円周」から「扇形の弧の長さ」を求めることができる。
「扇形の弧の長さ」の求め方の基本はわかったね??
それじゃあ、扇形の弧の長さの公式をみていこう!
扇形の半径をr、中心角をα、円周率をπとすると、
2πr×α/360
で「扇形の弧の長さ」を求められるんだ。 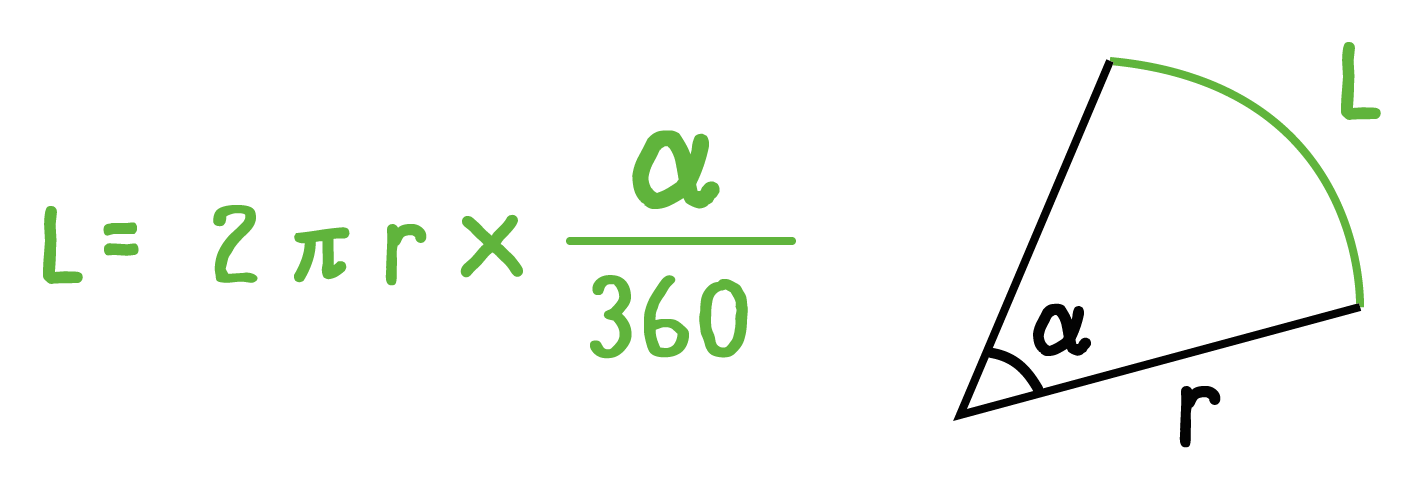
公式のうしろにある「α/ 360」という数値が「扇形が円の○○分の1になっている」ってことをあらわしているよ。
つまり、「円」という1枚のピザを何等分に切ったか??ということがわかる。
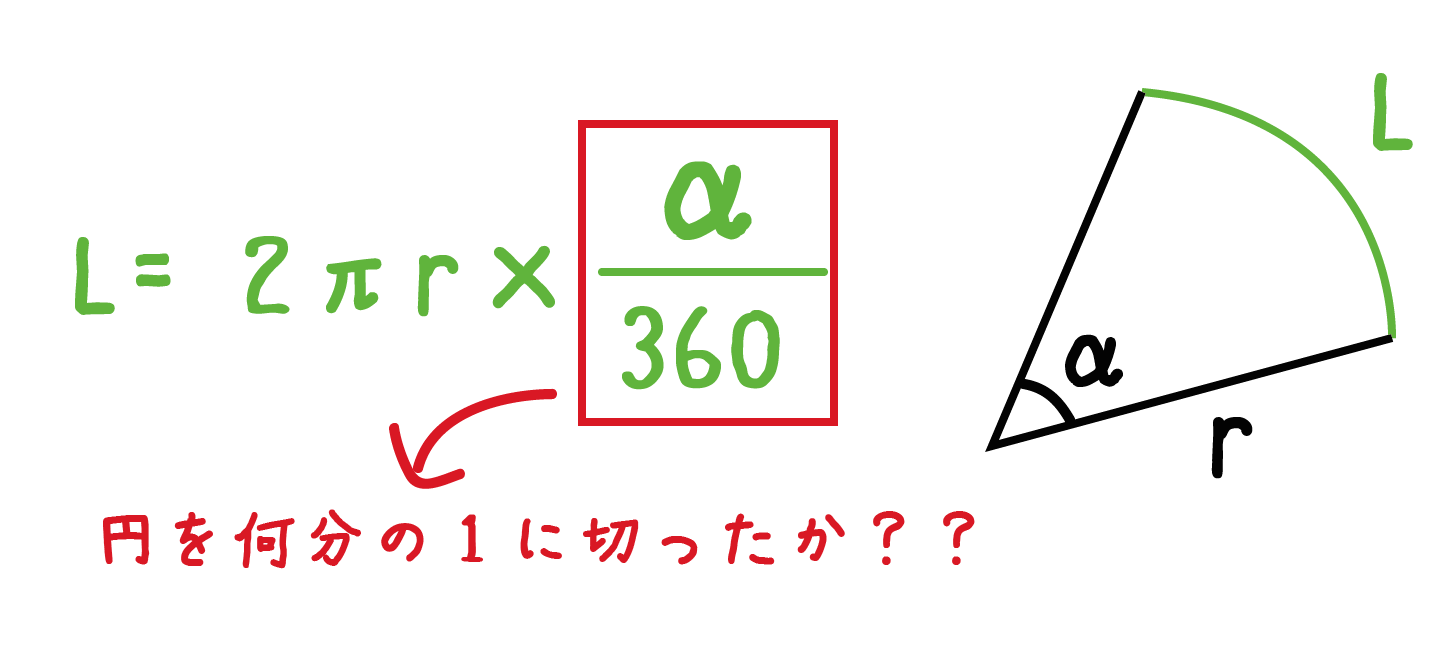
だから、こいつを円周の長さ「2πr」にかけてやると、「扇形の弧の長さ」を計算できるってことになるね。
たとえば、
半径3cm、中心角が30°の扇形がここにいたとしよう。
このとき、扇形の弧の長さLは、
L = 2π × 3 × 30/360
= π/ 2
になるよ。
こんな感じで「扇形の弧の長さ」をバンバン求めていこう!
さいごに復習しておこう。
扇形の弧の長さLの求め方は、
L = 2πr×α/360
だったね??
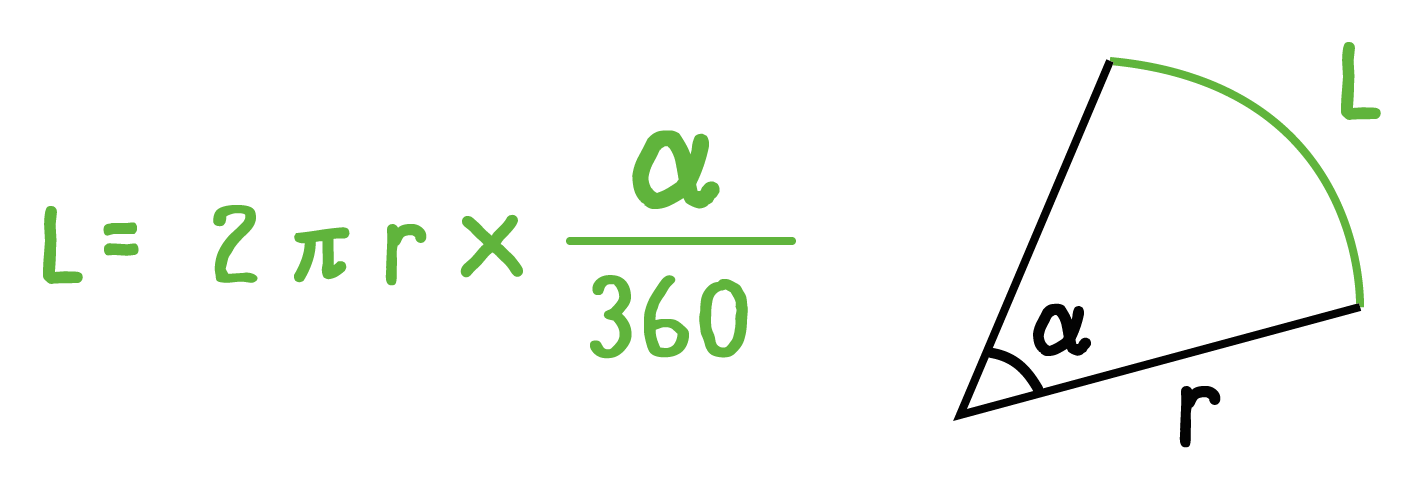
ピザのカロリーを計算するように、扇形の弧の長さを求められれば大丈夫。
時間があったら、扇形の面積の求め方も復習してみてね。
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよー。コーヒーは何度飲んでもうまいね。
「円とおうぎ形」という単元では、
という2つの図形について勉強していくよ。
前回まで、
っていう2つの公式をマスターしてきたね。
今日は、「扇形の面積」について詳しく勉強していこう。
「面積の求め方の公式」をおぼえていればテストでも楽勝さ。
~もくじ~
「おうぎ形の面積の求め方」はつぎの公式であらわされるんだ。
半径をr、面積をS、円周率をπ、中心角をαとすると、
S = πr² × α / 360
になるんだ。
つまり、
円周率×半径×半径×中心角÷360
ってわけさ。
たとえば、半径3cm、中心角が90度の扇形があったとしよう。扇形の公式をつかってやれば、
S = 3×3×π×90/360
= 9π/4
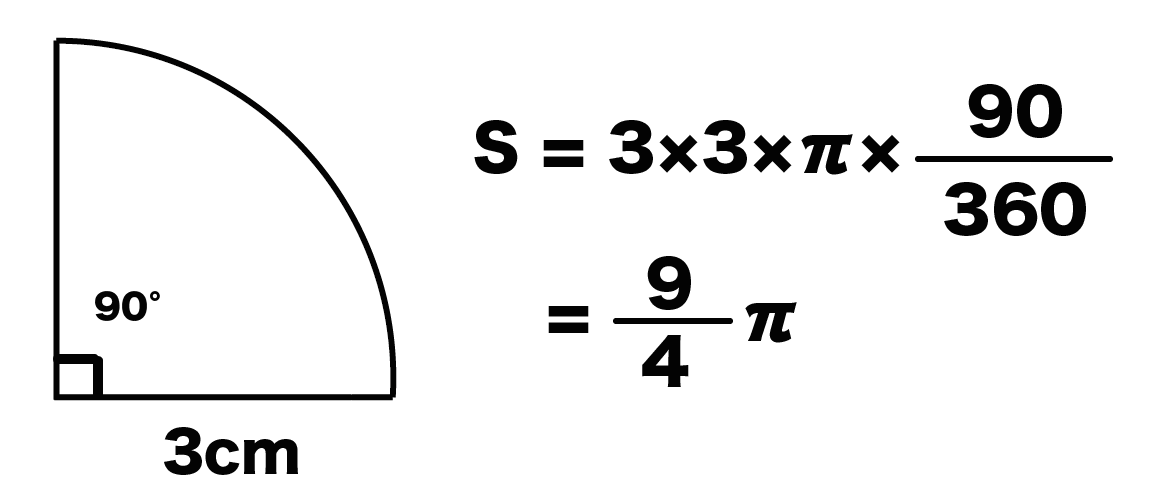
になるんだ。どんな扇形の面積でもバッチコイだね!!
扇形の面積の求め方はあんまり難しくない。シンプルさ。
ただ、半径rの「円の面積」に「おうぎ形パワー」をかけているだけなんだ。
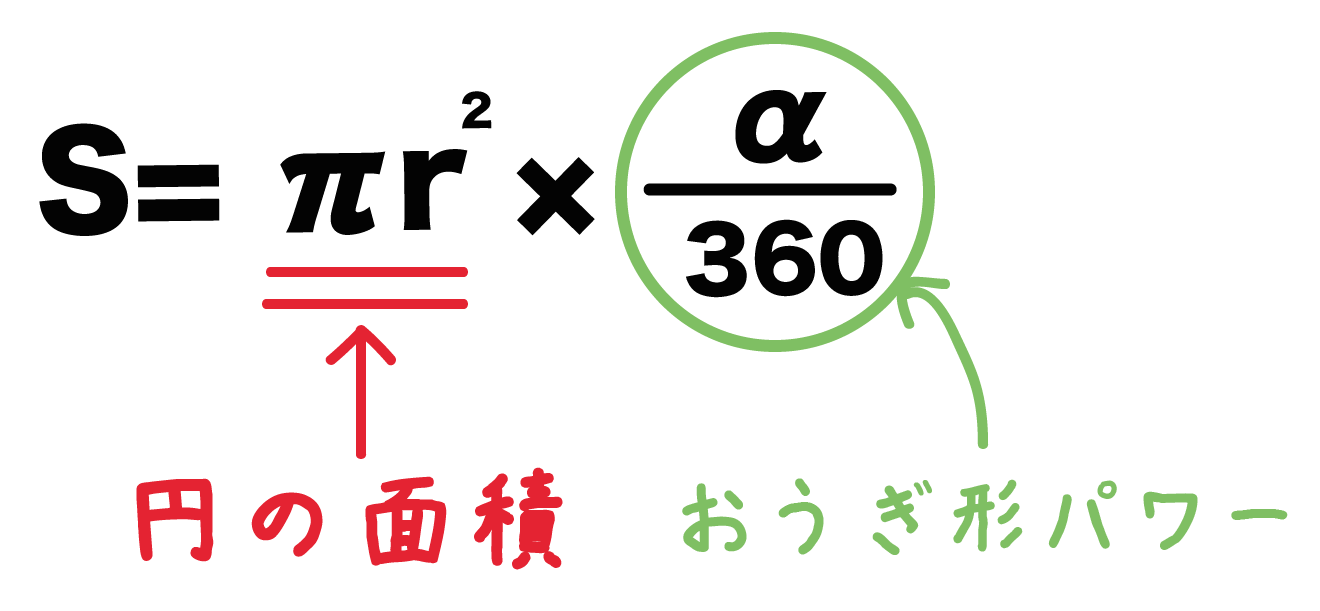
ここでいう「おうぎ形パワー」っていうのは「扇形の大きさ」をあらわしている指数のことさ。
扇形が大きければ大きいほど大きくなる。
おうぎ形パワーとは、
「同じ半径の円」に対して「扇形」がどれくらいの割合になっているか??
ということを表したものなんだ。
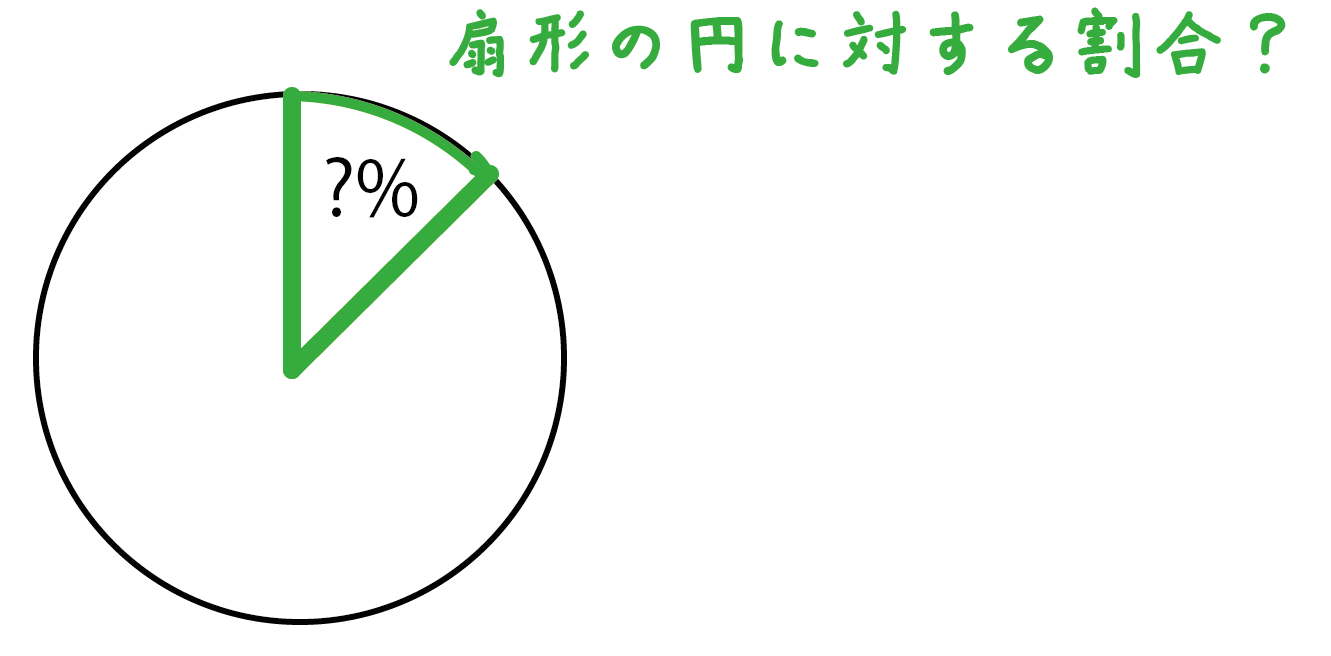
この割合を計算するためには、
「扇形の中心角」が360°中どれだけ大きいか??
ということをみればいい。だって、円の中心角はぐるっと回った360°だからね。
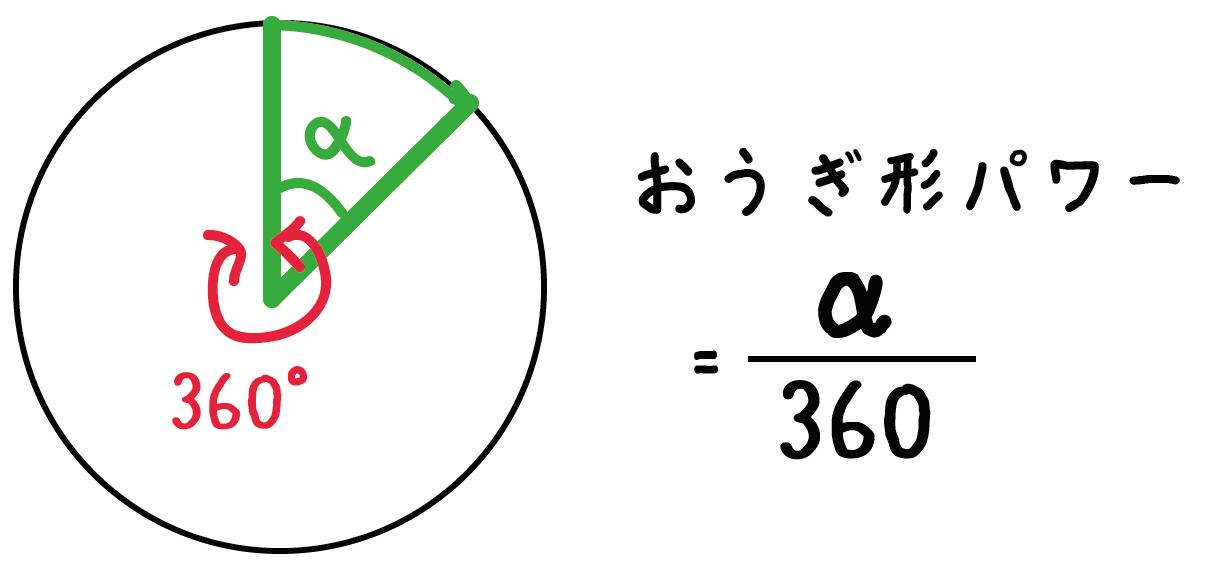
だから、おうぎ形パワーは中心角αを360°でわった、
α/360
になるんだ。
これはなんという偶然か、ピザを切り分けるときと一緒。

一枚まるまる1200kcalのピザがあったとしよう。こいつを6枚に切り分けると、カロリーはその1/6の200kcalになるでしょ??
これは一枚のピザにたいしてどれぐらいの大きさをしているか、ということを表しているんだ。
「扇形の面積の公式」を忘れたら「ピザ」を思い出そう。
扇形の面積の求め方はどうだった??
円の公式に毛がはえたようなもんだから、頑張れば覚えられそうだね。
S = πr² × α / 360
「円とおうぎ形」がテストにでるときに確認したいね。
おうぎ形の面積をマスターしたら次はおうぎ形の中心角を求めてみよう!
そんじゃねー
Ken
こんにちは、この記事をかいてるKenだよ。チョコレートに惚れ直したね。
「円周の長さの公式」ってなかなか覚えられない??
教科書には、
「円周の長さ = 直径 × 円周率」
っていう計算式が公式としてのっているね。
たとえば、直径3cmの円があったとすると、円周の長さは、
3 × 3.14 = 9.42[cm]
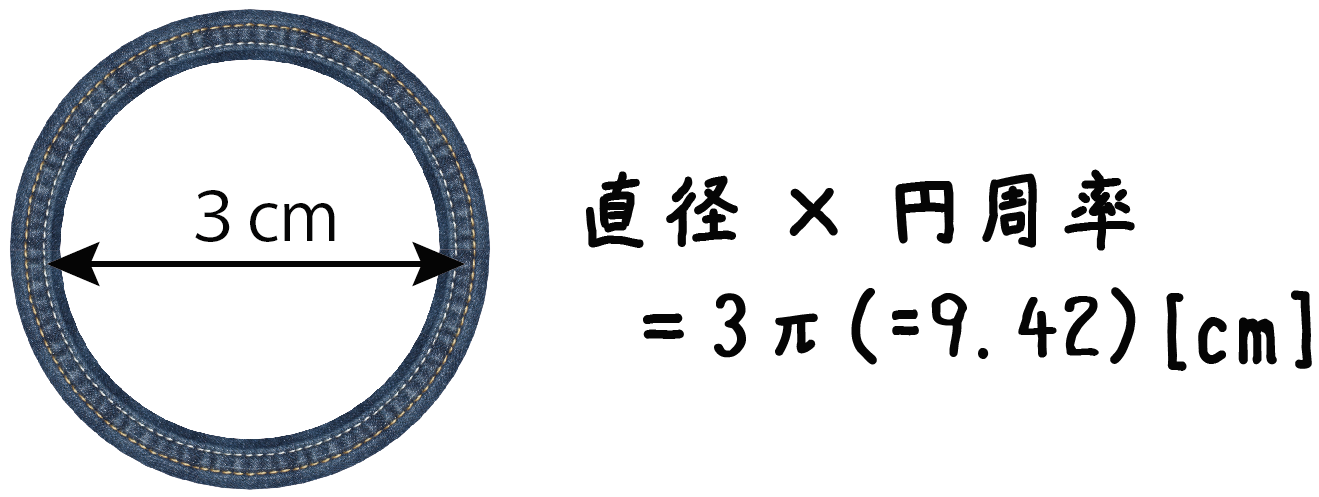
になる。つまり、この円をハサミで切ってあげると、
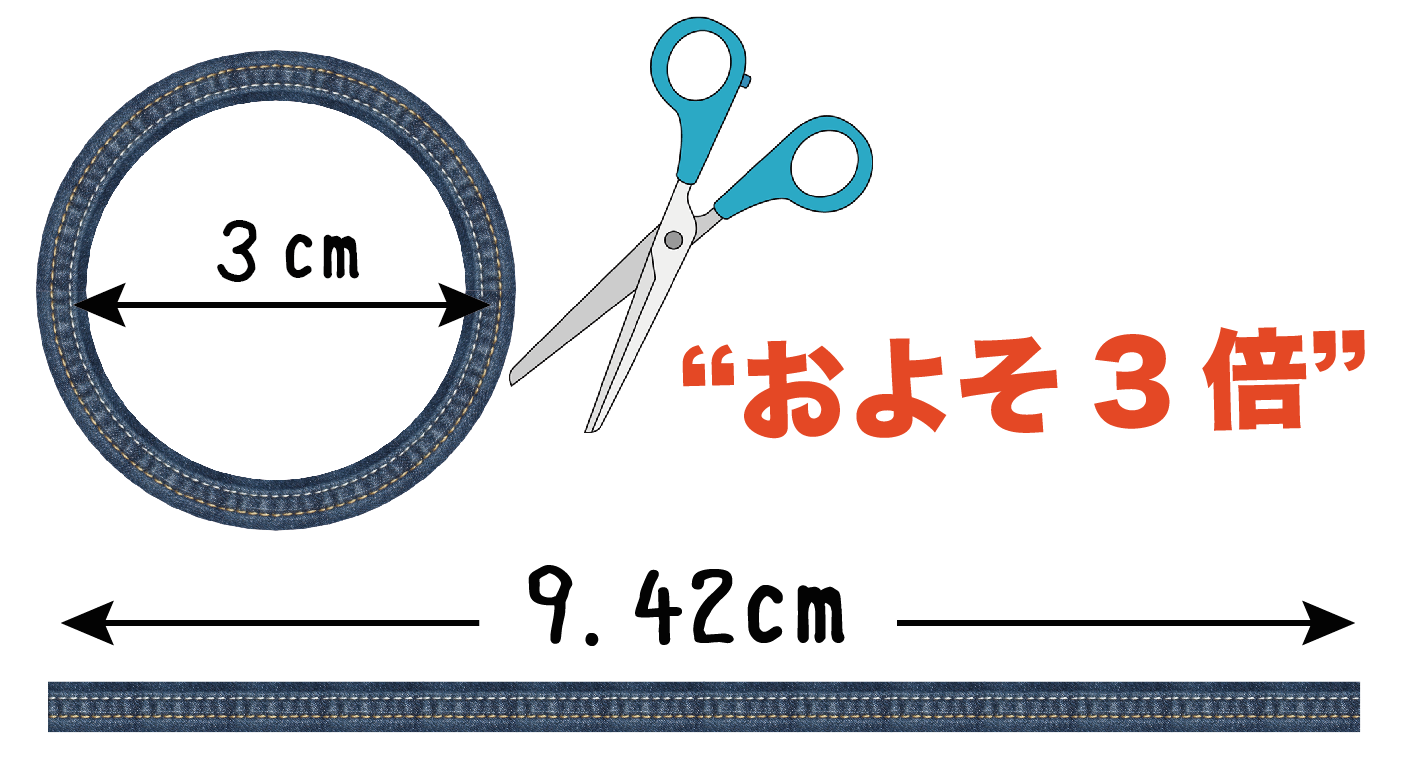
おおよそ、直径の3倍ぐらいの長さになっているってことだ。
直径と円周率をかけるだけ。
チョー便利な計算公式。だけど、どうやって覚えたらいいんだろう!??
「円周の長さの公式」をおぼえるためには何もいらない。
語呂合わせも裏技も必要ない。
円周率の意味を思い出すだけ
で円周の長さを求めることができるんだ。
円周率の意味って、
「円周の長さ」が「直径」の何倍になっているかを表した数値
だったよね??
つまり、直径に円周率をかけるだけで「円周の長さ」を求めることができるんだ。
だって、円周率って「直径」の「円周」に対する比のことだからね。
だから、
円周の長さ = 直径 × 円周率
っていう公式はある意味当たり前のこと。
円周率の意味さえおさえておけば、どうってことない公式さ。
ここまでは算数でも勉強してきた。
ここからは「中学生の数学」を勉強していこう。
中学数学でのあたらしいミッションは、
「円周の公式」を文字式であらわす
ということ。
なぜこんなことをするのかというと、文字式であらわしたほうが断然かっちょいいからだ。うん。ぜったいそう。
中学では次のように「円周の長さ」の公式をあらわすことにしているよ。
l = 2πr
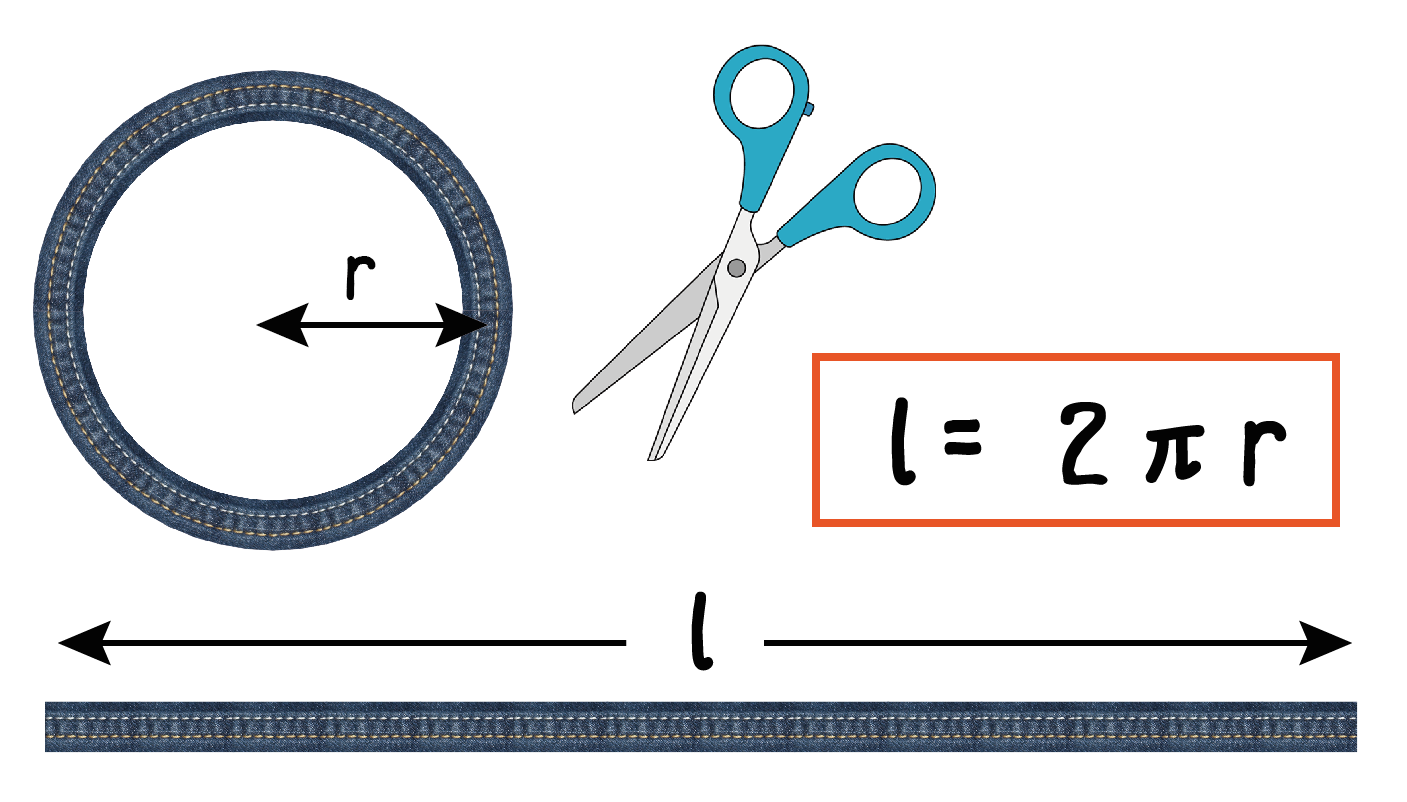
「r」という文字が「円の半径」であることに注意してね。直径は半径の2倍で「2r」になるんだ。だから、
円周の長さ = 直径 × 円周率
っていう公式を「r」と「l」と「π」であらわしてやると、
l = 2πr
になる。
「π」はどの文字よりも優先して先に書いてあげてね。
円周の公式はシンプルだけど意外に忘れやすい。
円周の公式を忘れたら、「円周率の意味」をおもいだしてみてね。
「l = 2πr」でバンバン円周の長さを計算していこう!
そんじゃねー
Ken
☆1分でわかる!円周の求め方を動画にしてみたよ☆
よかったらみてみてね↓↓
こんにちは、この記事を書いてるKenだよー。ひさしぶりに服を買ったね。
「円とおうぎ形」っていう単元に入ると、
円の面積を求めろおお!
っていう問題がたくさんでてくるんだ。
だって、ここでは「円」と「おうぎ形」が主役だからね。めんどうだけど、しょうがないね。
だけれども、一度公式をおぼえてしまえば、あとは公式の通りに計算するだけでいい。
ってことは、
円の面積の公式を一度おぼえて忘れなければいいってことなんだ。

今日は、「円の面積の求め方」の公式を一生忘れないようにするために便利な、
円の面積の公式の覚え方
を紹介するね。
テスト前に参考にしてみてー
小学校で「円の面積の求め方」の公式を勉強してきたよね??
たしか、
円の面積 = 半径 × 半径 × 円周率
ってならったはずだ。
たとえば、半径3cmの円がいたとすると、コイツの面積は、
3×3×3.14 = 28.26[cm2]
になるんだったね??
円の面積 = 半径 × 半径 × 円周率
っていう公式さえ覚えていればどうにかなるけど、これを忘れるとイタい。あせる。テストでいい点はとれない・・・・
どうしよ・・・・
公式を覚えられない中学生のために、裏技を開発してみた。
いわゆる、語呂、というやつだ。
フレーズを暗記するだけで「円の面積の求め方」を覚えられるというわけ。
これは心強いね。
とりあえず、
ラーメン屋に2人で行ったときのシチュエーションを想像してくれ。

http://www.kome100.ne.jp/main/contents/cec/f-ccc1/f-cpd1/f-cqb1/IPA-ccc660.htmより
友だちと2人で、だ。2人で。
さっそく美味そうなラーメンを注文し、2人同時にラーメンを食べ始めたんだ。

すると、
一緒にきていた友だちのラーメンを食べるスピードが異様に速い。
速すぎるじゃないか。

あまりの驚きを隠せないキミ。
そこで、ついつい耐えきれなくなって、次の「衝撃のツッコミ」を入れたんだ。

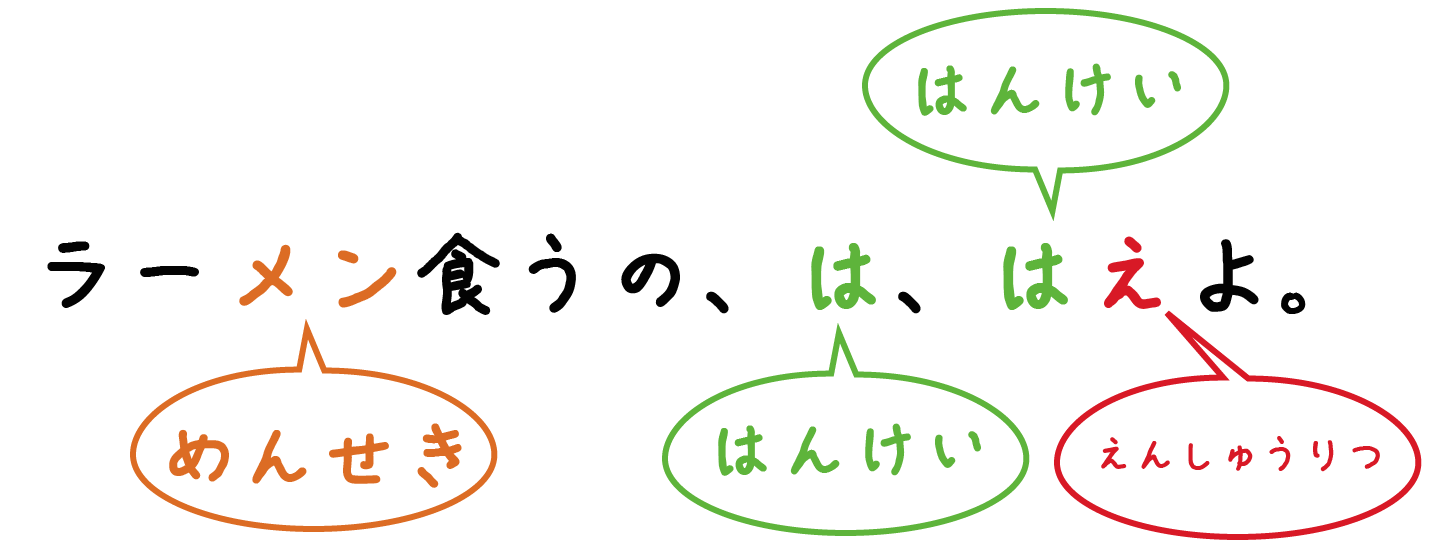
ラーメン食うの、は、はえよ!!
って。
え。ふつうの「ツッコミ」にみえるって??
たしかにそうだ。円の面積の公式なんかとぜんぜん関係ないようにみえる。
だがしかし、このフレーズに重大なヒント・手がかりが隠されているんだ。
もう一度、さっきの名台詞を確認してみると、
ラーメン食うの、は、はえよ!!
そろそろ、キーワードに気づいたかい??
そうだ。
じつは、
(円のめんせき)= (はんけい)×(はんけい)×(えんしゅうりつ)
っていう円の公式にでてくるキーワードの頭文字と偶然に一致している。
ラーメン屋のシチュエーションを頭に浮かべるだけで、円の面積の公式が覚えられるんだ。
ね? クソ便利じゃない??。
「円の面積の求め方」の公式も大丈夫。
あとはテスト中にラーメン屋のシーンを思い浮かべるだけさ。
あ、でも、中学校の数学では「円の面積の公式」はもう少しカッコいいのを使うよ。
言ってることは同じなんだけど、文字式で公式をあらわすことにしてるんだ。
円の面積を「S」、半径を「r」、円周率をπとすると、

S = πr^2
ってあらわすことができるんだ。やってることは、
面積=半径×半径×円周率
と同じこと。ただ、「円の面積の公式」を文字式であらわしているだけだよ。
なぜ面積がSなのかというと、「面積」を英語にすると「Surface」になるからだ。おなじように、半径がrなのも英語の「radius(半径)」からきてるんだ。
テストで忘れそうになったらラーメン屋の風景を思い浮かべてね。
「円の面積の公式」は導きだすのはちょっとむずかしい。
だから、公式をおぼえておくと、むちゃくちゃ便利なんだ。
ラーメン食うの、はっ、はえよ!!
っていう「ツッコミ」を忘れずにテストにのぞみたいね。
そんじゃねー
Ken