【方程式の利用】一次方程式の文章題の4つの解き方
一次方程式の文章題の解き方がいまいちわからない。。
こんにちはー!みそ汁なら作れるKenだよ!
方程式の解き方はマスターできたかな?? まだちょっと心配だなあ・・ってときは次の記事読んでみてね。
- 【中1数学】方程式の解ってどういうこと??〜方程式を「解く」とは〜
- 方程式を解くのに便利!4つの等式の性質
- 【中学数学】1次方程式(xの方程式)の解き方の3つの手順〜基礎編〜
- 【中1数学】分数をふくむ方程式の解き方
- 【中1数学】小数をふくむ一次方程式の解き方
ただ、中1数学の方程式は解き方を覚えるだけじゃダメなんだ。
その解き方をつかって、いかに文章題を正確に解いていくかがテストの勝負の分かれ目になるよ。
一次方程式文章題の4つの解き方
今日は「1次方程式の文章題の解き方」を4つ紹介するね!
ポイントを押さえればむずかしい文章題がでても大丈夫。落ち着けばきっと解けるはず!
次の文章題を例として解き方を確認してみよう!
解き方1. とりあえず図を描いてみる。
方程式の文章題が苦手だと思ったら、とりあえず図を描いてみよう。
意味がないときもあるけど、図を描くことで頭がスッキリするよ。解き方をひらめくときがあるんだ。
なにもせずに文章題を何度も読み返すより、
とりあえず図を描く
ってことはかなりお得。おそれずに前にすすんでみよう。
そうだなあ、この文章題だとちょっと難しいけど図を描いてみようか。
3年B組の教室にはとりあえず義理チョコがある。

だけど、具体的にチョコが何個あるかっていうのはまだわかってないね?
そんで、3年B組の男子生徒に2個ずつ配ると9個チョコが余っちゃうらしいんだ。男子生徒の数もチョコの数と同じようにまったく不明って状態。

だったら違う方法で!
ってことで、男子生徒に3個ずつ義理チョコを配ってみると、
ちょっとあげすぎたらしく、
4個チョコが足りないってことになっちゃうんだ。
そんで、この文章題で求めなきゃいけないのは、
3年B組の男子生徒の数!
だよね??

こうやって図を描いてみると、文字だけの文章題がちょっと現実っぽくなるでしょ??
頭がこんがらがったら図を描いてみるのは方程式の文章題の王道だね。
解き方2. 求める値を「x」にする!!
一次方程式の文章題で大切なのは、
どの値をxとするか???
ということ。これによって、方程式のカタチが変わってくるし、問題を間違える可能性も小さくなったり大きくなったりする。
文章題にはいろいろな数があってわかりにくいけど、じつはだいたいウマくいく鉄則があるんだ。
それは、
文章題で求める値をxとする
という解き方。これならば、文章題にそって方程式をたてて、それを解いてしまえばそれが文章題の答えにもなるんだ。
お得だし、カンタンだし、x選びに迷わなくていいよね。
これでうまくいかない例外もあるけど、95%の確率でうまくいくね。
経験上。
だから、とりあえず問題で求められている値をxと置いてみよう!
さっきの義理チョコの例題だったら、
「3年B組の男子生徒の数」
を求めるんだったよね?? だから、この文章題でも「男子生徒の数」を「x人」とおいてみよう。
これが方程式の文章題をさくさく解く第一ステップさ!
解き方3. 等しくなる2つの値をみつける!
方程式をつくるってことは、
「天秤を釣り合わせる」のと同じなんだ。
だから、
何と何が等しくなりそうか??
ってことを見極めなきゃいけない。さっきの義理チョコ文章題で等しくなりそうな2つの値ってどれだろうか??
この文章題をよーく見つめていると、
男子に何個配ろうが、義理チョコの数はかわらない!!
っていうことに気づくよね?!? 男子の気持ちになればわかるはず。
だから、この文章題では、
男子に2個ずつ配った場合と、
3個ずつ配った場合の、
2つの場合においても義理チョコの数は変わらない
ってことを表してやればいいんだ。
男子生徒の数をxとしているから、
2個ずつあげたときは「2x」個のチョコを男子たちにあげたことになるよね?? それで、義理チョコが9個余っているわけだから、このときの義理チョコ数は「2x + 9」と表せるんだ。
同じように、
3個ずつあげたときは「3x」個のチョコを男子にあげたことになるね。でも、結果的にチョコが4個足らなくなったらしいから、義理チョコは3xよりも4個少ない「3x – 4」って表せるね!
2つの場合の義理チョコ全体の数は等しいから、
2x + 9 = 3x -4
っていう方程式が立てられるね!
この方程式をていねいにゆっくり解いてあげればいんだ。
ね? なんだかできそうな気がしてきたでしょ??
解き方4. 方程式の解はほんとうに大丈夫??
文章題からつくった方程式を解いておしまい!!
って言いたいところだけど、これで文章題は終わらないんだ。
あと一つやることがあるんだよねー。
それは、
方程式の解が文章題の答えとして妥当かチェックする、
ということ。文章題と関係ない方程式なら、どんな値がでても何も文句はなかったけれど、文章題はひと味違う。
文章題にちゃんとフィットした答えじゃなきゃ正解じゃないんだ。
たとえば、先ほどの義理チョコ文章題の例をみてみよう。
無事に方程式をつくり、解いてみたら、
x = -13
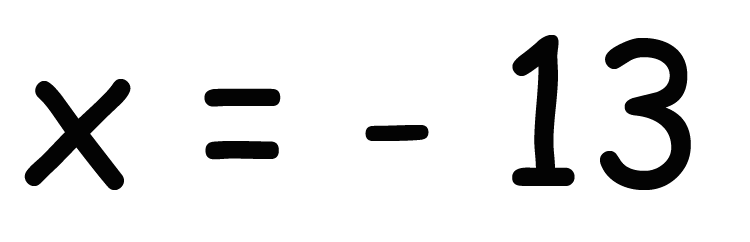
っていう方程式の解が得られたとしよう。えっと、だから、この文章題の答えは-13っと・・・・・
ちょ、
ちょと待って!!
xって何だったか確認してみて!!
たしか、xを「3年B組の男子生徒の数」って置いたよね!
ってことはもしxが「-13」だとすると、
男子生徒が「-13人」ってことになっちゃう!!
男子生徒はもともと人間の仲間だから、男子が-13人っていうと・・・・消えてるのか??。 ってことになっちゃう。人間の数にマイナスもクソもないよね??
だから当然、マイナスが解だったらおかしいってことに気づくはずだ。ミスに気づいたらどのプロセスで間違えてしまったのかチェックしてみよう!!
ふつうの計算問題だったら気づかないミスも、文章題なら気づけるんだ。
解が文章題の答えとして妥当かどうか確認してみよう!!
一次方程式文章題の解き方もオッケー!!
1次方程式文章題の解き方はどうだったかな?? ゆっくりやればできそうな気がするでしょ??
文章題にはいくつか出題のパターンがあるから、問題集とかテキストの演習問題を何度か解いてみて! きっと文章題マスターになっているはずだ!
次回は「速さ」にかんする文章題の解き方を解説していくね。
そんじゃねー!!
Ken