
中学数学の「データの活用」で出てくる箱ひげ図。
名前のインパクト、強すぎますよね。
箱に、ひげ、っすからね。
たぶん、こんなキャラクターイメージしちゃったんじゃないっすか。

でも、いえ。
箱ひげ図はキャラ名ではありません。
数学用語の一種なんです。
えっ、名前からしてゼッタイ難しそうですって??
安心してください。
箱ひげ図は、
四分位数がわかっていれば描けます。
今日は、
「箱ひげ図の書き方(中学数学)」
を、ステップを踏んでわかりやすく解説します。
~もくじ~
まず基本から。
箱ひげ図とは、
データの散らばり方を、ひと目で表す図
です。
サンプルを出すとこんな感じっすね。
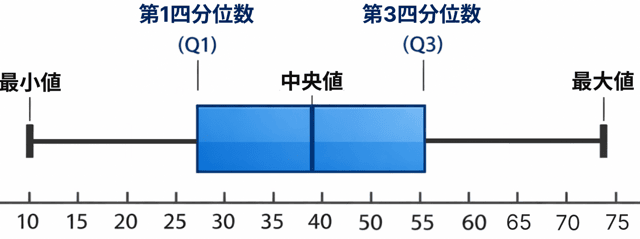
どう?? 全然ヒゲっぽくないでしょ。
この箱ひげ図は、
が一気にわかるのが特徴。
だからテストでもよく出るんすね。
箱ひげ図を書くために必要なのは、次の5つの数です。
この5つがそろえば、箱ひげ図は完成します。
えっ。ちょっと無理??
そんなときは中央値の求め方、
四分位数の求め方を復習しておきましょう。
では、実際に書いていきましょう。
まず、次のようなデータがあるとします。
9, 3, 11, 6, 5, 8, 13
箱ひげ図の書き方は次の6ステップ。
オッケー、まずは小さい順に並び替え。
すると、
3, 5, 6, 8, 9, 11, 13
こうなりますね。
次は、四分位数を求めます。
すると、こんな感じ。

やり方は四分位数の求め方を読んでみてね。
値の範囲が入るように、横に数直線を書きます。
ルールは簡単。
最小値〜最大値を必ず含むようにすればいいんす。
なので、数直線は「3 〜 13」をカバーする範囲にします。
メモリの間隔は・・・そうだな、2にしておこうか。辛いし。
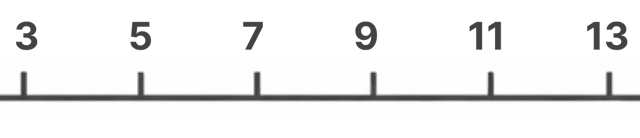
右端の矢印ヘッドは書かなくて大丈夫。
オッケー、次はいよいよ箱です。
まず、Q1 から Q3 までを「箱」で囲みます。
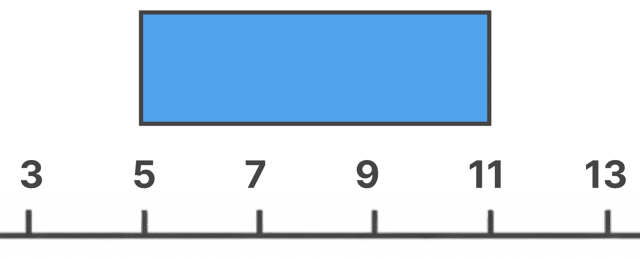
今回は
でしたよね。だから、こんな感じのボックスが登場。
そして、箱の中に中央値の線を引こう。
今回は
だから、こんな感じ。
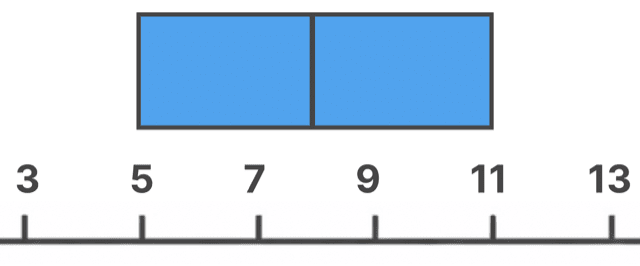
さて、お待ちかねのひげ、きました。
箱ひげ図の「ひげ」って、これっすね。
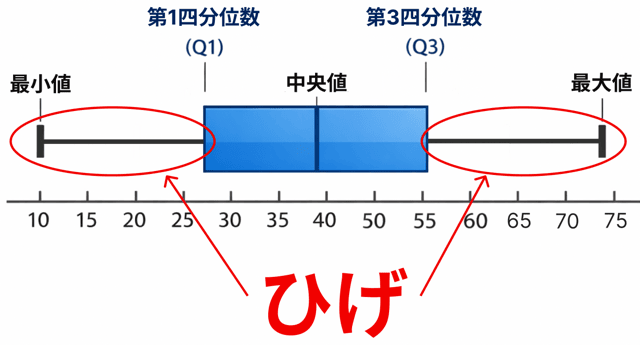
ひげの書き方は
箱の左端(Q1)から最小値まで線を引く。
箱の右端(Q3)から最大値まで線を引く。
です。
今回の場合は、
でしたから、こんな感じ。
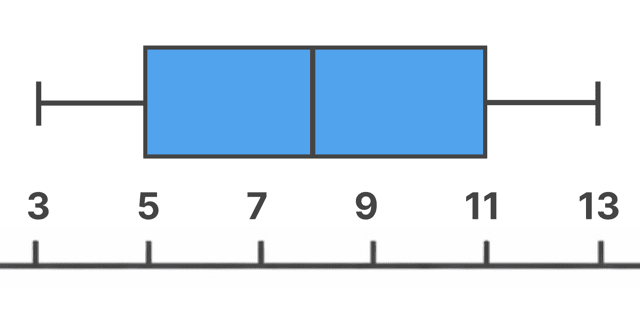
うん、はい。
これで、
箱ひげ図の完成!

テストで多いミスをまとめます。
特に、
箱は Q1 ~ Q3、ひげは端まで。
ここを間違えないようにしましょう。
箱ひげ図を見ると、
がすぐにわかります。
箱が長い → ばらつきが大きい
箱が短い → データが集中
という見方も、テストでよく聞かれますので要記憶。
箱ひげ図は、
だけでした。
見た目は難しそうですが、中身はシンプル。

そんじゃねー

中学数学で出てくる「四分位範囲」。
名前からして強そうですよね。
四分位??
範囲??
なにそれ???
しかも問題を見てみると、
でやり方が変わるっぽい…。
ってことで今日は、
「四分位範囲の求め方(奇数・偶数)」
を、中学生向けにわかりやすく解説します。
~もくじ~
四分位範囲とはずばり、
データの散らばり具合を表す数
です。
平均との差とはちょっとちがって、
「真ん中の50%が、どれくらい広がっているか」
を見るための指標なのです。
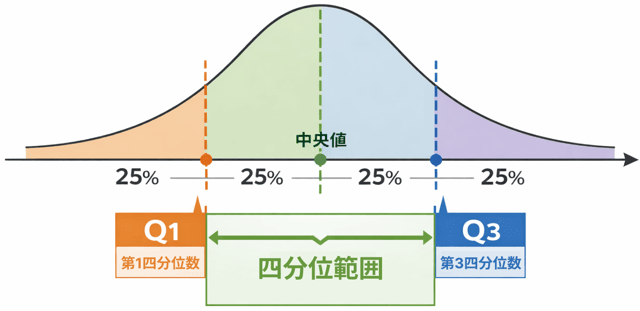
そのために使うのが、
です。
つまり、四分位範囲を出すには、先に四分位数を求める必要があります。
やることはこの3ステップ。
詳しいやり方はこちらの四分位数の求め方の記事で復習しておきましょう。
四分位範囲の求め方の公式はこれ ↓
四分位範囲 = 第3四分位数 − 第1四分位数
そう、これだけです。
引き算1回です。
たとえば、四分位数の求め方を駆使して頑張った結果、
が得られたとします。

さて、四分位範囲の求め方は
四分位範囲 = 第3四分位数 − 第1四分位数
でしたね?
この公式にもろもろの値をぶち込んでみると、
四分位範囲
= 11 – 5
= 6
になります。
つまり、四分位範囲は6!
この
四分位範囲 = 第3四分位数 − 第1四分位数
という求め方はデータの個数が奇数だろうが偶数だろうが同じ。
問題は、
第3四分位数と第1四分位数の求め方が偶数と奇数の場合で異なるってことですね。
そこらへんの事情は、さっきからチラチラ登場している四分位範囲の求め方で復習しておいてくださいね。
はい、四分位範囲は、
が全部つながった用語でした。最後に紛らわしい「四分位数」と「四分位範囲」の違いをおさらいしておきましょう。
| 項目 | 四分位数 | 四分位範囲 |
|---|---|---|
| 意味 | データを4等分するときの区切りとなる数 | 真ん中50%のデータがどれくらい広がっているかを表す量 |
| 種類 | 第1四分位数(Q1) 第2四分位数(Q2・中央値) 第3四分位数(Q3) |
1種類のみ |
| 求め方 | データを小さい順に並べ、 4等分した位置の値を求める |
第3四分位数 − 第1四分位数 (Q3 − Q1) |
| 役割 | データの区切りの位置を知る | データのばらつきの大きさを知る |
| 単位 | 元のデータと同じ | 元のデータと同じ |
| 箱ひげ図での表し方 | 箱や線の区切りの位置 | 箱の横の長さ |

そんじゃねー

中学数学で登場する「四分位数(しぶんいすう)」。
中央値はなんとなくわかるけど、
四分位数??
なんか急に専門用語っぽい〜
なんて思っちゃいますよね。
しかも問題をよく見ると、
で、やり方が変わるみたいで混乱しがちです。
今日は、
「四分位数の求め方(奇数・偶数それぞれ対応)」
を中学生向けにやさしく解説します。
~もくじ~
そもそもからいきましょう。
四分位数とはずばり、
データを4つに分けたときの区切りになる数
です。
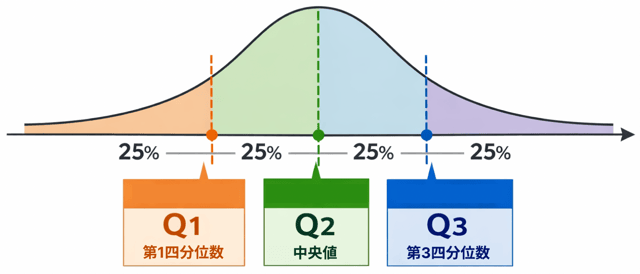
ポイントはここ ↓
小さい順に並べたデータを4等分する
ってこと。
そのときに出てくるのが、
です。
中学数学では、Q1 と Q3 を求められることが多いです。
四分位数は、次の3ステップで求めます。
ここから、奇数か偶数かで少しだけ分かれますよ。
たとえば、次のデータの四分位数を求めてみましょう。
9, 3, 11, 6, 5, 8
まず、小さい順に並べます。
すると、
3, 5, 6, 8, 9, 11
になる。
そして、データの真ん中は「8」。
これが中央値(Q2)ってわけっすね。
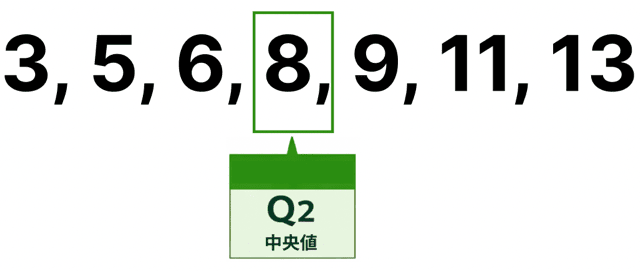
そして、中央値を除いて左右に分けます。
それぞれの中央値は、

これで四分位数が求まりましたね。
次は偶数の場合です。
6, 13, 5, 9, 3, 8, 11
さて、もう一度小さい順に並べます。
3, 5, 6, 8, 9, 11, 13
この場合だと、真ん中2つは「6」と「8」。
この2つの平均が中央値(Q2)になるんすね!
つまり、
(6 + 8) ÷ 2 = 7
です。

だがしかし、
中央値の値は、分けるための目安
として使うってポイントに注意です。
「左右それぞれの中央値を求める」っていう最後のステップでは、中央値は一旦脇に置来ましょう。
ってことで、中央値を無視して左右にわけると、
それぞれの中央値は、
となります。
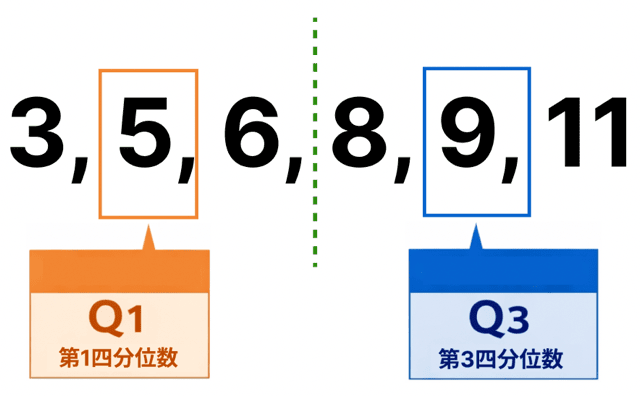
テストで間違えやすいポイントをまとめます。
この4つを意識すればOKです。
四分位数は、
だけでした。
このあと、
へとつながっていきます。

そんじゃねー

さて、中1数学で出てくる「累積度数」。
累積相対度数の話を聞いたあとだと、
え、今度は相対じゃないの?
なにを足すの???
ってなりますよね。
今日は、
「累積度数の求め方」
について、できるだけわかりやすく解説します。
よかったら参考にしてください。
~もくじ~
累積度数とはずばり、
小さい階級から順に、度数を足していった数
です。
……はい、名前は強いですが、やっていることはシンプル。
言葉をいいかえると、
「ここまでで、何回(何人)あるか」
を表した数です。
ポイントはこの2つだけ。
相対度数は、今回は使いません。
では、これまでと同じ「マメつかみゲーム」の度数分布表を使って考えてみましょう。

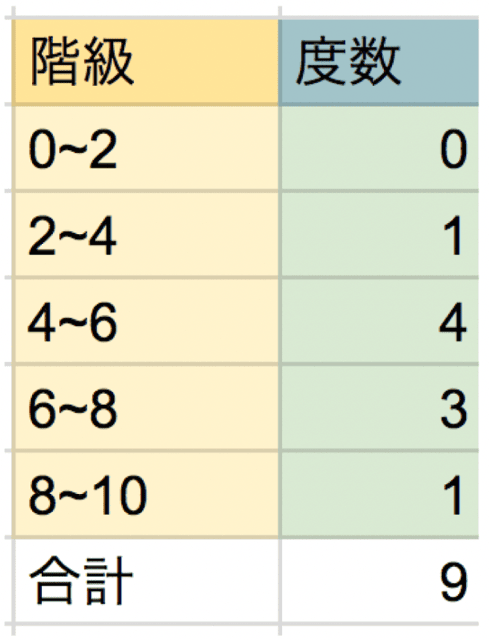
累積度数の求め方はズバリ、
一番小さい階級から順に、度数を足すだけ!
です。
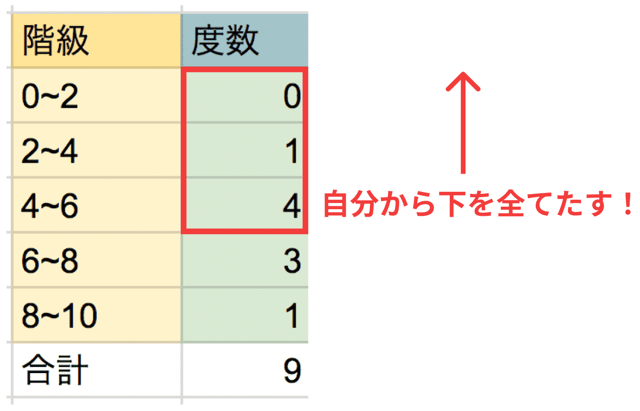
たとえば、今回の場合だと
となります。
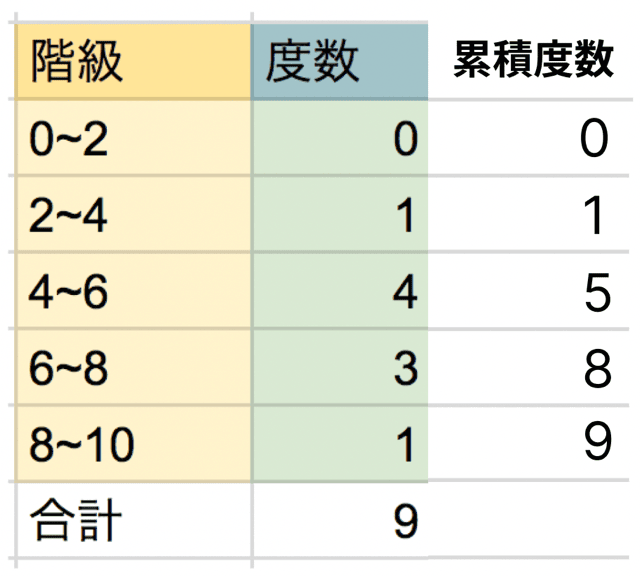
このように、
前の累積度数に、次の度数を足す
という作業をくり返すだけでOKです。
累積度数を見ると、
「〇〇未満の回数」「〇〇以下の人数」
がすぐに分かります。
たとえば、
という読み取りができます。
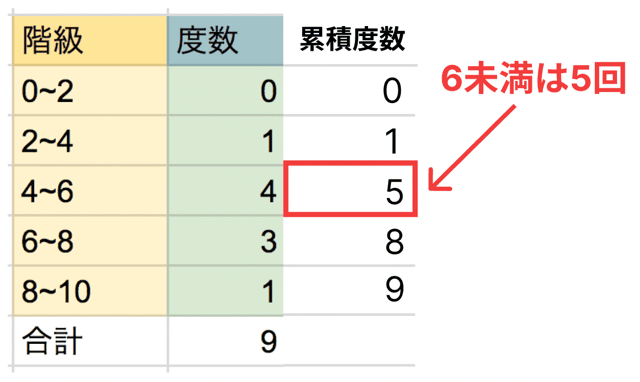
「未満・以下」という言葉が出てきたら、
累積度数の出番です。
ここで、よくある混乱、
累積度数と累積相対度数の違いを整理しておきましょう。
| 種類 | 足すもの | 表すもの |
|---|---|---|
| 累積度数 | 度数 | 回数・人数 |
| 累積相対度数 | 相対度数 | 割合 |
どちらも累積から始まる紛らわしいワーズですが、
「小さい階級から足す」
という考え方は同じです。
ズバリ、
足すものがちがうだけ。

まとめです。
累積度数は、
だけでした。
ついでに累積相対度数も復習しておきましょうね。
そんじゃねー

さて、中1数学で「累積相対度数」を勉強しますよ。
そう、出ました。
累積??
相対??
度数!?!?
相対度数の時点で怪しかったのに、さらに「累積」が追加。
もう頭がパンクしそうですよね。
今日は、
「累積相対度数の求め方」
を、できるだけやさしく解説します。
よかったら参考にしてください。
~もくじ~
累積相対度数とはずばり、
小さい階級から順に、相対度数を足していったもの
です。
……またしても、わかりませんね。
言葉をいいかえると、
「この階級までで、全体の何%になるか」
を表した数なのです。
ポイントはこの2つ。
これだけ覚えておけばOKです。
では、相対度数のときと同じ具体例「マメつかみゲーム」の度数分布表を使って考えてみましょう。

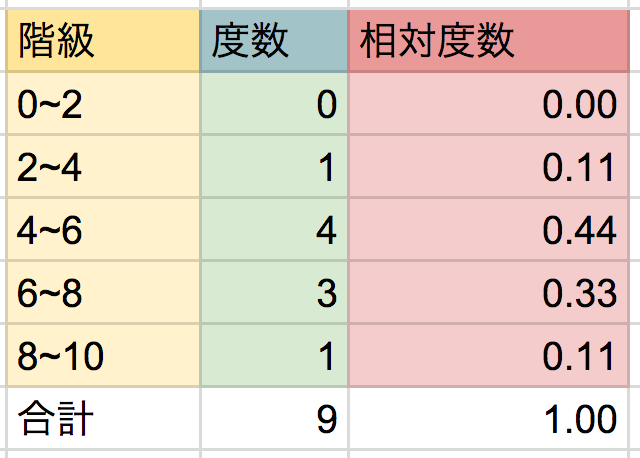
累積相対度数の求め方はズバリ、
一番小さい階級から順に、相対度数を足すだけ!
です。
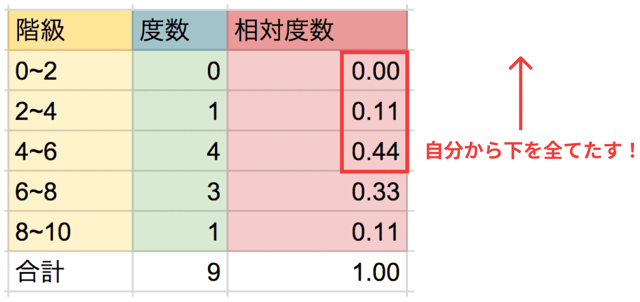
たとえば、今回の場合だと
になりますね。
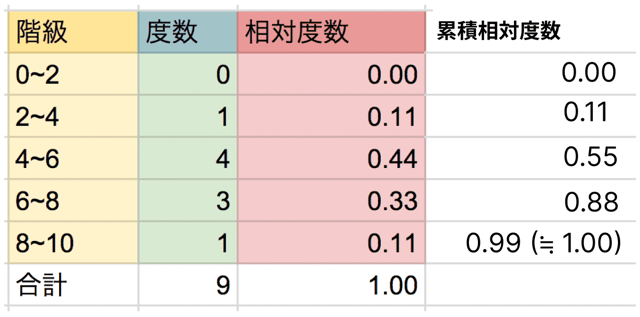
このように、
前の累積相対度数に、次の相対度数を足す
という作業をくり返すだけでいいんです。
えっ、累積相対度数がなんの役に立つか、ですって??
じつは累積相対度数を見れば、
「この値以下の人が、全体の何割か」
が一発でわかります。
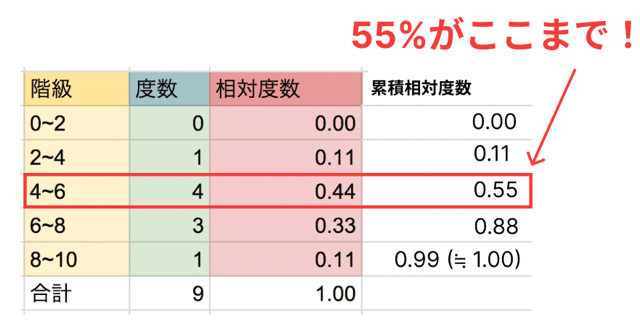
たとえば、
という感じで使われますよ。
累積相対度数で気をつけるポイントは2つあります。
累積相対度数は、最後の階級で必ず「1」になります。
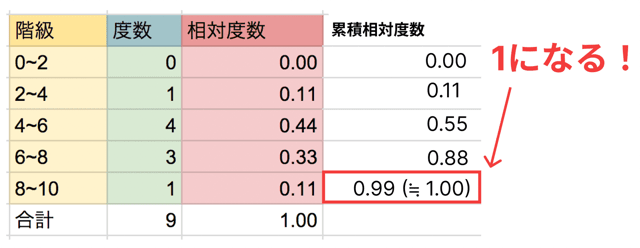
なぜなら、全体の100%を足し切った状態だからです。
計算ミスをしていないかどうか、最後が1になっているか必ずチェックしましょう。
今回の「マメつかみゲーム」でも、
8~10 の累積相対度数 → 0.88 + 0.11 = 0.99 ≒ 1.00
となっていますね。最後の累積相対度数は1です。
累積相対度数は、順番が命です。
大きい階級から足したり、途中を飛ばしたりするとアウト。
必ず、
小さい階級 → 大きい階級
の順番で足しましょう。
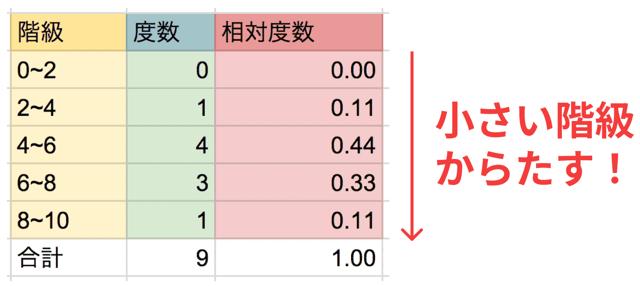
今回の「マメつかみゲーム」でも、
大きい階級の「8~10」から足しちゃダメってことですね。
以上です。
累積相対度数は、
でしたね。

次は「中央値」を勉強しましょう。
そんじゃねー
「一次方程式」には色々なタイプがあるけど、中には
分数と小数の両方を含む厄介な奴
がいるんだよね。
例えば次のような問題さ。
次の方程式を解け。
$$\frac{x}{4}-\frac{2x-7}{3}=x + 3.5$$
次のステップを踏むと解けるよ。
最初にすべきことは
「小数」を「分数」にすることだ。
これによって、分数だけの方程式に進化させるのさ。
分数だけの方程式にしてあげればもう大丈夫。分数を含む方程式の解き方なら知っているもんね。
この問題でいうと、小数の$3.5$を分数にして$\frac{35}{10}$にするんだ。
これで分数だけの方程式のできあがり。
$$\frac{x}{4}-\frac{2x-7}{3}=x + 3.5$$
$$\frac{x}{4}-\frac{2x-7}{3}=x + \frac{35}{10}$$
あとは、分数を含む方程式の解き方でとくだけ。
セオリー通り、分母の最小公倍数を両辺にかけて分数を消し去ろう。
例題では、
っていう3つの分数項があるから、こいつらの分母に注目。
分母の4、3、10の最小公倍数は「60」だね。
よって、方程式の両辺に60をかけると、
$$\frac{x}{4}-\frac{2x-7}{3}=x + \frac{35}{10}$$$$15x-20(2x-7)=60x +210$$
になる。
方程式から分数がなくなったから、あとはいつも通りに一次方程式を解くだけ。
$$15x-20(2x-7)=60x +210$$
この状態では、()を含む方程式になっているから、分配法則でカッコを展開しよう。
$$15x-20(2x-7)=60x +210$$$$15x-40x + 140=60x +210$$
$$-85x =70$$
$$x =-\frac{14}{17}$$
になるはずだね。
こんな感じで、小数を分数にしてやれば、あら不思議。
小数と分数が含まれていようが、分数だけの方程式に様変わりだ。
テスト前によーく復習しておこう。
そんじゃねー
Ken
立体の問題ではこんな問題もあるっぽいよ。
次の立体の表面積を求めよ。
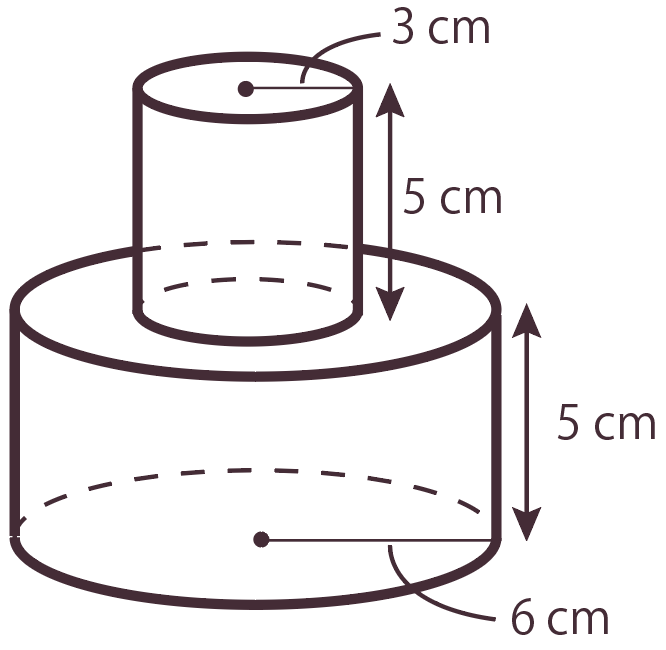
なんと、
円柱を2つ重ねた立体
の登場だ。
しかも「表面積」を求めろ、と。
今まで口を酸っぱく、
表面積を求める前に展開図をかこう
と言ってきたけど、この問題はちょっと例外。
なぜなら、展開図をかくのがむずいからね。
展開図はスルーしよう。
その代わり、
「底面積」と「側面積」を別々に計算して最後に足す
っていう解き方がおすすめ。
まず底面積を求めよう。
底面は、
の3つだね。
こいつらの面積を計算して最後に足せばいいんだ。
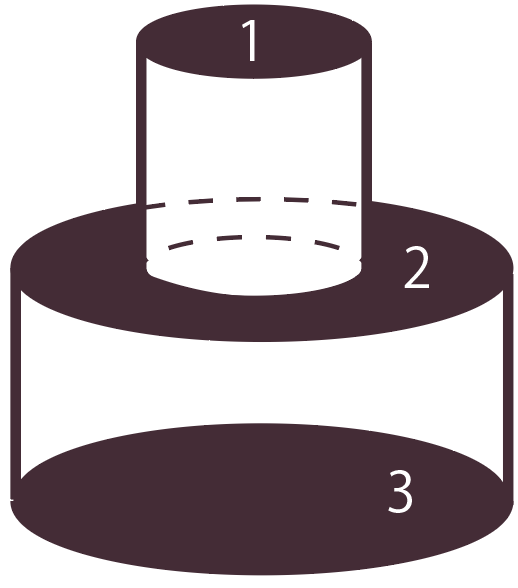
まず、小さい円柱の上面の底面積(上図1)。
半径3 cmの円だから、円の面積公式「半径×半径×円周率」で計算すると、
$$3×3×π$$
$$= 9π[cm^2]$$
だ。

次は真ん中のドーナッツのような図形(上図2)。
大きい円(半径6cm)から、小さい円(半径3 cm)の面積を引けばいいね。
(大きい円の面積) – (小さい円の面積)で計算すると、
$$ (6×6×π)- (3×3×π)$$
$$= 27π[cm^2]$$
になるね。
最後は下に敷かれているでかい円の面積。
こいつは半径6cmの円だから「半径×半径×円周率」で面積を計算すると、
$$6×6×π$$
$$= 36π[cm^2]$$
になる。
これらの底面積をぜーんぶ足してやると、
$$9π + 27π + 36π$$
$$= 72π[cm^2]$$
になるね。
次は側面積を求めよう。
「上の円柱の側面(1)」と「下の円柱の側面(2)」の面積を足せばいいんだ。
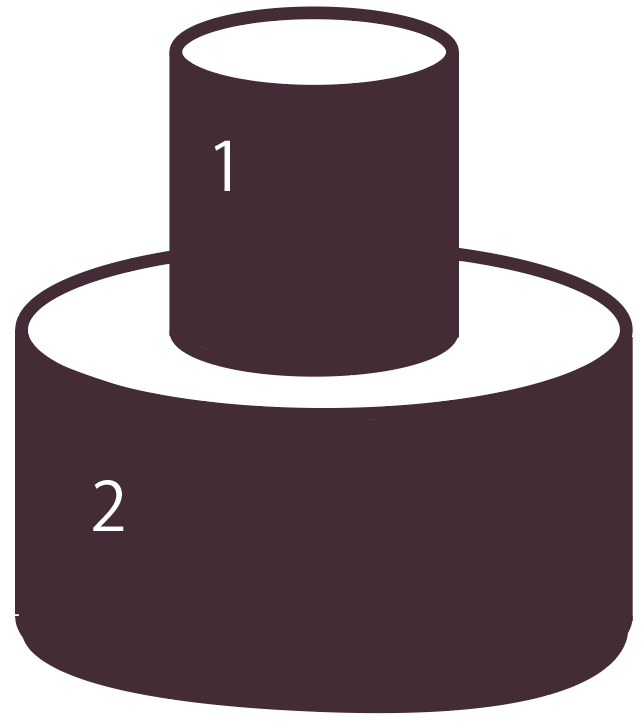
ここで円柱の側面積の求め方の復習ね。
直径×高さ×円周率
で計算できたよね?
上下の円柱の側面積を「(小さい円柱の表面積)+(大きい円柱の表面積)」で足すと、
$$(6π × 5)+ (12π × 5)$$
$$= 30π + 60π$$
$$= 90π[cm^2]$$
になる。
あとは底面積と側面積を足すだけ。
「底面積+側面積」を計算すると、
$$72π + 90π$$
$$= 162π [ cm² ]$$
になるはず。
こんな感じで、円柱が2つくっついていようが、基本は変わらない。
表面積を求めるために、底面積と側面積を足すのさ。
そんじゃねー
Ken
よくテストに出てくるのが「式の値」。
シンプルにいうと、
ある値を文字式に代入する
という問題だ。
今日は式の値の応用問題に挑戦しよう。
いきなり数字を代入したいだろうけど、ちょっと待った!
代入前にやることがあるんだ。
それは、
求めやすいように文字式を変形させること。
計算が楽になったり、問題の突破口が開けたりするよ。
例題だと、
$$2x² + xy + 2y²$$
の値を求めたいよね。
ただ、このままだと求めにくいから、文字式を変形させてあげよう。
がわかっているから、これらを使って値を出しやすいように式を変形。
具体的にいうと、
$$2x² + xy + 2y²$$
$$= 2(x+y)² – 3xy$$
のように「$x + y$」と「$xy$」だけであらわすといいね。
これなら代入しやすくなる。
あとは代入するだけ。
$$2(x+y)² – 3xy$$
に
を代入して、
$$2(x+y)² – 3xy$$
$$= 2 × 1² – 3 × (-3)$$
$$= 2 + 9$$
$$= 11$$
になるね。
こんな感じで、式の値のコツは、
代入前に式をいかに変形させるか
ってこと。
代入前に式の形を整えてみよう。
そんじゃねー
Ken
ルート関係でよく出てくるのはこの問題。

一度解きほぐせばすぐに解けるようになるよ。
知っておきたいのは、
ルートの中身が「何かの2乗」になれば自然数になること。
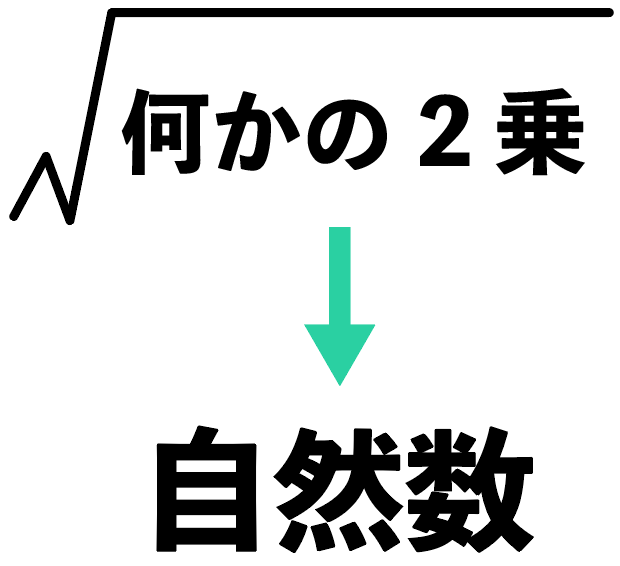
ルートの中身が何かの2乗なら、ルートが外れて自然数になるよね。
例えば、$\sqrt{5}$の2乗だったら、ルートが外れて自然数「5」になるはず。
例題ではルートの中身が「$54a$」だったから、「$54a$」が何かの数字を2乗になるように、$a$を調整すればいい。
ルートの中身を素因数分解しよう。
例題では、ルートの中身が
$54a$
だったから、$a$の前にある54を素因数分解しよう。

詳しくは「素数分解のやり方」で復習してみてね。
素因数分解すると、
$$54 = 2 × 3³$$
になるね。
素因数の指数に注目しよう。
指数とは、
数字についている乗数のこと
だ。
例えば「$3^2$」なら「2」が指数ってこと。
例題では54が
$$2 × 3³$$
に素因数分解できた。
それぞれの因数の「2」と「3」の指数をみると、
になってる。
どの因数の指数も「奇数」ってことだ。
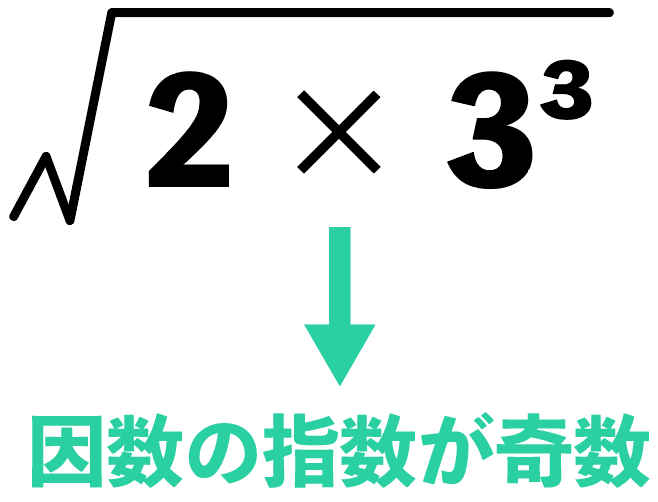
ルートが自然数になるのは、
ルートの中身が「何かの2乗」になるとき
だ。
この場合だと「2」と「3」の指数がぜんぶ偶数になるときさ。
指数が偶数になるパターンは複数考えられるけど、最小の労力で済むのが、
「2」と「3」を1つずつかける方法。
これによって、「$54 = 2 × 3³$」が
$$2² × 3⁴$$
になって、因数の指数がすべて偶数になるね。

だから、54にかける$a$は「 2と3を1個ずつかけた」6が正解だ。
$a$を6とすれば、$\sqrt{54a}$は18という自然数になるはず。

こんな感じでルートの問題と見せかけて、
素因数分解の応用問題だったわけだ。
テストに出やすいからよく復習しておこう。
そんじゃねー
Ken
一次方程式で出てきやすいのが
かっこ()
がついたバージョン。
例えばこんなやつかな↓
次の方程式を解いて。
$$5 ( x + 1 ) = 3 ( 2x -3 )$$
解き方は次の3ステップだよ。
「かっこ」がついていたら、分配法則を使おう。
「分配法則」とは、
かっこ内の項に1つ1つかけて、すべて足す
という計算方法だったね。
たとえば、
$$a × ( b + c )$$
という式があったしよう。
この時、かっこ前の「a」を、中身の「b」と「c」にかけて、そして足して、
$$a × ( b + c )$$
$$= a × b + a × c$$
になるのさ。
例題で分配法則を使うと、
$$5 ( x + 1 ) = 3 ( 2x -3 )$$
$$5x + 5 = 6x – 9$$
になるはず。
かっこを外したら、あとは移項するだけ。
左に文字、右に数字を移項してみよう。
移項とは、
= の反対側に項を移動させる作業
のことだったね。
例題を移項で整理すると、
$$5x + 5 = 6x – 9$$
$$5x – 6x = -9 – 5$$
$$- x = – 14$$
になるはず。
「xの係数」で割ろう。
例題では、xの係数が「-1」 だから両辺を「-1」で割ると、
$$- x = – 14$$
$$x = 14$$
になる。これでやっとxが求められたね。
でもでもでもさ?
たまに、
かっこ前に「分数」がある問題
も出るよね。
例えば次のようなやつ↓
次の方程式を解いて。$$\frac{1}{3}(x + 2)= \frac{1}{2}(2x + 1)$$
さっきと解き方は同じだけど、分配法則の前に、
分数を消し去る
という手順が必要さ。
つまり、
分母の「最小公倍数」を両辺にかけるんだ。
例題だと、分母の「3」と「2」の最小公倍数は「6」。
よって、6を両辺にかけると、
$$\frac{1}{3}(x + 2)= \frac{1}{2}(2x + 1)$$
$$6 × \frac{1}{3}(x + 2)=6 × \frac{1}{2}(2x + 1)$$
$$2 ( x + 2 ) = 3 ( 2x + 1 )$$
になるね。
さっきと同じ「かっこつきの方程式」になったから、同じように解いて、
$$2 ( x + 2 ) = 3 ( 2x + 1 )$$$$2x + 4 = 6x + 3$$$$-4x = -1$$
$$x = \frac{1}{4}$$
と出る。
あと、もう1つ出てきやすいのが、
掛け算じゃなくて「割り算」のパターン。
たとえば、次のような問題かな。
次の方程式を解いてね。$$(x + 4)÷ 2 = (2x + 1)÷ 3$$
この手の問題では、
「割り算」を「掛け算」に直すといいよ。
ずばり、
「÷」後の数字を分母にした分数をかればいいんだ。
例題だと、
$$(x + 4)÷ 2 = (2x + 1)÷ 3$$
$$(x + 4)× \frac{1}{2} = (2x + 1)× \frac{1}{3}$$
になる。
これは「分数がかっこの前についているパターン」と同じさ。
さっきと同じように、分母の最小公倍数を両辺にかければいいんだ。
$$(x + 4)× \frac{1}{2} = (2x + 1)× \frac{1}{3}$$
$$(x + 4)× \frac{1}{2} × 6= (2x + 1)× \frac{1}{3}× 6$$
$$3 ( x + 4 ) = 2 ( 2x + 1 )$$
$$3x + 12 = 4x + 2$$
$$-x = -10$$
$$x = 10$$
テストに割と出やすいからよーく復習しておこう。
そんじゃねー
Ken
「一次関数の利用」で必ず出てくるのが、
点が動く問題。
ちまたでは、
動点の問題
と呼ばれているやつだ。
一番テストに出てくるのは「1つの点が動くパターン」。
だけど、厄介なことに、たまーに、
「2つの点が動く」問題が出ることもある。
例えば次のような問題さ。
AD = 4 cm、BC = 6 cm、 CD = 4 cm、∠C = ∠D = 90°の台形ABCDがある。
2点P、QはそれぞれA、Cを同時に出発し、点Pは辺AD上を、点Qは辺BC上をどちらも毎秒 1 cmの速さで動く。
端まで行けば折り返し、12秒間動くものとする。点P、Qが動き始めてからx秒後の4点A、B、P、Qを結んでできる図形の面積をy cm² とする。
(1) 0 ≤ x ≤ 12のとき、xとyの関係を表すグラフをかきなさい。
(2)四角形ABQPの面積が、台形ABCDの面積の4分の1になるのは点P、Qが動き始めてから何秒後ですか。
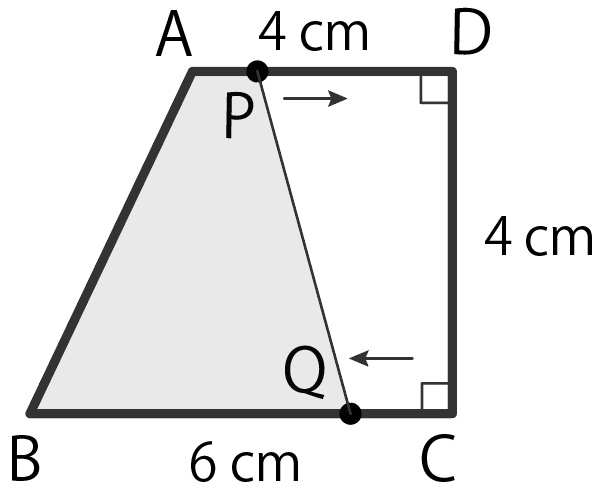
今日はこの応用問題を気合いで乗り切っていこう。
一次関数の動点では、
変域がいくつできるのか?
と見通しをつけるといいよ。
この問題では
点PがAから、点QがCから毎秒1cmの速さで動く
という条件があるね?
しかも、辺の端まできたら折り返して、12秒間動く、らしい。
12秒で四角形ABQPの面積 (y)はどのように変化するんだろう??
分け方のポイントは、
動点が頂点に到着するタイミングで分ける
だよ。
ADはBCより短いから最初に、点PがDに着く。
そして、点Pに遅れてちょっとして点QがBに辿り着く。
PとQは、頂点にたどり着くタイミングが微妙に異なるから、4つの変域が考えられそう。
それぞれの変域で、四角形ABCDの面積の変化をみればいいんだ。
まずはPがAを出発してからDに着くまで。
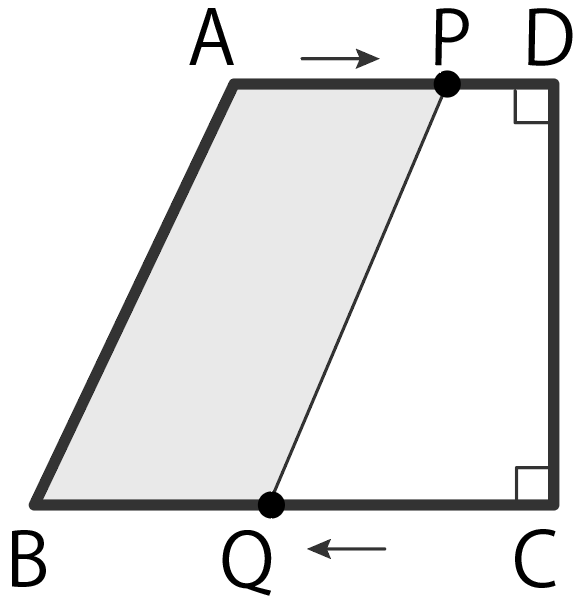
図をかくとわかるけど、四角形ABQPは台形になる。
で、面積を求めるために、
という辺の長さが必要だね。
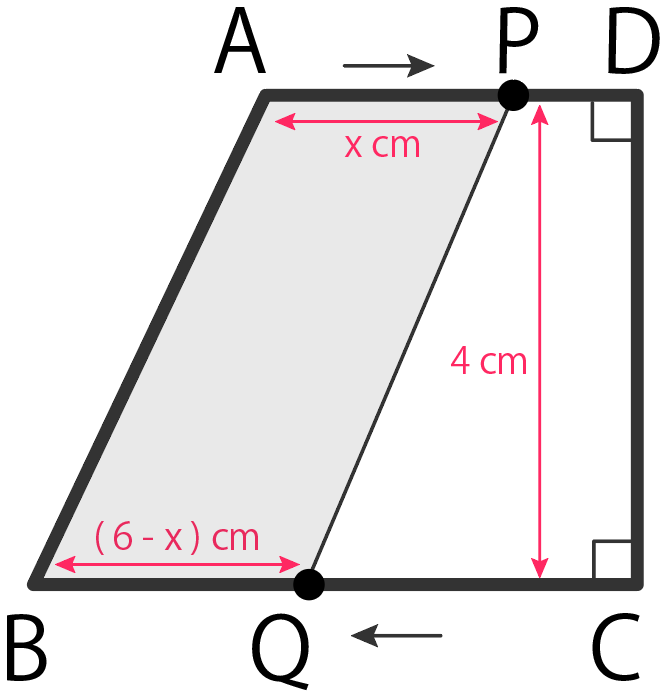
ポイントはBQの長さ。
QはCからスタートしてBに向かっているから
$$CQ= x cm$$
そして、そいつをBCの長さ 6 cm から引いたやつがCQの長さになるから、
$$BQ= BC – CQ$$
$$= 6 – x$$
になる。
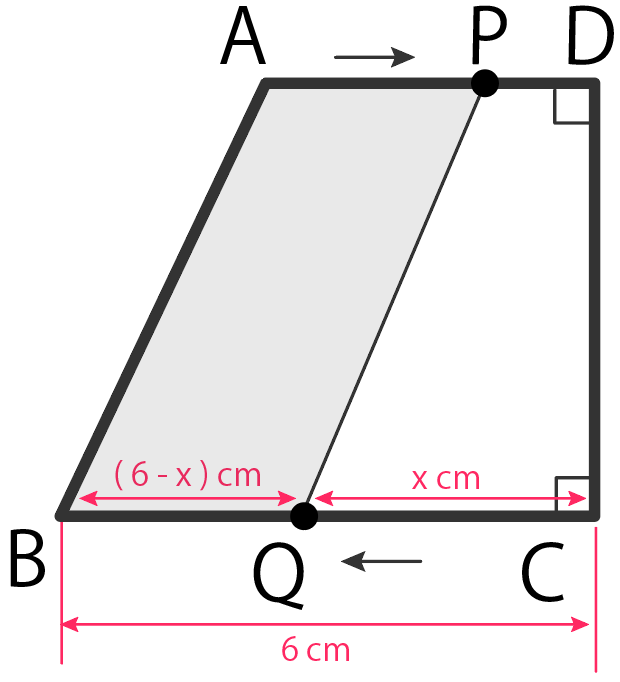
さて。ここで台形ABQPの面積yを計算しよう。
(上の辺+下の辺)×(高さ)÷2
だったから、
$$y = (AP+BQ)× DC ÷ 2$$
$$= (x +6 -x)× 4 ÷ 2$$
$$= 12$$
になる。
0〜4秒では、台形ABQPの面積はずーっと12ってこと。
PがDに到着して、折り返しを始めたら、四角形ABQPの面積は変化するよ。
この場合、APの長さが変化してきていて、
$$8 – x$$
になってるはず。
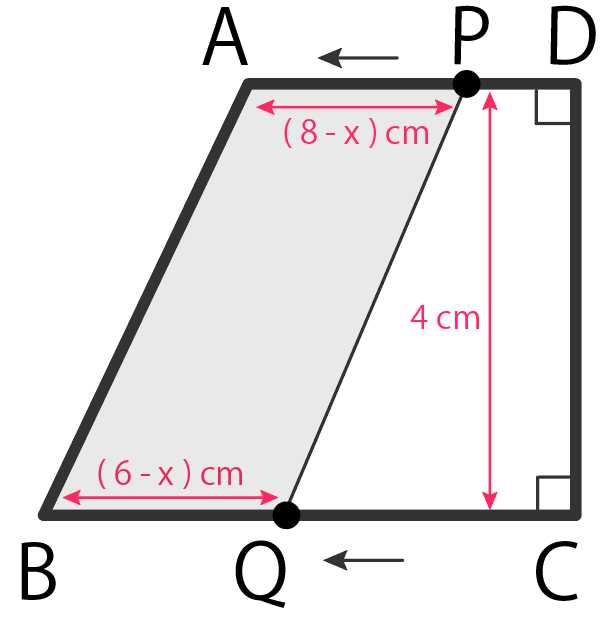
ADを2倍した長さから、Pが動いた距離「x」を引くとAPになるね。
ただ、相変わらず四角形ABQPは台形さ。
同じように台形の面積 y を計算すると、
$$y = (AP+BQ)× DC ÷ 2$$
$$= (8-x +6 -x)× 4 ÷ 2$$
$$= -4x + 28$$
になる。
この式から分かるのは、
このフェーズ($0 ≤ x ≤ 4$)では時が経つにつれて面積が小さくなるってこと。
お次はPがDに到着して、PがAに戻るまでの時間。
6〜8 秒までだね。
ここでのポイントは、BQの長さが変化していること。
QはBに到着して、折り返しているから、
BQ=
Qが進んだ距離 – BCの長さ
= x – 6
になる。
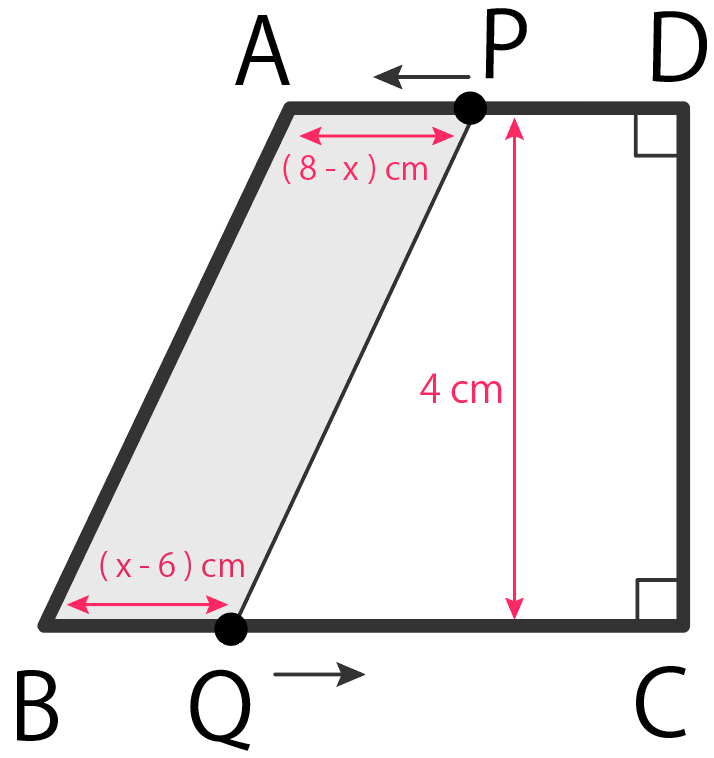
すると、四角形ABQP(というか台形)の面積yを計算すると、
$$y = (AP+BQ)× DC ÷ 2$$
$$= (8-x +x – 6)× 4 ÷ 2$$
$$= 4$$
になるね。
あら不思議。
またまた面積yが一定になっちゃった。
最後はQがCに戻るまで。
このタイミングは、Pが2回目にDに到着するタイミングでもあるとも言えるね。
変域で表すと
$$8 ≤ x ≤ 12$$
になる。
この時ポイントは、APの長さが変化していること。
PはAに到着して、折り返してDを目指しているはず。
だから、
APの長さ
=Pが進んだ距離 – ADの2倍の距離
= x – 8
になる。
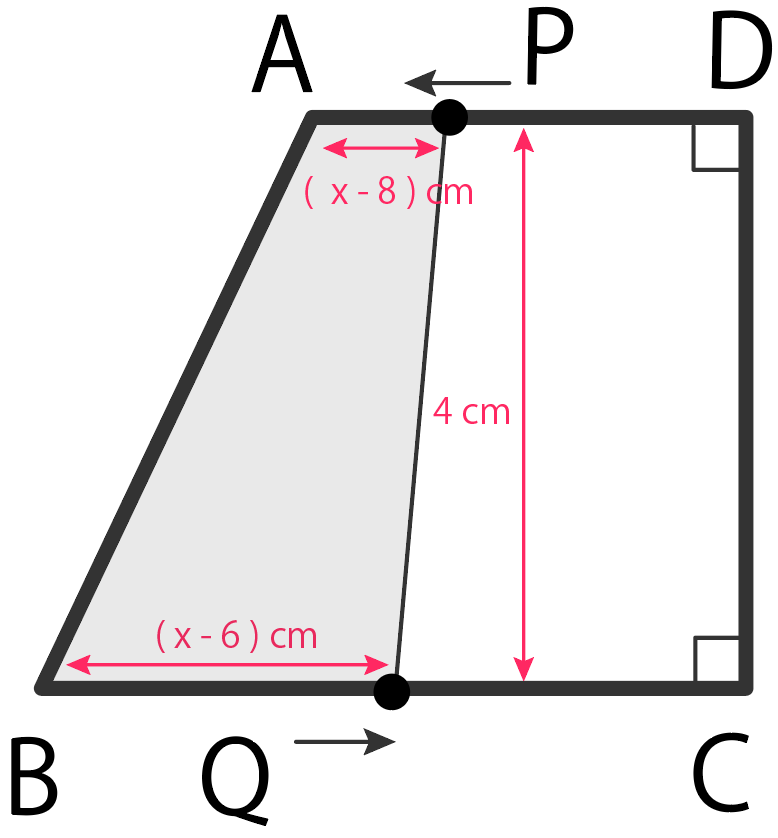
四角形ABQP(というか台形)の面積yを計算すると、
$$y= (AP+BQ)× DC ÷ 2$$
$$= (x – 8 +x – 6)× 4 ÷ 2$$
$$= 4x – 28$$
になる。
ふう、これで全部の変域における関数式が出せたぜ。
それぞれの式をグラフにするとこんな感じ。
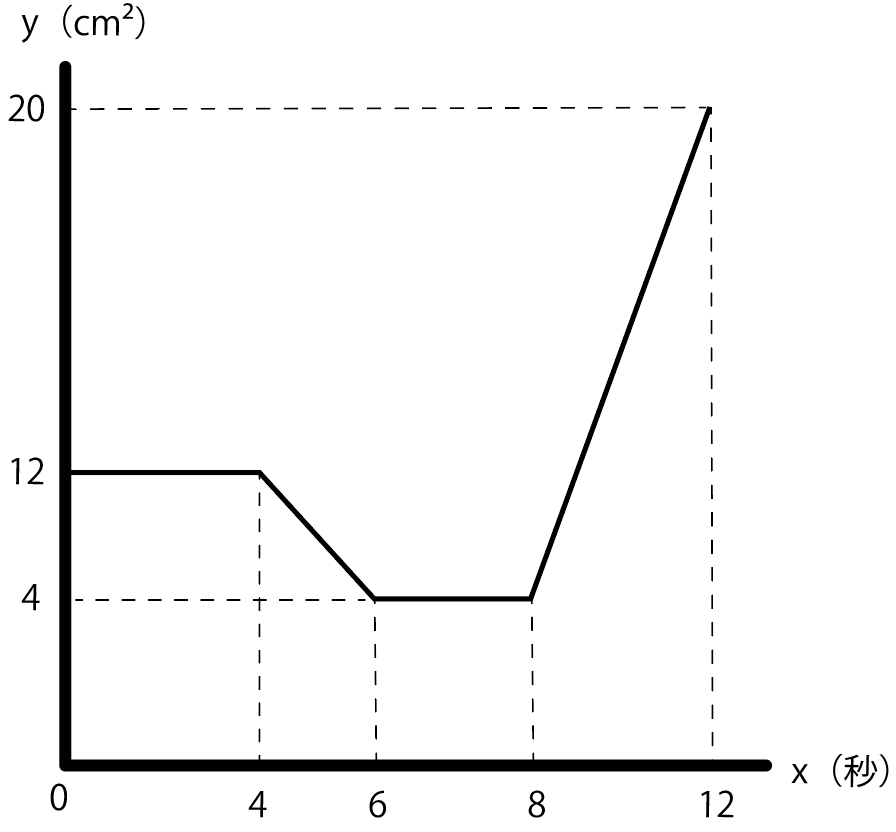
あと1つやることがある。
それは、例題の(2)の
四角形ABQPの面積が、台形ABCDの面積の4分の1になるのはいつ?
に答えること。
つまり、これ、
yが特定の値になる時のxを求めよ
という問題だ。
まずは「台形ABCDの面積の4分の1」がいくつか探っていこう。
台形ABCDは上辺が4、下辺が6、高さが4の台形だから、
$$(4 + 6 )× 4 ÷ 2$$
$$= 20 cm²$$
という面積になる。この4分の1は「$5 cm²$」だ。
ここで、さっき適当にかいたグラフに注目。
yが「5 」になっている箇所を探してみると、2つヒットだ。
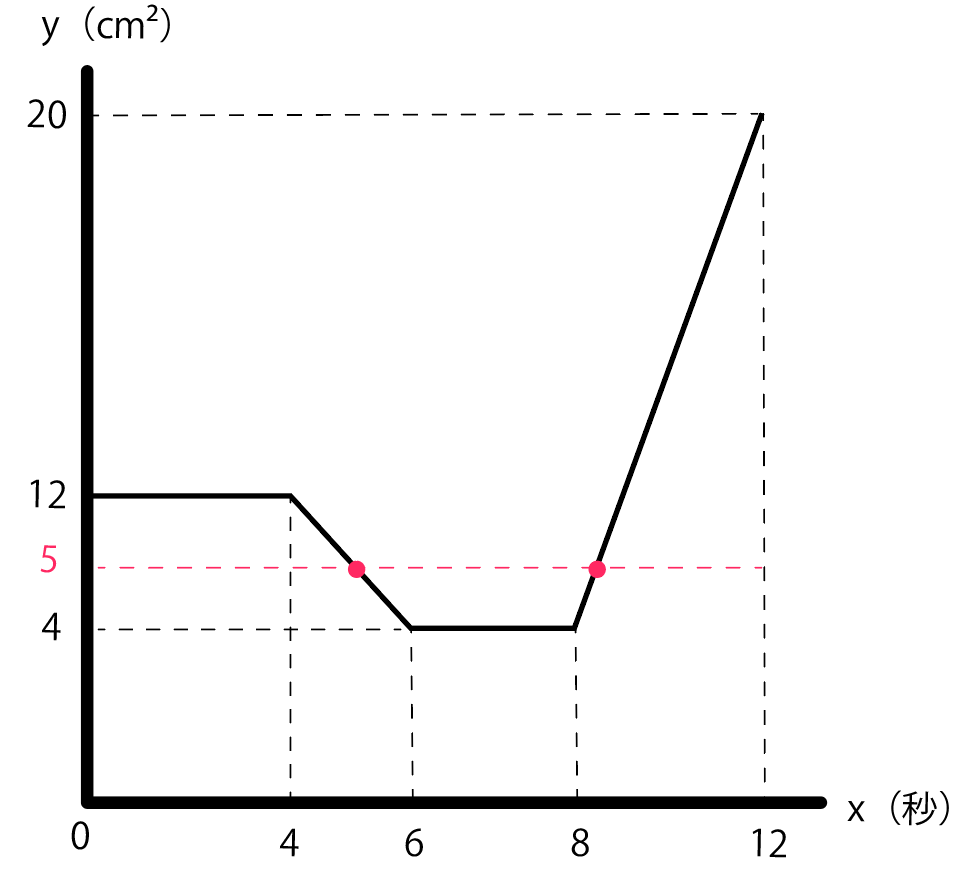
という2つの変域でyが5になる瞬間があるじゃないか。
ということで、これら2つの変域の関数にそれぞれ$y=5$を代入して、その時のxを求めればいいことになる。
まず、QがBに着くまで($4 ≤ x ≤ 6$)の場合。
$$y = -4x + 28$$
に $y = 5$を代入すると、
$$5 = -4x + 28$$
$$x= \frac{23}{4}$$
になるね。
あと1つは、QがCに戻るまで($8 ≤ x ≤ 12$)の場合。
$$y = 4x -28$$
に$y = 5$を代入しよう。
すると、
$$5 = 4x -28$$
$$x = \frac{33}{4}$$
になる。
ってことで、四角形ABQPの面積yが$5 cm²$になる時間は、
の2つだ。
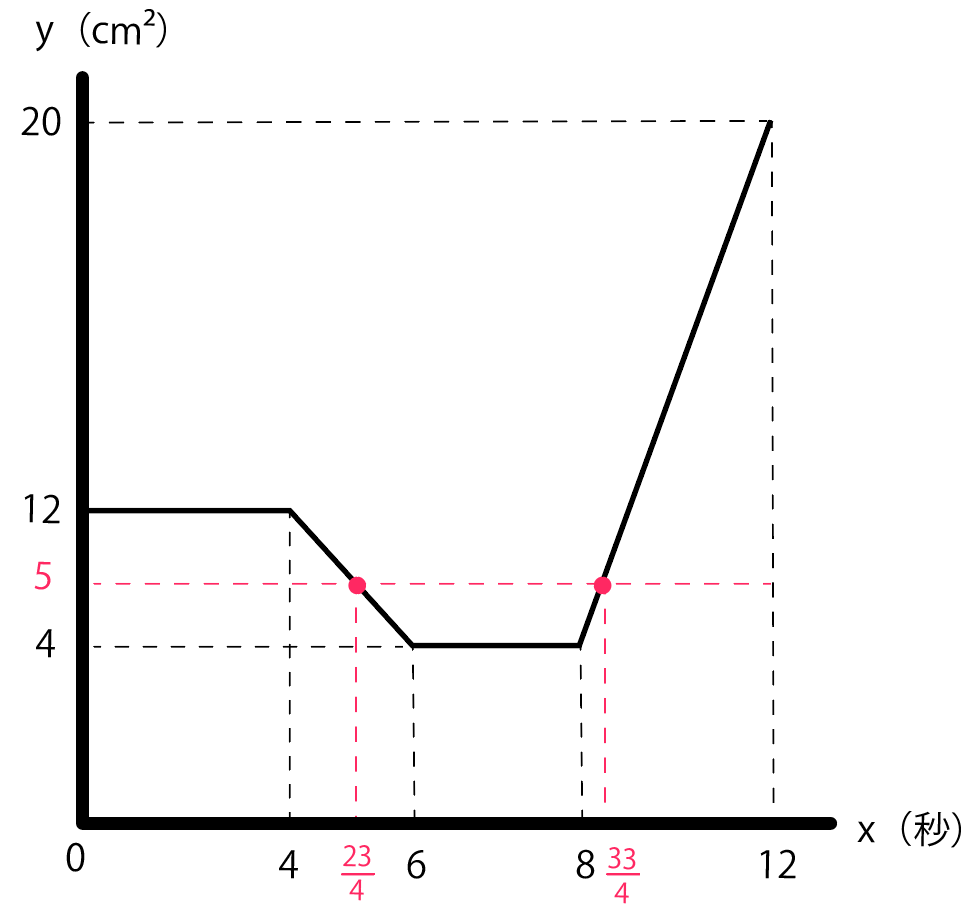
いやーほんとおつかれさま。
動点が2つあるとこんなに厄介だとは思わんかったな。
応用問題では出現することがあるから対策しておこう。
そんじゃねー
Ken
前回、「平行な2直線の求め方」を勉強してきたね?
今回はそれと似たようなやつで、
ある直線に「垂直な」式を求める問題
にチャレンジしよう。
例えば、次のような問題↓
状況を図にかくとこんな感じ。
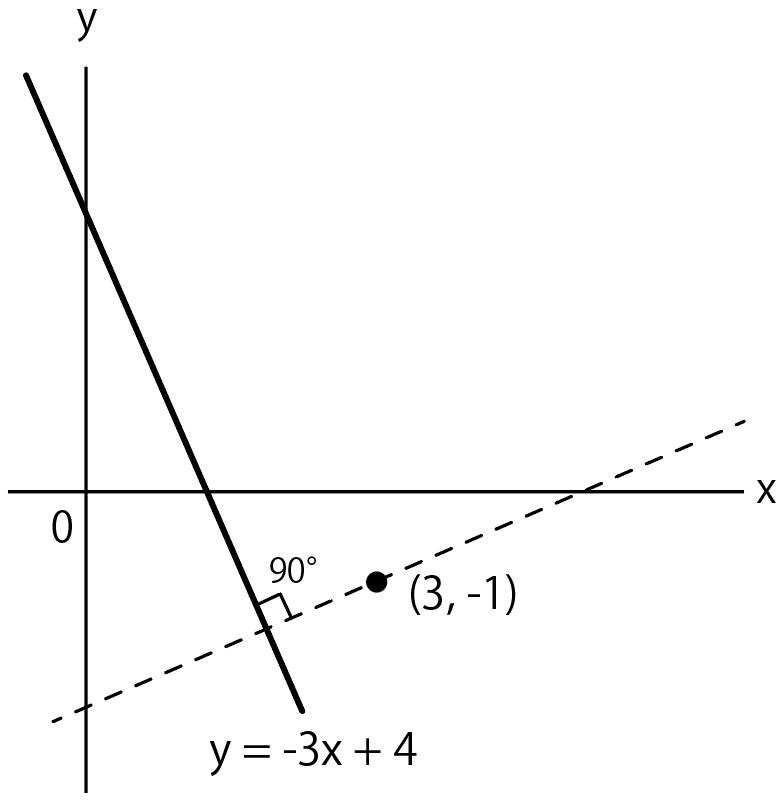
点線になっている一次関数の式を求めるんだ。
この手の問題は次の方法で解けるはず。
2直線が垂直だったらわかること。
それは、
2直線の傾きをかけたら 「- 1」になる
こと。
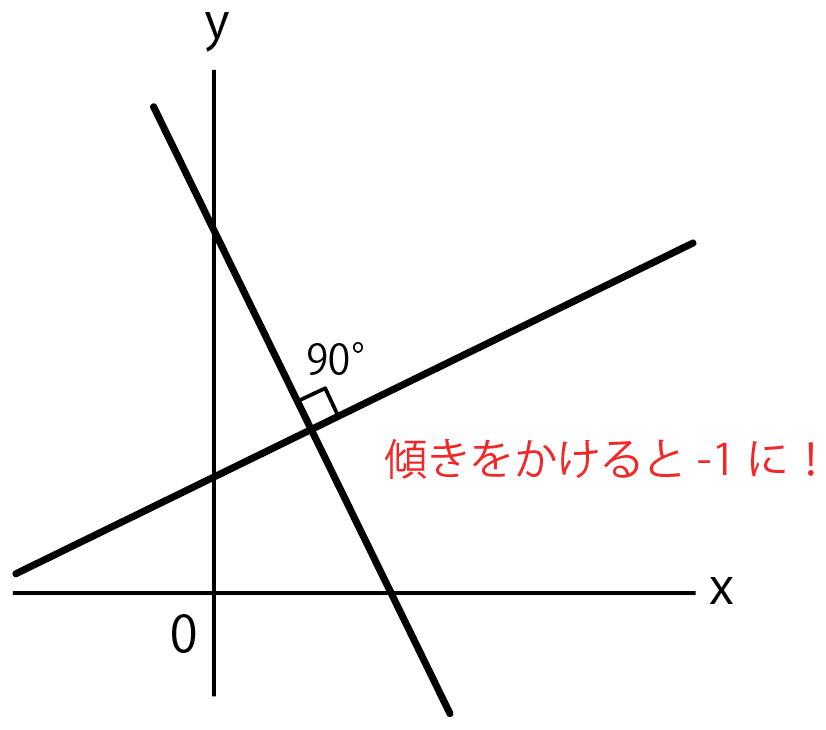
例えば「$y = – 3x + 4$」に垂直な直線の傾きを考えてみよう。
傾き「- 3」にかけたら 「- 1」になる傾きを求めればいいんだ。
求めたい直線の傾きを「a」とすると、
$$- 3 a = -1$$
$$a = \frac{1}{3}$$
と出てくるね。

って感じで、垂直ってヒントから、一次関数の傾きがわかっちまうんだ。
さっきのステップで$y = ax + b$の傾きが分かった。
あとは座標を代入して「切片b」を求めよう。
例題では
点(3, – 1)を通る
っていうヒントがあったから、この座標を代入しよう。
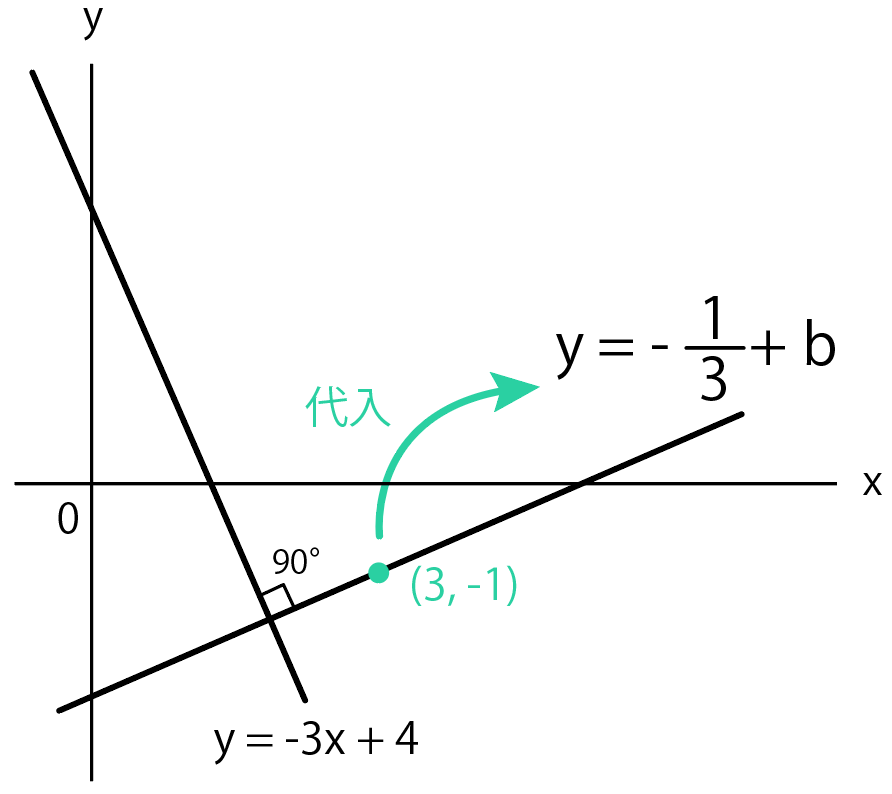
すでに傾きは$\frac{1}{3}$とわかったから、
$$y = \frac{1}{3} x + b$$
$$-1 = \frac{1}{3} × 3 + b$$
$$b = -2$$
となるね。
ここで疑問に思うのが、
垂直な2直線の傾きをかけたらなぜ「- 1」になるのか?
ってこと。
シンプルでわかりやすいけど、理由を教えてもらえないとしっくりこないよね。
これを証明するには、中学3年生でならう三平方の定理を使うよ。
例えば$y =mx$、$y = nx$という1次関数(比例)があったとしよう。
そして、直線上にx座標が「1」の点A、Bがあるシチュエーションを想像してくれ。
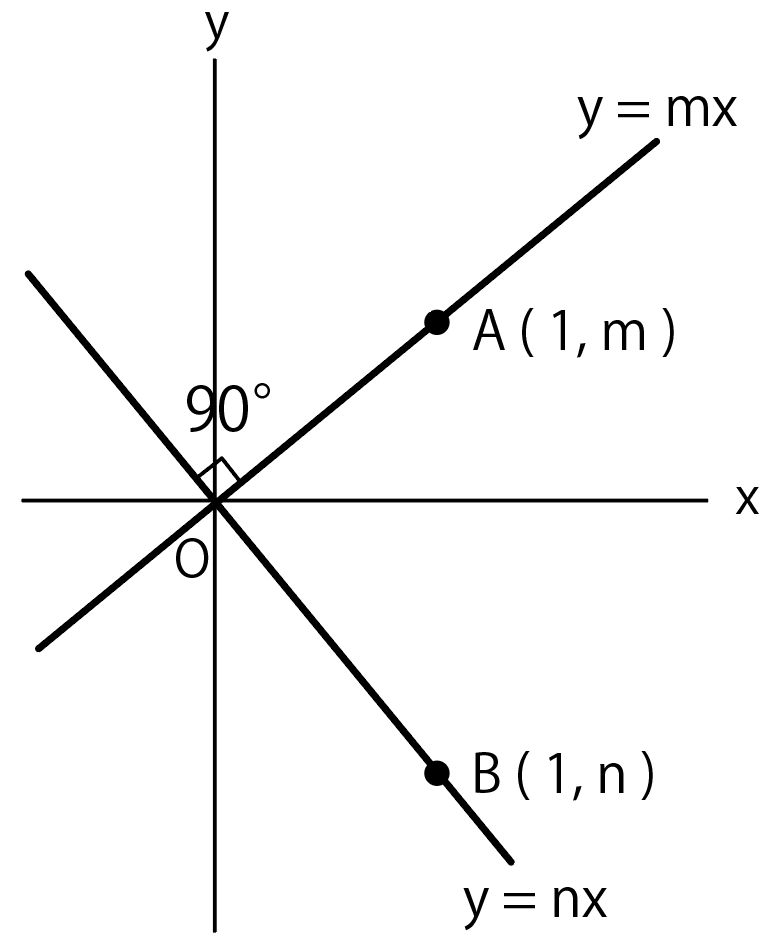
このとき、ABの長さはAのy座標からBのy座標を引いて
$$m – n$$
になるはず。
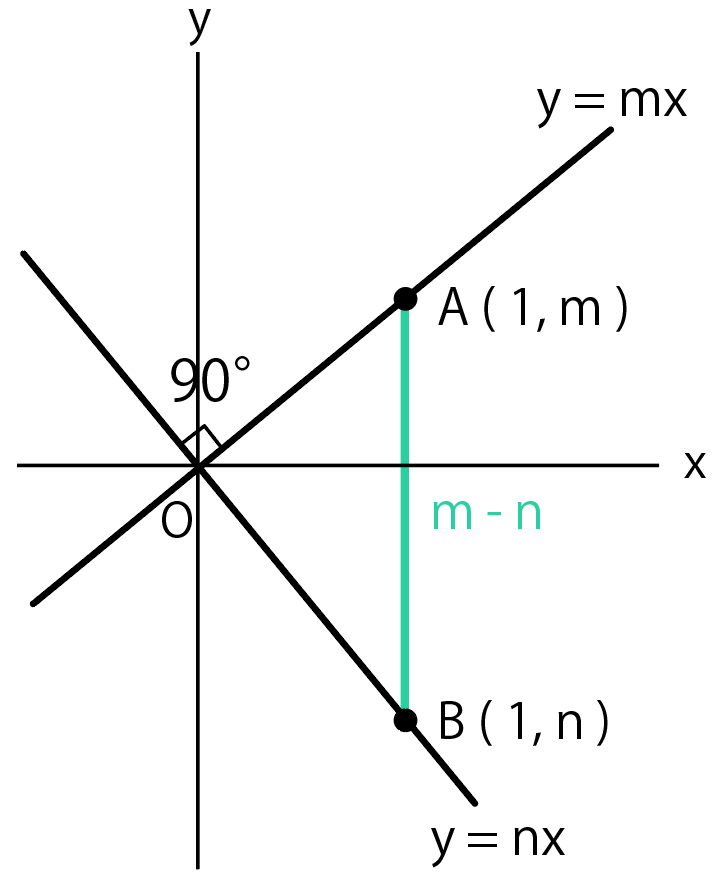
三平方の定理を使うと
$$OA =\sqrt{(1² + m²)} $$
$$OB = \sqrt{(1² + n²)}$$
と計算できる。
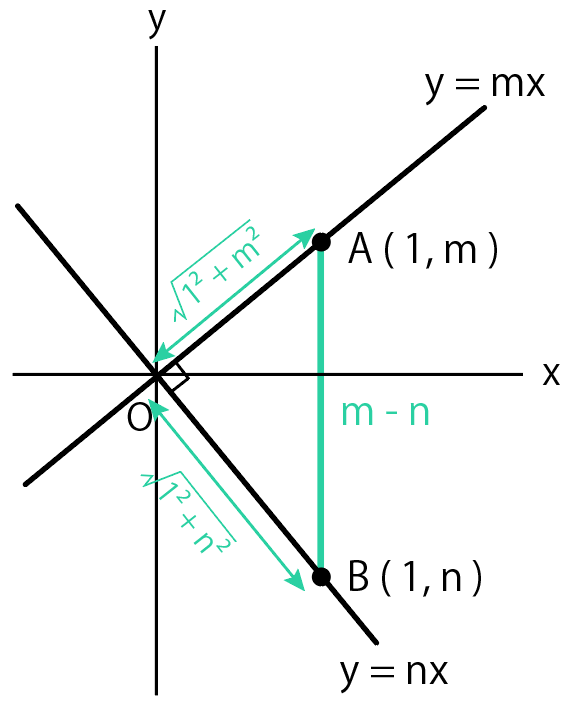
直角三角形OABに注目して、三平方の定理を使うと、
$$AB² = OA² + OB²$$
$$(m – n)^2 = {\sqrt{(1² + m²)}}^2 + {\sqrt{(1² + n²)}}^2$$
$$2mn = -2$$
$$mn = -1$$
となる。
「m」と「n」は垂直な直線の傾きだから、
垂直な2直線の傾きをかけると-1になる
って証明できるね。
こんな感じで、垂直な直線の傾きをかけると -1 になるから便利。
ついでに、なぜそうなるのかを理解しておけば怖いものなしだ。
テストに出てきやすいからよーく復習しておこう。
そんじゃねー
Ken