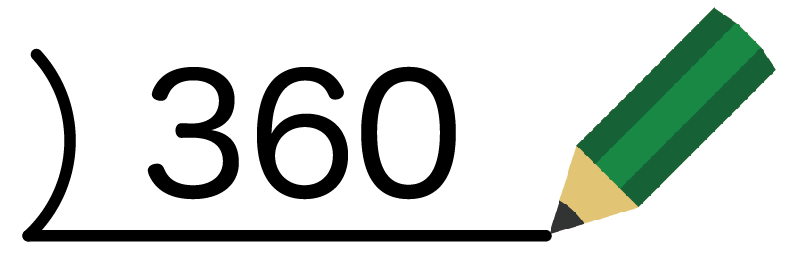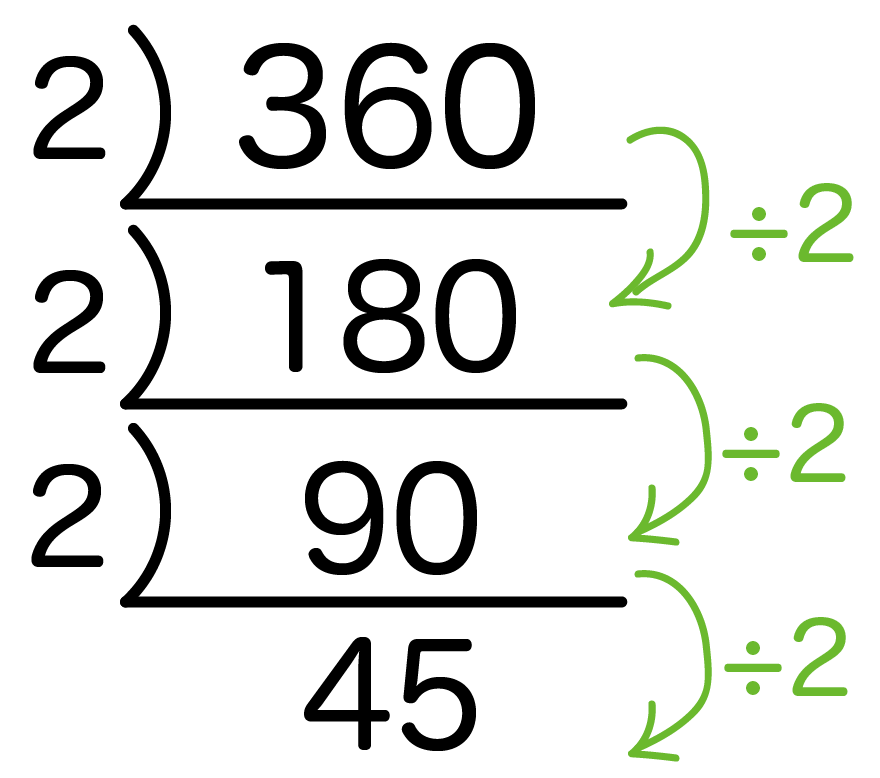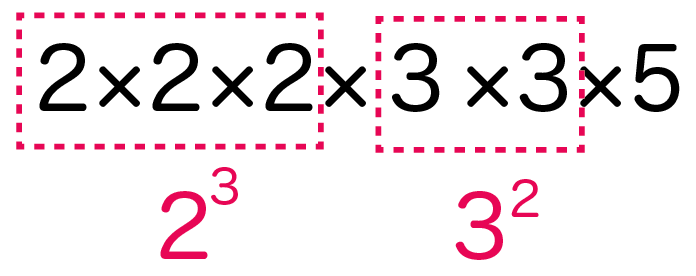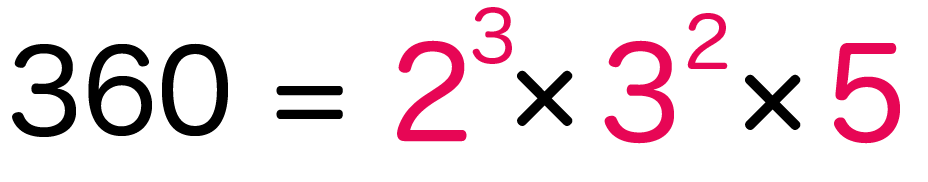素因数分解のやり方・解き方がわからん！？
こんにちは！この記事をかいているKenだよ。塩は大事だね。
ってことは習ったね。
だけどさ、
実際、素因数分解ってどうやるんだろう？？
やり方なんてぜんぜんイメージできないよね。
だって、素因数分解したことないんだもん。
そこで今日は、
素因数分解のやり方を5ステップで解説してみたよ。
よかったら参考にしてみて。
素因数分解のやり方がわかる5ステップ
素因数分解のやり方はずばり、
素数でわりまくって、割れた素数を集めて因数にする
方法だ。
だから、素因数分解で大切なのは、
素数で割りまくる根性
と、
素数かどうか見分ける力
なんだ。
この2つさえあれば素因数分解なんて楽勝さ。
素因数分解は5ステップでできちゃうよ。
- 自然数をかく
- 線をかく
- 素数でわりまくる
- 割れた素数を×でつなげる
- 指数でまとめる
例として、自然数の360を素因数分解してみよう！
Step1. 自然数をかく
まず、素因数分解したい自然数をかいてみよう。
鉛筆でもシャープペンでもいいからかいてみて。
例題でいうと、
360
だね。
うまくかけたらつぎにいこう。
Step2. 線をかく
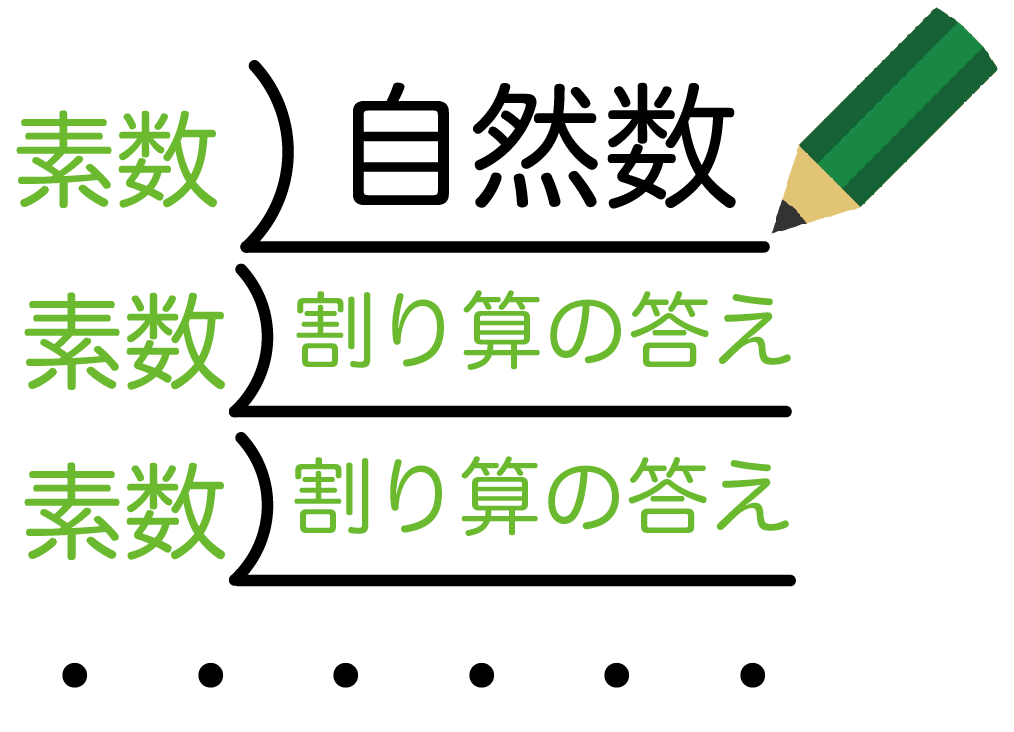
つぎは素因数分解するための準備。
自然数の周りに線をかいてみて。
これは素数で割りまくるための道具なんだ。
この線の横に、自然数を割る素数、
自然数の下にその割り算の答えをかいていくんだ。
もし、「割り算の答え」が素数でわれるようだったら、
こんな感じで下に続けていって、素数でわりまくるんだ。
例題でもおんなじさ。
360の下にこのきんとんうんのような線をちょこっとかいてあげよう。
これが第2ステップ！！
Step3. 小さい素数から順番にわりまくる！
いよいよ素因数分解の山場。
素数でわりまくる
っていうステップだ。
ここでのコツは、
小さい素数から割りまくる
ってこと。
つまり、素数でいちばん小さい「2」から割りまくるのさ。
2で割り切れなくなったら3、
3で割り切れなくなったら5、
・・・・
というように徐々に素数を大きくしていこう。
割り算の答えが1になるまで続けてみてね。
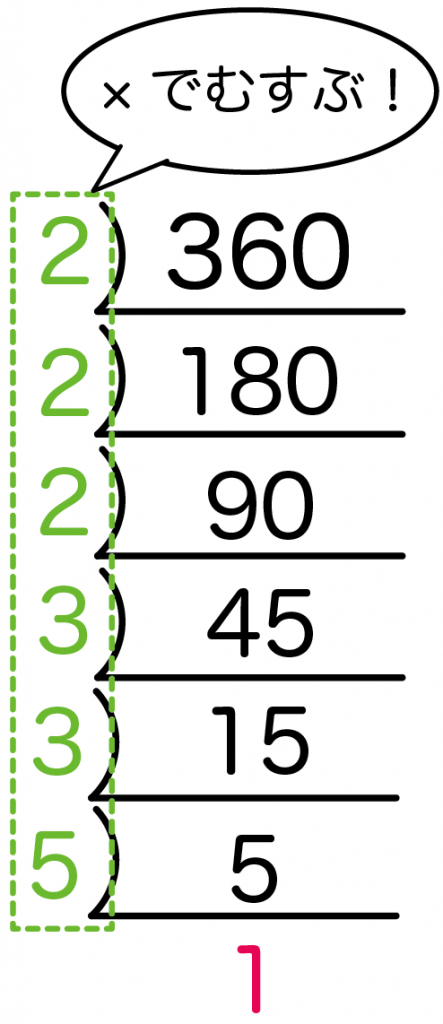
例題の「360」もまずは素数2でわりまくってみよう。
すると、
- 360÷2 = 180
- 180÷2 = 90
- 90÷2 = 45
っていう感じで3回われたね！
45は残念ながら2で割り切れないから3にバトンタッチだ。
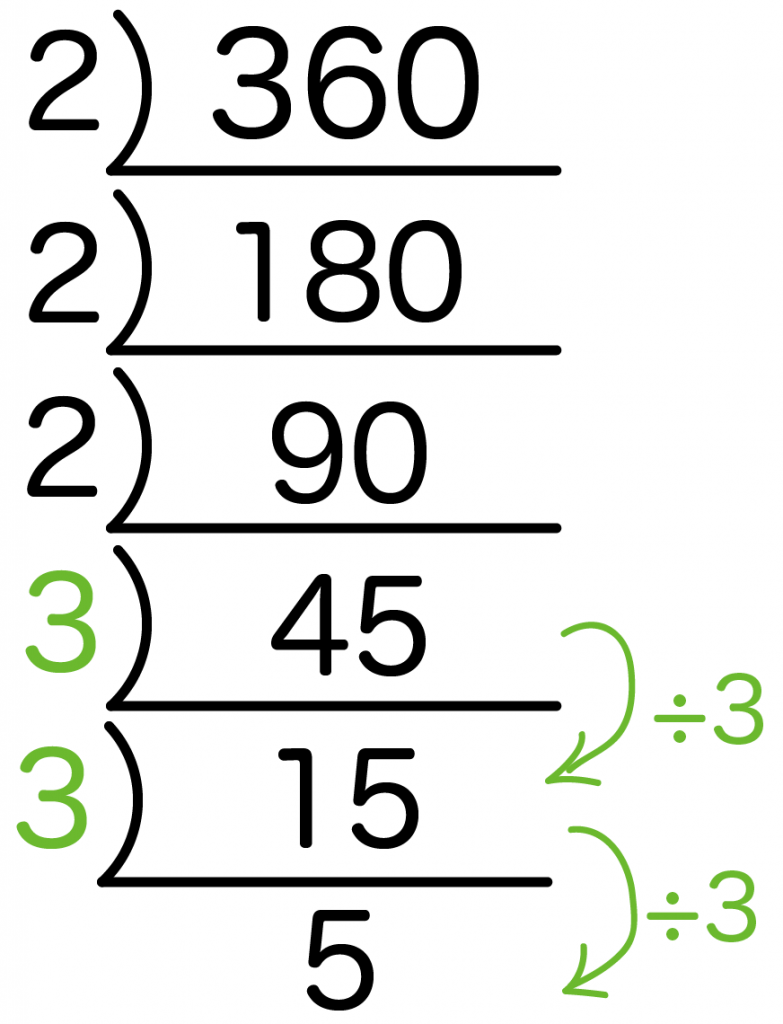
おなじように、3で割りまくってみると、
- 45÷3 = 15
- 15÷3 = 5
っていう感じで2回われたね。
お次は素数の5の出番。
おなじように割り算の答えをわってみると、
- 5÷5 = 1
・・・
おや！
1がでてきたね！
割り算の答えが1になったからストップ。
Step4. 割った素数を×でむすぶ
割ってきた素数を集めるフェーズだ。
左の素数をかきあつめて「×」でむすんでみよう。
たとえば、自然数が素数1から素数nまでわれちゃったとしよう。
このとき、割れちゃった素数を「×」でむすんでやると、
素数1×素数2×素数3×・・・×素数n
になるね。
これを360の素因数分解でもやってみよう。
割った素数はぜんぶで、
- 2
- 2
- 2
- 3
- 3
- 5
の6つだね？？
こいつらを「×」でむすんでやると、
360 = 2×2×2×3×3×5
になるね。
Step5. 指数でまとめる
最後は指数でシンプルにしよう。
同じ素数を指数でまとめればいいのさ。
360の素因数分解でいうと、
- 2
- 3
が指数でまとめられそうだね。
指数でコンパクトにしてやると、
360 = 2^3 × 3^2 × 5
になるはずだ。
おめでとう！
これで素因数分解のやり方もマスターだね。
まとめ：素因数分解のやり方は根性で乗り切れ！
素因数分解は基本的に、
素数で自然数をわりまくって、
あつめて、
かけ算にしてやるだけ。
あとは指数でととのえればよし。
素因数分解はいろいろな計算に使えて便利。
やり方・解き方はおぼえておこうね。
そんじゃねー
Ken
