【中1数学】累積相対度数の求め方をわかりやすく解説
「累積相対度数の求め方」を教えてほしい!!

さて、中1数学で「累積相対度数」を勉強しますよ。
そう、出ました。
累積??
相対??
度数!?!?
相対度数の時点で怪しかったのに、さらに「累積」が追加。
もう頭がパンクしそうですよね。
今日は、
「累積相対度数の求め方」
を、できるだけやさしく解説します。
よかったら参考にしてください。
~もくじ~
- 累積相対度数とはなにか??
- 「累積相対度数の求め方」
- 累積相対度数の2つの注意点
中学数学の「累積相対度数」とはなにもの??
累積相対度数とはずばり、
小さい階級から順に、相対度数を足していったもの
です。
……またしても、わかりませんね。
言葉をいいかえると、
「この階級までで、全体の何%になるか」
を表した数なのです。
ポイントはこの2つ。
- 小さい階級から順番に
- 相対度数を足していく
これだけ覚えておけばOKです。
累積相対度数の求め方がわかる3ステップ
では、相対度数のときと同じ具体例「マメつかみゲーム」の度数分布表を使って考えてみましょう。

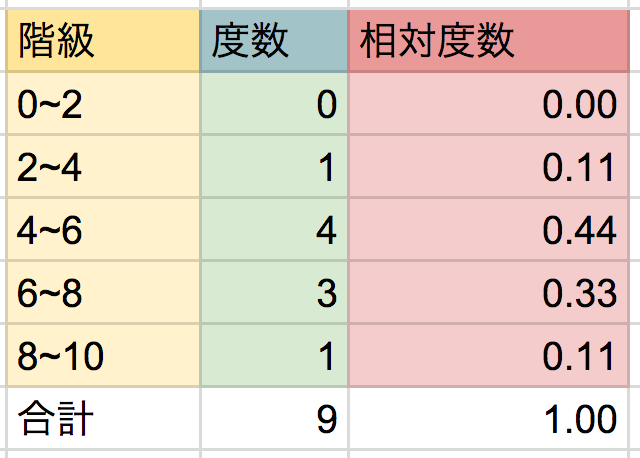
累積相対度数の求め方はズバリ、
一番小さい階級から順に、相対度数を足すだけ!
です。
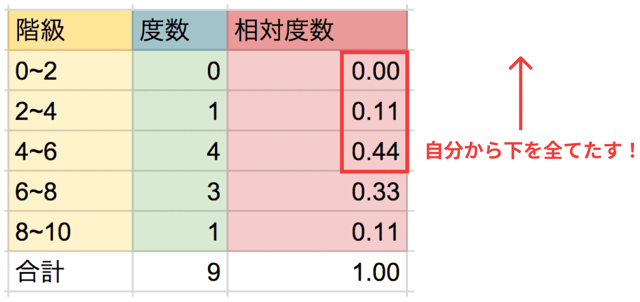
たとえば、今回の場合だと
- 0~2 の累積相対度数 → 0.00
- 2~4 の累積相対度数 → 0.00 + 0.11 = 0.11
- 4~6 の累積相対度数 → 0.11 + 0.44 = 0.55
- 6~8 の累積相対度数 → 0.55 + 0.33 = 0.88
- 8~10 の累積相対度数 → 0.88 + 0.11 = 0.99 ≒ 1.00
になりますね。
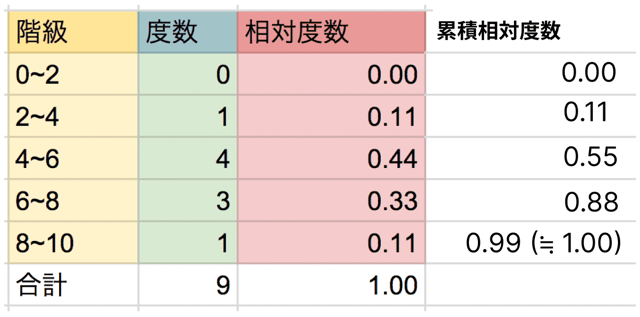
このように、
前の累積相対度数に、次の相対度数を足す
という作業をくり返すだけでいいんです。
累積相対度数で何がわかるの??
えっ、累積相対度数がなんの役に立つか、ですって??
じつは累積相対度数を見れば、
「この値以下の人が、全体の何割か」
が一発でわかります。
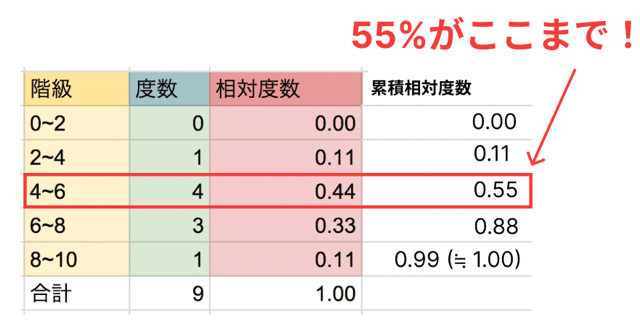
たとえば、
- 累積相対度数が 0.55 → 55%の人がそこまで
- 0.50 に近いところ → 中央値の目安
という感じで使われますよ。
「累積相対度数の求め方」における2つの注意点
累積相対度数で気をつけるポイントは2つあります。
最後は必ず「1」になる
累積相対度数は、最後の階級で必ず「1」になります。
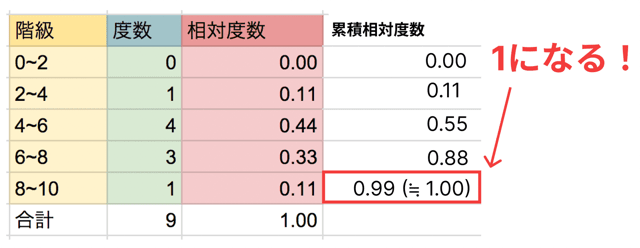
なぜなら、全体の100%を足し切った状態だからです。
計算ミスをしていないかどうか、最後が1になっているか必ずチェックしましょう。
今回の「マメつかみゲーム」でも、
8~10 の累積相対度数 → 0.88 + 0.11 = 0.99 ≒ 1.00
となっていますね。最後の累積相対度数は1です。
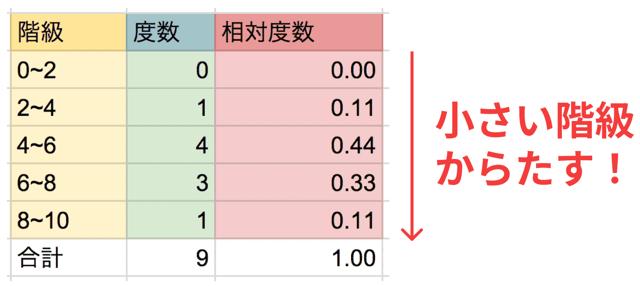
2. 小さい階級から足す
累積相対度数は、順番が命です。
大きい階級から足したり、途中を飛ばしたりするとアウト。
必ず、
小さい階級 → 大きい階級
の順番で足しましょう。
今回の「マメつかみゲーム」でも、
大きい階級の「8~10」から足しちゃダメってことですね。
累積相対度数の求め方、これでOK!
以上です。
累積相対度数は、
- 相対度数を求める
- 小さい階級から順に足す
でしたね。

次は「中央値」を勉強しましょう。
そんじゃねー




