やあ、Dr.リードだよ。今日は「逆」だよ。逆。
これまで勉強してきた、三平方の定理には、
三平方の定理(ピタゴラスの定理)の逆
っていうのがあるんだ。

逆は中2数学で習ったやつだったね。
忘れてるやつも多いと思うから、逆を復習しつつ、
三平方の定理でも逆が言えるのか??
を見ていこう。
=もくじ=
まずは数学の「逆」を復習してみよう。
数学の「逆」とはずばり、
ある命題の「仮定」と「結論」を入れ替えたもの
なんだ。
数学の命題とは、「正しいか、正しくないかを考える事柄のこと」だったね。
たとえば、次のような命題があるとするよ。
x =2, y = 3 ならば x+y = 5

仮定と結論をいれかえて、逆を作ってみると、
x+y = 5 ならば x =2, y = 3
になるね。

この命題の逆は正しいかな?
「x+y=5」を満たすxとyの組み合わせって「x=2, y = 3」以外にもありそうだよね?
たとえば、「x = 0、 y = 5」とかね。
だから、この場合は逆にすると命題が成り立たないね。
この例みたいに、
ある命題は正しいけど、逆は正しい場合もあるし、正しくない場合も両方あり得るんだ。
では、三平方の定理の逆はどうだろ。
三平方の定理(ピタゴラスの定理)とはこうだったな。
【三平方の定理(ピタゴラスの定理)】
直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、
a²+b² = c²
が成り立つ。

この三平方の定理(ピタゴラスの定理)で逆をつくってみようか。
三平方の定理の仮定と結論は、
だ。
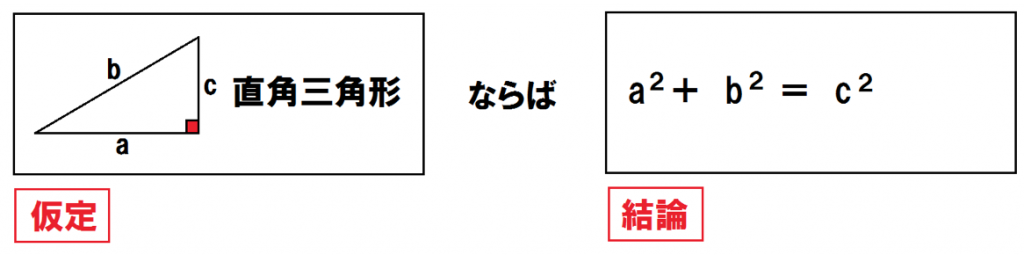
この逆をつくってみると、
になるね。
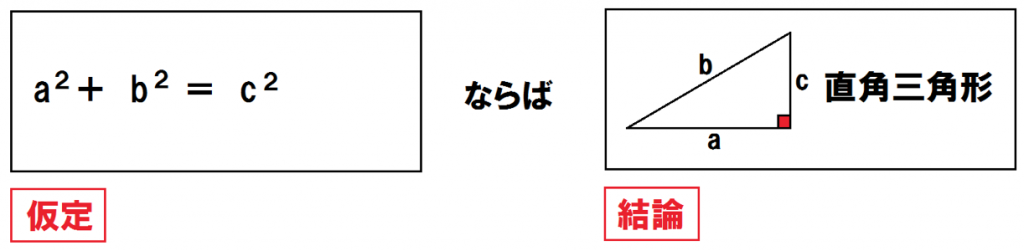
つまり、三平方の定理(ピタゴラスの定理)の逆は、
「a²+b² = c²」ならば「直角三角形である」
だ。
はてさて、これは正しいのかな?
三平方の定理の逆の証明してみるか。

わかりきってても、きっちりいくぜぃ。
下の図のような△ABCと△DEFがある。
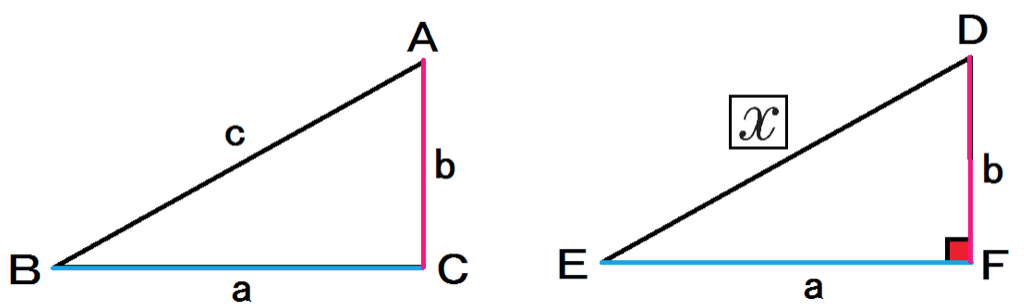
【仮定】
△ABCにおいて a²+b² = c²
△DEFは直角三角形である。
【証明】
△ABC と△DEF について、
仮定より、 a²+b² = c²・・・(1)
△DEFは直角三角形なので 三平方の定理より
a²+b² = x² ・・・(2)
(1)・(2)より、
c² = x²
c も x も正の数なので 、
c = x
△ABCと △DEF の3つの辺がそれぞれ等しいので、
△ABC ≡△DEF
よって ∠BCA =∠EFD=90°
したがって、
△ABC は直角三角形である。
この証明からわかるのは、
三平方の定理の逆も正しい!
ってこと。
中学生ならこの証明で十分かな!

三平方の定理の逆をつかった問題を解いてみよう。
練習問題
次の1辺の三角形があります。直角三角形となるのはどれですか。
(1) 3 cm 4 cm 5 cm
(2) 2 cm √7 cm √10 cm
(3) 15 cm 13 cm 7 cm
(4) 2 cm 2 cm √6 cm
(5) 2√5 cm 2√6 cm 2√7 cm
(6) 2√5 cm 2√5 cm 2√10 cm
2ステップで解けちゃうぜ。
一番長い斜辺は5 cmだから、斜辺の2乗は5² = 25。
他の2辺のに乗の和は、
3² + 4² = 25
になるね。
三平方の定理が成り立つから、直角三角形である!

斜辺は√10cmだから、斜辺の2乗は、
(√10)² = 10
になる。
他の2辺の2乗の和は、
2² + (√7)² = 11
三平方の定理が成り立たないから、直角三角形ではない。

一番長い辺の斜辺は15 cm。
斜辺の2乗は 15² = 225。
他の2編の2乗の和は、
7² + 13² = 218
三平方の定理が成り立たないから直角三角形ではない。

斜辺は√6 cmだから、斜辺の2乗は、
(√6)² = 6
になる。
他の2辺の2乗の和は、
2² + 2² = 8
三平方の定理が成り立たないから直角三角形ではない。

斜辺は2√7 cmだ。
斜辺の2乗は(√7)² = 7
他の2辺の2乗の和は、
(2√5)² + (2√6)² = 44
三平方の定理が成り立たないから直角三角形ではない。

斜辺は2√10 cmだから、斜辺の2乗は (2√10)² = 40になる。
他の2辺の2乗の和は、
(2√5)² + (2√5)² = 40
三平方の定理が成り立つから、直角三角形。

三平方の定理の逆はどうだったかな?
散々「ピタゴラスった!」から慣れたようだね。
つぎは立体で三平方の定理を使えるようになってみよう!
それじゃあな!
Dr.リード
やあやあ、Dr.リードだよ。
3年生の数学もいよいよ大詰め。
今日は、高校入試でよく出てくる、
正四角錐の高さを求める問題
を解説していくぞ。
正四角錐って、底面が正方形で、先っちょが尖ってる立体のことだったね。

ちょうど、エジプトのピラミッドが正四角錐だな。
正四角錐の高さを求めるためには、中3で勉強した三平方の定理も使っていくぞ。
正四角錐の高さの求め方はつぎの4ステップだ。
つぎの例題をいっしょに解いていこう。
練習問題
つぎの正四角錐の立体の高さを求めなさい。
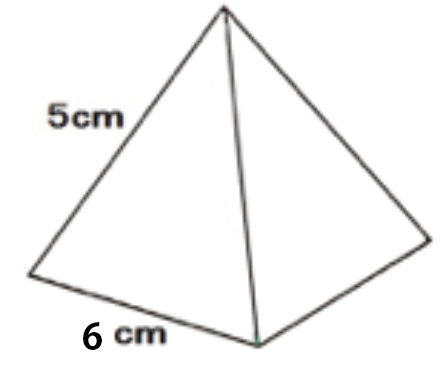
まずは、補助線をガンガン入れる。直角にも印をつけるといい。
正四角錐の中の直角三角形を見つけやすくするためだ。
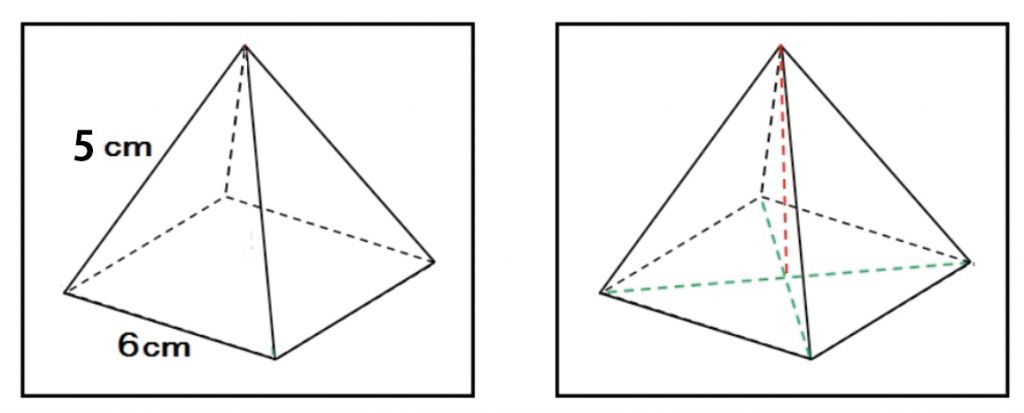
つぎは、正四角錐の底面に注目してみよう。
底面の正方形の対角線の長さを計算していくんだ。
底面は1辺が6cmの正方形だったな?
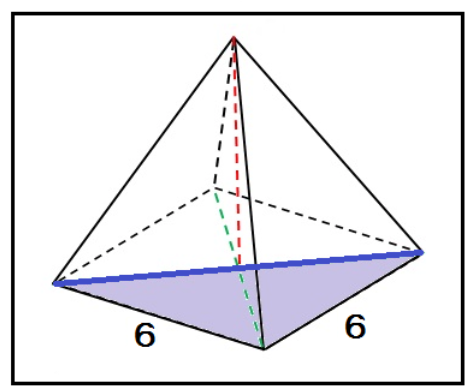
この正方形の半分の直角三角形で三平方の定理を使ってやると、
6² + 6² = x²
x = √72 = 6√2
になるぞ。
ってことは、正四角錐の底面の対角線の半分の長さは、
6√2÷2 = 3√2
だ。
つぎは、正四角錐の頂点からの垂線に注目。
垂線をふくむ直角三角形を探して、三平方の定理を使えばいいんだ。
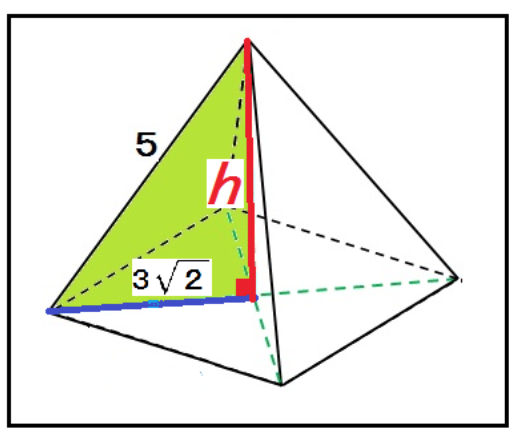
さっき見つけた正四角錐の頂点からの高さを求めてみよう。
使うのは、もちろん、
三平方の定理!
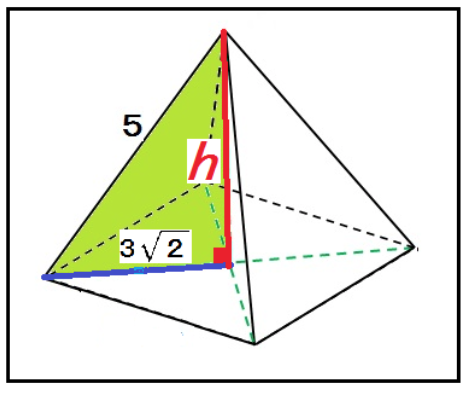
正四角錐の頂点からの高さをhとしてやると、
5² = (3√2)² + h²
h = √7
になるね。
つまり、この正四角錐の高さは√7 cmってわけ!
正四角錐の高さの求め方はどうだったかな?
つぎの4ステップで計算できちゃったな。
入試問題によく出てくるから復習しておこう。
正四角錐の高さが計算できたら次は円錐の高さに挑戦してみよう。
じゃあな
Dr.リード
どうも、Drリードだぞい。
中3数学では、
三平方の定理(ピタゴラスの定理)を勉強してきたよな?
簡単に復習すると、
直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、
a²+ b² = c² が成り立つ
ってやつだったな。

さあ、この定理を使いこなせるようになるんだぞ。
今回はそのための基礎トレーニングだ。
三平方の定理をつかった問題でよく出てくるのは、
直角三角形の辺の長さを求める問題。
今日はこの問題を4つのパターンに分けてみたぞ。
問題集では、いろいろな直角三角形がでてくるし、簡単なのも難しいのも混じっているからな。
初めは解けなくっても、がっくりこないで、
負けんぞ!!
と構えとけ。

まず1つ目の問題は、
直角三角形の辺の長さを三平方の定理の公式で求めるタイプ。
これは、
三平方の定理の公式に、辺の長さを代入して計算するだけだから簡単だ。
たとえば、つぎの練習問題な。
練習問題1.
つぎの直角三角形の辺の長さxを求めてください。
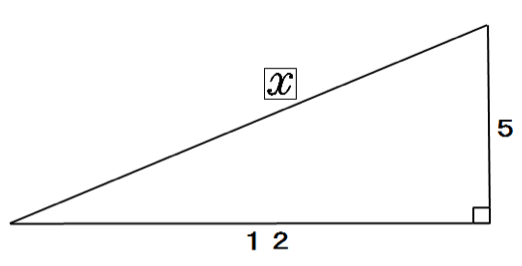
辺の長さが2桁でも気にすんな。
三平方の定理(ピタゴラスの定理)の公式にぶち込めばいいんだ。
x² = 5² + 12²
x = 13
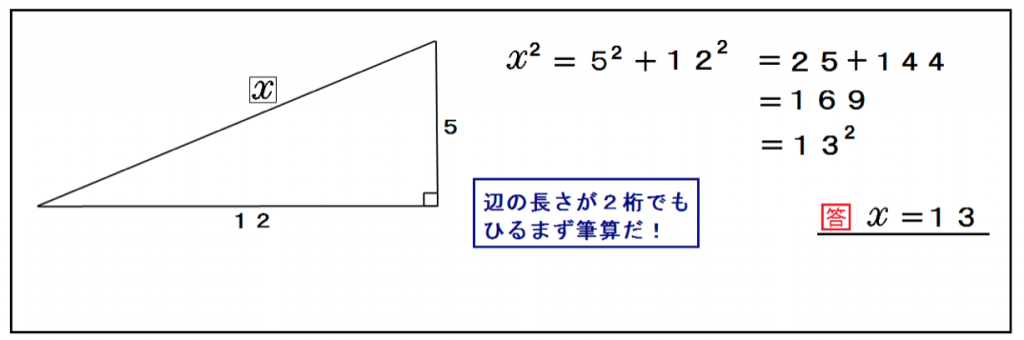
直角三角形と言えども、いつも右下に直角が来るとは限らんぞ。
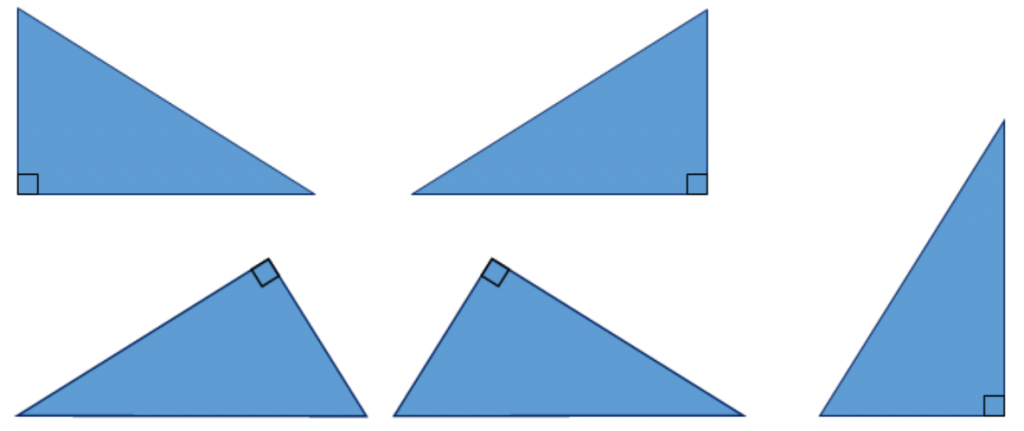
なっ。向きが変わると、斜辺がどれなのかうっかりしてしまうよ。
要注意だな。
2つ目のタイプは、
三平方の定理の計算に「平方根・ルートの計算」が混じってるやつだ。
たとえば、次のような練習問題。
練習問題2.
つぎの直角三角形の辺の長さxを求めてください。
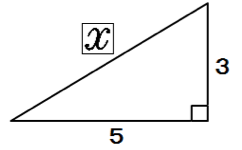
三平方の定理で直角三角形の辺の長さを計算してみると、
x² = 3² + 5²
x = √34
になるね。

答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。
つぎは、直角二等辺三角形の辺の長さを三平方の定理で計算する問題。
たとえば、三平方の定理を発見したピタゴラスも悩んだと知られる次の問題だ。
練習問題3.つぎの直角三角形の辺の長さxを求めてください。
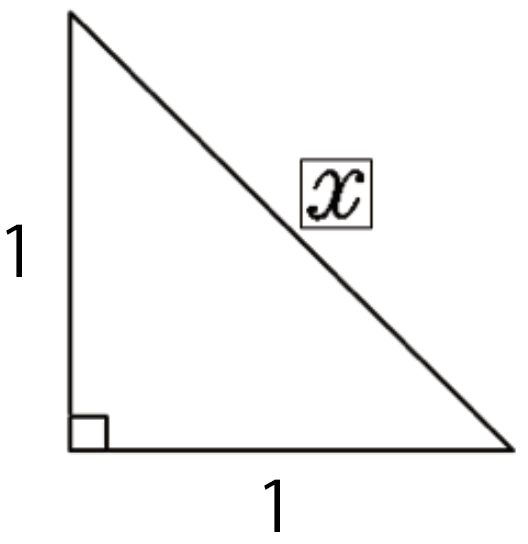
直角二等辺三角形だけど、さっきの計算問題と同じだ。
三平方の定理の公式を使ってやると、
x² = 1² + 1²
x = √2
になるぞ。
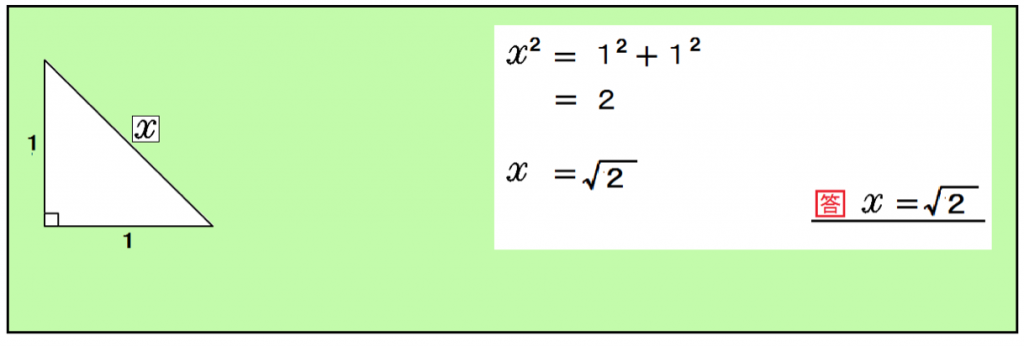
この直角二等辺三角形からピタゴラスは「無理数」を発見したと言われているんだ。
でも、ピタゴラスの生きてた時代は、まだまだ自然科学より宗教の勢力の方が主流でな。
ピタゴラス学派がうっかり、そして見事にピタゴラスの定理を見つけたんだが、
2乗して2になる数なんて、まだ見つかってなかった。
やや、これを発表したら、世の中大変なことになる・・・・
ってんで、長いこと秘密にしてたらしいぞ。

今は平和だ。
無理数はある!!と大声で言えるいい時代だ。(。)
つぎは、
直角三角形が2つくっついてる問題な。
たとえば、次の練習問題だ。
練習問題4.
つぎの直角三角形の辺の長さxを求めてください。
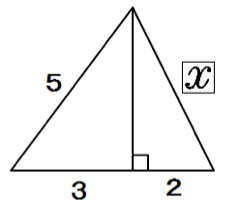
このタイプの問題では、高さを新しい文字で置いて2つの三角形の辺を出していくぞ。
まず、大きい三角形の高さをyとしてみよう。
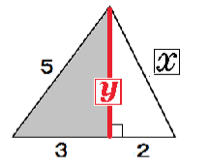
まず、灰色の直角三角形でyを計算してみる。
5² = 3² + y²
y = 4
そして、残りの白い直角三角形でxを出せばいいのさ。
x² = 4² + 2²
x = 2√5
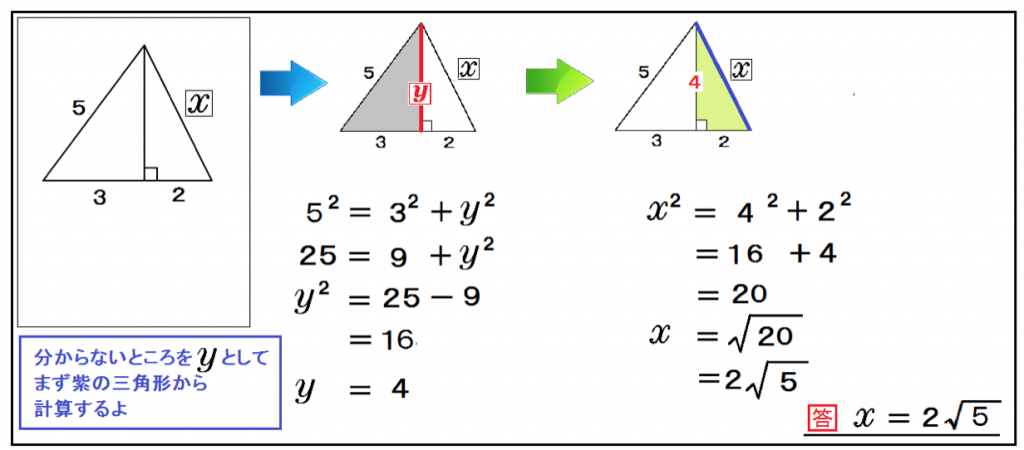
解き方大体わかっただろ??
じゃあつぎの計算問題にもチャレンジしよう。
練習問題5.
つぎの直角三角形の辺の長さxを求めてください。
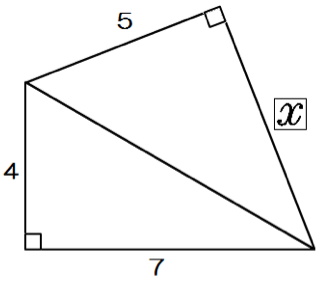
この問題も解き方はおんなじだ。
まず、真ん中の辺をyとして、yから計算すればいいんだね。
y² = 4² + 7²
y = √65
つぎはxを計算!
65 = 5² + x²
x = 2√10
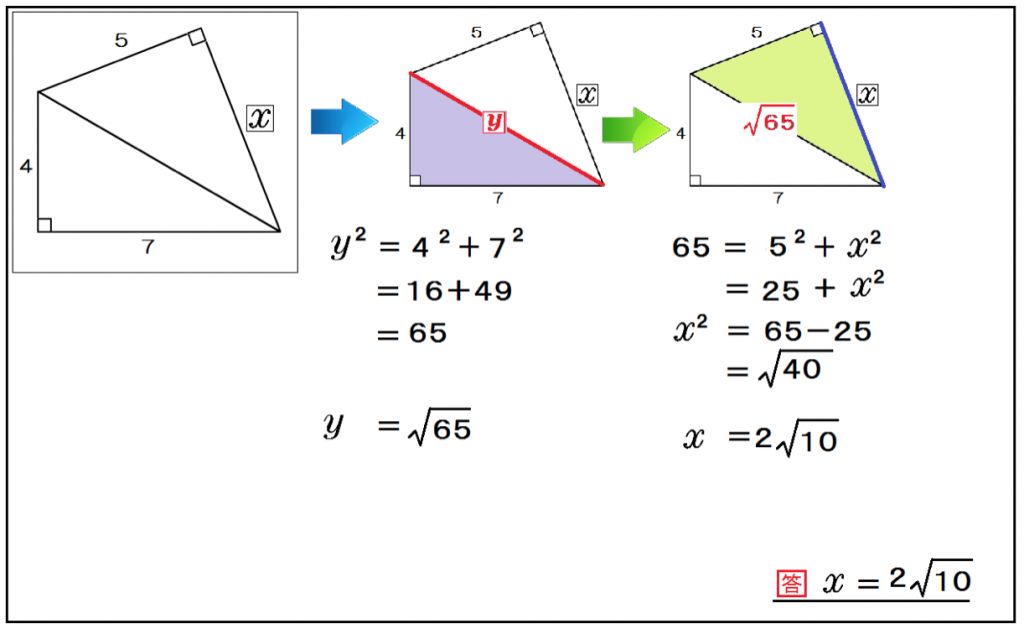
三平方の定理で、直角三角形の辺の長さを求める問題はどうだった?
今日勉強した問題のパターンは4つだったな?
これだけの基本パターンやったら、少しは自信がついたな。
慣れるまではピタゴラスの定理の式に丁寧に数値を代入してくれ。


それじゃあな
Drリード
こんにちは!この記事を書いているKenだよ。電気最高。
中学3年生になると、
三平方の定理
を勉強していくよね??
この定理は今から2500年ぐらい前に活躍した「ピタゴラス」っていう数学者が発見した定理だから、
ピタゴラスの定理
とも呼ばれてるやつね。
発見者の名前がついてるわけ。
この三平方の定理(ピタゴラスの定理)とは何かっていうと、
直角三角形の3つの辺の関係を表した公式
なんだ。
もうちょっと具体的にいうと、直角三角形には、
斜辺の2乗は、直角をはさむ辺を2乗して足したものと等しい
っていう関係があるんだ。
たとえば、斜辺の長さがc、その他の辺の長さがa・bの直角三角形ABCがあっとすると、
a² + b² = c²
っていう公式が成り立っているんだ。

たとえば、斜辺の長さが15cm、その他の辺の長さが12cm、9cmの直角三角形ABCをイメージしてみて。
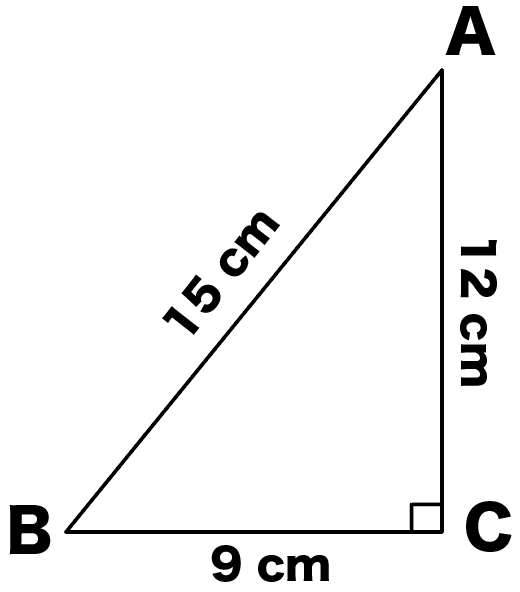
斜辺ABの2乗は、
AB²=15² = 225
一方、その他の辺のBCとACの2乗して足してみると、
AC²+ BC²
= 12² + 9² = 144 + 81 =225
だね!
おっ。両方225になって等しくなってんじゃん!
ピタゴラスの定理の公式すごいな。。
>>三平方の定理(ピタゴラスの定理)の証明はこちら
でもさ、
三平方の定理(ピタゴラスの定理)の公式のすごさがいまいちわからないよね??
ぜんぜん生活に役に立ったないじゃん!
って思ってない??
じつは、三平方の定理(ピタゴラスの定理)のすごいところは、
直角三角形の2辺の長さがわかれば、残りの辺の長さがわかる
ってところなんだ。
たとえば、斜辺の長さ13cm、その他一辺の長さが5cmの直角三角形DEFがあったとしよう。
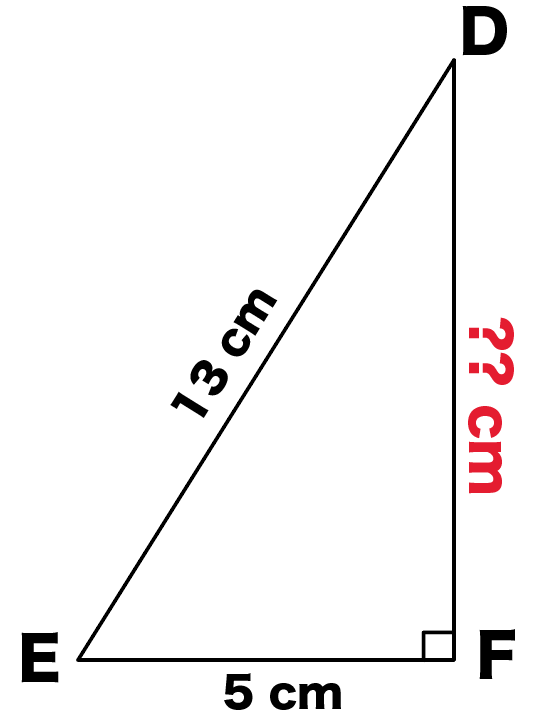
DFの長さって問題にも書いてないし、誰も教えてくれてないよね??
でも、大丈夫。
三平方の定理(ピタゴラスの定理)を使えば求められるんだ。
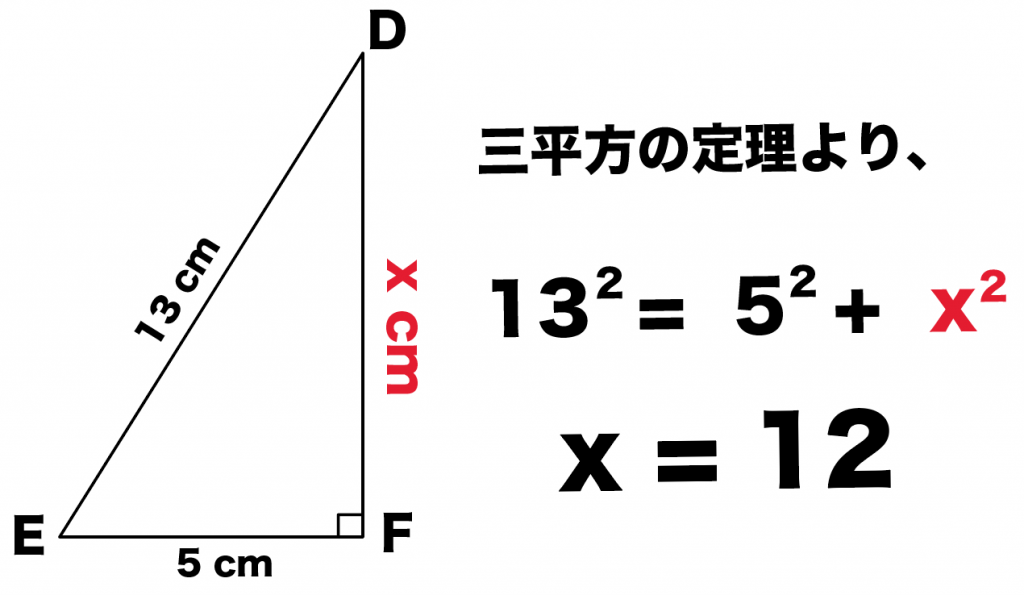
DFの長さをxcmとして、三平方の定理(ピタゴラスの定理)に代入してみると、
13² = 5² + x²
x = 12
あら不思議!
長さがわからない直角三角形の辺を求めることができたね。
>>三平方の定理(ピタゴラスの定理)の計算問題にチャレンジ!!
三平方の定理(ピタゴラスの定理)の公式はめちゃくちゃ便利。
この公式なら、
だって計算できちゃうんだ。
入試問題や定期テストでむちゃくちゃよく出てくる定理だから、しっかりと覚えておこうね。
そんじゃねー
Ken
こんにちは!この記事をかいてるKenです。良薬は苦しだね。
直角三角形の辺の比の問題でよく出てくるパターンの1つに、
3: 4: 5の直角三角形
っていうのがあるんだ。
これは文字通り、
3つの辺の比が3:4:5になってる直角三角形のことね。
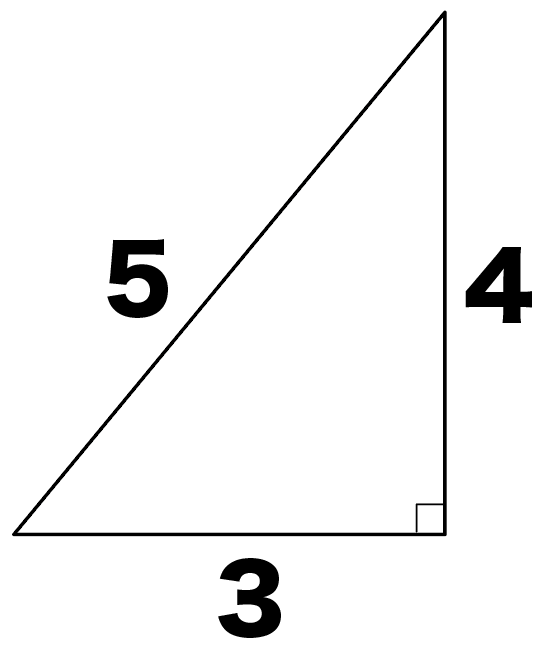
たとえば、辺の長さが、
になってる直角三角形。
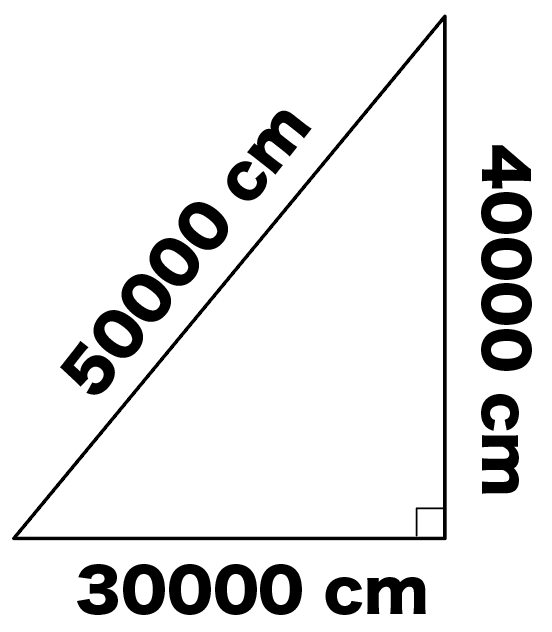
辺の長さの比を取ってみると、
30000 : 40000 : 50000
= 3 : 4 :5
になってるでしょ??
今日はこんな感じで、
3:4:5の直角三角形の辺の長さを求める問題
の解き方紹介していくよ。
よかったら参考にしてみてね。
3:4:5の直角三角形の辺の比の問題は3種類あるよ。
一つ目のパターンは、
斜辺以外の辺の比が3:4の問題だね。
直角三角形の辺の比を使えば、三平方の定理より早く解けちゃうんだ。
たとえば、つぎのような練習問題ね。
練習問題
直角三角形の辺の長さxを求めなさい。
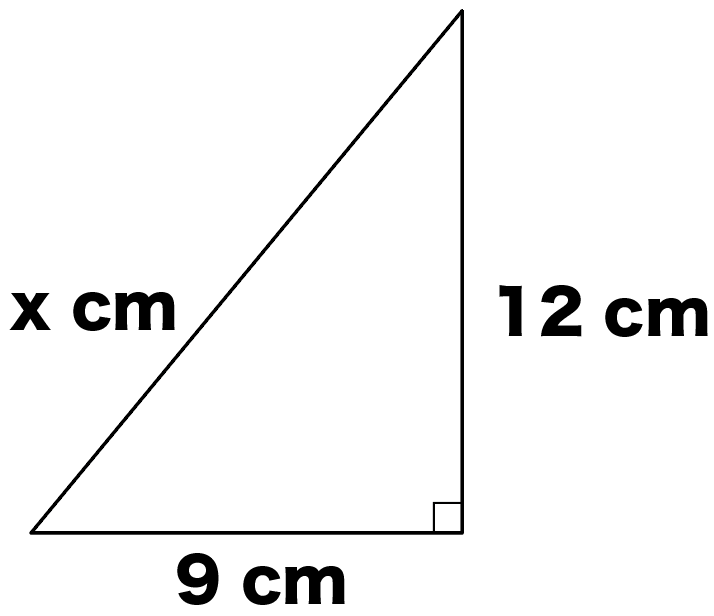
直角三角形の斜辺以外の辺の比をみてみると、
9 : 12
= 3 : 4
になってるよね??
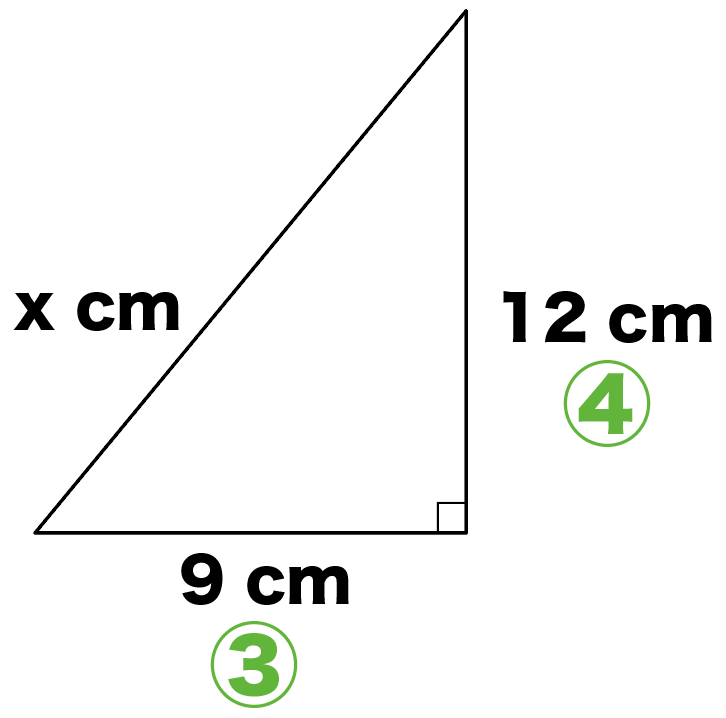
ってことは、これは紛れもなく3:4:5の直角三角形。
この手の問題では、
「1番小さい辺の長さ」に3分の5をかければ斜辺の長さを計算できるんだ。
なぜなら、
(斜辺の長さ):(1番小さい辺の長さ)= 5 : 3
になってるはずだからね。
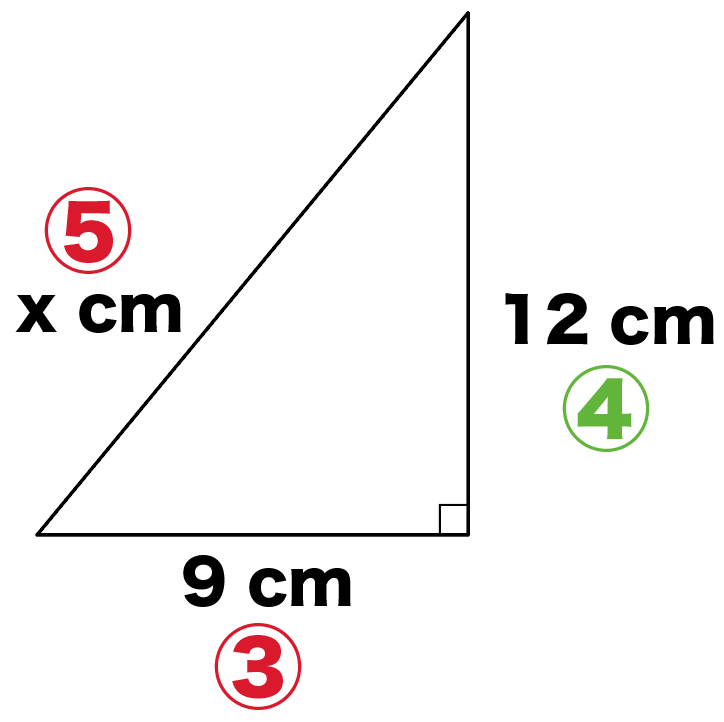
ってことで、1番小さい辺の「9 cm」に3分の5をかけてやると、
9× 5/3
= 15 cm
に斜辺はなるね。
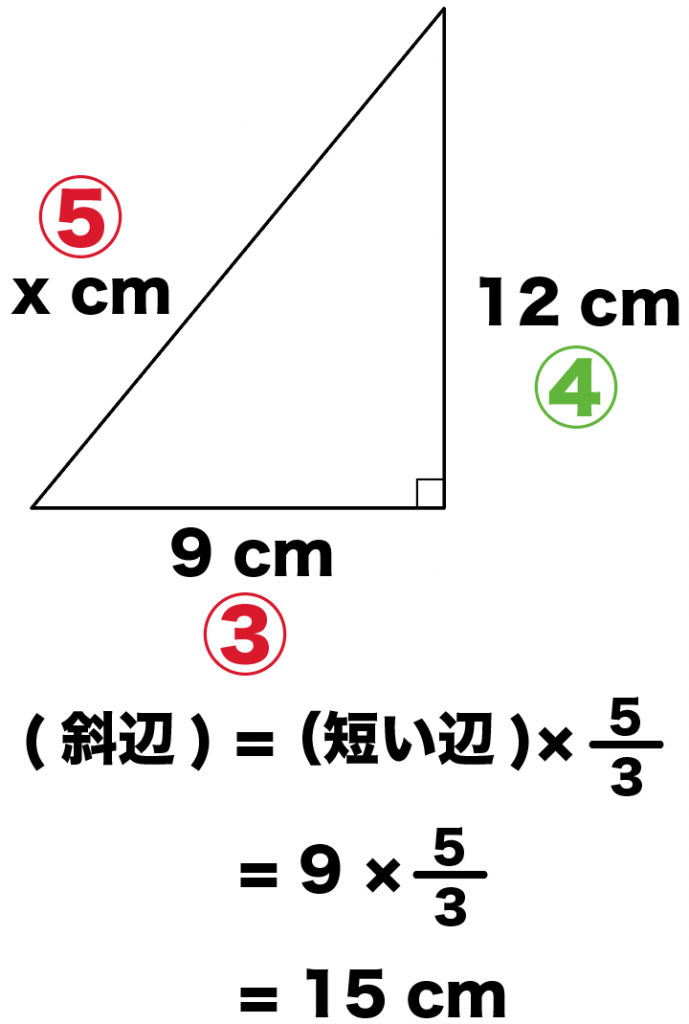
三平方の定理を使うより早くて簡単だ。
つぎは「斜辺」と「その他の辺」の比が5:4の問題ね。
練習問題
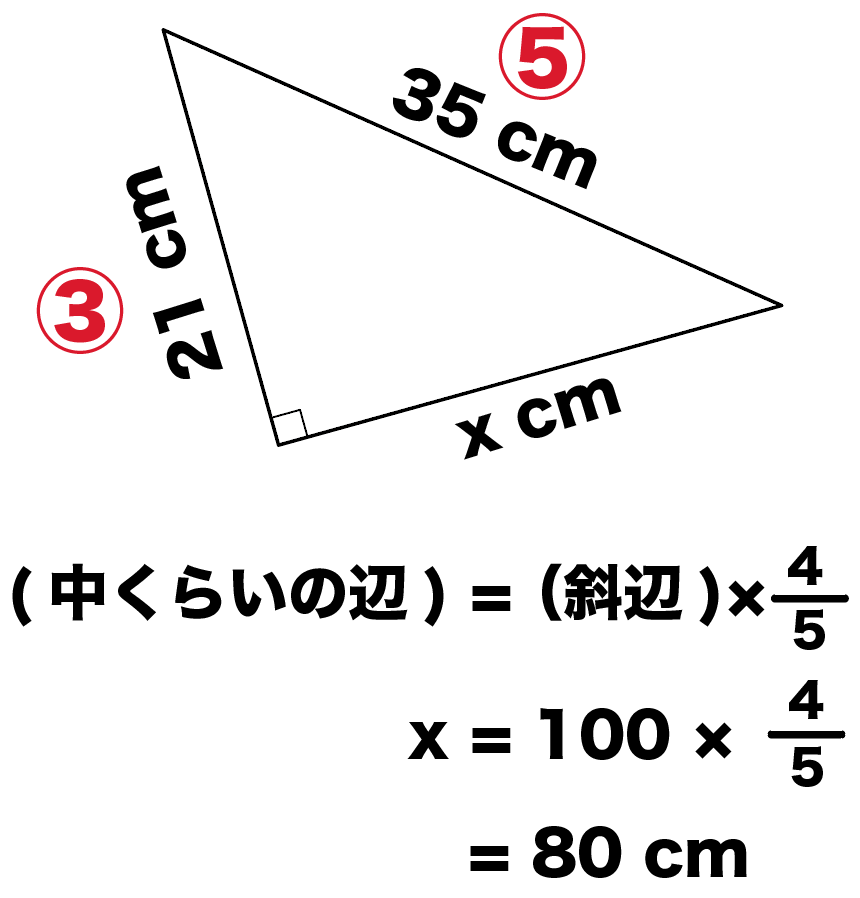
つぎの直角三角形の辺の長さxを求めなさい。
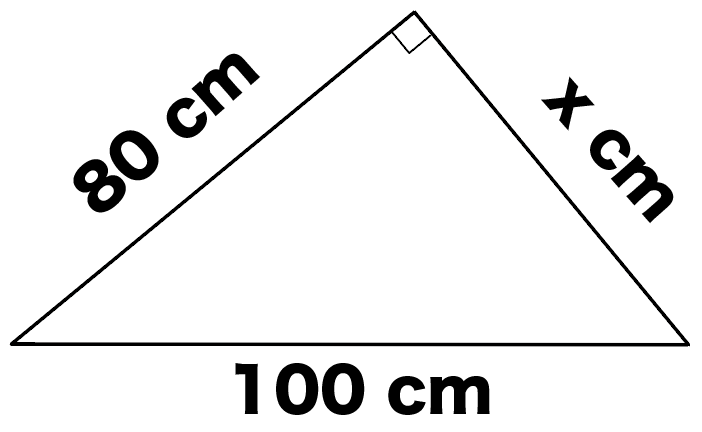
この問題では、「斜辺」と「もう1辺の長さ」の辺の比が、
100 : 80
= 5 : 4
になってるよね??
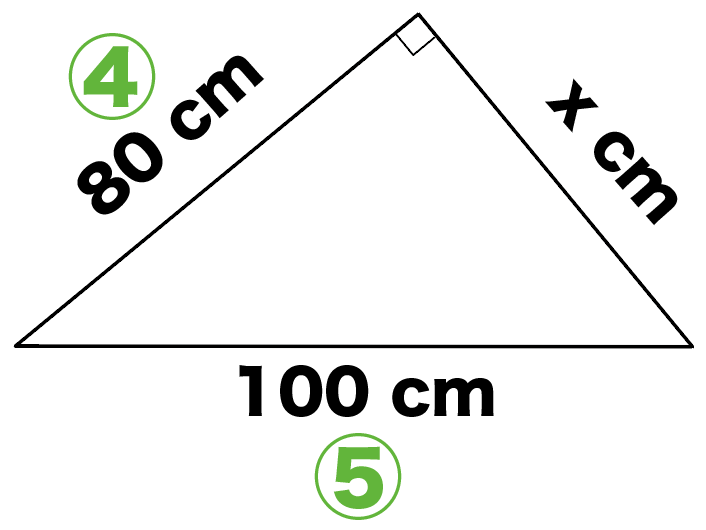
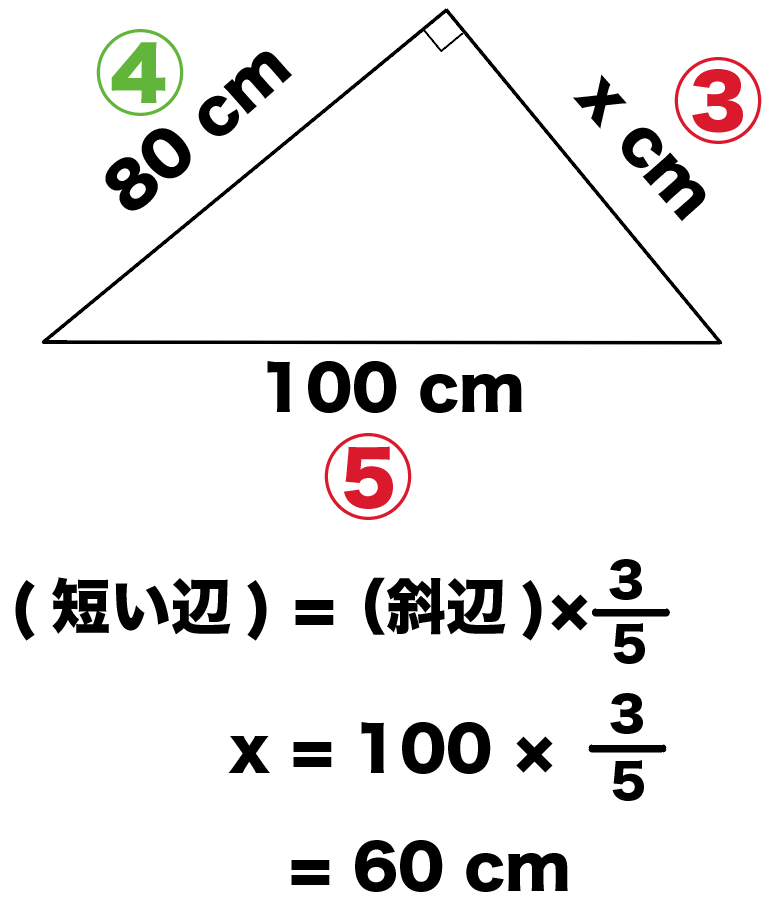
ってことは、直角三角形の辺の比は3:4:5になるはずだから、
「斜辺の長さ」に5分の3をかければ残りの辺の長さを計算できちゃうね。
ってことで、残りの辺の長さxは、
x = 100×5分の3
= 60 cm
になるね。
最後は、「斜辺」と「その他の辺」の比が5:3になってる問題ね。
たとえば、つぎのようなやつ。
練習問題
つぎの直角三角形の辺の長さxを求めなさい。
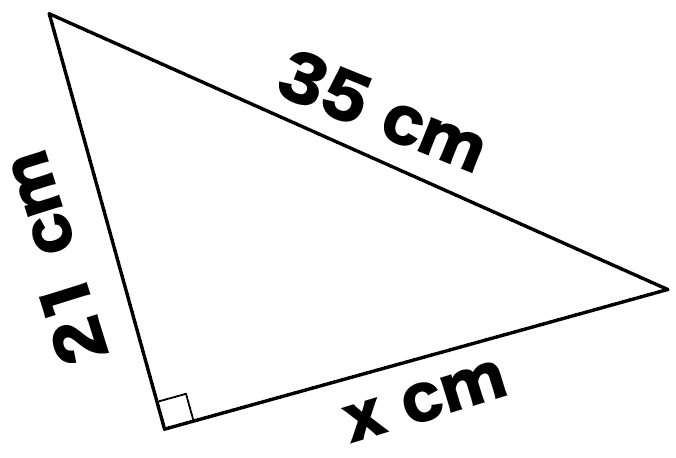
直角三角形の「斜辺」と「その他の一辺の長さ」の比を出してみると、
35 : 21
= 5 : 3
になってるよね?
ってことはこの直角三角形も3:4:5のタイプ。
斜辺と残りの辺の長さの比は、
5: 4
になってるはずだから、斜辺に5分の4をかければ辺の長さが出てくる。
実際に計算してみると、
x = 35×4/5
= 28 cm
になるね。
辺の比が3:4:5の直角三角形の問題はどうだったかな??
全部で、
の3パターンあったけど、やってることは全部一緒。
3:4:5の辺の比を使って分数の掛け算すればいいのさ。
コツは、
辺の比が3:4:5になってることをいかに早く見つけるか
だ。
問題をたくさんといて解き方に慣れていこう。
そんじゃねー
Ken
どうも!ぺーたーだよ。
中3数学では、
三平方の定理(ピタゴラスの定理)
っていう単元を勉強するよ。
この章が終われば、中3年の数学はほぼ終わり。あともう少し頑張って勉強していこうね。
今回はこの三平方の定理を使った計算問題のうち、
よく出てくる問題の解き方
を3つ紹介するよ。
よかったら参考にしてみて。
=もくじ=
まず問題を解く前に、
三平方の定理(ピタゴラスの定理)を復習しておこう。
これがわからないと問題解けないからね。
三平方の定理(ピタゴラスの定理)とはズバリ、
直角三角形の各辺同士の関係を表した公式
だったよね??
具体的にいうと、
直角三角形の直角を挟む2辺の長さをa、b、
斜辺の長さをcとおくと、
$$a² + b² = c²$$
になるってやつね。

三平方の定理は直角三角形のときに使える
っていうことがとっても大事だよ。
慣れてないと、ふつうの三角形でも使っちゃう人がいるからね。
早速、三平方の定理(ピタゴラスの定理)を使って問題を解いていこう。
今回紹介する問題は次の3つね。
まず三平方の定理(ピタゴラスの定理)を使って、
直角三角形の斜辺を計算する問題
を解いていくよ。
例えば、次のような問題ね。
練習問題1.
次の直角三角形ABCのxの長さを求めなさい。

この問題は直角三角形の斜めの辺、
つまり「斜辺の長さ」を求める問題だ。
三平方の定理はa² + b² = c²だったね。
今は斜辺がx、底辺と高さが3cm、1cmだから、
$$3² + 1² = x²$$
っていう式が成り立つんだ。
あとはこいつを計算してみよう。
$$3² + 1² = x²$$
$$9 + 1 = x²$$
$$x² = 10$$
$$x = ±\sqrt{10}$$
辺の長さがマイナスになることは絶対にないから、
$$x =\sqrt{10}$$
ってことね。

これが一番ベーシックな計算問題だ。
じゃあつぎ行ってみよう!
次は斜辺以外がわからないパターンだね。
例えば、つぎのような計算問題。
練習問題2.
次の直角三角形ABCのxの長さを求めなさい。

この問題では、斜辺の長さがすでにわかってるね。
まあ、こいつも三平方の定理(ピタゴラスの定理)で計算をすればよくて、
$$4² + x² = 6²$$
$$x² = 20$$
$$x = 2\sqrt{5}$$
になるね。

最後はちょっと難しい問題。
直角三角形の中に、直角三角形がいる??
っていう問題なんだ。
練習問題3.
次の直角三角形ABCのxの長さを求めなさい。

この問題はいくつか段階を追って答えを出すんだ。
まず△ADCに注目。
こいつは直角三角形だよね??
ってことは、三平方の定理で残りの辺の長さが求められるんだ。
斜辺が2√5㎝、高さが4㎝だから、
$$y² + 4² = (2\sqrt{5})²$$
$$y = 2$$
になるね。

図で表すとこうなる。

じゃ、次は大きい△ABCに注目。
BCの長さをzとすると、
x㎝を求めるには、z㎝からyの2㎝引けばいいよね?
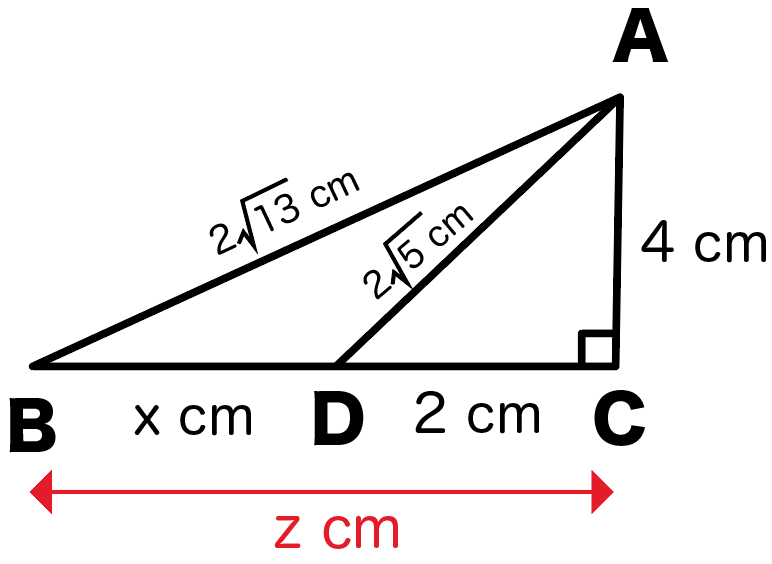
だからzの値が出れば答えまでもう少し!
直角三角形だから三平方の定理(ピタゴラスの定理)が使えるんだ。
斜辺が2√13cm、高さが4㎝だから、
$$z² + 4² = (2\sqrt{13})²$$
$$z = 6$$
になるね。
ってことは、xcmの長さは、そこからyの2cmを引いてやって、
$$x = 6 -2$$
$$= 4$$
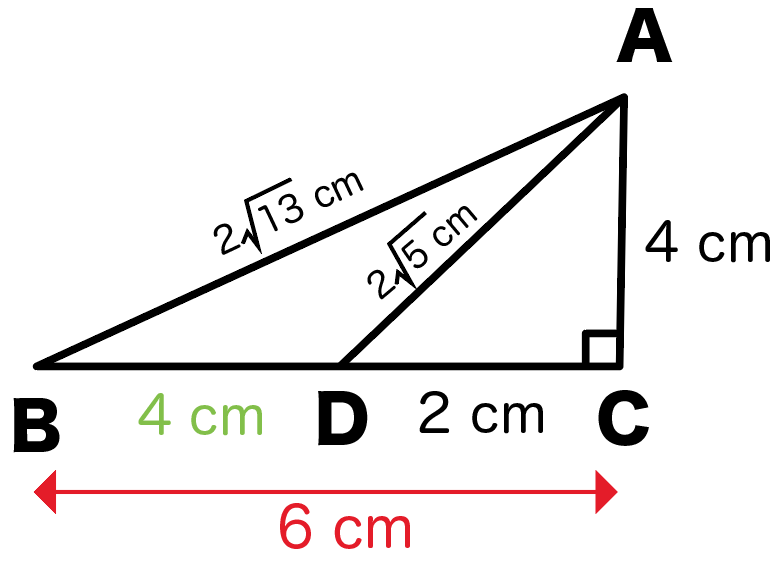
答えは4cmだ!
お疲れ!
三平方の定理(ピタゴラスの定理)の計算問題はどうだったかな??
今回マスターした計算問題の解き方は次の3つだったね。
三平方の定理の問題は解きまくってマスターしていこう。
またねー
ぺーたー
こんにちは!ぺーたーだよ。
今日は三平方の定理を使って、
座標上の2点の距離を計算する方法を勉強していこう!
関数が苦手な子は、
「えー、絶対やだ!」
とか思っちゃうかもしれないけど、
三平方の定理がしっかりわかっていれば、そんなに難しくないよ。
頑張ってやってみよう!
三平方の定理を使えば、2点間の距離は3ステップで計算できるよ。
次の例題を一緒に考えてみよう。
練習問題
2点A(-1,5), B(2,1)の間の距離を求めてください。
まずは座標と点を図にしてみて。
図がかかれてたらスキップしてもOKだけどね
練習問題でも図をかいてみようか。
まず、 座標軸をスラーっとかいてあげて、

2点の座標をポチッと打ってあげる。

だいたいこんな感じだよね。
直線ABを長さを求めるのが目標だ。
次は三平方の定理を使うために、
直角三角形を作ってみよう。
「求めたい2点の距離」を斜辺とする直角三角形を作ればいいのさ。
練習問題をみてみて。
ABを斜辺とする直角三角形を作るには、
2点から垂線を引いてやればいいね。
まず、Aからy軸と平行な垂線をひいてみて。
要はAから縦方向に線をひくんだ。

それがかけたら、Bからx軸に平行な垂線をひいてみて!
つまり、横方向の垂線ってことね。

そしたら、
2つの垂線の交点をCとしよう。
Cの座標はAのx座標、Bのy座標と同じだから、
(-1,1)
ってわけさ。

これで、 ABを斜辺とする直角三角形ABCがかけたね。

最後は三平方の定理で斜辺を求めるだけ!
練習問題では、
ACは2点のy座標の差、
BCはx座標の差だよね??
つまり、
になるはず。

あとはABをxとおいて、三平方の定理で計算すればいいね。
4²+3²=x²
こいつを計算すると、
x = 5
になる。
つまり、
AB = 5ってこと。

だからこの座標上の2点の距離は、
5
になるってことね。
おめでとう!
座標の2点間の距離はゲットできたかな??
最後に解き方を復習しておこう。
難しい作業もないから頑張ればできるはず。
グラフは書いた方がわかりやすいから忘れずに。
これでおしまい!
ぺーたー
どーもー!ぺーたーだよ。
立方体の対角線の長さの求め方には公式があるって知ってたかな??
立方体の1辺の長さをaとすると、
√3 a
で対角線の長さが求められるんだ。

つまり、
立方体の辺の長さに「√3」をかけるだけでいいんだ。
たとえば、1辺の長さが4cmの立方体があったとしよう。
すると、この対角線の長さは、
4√3
になるってわけ。

ね??すごい簡単な計算公式でしょ??
でもさ、ちょっと待って。
立方体の対角線の公式が簡単ってのはわかったけどさ、
なんでこの公式が使えるんだろう!??
って思わない??
公式忘れたら一発KOだよね。
そこで今日は、
公式を使わないで立方体の対角線の長さを出す方法
もみていくよ。
さっきの1辺が4cmの立方体の対角線の長さを出していこう。

だいたい直方体の対角線の長さの求め方と一緒なんだけどねw
まずは立方体の底面の対角線の長さを求めてみよう。
さっきの立方体でも底面に対角線を書き込んでみて。

△FGHに注目してみると、
この三角形は直角三角形ってことがわかるね。
ってことは三平方の定理が使えるはず。

△FGHを抜き出すとこんな感じだ。
この直角三角形で三平方の定理を使ってみよう。
斜辺をxとしておくと、式はこうなるね。
4²+4²=x²
こいつを計算すると、
x = 4√2
になるね。

三平方の定理を使って対角線を求めたけど、
別のやり方でも求めることができるんだ。
△FGHって直角二等辺三角形だよね。
直角二等辺三角形の比って覚えてるかな?
1:1:√2
ってやつだよ!

こいつをこの問題に当てはめると、
4㎝の辺と斜辺の比が「1:√2」だから、
4:x=1:√2
っていう比の式が立てられるんだ。

計算はこっちのほうがずっと楽だね!
次は立方体の対角線が計算できそうな直角三角形を見つけよう。
具体的にいうと、
を辺に持つ直角三角形だね。
さっきの立方体でいうと、
直角三角形AEGのこと。

なぜなら、
になってるからね。
次は立方体の対角線を求めていくよ。
さっき見つけた直角三角形で三平方の定理を使えばいいのさ。
奥行きがあってわかりにくいかもしれないから、
△ AEGの部分を抜き出してみるよ。

2辺の長さがわかってるから三平方の定理を使ってみよう。
AEは立方体の辺だから4㎝、AGを y cm とすると、
4²+(4√2)²=y²
になるね。
これをyについて解くと、
y = 4√3
になる。

ってことで、この立方体の対角線 AGの長さは「4√3 cm」になるのさ。

どう??できたかな??
立方体の対角線の長さの求め方は、
の3ステップだったね??
最初にも言ったけど、立方体の対角線の求め方は、
直角三角形の対角線の求め方とだいたい一緒。
どっちかできれば空間図形の対角線は大丈夫だね。
今日はこれでおしまい!
またねー
ぺーたー
こんにちは!ぺーたーだよ。
三平方の定理を使うと、
直方体の対角線の長さの公式を導けるって知ってた??
実は、対角線の長さには次の公式があるんだ。
直方体のそれぞれの長さを、
とすると、対角線の長さは、
√(a² + b² + c²)
になるよ。
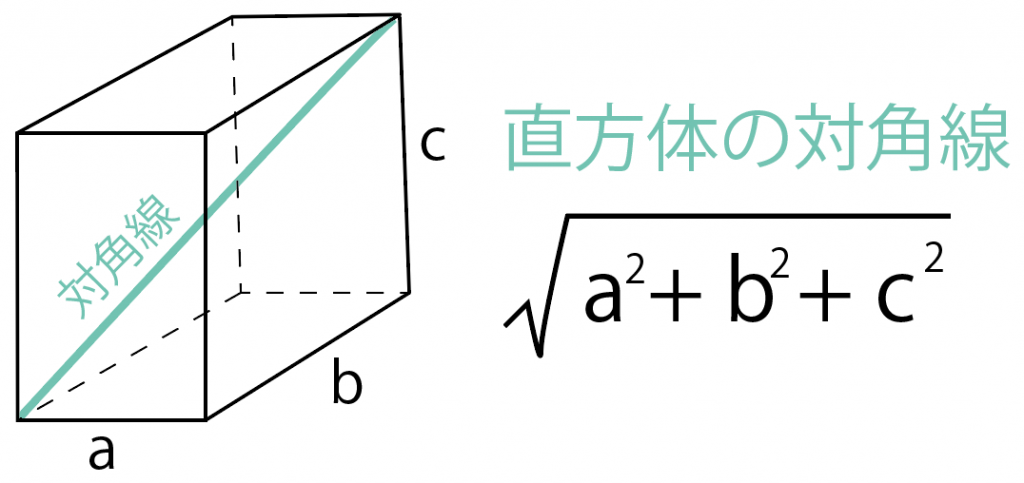
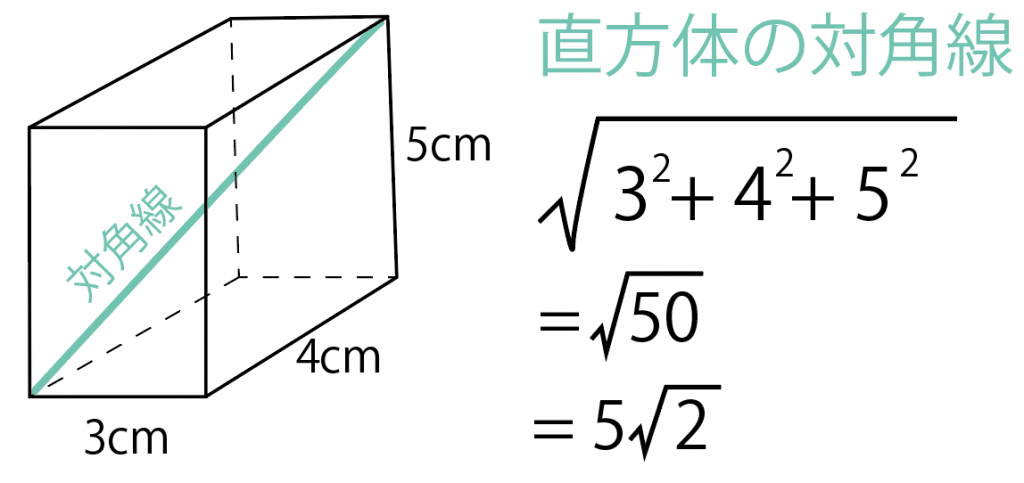
たとえば、
の直方体があったとしよう。
こいつに直方体の対角線の公式を使ってやると、
対角線
= √(a² + b² + c²)
=√(3² + 4² + 5²)
= 5√2
になる。
どう??
すぐに直方体の対角線の長さ求められたでしょ??
でもね、公式を使うときには、
なぜその公式が使えるのか??
を知っておくといいよ。
公式を忘れても大丈夫なようにね。
だから今日は最後に、
公式を使わずに直方体の対角線を求めてみよう。
さっそく、公式なしで直方体の対角線の長さを出してみようか。
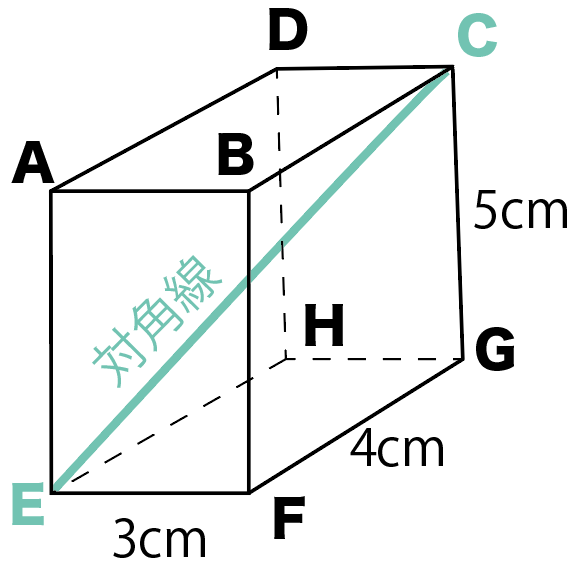
この問題では、対角線ECを求めてみよう。
まず最初は、
底面の対角線を引いてみよう。
なんでそんなのひかなきゃいけないの?
って思うかもしれないけど、
その理由はあとでわかるからちょっとがまんしてね!
底面に対角線をひくとこうなるね。
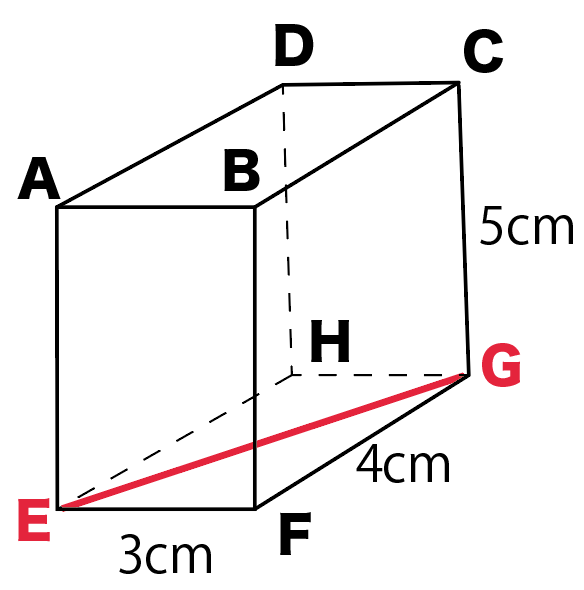
対角線ECを求めるために、
底面の対角線はEG
を引くってことね。
次は、底面の対角線の長さを計算してみよう。
えっ。
どうやって出すのかって??
こういうときは、
底面にできた三角形に注目してみて。
さっきの直方体でいうと、
△EFG
だね。
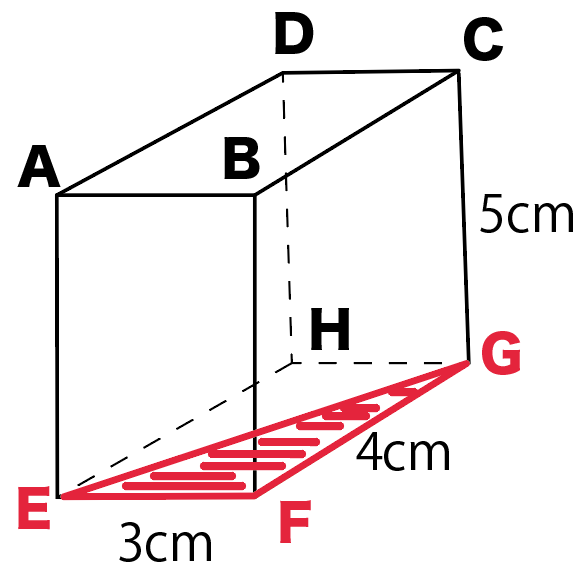
この三角形は上から見るとわかると思うけど、
直角三角形になってるよね。
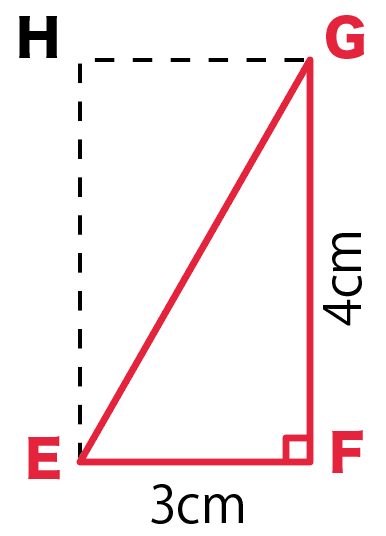
てことは、
三平方の定理で「斜辺EGの長さ」を求めることができるんだ。
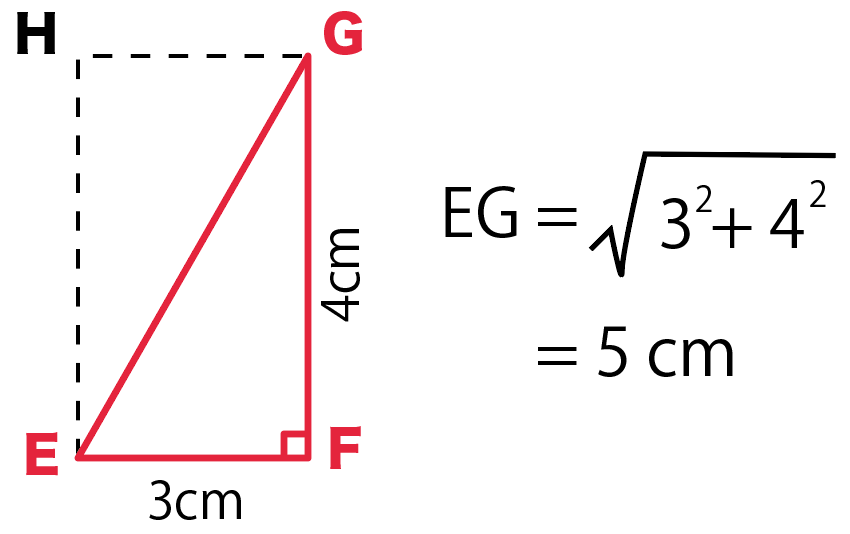
三平方の定理を使ってやると、
EG² = EF² + FG²
EG² = 3² + 4²
EG = 5 cm
になるね。
いよいよ本題の直方体の対角線の長さを求めるよ。
まず、求めたい直方体の対角線をさっきの図に書き込んでみよう。
対角線を書き込んだことで、また新しい三角形ができるよね??
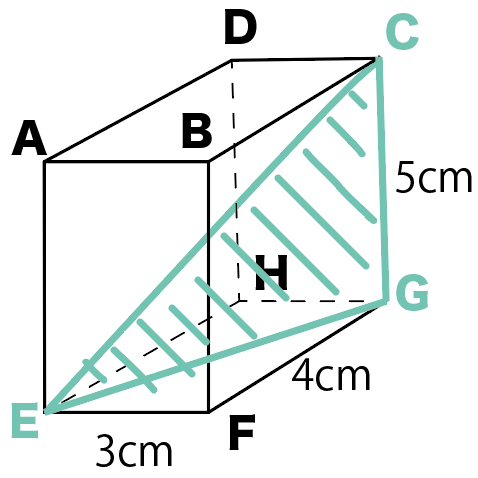
直方体の高さの辺と、底面の対角線でできる直角三角形ECGだ。
この三角形を取り出すと下みたいになるよ。
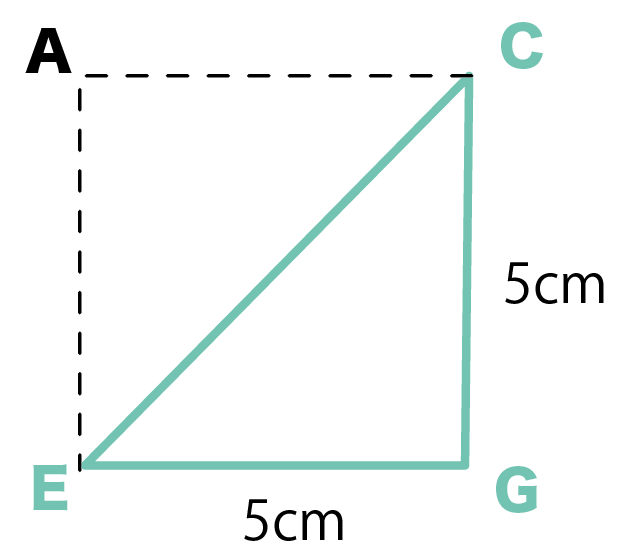
ここで、さっき求めた底面の対角線を使うんだ。
底面の対角線EGは5㎝だったね。
こいつを先に出しておかないと、うまく式が立てられず、計算できないんだ。
だから、底面の対角線を求めておくのはとっても大事ってわけ!
さっきと同じように三平方の定理を使うと、斜辺 ECの長さは、
EC² = CG² + FG²
EC² = 5² + 5²
EC = 5√2 cm
になるね。
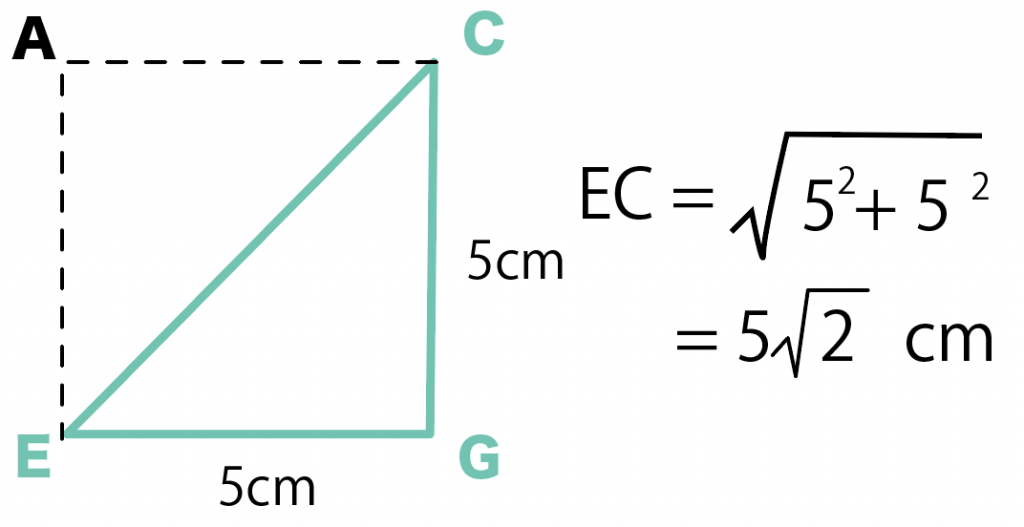
つまり、
この直方体の対角線の長さは「5√2 cm」になるってわけ!
直方体の対角線の求め方はわかったかな?
の2ステップでオッケー。
都合のいい直角三角形を見つけて、三平方の定理を使えれば全く問題ないね。
じゃあ、今日はここまでにしようか。
またね!お疲れさま!
ペーター