中学生でもわかる!三平方の定理(ピタゴラスの定理)の公式の4つの証明
中学生でもわかる三平方の定理(ピタゴラスの定理)の証明って??
こんにちは!Dr.リードだぞいっ。
今回のテーマは三平方の定理(ピタゴラスの定理)だ。
聞いたことあるかな?
紀元前572年ごろのギリシア人のピタゴラスさんが発見したから「ピタゴラスの定理」っていうんだな。
今日はその三平方の定理(ピタゴラスの定理)の使い方じゃなくて、
なぜ、三辺平方の定理が使えるのか?を証明していくぞ。
中学生でもわかる!三平方の定理(ピタゴラスの定理)の4つの証明
三平方の定理の証明法は100以上、いやもっとそれ以上あるといわれている。
中でも、中学生にも分かりやすい4つの証明を紹介していくぞ。
- 小さな三角形を使う証明
- 小さな三角形と正方形を使う証明
- 正方形を2つ使う証明
- 直角三角形の相似を利用する証明
今回は姉上といっしょに三平方の定理(ピタゴラスの定理)の証明をみていこう。

その1. 「直角二等辺三角形を使った証明」
まず1つ目の証明は、
小さな直角三角形二等辺三角形
を使った証明だ。
直角三角形を4枚合わせると、
正方形になるよな?
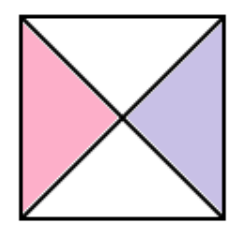
んで、この正方形をもっとつなぎ合わせると、もっとでかい四角形ができるね。
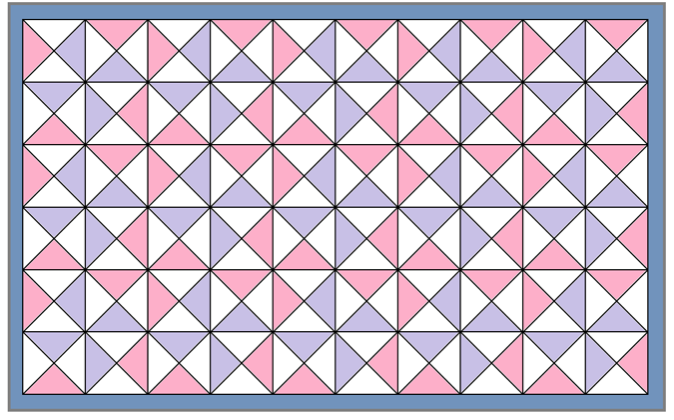
この証明では、パッチワークみたいな感じで、小さい直角二等辺三角形を使っていくぞ。
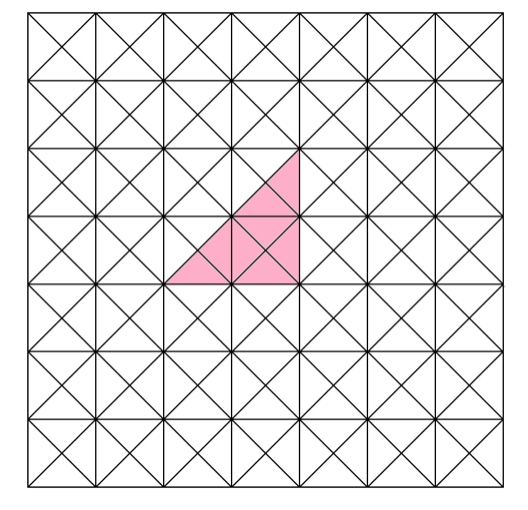
まずは、中ほどにピンクの生地8枚使って、直角三角形を作ってくだされ。

ついでに3種類、イエロー、パープル、ミントグリーンも使って、ピンクの三角形の各辺がくっついた正方形を作ってくだされ。
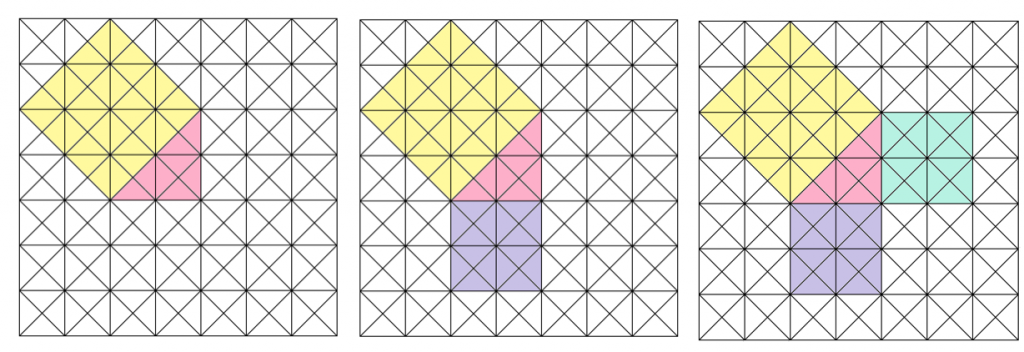
それぞれの色にふくまれる直角二等辺三角形の数を数えてみよう。
- 黄色:32個
- パープル:16個
- ミントグリーン:16個
「黄色の枚数」と「パープル+ミントグリーン」の枚数が一緒ってことに気づくかな?
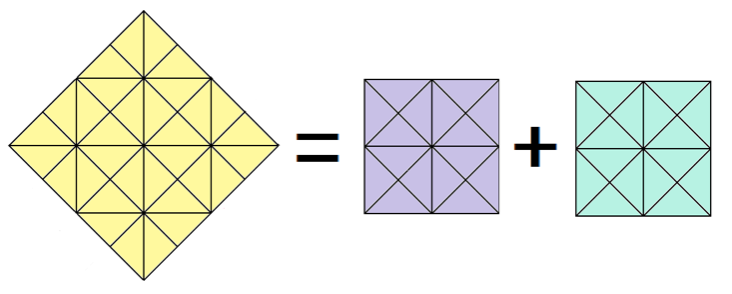
黄色い正方形の1辺をb、
パープル・ミントグリーンの正方形の1辺をaとすると、
b² = a² + a²
になってるはずだね。
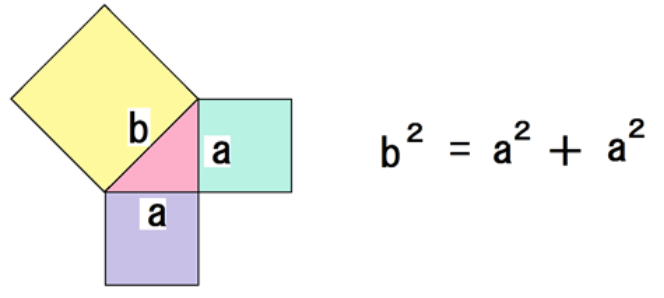
このことから、
赤の直角二等辺三角形の斜辺の2乗が、他の2辺の2乗の和になってる
って言えるね。
おお、これって三平方の定理じゃん!!
その2. 正方形と直角三角形を使った証明
つぎの三平方の定理(ピタゴラスの定理)証明は、
- 正方形
- 直角三角形
の2つを使っていくよ。
こんな感じのパッチワークを想像してくれ。
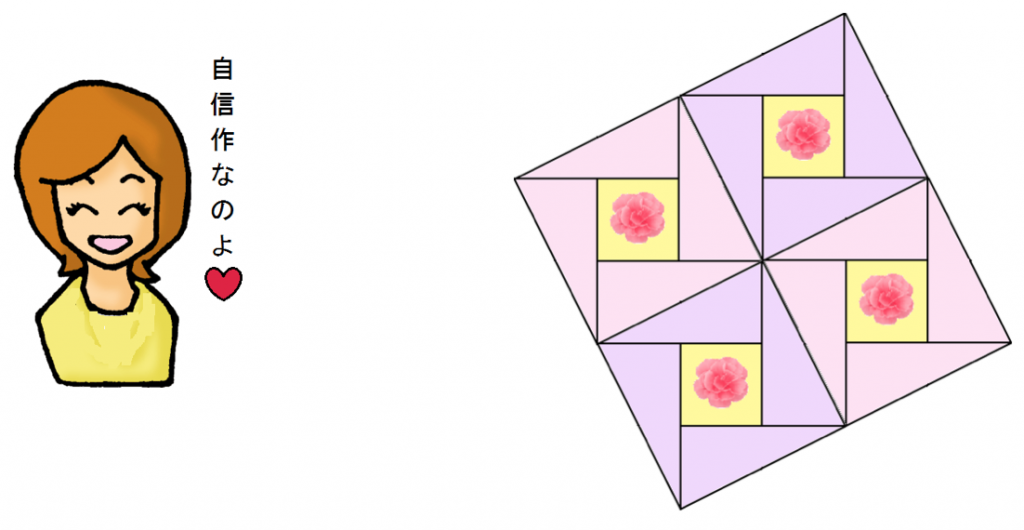
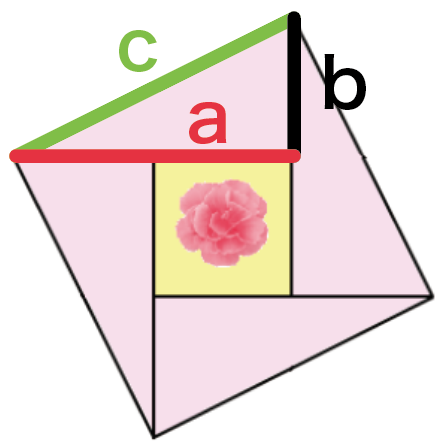
これの一番基本となるピースに注目。
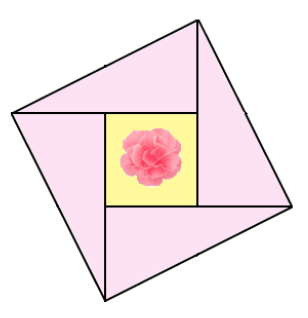
今回は、この、
- 正方形1つ
- 直角三角形4つ
が合体して正方形になってる図形を使っていくんだ。
1つの直角三角形の辺の長さをそれぞれ、
- a
- b
- c
としてやろう。
まず、下のようにピンクの三角形を右下へ動かしてみる。
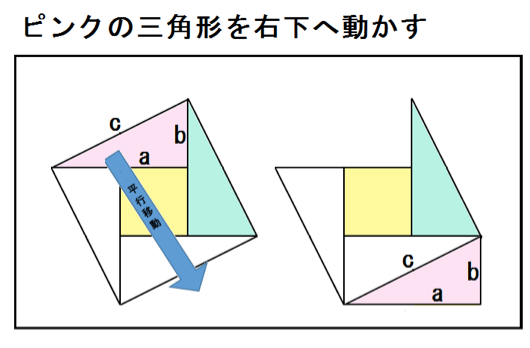
つぎは、水色の三角形を左下へ動かしてみる。
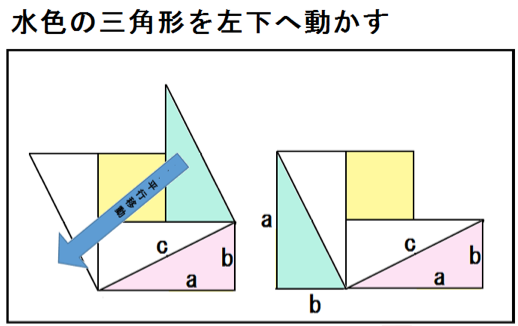
ここで、こいつを2つの正方形、
- 1辺がaの正方形
- 1辺がbの正方形
に分けてみると、
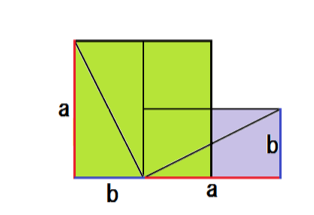
こいつの面積は、
a² + b²
になるよね?
んで、もともとは1辺がcの正方形だったはずだから、
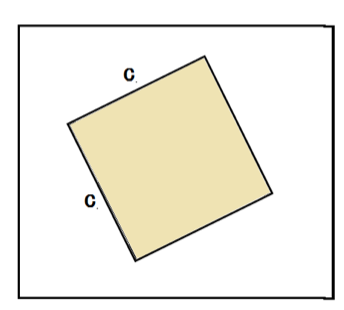
c² = a² + b²
っていう式が成り立つね。
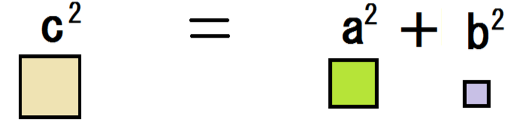
ここで、左上の基本のピンクの直角三角形に注目てしてみて。
cは斜辺、aとbはその他の2辺の長さになってるよね?
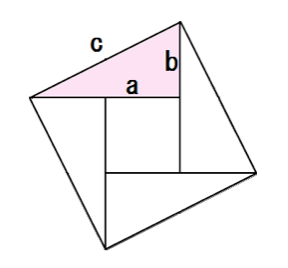
おお、みごと、三平方の定理の式になりました。

その3. 正方形を2つ使う証明
つぎの三平方の定理(ピタゴラスの定理)の証明は、
正方形を2つ使うパターン。
- 1辺が(a+b)
- 1辺がc
の2つの正方形をイメージしてみよう。
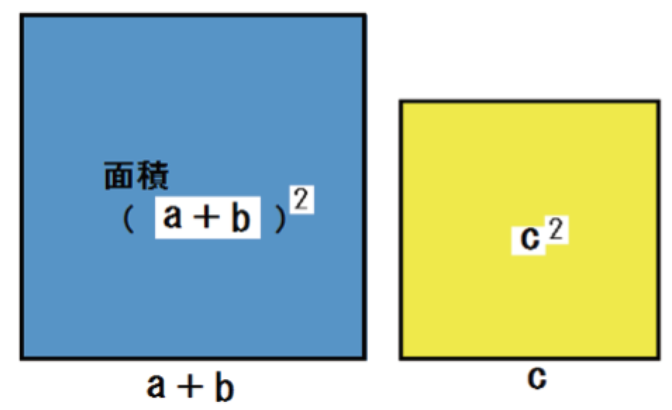
こいつをこんな風に重ねてみた。
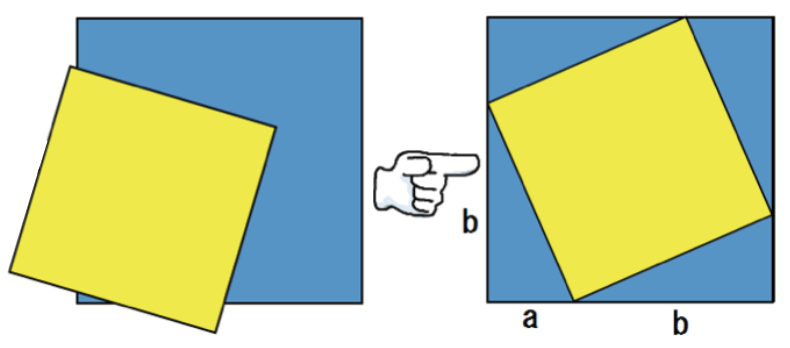
それぞれの面積を出すと、
- 青色正方形の面積 = (a+b)²
- 黄色い正方形の面積 = c²
- 青い直角三角形の面積 = ½ × a × b × 4 = 2ab
真ん中の黄色い正方形は、青い正方形から4つの直角三角形を引いたものだから、
c² = (a+b)² -2ab
c² = a²+2ab +b² -2ab
c² = a²+b²
1つの直角三角形でみると、
cは斜辺でaとbはその他の辺だね。
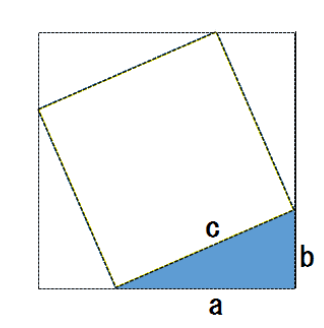
おお、これも見事三平方の定理の式になったぞ。
その4. 直角三角形の相似を使う証明
相似の証明を使って、三平方の定理を証明することもできるんだよ。
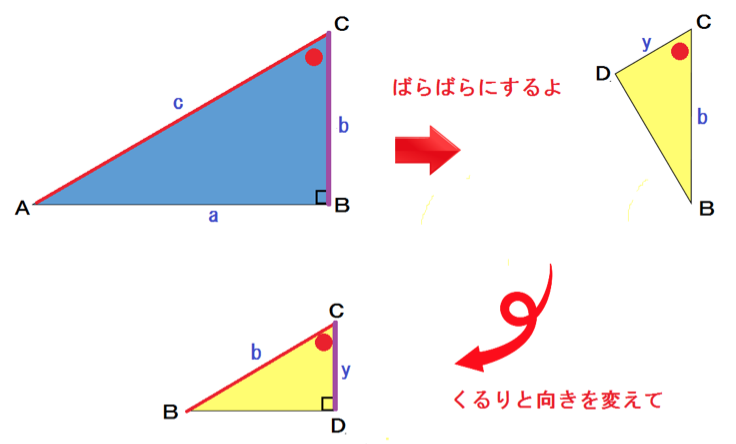
つぎのような直角三角形△ABCがある。
Bから辺ACに垂線を下ろし、交点をDとするね。
AD = x 、DC = y としておく。
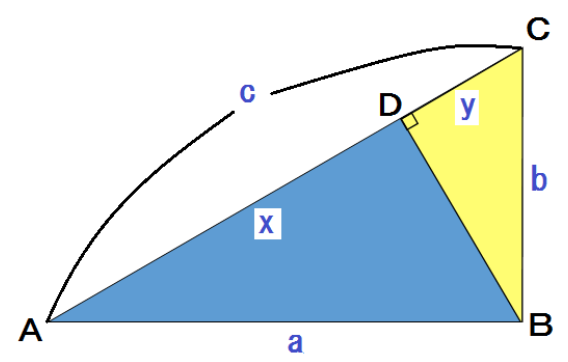
見やすいように図形をバラバラにすると、
相似な三角形が3個も隠れてるんだ。
△ABCと△ADBについて、
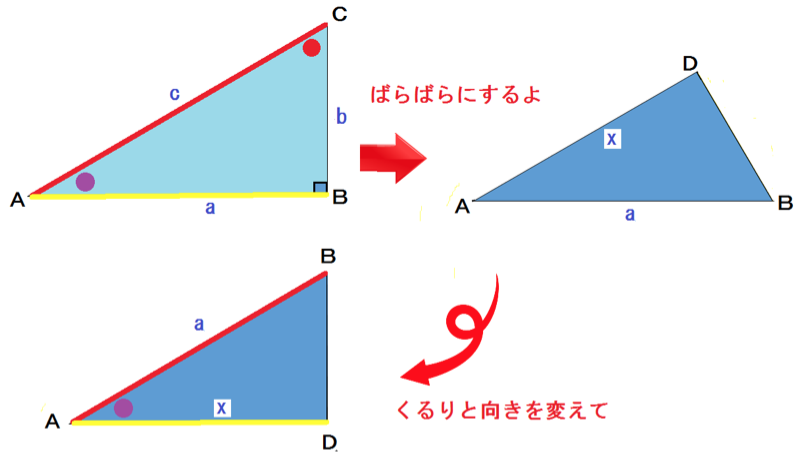
仮定より、
∠ABC = ∠ADB = 90°・・・①
また、
∠CAB = ∠BAD(共通)・・・②
①②より、
2組の角がそれぞれ等しいので、
△ABC∼△ADB
よって、対応する辺の比はそれぞれ、
c : a = a : x
a² = cx・・・③
になる。
また、
△ABCと△BDCについて、
仮定より、
∠ABC = ∠BDC = 90°・・・④
また、
∠CAB = ∠BAD(共通)・・・⑤
④⑤より、
2組の角がそれぞれ等しいので、
△ABC∼△BDC
よって、対応する辺の比はそれぞれ、
c : b = b : y
b² = cy・・・⑥
になる。
③+⑥を計算すると、
a² + b² = cx + cy
a² + b² = c (x + y)
a² + b² = c²
おお、これも見事三平方の定理の式になったぞ。
まとめ:三平方の定理(ピタゴラスの定理)の証明はまだまだあるぞ!
三平方の定理(ピタゴラスの定理)の証明はどうだっかな?
勉強したのは4つだったね。
- 小さな三角形を使う証明
- 小さな三角形と正方形を使う証明
- 正方形を2つ使う証明
- 直角三角形の相似を利用する証明
しっくりきたやつを覚えておこう。
ピタゴラスは数学者じゃなくて、ピタゴラス学派っていうギリシャの宗教教団のリーダーだったんだ。
数学者・哲学者・音楽家と様々な顔を持っていたらしいよ。
なかなかやるな、ピタゴラス。

それじゃあ!
Dr.リード


