三平方の定理(ピタゴラスの定理)の計算問題 の3つの解き方
三平方の定理(ピタゴラスの定理)の計算問題の解き方教えて!
どうも!ぺーたーだよ。
中3数学では、
三平方の定理(ピタゴラスの定理)
っていう単元を勉強するよ。
この章が終われば、中3年の数学はほぼ終わり。あともう少し頑張って勉強していこうね。
今回はこの三平方の定理を使った計算問題のうち、
よく出てくる問題の解き方
を3つ紹介するよ。
よかったら参考にしてみて。
=もくじ=
- 三平方の定理(ピタゴラスの定理)の復習
- 三平方の定理を使った3つの問題の解き方
三平方の定理(ピタゴラスの定理)ってなんだっけ??
まず問題を解く前に、
三平方の定理(ピタゴラスの定理)を復習しておこう。
これがわからないと問題解けないからね。
三平方の定理(ピタゴラスの定理)とはズバリ、
直角三角形の各辺同士の関係を表した公式
だったよね??
具体的にいうと、
直角三角形の直角を挟む2辺の長さをa、b、
斜辺の長さをcとおくと、
$$a² + b² = c²$$
になるってやつね。

三平方の定理は直角三角形のときに使える
っていうことがとっても大事だよ。
慣れてないと、ふつうの三角形でも使っちゃう人がいるからね。
三平方の定理(ピタゴラスの定理)を使った3つの計算問題の解き方
早速、三平方の定理(ピタゴラスの定理)を使って問題を解いていこう。
今回紹介する問題は次の3つね。
- 斜辺を計算する問題
- 斜辺以外を求める問題
- 直角三角形の中に直角三角形がいる問題
計算問題1. 「斜辺の長さを計算する問題」
まず三平方の定理(ピタゴラスの定理)を使って、
直角三角形の斜辺を計算する問題
を解いていくよ。
例えば、次のような問題ね。
練習問題1.
次の直角三角形ABCのxの長さを求めなさい。

この問題は直角三角形の斜めの辺、
つまり「斜辺の長さ」を求める問題だ。
三平方の定理はa² + b² = c²だったね。
今は斜辺がx、底辺と高さが3cm、1cmだから、
$$3² + 1² = x²$$
っていう式が成り立つんだ。
あとはこいつを計算してみよう。
$$3² + 1² = x²$$
$$9 + 1 = x²$$
$$x² = 10$$
$$x = ±\sqrt{10}$$
辺の長さがマイナスになることは絶対にないから、
$$x =\sqrt{10}$$
ってことね。

これが一番ベーシックな計算問題だ。
じゃあつぎ行ってみよう!
計算問題2. 「斜辺以外の長さを求める問題」
次は斜辺以外がわからないパターンだね。
例えば、つぎのような計算問題。
練習問題2.
次の直角三角形ABCのxの長さを求めなさい。

この問題では、斜辺の長さがすでにわかってるね。
まあ、こいつも三平方の定理(ピタゴラスの定理)で計算をすればよくて、
$$4² + x² = 6²$$
$$x² = 20$$
$$x = 2\sqrt{5}$$
になるね。

計算問題3. 「直角三角形の中に直角三角形がいる問題」
最後はちょっと難しい問題。
直角三角形の中に、直角三角形がいる??
っていう問題なんだ。
練習問題3.
次の直角三角形ABCのxの長さを求めなさい。

この問題はいくつか段階を追って答えを出すんだ。
まず△ADCに注目。
こいつは直角三角形だよね??
ってことは、三平方の定理で残りの辺の長さが求められるんだ。
斜辺が2√5㎝、高さが4㎝だから、
$$y² + 4² = (2\sqrt{5})²$$
$$y = 2$$
になるね。

図で表すとこうなる。

じゃ、次は大きい△ABCに注目。
BCの長さをzとすると、
x㎝を求めるには、z㎝からyの2㎝引けばいいよね?
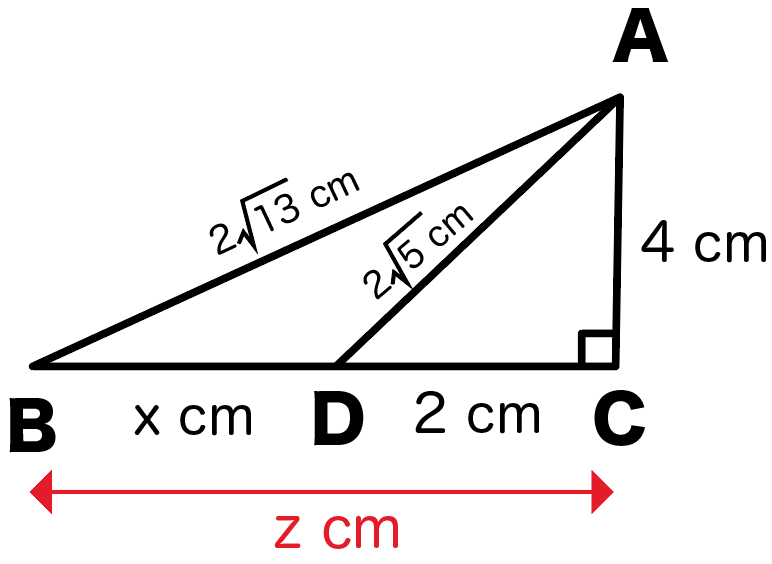
だからzの値が出れば答えまでもう少し!
直角三角形だから三平方の定理(ピタゴラスの定理)が使えるんだ。
斜辺が2√13cm、高さが4㎝だから、
$$z² + 4² = (2\sqrt{13})²$$
$$z = 6$$
になるね。
ってことは、xcmの長さは、そこからyの2cmを引いてやって、
$$x = 6 -2$$
$$= 4$$
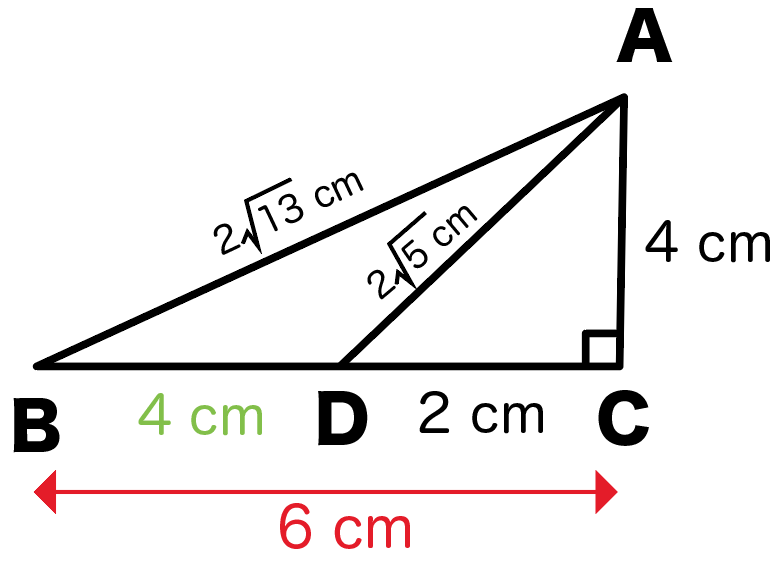
答えは4cmだ!
お疲れ!
まとめ:三平方の定理(ピタゴラスの定理)の計算問題の解き方はワンパターン!
三平方の定理(ピタゴラスの定理)の計算問題はどうだったかな??
今回マスターした計算問題の解き方は次の3つだったね。
- 斜辺を求める問題
- 斜辺以外を求める問題
- 直角三角形の中に直角三角形問題
三平方の定理の問題は解きまくってマスターしていこう。
またねー
ぺーたー


